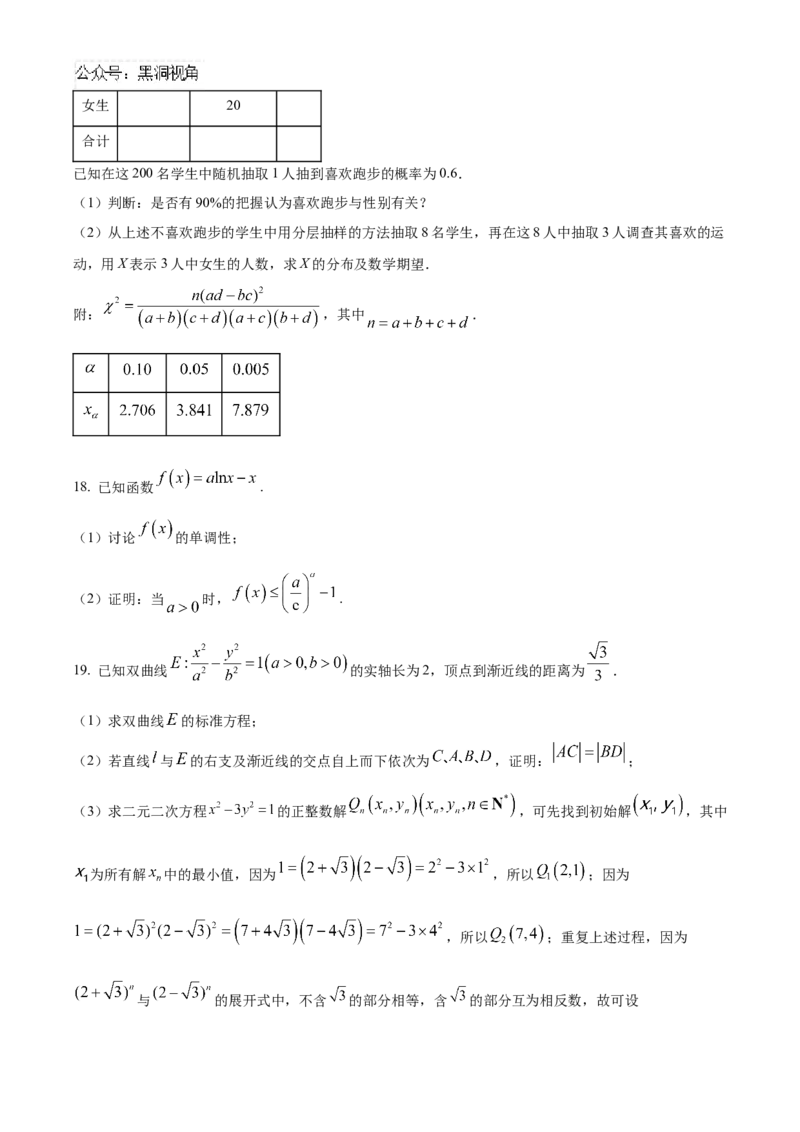文档内容
高三数学
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有
一项是符合要求的.
1. 集合 ,集合 ,则 ( )
A. B. C. D.
2. 函数 是定义在 上的奇函数,当 时, ,则 ( )
A. B. 2 C. D.
3. 展开式中第6项 的二项式系数是( )
A. B. C. D.
4. 已知函数 是定义在 上的增函数,则满足 的x的取值范围是( )
.
A B. C. D.
5. 体育课上甲、乙两名同学进行投篮比赛(甲、乙各投篮一次),甲投中的概率为0.7,乙投中的概率为
0.8,则甲、乙两人恰好有一人投中的概率为( )
A. 0.38 B. 0.24 C. 0.14 D. 0.5
6. 函数 在区间 上单调递增,则实数a的取值范围是( )
A. B. C. D.
7. 函数 的图像恒过定点 ,若点 在直线 上,其中
,则 的最小值为( )A. 4 B.
C. D. 8
8. 已知函数 是R上的偶函数,对于 都有 成立,且 ,
当 ,且 时,都有 .则给出下列命题:
① ;②函数 图象的一条对称轴为 ;
③函数 在 上为严格减函数;④方程 在 上有4个根;
其中正确的命题个数为( )
A. 1 B. 2 C. 3 D. 4
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符
合题目要求.全选对的得6分,部分选对的得部分分,有选错的得0分.
9. 在下列函数中,既是偶函数又在 上单调递增的函数有( )
.
A B.
C. D.
10. 已知函数 ,则( )
A. 在 单调递增
B. 有两个零点
C. 的最小值为
D. 在 点处切线为
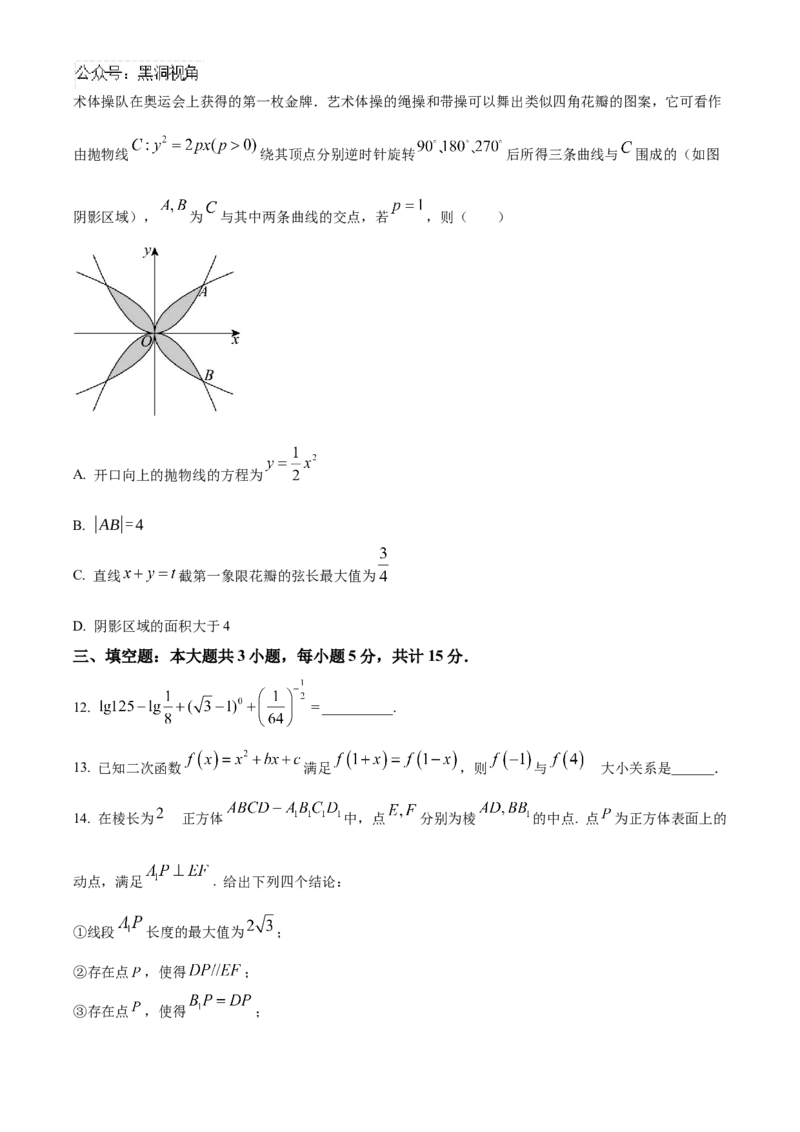
11. 在2024年巴黎奥运会艺术体操项目集体全能决赛中,中国队以69.800分的成绩夺得金牌,这是中国艺术体操队在奥运会上获得的第一枚金牌.艺术体操的绳操和带操可以舞出类似四角花瓣的图案,它可看作
由抛物线 绕其顶点分别逆时针旋转 后所得三条曲线与 围成的(如图
阴影区域), 为 与其中两条曲线的交点,若 ,则( )
A. 开口向上的抛物线的方程为
B. |AB|=4
C. 直线 截第一象限花瓣的弦长最大值为
D. 阴影区域的面积大于4
三、填空题:本大题共3小题,每小题5分,共计15分.
12. __________.
13. 已知二次函数 满足 ,则 与 大的小关系是______.
的
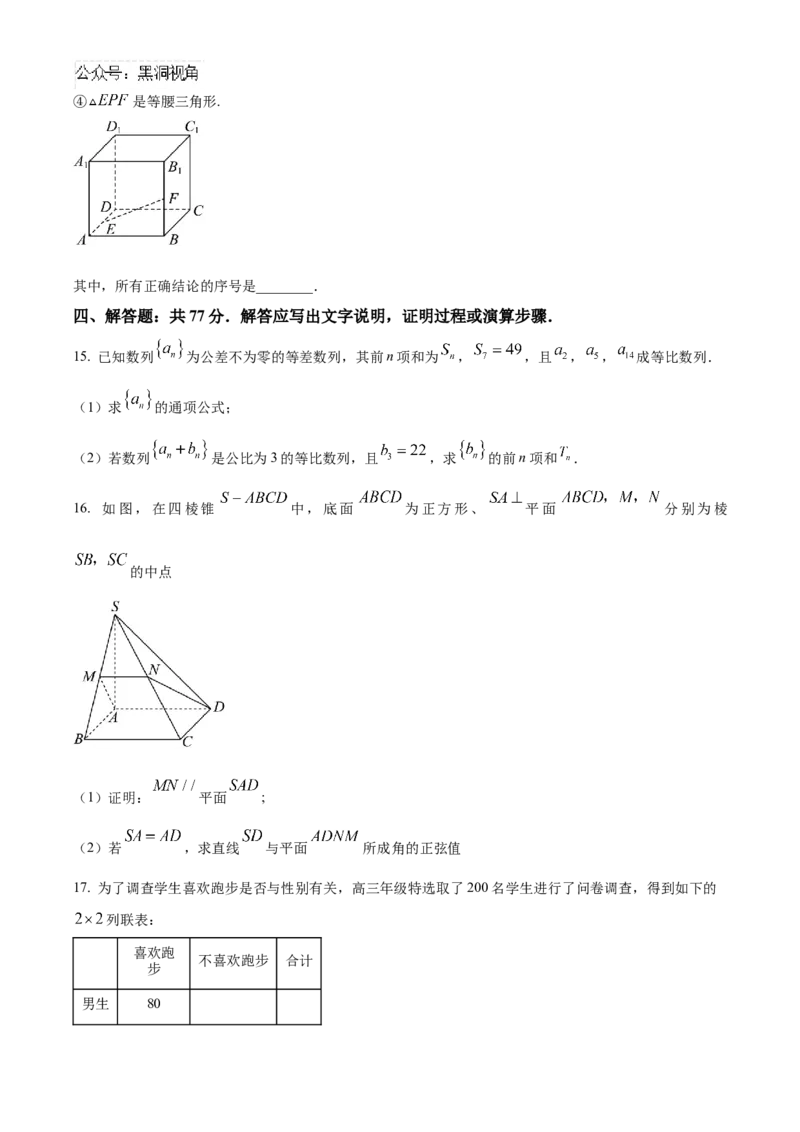
14. 在棱长为 正方体 中,点 分别为棱 的中点. 点 为正方体表面上的
动点,满足 . 给出下列四个结论:
①线段 长度的最大值为 ;
②存在点 ,使得 ;
③存在点 ,使得 ;④ 是等腰三角形.
其中,所有正确结论的序号是________.
四、解答题:共77分.解答应写出文字说明,证明过程或演算步骤.
15. 已知数列 为公差不为零的等差数列,其前n项和为 , ,且 , , 成等比数列.
(1)求 的通项公式;
(2)若数列 是公比为3的等比数列,且 ,求 的前n项和 .
16. 如图,在四棱锥 中,底面 为正方形、 平面 分别为棱
的中点
(1)证明: 平面 ;
(2)若 ,求直线 与平面 所成角的正弦值
17. 为了调查学生喜欢跑步是否与性别有关,高三年级特选取了200名学生进行了问卷调查,得到如下的
列联表:
喜欢跑
不喜欢跑步 合计
步
男生 80女生 20
合计
已知在这200名学生中随机抽取1人抽到喜欢跑步的概率为0.6.
(1)判断:是否有90%的把握认为喜欢跑步与性别有关?
(2)从上述不喜欢跑步的学生中用分层抽样的方法抽取8名学生,再在这8人中抽取3人调查其喜欢的运
动,用X表示3人中女生的人数,求X的分布及数学期望.
附: ,其中 .
18. 已知函数 .
(1)讨论 的单调性;
(2)证明:当 时, .
19. 已知双曲线 的实轴长为2,顶点到渐近线的距离为 .
(1)求双曲线 的标准方程;
(2)若直线 与 的右支及渐近线的交点自上而下依次为 ,证明: ;
(3)求二元二次方程 的正整数解 ,可先找到初始解 ,其中
为所有解 中的最小值,因为 ,所以 ;因为
,所以 ;重复上述过程,因为
与 的展开式中,不含 的部分相等,含 的部分互为相反数,故可设,所以 .若方程 的正整数解
为 ,且初始解 ,则 的面积是否为定值?若是,请求出该定值,并说明理由.