文档内容
高三入学摸底测试数学
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项,只有一项是
符合题目要求的.
1. 命题 的否定为( )
A. x>0,x2+x+1>0 B. x<0,x2+x+1>0
C. ∀x>0,x2+x+1>0 D. ∀x≤0,x2+x+1>0
∃ ∃
2. 设 , ,若 ,则实数 的值的个数为(
)
A. 2 B. 3 C. 4 D. 5
3. 已知 展开式的二项式系数之和为64,则展开式的第5项是( )
A. 6 B. 15 C. D.
4. 已知盒子中有6个大小相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两球,每次取
一球,记第一次取出的球的数字是 ,第二次取出的球的数字是 .若事件 “ 为偶数”,事件
“ , 中有偶数且 ”,则 ( )
A. B. C. D.
5. 设等差数列 的公差为 ,则“ ”是“ 为递增数列”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
6. 已知 , ,且 ,则 的最小值是( )
A. 4 B. 5 C. 7 D. 97. 过双曲线 左焦点 作圆 的切线,切点为 ,直线 交直
的
线 于点 .若 ,则双曲线 的离心率为( )
A. B. C. D.
8. 已知函数 ,若关于 的不等式 恒成立,则实数 的取值
范围( )
A. B. C. D.
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对得6分,部分选对的得部分分,选错得0分.
9. 下列命题中,正确的是( )
A. 已知随机变量 服从正态分布 ,若 ,则
B. 若甲、乙两组数据的相关系数分别为0.66和 ,则甲组数据的线性相关性更强
C. 用 表示 次独立重复试验中事件 发生的次数, 为每次试验中事件 发生的概率,若
,则
D. 已知随机变量 的分布列为 ,则
10. 已知函数 ,则下列说法正确 的有( )
A. 若 是 上的增函数,则
B. 当 时,函数 有两个极值C. 当 时,函数 有两零点
D. 当 时, 在点 处的切线与 只有唯一个公共点
11. 在正三棱柱 中, ,点P满足 ,其中
,则( )
A. 当 时, 最小值为
B. 当 时,三棱锥 的体积为定值
C. 当 时,平面 平面
D. 若 ,则P的轨迹长度为
三、填空题:本大题共3小题,每小题5分,共15分.
12. 抛物线 的准线方程是___________________.
13. 由0,1,2,3,4,5这6个数字可以组成______个无重复数字的四位偶数.(用数字作答).
14. 甲、乙、丙三个人去做相互传球训练,训练规则是确定一人第一次将球传出,每次传球时,传球者都
等可能地将球传给另外两个人中的任何一人,每次必须将球传出.如果第一次由甲将球传出,设 次传球
后球在甲手中的概率为 ,则 ______; ______.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 如图所示,在四棱锥 中,底面 为直角梯形, , ,侧面
底面 且 , 为 中点.(1)求证: ;
(2)求二面角 的正弦值.
16. 为了了解高中学生课后自主学习数学时间(x分钟/每天)和他们的数学成绩(y分)的关系,某实验小
组做了调查,得到一些数据(表一).
编号 1 2 3 4 5
学习时间 3 6
40 50 70
x 0 0
数学成绩 6 9
78 85 108
y 5 9
(1)求数学成绩 与学习时间 的相关系数(精确到0.001);
(2)请用相关系数说明该组数据中 与 之间的关系可用线性回归模型进行拟合,并求出 关于 的回
归直线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩(参考数据:
, 的方差为200);
(3)基于上述调查,某校提倡学生周末在校自主学习.经过一学期的实施后,抽样调查了220位学生.按照
是否参与周末在校自主学习以及成绩是否有进步统计,得到 列联表(表二).依据表中数据及小概率
值 的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.
没有进步 有进步 合计
参与周末在校自主学习 35 130 165
未参与周末不在校自主学习 25 30 55
合计 60 160 220附:方差: 相关系数:
回归方程 中斜率和截距的最小二乘估计公式分别为 , ,
.
.
0.10 0.05 0.010 0005 0.001
2.706 3.841 6.635 7.879 10.828
17. 设数列{a }的前 项和为 ,且满足 .
n
(1)求{a }的通项公式;
n
(2)设 ,数列{b }的前 项和为 ,若对任意的 恒成立,求 的取
n
值范围.
18. 已知椭圆 左焦点为 ,离心率为 ,以坐标原点 为圆心, 为半径
作圆使之与直线 相切.
(1)求 的方程;
(2)设点 , , 是椭圆上关于 轴对称 的两点, 交 于另一点 ,
①证明:直线 经过定点;
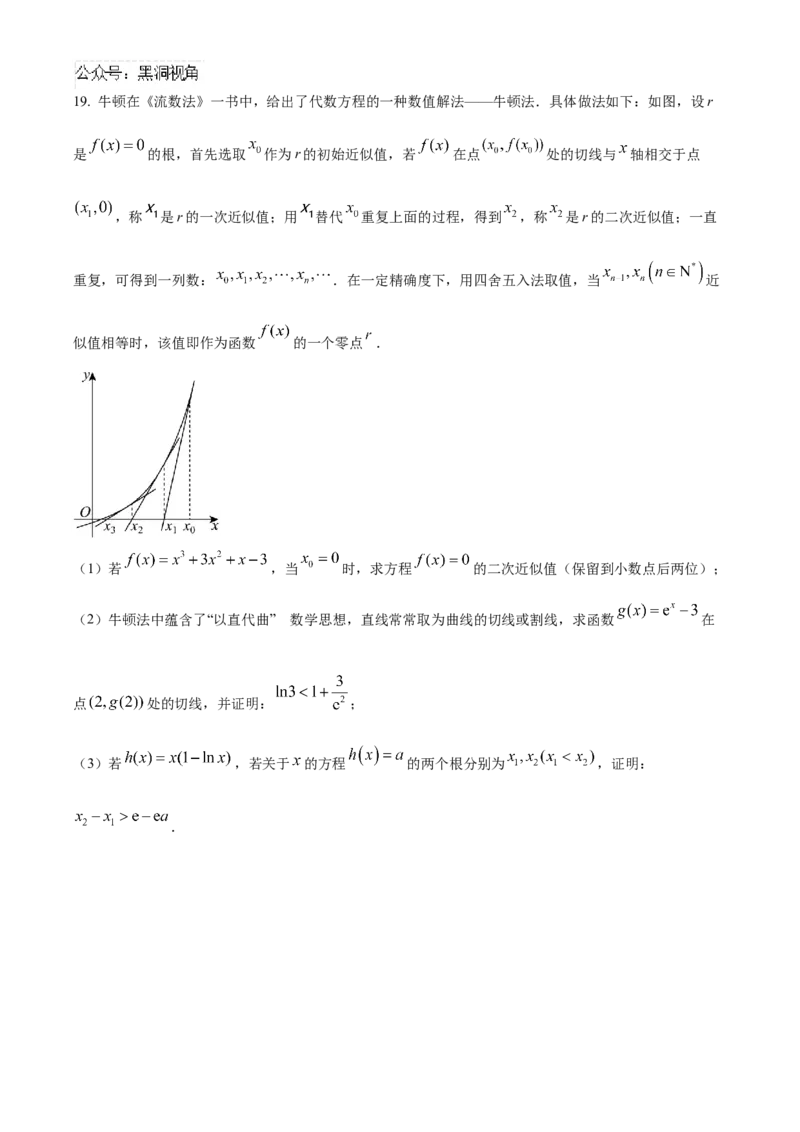
②求 的内切圆半径的范围.19. 牛顿在《流数法》一书中,给出了代数方程的一种数值解法——牛顿法.具体做法如下:如图,设r
是 的根,首先选取 作为r的初始近似值,若 在点 处的切线与 轴相交于点
,称 是r的一次近似值;用 替代 重复上面的过程,得到 ,称 是r的二次近似值;一直
重复,可得到一列数: .在一定精确度下,用四舍五入法取值,当 近
似值相等时,该值即作为函数 的一个零点 .
(1)若 ,当 时,求方程 的二次近似值(保留到小数点后两位);
的
(2)牛顿法中蕴含了“以直代曲” 数学思想,直线常常取为曲线的切线或割线,求函数 在
点 处的切线,并证明: ;
(3)若 ,若关于 的方程 的两个根分别为 ,证明:
.