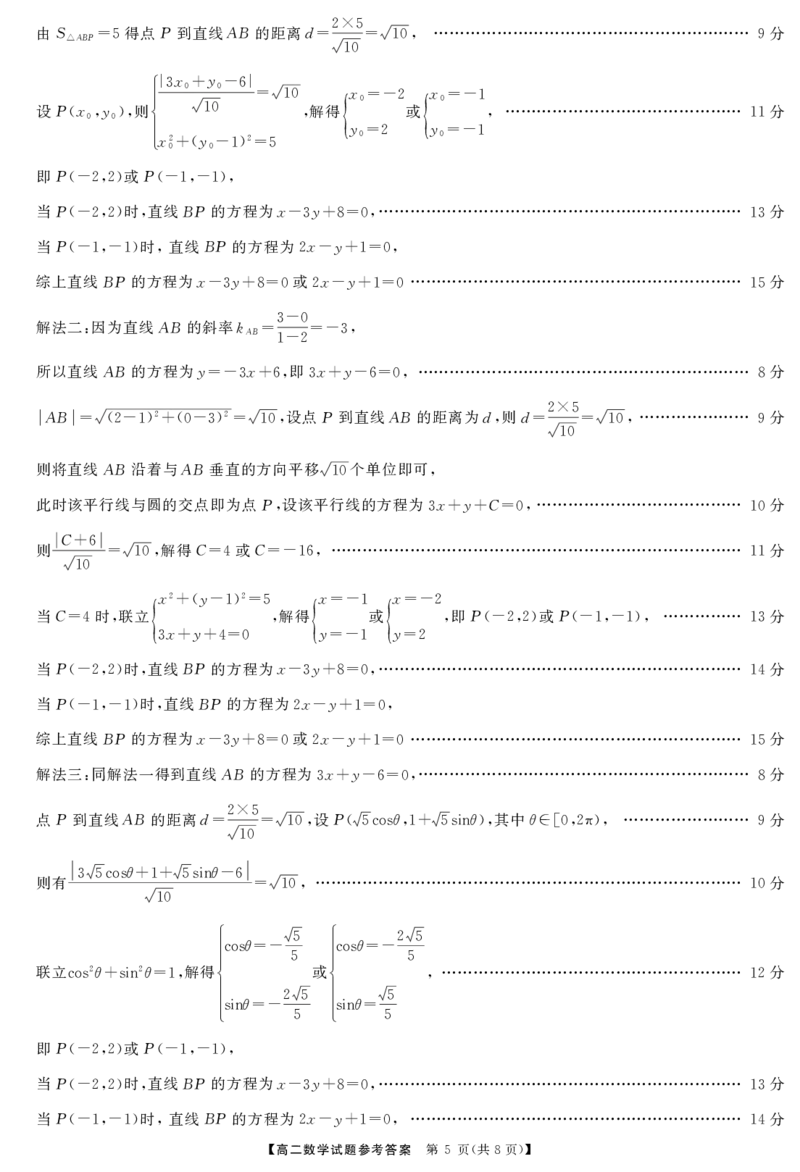文档内容
{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}湖湘名校教育联合体 年下学期高二 月大联考数学
2024 10
参考答案、提示及评分细则
.【答案】
1 B
【解析】a b .
=1×1+1×(-1)+0×2=0
.【答案】
2 B
【解析】由题知 点 在直线l 上 逆时针旋转 直线l 与直线l 垂直 斜率为 所以直线l 方程为
, (0,1) 1 , 90°, 2 1 , -1, 2
x y .
+ -1=0
.【答案】
3 D
【解析】圆C 圆心为 圆C 圆心为 两圆心的距离d 2 2 r r
1 (0,0), 2 (2,3), = (2-0)+(3-0)= 13,1=2,2=3,
知两圆相交 选 .
1< 13<5, , D
.【答案】
4 C
【解析】因为椭圆的右焦点坐标为 所以λ λ 则λ .
(2,0), >5,-5=4, =9
.【答案】
5 C
【解析】 ABCD四点共面 x y 1 x y 1
∵ , , , ,∴ + + =1,+ =
2 2
(x y)
xy + 2 1 1 xy 1当且仅当x 1y 1时取得等号 xy的最大值为1.
∵2 ≤2 =2× = ,∴2 ≤ = ,= ,2
2 16 8 8 4 4 8
.【答案】
6 A
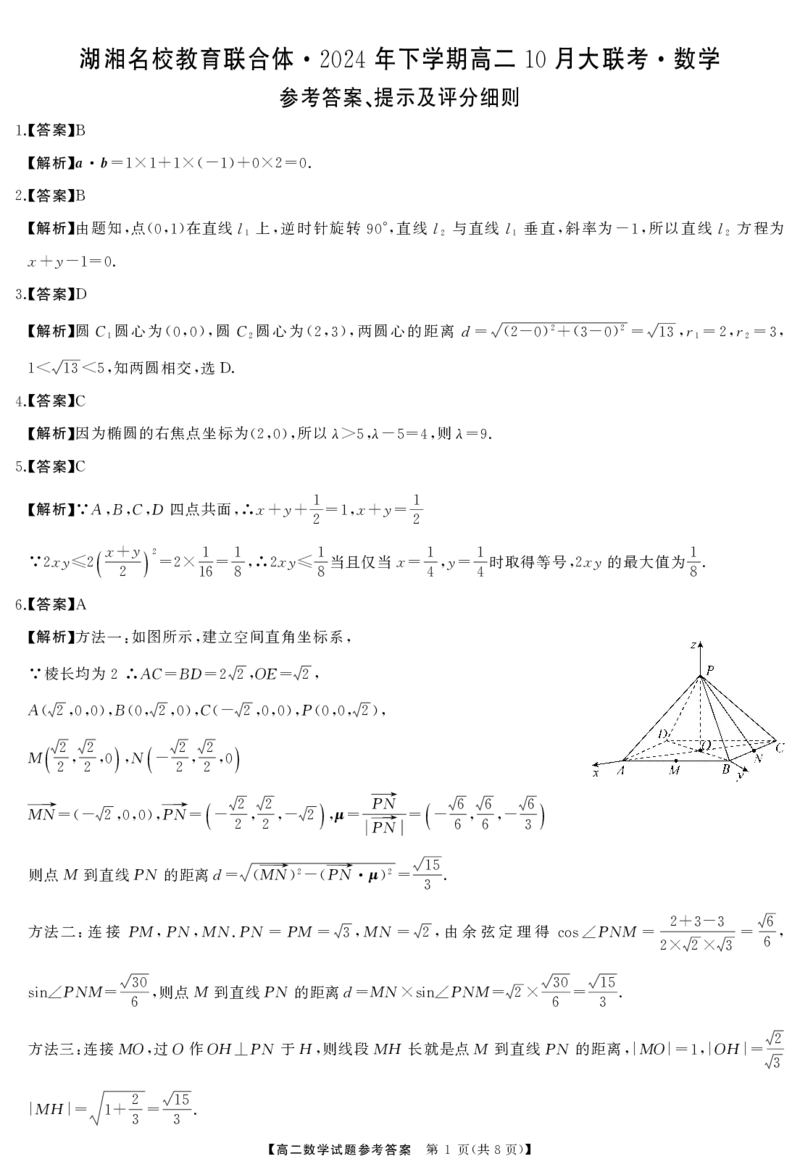
【解析】方法一 如图所示 建立空间直角坐标系
: , ,
棱长均为 AC BD OE
∵ 2∴ = =22, = 2,
A B C P
(2,0,0), (0,2,0), (- 2,0,0), (0,0,2),
( ) ( )
M 2 2 N 2 2
, ,0 , - , ,0
2 2 2 2
( ) PN→ ( )
MN→ PN→ 2 2 μ 6 6 6
=(- 2,0,0), = - , ,- 2 ,= PN→ = - , ,-
2 2 6 6 3
则点M 到直线PN的距离d MN→ 2 PN→ μ2 15.
= ( )-( )=
3
方法二 连接PM PN MN.PN PM MN 由余弦定理得 PNM 2+3-3 6
: , , = = 3, = 2, cos∠ = = ,
2× 2× 3 6
PNM 30 则点M 到直线PN的距离d MN PNM 30 15.
sin∠ = , = ×sin∠ = 2× =
6 6 3
方法三 连接MO 过O作OH PN于H 则线段MH 长就是点M 到直线PN 的距离 MO OH 2
: , ⊥ , ,| |=1,| |=
3
MH 2 15.
| |= 1+ =
3 3
高二数学试题参考答案 第 页 共 页
【 1 ( 8 )】
{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}.【答案】
7 B
ì
【解析】由题可知fx í
ïï
-
x
,
x
≥0 fa x2 fx 可转化为fa x2 f x fx 在R上单调递
,()=ïï ,(- )≥ 2 () (- )≥ (2 ), ( )
î xx
- ,<0
减a x2 x 使得a x2 x恒成立 得到 x2 x 解得x的解集为 .
,- ≤2 , ≤ +2 , 3≤ +2 , :(-∞,-3]∪[1,+∞)
.【答案】
8 A
【解析】由题可知AO AB ABD为等腰直角三角形. 动点Q在 ACD内运动 BQ 过点B向
2=2, =4,△ ∵ △ , = 10,
AD作垂线 垂足为点M BM 过M 向DC作垂线 垂足为N MN 2 66 点Q在以M 为圆心
, , =22, , , = > 2,∴ ,
11
为半径的半圆上 点Q的轨迹长度为 .
2 ,∴ 2π
.【答案】
9 AD
【解析】对于 选项 A 1T 11π 5π π T ω 正确
A , =2, = - = , =π,=2,A ;
2 12 12 2
( ) ( )
对于 选项 将点 5π 代入解析得 5π φ 解得 φ π 错误
B , ,-2 ,-2=2cos2× + , = ,B ;
12 12 6
k
对于 选项 令 x π k k Z 得x π πk Z 当k 时x π 错误
C , 2 + = π,∈ , =- + ,∈ , =0 ,=- ,C ;
6 12 2 12
é ù é ù
对于 选项x ê ê π π ú ú x π ê ê 5π π ú ú [ ] 正确.
D ,∈ë- ,- û,2 + ∈ë- ,- û⊆ -π,0 ,D
2 6 6 6 6
.【答案】
10 ABC
【解析】对于 选项 过E M B三点在同一个平面 F在平面外 直线EF与MB为异面直线 正确
A , , , , , ,A ;
EF→ FG→ FG→
对于 选项 可以建系用空间向量表示 也可以在截面正六边形中 利用投影得 1FG→ 故
B , , , FG→ FG→ = , B
2
正确
;
对于 选项 AQ→ AA→ 1AC→ AA→ 1 AA→ AB→ BC→ 变形得 AQ→ AB→ AD→ AA→ 正确
C , = 1+ 1 = 1+ (1 + + ), 4 = + +3 1,C ;
4 4
对于 选项 以点D为坐标原点 DADCDD 分别为xyz轴建系可得 E F G
D , , , , 1 ,, , (2,0,1), (1,0,0), (0,2,1),
M 设P t 平面PGM 的法向量n xyz
(2,1,2), (0,,0), =(,,),
{n GM→
=0
由 可求得一个n t t
, =(3- ,2,2-4),
n GP→
=0
要使EF 面PGM 则n EF→ 且EF 面PGM
∥ , =0 ⊄ ;
由n EF→ 解得t 此时EF 面PGM 不合题意 或直接由几何法也可得出 故 错误.
=0 =1, ⊂ , ( ), D
.【答案】
11 ABD
【解析】对于 选项 圆C的圆心为 半径为 AB R2 d2 故 正确
A , (1,1), 2, =2 - = 6, A ;
对于 选项 圆C x 2 y 2 设点Pt t 以CP为直径的圆的方程为 x x t
B , :(-1)+(-1)=2①, (,-1- ), ( -1)( - )+
高二数学试题参考答案 第 页 共 页
【 2 ( 8 )】
{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}y y t 化简为x2 t x y2 ty 得切点弦AB的方程为tx y x
(-1)(+1+ )=0, -(+1)+ + -1=0②,②-① (- )+1-
ì
ï
x 1
{x y ï ï =
- =0 3
y 与t无关 得 解之得í 正确
-2 =0, , , ï ,B ;
x y
1- -2 =0 ïïy 1
î =
3
( )
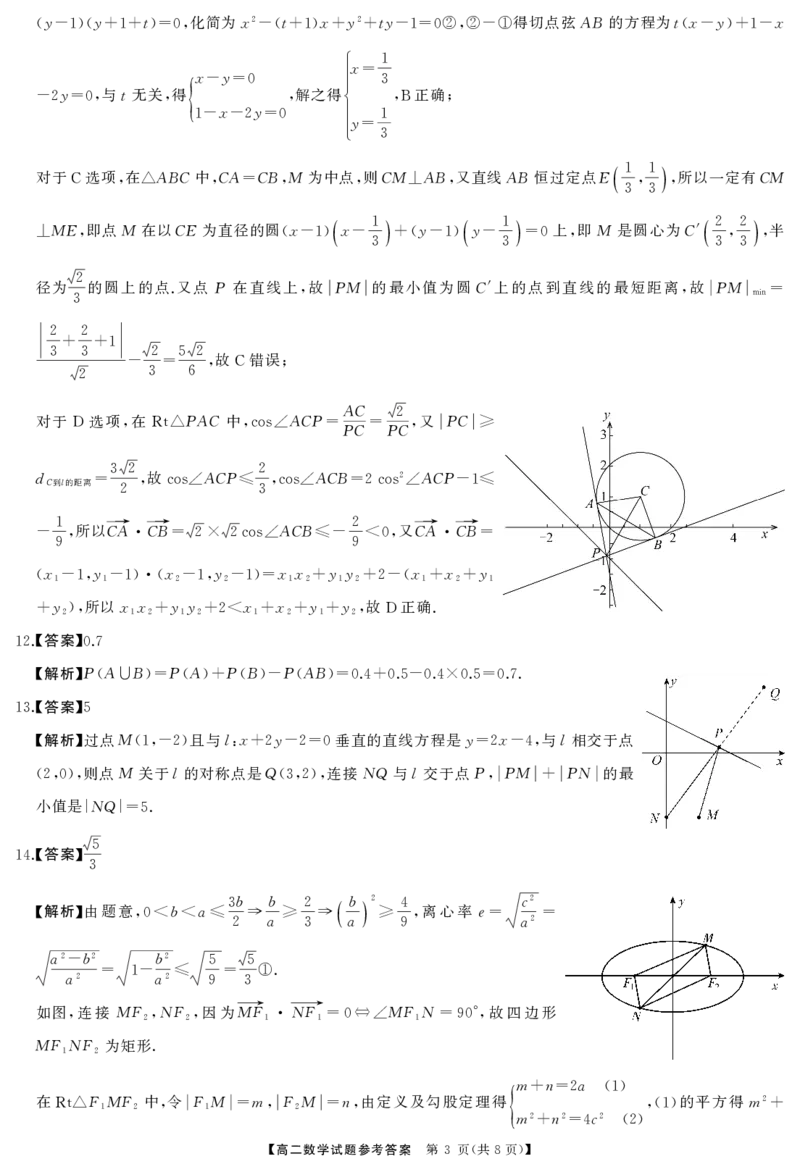
对于 选项 在 ABC中 CA CB M 为中点 则CM AB 又直线AB恒过定点E 1 1 所以一定有CM
C , △ , = , , ⊥ , , ,
3 3
( ) ( ) ( )
ME 即点M 在以CE为直径的圆x x 1 y y 1 上 即M 是圆心为C′ 2 2 半
⊥ , (-1) - +( -1) - =0 , , ,
3 3 3 3
径为 2的圆上的点.又点P 在直线上 故 PM 的最小值为圆C′上的点到直线的最短距离 故 PM
, , min=
3
2 2
+ +1
3 3 2 52 故 错误
- = , C ;
2 3 6
AC
对于 选项 在 PAC中 ACP 2 又 PC
D , Rt△ ,cos∠ =PC=PC, ≥
d C到l的距离 = 32 , 故 cos∠ ACP ≤ 2 ,cos∠ ACB =2cos 2 ∠ ACP -1≤
2 3
1 所以CA→ CB→ ACB 2 又CA→ CB→
- , = 2× 2cos∠ ≤- <0, =
9 9
x y x y xx yy x x y
(1-1,1-1)(2-1,2-1)= 1 2+ 1 2+2-(1+ 2+ 1
y 所以xx yy x x y y 故 正确.
+ 2), 1 2+ 1 2+2< 1+ 2+ 1+ 2, D
.【答案】.
12 07
【解析】PA B PA PB PAB . . . . ..
( ∪ )= ( )+ ( )- ( )=04+05-04×05=07
.【答案】
13 5
【解析】过点M 且与lx y 垂直的直线方程是y x 与l相交于点
(1,-2) :+2 -2=0 =2 -4,
则点M 关于l的对称点是Q 连接NQ与l交于点P PM PN 的最
(2,0), (3,2), , +
小值是 NQ .
| |=5
.【答案】5
14
3
b b (b)2 c2
【解析】由题意 b a 3 2 4 离心率e
,0< < ≤ ⇒a≥ ⇒ a ≥ , = a2 =
2 3 9
a2 b2 b2
- 5 5 .
a2 = 1-a2≤ = ①
9 3
如图 连接 MF NF 因为MF→ NF→ MFN 故四边形
, 2, 2, 1 1=0⇔∠ 1 =90°,
MFNF 为矩形.
1 2
{m n a
在 FMF 中 令 FM m FM n 由定义及勾股定理得 + =2 (1) 的平方得m2
Rt△ 1 2 , 1 = , 2 = , ,(1) +
m2 n2 c2
+ =4 (2)
高二数学试题参考答案 第 页 共 页
【 3 ( 8 )】
{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}m2 n2 c2
n2 mn a2 代入 式得mn a2 c2 将 除以 式得 + 4 .又 MF
+2 =4 , (2) =2 -2 (3), (2) (3) , mn = a2 c2 1 ≥
2 -2
m m2 n2 m n m m2 n2
NF 则 .左边y + 1易知在 上单调递增 故y + 1
2 1 , n≥2 = mn =n+m=n+m [2,+∞) , = mn ≥2+ =
2
n
c2 c2
5 所以 4 5 整理得 c2 a2 所以e 5 5 由 得e 5.
, a2 c2≥ , 9 ≥5 , = a2≥ = ②, ①② =
2 2 -2 2 9 3 3
.【解析】 因为b A a B
15 (1) (1-cos )= 3 sin ,
由正弦定理可得 B A A B. 分
sin (1-cos )= 3sin sin 2
又因为B 则 B
∈(0,π), sin ≠0,
( ) ( )
所以 A A.整理得 A π 即 A π 1. 分
1-cos = 3sin 2sin + =1, sin + = 4
6 6 2
( )
因为A 所以A π π 7π 分
∈(0,π), + ∈ , , 5
6 6 6
所以A π 5π 所以A 2π. 分
+ = , = 6
6 6 3
在 ABC中a a2 b2 c2 bc A 且b
(2) △ ,=27, = + -2 cos , =2,
则有 c2 c 解得c 舍去负值 . 分
28=4+ +2 , =4( ) 8
方法 由面积有S S S 分
1: △ ABC = △ ABD + △ ACD, 10
1bc BAC 1b AD CAD 1c AD BAD 分
sin∠ = sin∠ + sin∠ , 12
2 2 2
即 AD AD 则AD 4 线段AD的长是4. 分
2×4=2 +4 , = , 13
3 3
CD AC
方法 由内角平分线定理有| | | | 1
2: DB = AB = ,
| | | | 2
则AD→ 1AB→ 2AC→ 分
= + , 10
3 3
AD→ 2 1 c2 4 b2 2cb 16 分
| |= × + × - = , 12
9 9 9 9
所以AD 4 线段AD的长是4. 分
= , 13
3 3
.【解析】 由题意 设圆C的标准方程为x2 y a2 r2 分
16 (1) , +(- )= , 2
代入点A B 解之得a r 分
(2,0), (1,3), =1,= 5, 4
故圆C的标准方程为x2 y 2 . 分
+(-1)=5 6
也可由几何性质法求得线段AB的垂直平分线与y轴的交点 为圆心 再求出半径r 写出标准方
( (0,1) , = 5,
程.
)
解法一 直线AB的方程为 x y AB 分
(2) : 3 + -6=0, = 10, 8
高二数学试题参考答案 第 页 共 页
【 4 ( 8 )】
{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}由S 得点P到直线AB的距离d 2×5 分
△ ABP =5 = = 10, 9
10
ì ï x y
ï
|3 0+ 0-6| {x {x
设P ( x 0, y 0), 则í ï 10
= 10
, 解得
0=-2
或
0=-1
, 11 分
ï y y
îx2 y 2 0=2 0=-1
0+(0-1)=5
即P 或P
(-2,2) (-1,-1),
当P 时 直线BP的方程为x y 分
(-2,2) , -3 +8=0, 13
当P 时 直线BP的方程为 x y
(-1,-1) , 2 - +1=0,
综上直线BP的方程为x y 或 x y 分
-3 +8=0 2 - +1=0 15
解法二 因为直线AB的斜率k 3-0
: AB = =-3,
1-2
所以直线AB的方程为y x 即 x y 分
=-3 +6, 3 + -6=0, 8
AB 2 2 设点P到直线AB的距离为d 则d 2×5 分
= (2-1)+(0-3)= 10, , = = 10, 9
10
则将直线AB沿着与AB垂直的方向平移 个单位即可
10 ,
此时该平行线与圆的交点即为点P 设该平行线的方程为 x y C 分
, 3 + + =0, 10
C
则 +6 解得C 或C 分
= 10, =4 =-16, 11
10
{x2 y 2 {x {x
+(-1)=5 =-1 =-2
当C 时 联立 解得 或 即P 或P 分
=4 , , , (-2,2) (-1,-1), 13
x y y y
3 + +4=0 =-1 =2
当P 时 直线BP的方程为x y 分
(-2,2) , -3 +8=0, 14
当P 时 直线BP的方程为 x y
(-1,-1) , 2 - +1=0,
综上直线BP的方程为x y 或 x y 分
-3 +8=0 2 - +1=0 15
解法三 同解法一得到直线AB的方程为 x y 分
: 3 + -6=0, 8
点P到直线AB的距离d 2×5 设P θ θ 其中θ 分
= = 10, (5cos,1+ 5sin ), ∈[0,2π), 9
10
θ θ
则有 35cos+1+ 5sin -6 分
= 10, 10
10
ì ì
ï ï
ï θ 5 ï θ 25
ïcos=- ïcos=-
5 5
联立 2θ 2θ 解得í 或í 分
cos +sin =1, ï ï , 12
ï ï
ï θ 25 ï θ 5
îsin =- îsin =
5 5
即P 或P
(-2,2) (-1,-1),
当P 时 直线BP的方程为x y 分
(-2,2) , -3 +8=0, 13
当P 时 直线BP的方程为 x y 分
(-1,-1) , 2 - +1=0, 14
高二数学试题参考答案 第 页 共 页
【 5 ( 8 )】
{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}综上直线BP的方程为x y 或 x y 分
-3 +8=0 2 - +1=0 15
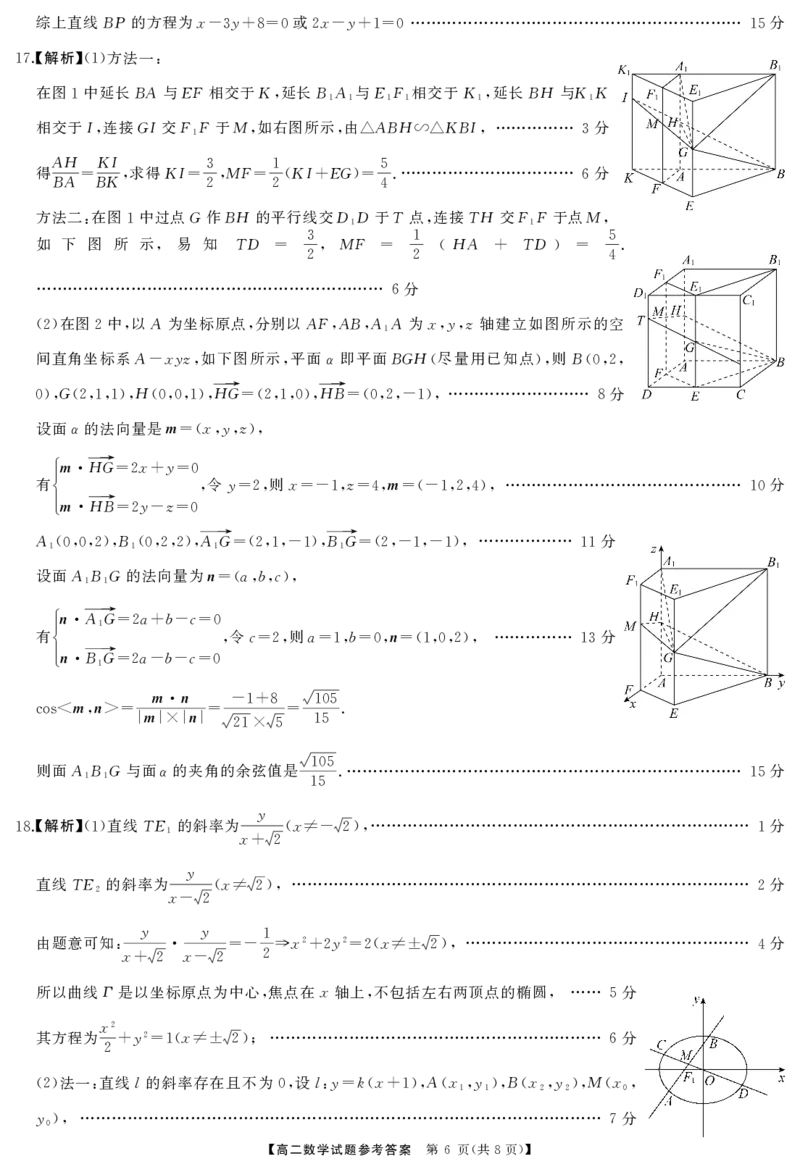
.【解析】 方法一
17 (1) :
在图 中延长BA与EF相交于K 延长BA 与EF 相交于K 延长BH 与KK
1 , 1 1 1 1 1, 1
相交于I 连接GI交FF于M 如右图所示 由 ABH KBI 分
, 1 , , △ ∽△ , 3
AH KI
得 求得KI 3 MF 1 KI EG 5. 分
BA=BK, = , = ( + )= 6
2 2 4
方法二 在图 中过点G作BH 的平行线交DD于T点 连接TH 交FF于点M
: 1 1 , 1 ,
如 下 图 所 示 易 知 TD 3 MF 1 HA TD 5.
, = , = ( + ) =
2 2 4
分
6
在图 中 以A为坐标原点 分别以AFABAA为xyz轴建立如图所示的空
(2) 2 , , , , 1 ,,
间直角坐标系A xyz 如下图所示 平面α即平面BGH 尽量用已知点 则B
- , , ( ), (0,2,
G H HG→ HB→ 分
0), (2,1,1), (0,0,1), =(2,1,0), =(0,2,-1), 8
设面α的法向量是m xyz
=(,,),
ì
ïïm
HG→
=2
x
+
y
=0
有í 令y 则x z m 分
ïï , =2, =-1,=4, =(-1,2,4), 10
îm HB→ y z
=2 - =0
A B AG→ BG→ 分
1(0,0,2),1(0,2,2),1 =(2,1,-1),1 =(2,-1,-1), 11
设面ABG的法向量为n abc
1 1 =(,,),
ì
ï ï n A 1 G→ =2 a + b - c =0
有í 令c 则a b n 分
ïï , =2, =1,=0,=(1,0,2), 13
în BG→ a b c
1 =2 - - =0
m n
mn -1+8 105.
cos< ,>= m n = =
| |×|| 21× 5 15
则面ABG与面α的夹角的余弦值是 105. 分
1 1 15
15
y
.【解析】 直线TE 的斜率为 x 分
18 (1) 1 x (≠- 2), 1
+ 2
y
直线TE 的斜率为 x 分
2 x (≠ 2), 2
- 2
y y
由题意可知 1 x2 y2 x 分
: x x =- ⇒ +2 =2(≠± 2), 4
+ 2 - 2 2
所以曲线Γ是以坐标原点为中心 焦点在x轴上 不包括左右两顶点的椭圆 分
, , , 5
x2
其方程为 y2 x 分
+ =1(≠± 2); 6
2
法一 直线l的斜率存在且不为 设ly kx Ax y Bx y M x
(2) : 0, := ( +1), (1,1), (2,2), (0,
y 分
0), 7
高二数学试题参考答案 第 页 共 页
【 6 ( 8 )】
{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}ì ïx2
ï y2
联立í2 + =1 整理得 k2x2 k2x k2 Δ k2 恒成立 分
ï , (1+2 ) +4 +2 -2=0, =8 +8>0 , 9
ï
îy kx
= (+1)
ì ï k2
x x 4
ï ï 1+ 2=- 1+2 k2 k2
且í 则 AB k2 x x 22( +1) 分
ï , = 1+ 1- 2 = k2 , 10
ïïxx 2
k2
-2
1+2
î 1 2= k2
1+2
ì ï k2
x 2
ï ï 0=- 1+2 k2 k2 k
则í 即M 2 k 1 分
ï , (- k2 , k2 ),OM =-k, 11
k 1+2 1+2 2
ïïy
î 0= k2
1+2
x2 k2
直线CD的方程为y 1x 与 y2 x 联立得x2 4 分
=-k , + =1(≠± 2) = k2 , 12
2 2 1+2
设点Cx y D x y 到直线ly kx 的距离分别为d d
(3,3), (- 3,- 3) := (+1) 1,2,
kx y k kx y k kx y k2
则d 3- 3+ d - 3+ 3+ d d 2 3-2 3 2 2 +1 分
1= k2 ,2= k2 ,1+ 2= k2 = k2 , 14
+1 +1 +1 +1
k2 k2
四边形ACBD面积S 1 AB d d 1 22( +1) 2 2 +1
=
2
(1+ 2)=
2
×
1+2
k2 × k2
+1
1
k2
+1 1 2 分
=22× k2 =22 +k2 , 16
2 +1 2 2 +1
又k2 所以S 故四边形ACBD面积的取值范围为 . 分
>0, ∈(2,22), (2,22) 17
法二 易知直线l的斜率存在且不为 设lx my Ax y Bx y Mx y 分
: 0, := -1, (1,1), (2,2), (0,0), 7
ì ïx2
代入点得í ï ï 2
1
+
y2
1=1 相减得( x 1- x 2)( x 1+ x 2) y y y y 分
ï , +(1- 2)(1+ 2)=0, 8
ïï
x2
2 y2
2
î + 2=1
2
整理得k k 1 分
OM AB =- ①; 9
2
{x my
= -1 m
联立 得 m2 y2 my 所以y y 2 yy -1 .
, ( +2) -2 -1=0, 1+ 2=m2 ,1 2=m2
x2 y2 +2 +2
+2 -2=0
m2
AB m2 y y 22( +1) 分
= 1+ 1- 2 = m2 ; 11
+2
设C ( x 3, y 3), D (- x 3,- y 3), 由 ① 得k OM k AB =- 1 , 直线CD方程为x =-m 2y , 12 分
2
ì ïx2
ï ï 2 +
y2
=1 m2 m2 m
联立í 解之得y2 即 y . 分
ï
ïïx 2y
, =m2
+2
, 3 = m2
+2
= m2
+2
13
î =-m
高二数学试题参考答案 第 页 共 页
【 7 ( 8 )】
{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}设点Cx y D x y 到直线lx my 的距离分别为d d
(3,3), (- 3,- 3) := -1 3,4,
2y my
x my x my x my 2(-m 3)-2 3
则d 3- 3+1 d - 3+ 3+1 d d 2 3-2 3
3 = m2 , 4 = m2 , 3 + 4 = m2 = m2 =
+1 +1 +1 +1
4 m y
m+2 3 m2
2 +2 分
m2 = m2 15
+1 +1
m2
所以四边形ACBD的面积S 1 AB d d 22 +1 1 分
=
2
(3+ 4)= m2
+2
=22 1-m2
+2
, 16
又m2 所以m2 1 1 1 1
>0, +2>2⇒0<m2 < ⇒ <1-m2 <1,
+2 2 2 +2
所以S 故四边形ACBD面积的取值范围为 . 分
∈(2,22), (2,22) 17
.【解析】 card M S { } 集合M 有
19 (1)∵ ( )=4, = 1,2,3,4,5 ∴ :{1,2,3,4},{1,2,3,5},{1,2,4,5},{1,3,4,5},
. 分
{2,3,4,5} 4
取M { } 对于任意的xyz M 满足x y z McardM 分
(2) = 6,7,8,9,,15 , ,,∈ , + + ∉ , ( )=10, 6
当cardM 时 集合M 中的元素取从大到小对应cardM 的个数 均成立 分
( )<10 , ( ) , , 7
下证当 cardM 不成立
11≤ ( )≤15 ,
作三元子集M { } M {k k k} k 分
0= 5,10,15 , k = ,10- ,10+ (=1,2,3,4), 8
则S M M M M M 对S的任意一个 元子集S 必包含某个M
= 0∪ 1∪ 2∪ 3∪ 4, 11 1, k,
若M S 则有 成立 与x y z S 矛盾 分
0⊆ 1, 15=5+5+5 , + + ∉ 1 ; 10
若M k ⊆ S 1( k =1,2,3,4), 则元素 10+ k = k + k +(10- k ) 与x + y + z ∉ S 1 矛盾 ,
cardM 的最大值为 分
∴ ( ) 10; 11
(3)( 反证法 ) 假设对任意的i < j , card ( M i ∩ M j)=2 或card ( M i ∩ M j)=0, 12 分
若cardM M 三元子集至少有n 个 与元素只有n个矛盾 分
① ( i ∩ j)=0, +1 , , 13
若cardM M
② ( i ∩ j)=2,
若cardM M cardM M 则cardM M 分
( 1∩ 2)=2, ( 2∩ 3)=2, ( 1∩ 3)=2, 14
将M M M M 分成若干组 每组中的两个三元子集都有 个公共元素 不同组中无公共元素.
1, 2,, n, n +1 , 2 ,
下证 任取一组有k个三元子集 有m个元素 则k m 分
, , , < , 15
当k 时 m 则k m
=1 , =3, < ,
当k 时k m m 分
≥2 ,≤4+( -4)= , 16
而三元子集有n 个 至少要有n 个元素 矛盾.
+1 , +1 ,
一定存在两个不同的子集M M 使得cardM M . 分
∴ i, j, ( i ∩ j)=1 17
高二数学试题参考答案 第 页 共 页
【 8 ( 8 )】
{#{QQABJQaAggAAQIBAAAgCEwVoCgAQkAGACYgGhBAMIAAAiANABCA=}#}