文档内容
参考答案与试题解析
1.B 2.D 3.A. 4.B 5.B.
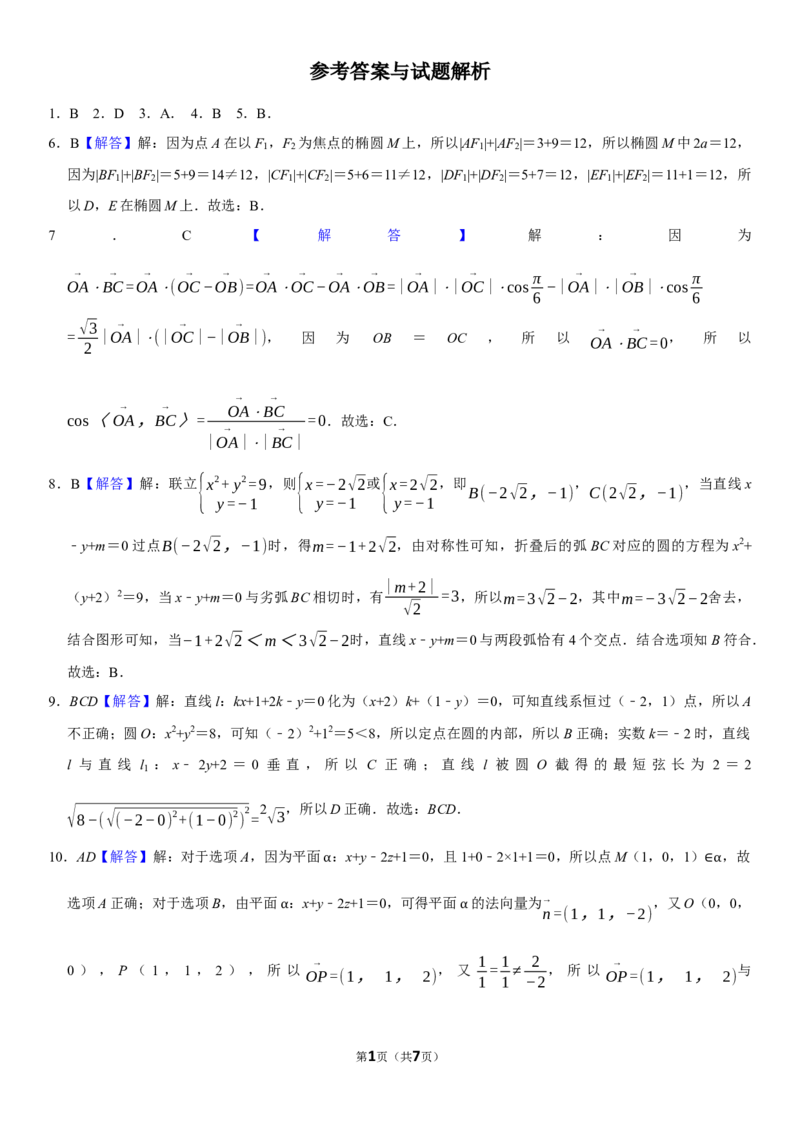
6.B【解答】解:因为点A在以F ,F 为焦点的椭圆M上,所以|AF |+|AF |=3+9=12,所以椭圆M中2a=12,
1 2 1 2
因为|BF |+|BF |=5+9=14≠12,|CF |+|CF |=5+6=11≠12,|DF |+|DF |=5+7=12,|EF |+|EF |=11+1=12,所
1 2 1 2 1 2 1 2
以D,E在椭圆M上.故选:B.
7 . C 【 解 答 】 解 : 因 为
→ → → → → → → → → → → π → → π
OA⋅BC=OA⋅(OC−OB)=OA⋅OC−OA⋅OB=|OA|⋅|OC|⋅cos −|OA|⋅|OB|⋅cos
6 6
√3 → → → → →
=
2
|OA|⋅(|OC|−|OB|), 因 为 OB = OC , 所 以 OA⋅BC=0 , 所 以
→ →
→ → OA⋅BC
cos〈OA,BC〉= =0.故选:C.
→ →
|OA|⋅|BC|
8.B【解答】解:联立{x2+ y2=9,则{x=−2√2或{x=2√2,即 , ,当直线x
B(−2√2,−1) C(2√2,−1)
y=−1 y=−1 y=−1
﹣y+m=0过点B(−2√2,−1)时,得m=−1+2√2,由对称性可知,折叠后的弧BC对应的圆的方程为x2+
|m+2|
(y+2)2=9,当x﹣y+m=0与劣弧BC相切时,有 =3,所以m=3√2−2,其中m=−3√2−2舍去,
√2
结合图形可知,当−1+2√2<m<3√2−2时,直线x﹣y+m=0与两段弧恰有4个交点.结合选项知B符合.
故选:B.
9.BCD【解答】解:直线l:kx+1+2k﹣y=0化为(x+2)k+(1﹣y)=0,可知直线系恒过(﹣2,1)点,所以A
不正确;圆O:x2+y2=8,可知(﹣2)2+12=5<8,所以定点在圆的内部,所以B正确;实数k=﹣2时,直线
l 与 直 线 l : x﹣ 2y+2 = 0 垂 直 , 所 以 C 正 确 ; 直 线 l 被 圆 O 截 得 的 最 短 弦 长 为 2 = 2
1
√ 8−(√(−2−0) 2+(1−0) 2 ) 2 = 2 √3 ,所以D正确.故选:BCD.
10.AD【解答】解:对于选项A,因为平面 :x+y﹣2z+1=0,且1+0﹣2×1+1=0,所以点M(1,0,1) ,故
α ∈α
选项A正确;对于选项B,由平面 :x+y﹣2z+1=0,可得平面 的法向量为→ ,又O(0,0,
n=(1,1,−2)
α α
→ 1 1 2 →
0 ) , P ( 1 , 1 , 2 ) , 所 以 OP=(1, 1, 2) , 又
1
=
1
≠
−2
, 所 以 OP=(1, 1, 2) 与
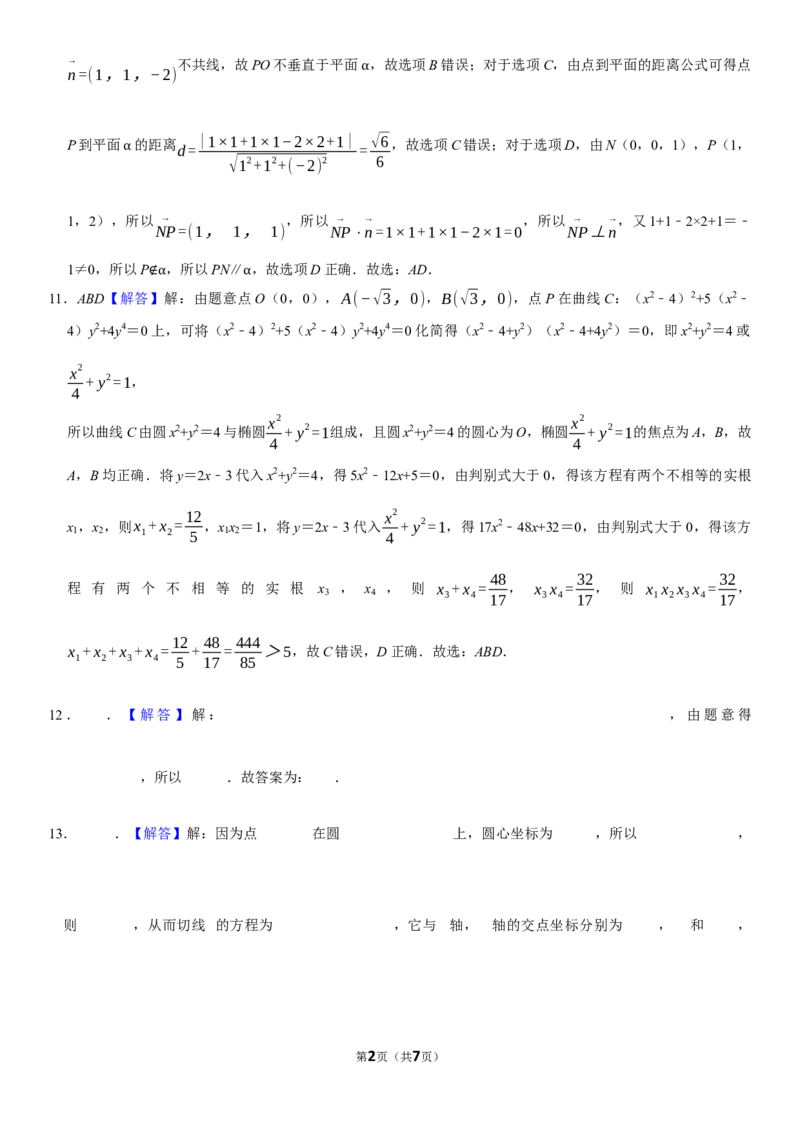
第1页(共7页)→ 不共线,故PO不垂直于平面 ,故选项B错误;对于选项C,由点到平面的距离公式可得点
n=(1,1,−2)
α
P到平面 的距离
d=
|1×1+1×1−2×2+1|
=
√6,故选项C错误;对于选项D,由N(0,0,1),P(1,
√12+12+(−2) 2 6
α
1,2),所以 → ,所以 → → ,所以 → →,又1+1﹣2×2+1=﹣
NP=(1, 1, 1) NP⋅n=1×1+1×1−2×1=0 NP⊥n
1≠0,所以P ,所以PN∥ ,故选项D正确.故选:AD.
11.ABD【解答∉】α解:由题意点αO(0,0),A(−√3,0),B(√3,0),点P在曲线C:(x2﹣4)2+5(x2﹣
4)y2+4y4=0上,可将(x2﹣4)2+5(x2﹣4)y2+4y4=0化简得(x2﹣4+y2)(x2﹣4+4y2)=0,即x2+y2=4或
x2
+ y2=1,
4
x2 x2
所以曲线C由圆x2+y2=4与椭圆 + y2=1组成,且圆x2+y2=4的圆心为O,椭圆 + y2=1的焦点为A,B,故
4 4
A,B均正确.将y=2x﹣3代入x2+y2=4,得5x2﹣12x+5=0,由判别式大于0,得该方程有两个不相等的实根
12 x2
x ,x ,则x +x = ,x x =1,将y=2x﹣3代入 + y2=1,得17x2﹣48x+32=0,由判别式大于0,得该方
1 2 1 2 5 1 2 4
48 32 32
程 有 两 个 不 相 等 的 实 根 x , x , 则 x +x = , x x = , 则 x x x x = ,
3 4 3 4 17 3 4 17 1 2 3 4 17
12 48 444
x +x +x +x = + = >5,故C错误,D正确.故选:ABD.
1 2 3 4 5 17 85
12. .【解答】解: ,由题意得
,所以 .故答案为: .
13. .【解答】解:因为点 在圆 上,圆心坐标为 ,所以 ,
则 ,从而切线 的方程为 ,它与 轴, 轴的交点坐标分别为 , 和 ,
第2页(共7页)故所求三角形的面积为 .故答案为: .
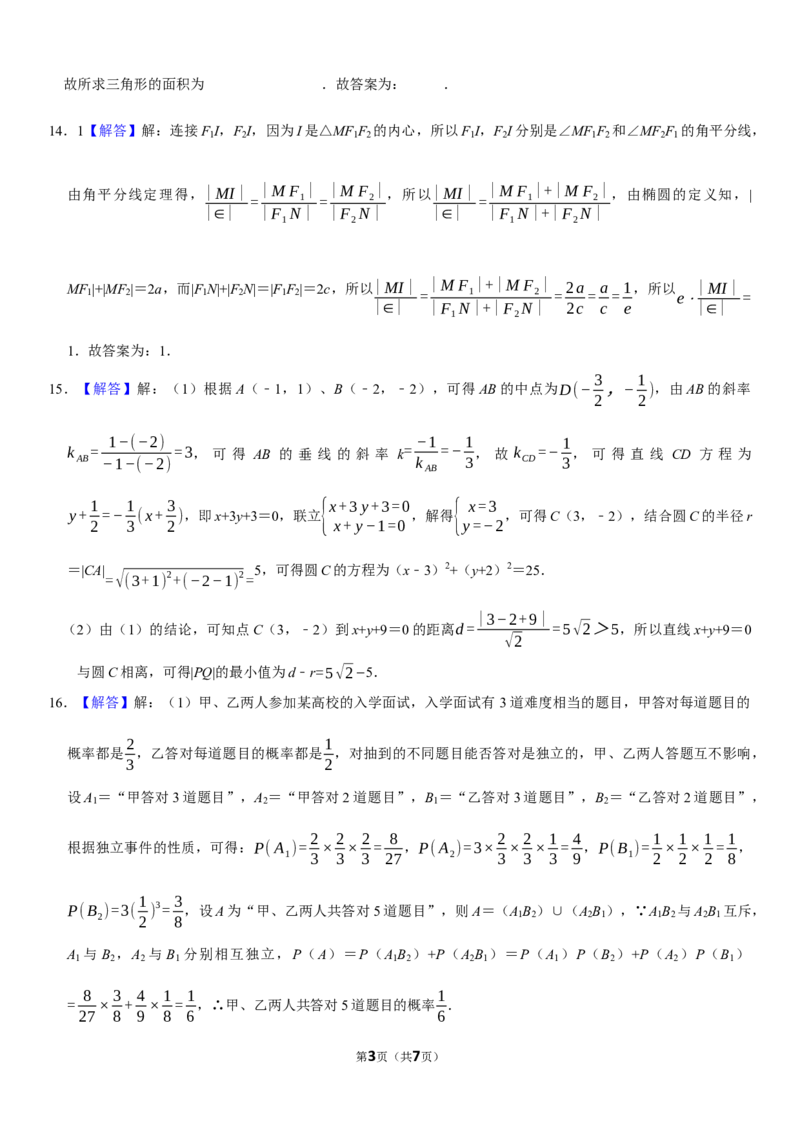
14.1【解答】解:连接F I,F I,因为I是△MF F 的内心,所以F I,F I分别是∠MF F 和∠MF F 的角平分线,
1 2 1 2 1 2 1 2 2 1
由角平分线定理得,|MI| |M F | |M F | ,所以|MI| |M F |+|M F | ,由椭圆的定义知,|
= 1 = 2 = 1 2
|∈| |F N| |F N| |∈| |F N|+|F N|
1 2 1 2
MF |+|MF |=2a,而|F N|+|F N|=|F F |=2c,所以|MI| |M F |+|M F | 2a a 1,所以 |MI|
1 2 1 2 1 2 = 1 2 = = = e⋅ =
|∈| |F N|+|F N| 2c c e |∈|
1 2
1.故答案为:1.
3 1
15.【解答】解:(1)根据A(﹣1,1)、B(﹣2,﹣2),可得AB的中点为D(− ,− ),由AB的斜率
2 2
1−(−2) −1 1 1
k = =3, 可 得 AB 的 垂 线 的 斜 率 k = =− , 故 k =− , 可 得 直 线 CD 方 程 为
AB −1−(−2) k 3 CD 3
AB
1 1 3 {x+3 y+3=0 { x=3
y+ =− (x+ ),即x+3y+3=0,联立 ,解得 ,可得C(3,﹣2),结合圆C的半径r
2 3 2 x+ y−1=0 y=−2
=|CA| 5,可得圆C的方程为(x﹣3)2+(y+2)2=25.
=√(3+1) 2+(−2−1) 2=
|3−2+9|
(2)由(1)的结论,可知点C(3,﹣2)到x+y+9=0的距离d= =5√2>5,所以直线x+y+9=0
√2
与圆C相离,可得|PQ|的最小值为d﹣r=5√2−5.
16.【解答】解:(1)甲、乙两人参加某高校的入学面试,入学面试有 3道难度相当的题目,甲答对每道题目的
2 1
概率都是 ,乙答对每道题目的概率都是 ,对抽到的不同题目能否答对是独立的,甲、乙两人答题互不影响,
3 2
设A =“甲答对3道题目”,A =“甲答对2道题目”,B =“乙答对3道题目”,B =“乙答对2道题目”,
1 2 1 2
2 2 2 8 2 2 1 4 1 1 1 1
根据独立事件的性质,可得:P(A )= × × = ,P(A )=3× × × = ,P(B )= × × = ,
1 3 3 3 27 2 3 3 3 9 1 2 2 2 8
1 3
P(B )=3( ) 3= ,设A为“甲、乙两人共答对5道题目”,则A=(A B )∪(A B ),∵A B 与A B 互斥,
2 2 8 1 2 2 1 1 2 2 1
A 与 B ,A 与 B 分别相互独立,P(A)=P(A B )+P(A B )=P(A )P(B )+P(A )P(B )
1 2 2 1 1 2 2 1 1 2 2 1
8 3 4 1 1 1
= × + × = ,∴甲、乙两人共答对5道题目的概率 .
27 8 9 8 6 6
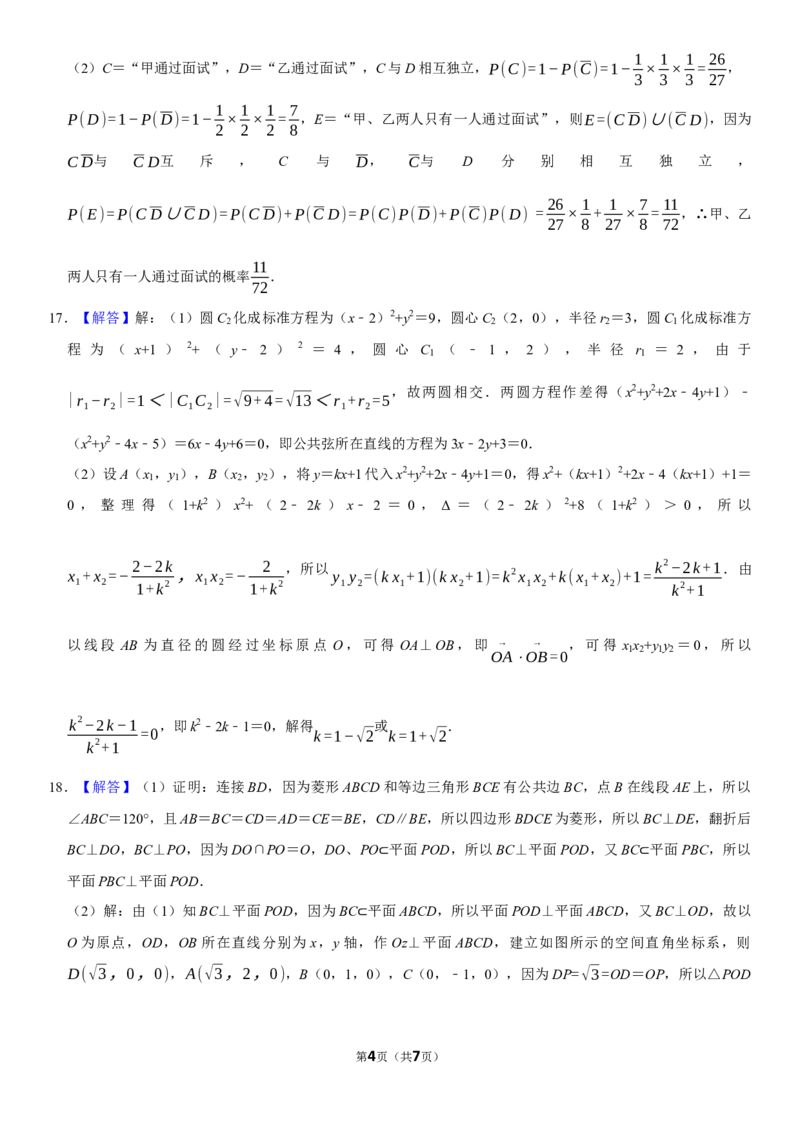
第3页(共7页)1 1 1 26
(2)C=“甲通过面试”,D=“乙通过面试”,C与D相互独立,P(C)=1−P(C)=1− × × = ,
3 3 3 27
1 1 1 7
P(D)=1−P(D)=1− × × = ,E=“甲、乙两人只有一人通过面试”,则E=(CD)∪(CD),因为
2 2 2 8
CD与 CD互 斥 , C 与 D, C与 D 分 别 相 互 独 立 ,
26 1 1 7 11
P(E)=P(CD∪CD)=P(CD)+P(CD)=P(C)P(D)+P(C)P(D) = × + × = ,∴甲、乙
27 8 27 8 72
11
两人只有一人通过面试的概率 .
72
17.【解答】解:(1)圆C 化成标准方程为(x﹣2)2+y2=9,圆心C (2,0),半径r =3,圆C 化成标准方
2 2 2 1
程 为 ( x+1 ) 2+ ( y﹣ 2 ) 2 = 4 , 圆 心 C ( ﹣ 1 , 2 ) , 半 径 r = 2 , 由 于
1 1
,故两圆相交.两圆方程作差得(x2+y2+2x﹣4y+1)﹣
|r −r |=1<|C C |=√9+4=√13<r +r =5
1 2 1 2 1 2
(x2+y2﹣4x﹣5)=6x﹣4y+6=0,即公共弦所在直线的方程为3x﹣2y+3=0.
(2)设A(x ,y ),B(x ,y ),将y=kx+1代入x2+y2+2x﹣4y+1=0,得x2+(kx+1)2+2x﹣4(kx+1)+1=
1 1 2 2
0 , 整 理 得 ( 1+k2 ) x2+ ( 2﹣ 2k ) x﹣ 2 = 0 , Δ = ( 2﹣ 2k ) 2+8 ( 1+k2 ) > 0 , 所 以
2−2k 2 ,所以 k2−2k+1.由
x +x =− ,x x =− y y =(kx +1)(kx +1)=k2x x +k(x +x )+1=
1 2 1+k2 1 2 1+k2 1 2 1 2 1 2 1 2 k2+1
以线段 AB 为直径的圆经过坐标原点 O,可得 OA⊥OB,即 → → ,可得 x x +y y =0,所以
1 2 1 2
OA⋅OB=0
k2−2k−1 ,即k2﹣2k﹣1=0,解得 或 .
=0 k=1−√2 k=1+√2
k2+1
18.【解答】(1)证明:连接BD,因为菱形ABCD和等边三角形BCE有公共边BC,点B在线段AE上,所以
∠ABC=120°,且AB=BC=CD=AD=CE=BE,CD∥BE,所以四边形BDCE为菱形,所以BC⊥DE,翻折后
BC⊥DO,BC⊥PO,因为DO∩PO=O,DO、PO 平面POD,所以BC⊥平面POD,又BC 平面PBC,所以
平面PBC⊥平面POD. ⊂ ⊂
(2)解:由(1)知BC⊥平面POD,因为BC 平面ABCD,所以平面POD⊥平面ABCD,又BC⊥OD,故以
O为原点,OD,OB所在直线分别为 x,y轴⊂,作Oz⊥平面ABCD,建立如图所示的空间直角坐标系,则
D(√3,0,0),A(√3,2,0),B(0,1,0),C(0,﹣1,0),因为DP=√3=OD=OP,所以△POD
第4页(共7页)√3 3 → → √3 3
为等边三角形,∠POD=60°,所以P( ,0, ),所以
BA=
(√3,1,0),
BP=
( ,﹣1, ),
2 2 2 2
→ →
{
m⋅BA=√3x+ y=0
→ (0,2,0),设平面PAB的法向量为→ (x,y,z),则 ,令x=﹣1,则y
CB= m= → → √3 3
m⋅BP= x−y+ z=0
2 2
, z , 所 以 → ( ﹣ 1 , , ) , 设 平 面 PBC 的 法 向 量 为 → ( a , b , c ) , 则
=√3 =√3 m= √3 √3 n=
→ →
{
n⋅CB=2b=0
→ → √3 3
,令a=√3,则b=0,c=﹣1,所以→
n=
(√3,0,﹣1),设平面PAB与平面PBC
n⋅BP= a−b+ c=0
2 2
→ →
夹角为 ,则cos =|cos → , → |=
|m⋅n|
=
|−√3−√3|
=
√21
,故平面PAB与平面PBC夹角的余弦
<m n> → → √7×2 7
|m|⋅|n|
θ θ
√21
值为 .
7
(3)解:由(2)知P在平面xOz上,且OP ,不妨设P( cos ,0, sin ), (0, ),则 →
=√3 √3 √3 AP=
α α α∈ π
( cos ,﹣2, sin ), → ,设平面PBC的法向量为→ (x ,y ,
√3 −√3 √3 BP=(√3cosα,−1,√3sinα) m = 1 1
1
α α
→ →
{
z 1 ),则
m
1
⋅CB=2y
1
=0
,取x 1 =sin ,得 m → = (sin ,0,﹣cos ),设PA与平面
→ →
1
m ⋅BP=√3cosαx −y +√3sinαz =0
1 1 1 1 α α α
π → →
PBC的夹角为 ( [0, ]),则sin =|cos , |
2
<AP m
1
>
φ φ∈ φ
→ →
|AP⋅m | √3sinα √ 3sin2α √3(1−cos2α),令t=10﹣6cos [4,
= 1 = = =
→ → √3(cosα−1) 2+4+3sin2α×1 10−6cosα 10−6cosα
|AP|⋅|m | α∈
1
16],则cos 10−t,所以 √ 1−( 10−t ) 2
= 6 √−t2+20t−64
6 sinφ=√3× =√3×
α t 36t
√3 √ 64 √3 √3 1
= × 20−(t+ )≤ ×√20−16= ,当且仅当t=8,即cosα= 时,等号成立,所以直线PA与平面
6 t 6 3 3
√3
PBC夹角正弦值的最大值为 .
3
第5页(共7页)c √2
19.【解答】解:(1)由题意得:e= = ,2c=2,又a2=b2+c2,则a=√2,b2=1,所以椭圆的标准方程
a 2
x2
为: + y2=1;
2
{
y=x+1
(2)证明:易知F(﹣1,0),l:y=x+1,设A(x ,y ),B(x ,y ),由 ,得3x2+4x=0,
1 1 2 2 x2
+ y2=1
2
4 2 4
解 得 x =0,x =− , 则 |MA|⋅|BF|=√2|x +2|⋅√2|x +1|=2× ×1= ,
1 2 3 1 2 3 3
1 4
|MB|⋅|AF|=√2|x +2|⋅√2|x +1|=2×2× = ,所以|MA|•|BF|=|MB||AF|;
2 1 3 3
(3)若直线l,m中两条直线分别与两条坐标轴垂直,则其中有一条必与直线x=﹣2 平行,所以直线l的斜率
1
存在且不为零,设直线l方程为 y=k(x+1),则直线m的方程为y=− (x+1),k≠0,设A(x ,y ),B
1 1
k
{y=k(x+1)
(x ,y ),由 ,消去y得(1+2k2)x2+4k2x+2k2﹣2=0,则Δ=16k4﹣8(1+2k2)(2k2﹣2)>0,
2 2 x2
+ y2=1
2
4k2 2k2−2,易知x
>﹣2,x >﹣2,将x=﹣2代入直线l的方程得y=﹣k,即M
x +x =− ,x ⋅x = 1 2
1 2 1+2k2 1 2 1+2k2
( ﹣ 2 , ﹣ k ) , 则
4k2
− +4
1 1 1 1 1 x +x +4 1 1+2k2 2
+ = + = ( 1 2 )= ( )=
|MA| |MB| √1+k2|x +2| √1+k2|x +2| √1+k2 x x +2(x +x )+4 √1+k2 2k2−2 8k2 √1+k2
1 2 1 2 1 2 − +4
1+2k2 1+2k2
第6页(共7页)1 1 2 2|k|
同理 + = = ,所以 1 1 1 1 √1+2|k|+k2,
|NC| |ND| √ 1 2 √1+k2 + + + =2
1+(− ) |MA| |MB| |NC| |ND| 1+k2
k
√ 2
=2 1+ ≤2√2, 当 且 仅 当 1 , 即 k = ±1 时 , 等 号 成 立 , 所 以
1
=|k|
+|k| |k|
|k|
1 1 1 1
+ + + 的最大值为2√2.
|MA| |MB| |NC| |ND|
第7页(共7页)