文档内容
2025 年 9 月高二五校联考试题(数学)参考答案
《
所以 ,该方程组没有实数解,因此假设不成立,所以 也是空间的一个
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D D B C C B ABC ACD
题号 11
基底, 故 C 正确;对于 D,由题意得 , ,则 共线,
答案 CD
故点 不能构成三角形,故 D 正确.
8.B【详解】由正方形 ,得 ,而平面 平面
11.CD【详解】对于 A,因为 , ,
, 平面 ,得 平面 ,又四边形 是
所以 , ,
正方形,则直线 两两垂直,以点 为原点,直线 分
别为 轴建立空间直角坐标系, , 所以 ,因为 ,所以
,设与 都垂直的向量
,
,则 ,令 ,得 , 所以 ,所以 ,A 正确,对于 B,连接 , 由选项 A 知 ,
因为在平行四边形 中, ,所以四边形 为菱形,
所以 的最小值为 .
所以 ,因为 , 平面 ,
9.ABC【详解】对于 D,假设存在 ,使 ,则 ,解得 或 , 所以 平面 ,因为 平面 ,所以 ,
当 , , ,两直线重合,舍去, 因为 , ,所以 ,
当 时, ,即 , 所以 ,由于 ,
,即 ,两直线重合,舍去, 所以 ,所以 为直角三角形,即 ,因为 ,所以
所以不存在 ,使 ,故 D 错误. ,因为 , 平面 ,所以 平面 ,所以 B 正确,对
10.ACD【详解】对于 B,注意线面角的范围是 ,因为直线 的方向向量与平面 的法向量 于 C,因为四边形 为平行四边形,所以 为 的中点,
的夹角为 ,所以直线 与平面 所成的角为 ; 所以 ,所以 ,所以 C 错误,
对于 C,假设 不是空间一个基底, 对于 D,设 , ,因为在菱形 中, ,所以
那么存在实数 使得 成立. ,因为 ,
高二数学第 1 页 共 3 页所以
当截距相等且不为 时,设直线方程为 ,
,所以 ,所以 D 错误,
因为直线过点 ,则代入直线方程得, ,则直线方程为 ...............12 分
12. 13. 或 14. 【详解】设
所以直线方程为 或 ..........................................13 分
,其中 ,
16.【详解】(1) ,............................................2 分
,
,.................6 分
, ,
所以 ............................................7 分
因为 、 、 、 四点共线,则向量 、 、 共面,
设 为异面直线 与 所成的角,
由共面向量定理可知,存在 、 使得 ,
................10 分
即
..........................................12 分
,
所以, ,解得 . 所以异面直线 与 所成的角 .....................................15 分
15.(1)①解法 1:设 的中点为 ,由中点坐标公式可得 ,
17.【详解】(1)将直线 的方程整理得 ,........................1 分
由两点式得 所在直线方程为 ,即 ...............3 分
令 ,解得 所以直线 恒过点 .........................4 分
解法 2:设 的中点为 ,由中点坐标公式可得 ,
则 ,
则定点 到直线 的距离为 .........................7 分
所以 所在直线方程为 ,即 .
(2)由(1)可得直线 过定点,设定点为 .
②因为 , ,
当 时,点 到直线 的距离最大,........................9 分
所以 边上的高所在直线方程为 ,即 ...............6 分
且最大距离 ,即点 到直线 的最大距离为 .........................11 分
(2)【详解】(1)当截距为 时,设直线方程为 ,
此时 ,直线 的斜率 ,解得 ..........15 分(写对一个斜率给 1 分)
因为直线过点 ,则 ,解得 ,所以直线方程为 ;............9 分
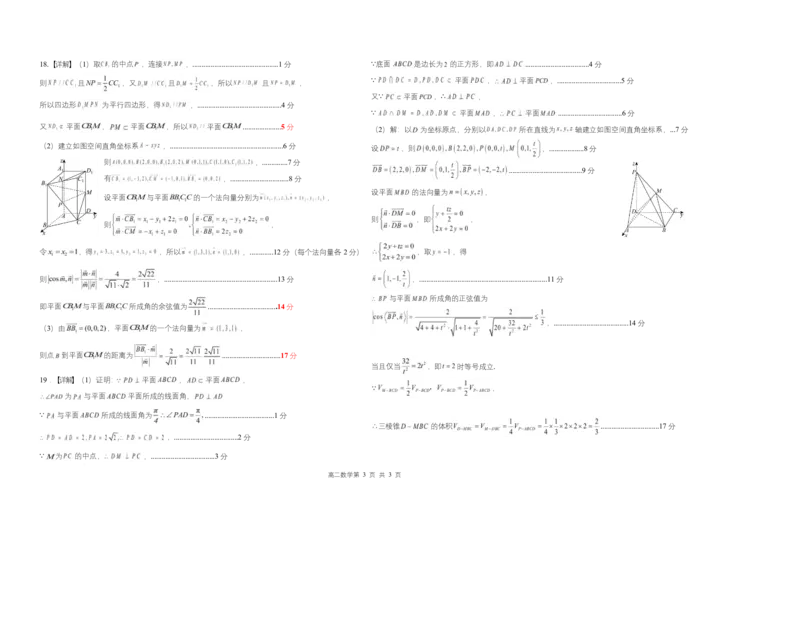
高二数学第 2 页 共 3 页18.【详解】(1)取 的中点 ,连接 ,...............................................1 分 ∵底面 是边长为 的正方形,即 ...................................4 分
∵ 平面 , 平面 ,...................................5 分
则 且 ,又 且 ,所以 且 ,
又∵ 平面 ,∴ ,
所以四边形 为平行四边形,得 ,..............................................4 分
∵ 平面 , 平面 ...................................6 分
又 平面 , 平面 ,所以 平面 .....................5 分
(2)解:以 为坐标原点,分别以 所在直线为 轴建立如图空间直角坐标系,...7 分
(2)建立如图空间直角坐标系 ,..............................................................6 分
设 ,则 ,...................8 分
则 ,..............7 分
........................................9 分
有 ,................................8 分
设平面 的法向量为 ,
设平面 与平面 的一个法向量分别为 ,
则 ,即 ,
则 ,
令 ,得 ,所以 ,.............12 分(每个法向量各 2 分) ,取 ,得
则 ,..............................................................13 分 ,......................................................................11 分
与平面 所成角的正弦值为
即平面 与平面 所成角的余弦值为 ......................................14 分
,.........................................14 分
(3)由 ,平面 的一个法向量为 ,
则点 到平面 的距离为 ................................17 分
当且仅当 ,即 时等号成立.
19.【详解】(1)证明: 平面 , 平面 ,
,
为 与平面 平面所成的线面角,
∵ 与平面 所成的线面角为 ......................................1 分
三棱锥 的体积 ................................17 分
,...................................2 分
∵ 为 的中点, ,...................................3 分
高二数学第 3 页 共 3 页