文档内容
完成时间: 月 日 天气:
作业 05 平面向量的数量积及极化恒等式的应用
1.平面向量的数量积
设两个非零向量a,b的夹角为θ,
定义
则数量|a||b|cos θ叫做a与b的数量积,记作a·b
|a|cos θ叫做向量a在b方向上的投影,
投影
|b|cos θ叫做向量b在a方向上的投影
几何
数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cos θ的乘积
意义
2. 向量数量积的运算律
(1)a·b=b·a.
(2)(λa)·b=λ(a·b)=a·(λb).
(3)(a+b)·c=a·c+b·c.
3.平面向量数量积的有关结论
已知非零向量a=(x ,y ),b=(x ,y ),a与b的夹角为θ.
1 1 2 2
结论 几何表示 坐标表示
模 |a|= |a|=
夹角 cos θ= cos θ=
a⊥b的充要条件 a·b=0 x x +y y =0
1 2 1 2
|a·b|与|a||b|的关系 |a·b|≤|a||b| |x x +y y |≤
1 2 1 2
4.极化恒等式
学科网(北京)股份有限公司恒等式右边有很直观的几何意义:
向量的数量积可以表示为以这两个向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的
,
恒等式的作用在于向量的线性运算与数量积之间的联系
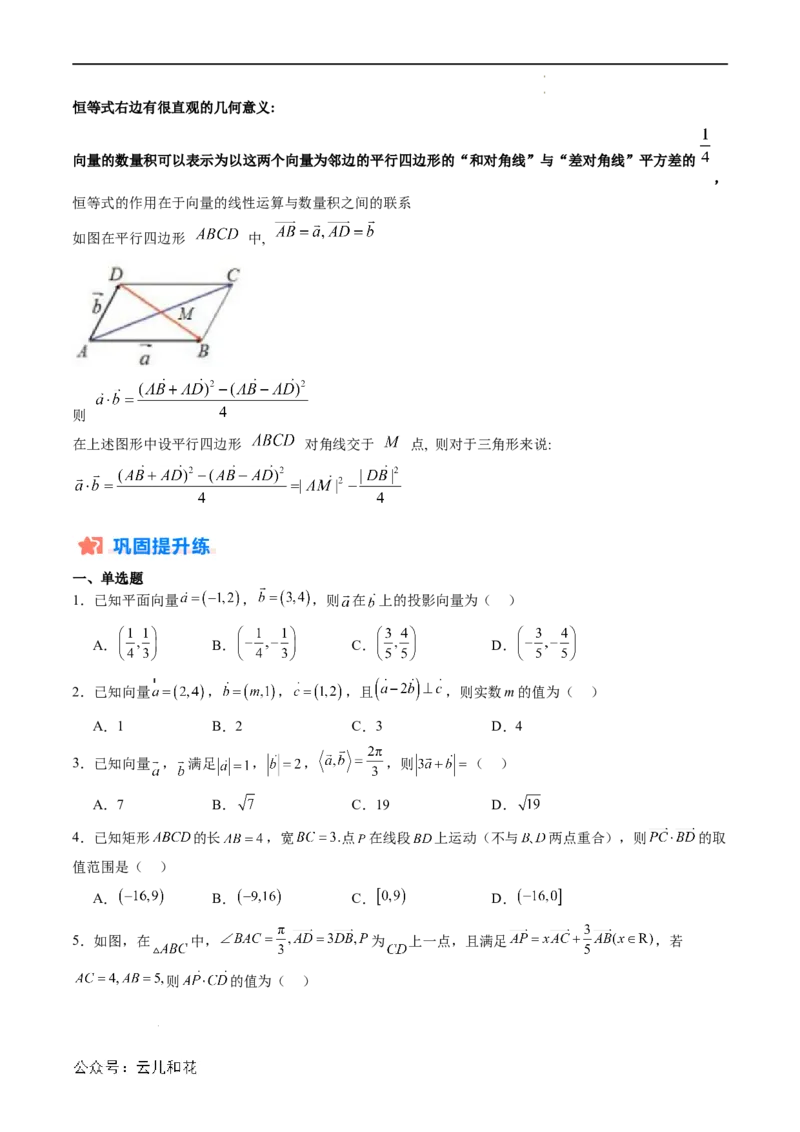
如图在平行四边形 中,
则
在上述图形中设平行四边形 对角线交于 点, 则对于三角形来说:
一、单选题
1.已知平面向量 , ,则 在 上的投影向量为( )
A. B. C. D.
2.已知向量 , , ,且 ,则实数m的值为( )
A.1 B.2 C.3 D.4
3.已知向量 , 满足 , , ,则 ( )
A.7 B. C.19 D.
4.已知矩形 的长 ,宽 .点 在线段 上运动(不与 两点重合),则 的取
值范围是( )
A. B. C. D.
5.如图,在 中, 为 上一点,且满足 ,若
则 的值为( )
学科网(北京)股份有限公司A. B. C. D.
二、多选题
6.下面给出的关系式中,正确的是( )
A. B.
C. D.
7.已知平面向量 , ,则( )
A. B.
C. 在 上的投影向量的模为 D. 与 的夹角为锐角
8.已知向量 , ,下列结论正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则 在 上的投影向量为
三、填空题
9.已知 , ,且 ,则 .
10.如图,圆 为 的外接圆, , , 为边 的中点,则 .
四、解答题
学科网(北京)股份有限公司11.已知向量 ,且 与 的夹角为 ,
(1)求证:
(2)若 ,求 的值;
12.已知向量 满足 , .
(1)求 ;
(2)求 ;
(3)若向量 与向量 的方向相反,求实数 的值.
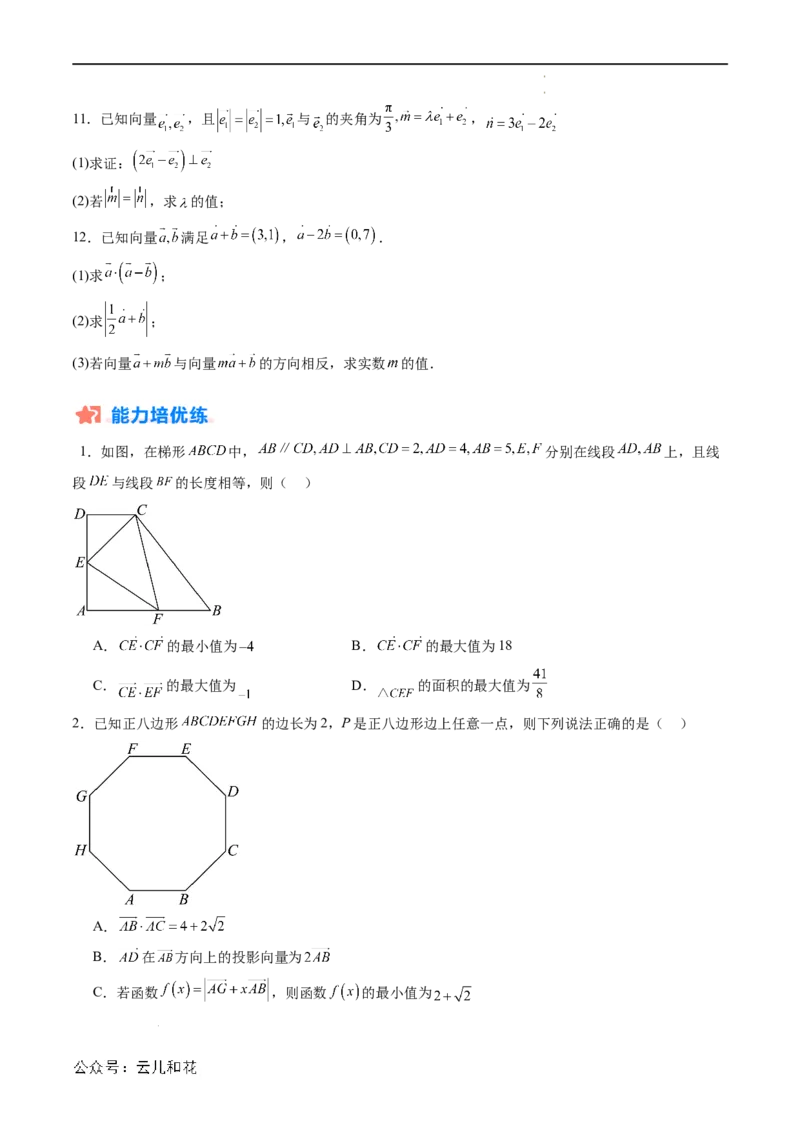
1.如图,在梯形 中, 分别在线段 上,且线
段 与线段 的长度相等,则( )
A. 的最小值为 B. 的最大值为18
C. 的最大值为 D. 的面积的最大值为
2.已知正八边形 的边长为2,P是正八边形边上任意一点,则下列说法正确的是( )
A.
B. 在 方向上的投影向量为
C.若函数 ,则函数 的最小值为
学科网(北京)股份有限公司D.
3.平面向量 满足 ,且 ,则 的最小值为 .
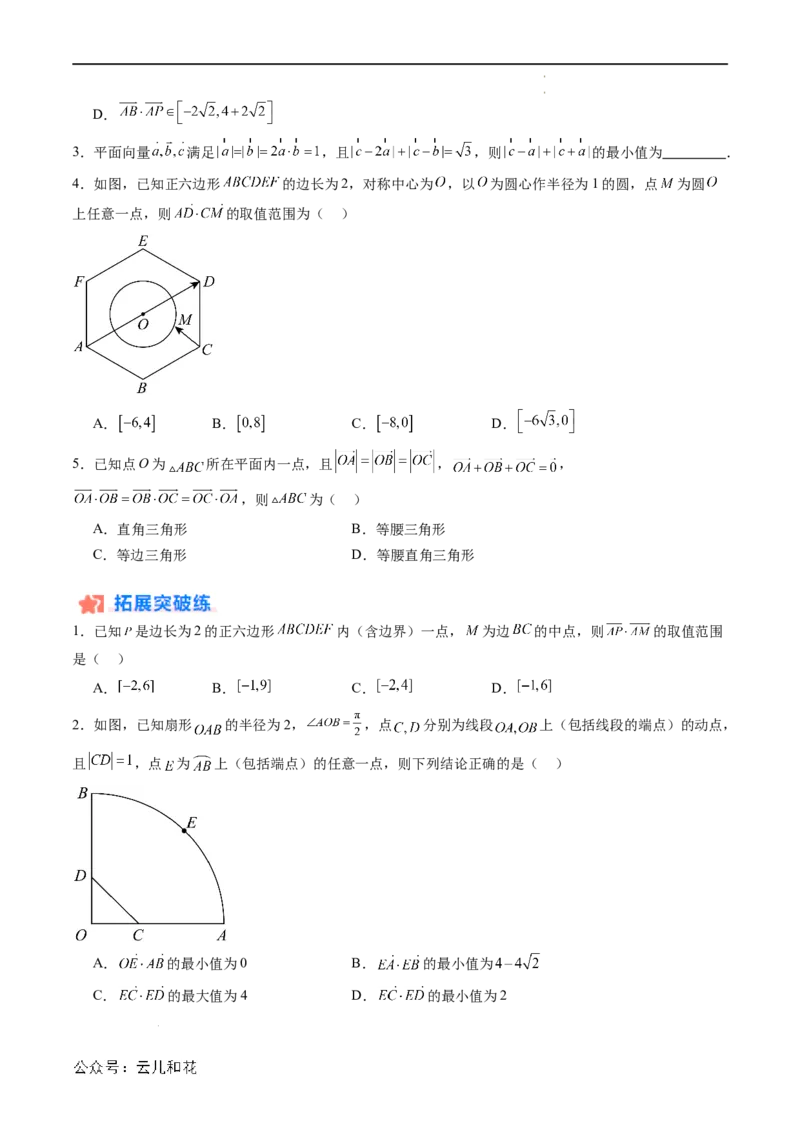
4.如图,已知正六边形 的边长为2,对称中心为 ,以 为圆心作半径为1的圆,点 为圆
上任意一点,则 的取值范围为( )
A. B. C. D.
5.已知点O为 所在平面内一点,且 , ,
,则 为( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
1.已知 是边长为2的正六边形 内(含边界)一点, 为边 的中点,则 的取值范围
是( )
A. B. C. D.
2.如图,已知扇形 的半径为2, ,点 分别为线段 上(包括线段的端点)的动点,
且 ,点 为 上(包括端点)的任意一点,则下列结论正确的是( )
A. 的最小值为0 B. 的最小值为
C. 的最大值为4 D. 的最小值为2
学科网(北京)股份有限公司3. 中, , , 是 外接圆圆心,是 的最大值为( )
A.1 B. C.3 D.5
1.(2022·全国·高考真题)已知向量 满足 ,则 ( )
A. B. C.1 D.2
2.(2023·全国·高考真题)已知向量 , 满足 , ,则 .
3.(2022·北京·高考真题)在 中, .P为 所在平面内的动点,且
,则 的取值范围是( )
A. B. C. D.
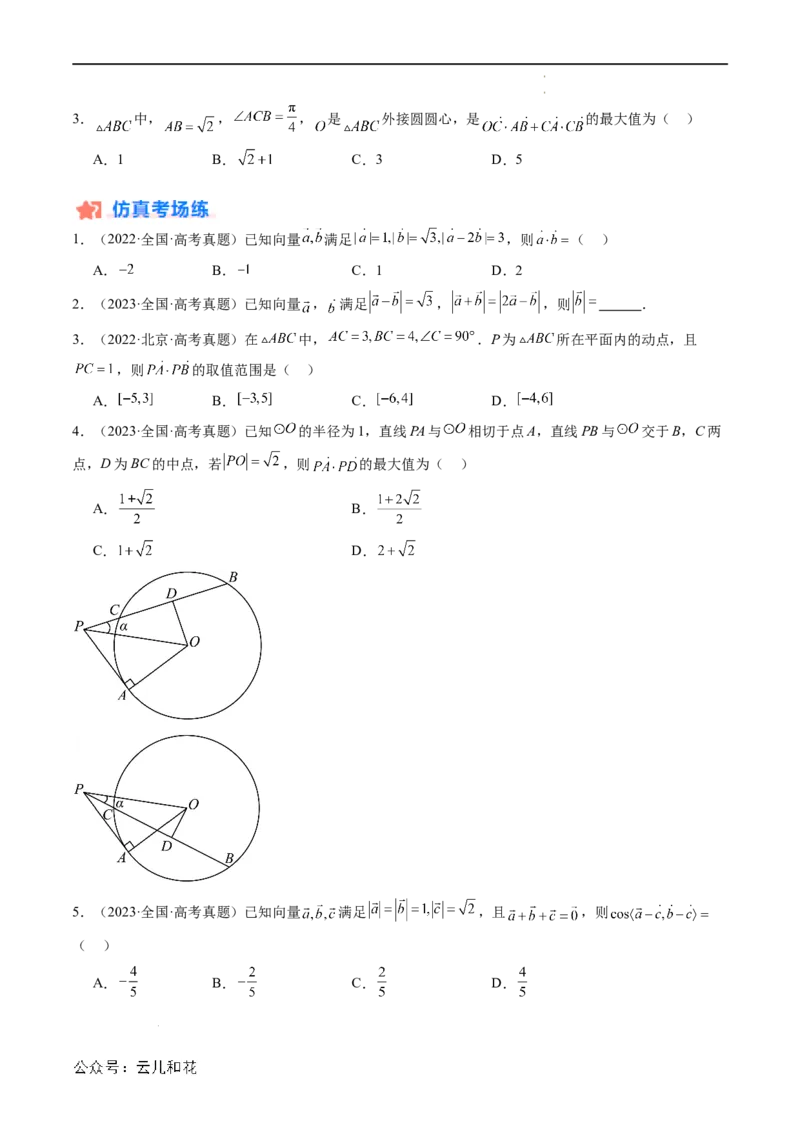
4.(2023·全国·高考真题)已知 的半径为1,直线PA与 相切于点A,直线PB与 交于B,C两
点,D为BC的中点,若 ,则 的最大值为( )
A. B.
C. D.
5.(2023·全国·高考真题)已知向量 满足 ,且 ,则
( )
A. B. C. D.
学科网(北京)股份有限公司