文档内容
2024-2025 学年高二第二学期六校联合体 3 月调研测试
高二数学
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选
项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.18×17×…×4 可表示为 ( )
A.A1518 B.A1418 C.C1518 D.C1418
2.如果 AB<0,BC>0,那么直线 Ax+By+C=0 不通过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若数列{a}是等比数列,且 a>0,a·a=9 则 log3a+log3a 的值为 ( )
n n 4 5 1 8
A.1 B.2 C.3 D.4
4.已知直线 l 的方向向量为 a=(1,-1,λ),平面α的一个法向量为 n=(-2,2,1),若 l
⊥α,则λ的值是 ( )
A.-2 B.-12 C.1 D.4
5.设 a,b∈R,若直线 ax+by=1 与圆 x2+y2=2 相切,则点 P(a,b)与圆的位置关系是
( )
A.点在圆上 B.点在圆外 C.点在圆内 D.不能确定
6.已知双曲线的对称中心为坐标原点,对称轴为坐标轴,若双曲线的离心率为 5,则双曲
线的渐近线方程为 ( )
A.y=±2x B.y=±33x
C.y=±33x 或 y=±3x D.y=±12x 或 y=±2x
7.现提供红、黄、蓝、绿四种颜色给一个四棱锥的五个面涂色,且相邻(两个面有公共边)
的两个面所涂颜色不相同,则不同的涂色方案的种数为 ( )
A.24 种 B.48 种 C.72 种 D.144 种
8.已知函数 y=ax 与 y=ex 有两条公共切线,则实数 a 的取值范围是 ( )
第 1 页 / 共 4 页A.(0,2e) B.(0,e)
C.(-∞,0)∪(0,2e) D.(-∞,0)∪(0,e)
二、选择题:本大题共 3 小题,每小题 6 分,共 18 分.在每小题给出的四个选
项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上.全部选
对得 6 分,部分选对得部分分,不选或有错选的得 0 分.
9.已知函数 f(x)=13x3-2x2+3x,下列说法正确的有 ( )
A.函数 f(x)在 x=0 处的切线方程为 y=
3x B.函数 f(x)在[1,3]单调递增
C.函数 f(x)在[0,2]上的最大值为 23
D.若方程 f(x)=a 仅有 1 个解,则 a 的取值范围是 a<0 或 a>43
10.五一假期即将来临,小张,小李,小王,小赵,小孙五名同学决定到南京的著名景点“夫
子庙”、“中山陵”、“玄武湖”游玩,每名同学只能选择一个景点,则下列说法正确
的有 ( )
A.所有可能的方法有 125 种
B.若小张同学必须去“夫子庙”,则不同的安排方法有 81
种 C.若每个景点必须有同学去,则不同的安排方法有 150
种
D.若每个景点必须有同学去,且小张和小李不去同一个景点,则不同的安排方法有
114 种
11.已知在平行六面体 ABCD-ABC D 中,AB=1,AD=AA=2,且∠AAB=∠AAD=
1 1 1 1 1 1 1
∠BAD=60°,则下列说法正确的有 ( )
→ → → →
. = - +
A BD1 AD AB AA1
B.线段 BD 的靠近点 B 的三等分点 Q 在平面 AC B
1 1 1 1
内 C.线段 AC 的长度为 39+8
1
D.直线 AC 与直线 DB 所成角的余弦值为 51451
1
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.请把答案填写在答题卡
相应位置上.
12.若(a+b)n 的展开式中,只有第 5 项的二项式系数最大,则 n 的值为▲________.
13.5 位身高互不相同的同学站成一排照相,要求身高最高的同学站中间,从中间往两边身
高依次递减,则不同的站法有▲________种.
14.已知 F 是抛物线 C:y2=2px(p>0)的焦点,M 是抛物线的准线与 x 轴的交点,且过点 M
的直线 l 与 E 相切于点 P,|PF|=4.则抛物线 C 的方程为▲________.
四、解答题:本大题共 5 小题,共 77 分.请在答题卡指定区域内作答,解答时
应写出必要的文字说明,证明过程或演算步骤.
15.(本题满分 13 分)
已知(1-2x)10=a+ax+ax2+···+a x10.
0 1 2 10
第 2 页 / 共 4 页(1)求 a 的值;
2
(2)求 a+a+···+a 的值;
0 1 10
(3)求|a|+|a|+···+|a |的值.
1 2 10
16.(本题满分 15 分)
已知{a}是公差不为 0 的等差数列,a4=7,a1,a2,a5 成等比数列.{bn}为公比为 2
n
的等比数列
(1)求数列{an}的通项公式;
(2)数列{bn}的前 n 项和为 Sn,若 S6=126,记数列{cn}满足 cn=nna,n 为奇数 b,n
为偶数),
求数列{cn}的前 2n 项和 T2n.
17.(本题满分 15 分)
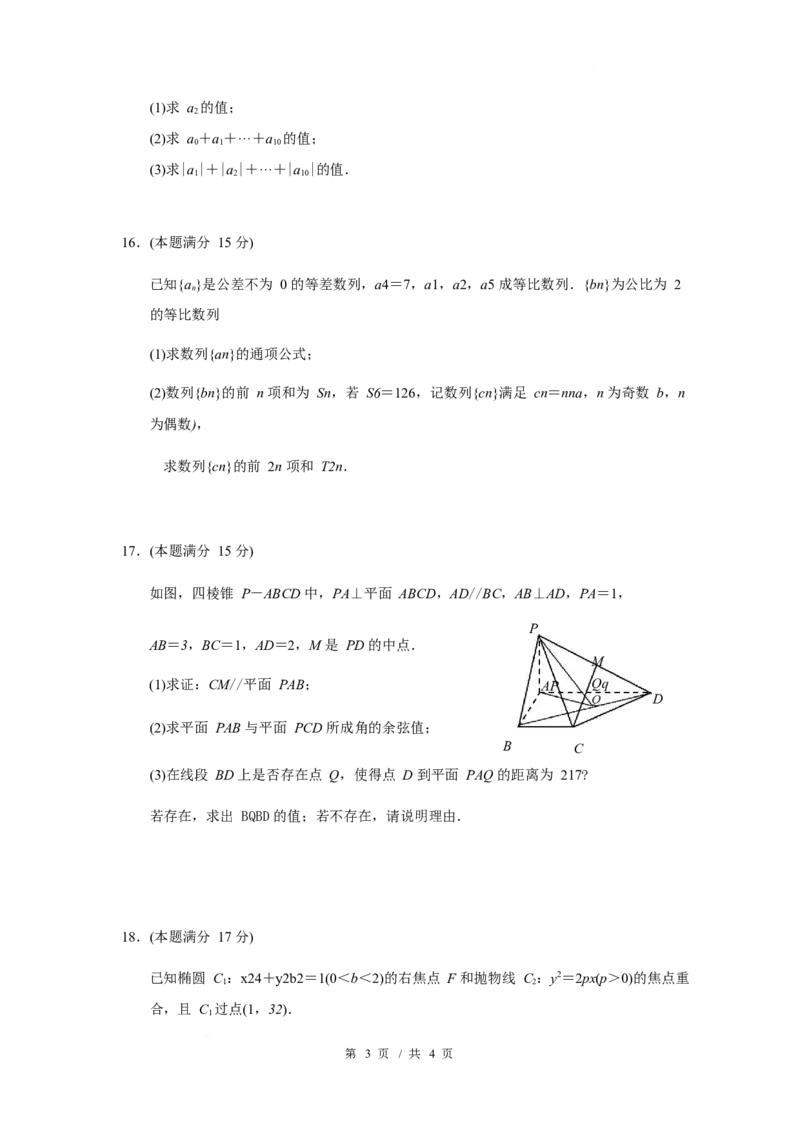
如图,四棱锥 P-ABCD 中,PA⊥平面 ABCD,AD//BC,AB⊥AD,PA=1,
P
AB=3,BC=1,AD=2,M 是 PD 的中点.
M
(1)求证:CM//平面 PAB; AP Qq
Q D
(2)求平面 PAB 与平面 PCD 所成角的余弦值;
B C
(3)在线段 BD 上是否存在点 Q,使得点 D 到平面 PAQ 的距离为 217?
若存在,求出 BQBD 的值;若不存在,请说明理由.
18.(本题满分 17 分)
已知椭圆 C :x24+y2b2=1(0<b<2)的右焦点 F 和抛物线 C :y2=2px(p>0)的焦点重
1 2
合,且 C 过点(1,32).
1
第 3 页 / 共 4 页(1)求 C 和 C 的方程;
1 2
(2)过点 F 作直线 l 分别交椭圆 C 于点 A,B,交抛物线 C 于点 P,Q,是否存在常数λ
1 2
和μ,使得μ|AB|+λ|PQ|为定值?若存在,求出λμ的值;若不存在,说明理由.
19.(本题满分 17 分)
m
我们学过组合数的定义,Cn =n(n-1)(n-2)…(n-m+1)m!,其中 m∈N,n∈N*,并
m
且 m≤n.牛顿在研究广义二项式定理过程中把二项式系数 C 中的下标 n 推广到任意实
n
m
数,规定广义组合数 Cx =x(x-1)…(x-m+1)m!是组合数的一种推广,其中 m∈N,x
0
∈R,且规定 C =1.于是广义二项式定理可写成:
x
0 1 2 3 n
(1+x)α=C +C ·x1+C ·x2+C ·x3+…+C ·xn+…,其中|x|<1.等式右端有无穷
α α α α α
项.
6 2
(1)求 C 和 C 的值.
4 0.5
(2)计算 1.11.8 的近似值,保留到小数点后 2 位.
20 0 19 1 18 2 1 19 0 20
(3)求 C ·C +C ·C +C ·C +…+C ·C +C ·C 的值.
0.7 1.3 0.7 1.3 0.7 1.3 0.7 1.3 1.7 1.32024-2025 学年高二第二学期六校联合体 3 月调研测试
高二数学参考答案
一、单选题
1-8 A B B B C D C A
二、多选题
9-11 AD BCD ABD
三、填空题
12.8 13.6 14.y2=8x
四、解答题
15.(1)T=C210·18·(-2x)2=180x2,所以 a=180. 4 分
3 2
(2)令 x=1,则(-1)10=a+a+···+a ,即 a+a+···+a =1. 8 分
0 1 10 0 1 10
(3)法 1.由题意知 a,a,…,a<0,a,a,…,a >0,
1 3 9 2 4 10
所以|a|+|a|+···+|a |=-a+a-a+a-···-a+a ,
1 2 10 1 2 3 4 9 10
令 x=0,可得 a=1; 10 分
0
令 x=-1,可得 a-a+a-a+a-···-a+a =310=59049, 12 分
0 1 2 3 4 9 10
所以原式=59048.(写 310-1 也算对) 13 分
法 2.令 x=0,可得 a=1; 10 分
0
考虑(1+2x)10 的展开式,令 x=1,得|a|+|a|+|a|+···+|a |=310=59049, 12 分
0 1 2 10
所以原式=59048.(写 310-1 也算对) 13 分
16.解:(1)数列{a}是等差数列,设首项为 a 公差为 d(d≠0)
n 1
因为 a=7,所以 a+3d=7 ① 1 分
4 1
因为 a,a,a 成等比数列,所以(a+d)2=a·(a+4d)
1 2 5 1 1 1
因为 d≠0,所以 d=2a ② 3 分
1
由①②得 a=1,d=2, 5 分
1
所以 a=2n-1 6 分
n(2)因为数列{b}为公比为 2 的等比数列,
n
由 S=126 得 b1(1-26)1-2=126,所以 b=2,则 b=2n, 9 分
6 1 n
所以 c=\a\ac(2n2,n-n为1,偶n数为)奇数 11 分
n
所以 T =(a+a+···+a )+(b+b+···+b )
2n 1 3 2n-1 2 4 2n
=n+n(n-1)2×4+4(1-4n)1-4
=2n2-n+4(4n-1)3 15 分
→ →
,
→
17. (1) 法 1.如图,以{ AD, }为正交基底,建立空间直角坐标系,
则 A(0,0,0),B(3,0,0),C(3,1,-1),D(0,2,0),P(0,0,1),M(0,1,12)
→
由题意:平面 PAB 的法向量为 n1=(0,1,0), =(-3,0,32) 2 分
→
→
,
因为 n1· =0,所以 n1⊥CM 3 分
又因为 CM 平面 PAB,所以 CM//平面 PAB. 4 分
(注:不写“CM 平面 PAB”扣 1 分)
∥
法 2.取 AB 的中点 E,连接 ME,因为 M 是 PD 的中点, 所以 = 12AD.
ME
∥ ∥
又因为 BC= 12AD,所以 = BC,
ME
所以四边形 BCME 是平行四边形,所以 CM∥BE. 2 分
又因为 CM 平面 PAB,BE 平面 PAB,
所以 CM//平面 PAB. 4 分
z
P
(注:不写“CM 平面 PAB”扣 1 分)
M
A D
Q y
B C
x
(2)由题意:平面 PAB 的法向量为 n1=(0,1,0),设平面 PCD 的法向量为 n2=(x,y,z)
→ → → →
=(3,1,-1) , =(0,2,-1),由 ·n2=0, ·n2=0,可得\r(3 2y-z=0,令 y=1,则 n2=(33,1,2) 6 分
所以 cos<n1,n2>=113)+1+4=34. 8 分
所以,平面 PAB 与平面 PCD 所成二面角的余弦值为 34. 9 分
→ → → → → →
(3)设 BQBD=λ,则 =λ , = +λ =(3-3λ,2λ,0) , =(0,0,
1),
→ →
设平面 PAQ 的法向量为 n3=(x,y,z),则 n3· =0,n3· =0,
0 0 0
可得 (\r(3)λ z0=0,令 y=1,所以 n3=(-2λ3,1,0). 11 分
0
因为点 D 到平面 PAQ 的距离为 217,
→
所以 d=3PD3|n·||n|=4λ23(1-λ)2
+12=2127.……………………………………………13 分
解得λ=12. 14 分
所以存在点 Q,使得点 D 到平面 PAQ 的距离为 217,此时 BQBD=12. 15 分
(注:在底面内过点 D 作直线 AQ 的垂线,由几何知识得 BQBD=12 也得满分,用等体积法
V =V 求得 BQBD=12 也得满分)
P-AQD D-PAQ
18.(1)因为椭圆 C 过点(1,32),所以{14+94b2=1,所以 b2=3,
1
所以 C 方程:x24+y23=1. 2 分
1
又因为椭圆 C 的右焦点 F(1,0),
1
所以 p2=1,p=2,所以 C 方程:y2=4x. 4 分
2
(2)解:方法一:假设存在这样的 l,
设直线 l 的方程为:x=my+1,A(x,y),B(x,y),
1 1 2 2\a\ac\co31x\2h+s 24\ vys22=( x1=2)my+1 3(m2y2+2my+1)+4y2=12,(3m2+4)y2+6my-9=0.
Δ=36m2+36(3m2+4)=144(m2+1),
∴|AB|=1+m2·|y-y|=1+m2·m2+1)3m2+4=12(m2+1)3m2+4. 8 分
1 2
设 P(x,y),Q(x,y),
3 3 4 4
\a\ac\co1\hys22=\ v s42x()x=my+1 y2=4my+4,y2-4my-4=0,Δ=16m2+16,
∴|PQ|=1+m2·|y-y|=1+m2·16m2+16=4(m2+1), 12 分
3 4
∴μ|AB|+λ|PQ|=(3m2+4)μ12(m2+1)+λ4(m2+1)=(3m2+4)μ+3λ12(m2+1)=C(C 为定
值). 15 分
∴3m2(4C-μ)+(12C-3λ-4μ)=0,任意的实数 m 恒成立
∴ 12C\a-\ac3(λ4-C=4μμ,=0.)得到\ a3\ aλc(=μ-=44CC.,)∴当λμ=-13 时μ|AB|+λ|PQ|为定值.
17 分
方法二:设 l 倾斜角为θ,
∴|AB|=2ab2a2-c2cos2θ=2×2×34-cos2θ=124-cos2θ, 8 分
|PQ|=2psin2θ=4sin2θ, 12 分
∴μ|AB|+λ|PQ|=(4-cos2θ)μ12+λsin2θ4=4μ+3λsin2θ-μcos2θ12 为定值, 15 分
∴3λ=-μ时即λμ=-13 时,μ|AB|+λ|PQ|为定值. 17 分
(注:用焦半径公式需要证明,不证明则每种情况扣 2 分.)
6
19.(1)C =4×3×2×1×0×(-1)6!=0 2 分
4
2
C =0.5×(-0.5)2!=-18(写-0.125 也对) 4 分
0.5
(2)1.11.8=(1+0.1)1.81 2 3
=1+C1.8·0.1+C1.8·0.12+C1.8·0.13+… 6 分
=1+0.18+0.0072-0.000048+…
≈1.19 10 分
(注:只要有展开过程就得 2 分,后面需至少保留前 3 项)
(3)考虑(1+x)2=(1+x)0.7·(1+x)1.3 的展开式中,x20 的系数. 13 分
左式为 1+2x+x2,x20 的系数为 0,
20 0 19 1 18 2 1 19 0 20
右式中 x20 的系数为 C0.7·C1.3 +C0.7·C1.3 +C0.7·C1.3 +…+C0.7·C1.3 +C1.7·C1.3 , 15 分
20 0 19 1 18 2 1 19 0 20
所以 C0.7·C1.3 +C0.7·C1.3 +C0.7·C1.3 +…+C0.7·C1.3 +C1.7·C1.3 =0. 17 分