宝鸡中学2022级高三第一学期月考三考试参考答案-数学_2024-2025高三（6-6月题库）_2024年12月试卷_1203陕西省宝鸡市宝鸡中学2024-2025学年高三上学期12月月考

宝鸡中学 2022 级高三月考三考试参考答案
一.选择题
1 2 3 4 5 6 7 8 9 10 11
D A B C C D A A AD BD BCD
二.填空题
4 48
12.  13. 14.10
3 5
三解答题
15.解：(1)因为acos(BC)acosA2 3csinBcosA ，
所以acosBcosC asinBsinC a(cosBcosC sinBsinC)2 3csinBcosA ，
即 asinBsinC  3csinBcosA ，
由正弦定理得： sinAsinBsinC  3sinCsinBcosA ，
显然sinC 0，sinB 0，所以sinA 3cosA，所以tanA 3 ，
 
因为 A(0, )，所以A . 分
2 3
----------------------------------------a-----------b--------------------6
(2)因为ABC 外接圆的半径为 3 ，所以由正弦定理得：   2 3 ，
sin A sinB
所以a3，b2 3sinB，
b2 a2 a2 3 3 3
所以 b 2 3sinB 2 3(sinB )，
b b 2sinB 4sinB
 
0 B

 2   1
因为ABC 为锐角三角形，所以 ，解得  B  ，即sinB( ,1).
 2  6 2 2
0 B
 3 2
3 1
令 f(x) x ，x( ,1)，
4x 2
3 1 3 3
根据对勾函数的性质可知，函数 f(x) x 在( , )上单调递减，在( ,1)上单调
4x 2 2 2
第 页，共 页
1 6
{#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}1 3 7
递增，且 f( )2， f( ) 3 ， f(1) ，
2 2 4
3
所以 f (x)[ 3,2),即sinB [ 3,2),
4sinB
3 b2 a2
所以2 3(sinB )[6,4 3),即 的取值范围为[6,4 3). ------------13分
4sinB b
16. (1)证明：因为AAC60， AC 1，AA 2，由余弦定理得
1 1
AC  12 22 212cos60  3，
1
所以 AA2  AC2  AC2，所以 AC  AC ，又因为 AC  AB，
1 1 1 1
又因为 AC  AB  A，所以 AC 平面ABC. 分
1
(2)解：由已知和(1)得，CA、CB、CA两两垂直--，--------------------------------------6
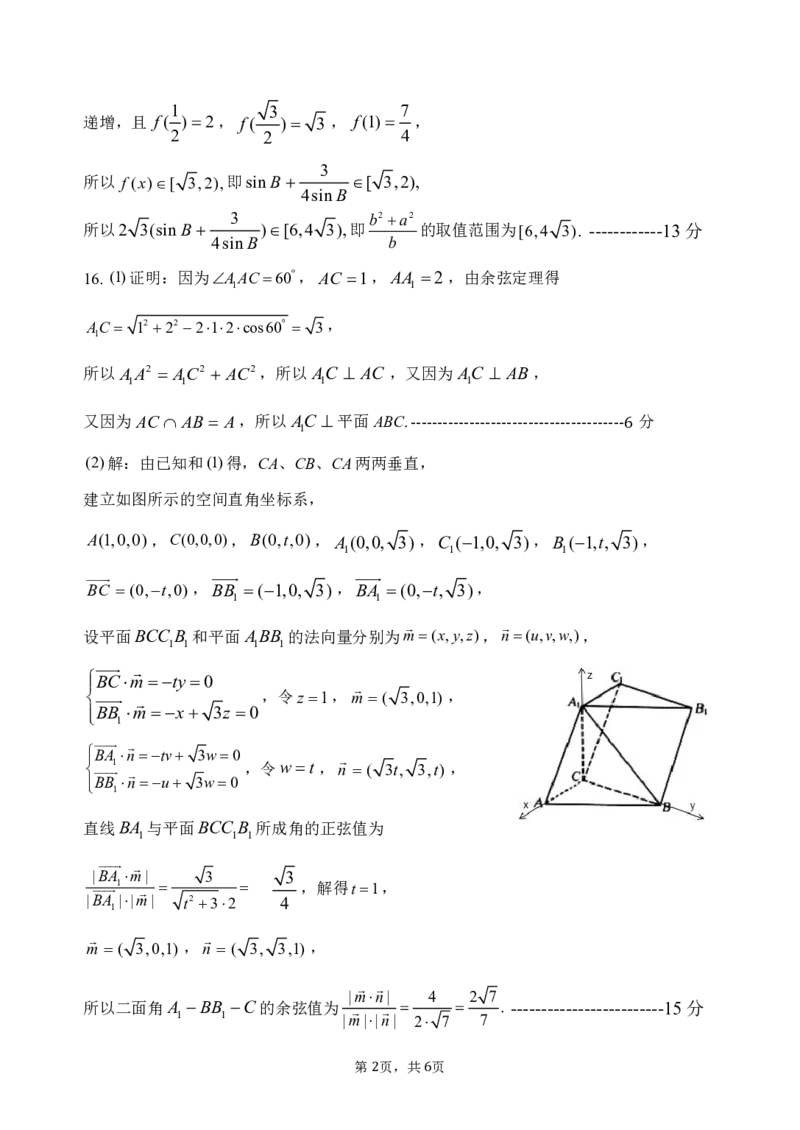
建立如图所示的空间直角坐标系，
A(1,0,0)，C(0,0,0)，B(0,t,0)， A(0,0, 3) ，C (1,0, 3)，B (1,t, 3)，
1 1 1
  
BC  (0,t,0)，BB (1,0, 3)，BA (0,t, 3)，
1 1
 
设平面BCC B 和平面 ABB 的法向量分别为m(x,y,z)，n(u,v,w,)，
1 1 1 1


 BCmty 0

  ，令z 1，m  ( 3,0,1) ，
BB mx 3z 0
1
 
   B  A  1 n  tv 3w0 ，令wt ，n   ( 3t, 3,t) ，
BB nu 3w0
1
直线BA 与平面BCC B 所成角的正弦值为
1 1 1
 
|BA m| 3 3
1

  ，解得t 1，
|BA ||m| t2 32 4
1
 
m  ( 3,0,1) ，n  ( 3, 3,1)，
 
|mn| 4 2 7
所以二面角 A BB C的余弦值为     . -------------------------15分
1 1 |m||n| 2 7 7
第 页，共 页
2 6
{#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}17.解：(1)因为抛物线x2  4y 的焦点为(0,1)，
所以椭圆C的下顶点 A(0,1)，可得b1，
3 1 3
因为椭圆C经过点B(1, )， 所以  1， 解得a2 4，
2 a2 4
x2
则椭圆C的方程为  y2 1. 分
4
---------------------------------------------------------6
证明：当直线PQ的斜率不存在时，
(2)
不妨设P(x ,y )， 此时Q(x ,y )，
0 0 0 0
y 1 y 1 1y2 1 x2
则k k  0  0  0  ， 整理得 0  y2 1，
AP AQ x x x2 2 2 0
0 0 0
x2 x2
由 0  y2 1与 0  y2 1解得x 0不符题意，所以直线PQ的斜率存在，
2 0 4 0 0
因为直线AP，AQ斜率同号， 所以直线PQ的斜率存在且不为0，
不妨设直线PQ的方程为 y  kxm，P(x,y )，Q(x ,y )，
1 1 2 2
x2
  y2 1
联立 4 ，消去y并整理得(14k2)x2 8kmx4m2 40，

y  kxm
此时16(4k2 m2 1)0， 即4k2 1 m2，
8km 4m2 4
由韦达定理得x  x  ，x x  ，
1 2 14k2 1 2 14k2
所以
4m2 4 8km m2 4k2
y y (kx m)(kx m)k2xx km(x x )m2 k2 km m2 
1 2 1 2 1 2 1 2 14k2 14k2 14k2
8km 2m
y  y k(x x )2mk 2m ，
1 2 1 2 14k2 14k2
第 页，共 页
3 6
{#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}y 1 y 1 y y (y  y )1 1
此时k k  1  2  1 2 1 2  ，
AP AQ x x xx 2
1 2 1 2
整理得2y y 2(y  y )2xx ，
1 2 1 2 1 2
m2 4k2 4m 4m2 4
即2  2 ， 解得m  1或m3，
14k2 14k2 14k2
当m  1时，直线PQ方程为 y  kx1， 令x0， 解得y1，
所以直线PQ恒过定点(0,1)，不符合题意，
当m3时，直线PQ方程为 y kx3，令x0， 解得 y 3，
所以直线PQ恒过定点(0,3)，符合题意，
综上所述，直线PQ恒过定点(0,3). 分
-------------------------------------------------15
18.解：(1)由题意得这三人中这一周恰好有一人选择A健身中心健身的概率
1 1 2 1 1 2 1 1 2 7
P (1 )(1 )(1 ) (1 )(1 )(1 )  ；---------------4分
2 3 3 2 3 3 2 3 3 18
(2)记事件C：丁周六选择A健身中心，事件D：丁周日选择B健身中心，
 1 1 3  2 1
则P(C)P(C) ,P(D|C)1  ,P(D|C)1  ，
2 4 4 3 3
  1 3 1 1 13
由全概率公式得P(D)P(C)P(D|C)P(C)P(D|C)     ，
2 4 2 3 24
13
故丁周日选择B健身中心健身的概率为 ；-----------------------------------10分
24
(3)设从全校学生中随机抽取1人，抽取到的学生是健身效果不佳的学生的概率为p，则
p  0.02，
设抽取次数为X，则X的分布列为：
X 1 2 3 n1 n
P p (1 p)p (1 p)2p ⋯ (1 p)n2 p (1 p)n1
⋯
第 页，共 页
4 6
{#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}故E(X) p(1 p)p2(1 p)2p3(1 p)n2p(n1)(1 p)n1n，
又(1 p)E(X)(1 p)p(1 p)2p2(1 p)3p3(1 p)n1p(n1) (1 p)nn，
两式相减得 pE(X) p(1 p)p(1 p)2p(1 p)n2p(1 p)n1p，
所以
1(1 p)n 1(1 p)n 10.98n
E(X)1(1 p)(1 p)2 (1 p)n2 (1 p)n1    ，
1(1 p) p 0.02
10.98n
所以E(X) 在nN*时单调递增，
0.02
10.9829 10.557
可知当n 29时，E(X)  22.15，
0.02 0.02
10.9830 10.545
当n30时，E(X)  22.75，
0.02 0.02
10.9831 10.535
当n 31时，E(X)  23.25，
0.02 0.02
若抽取次数的期望值不超过23，则n的最大值为30. ------------------------------------17分
1
19. (1)证明：当ae时， f (x)  ex lnx ， f(x)ex(lnx )，
x
1 1 1 x1
设 p(x)lnx ，则 p(x)   ，
x x x2 x2
当0 x1时， p(x)0，当x1时， p(x)0，
所以 p(x)在(0,1)上单调递减，在(1,)上单调递增，
故 p(x) p(1)10，所以 f(x) 0，所以 f(x)为增函数．-------------------4分
1
(2)解：(i)设aet(t0)，则 f(x) etxlnx，
t
etx etx 1
则 f(x)etxlnx  (xlnx ).
tx x t
设g(x)xlnx，则g(x)1lnx，
第 页，共 页
5 6
{#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}1
当x(0, )时，g(x)0，g(x)单调递减，
e
1
当x( ,)时，g(x)0，g(x)单调递增，
e
1 1
所以g(x)  g( )  ，
min e e
1
当t 0时，令g(x) ，由g(1)0，且g(x)在(1,)上单调递增，
t
1
故g(x) 仅有一个零点x ，不符合题意；
t 0
1
当t 0时，g(x)[ ,),
e
1 1 1
①当t„e时，则
„
 ，此时g(x)  ， f(x) 0， f(x)单调递增，不符合题意；
t e t
1 1 1
②当t e时，则  0，此时g(x) 存在两个零点x x ，
e t t 1 2
1 1
当x(0,x )时g(x) ， f(x) 0；当x(x ,x )时，g(x) ， f(x) 0；
1 t 1 2 t
1
当x(x ,)时，g(x) ， f(x) 0， f(x)存在两个极值点，符合题意．
2 t
综上可知，a(ee,). 分
--------------------1--------------------------1-------------------------11
(ii)由(i)可知M  f(x )，且x (0, )，满足x lnx  ，
1 1 e 1 1 t
1
1 
故M  f(x ) etx1lnx x (lnx )2e lnx1 ，
1 t 1 1 1
设r lnx (1,)，则 1 r 2lnrr 1，
1 M er r2 e r
1 2 1 (r1)2
设h(r)2lnrr ，则h(r) 1  0，
r r r2 r2
故h(r)单调递减，且h(1)0，则h(r)(,0)，
即
M e
2lnrr 1
r(1,0).
------------------------------------------------------------17分
第 页，共 页
6 6
{#{QQABLYQEggiIABAAAAgCAw0iCkAQkgGCAYgOBEAIMAAASQNABAA=}#}