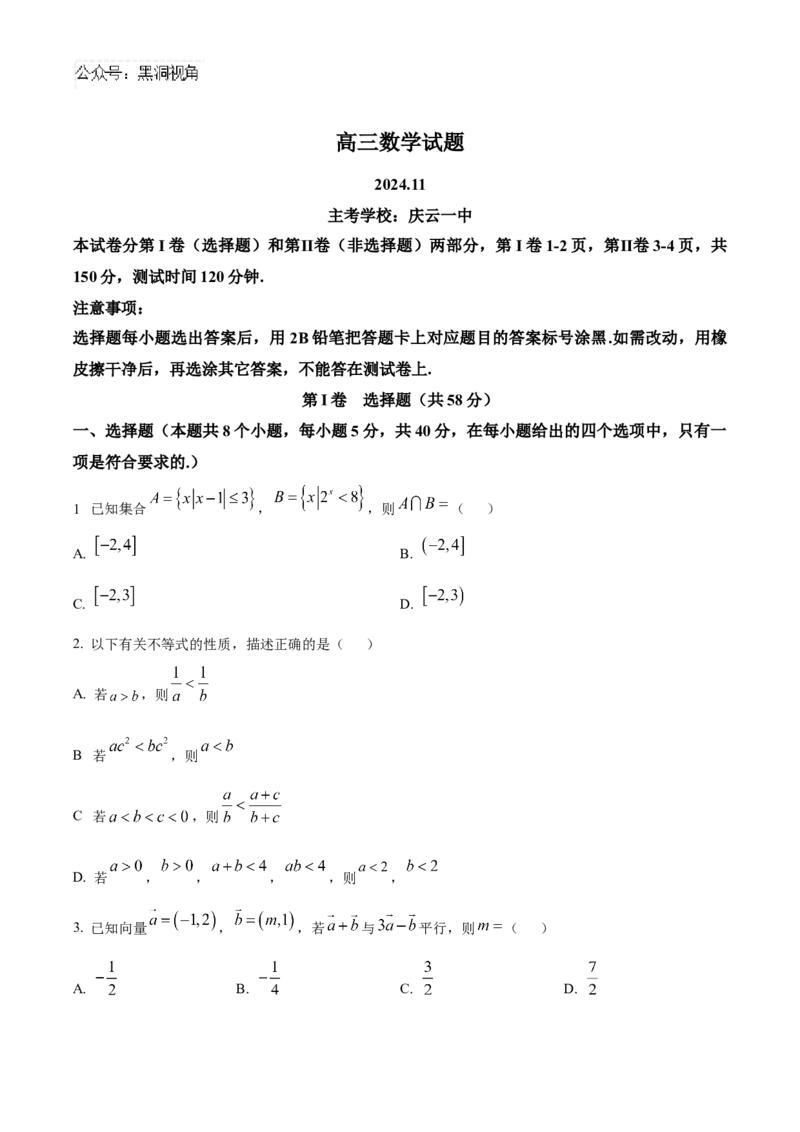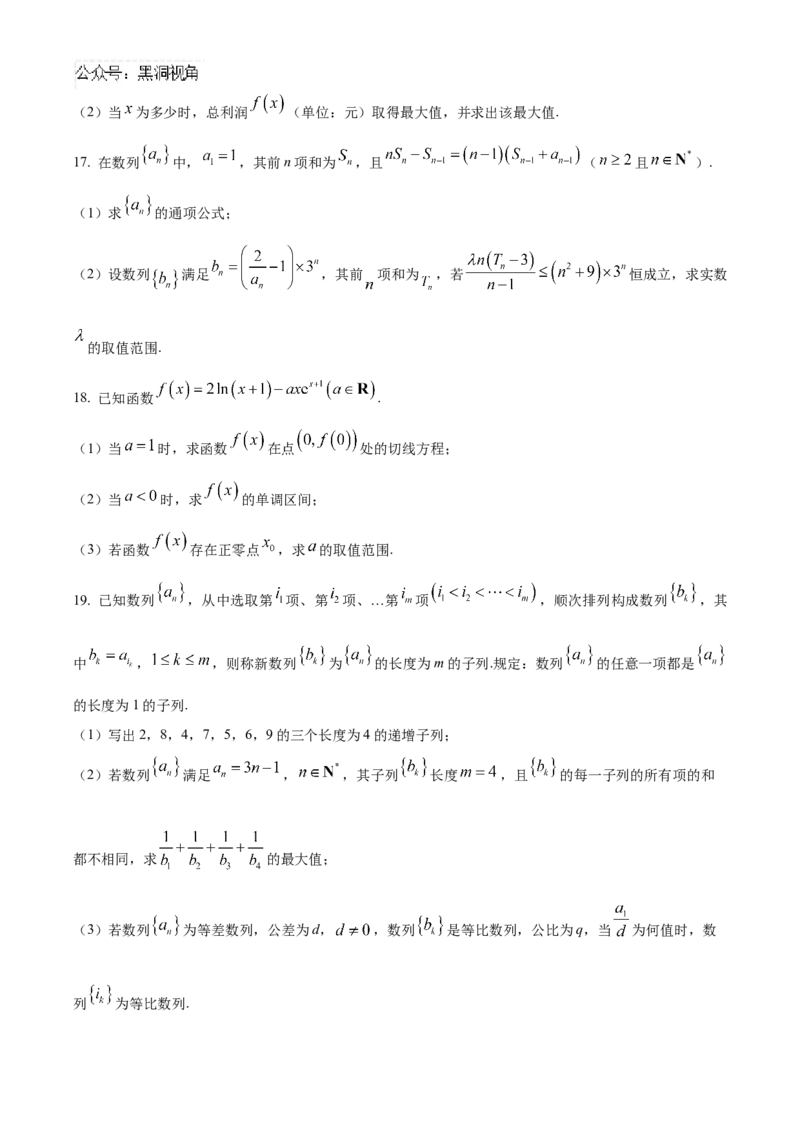文档内容
高三数学试题
2024.11
主考学校:庆云一中
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第 I卷1-2页,第Ⅱ卷3-4页,共
150分,测试时间120分钟.
注意事项:
选择题每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡
皮擦干净后,再选涂其它答案,不能答在测试卷上.
第I卷 选择题(共58分)
一、选择题(本题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一
项是符合要求的.)
.
1 已知集合 , ,则 ( )
A. B.
C. D.
2. 以下有关不等式的性质,描述正确的是( )
A. 若 ,则
.
B 若 ,则
.
C 若 ,则
D. 若 , , , ,则 ,
3. 已知向量 , ,若 与 平行,则 ( )
A. B. C. D.4. 已知等差数列 的前n项和为 , , ,则 ( )
A. 180 B. 200 C. 220 D. 240
5. 已知 : , : ,若 是 的充分不必要条件,则a的取值范围是( )
A. B.
C. D.
6. 已知关于 函数 在 上单调递增,则实数 的取值范围是( )
的
A. B.
C. D.
7. 已知函数 ,若方程 在区间 上恰有3个实数根,则 的取
值范围是( )
A. B.
C. D.
8. 已知函数 ,若函数 有三个不同的零点,则实数a的取值
范围是( )
A. B..
C D.
二、选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.)
9. 下列结论正确的是( )
A.
B. ,
C. 若 , ,
D. 的值域为
10. 已知函数 ,则( )
A. 函数 有两个零点
B. 是 的极小值点
C. 是 的对称中心
D. 当 时,
11. 已知数列 的各项均为负数,其前 项和 满足 ,则( )
A. B. 为递减数列C. 为等比数列 D. 存在大于 的项
第Ⅱ卷非选择题(共92分)
三、填空题(本题共3小题,每小题5分,共15分)
12. 已知正三角形 的边长为2, 为 中点, 为边 上任意一点,则 ______.
13. 设 ,当 时, ,则 ______.
14. 已知函数 的定义域为 , , 为偶函数,且 ,
则 ______, ______.
四、解答题(本题共5小题,共77分,解答应写出必要的文字说明、证明过程或演算步骤.)
15. 已知 中的三个角 的对边分别为 ,且满足 .
(1)求 ;
(2)若 的角平分线 交 于 , ,求 面积的最小值.
16. 某企业计划引入新的生产线生产某设备,经市场调研发现,销售量 (单位:台)与每台设备的利
润 (单位:元, )满足: (a,b为常数).当每台设备的利润为36
元时,销售量为360台;当每台设备的利润为100元时,销售量为200台.
(1)求函数 的表达式;(2)当 为多少时,总利润 (单位:元)取得最大值,并求出该最大值.
17. 在数列 中, ,其前n项和为 ,且 ( 且 ).
(1)求 的通项公式;
(2)设数列 满足 ,其前 项和为 ,若 恒成立,求实数
的取值范围.
18. 已知函数 .
(1)当 时,求函数 在点 处的切线方程;
(2)当 时,求 的单调区间;
(3)若函数 存在正零点 ,求 的取值范围.
19. 已知数列 ,从中选取第 项、第 项、…第 项 ,顺次排列构成数列 ,其
中 , ,则称新数列 为 的长度为m的子列.规定:数列 的任意一项都是
的长度为1的子列.
(1)写出2,8,4,7,5,6,9的三个长度为4的递增子列;
(2)若数列 满足 , ,其子列 长度 ,且 的每一子列的所有项的和
都不相同,求 的最大值;
(3)若数列 为等差数列,公差为d, ,数列 是等比数列,公比为q,当 为何值时,数
列 为等比数列.高三数学试题
2024.11
主考学校:庆云一中
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第 I卷1-2页,第Ⅱ卷3-4页,共
150分,测试时间120分钟.
注意事项:
选择题每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡
皮擦干净后,再选涂其它答案,不能答在测试卷上.
第I卷 选择题(共58分)
一、选择题(本题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一
项是符合要求的.)
【1题答案】
【答案】D
【2题答案】
【答案】B
【3题答案】
【答案】A
【4题答案】
【答案】C
【5题答案】
【答案】A
【6题答案】
【答案】D
【7题答案】
【答案】C
【8题答案】
【答案】B
二、选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.)
【9题答案】
【答案】BC
【10题答案】
【答案】ABD
【11题答案】
【答案】ABD
第Ⅱ卷非选择题(共92分)
三、填空题(本题共3小题,每小题5分,共15分)
【12题答案】
【答案】3
【13题答案】
【答案】
【14题答案】
【答案】 ①. 1 ②. -2026
四、解答题(本题共5小题,共77分,解答应写出必要的文字说明、证明过程或演算步骤.)
【15题答案】
【答案】(1)
(2)
【16题答案】
【答案】(1)
(2)当 为100元时,总利润取得最大值为20000元.
【17题答案】【答案】(1)
(2) .
【18题答案】
【答案】(1)
(2)单增区间是 ,无单减区间;
(3) .
【19题答案】
【答案】(1)2,4,7,9;2,4,5,6;2,4,5,9;
(2)
(3)