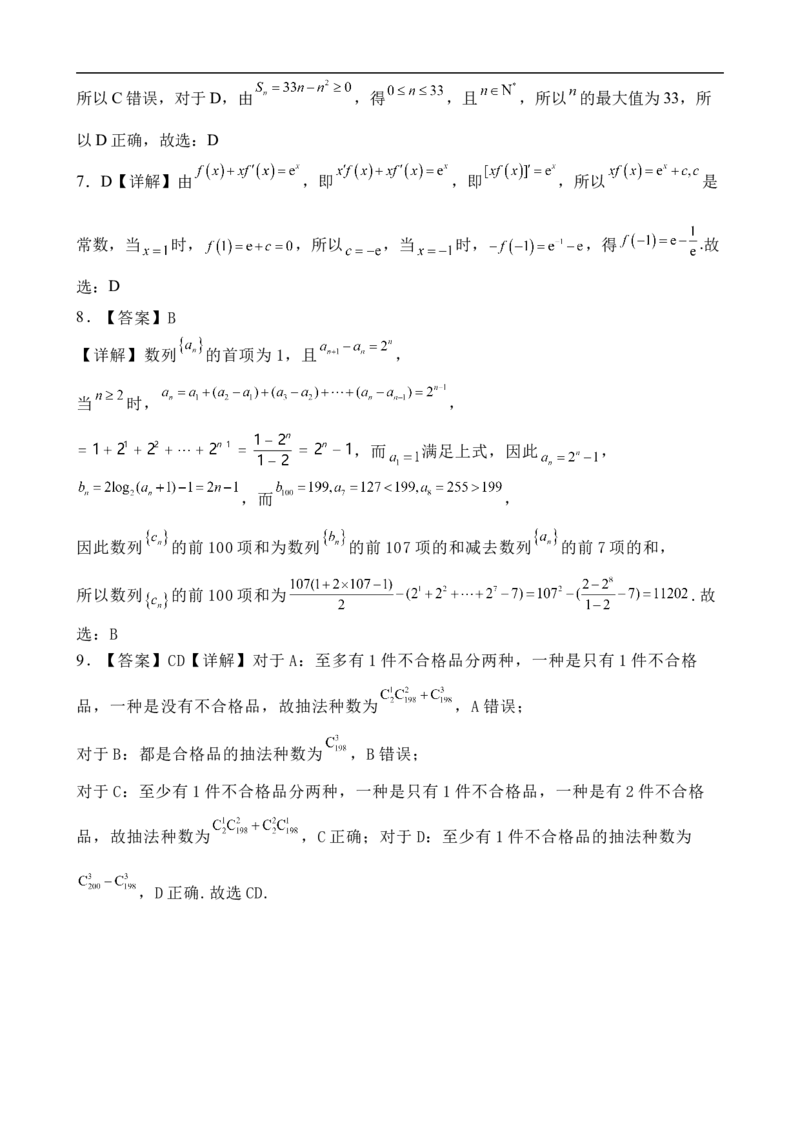文档内容
高二数学试卷
一、单选题(每小题5分,计40分)
1.已知函数 在 上可导,若 ,则 ( )
A.9 B.12 C.6 D.3
2.已知抛物线 的焦点为F,若抛物线上的点 与点F间的距离为3,则
( )
A. B. C. 或 D.4或
3.已知数列 满足 ,且 , ,则 ( )
A. B. C. D.
4.已知双曲线 的左、右焦点分别为 , 为 的右支上一点,
,则 的离心率为( )
A. B. C. D.
5.已知实数 满足 ,则 的最大值为( )
A. B. C. D.
6.设数列 的前 项和为 ,则下列说法正确的是( )
A. 是等比数列 B. 成等差数列,公差为
C.当且仅当 时, 取得最大值 D. 时, 的最大值为33
7.当 时,设函数 存在导数 ,且满足 ,若 ,则
( )A. B. C.0 D.
8.已知数列 的首项为1,且 ,设数列 中不在数
列 中的项按从小到大的顺序排列构成数列 ,则数列 的前100项和为( )
A.11449 B.11202 C.11209 D. 11195
二、多选题(每小题6分,计18分)
9.某工厂生产的200个零件中,有198件合格品,2件不合格品,从这200个零件中任
意抽出3件,则抽出的3个零件中( )
A.至多有1件不合格品的抽法种数为
B.都是合格品的抽法种数为
C.至少有1件不合格品的抽法种数为
D.至少有1件不合格品的抽法种数为
10.已知在首项为1,公差为d的等差数列 中, 、 、 是等比数列 的前三项,
数列 的前n项和为 ,则( )
A. 或 B. C. 是等差数列 D.
11.甲、乙、丙三人相互做传球训练,第一次由甲将球传出,每次传球时,传球者都等
可能地将球传给另外两个人中的任何一人,下列说法正确的是( )
A.2次传球后球在丙手上的概率是
B.3次传球后球在乙手上的概率是
C.3次传球后球在甲手上的概率是
D.n次传球后球在甲手上的概率是三、填空题(每小题5份,计15分)
12.已知 的二项展开式中各项系数和为 ,则展开式中常数项的值为 .
13已知直线l分别与曲线 , 相切于点 , ,则 的值
为 .
14.如图,经过边长为1的正方体的三个项点的平面截正方体得到一个正三角形,将这
个截面上方部分去掉,得到一个七面体,则这个七面体内部能容纳的最大的球半径是
.
四、解答题(共5小题,计77分)
15.中国在第75届联合国大会上承诺,努力争取 2060年之前实现碳中和(简称“双碳目
标”).新能源电动汽车作为战略新兴产业,对于实现“双碳目标”具有重要的作用.赛
力斯汽车有限公司为了调查客户对旗下 AITO问界M7的满意程度,对所有的意向客户发
起了满意度问卷调查,将打分在 80分以上的客户称为“问界粉”.现将参与调查的客户
打分(满分100分)进行了统计,得到如下的频率分布直方图:
(1)估计本次调查客户打分的中位数(结果保留一位小数);
(2)按是否为“问界粉”比例采用分层抽样的方法抽取10名客户前往重庆赛力斯两江智
慧工厂参观,在10名参观的客户中随机抽取2名客户赠送价值2万元的购车抵用券.记
获赠购车券的“问界粉”人数为 ,求 的分布列和数学期望 .
16.已知数列 满足 , .
(1)证明:数列 为等差数列,并求通项 ;(2)求数列 的前n项和 .
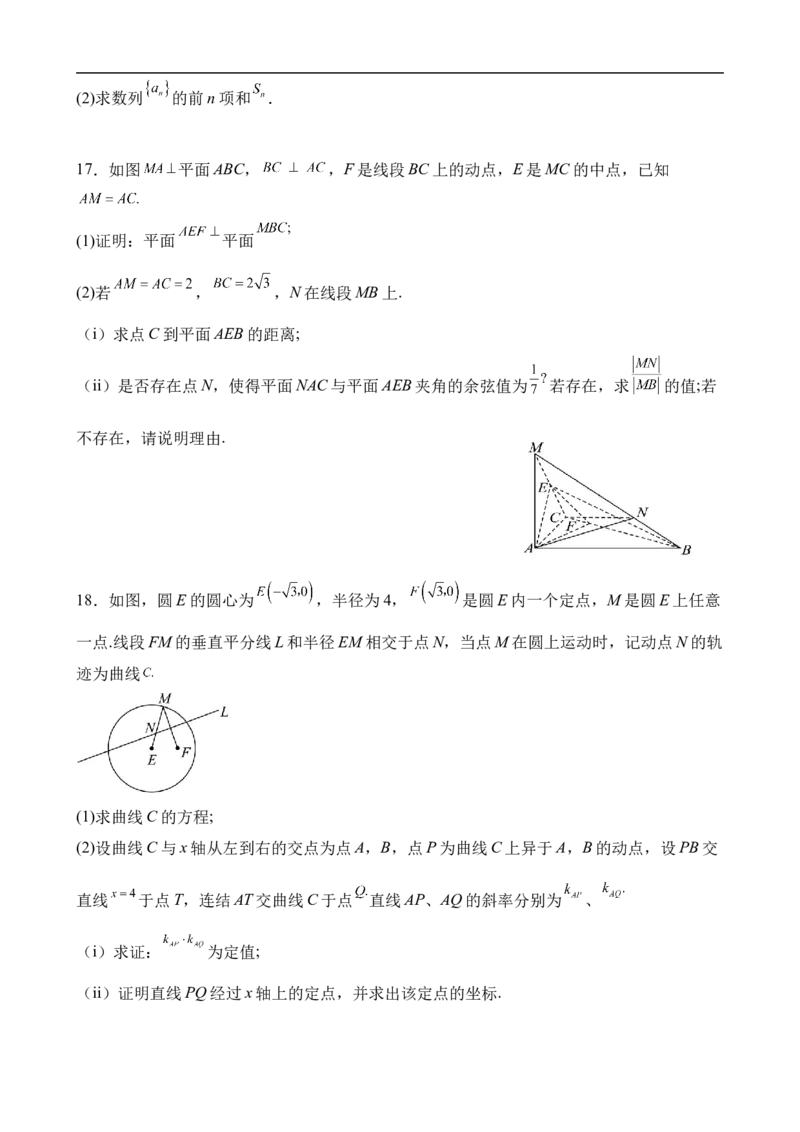
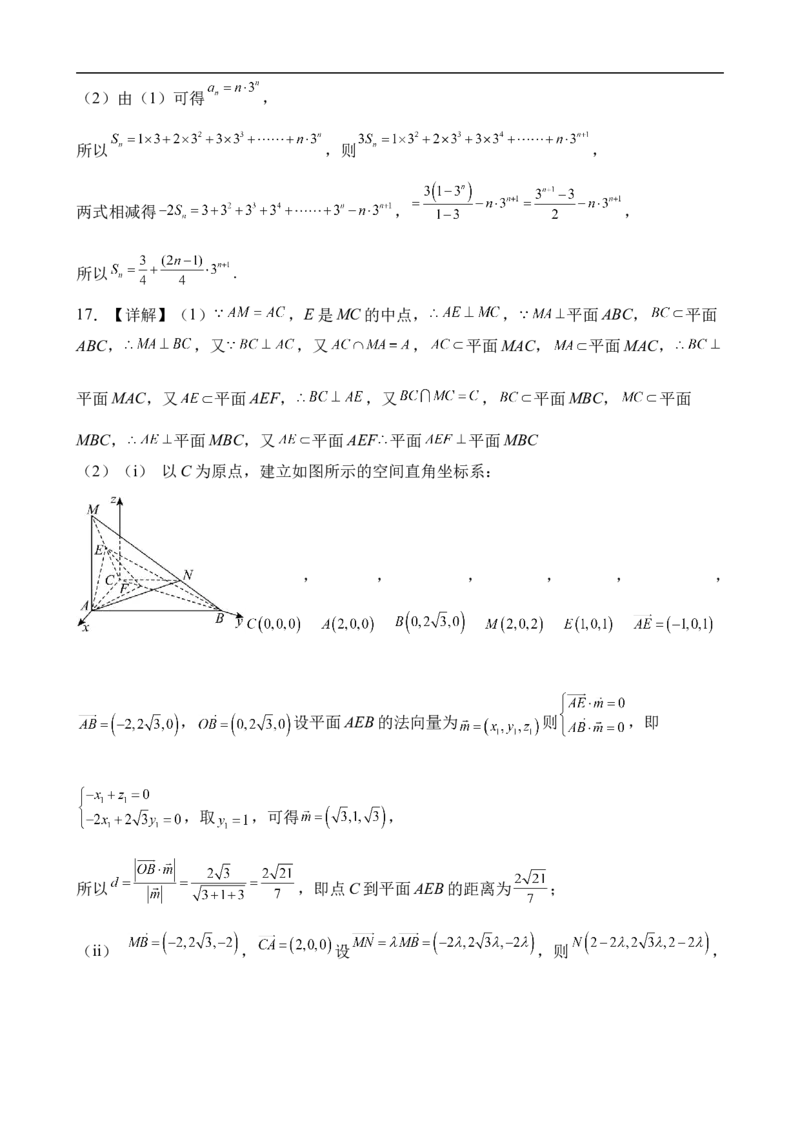
17.如图 平面ABC, ,F是线段BC上的动点,E是MC的中点,已知
(1)证明:平面 平面
(2)若 , ,N在线段MB上.
(i)求点C到平面AEB的距离;
(ii)是否存在点N,使得平面NAC与平面AEB夹角的余弦值为 若存在,求 的值;若
不存在,请说明理由.
18.如图,圆E的圆心为 ,半径为4, 是圆E内一个定点,M是圆E上任意
一点.线段FM的垂直平分线L和半径EM相交于点N,当点M在圆上运动时,记动点N的轨
迹为曲线
(1)求曲线C的方程;
(2)设曲线C与x轴从左到右的交点为点A,B,点P为曲线C上异于A,B的动点,设PB交
直线 于点T,连结AT交曲线C于点 直线AP、AQ的斜率分别为 、
(i)求证: 为定值;
(ii)证明直线PQ经过x轴上的定点,并求出该定点的坐标.19.对于函数 ,我们无法直接求出它的零点,数学家牛顿用设切线的方法
解决了这个问题.设函数的零点为 ,如果可以找到一步步逼近 的 , , ,…, ,使
得当 时, ,则可把 看做函数 的近似解,这个方法被称为“牛顿法”.
具体步骤为:选取合适的 ,在横坐标为 的点作 的切线,切线与 轴的交点的横坐标
即 ,再用 代替 ,重复上面的过程得到 ,如此循环计算出 .我们知道 在
处的切线的斜率为 ,由此写出切线方程 ,因为
,所以令 得切线与 轴交点的横坐标 ,同理得
, ,以此类推,可以得到 .
(1)对于函数 ,当 时,求 , 的值;
(2)已知函数 的定义域R.
(i)对于函数 ,若 为公差不为零的等差数列,求证: 无零点;
(ii)当 时,运用“牛顿法”证明:高二数学答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A B D D D B CD AC
题号 11
答案 ACD
1.B【详解】由导数定义可知:
,
故 .故选:B.
2.C解析:抛物线 开口向左,依题意,抛物线上的点 与点F间的距离
为3,所以 , ,抛物线方程为 ,令 ,得 ,解得 ,故选:C.
3.【详解】由 可得: ,若 ,则
,与题中条件矛盾,故 ,所以 ,也即数列
是以 为首项,以 为公比的等比数列,所以 ,则有
,
也即 ,所以 ,故选: .
4.B【详解】依题意得 ,则 的离心率为
故选:B.
5.D【详解】设 ,将其看作直线 ,由直线 与圆
有公共点,得圆心 到直线的距离小于或等于圆的半径 ,
即 ,解得 ,所以 的最大值为 ,
即 的最大值为 故选:D
6.D【详解】因为 ,所以数列 是以 为公差,32为首项的等差数列,
所以 ,所以 ,所以当 时, ,所以
,
因为 ,所以 ,对于A,因为 ,
所以 是以 为公差的等差数列,所以A错误,对于B,因为 ,所以
,所以 ,
因为 ,所以 成等差数列,公差为 ,所以B错误,对于
C, ,对称轴为 ,因为 ,所以当 或 时, 取得最大值,所以C错误,对于D,由 ,得 ,且 ,所以 的最大值为33,所
以D正确,故选:D
7.D【详解】由 ,即 ,即 ,所以 是
常数,当 时, ,所以 ,当 时, ,得 .故
选:D
8.【答案】B
【详解】数列 的首项为1,且 ,
当 时, ,
,而 满足上式,因此 ,
,而 ,
因此数列 的前100项和为数列 的前107项的和减去数列 的前7项的和,
所以数列 的前100项和为 .故
选:B
9.【答案】CD【详解】对于A:至多有1件不合格品分两种,一种是只有1件不合格
品,一种是没有不合格品,故抽法种数为 ,A错误;
对于B:都是合格品的抽法种数为 ,B错误;
对于C:至少有1件不合格品分两种,一种是只有1件不合格品,一种是有2件不合格
品,故抽法种数为 ,C正确;对于D:至少有1件不合格品的抽法种数为
,D正确.故选CD.10.【答案】AC【详解】由题意 ,则 ,整理得 ,可得 或
,当 时, , ,则 ,即 是等差数列,此时 ;当 时,
, ,则 ,即 是等差数列,
此时 ,易知公比为4,故 ;综上,A、C对,B、D错.
故选:AC
11.【答案】ACD【详解】第一次甲将球传出后,2次传球后的所有结果为:甲乙甲,甲
乙丙,甲丙甲,甲丙乙,共4个结果,它们等可能,2次传球后球在丙手中的事件有:
甲乙丙, 1个结果,所以概率是 ,故A正确;
第一次甲将球传出后,3次传球后的所有结果为:甲乙甲乙,甲乙甲丙,甲乙丙甲,甲乙
丙乙,甲丙甲乙,甲丙甲丙,甲丙乙甲,甲丙乙丙,共 8个结果,它们等可能,3次传
球后球在乙手中的事件有:甲乙甲乙,甲乙丙乙,甲丙甲乙,3个结果,所以概率为 ,
故B错误;
3次传球后球在甲手上的事件为:甲乙丙甲,甲丙乙甲,2个结果,所以概率为 ,故
C正确;n次传球后球在甲手上的事件记为 ,则有 ,令 ,则
于是得 ,
故 ,则 ,而第一次由甲传球后,球不可能在甲手中,即
,则有 ,数列 是以 为首项, 为公比的等比数列,所以
即 ,故D正确.
故选ACD.
12.【答案】【详解】 的二项展开式中各项系数和为1024,即 ,
.设 的二项展开式的通项为 ,则 ,
令 ,得 ,故展开式中常数项的值为 .
故答案为:210.
13.答案:1解析:由 , ,有 , ,
在点 处的切线方程为 ,
在点 处的切线方程为 ,
则有 ,得 ,
所以 ,可得 .
故答案为:1.
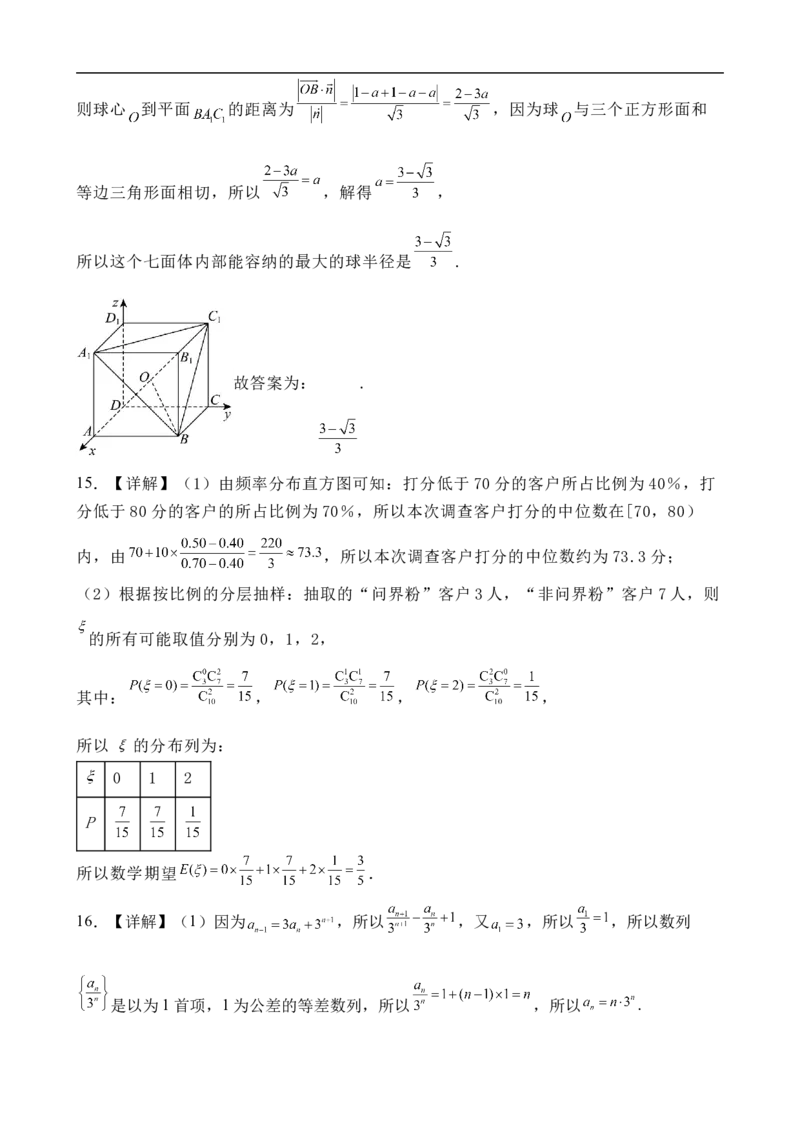
14.【答案】
【详解】如图,七面体为正方体 截去三棱锥 的图形,
由正方体的结构特征可得这个七面体内部能容纳的球最大时,
该球与三个正方形面和等边三角形面相切,且球心在体对角线 上,
如图,以点 为原点建立空间直角坐标系,则 ,
设球心 ,故 ,
设平面 的法向量为 ,则有 ,可取 ,则球心 到平面 的距离为 ,因为球 与三个正方形面和
等边三角形面相切,所以 ,解得 ,
所以这个七面体内部能容纳的最大的球半径是 .
故答案为: .
15.【详解】(1)由频率分布直方图可知:打分低于70分的客户所占比例为40%,打
分低于80分的客户的所占比例为70%,所以本次调查客户打分的中位数在[70,80)
内,由 ,所以本次调查客户打分的中位数约为73.3分;
(2)根据按比例的分层抽样:抽取的“问界粉”客户3人,“非问界粉”客户7人,则
的所有可能取值分别为0,1,2,
其中: , , ,
所以ξ的分布列为:
0 1 2
P
所以数学期望 .
16.【详解】(1)因为 ,所以 ,又 ,所以 ,所以数列
是以为1首项,1为公差的等差数列,所以 ,所以 .(2)由(1)可得 ,
所以 ,则 ,
两式相减得 , ,
所以 .
17.【详解】(1) ,E是MC的中点, , 平面ABC, 平面
ABC, ,又 ,又 , 平面MAC, 平面MAC,
平面MAC,又 平面AEF, ,又 , 平面MBC, 平面
MBC, 平面MBC,又 平面AEF 平面 平面MBC
(2)(i) 以C为原点,建立如图所示的空间直角坐标系:
, , , , , ,
, 设平面AEB的法向量为 则 ,即
,取 ,可得 ,
所以 ,即点C到平面AEB的距离为 ;
(ii) , 设 ,则 ,,设平面NAC的法向量为 则 ,即
,
令 。可得 ,
,化简得 ,解得 或 ,
或 .
18.【详解】(1)由题意可知, ,由椭圆定义可得,点
N的轨迹是以E, F为焦点的椭圆,且长轴长 ,焦距 ,
所以 ,因此曲线C方程为
(2)证明: 设 , , ,由题可知 , ,如下图所示,则
, ,而 ,于是 ,
所以 ,又 ,则 ,
因此 为定值;
由题意可知,直线PQ不可能与 轴平行,
设直线PQ的方程为 , , ,易知由 ,得 , ,得 所以
由 可知, ,
即 ,
将 代入化简得 ,解得 或 舍去 ,
所以直线PQ的方程为 ,因此直线PQ经过定点
19.【详解】(1) ,故 ,
;
(2)(i)因为 ,而 为公差不为0的等差数列,所以
为非零常数.设 .可得 .并且 .
所以 .用此类推,得 ,因为 为常数,所以当 时,,即 :当 时, ,即 .
所以 不存在,即 无零点.
(ii) ,所以 .
对于函数 ,即 ,因为 ,所以
,以此类推,得
,
令 ,由等比数列求和公式得
,
因此 .
时, ,即 ,所以 .