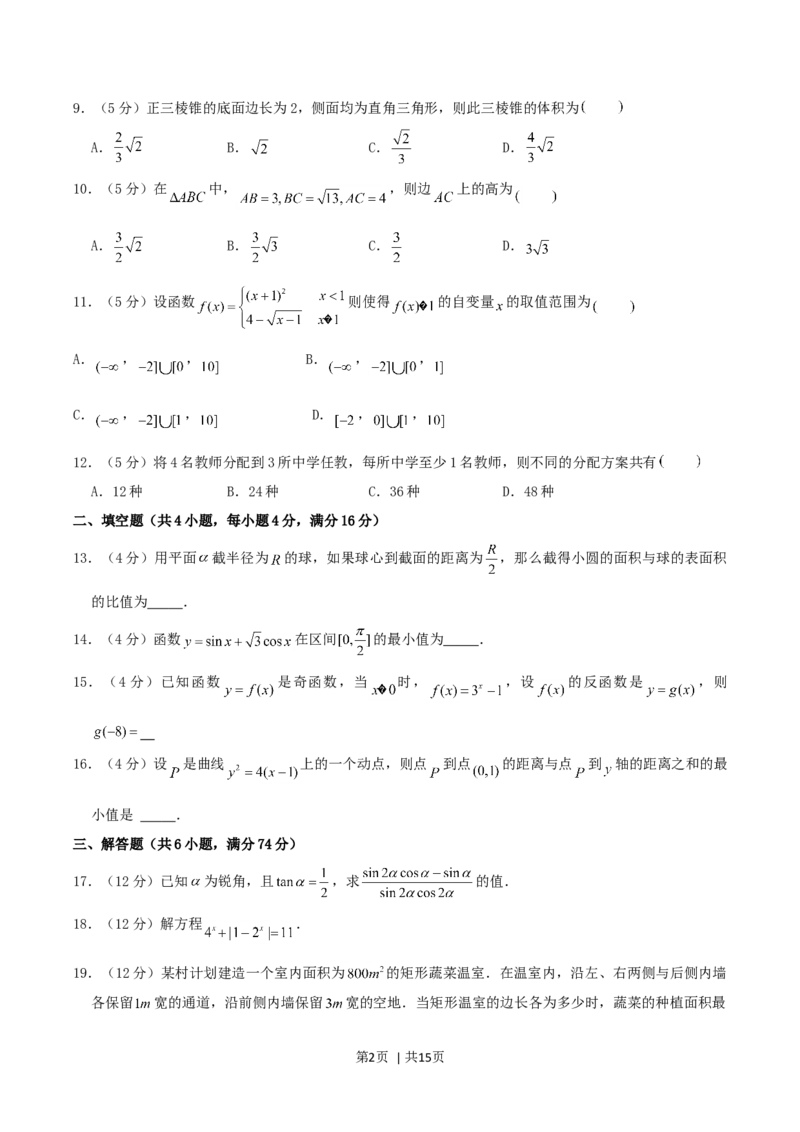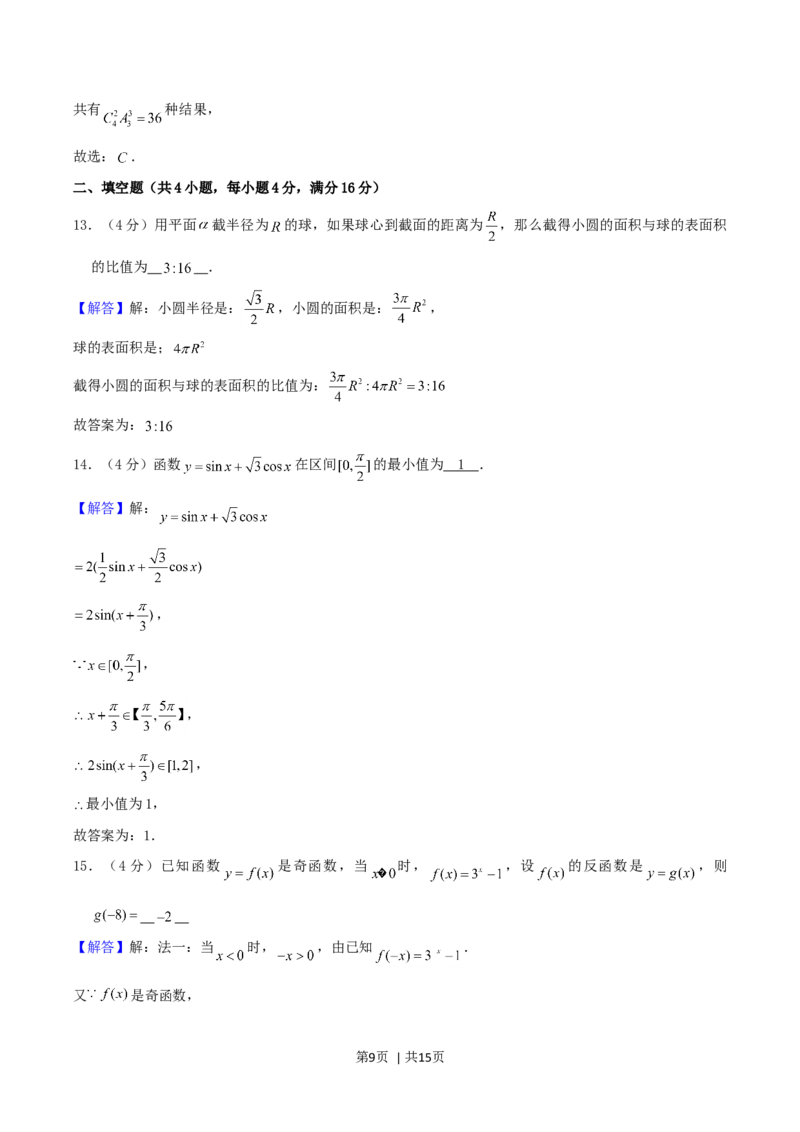文档内容
2004 年陕西高考理科数学真题及答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)设集合 , , , , , ,则集
合 中元素的个数为
A.1 B.2 C.3 D.4
2.(5分)函数 的最小正周期是
A. B. C. D.
3.(5分)设数列 是等差数列, , , 是数列 的前 项和,则
A. B. C. D.
4.(5分)圆 在点 处的切线方程为
A. B. C. D.
5.(5分)函数 的定义域是
A. , , B. , ,
C. , , D. , ,
6.(5分)设复数 的幅角的主值为 ,虚部为 ,则
A. B. C. D.
7.(5分)设双曲线的焦点在 轴上,两条渐近线为 ,则双曲线的离心率
A.5 B. C. D.
8.(5分)不等式 的解集为
A. B. , ,
C. D. , ,
第1页 | 共15页9.(5分)正三棱锥的底面边长为2,侧面均为直角三角形,则此三棱锥的体积为
A. B. C. D.
10.(5分)在 中, ,则边 上的高为
A. B. C. D.
11.(5分)设函数 则使得 的自变量 的取值范围为
A. , , B. , ,
C. , , D. , ,
12.(5分)将4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有
A.12种 B.24种 C.36种 D.48种
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)用平面 截半径为 的球,如果球心到截面的距离为 ,那么截得小圆的面积与球的表面积
的比值为 .
14.(4分)函数 在区间 的最小值为 .
15.(4分)已知函数 是奇函数,当 时, ,设 的反函数是 ,则
16.(4分)设 是曲线 上的一个动点,则点 到点 的距离与点 到 轴的距离之和的最
小值是 .
三、解答题(共6小题,满分74分)
17.(12分)已知 为锐角,且 ,求 的值.
18.(12分)解方程 .
19.(12分)某村计划建造一个室内面积为 的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙
各保留 宽的通道,沿前侧内墙保留 宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最
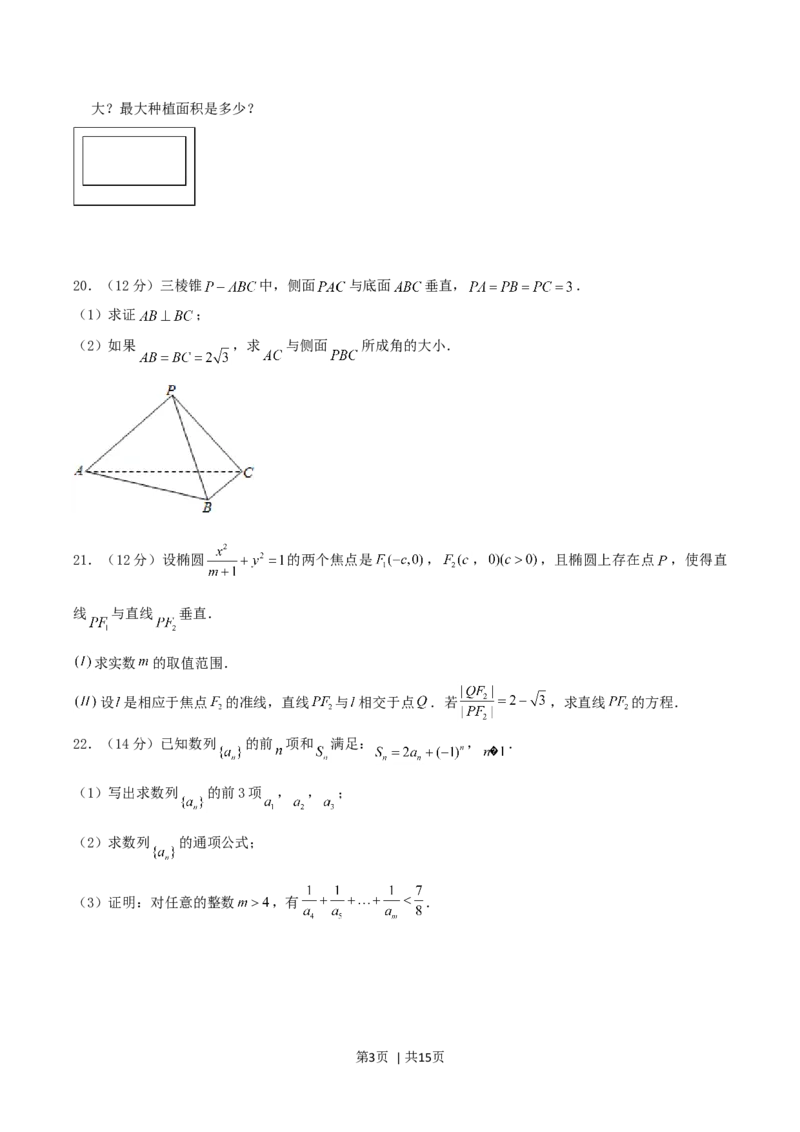
第2页 | 共15页大?最大种植面积是多少?
20.(12分)三棱锥 中,侧面 与底面 垂直, .
(1)求证 ;
(2)如果 ,求 与侧面 所成角的大小.
21.(12分)设椭圆 的两个焦点是 , , ,且椭圆上存在点 ,使得直
线 与直线 垂直.
求实数 的取值范围.
设 是相应于焦点 的准线,直线 与 相交于点 .若 ,求直线 的方程.
22.(14分)已知数列 的前 项和 满足: , .
(1)写出求数列 的前3项 , , ;
(2)求数列 的通项公式;
(3)证明:对任意的整数 ,有 .
第3页 | 共15页2004年高考数学试卷(理科)
参考答案与试题解析
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)设集合 , , , , , ,则集
合 中元素的个数为
A.1 B.2 C.3 D.4
【解答】 解:根据题意, , , , ,
将 代入 ,
得 ,△ ,
所以方程组有两组解,
因此集合 中元素的个数为2个,
故选: .
2.(5分)函数 的最小正周期是
A. B. C. D.
【解答】解:对于 , ,
函数 是函数 轴上方的图象不动将 轴下方的图象向上对折得到的,如图示,故
,
故选: .
第4页 | 共15页3.(5分)设数列 是等差数列, , , 是数列 的前 项和,则
A. B. C. D.
【解答】解: ,
,
得 ,
故选: .
4.(5分)圆 在点 处的切线方程为
A. B. C. D.
【解答】解:法一:
.
该二次方程应有两相等实根,即△ ,解得 .
,
即 .
法二:
点 在圆 上,
第5页 | 共15页点 为切点,从而圆心与 的连线应与切线垂直.
又 圆心为 , .
解得 ,
切线方程为 .
故选: .
5.(5分)函数 的定义域是
A. , , B. , ,
C. , , D. , ,
【解答】解:
或 .
的定义域为 , , .
故选: .
6.(5分)设复数 的幅角的主值为 ,虚部为 ,则
A. B. C. D.
【解答】解: 复数 的幅角的主值为
设复数
虚部为
第6页 | 共15页故选: .
7.(5分)设双曲线的焦点在 轴上,两条渐近线为 ,则双曲线的离心率
A.5 B. C. D.
【解答】解:依题意可知 ,求得
故选: .
8.(5分)不等式 的解集为
A. B. , ,
C. D. , ,
【解答】解:
即 即 ,
解得 ,即 , ,
解法二:
解得 , ,
故选: .
9.(5分)正三棱锥的底面边长为2,侧面均为直角三角形,则此三棱锥的体积为
A. B. C. D.
【解答】解:由题意正三棱锥的底面边长为2,侧面均为直角三角形,
可知:侧棱长为 ,三条侧棱两两垂直,
第7页 | 共15页所以此三棱锥的体积为
故选: .
10.(5分)在 中, ,则边 上的高为
A. B. C. D.
【解答】解:由点 向 作垂线,交点为 .
设 ,则 ,
,解得
故选: .
11.(5分)设函数 则使得 的自变量 的取值范围为
A. , , B. , , C. , , D.
, ,
【解答】解: 等价于 解得: 或 .
或 解得:
综上所述, 或 .
故选: .
12.(5分)将4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有
A.12种 B.24种 C.36种 D.48种
【解答】解:将4名教师分配到3所中学任教,每所中学至少1名教师,
只有一种结果1,1,2,
首先从4个人中选2个作为一个元素,
使它与其他两个元素在一起进行排列,
第8页 | 共15页共有 种结果,
故选: .
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)用平面 截半径为 的球,如果球心到截面的距离为 ,那么截得小圆的面积与球的表面积
的比值为 .
【解答】解:小圆半径是: ,小圆的面积是: ,
球的表面积是;
截得小圆的面积与球的表面积的比值为:
故答案为:
14.(4分)函数 在区间 的最小值为 1 .
【解答】解:
,
,
,
,
最小值为1,
故答案为:1.
15.(4分)已知函数 是奇函数,当 时, ,设 的反函数是 ,则
【解答】解:法一:当 时, ,由已知 .
又 是奇函数,
第9页 | 共15页,即 .
.
.
法二:当 时, ,由已知 .
又 是奇函数,
,即 .
.根据反函数定义
令 得 ,即:
答案为:
16.(4分)设 是曲线 上的一个动点,则点 到点 的距离与点 到 轴的距离之和的最
小值是 .
【解答】解: 的图象是以 轴为准线, 为焦点的抛物线, 当点 为 点与 点的
连线与抛物线的交点时,距离和最小,
最小值为: .
故答案为: .
三、解答题(共6小题,满分74分)
17.(12分)已知 为锐角,且 ,求 的值.
第10页 | 共15页【解答】解: , 为锐角
.
18.(12分)解方程 .
【解答】解:当 时,有: ,
化简得: ,
解之得: 或 (舍去).
又 得 ,故 不可能舍去.
当 时,有: ,
化简得: ,
解之得: 或 (舍去)
, ,
综上可得,原方程的解为 .
19.(12分)某村计划建造一个室内面积为 的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙
各保留 宽的通道,沿前侧内墙保留 宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最
大?最大种植面积是多少?
【解答】解:设矩形温室的左侧边长为 ,后侧边长为 ,则 .
蔬菜的种植面积
.
所以
当且仅当 ,即 , 时,
第11页 | 共15页.
答:当矩形温室的左侧边长为 ,后侧边长为 时,蔬菜的种植面积最大,最大种植面积为 .
20.(12分)三棱锥 中,侧面 与底面 垂直, .
(1)求证 ;
(2)如果 ,求 与侧面 所成角的大小.
【解答】解:(1)证明:取 中点 ,连接 、 .
又 侧面 底面
底面
又
为直角三角形
(2)解:取 的中点为 ,连接 , ,所以有 ,
由(1)有 平面 , ,由三垂线定理得
平面 平面 ,又 .
是等腰直角三角形,取 的中点 ,连接 ,
则 ,又 平面 平面 ,且交线是 , 平面
即为 与平面 所成的角
.
故 与平面 所成的角为 .
第12页 | 共15页21.(12分)设椭圆 的两个焦点是 , , ,且椭圆上存在点 ,使得直
线 与直线 垂直.
求实数 的取值范围.
设 是相应于焦点 的准线,直线 与 相交于点 .若 ,求直线 的方程.
【解答】解:(1) 直线 直线
以 为圆心以 为半径的圆: 与椭圆: 有交点.即 有解
又
(2)设 , ,直线 方程为: ,
直线 的方程为: ,
准线 的方程为 ,
设点 的坐标为 , ,则 ,
②
解可得 ,从而 , , ,
第13页 | 共15页则 或 ,
得到 的方程 或 .
22.(14分)已知数列 的前 项和 满足: , .
(1)写出求数列 的前3项 , , ;
(2)求数列 的通项公式;
(3)证明:对任意的整数 ,有 .
【解答】解:(1)当 时,有: ;
当 时,有: ;
当 时,有: ;
综上可知 , , ;
(2)由已知得:
化简得:
上式可化为:
故数列 是以 为首项,公比为2的等比数列.
故
数列 的通项公式为: .
第14页 | 共15页(3)由已知得:
故 .
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/4/23 19:41:17;用户:James;邮箱:15399095293;学号:8796782
第15页 | 共15页