重庆市南开中学高2024高三第六次质量检测数学试题_2024年2月_01每日更新_21号_2024届重庆市南开中学高三第六次质量检测_重庆市南开中学高2024届高三第六次质量检测数学

重庆市高2024届高三第六次质量检测 数 学 试 题 2024.2 命审单位: 重庆南开中学 注意事项: 1. 本试卷满分 150 分, 考试时间120 分钟。 2.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 3.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改 动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写 在本试卷上无效。 4. 考试结束后，将本试卷和答题卡一并交回。 一、单项选择题: 本题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中, 只有 一项符合题目要求. 1.已知集合 A{x|1 x3,B xN*x2 3x0},则 AB A. {x|0 x3} B. {x|1 x3}   C. 1,2   D. 0,1,2 2.已知复数 z 满足  z1  i2z1,则复数z 在复平面内对应的点位于 A.第一象限 B.第二象限 C.第三象限 D.第四象限            3.已知非零向量 a,b 满足 b 2 3 a ,且 a  3ab ,则 a 与 b 的夹角为  A. 6  B. 3 2 c. 3 5 D. 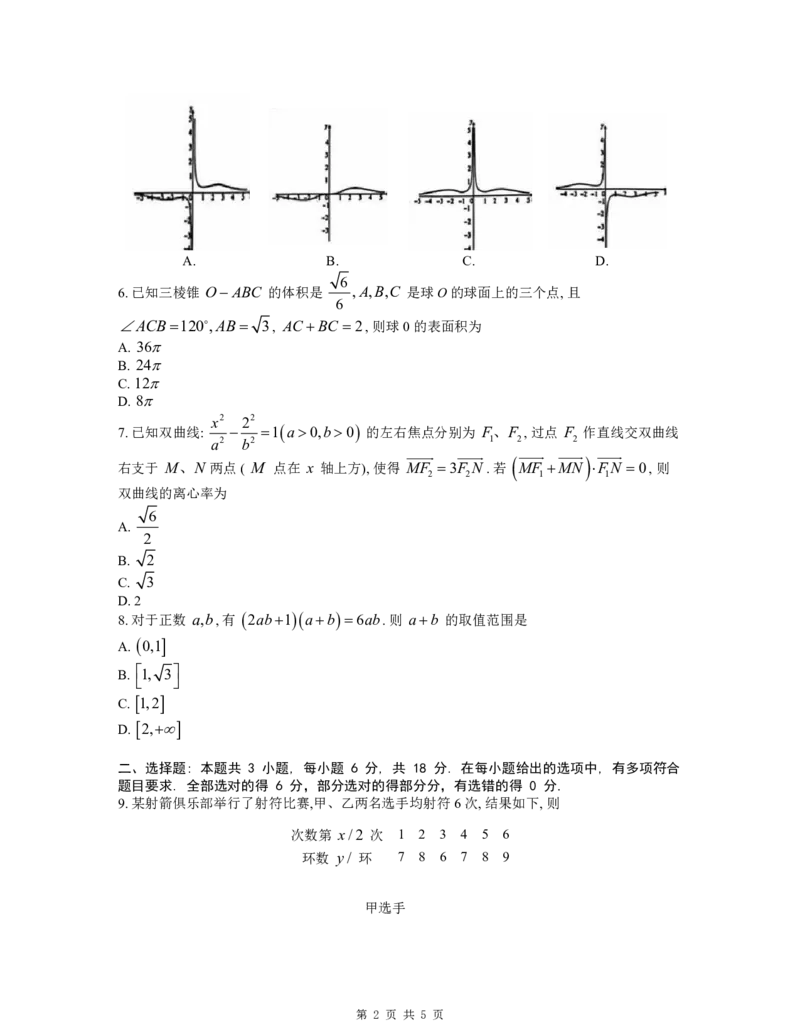6 4.已知等差数列  a  的前 n 项和为 S ,满足 a 3,3S 4S 12,则 a 等于 n n 2 4 3 1 A.10 B.11 C.12 D.13  1  ex x2  sin2x  2  5.函数 f  x  的部分图像大致为 e2x 1 第 1 页 共 5 页A. B. C. D. 6 6.已知三棱锥 OABC 的体积是 ,A,B,C 是球O的球面上的三个点,且 6 ACB120,AB 3, ACBC 2,则球0的表面积为 A. 36 B. 24 C. 12 D. 8 x2 22 7.已知双曲线:  1  a0,b0  的左右焦点分别为 F、F ,过点 F 作直线交双曲线 a2 b2 1 2 2        右支于 M、N 两点( M 点在 x 轴上方),使得 MF 3F N .若 MF MN FN  0,则 2 2 1 1 双曲线的离心率为 6 A. 2 B. 2 C. 3 D.2 8.对于正数 a,b,有  2ab1  ab 6ab.则 ab 的取值范围是   A. 0,1 B. 1, 3     C. 1,2 D.  2, 二、选择题: 本题共 3 小题, 每小题 6 分, 共 18 分. 在每小题给出的选项中, 有多项符合 题目要求. 全部选对的得 6 分，部分选对的得部分分，有选错的得 0 分. 9.某射箭俱乐部举行了射符比赛,甲、乙两名选手均射符6次,结果如下,则 次数第 x/2 次 1 2 3 4 5 6 环数 y/ 环 7 8 6 7 8 9 甲选手 第 2 页 共 5 页次数第 x/2 次 1 2 3 4 5 6 环数 y/ 环 9 7 6 8 6 6 乙选手 A.甲选手射击环数的第九十百分位数为8.5 B.甲选手射击环数的平均数比乙选手的大 C.从发挥的稳定性上看，甲选手优于乙选手 D.用最小二乘法求得甲选手环数 y 关于次数 x 的经验回归方程为 y 0.3xaˆ,则 aˆ 6.45 10.已知一圆锥的底面半径为 3,其侧面展开图是圆心角为 3 的扇形, A,B 为底面圆的一 条直径上的两个端点,则 A.该圆维的母线长为2 B.该圆锥的体积为 C.从 A 点经过圆锥的表面到达 B 点的最短距离为 2 3 D.过该圆锥的顶点作圆锥的截面,则截面面积的最大值为 3 11.平面解析几何的结论很多可以推广到空间中,如:  (1)平面上,过点 Q  x ,y  ,且以 m a,b  ab0  为方向向量的平面直线 l 的方程为 0 0 xx y y  0  0 ;在空间中,过点 Q  x ,y ,z  ,且以 m a,b,c  abc0  为方向向量的空 a b 0 0 0 xx y y zz 间直线 l 的方程为 0  0  0 . a b c  (2)平面上,过点 Q  x ,y  ,且以 n  m,n  mn0  为法向量的直线 l 的方程为 0 0  m  xx  n  y y 0;空间中,过点 Q  x ,y ,z  ,且以 n  m,n, p  mnp 0  为法 0 0 0 0 0 向量的平面 的方程为 m  xx n  y y  p  zz 0. 0 0 0 现已知平面:2x3y4z 5,平面 2x y 10 :x2y2z 0,l : ,l :6x4y13z1,则 1 yz 1 2 A. l // 1 B.// C. l  1 D. h  2 三、填空题: 本题共 3 小题, 每小题 5 分, 共 15 分. 12.已知圆 C:x2  y2 2x4y30 .直线 l:mx2ym20,若直线 l 与圆 C 交于 A,B 两点,则 AB 的最小值为_________. 13.2024年伊始，随着“广西沙糖桔”“马铃薯公主”等热梗不断 爆出，哈尔滨火爆出圈,成为旅游城市中的“顶流”。某班级五位 同学也准备共赴一场冰雪之约，制定了“南方小土豆，勇闯哈尔滨” 的出游计划，这五位同学准备在行程第一天圣索菲亚数堂,冰雪大世 第 3 页 共 5 页界，中央大街三个景点中选择一个去游玩,已知每个景点至少有一位同学会选.五位同学都会进 行选择并且只能选择其中一个景点,若学生甲和学生乙准备选同一个景点.则不同的选法种数是 ________. 14.设 f  x  是定义在 R 上的单调增函数,且满足 f 1x  f  x 7,若对于任意非零   1 1 实数 x 都有 f f  x  x 24.则 f  2024   f  x 3 x  ________. 四、解答题: 本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤. 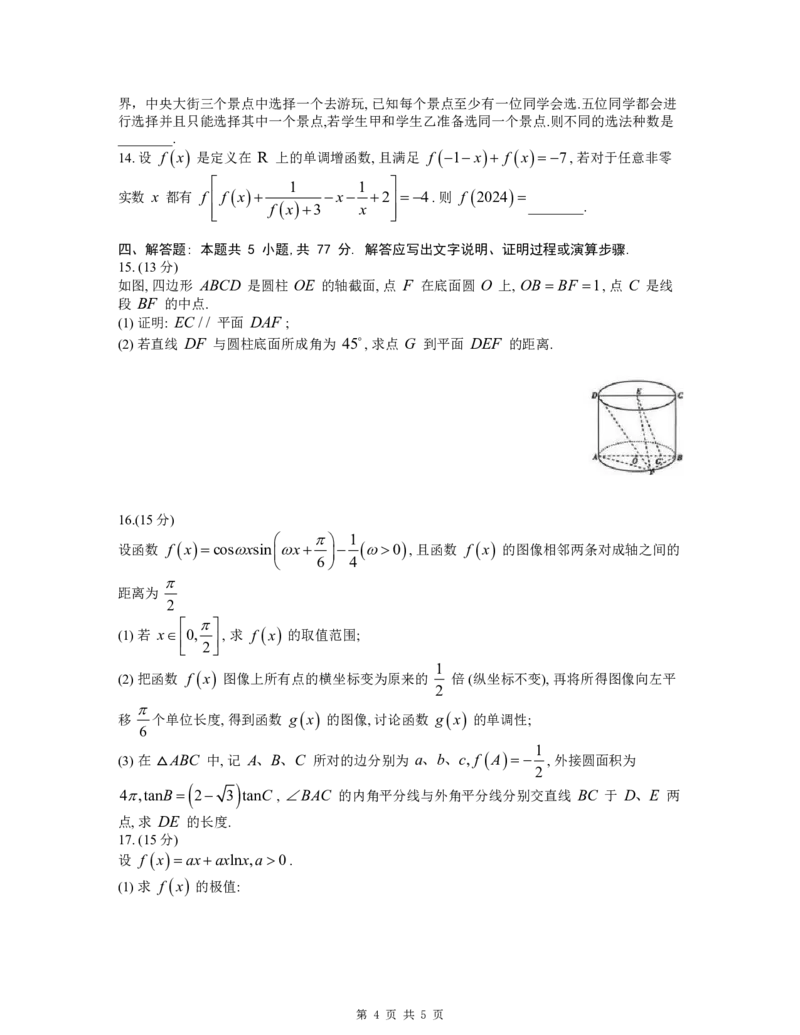15.(13分) 如图,四边形 ABCD 是圆柱 OE 的轴截面,点 F 在底面圆 O 上, OB  BF 1,点 C 是线 段 BF 的中点. (1)证明: EC// 平面 DAF ; (2)若直线 DF 与圆柱底面所成角为 45,求点 G 到平面 DEF 的距离. 16.(15分)   1 设函数 f  x cosxsin x   0  ,且函数 f  x  的图像相邻两条对成轴之间的  6 4  距离为 2   (1)若 x  0, ,求 f  x  的取值范围;  2 1 (2)把函数 f  x  图像上所有点的横坐标变为原来的 倍(纵坐标不变),再将所得图像向左平 2  移 个单位长度,得到函数 g  x  的图像,讨论函数 g  x  的单调性; 6 1 (3)在 ABC 中,记 A、B、C 所对的边分别为 a、b、c, f  A  ,外接圆面积为 2   4,tanB  2 3 tanC , BAC 的内角平分线与外角平分线分别交直线 BC 于 D、E 两 点,求 DE 的长度. 17.(15分) 设 f  x axaxlnx,a 0. (1)求 f  x  的极值: 第 4 页 共 5 页1  (2)若对于 x  , .存 f  x e2x 恒成立,求 a 的最大值. 2  18.(17分) 1 已知定点 A  1,0  ,B 1,0  .若动点 P 到 A  1,0  与到定直线 l :x4 的距离之比为 . 1 2 (1)求动点 P 的轨迹 C 的方程; (2)过点 B 作直线 l 交 C 于 M、N 两点( M 点在 x 轴的上方),过点 M 作 l 的垂线,垂 2 1 足为 Q.是否存在点 P,使得四边形 MNPQ 为荾形?若存在,请求出此时 l 的斜率;若不存在, 2 请说明理由; (3)若动点 P 在第一象限,延长 PA、PB 交 C 于 R、K 两点,求 PAK 与 PBR 内切圆 半径的差的绝对值的最大值. 19.(17分) 已知正项数列  a  满足: 4a2 a 5a a2 4a 5a 0,nN*,a 2. n n1 n n1 n n n1 1 1 (1)设 b a  ,试证明  b  为等比数列; n n a n n b 50 (2)设 c  n ,试证明 c c c  ; n b2 4 1 2 n 9 n 1 1 1 (3)设 A a2 a2 a2,B    ,是否存在 n 使得 32n2 A B  为整 n 1 2 n n a2 a2 a2 n n 1 2 n 数?如果存在,则求出 n 应满足的条件;若不存在,请给出理由. 第 5 页 共 5 页