文档内容
卓越联盟 2025-2026 学年第⼀学期⾼⼆第三次⽉考
数学试题
注意事项:
1. 答题前,考⽣务必将⾃⼰的姓名、考⽣号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每⼩题答案后,⽤铅笔把答题卡上对应题⽬的答案标号涂⿊ .如需改
动, ⽤橡⽪擦⼲净后, 再选涂其他答案标号.回答⾮选择题时,将答案写在答题卡上.写在本试
卷上 ⽆效.
3. 考试结束后,将本试卷和答题卡⼀并交回.
⼀ 、选择题:本题共 8 ⼩题,每⼩题 5 分,共 40 分. 在每⼩题给出的四个选项中, 只有⼀
项 是符合题⽬要求的.
1. 直线 的倾斜角为 ( )
A. B. C. D.
2
2. 数列 , , , , … 通项公式可能为 ( )
A. B. C. D.
3. 若 构成空间的⼀个基底 ,则下列向量不共⾯的是 ( )
A a B a E C a D
. , , . , , . , , . ,
(-3,7
4. 圆⼼为 , 半径为 4 的圆的标准⽅程为 ( )
A B.
C. D.
5. 若数列
的通项公式为 , 则 ta,} 的最⼩项和最⼤项分别为
( )
A.
,
C.
B , , D ,
6. 某体育场⼀角看台的座位共有⼗⼀排 ,从第⼀排到第⼗⼀排的座位数成等差数列, 且前两排的座位数与
第 1页/共 4页·
后两排的座位数之和为 80 ,则第六排的座位数为 ( )
A. 16 B. 18 C. 20 D. 22
7. 已知等差数列 的前 n 项和为s,
,
S1+ag=96
,
则s;= ( )
A 102 B 1(4 C 106 D 1(8
. . . .
8. 已知等⽐数列 前 n 项积为 , 0l , 且 T>1 ,则 n 的最⼩值为 ( )
A. 16 B. 15 C. 14 D. 13
⼆ 、选择题:本题共 3 ⼩题,每⼩题 6 分,共 18 分.在每⼩题给出的选项中,有多项符合题
⽬ 要求.全部选对的得 6 分, 部分选对的得部分分, 有选错的得 0 分.
9. ⻓轴⻓为 6, 离⼼率为 的椭圆的标准⽅程可能为 ( )
A. B. C. D.
n s, d u,: S,=s s
10. 已知等差数列 的各项均不为 0, 的前 项和为 ,公差为 , 且 , ,
则 ( )
A. S=S: B. d >0 C. S, 的最⼤值为 D. S, 的最⼩值为
11. 已知数列 lar) 的前 n 项和为 s.
, ,
且 2a, a⃞a⃞(cid:2)-3a,+9a=0
,
则 ( )
A. az=10ay B. 是等⽐数列
C. 数列 的前 100 项和为 5050 D.
三、填空题:本题共 3 ⼩题, 每⼩题 5 分, 共 15 分.
12. 向量a=(1,1,3)在向量b=(-1,-2,2) 上的投影向量的坐标为 .
13. 已知数列 的前 n 项和为s, , 且 s,=-n2-4n ,则 的通项公式为 .
14. 在数列 ta) 和 1e 中
, ,
b,=2"
,
且不等式 a,+b,>入 对任意 恒成⽴
,
则 :
的取
值范围为 .
四、解答题:本题共 5 ⼩题, 共 77 分.解答应写出⽂字说明、证明过程或演算步骤.
15. 在等差数列 中, , .
·
第 2页/共 4页(1) 的通项公式;
求
为正项等⽐数列, 且 , 求b; .
(2) ,
若
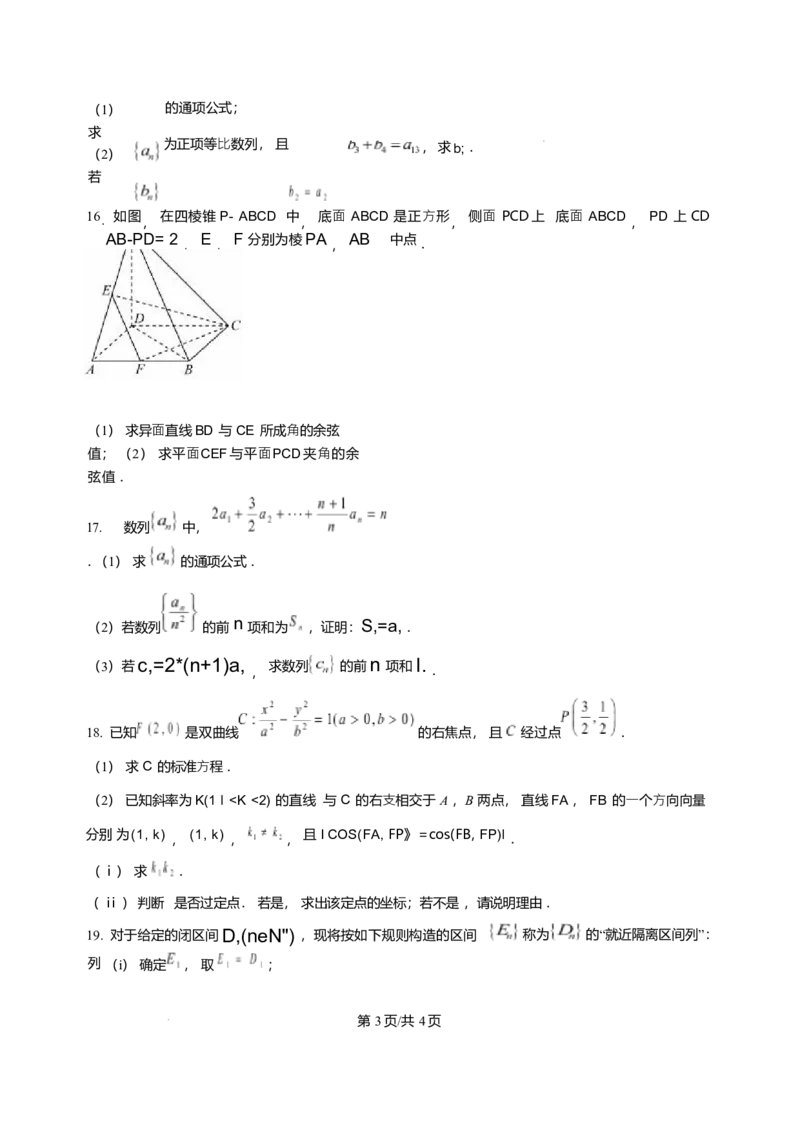
16. 如图
,
在四棱锥P- ABCD 中
,
底⾯ ABCD 是正⽅形
,
侧⾯ PCD上 底⾯ ABCD
,
PD 上CD
AB-PD= 2 E F 分别为棱PA AB 中点
, , , , .
(1) 求异⾯直线BD 与 CE 所成⻆的余弦
值; (2) 求平⾯CEF与平⾯PCD夹⻆的余
弦值 .
17. 数列 中,
. (1) 求 的通项公式 .
(2)若数列 的前 n 项和为 ,证明:S,=a, .
(3)若 c,=2*(n+1)a, 求数列 的前 n 项和 I.
, .
18. 已知 是双曲线 的右焦点, 且 经过点 .
(1) 求 C 的标准⽅程 .
(2) 已知斜率为K(1 l o
; 当 时, , 是递减数列 ,则 的最⼤项为 .
故选:B.
6. 某体育场⼀⻆看台的座位共有⼗⼀排 ,从第⼀排到第⼗⼀排的座位数成等差数列, 且前两排的座位数
与 后两排的座位数之和为 80 ,则第六排的座位数为 ( )
A. 16 B. 18 C. 20 D. 22
【答案】
C 【解
析】
【分析】 根据题意 ,利⽤等差数列的性质即可求解.
【详解】 假设从第⼀排到第⼗⼀排的座位数成等差数列 ,则
a1+a+a2+ao=4a=80 a=20
, 所以 得
, .
故选:C.
7. 已知等差数列 前 n 项和为s,
,
S1+ag=96
,
则 s;= ( )
A 102 B 1(4 C 106 D 1(8
. . . .
【答案】
B 【解
析】
【分析】根据等差数列的前 n 项和公式及通项公式列⽅程可得到⼀个关于u,d 的等式,整体代⼊s;的表
达 式中即可.
【详解】 设等差数列 的公差为 ,
由 ,得
, 所以 .
故选:B.
第 3页/共 16页n 0l >l n
8. 已知等⽐数列 的前 项积为 , , , 且 ,则 的最⼩值为 ( )
A. 16 B. 15 C. 14 D. 13
【答案】
C 【解
析】
【分析】 由题意可得 是递增数列且0l , 得 , 则 .
01
.
故 n 的最⼩值为
14. 故选:C.
⼆ 、选择题:本题共 3 ⼩题,每⼩题 6 分,共 18 分.在每⼩题给出的选项中,有多项符合题
⽬ 要求.全部选对的得 6 分, 部分选对的得部分分, 有选错的得 0 分.
9. ⻓轴⻓为 6, 离⼼率为 的椭圆的标准⽅程可能为 ( )
A. B. C. D.
【答案】
AC 【解
析】
【分析】 先根据已知条件求出a,b,c , 再根据焦点的位置分类讨
论. 【详解】 设椭圆的⻓轴⻓为2a, 短轴⻓为2b ,焦距为2c .
由 得 ,
所以椭圆的标准⽅程可能为 , .
·
第 4页/共 16页故选:AC.
10. 已知等差数列 的各项均不为 0, 的前 n 项和为s, ,公差为 d , 且 u,0 ; A 选 项 ,
S;-S;=5(2a+19d)=0 A 正确;CD 选项 得到 O0 B 正
, , , ,
确;
A 选项 S=5a,+10d, s;=15a,+105d 则 s;-s;=10a+95d=5(2a,+19d)=0
, ,
S=S:
故 A 正确;
, ,
2a+19d=0 a,+9d<0 a+10d>0
CD 选项 由于 故 ⼜ 所以
, , , , , ,
即 , , 故S, 的最⼩值为 sn , ⽆最⼤值 ,C 错误 ,D
正确 . 故选:ABD
11. 已知数列
lar)
的前
n
项和为
s.
, ,
且
2a, a⃞a⃞(cid:2)-3a,+9a=0
,
则 ( )
A. B. 是等⽐数列
C. 数列 的前 100 项和为 5050 D.
【答案】
ACD 【解
析】
【分析】变形得到 , 是公⽐为 3 的等⽐数列 ,从⽽得到 ,A 选
项,
第 5页/共 16页r-m
求出 ;B 选项 ,根据等⽐数列的定义进⾏判断;C 选项, ,从⽽利⽤等差数
列 求和公式得到答案;D 选项 ,放缩得到 , 由等⽐数列求和公式可得 .
【详解】 由 ,得 ,则 ,
所以 ,所以 是⾸项为 , 公⽐为 3 的等⽐数列
. 由 ,得 ,
n,-a a
A 选项, , ,所以 ,A 正确;
B 选项, 因为 , 不是常数 ,所以 不是等⽐数列 ,B 错
误; C 选项, 因为 ,所以 是等差数列,
所以 的前 100 项和为 5050 ,C 正确;
D 选项, 由 ,得 ,得
n=l
, 所以 ( 当且仅当 时, 等号成⽴).
故
, D 正确.
故选:ACD
三、填空题:本题共 3 ⼩题, 每⼩题 5 分, 共 15 分.
第 6页/共 16页·
12. 向量 在向量=(-1,-2,2) 上的投影向量的坐标为 .
【答案】
【解析】
【分析】 利⽤公式 计算即可.
b=(-1,-2,2)
【详解】 因为向量 向量
, ,
所以d-b=1x(-1)+1x(-2)+3x2=3
,
所以 在 上的投影向量的坐标为 .
,
故答案为: .
n
13. 已知数列 的前 项和为s, , 且 s,=-n2-4n ,则 的通项公式为0,- .
【答案】 -2n - 3
【解析】
【分析】 根据 求解即可 .
【详解】 当n 2 2 时,
. 当 n=l 时
,
a,=s=-5=-2-3
.
.
故答案为: -2n -3
.
14. 在数列 和 中 b,=2" 且不等式a,+b,>入对任意n e N, 恒成⽴ 则d 的取
, , ,
值范围为 .
【答案】
【解析】
第 7页/共 16页【分析】 构造函数 ,分析函数的单调性, 求出函数的最⼩值, 进⽽
求
出 的取值范围.
【详解】 设 ,
则
. 易得函数 为增函数 .
f(7)f(7
由 得
, , ,
:
所以 , 故 的取值范围为 .
,
故答案为:
四、解答题:本题共 5 ⼩题, 共 77 分.解答应写出⽂字说明、证明过程或演算步骤.
15. 在等差数列 中, ,
. (1) 求 的通项公式;
(2)若 为正项等⽐数列, 且 , b+b,=as , 求
b; . 【答案】(1) a,=3n-3
(2) 81
【解析】
【分析】(1) 由题⽬列⽅程组求出ap=0, d=3,所以a,=3n-3 .
(2) 结合( 1) 结果列⽅程组求出b,- l , g=3 , 所以 b;=hq'=81 .
【⼩问 1 详解】
设 的公差为 . 得
由 所以a,=3n-3
【⼩问 2 详解】
第 8页/共 16页设 的公⽐为 . 由
q=3 q=-4
得 ( 舍去)
,
bz=bg'=81
所以
. .
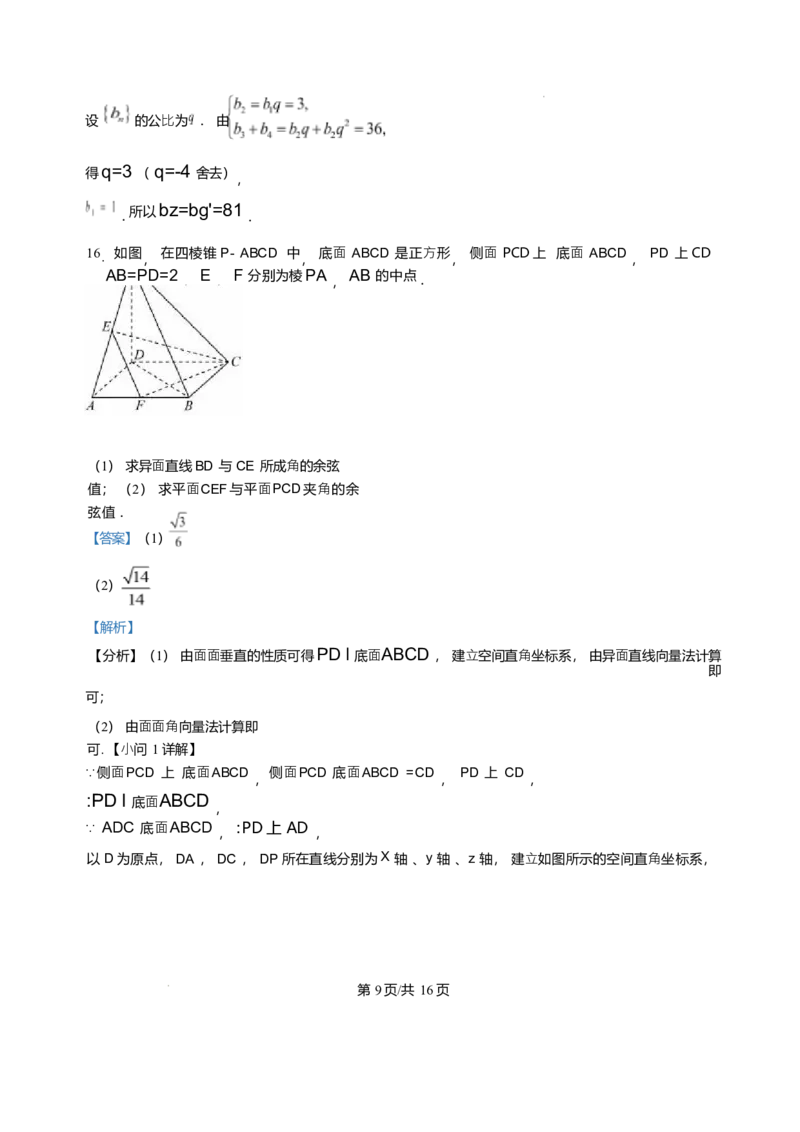
16. 如图
,
在四棱锥P- ABCD 中
,
底⾯ ABCD 是正⽅形
,
侧⾯ PCD上 底⾯ ABCD
,
PD 上CD
AB=PD=2 E F 分别为棱PA AB 的中点
, , , , .
(1) 求异⾯直线BD 与 CE 所成⻆的余弦
值; (2) 求平⾯CEF与平⾯PCD夹⻆的余
弦值 .
【答案】(1)
(2)
【解析】
【分析】(1) 由⾯⾯垂直的性质可得PD l 底⾯ABCD , 建⽴空间直⻆坐标系, 由异⾯直线向量法计算
即
可;
(2) 由⾯⾯⻆向量法计算即
可. 【⼩问 1 详解】
∵侧⾯PCD 上 底⾯ABCD 侧⾯PCD 底⾯ABCD =CD PD 上 CD
, , ,
:PD l ABCD
底⾯
,
∵ ADC 底⾯ABCD :PD上 AD
, ,
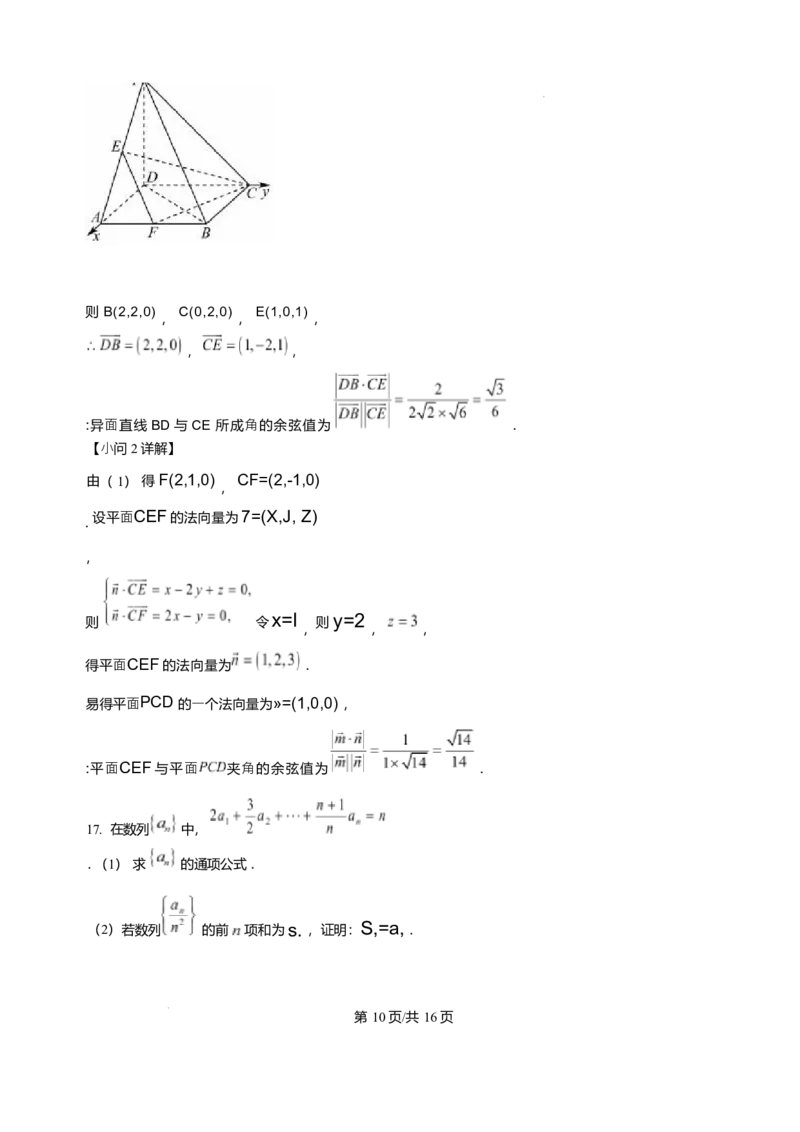
以 D为原点, DA , DC , DP 所在直线分别为X 轴 、y 轴 、z 轴, 建⽴如图所示的空间直⻆坐标系,
第 9页/共 16页则 B(2,2,0) C(0,2,0) E(1,0,1)
, , ,
, ,
:异⾯直线BD 与CE 所成⻆的余弦值为 .
【⼩问 2 详解】
由( 1) 得 F(2,1,0) CF=(2,-1,0)
,
设平⾯CEF的法向量为7=(X,J, Z)
.
,
x=l y=2
则 令 则
, , ,
得平⾯CEF的法向量为 .
易得平⾯PCD 的⼀个法向量为»=(1,0,0) ,
:平⾯CEF与平⾯ 夹⻆的余弦值为 .
17. 在数列 中,
. (1) 求 的通项公式 .
(2)若数列 的前 项和为s. ,证明: S,=a, .
第 10页/共 16页c,=2"(n+1)a, n
(3)若 求数列 的前 项和
,
I.
【答案】(1)
.
第 10页/共 16页T,=(n-1)x2"+4
(2) 证明⻅解析 ( 3)
【解析】
【分析】 ( 1)根据递推公式进⾏整理得到数列通项公式即可;
(2)通过对所需要的数列的通项公式进⾏裂项, 运⽤裂项相消的⽅法求和进⾏证明即
可; (3)运⽤错位相减的⽅法求解即可.
【⼩问 1 详解】
n=l
当 时
,
, 得
.
当n 之2
时 ,
,
,
两式相减得 ,则
n=l
. 当 时, 符合上式
, 所以 .
【⼩问 2 详解】
证明: 由( 1) 得 ,
所以 ,
s,=a
故
.
【⼩问 3 详解】
c,=2(n+1)a,=nx2""
由( 1) 得
,
T,=1x2+2x2'+…+(n-I)x2"+nx2"
则
,
,
所以
第 11页/共 16页,
T,=(n-1)x2"+4
所以
.
18. 已知 是双曲线 的右焦点, 且 经过点 .
(1) 求 C 的标准⽅程 .
(2) 已知斜率为K(l< K < 2) 的直线 与 C 的右⽀相交于 A ,B 两点, 直线FA , FB 的⼀个⽅向向量分
别
为(1, K) (1,K,) 且I COS(FA, FP》H COS(FB,
, , ,
FP)I . ( i ) 求 .
( ⅱ ) 判断 是否过定点. 若是, 求出该定点的坐标;若不是 ,请说明理由 .
【答案】(1)
(2)( i ) ; ( ⅱ ) 过定点(l,-1) .
【解析】
【分析】(1)根据条件列⽅程组求解;
(2)( i )根据数量积的定义化简 即可求出;
(k+m)'=l
( ⅱ ) 设直线 , 与双曲线⽅程联⽴ , 结合 ( i ) 可得出 , 再根
II 符合题意
. , , .
综上 l:y = kx+n = i(x-1)-I 所以 过定点(l,-I)
, , .
第 13页/共 16页19. 对于给定的闭区间D,(neN") ,现将按如下规则构造的区间列 称为 的“就近隔离区间
列”: (i) 确定 , 取 ;
(ii) 确定 ,若 D: 与 E 的交集为空集 ,则 E=D , 否则判断 D; 与 E 的交集是否为空集 ,若为空
集, 则 ,否则判断D; 与 的交集是否为空集 ,若为空集 ,则 , 以此类推 ,直
到找到 , 设 ;
(iii)确定E; ,若 与 E: 的交集为空集 ,则 ,否则判断 与 E: 的交集是否为空集 ,若
为 空集 ,则 , 以此类推, 直到找到 ,设 ;
(iv)依照(ii)(iii) 的⽅法依次确定E, EY, ,E, .
a=4, a:=4a, a=2am-a, D,-[a,,2a,], IE “
已知数列 满⾜ 区间 是 的 就近隔离
,
区间 列” .
(1) 求 的通项公式及EY,E, .
(2) 证明: v neN`,3keN",3·2"eE .
4'4'iE,, keN",n st;
(3) 设 是给定的正整数 求集合 中的元素之和
,
s(t) . 【答案】(1) a,=3n+l , ;
(2) 证明⻅解析; ( 3) .
【解析】
【分析】( 1) 根据给定的递推公式, 结合等差中项的意义求出通项公式, 再求出D,D,D,…,D, 即可
得
.
(2)令 , 利⽤ “就近隔离区间列” 的定义探求 , 求出数列 的通项 ,再⽐较⼤
得 ⼩
即可得证.
(3)按 的奇偶分类确定k 的最⼤取值, 再利⽤等⽐数列前 n 项和公式求出s(t) .
第 14页/共 16页【⼩问 1 详解】
a,+as=2a a
由 得 则 是等差数
, ,
列 设 的公差为 d 则 4d=az-aq=3a=12 解得 d=
, , ,
3 所以 a,=a+(n-I)d=3n+l
, ,
,
所以E=D=[4,8, E=D=[10,20], E;=D,=[22,44]
. 【⼩问 2 详解】
设 ,则 ,
meN", m>b, [a,,2a,]N[a,,2an]=D
设 且 则
,
即[3b,+1,6b,+2][Bm+1,6m+2]=z
, ,
3m+l>6b,+2
于是 即
, ,
⽽ me N' 则 m22b,+1 由 E, 的定义知
, , ,
即b.1=2b,+1 则
, , ,
b,+l=2" b,=2"-l
因此 是⾸项为 2, 公⽐为 2 的等⽐数列, , 即
E,=D,.,=[3:2"-2,32"-4]
, 则
,
⽽
,
w neN",3keN',3·2"eE
所以
. 【⼩问 3 详解】
4'eE, 32'-2 s234832""-4
由 得
,
当 n=l 时 4 4 22t 4 8 解得k=l ;
, , ,
n2 2 2""-(3·2"-2)=2"+2>0
当 时
, , ,
,
2k=n+2
, 即 则
,
,
·
第 15页/共 16页n t n
当 时 ,若 为奇数 ,则正整数 不存在;若 为偶数 ,则
, 因此当 为奇数时,
; 当 为偶数时,
,
所以
.
第 16页/共 16页