文档内容
2025-2026 学年度(上)阶段性考试(一)
高 2024 级 数学
考试时间:120 分钟 满分:150 分
一、单选题:本题共 8 个小题,每小题 5 分,共 40 分.在每小题给出的选项中,只有一项是符
合题目要求.
1. 我市某所高中每天至少用一个小时学习数学的学生共有 1200 人,其中一、二、三年级的人数比为
,要用分层随机抽样的方法从中抽取一个容量为 120 的样本,则应抽取的一年级学生的人数为(
)
A. 52 B. 48 C. 36 D. 24
【答案】C
【解析】
【分析】根据给定条件,利用分层抽样的抽样比列式计算即得.
【详解】依题意,应抽取的一年级学生的人数为 .
故选:C
2. 学校组织知识竞赛,某班 8 名学生的成绩(单位:分)分别是 65,60,75,78,86,84,90,94,则这
8 名学生成绩的 75%分位数是( )
A. 88 分 B. 84 分 C. 85 分 D. 90 分
【答案】A
【解析】
【分析】先对这 8 名学生的成绩按从小到大排列,然后用百分位数的定义求解即可.
【详解】8 名学生的成绩从小到大排列为:60,65,75,78,84,86,90,94,
因为 ,所以 75%分位数为第 6 个数和第 7 个数的平均数,
即 分.
故选:A.
3. 在一个实验中,某种豚鼠被感染 病毒的概率均为 ,现采用随机模拟方法估计三只豚鼠中被感染的
概率:先由计算机产生出 , 之间整数值的随机数,指定 1,2,3,4 表示被感染,5,6,7,8,9,0
表示没有被感染.经随机模拟产生了如下 20 组随机数:
192 907 966 925 271 932 812 458 569 683
第 1页/共 18页257 393 127 556 488 730 113 537 989 431
据此估计三只豚鼠都没被感染的概率为( )
A. 0.25 B. 0.4 C. 0.6 D. 0.75
【答案】A
【解析】
【分析】求得三只豚鼠都没有被感染的数量,结合题意,求解即可.
【详解】 组数据中,都不含 的数据有 5 个,分别是:907,966,569,556,989;
故三只豚鼠都没被感染的概率为: .
故选: .
4. 若 是两条不相同的直线, 是两个不同的平面,则下列命题中为真命题的是
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
【答案】C
【解析】
【分析】根据线面关系,对 A、B、D,都可能推出 l ,而 C,由面面平行的性质定理直接判断即可.
【详解】对 A、B、D,都可能推出 l ,所以不正确;
对 C,根据两个平面平行,则其中一个平面内的任意一条直线与另一个平面平行,所以 正确.
故选 C.
【点睛】本题考查了线面、面面平行的判定定理与性质定理的应用,考查了空间线面的位置关系,属于基
础题.
5. 已知 是空间的一个基底,则可以与向量 , 构成空间另一个基底的向量是
( )
A. B. C. D.
【答案】C
【解析】
【分析】根据空间基底、空间向量共面等知识确定正确答案.
第 2页/共 18页【详解】因为 ,
,
,
所以向量 , , 均与向量 , 共面,ABD 均不合题意;
假设 ,
则 ,无解,所以 与向量 , 不共面,C 符合题意.
故选:C
6. 向量 , , ,且 , ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】由向量的关系列式求解 , 的值,再运用向量的数乘及加法的坐标表示公式,结合向量的模公式
计算得出结果.
【详解】由 , ,则 ,解得 ,
, ,
,
故选:C.
7. 如图,某电子元件由 , , 三种部件组成,现将该电子元件应用到某研发设备中,经过反复测试,
, , 三种部件不能正常工作的概率分别为 , , ,各个部件是否正常工作相互独立,则该电子
元件能正常工作的概率是( )
第 3页/共 18页A. B. C. D.
【答案】B
【解析】
【详解】设上半部分正常工作为事件 ,下半部分正常工作为事件 ,该电子元件能正常工作为事件 ,
根据相互独立事件的概率公式求出 、 ,即可求出 、 ,再根据对立事件及独立事
件的概率公式计算可得.
【分析】设上半部分正常工作为事件 ,下半部分正常工作为事件 ,该电子元件能正常工作为事件 ,
则 , ,
,所以 ,
所以 ,
即该电子元件能正常工作的概率是 .
故选:B
8. 正方体 的棱长为 2,P 是空间内的动点,且 ,则 的最小值
为( ).
A. B.
C. D.
【答案】C
【解析】
【分析】取 的中点 M,连接 ,取 的中点 N,连接 ,则由已知条件可得动点 P 的轨迹为正
方体 的外接球,然后由向量的运算可得 ,从而可求得结果.
【详解】取 的中点 M,连接 ,
第 4页/共 18页则 ,则 ,即 ,
故动点 P 的轨迹为以 M 为球心, 为半径的球.
由正方体 的棱长为 2,可知正方体 外接球的半径为 3,
即动点 P 的轨迹为正方体 的外接球.
取 的中点 N,连接 ,
则
.
由题可知, ,则 , ,
则 .
所以 最小值为 ,
故选:C
二、多选题:本题共 3 个小题,共 18 分,在每小题给出的选项中,有多项符合题目要求.
9. 关于空间向量,以下说法正确的是( )
A. 若 ,则向量 , 的夹角是锐角
B. 空间中的三个向量,若有两个向量共线,则这三个向量一定共面
C. 若对空间中任意一点 O,有 ,则 P,A,B,C 四点共面
D. 若分别表示空间两向量的有向线段所在的直线是异面直线,则这两个向量不共面
【答案】BC
第 5页/共 18页【解析】
【分析】根据空间向量共面定理即可判断 B;根据 ,得到 ,即可判断 A;根据
判断四点共面即可判断 C;异面直线的平行线即可判断 D.
【详解】对 A,若 ,则 ,则向量 , 的夹角可以为 0 不是锐角,故 A 错误;
对 B,根据空间向量共面定理知:空间中三个向量,若有两个向量共线,则这三个向量一定共面,故 B 正
确.
对 C,因为 ,且 ,所以 四点共面,故 C 正确.
对 D,分别表示空间两向量的有向线段所在的直线是异面直线,则这两个向量是异面直线的平行线可以共
面,故 D 错误.
故选:BC.
10. 有 6 个相同的球,分别标有数字 1,2,3,4,5,6,从中不放回的随机取两次,每次取 1 个球,甲表
示事件“第一次取出的球的数字是奇数”,乙表示事件“第二次取出的球的数字是偶数”,丙表示事件“两次取
出的球的数字之和是奇数”,丁表示事件“两次取出的球的数字之和是偶数”,则( )
A. 乙发生的概率为 B. 丙发生的概率为
C. 甲与丁相互独立 D. 丙与丁互为对立事件
【答案】ACD
【解析】
【分析】先计算出甲乙丙丁的概率,故可判断 AC 的正误,再根据独立事件的乘法公式可判断 C 的正误,
根据对立事件的意义可判断 D 的正误.
【详解】设 为事件“第一次取出的球的数字是奇数”, 为事件“第二次取出的球的数字是偶数”,
为事件“两次取出的球的数字之和是奇数”, 为事件“两次取出的球的数字之和是偶数”,
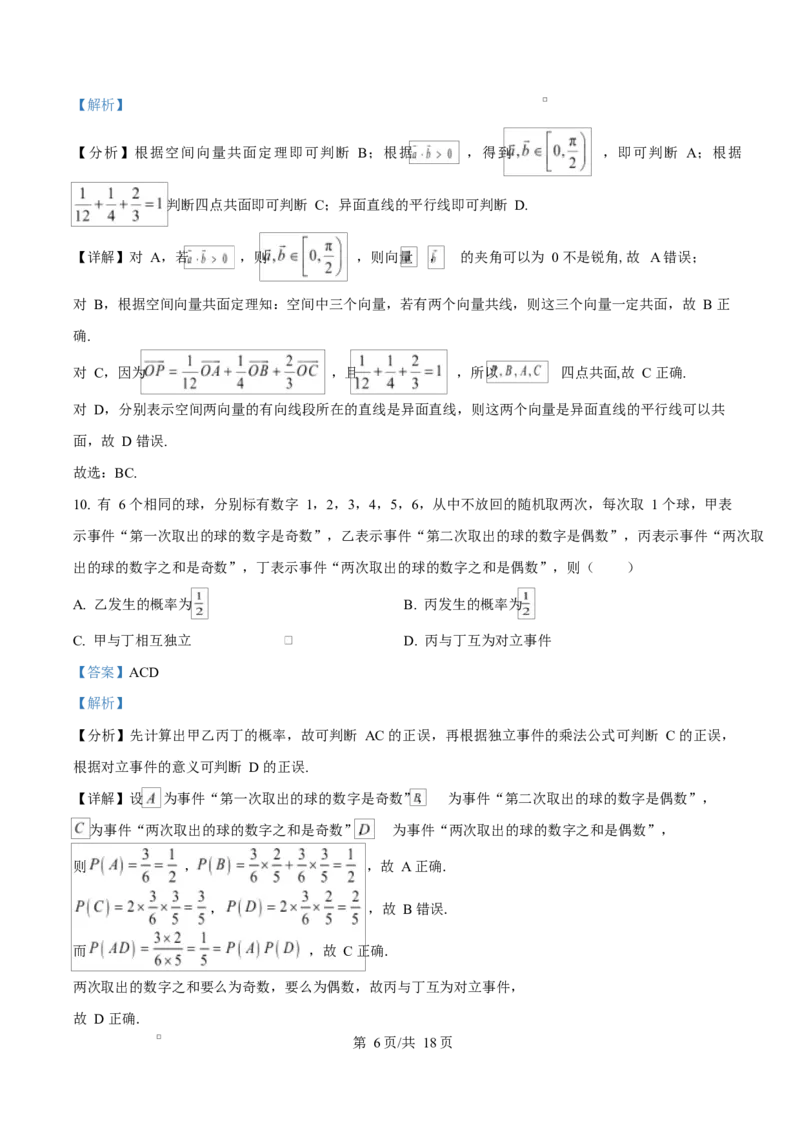
则 , ,故 A 正确.
, ,故 B 错误.
而 ,故 C 正确.
两次取出的数字之和要么为奇数,要么为偶数,故丙与丁互为对立事件,
故 D 正确.
第 6页/共 18页故选:ACD.
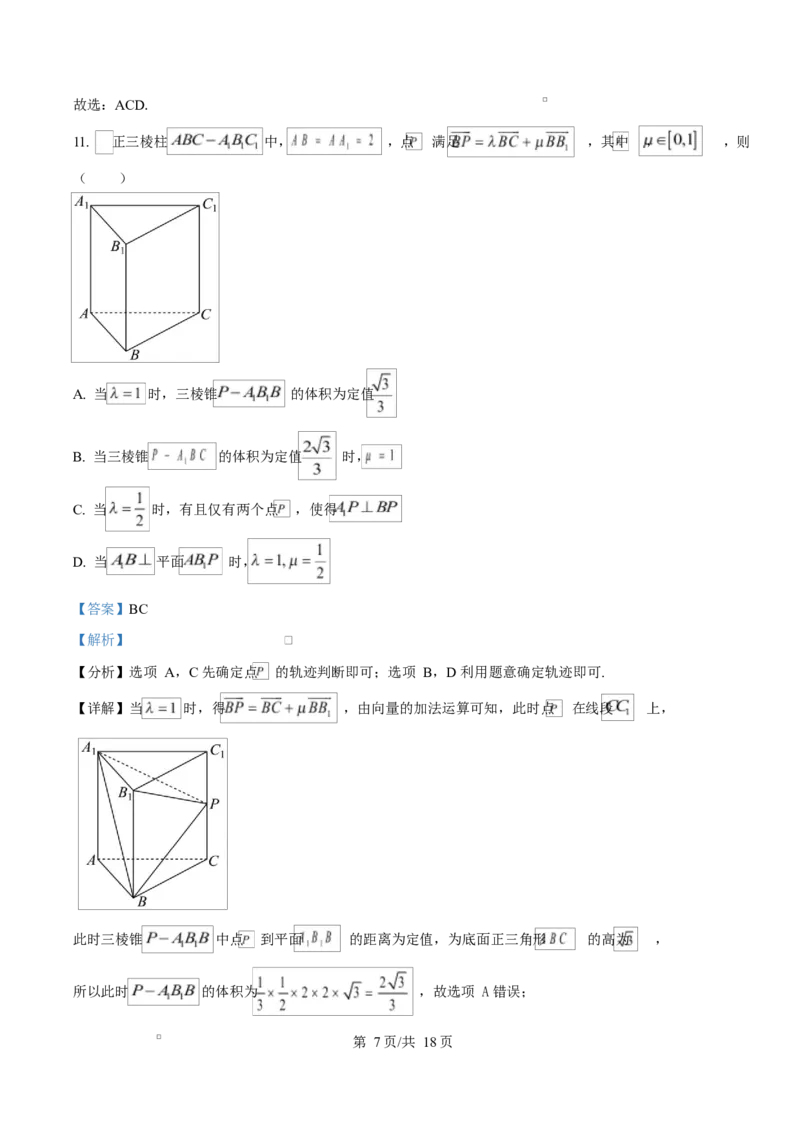
11. 正三棱柱 中, ,点 满足 ,其中 , ,则
( )
A. 当 时,三棱锥 的体积为定值
B. 当三棱锥 的体积为定值 时,
C. 当 时,有且仅有两个点 ,使得
D. 当 平面 时,
【答案】BC
【解析】
【分析】选项 A,C 先确定点 的轨迹判断即可;选项 B,D 利用题意确定轨迹即可.
【详解】当 时,得 ,由向量的加法运算可知,此时点 在线段 上,
此时三棱锥 中点 到平面 的距离为定值,为底面正三角形 的高为 ,
所以此时 的体积为 ,故选项 A 错误;
第 7页/共 18页由题易知,点 在正方形 内,所以点 到平面 的距离为定值 ,
当三棱锥 的体积为定值 时,可知
因为 ,所以点 到直线 的距离为 ,故此时点 在线段 上,
根据向量的线性运算可知 ,故选项 B 正确;
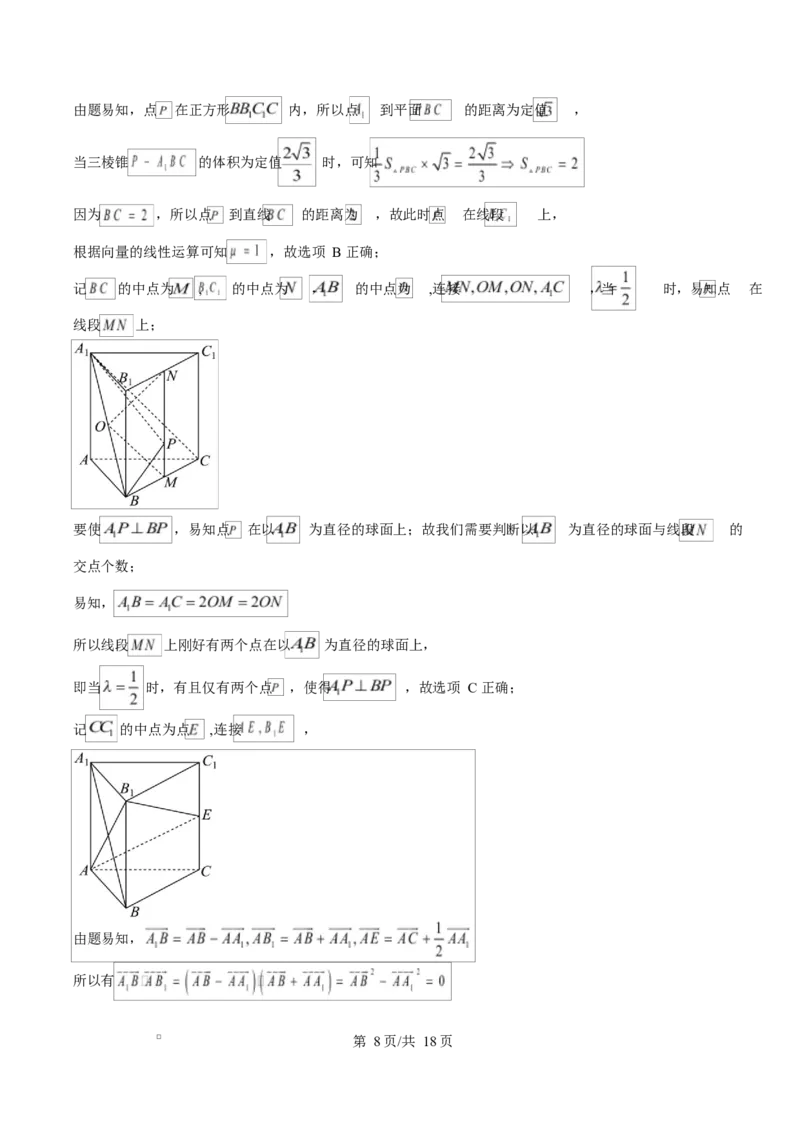
记 的中点为 , 的中点为 , 的中点为 ,连接 ,当 时,易知点 在
线段 上;
要使 ,易知点 在以 为直径的球面上;故我们需要判断以 为直径的球面与线段 的
交点个数;
易知,
所以线段 上刚好有两个点在以 为直径的球面上,
即当 时,有且仅有两个点 ,使得 ,故选项 C 正确;
记 的中点为点 ,连接 ,
由题易知,
所以有
第 8页/共 18页所以 ,
又 是平面 内的两条相交直线,所以 平面
又因为 平面 ,点 在正方形 内
所以易知点 在线段 上,此时 的值不确定,故选项 D 错误;
故选:BC
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12. 已知空间向量 , ,则向量 在向量 上的投影向量的坐标是______
【答案】
【解析】
【分析】根据题中条件,直接利用公式计算即可.
【详解】因为 , ,
所以
,
,
故向量 在向量 上的投影向量为
,
故答案为:
13. 我国古代认为构成宇宙万物的基本要素是金、木、水、火、土这五种物质,称为“五行”.古人构建了金生
水、水生木、木生火、火生土、土生金的相生理论,随机任取“两行”,则取出的“两行”相生的概率是_______
【答案】 ##0.5
【解析】
【分析】写出随机任取 “两行”共有多少种,再写出“两行”相生的可能情况,根据古典概型的概率计算求
第 9页/共 18页得答案.
【详解】由题意得,随机任取“两行”共有金木、金水、金火、金土、木水、木火、木土、水火、水土、火土
共 10 种,
其中取出的“两行”相生的情况有金生水、水生木、木生火、火生土、土生金共 5 种,
所以取出的“两行”相生的概率 ,
故答案为:
14. 设 , 是一个随机试验中的两个事件,且 , , ,则
_______
【答案】
【解析】
【分析】根据给定条件,利用概率的基本性质及互斥事件的概率公式列式求解.
【详解】由 ,得 ,解得 ,
由 ,得 ,解得 ,
由 ,得 ,解得 ,
所以 .
故答案为:
四、解答题:本题共 5 小题,共 77 分.解答应写出文字说明,证明过程或演算步骤.
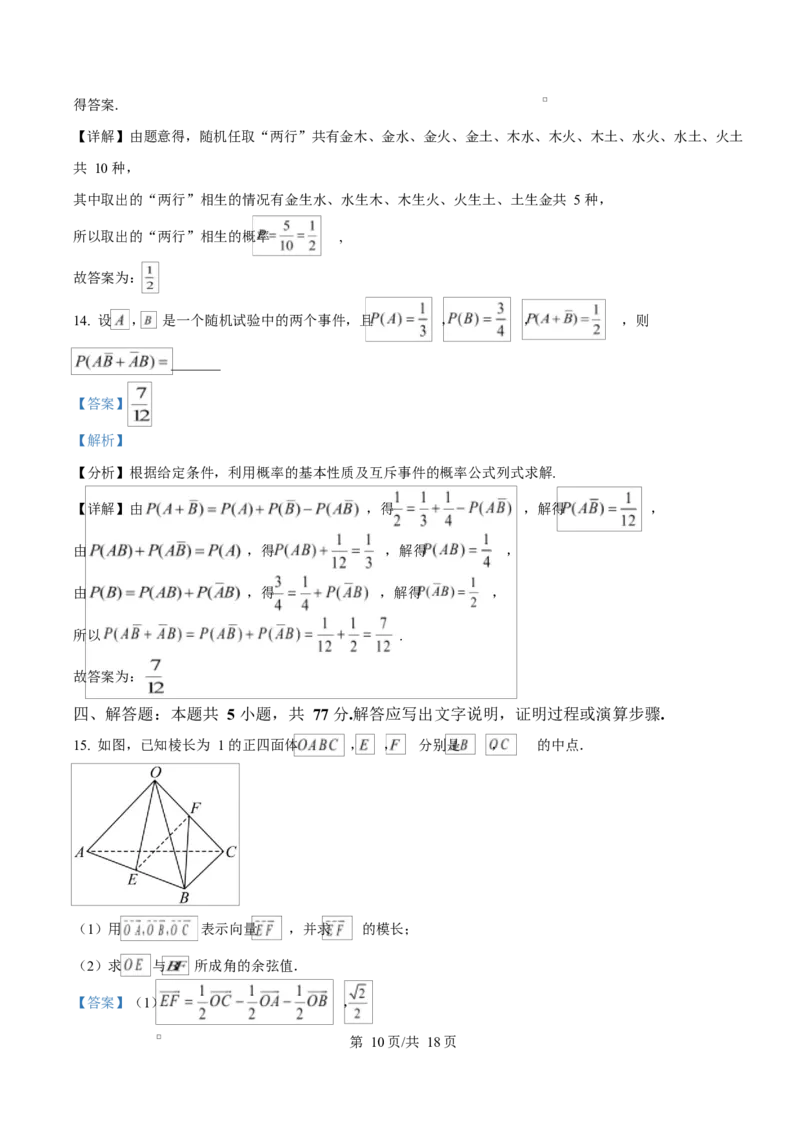
15. 如图,已知棱长为 1 的正四面体 , , 分别是 , 的中点.
(1)用 表示向量 ,并求 的模长;
(2)求 与 所成角的余弦值.
【答案】(1) ,
第 10页/共 18页(2)
【解析】
【分析】(1)利用向量的三角形法则即可表示出向量 ,两边同时平方即可求得结果.
(2)利用空间向量夹角的计算公式即可求得结果.
【小问 1 详解】
,
,所以
【小问 2 详解】
设 为异面直线 与 所成的角,
,所以异面直线 与 所成的角 .
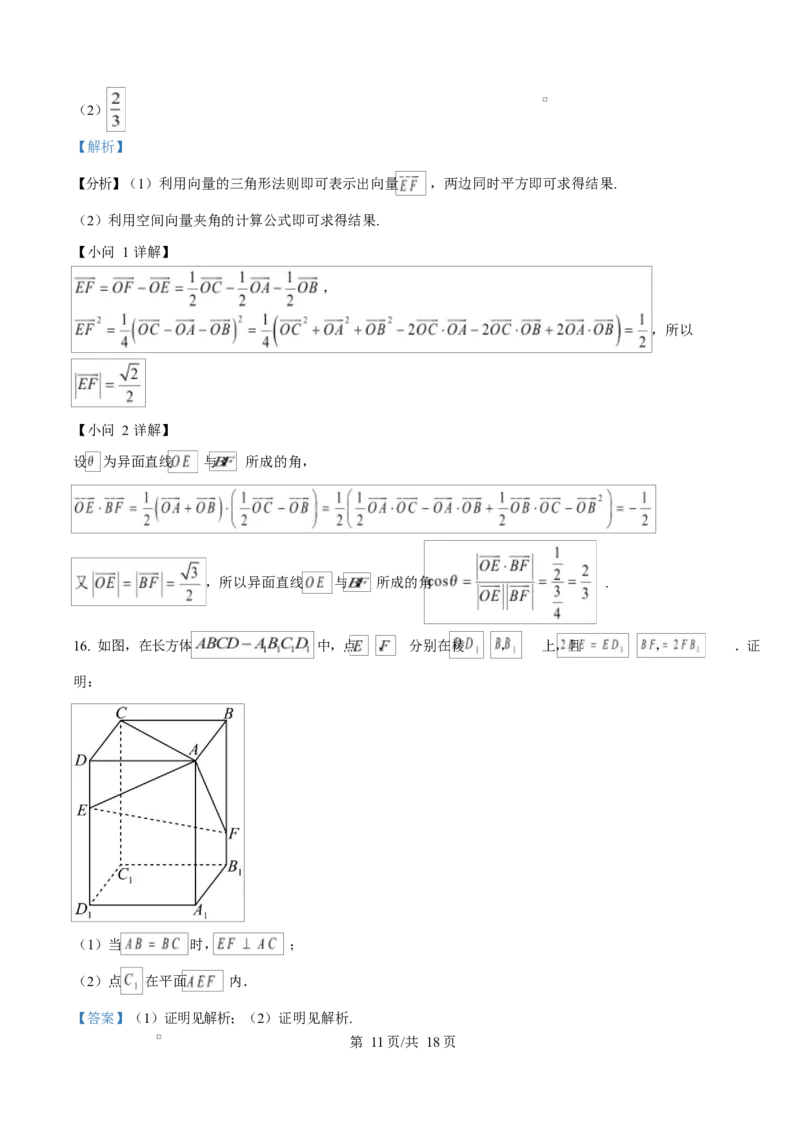
16. 如图,在长方体 中,点 , 分别在棱 , 上,且 , .证
明:
(1)当 时, ;
(2)点 在平面 内.
【答案】(1)证明见解析;(2)证明见解析.
第 11页/共 18页【解析】
【分析】(1)根据正方形性质得 ,根据长方体性质得 ,进而可证 平面 ,即
得结果;
(2)只需证明 即可,在 上取点 使得 ,再通过平行四边形性质进行证明即可.
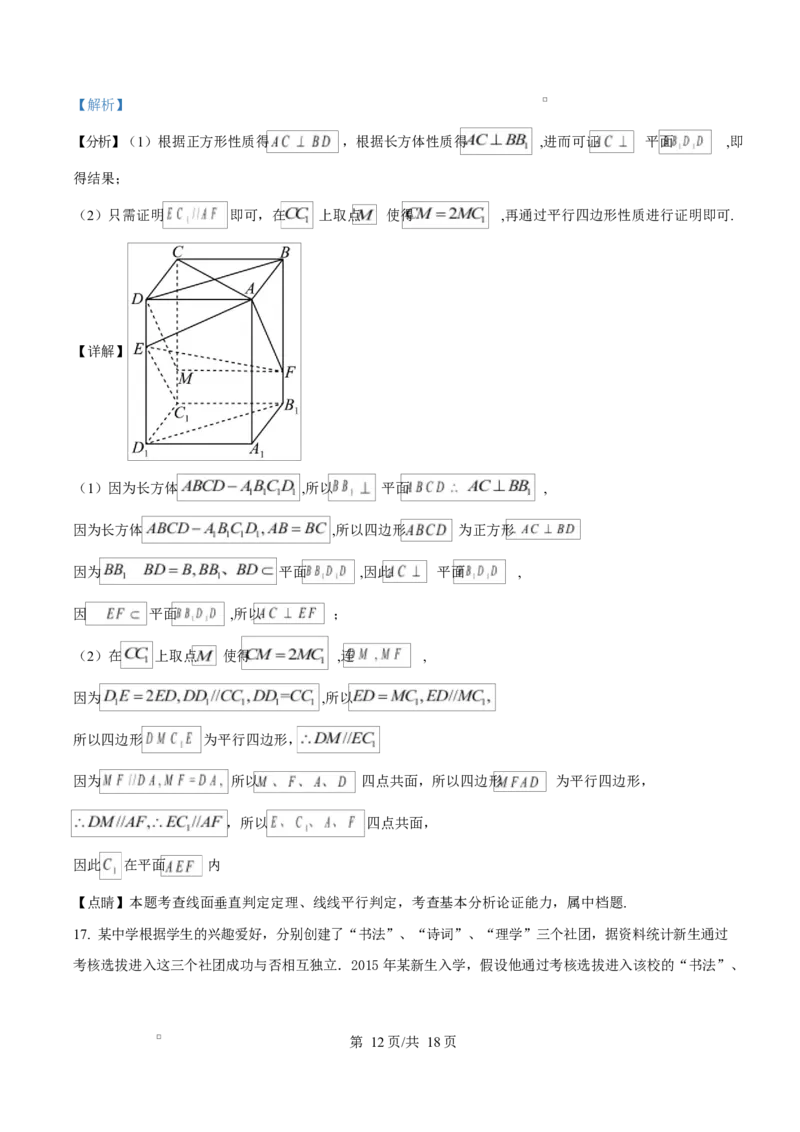
【详解】
(1)因为长方体 ,所以 平面 ,
因为长方体 ,所以四边形 为正方形
因为 平面 ,因此 平面 ,
因 平面 ,所以 ;
(2)在 上取点 使得 ,连 ,
因为 ,所以
所以四边形 为平行四边形,
因为 所以 四点共面,所以四边形 为平行四边形,
,所以 四点共面,
因此 在平面 内
【点睛】本题考查线面垂直判定定理、线线平行判定,考查基本分析论证能力,属中档题.
17. 某中学根据学生的兴趣爱好,分别创建了“书法”、“诗词”、“理学”三个社团,据资料统计新生通过
考核选拔进入这三个社团成功与否相互独立.2015 年某新生入学,假设他通过考核选拔进入该校的“书法”、
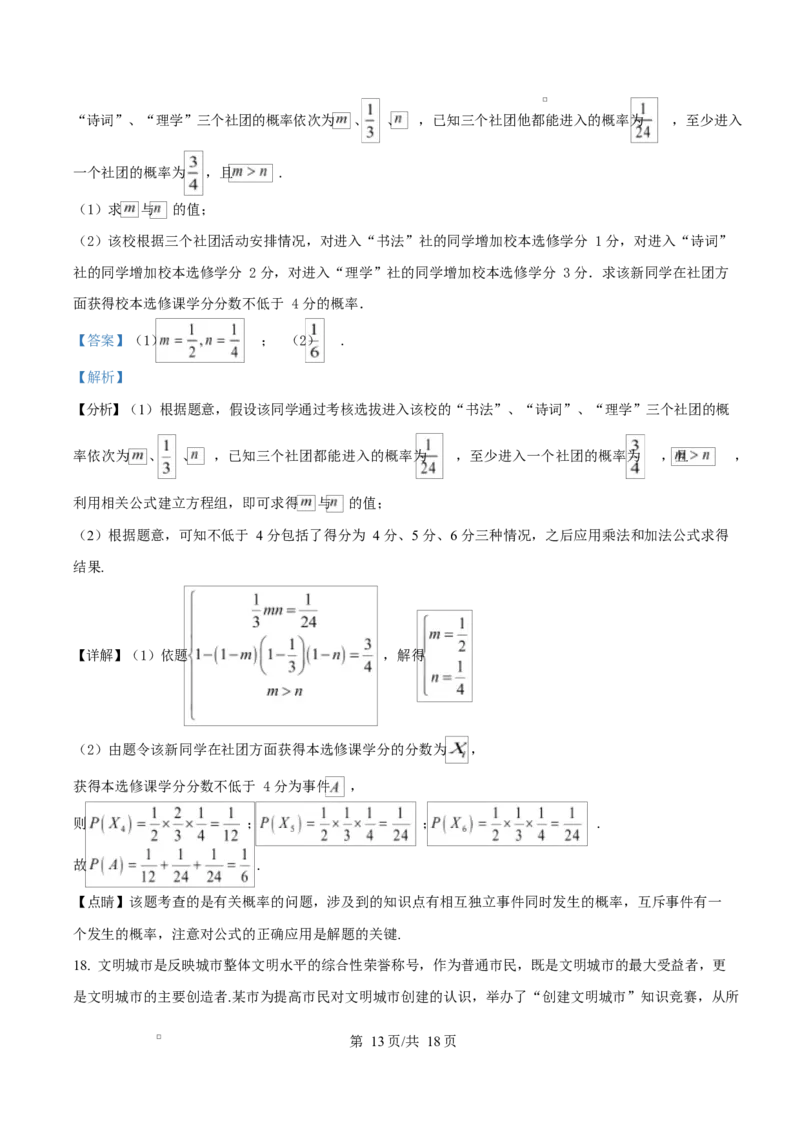
第 12页/共 18页“诗词”、“理学”三个社团的概率依次为 、 、 ,已知三个社团他都能进入的概率为 ,至少进入
一个社团的概率为 ,且 .
(1)求 与 的值;
(2)该校根据三个社团活动安排情况,对进入“书法”社的同学增加校本选修学分 1 分,对进入“诗词”
社的同学增加校本选修学分 2 分,对进入“理学”社的同学增加校本选修学分 3 分.求该新同学在社团方
面获得校本选修课学分分数不低于 4 分的概率.
【答案】(1) ; (2) .
【解析】
【分析】(1)根据题意,假设该同学通过考核选拔进入该校的“书法”、“诗词”、“理学”三个社团的概
率依次为 、 、 ,已知三个社团都能进入的概率为 ,至少进入一个社团的概率为 ,且 ,
利用相关公式建立方程组,即可求得 与 的值;
(2)根据题意,可知不低于 4 分包括了得分为 4 分、5 分、6 分三种情况,之后应用乘法和加法公式求得
结果.
【详解】(1)依题 ,解得
(2)由题令该新同学在社团方面获得本选修课学分的分数为 ,
获得本选修课学分分数不低于 4 分为事件 ,
则 ; ; .
故 .
【点睛】该题考查的是有关概率的问题,涉及到的知识点有相互独立事件同时发生的概率,互斥事件有一
个发生的概率,注意对公式的正确应用是解题的关键.
18. 文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更
是文明城市的主要创造者.某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所
第 13页/共 18页有答卷中随机抽取 100 份作为样本,将样本的成绩(满分 100 分,成绩均为不低于 40 分的整数)分成六段:
, , , 得到如图所示的频率分布直方图.
(1)求频率分布直方图中 的值;
(2)求样本成绩的众数,中位数和平均数;
(3)已知落在 的平均成绩是 54,方差是 7,落在 的平均成绩为 66,方差是 4,求两组成
绩合并后的平均数 和方差 .
【答案】(1) ;
(2)众数为 75,中位数为 75,平均数为 74;
(3)平均数为 62,方差为 37.
【解析】
【分析】(1)根据频率和为 1 求得 ;
(2)根据直方图,及众数、中位数、平均数求法求值;
(3)根据已知求样本总均值,再由总方差公式求样本总方差.
【小问 1 详解】
由每组小矩形的面积之和为 1,得 ,解得 ;
【小问 2 详解】
由 ,得样本成绩的众数为 75,
成绩落在 内的频率为 ,
成绩落在 内的频率为 ,
故中位数在 内,由 ,得样本成绩的中位数为 75,
由 ,
第 14页/共 18页得样本成绩的平均数为 74;
【小问 3 详解】
由频率分布直方图知,成绩在 的样本数为 ,
成绩在 的样本数为 ,
所以 ,
总方差为 .
19. 已知两个非零向量 , ,在空间任取一点 ,作 , ,则 叫做向量 , 的夹角,
记作 .定义 与 的“向量积”为: 是一个向量,它与向量 , 都垂直,它的模
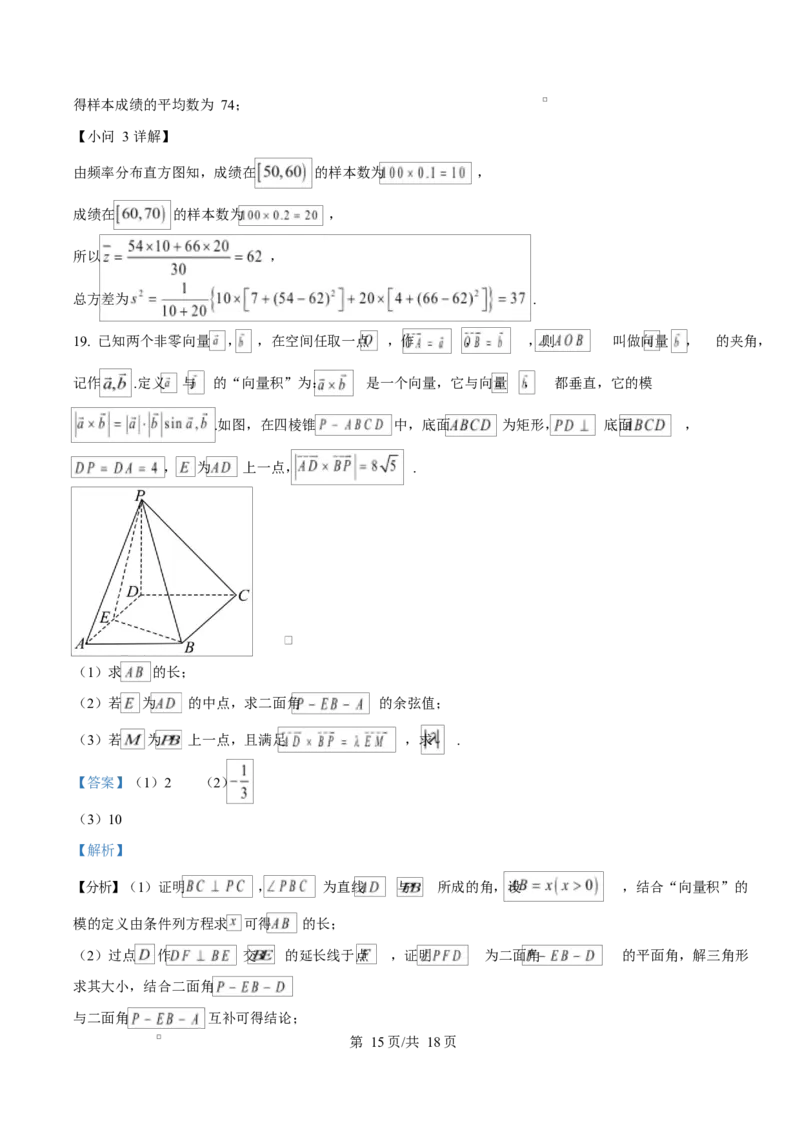
.如图,在四棱锥 中,底面 为矩形, 底面 ,
, 为 上一点, .
(1)求 的长;
(2)若 为 的中点,求二面角 的余弦值;
(3)若 为 上一点,且满足 ,求 .
【答案】(1)2 (2)
(3)10
【解析】
【分析】(1)证明 , 为直线 与 所成的角,设 ,结合“向量积”的
模的定义由条件列方程求 可得 的长;
(2)过点 作 交 的延长线于点 ,证明 为二面角 的平面角,解三角形
求其大小,结合二面角
与二面角 互补可得结论;
第 15页/共 18页(3)过点 作 ,证明 平面 ,过点 作 交 于点 ,证明
,结合条件可求 .
小问 1 详解】
因为底面 为矩形,
所以 , ,
因为 底面 , 底面 ,
所以 ,
又 , 平面 ,
所以 平面 ,
又 平面 ,所以 ,
因为 ,
所以 为直线 与 所成的角,即 ,
设 ,则 , ,
在 中 ,
又 ,所以 ,解得 或 (舍去),
所以 ;
【小问 2 详解】
在平面 内过点 作 交 的延长线于点 ,连接 ,
因为 底面 , 底面 ,所以 ,
又 , , 平面 ,
所以 平面 ,又 平面 ,所以 ,
所以 为二面角 的平面角,
因为 为 的中点,
所以 , ,
第 16页/共 18页所以 ,
设二面角 的平面角为 ,则 ,
所以 ,
即二面角 的余弦值为 ;
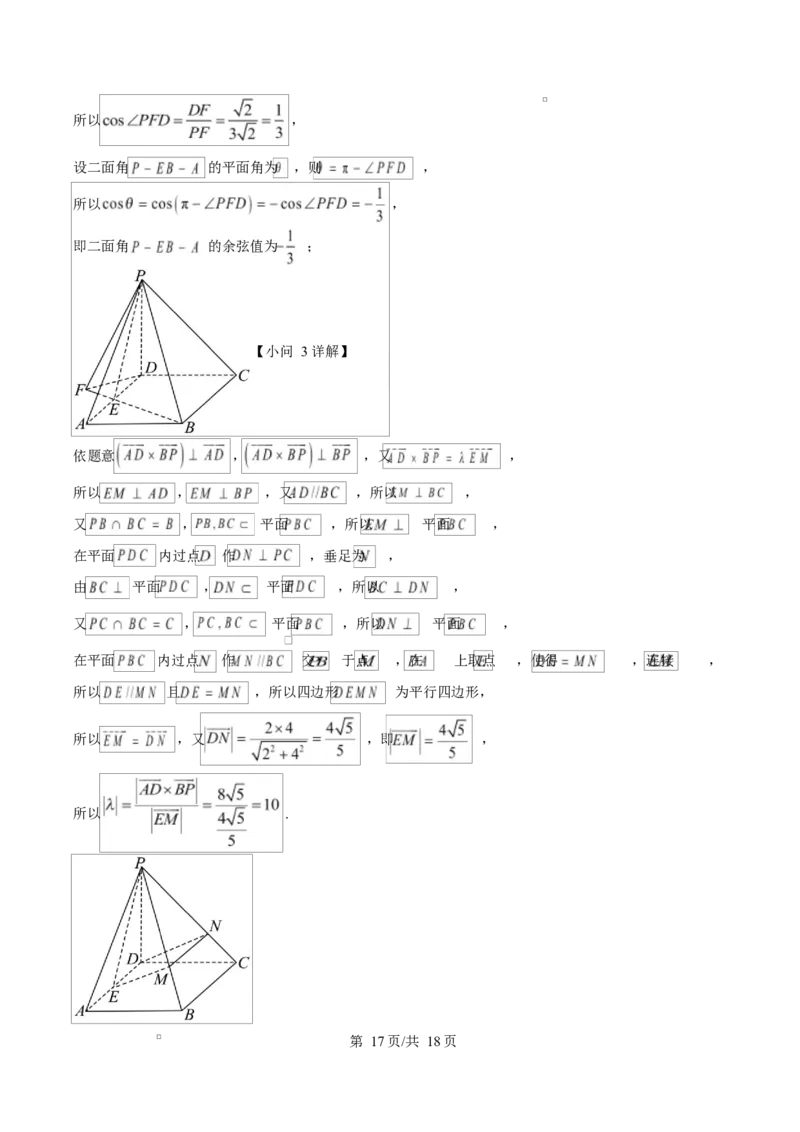
【小问 3 详解】
依题意 , ,又 ,
所以 , ,又 ,所以 ,
又 , 平面 ,所以 平面 ,
在平面 内过点 作 ,垂足为 ,
由 平面 , 平面 ,所以 ,
又 , 平面 ,所以 平面 ,
在平面 内过点 作 交 于点 ,在 上取点 ,使得 ,连接 ,
所以 且 ,所以四边形 为平行四边形,
所以 ,又 ,即 ,
所以 .
第 17页/共 18页【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义
去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象
看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变
才是制胜法宝.
第 18页/共 18页