2005年辽宁高考数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_辽宁

2005 年辽宁高考数学真题及答案 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择）题两部分，满分150分.考试用时120分钟. 第Ⅰ卷（选择题，共60分） 参考公式： 如果事件A、B互斥，那么 球的表面积公式 P(A+B)=P(A)+P(B) S 4R2 如果事件A、B相互独立，那么 P(A·B)=P(A)·P(B) 其中R表示球的半径 如果事件A在一次试验中发生的概率是 球的体积公式 4 P，那么n次独立重复试验中恰好发生k V  R3 球 3 次的概率P (k) CkPk(1P)nk 其中R表示球的半径 n n 一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有 一项是符合题目要求的. 1i 1．复数z  1.在复平面内，z所对应的点在 （ ） 1i A．第一象限 B．第二象限 C．第三象限 D．第四象限 2．极限lim f(x)存在是函数 f(x)在点x  x 处连续的 （ ） 0 xx 0 A．充分而不必要的条件 B．必要而不充分的条件 C．充要条件 D．既不充分也不必要的条件 3．设袋中有80个红球，20个白球，若从袋中任取10个球，则其中恰有6个红球的概率为 （ ） C4 C6 C6 C4 C4 C6 C6 C4 A． 80 10 B． 80 10 C． 80 20 D． 80 20 C10 C10 C10 C10 100 100 100 100 4．已知m、n是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列四个命 题：①若m ,m ,则//； ②若,,则//； ③若m,n,m//n,则//； ④若m、n是异面直线，m,m//,n ,n//,则// 其中真命题是 （ ） A．①和② B．①和③ C．③和④ D．①和④ 第1页 | 共11页5．函数y ln(x x2 1的反函数是 （ ） ex ex ex ex ex ex ex ex A．y  B．y   C．y  D．y   2 2 2 2 1a2 6．若log 0，则a的取值范围是 （ ） 2a 1a 1 1 1 A．( ,) B．(1,) C．( ,1) D．(0, ) 2 2 2 7．在R上定义运算:x y  x(1 y).若不等式(xa)(xa)1对任意实数x成立， 则 （ ） 1 3 3 1 A．1 a 1 B．0 a  2 C．  a  D．  a  2 2 2 2 8．若钝角三角形三内角的度数成等差数列，且最大边长与最小边长的比值为m，则m的范 围是 （ ） A．（1，2） B．（2，+∞） C．[3，+∞) D．（3，+∞） 9．若直线2x yc 0按向量a (1,1)平移后与圆x2  y2 5相切，则c的值为（ ） A．8或－2 B．6或－4 C．4或－6 D．2或－8 x x 10．已知y  f(x)是定义在R上的单调函数，实数x  x ， 1,a  1 2 , 1 2 1 x x  2 1 ，若| f(x ) f(x )|| f() f()|，则 （ ） 1 1 2 A． 0 B．0 C．01 D．1 11．已知双曲线的中心在原点，离心率为 3.若它的一条准线与抛物线 y2  4x的准线重 合， 则该双曲线与抛物线y2  4x的交点到原点的距离是 （ ） A．2 3+ 6 B． 21 C．1812 2 D．21 12．一给定函数y  f(x)的图象在下列图中，并且对任意a (0,1)，由关系式a  f(a ) 1 n1 n 得到的数列{a }满足a  a (nN*)，则该函数的图象是 （ ） n n1 n A B C D 第Ⅱ卷（非选择题 共90分） 第2页 | 共11页二、填空题：本大题共4小题，每小题4分，共16分. 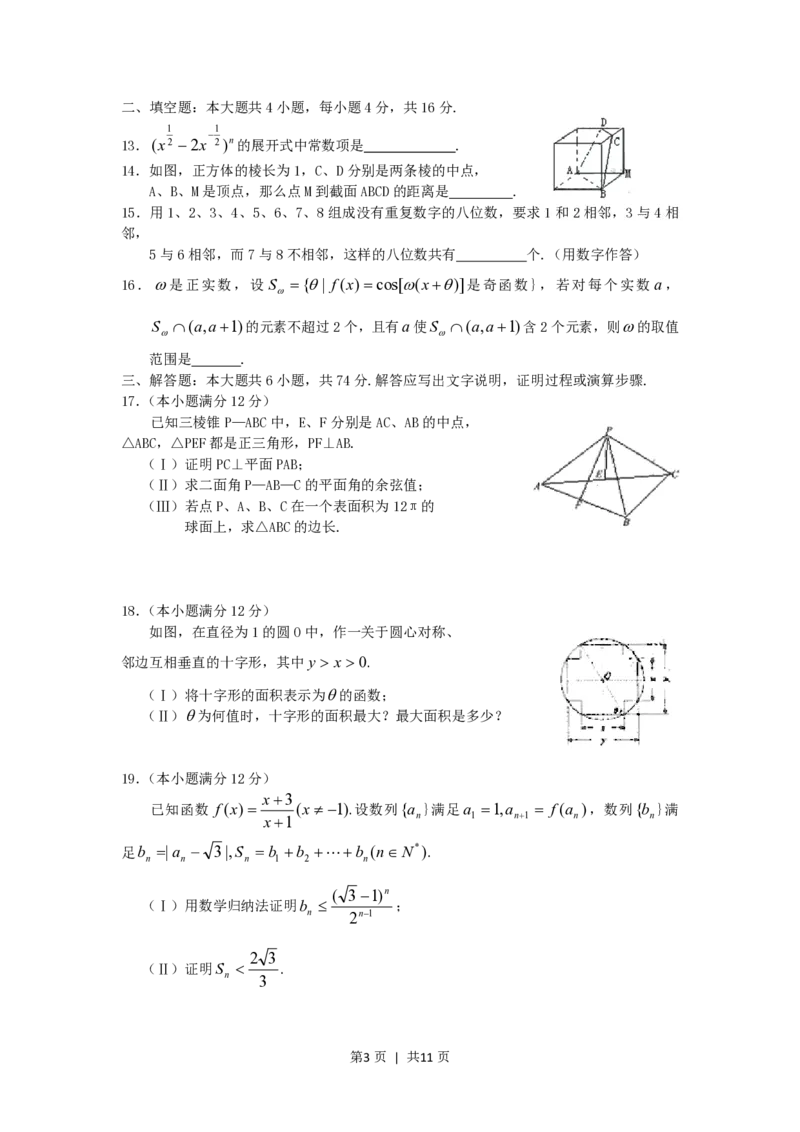1 1  13．(x2 2x 2)n的展开式中常数项是 . 14．如图，正方体的棱长为1，C、D分别是两条棱的中点， A、B、M是顶点，那么点M到截面ABCD的距离是 . 15．用1、2、3、4、5、6、7、8组成没有重复数字的八位数，要求1和2相邻，3与4相 邻， 5与6相邻，而7与8不相邻，这样的八位数共有 个.（用数字作答） 16．是正实数，设 S {| f(x) cos[(x)]是奇函数}，若对每个实数 a，  S (a,a1)的元素不超过2个，且有a使S (a,a1)含2个元素，则的取值   范围是 . 三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分） 已知三棱锥P—ABC中，E、F分别是AC、AB的中点， △ABC，△PEF都是正三角形，PF⊥AB. （Ⅰ）证明PC⊥平面PAB； （Ⅱ）求二面角P—AB—C的平面角的余弦值； （Ⅲ）若点P、A、B、C在一个表面积为12π的 球面上，求△ABC的边长. 18．（本小题满分12分） 如图，在直径为1的圆O中，作一关于圆心对称、 邻边互相垂直的十字形，其中y  x 0. （Ⅰ）将十字形的面积表示为的函数； （Ⅱ）为何值时，十字形的面积最大？最大面积是多少？ 19．（本小题满分12分） x3 已知函数 f(x)  (x  1).设数列{a }满足a 1,a  f(a )，数列{b }满 x1 n 1 n1 n n 足b |a  3|,S b b  b (nN*). n n n 1 2  n ( 31)n （Ⅰ）用数学归纳法证明b  ； n 2n1 2 3 （Ⅱ）证明S  . n 3 第3页 | 共11页20．（本小题满分12分） 某工厂生产甲、乙两种产品，每种产品都是经过第一和第二工序加工而成，两道工序 的加工结果相互独立，每道工序的加工结果均有A、B两个等级.对每种产品，两道工序的加 工结果都为A级时，产品为一等品，其余均为二等品. （Ⅰ）已知甲、乙两种产品每一道工序的加工结 概 工序 率 第一工序 第二工序 果为A级的概率如表一所示，分别求生产 产品 出的甲、乙产品为一等品的概率P 、P ； 甲 乙 甲 0.8 0.85 （Ⅱ）已知一件产品的利润如表二所示，用ξ、 乙 0.75 0.8 η分别表示一件甲、乙产品的利润，在 （I）的条件下，求ξ、η的分布列及 利 等级 润 一等 二等 Eξ、Eη； 产品 （Ⅲ）已知生产一件产品需用的工人数和资金额 甲 5（万元） 2.5（万元） 如表三所示.该工厂有工人40名，可用资. 乙 2.5（万元） 1.5（万元） 金60万元.设x、y分别表示生产甲、乙产 品的数量，在（II）的条件下，x、y为何 用 项目 量 工人（名） 资金（万元） 值时，z xE yE最大？最大值是多少？ 产品 甲 8 8 （解答时须给出图示） 乙 2 10 21．（本小题满分14分） x2 y2 已知椭圆  1(a b 0)的左、右焦点分别是F（－c，0）、F（c，0），Q是 a2 b2 1 2 椭圆外的动点，满足| FQ| 2a.点P是线段FQ与该椭圆的交点，点T在线段FQ上，并且 1 1 2 满足PT TF 0,|TF | 0. 2 2 c （Ⅰ）设x为点P的横坐标，证明| F P| a x； 1 a （Ⅱ）求点T的轨迹C的方程； （Ⅲ）试问：在点T的轨迹C上，是否存在点M， 使△FMF 的面积S=b2.若存在，求∠FMF 1 2 1 2 的正切值；若不存在，请说明理由. 22．（本小题满分12分） 函数y  f(x)在区间（0，+∞）内可导，导函数 f (x)是减函数，且 f (x) 0. 设 x (0,),y  kxm是曲线 y  f(x)在点（ x , f(x )）得的切线方程，并设函数 0 0 0 第4页 | 共11页g(x)  kxm. （Ⅰ）用x 、 f(x )、 f (x )表示m； 0 0 0 （Ⅱ）证明：当x (0,)时,g(x) f(x)； 0 3 2 （Ⅲ）若关于x的不等式x2 1 axb x3在[0,)上恒成立，其中a、b为实数， 2 求b的取值范围及a与b所满足的关系. 参考答案与评分标准 说明： 一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考， 如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细 则。 二、对解答题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题 的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数 的一半；如果后继部分的解答有较严重的错误，就不再给分。 三、解答右端所注分数，表示考生正确做到这一步应得的累加分数。 四、只给整数分数，选择题和填空题不给中间分。 一、选择题：本题考查基本知识和基本运算，每小题5分，满分60分. 1.B 2.B 3.D 4.D 5.C 6.C 7.C 8.B 9.A 10.A 11.B 12.A 二、填空题：本题考查基本知识和基本运算。每小题4分，满分16分。 2 13．－160 14． 15．576 16．(,2] 3 三、解答题 17．本小题主要考查空间中的线面关系，三棱锥、球的有关概念及解三角形等基础知识，考 查空间想象能力及运用方程解未知量的基本方法，满分12分. 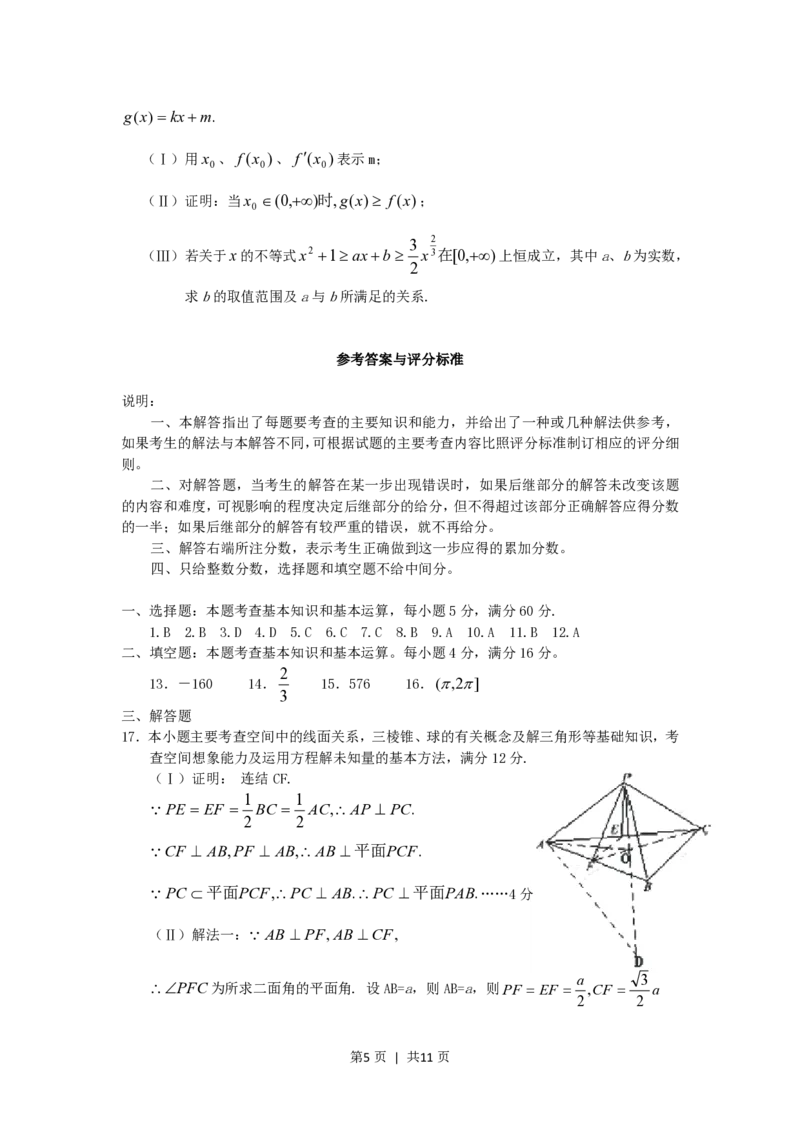（Ⅰ）证明： 连结CF. 1 1 PE  EF  BC  AC,AP  PC.  2 2 CF  AB,PF  AB,AB 平面PCF.  PC 平面PCF,PC  AB.PC 平面PAB.……4分  （Ⅱ）解法一： AB  PF,AB CF,  a 3 PFC为所求二面角的平面角. 设AB=a，则AB=a，则PF  EF  ,CF  a 2 2 第5页 | 共11页a 2 3 cosPFC   .……………………8分 3 3 a 2 解法二：设P在平面ABC内的射影为O. PAF≌PAE,PAB≌PAC.  得PA=PB=PC. 于是O是△ABC的中心. PFO为所求二面角的平面角. a 1 3 OF 3 设AB=a，则PF  ,OF   a. cosPFO   .…………8分 2 3 2 PF 3 （Ⅲ）解法一：设PA=x，球半径为R. PC 平面PAB,PA PB,   3x  2R. 4R2 12，R  3.得x  2.ABC的边长为2 2.………12  分 解法二：延长PO交球面于D，那么PD是球的直径. 连结OA、AD，可知△PAD为直角三角形. 设AB=x，球半径为R. 6 2 3 4R2 12,PD  2 3. PO OFtanPFO  x,OA  x,   6 3 2 3 6 6 ( x)2  x(2 3 x).于是x  2 2.ABC的边长为2 2.……12分 3 6 6 18．本小题主要考查根据图形建立函数关系、三角函数公式、用反三角函数表示角以及解和 三角函数有关的极值问题等基础知识，考查综合运用三角函数知识的能力. 满分12分. （Ⅰ）解：设S为十字形的面积，则S  2xyx2    2sincoscos2(  ).………………4分 4 2 1 1 5 1 （Ⅱ）解法一：S 2sincoscos2sin2 cos2  sin(2) , 2 2 2 2 2 5  其中arccos .………8分 当sin(2)1,即2 时,S最大.……10分 5 2  1 2 5 5 1 所以，当  arccos 时,S最大. S的最大值为 .…………12分 4 2 5 2 解法二： 因为S 2sincoscos2, 所以S2cos22sin22sincos  2cos2sin2.……………………8分 令S′=0，即2cos2sin20,  1 可解得  arctan(2) ………………10分 2 2 第6页 | 共11页 1 5 1 所以，当  arctan(2)时，S最大，S的最大值为 . …………12分 2 2 2 19．本小题主要考查数列、等比数列、不等式等基本知识，考查运用数学归纳法解决有关问 题的能力，满分12分。 2 （Ⅰ）证明：当x 0时, f(x) 1 1. 因为a=1， 1 x1 所以a 1(nN*). ………………2分 n ( 31)n 下面用数学归纳法证明不等式b  . n 2n1 （1）当n=1时，b= 31，不等式成立， 1 ( 31)k （2）假设当n=k时，不等式成立，即b  . k 2k1 ( 31)|a  3| 那么 b |a  3| k ………………6分 k1 k1 1a k 31 ( 31)k1  b  . 2 k 2k 所以，当n=k+1时，不等也成立。 根据（1）和（2），可知不等式对任意n∈N*都成立。 …………8分 ( 31)n （Ⅱ）证明：由（Ⅰ）知， b  . n 2n1 ( 31)2 ( 31)n 所以 S b b  b ( 31)   n 1 2  n 2  2n1 31 1( )n 2 1 2 ( 31) …………10分 ( 31)  3. 31 31 3 1 1 2 2 2 故对任意nN,S  3.………………（12分） n 3 20．（本小题主要考查相互独立事件的概率、随机变量的分布列及期望、线性规划模型的建 立与求解等基础知识，考查通过建立简单的数学模型以解决实际问题的能力，满分12 分. 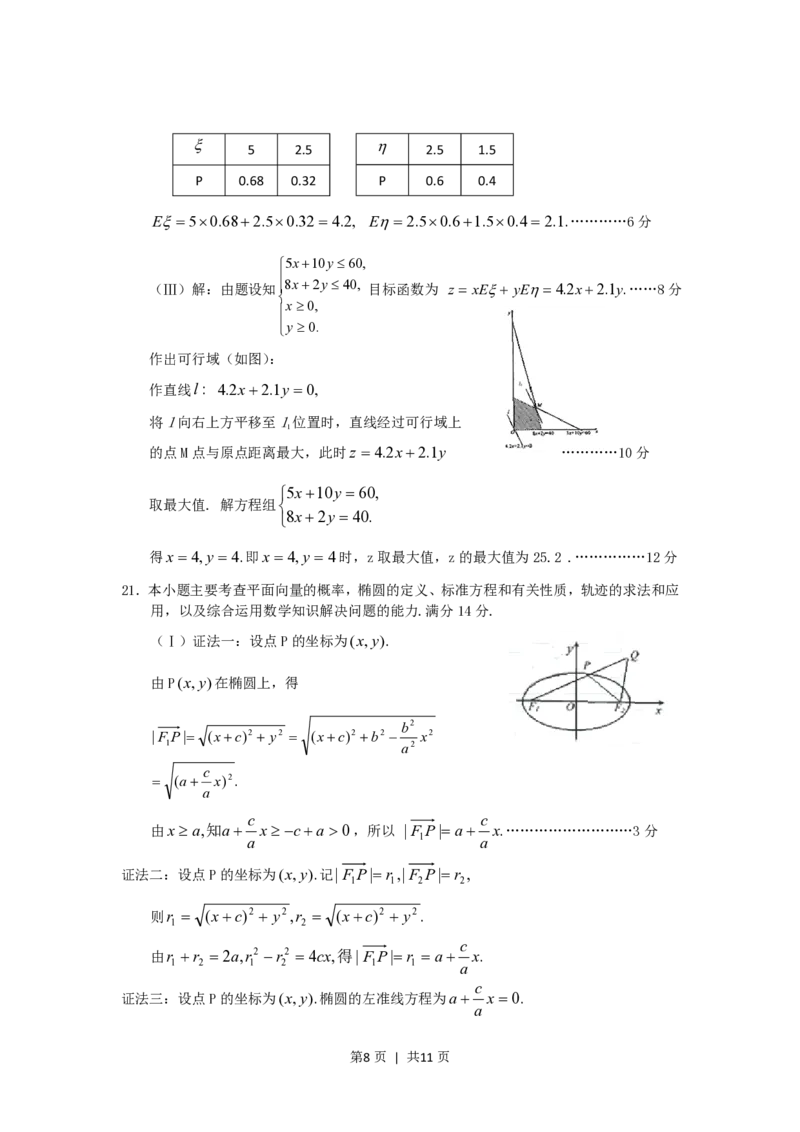（Ⅰ）解：P 0.80.850.68, P 0.750.80.6.…………2分 甲 乙 （Ⅱ）解：随机变量、的分别列是 第7页 | 共11页  5 2.5 2.5 1.5 P 0.68 0.32 P 0.6 0.4 E50.682.50.32 4.2, E 2.50.61.50.4  2.1.…………6分 5x10y60,  （Ⅲ）解：由题设知8x2y40, 目标函数为 z  xE yE4.2x2.1y.……8分  x0,   y0. 作出可行域（如图）： 作直线l: 4.2x2.1y 0, 将l向右上方平移至l位置时，直线经过可行域上 1 的点M点与原点距离最大，此时z  4.2x2.1y …………10分 5x10y 60, 取最大值. 解方程组 8x2y  40. 得x  4,y  4.即x  4,y  4时，z取最大值，z的最大值为25.2 .……………12分 21．本小题主要考查平面向量的概率，椭圆的定义、标准方程和有关性质，轨迹的求法和应 用，以及综合运用数学知识解决问题的能力.满分14分. （Ⅰ）证法一：设点P的坐标为(x,y). 由P(x,y)在椭圆上，得 b2 |FP| (xc)2  y2  (xc)2 b2  x2 1 a2 c  (a x)2. a c c 由x  a,知a x  ca 0，所以 | F P| a x.………………………3分 a 1 a 证法二：设点P的坐标为(x,y).记| F P| r ,| F P| r , 1 1 2 2 则r  (xc)2  y2,r  (xc)2  y2. 1 2 c 由r r  2a,r2 r2  4cx,得| F P| r  a x. 1 2 1 2 1 1 a c 证法三：设点P的坐标为(x,y).椭圆的左准线方程为a x 0. a 第8页 | 共11页由椭圆第二定义得 |F 1 P|  c ，即|FP| c |x a2 ||a c x|. a2 a 1 a c a |x | c c c 由x  a,知a x  ca 0，所以| F P| a x.…………………………3分 a 1 a （Ⅱ）解法一：设点T的坐标为(x,y). 当|PT |0时，点（a，0）和点（－a，0）在轨迹上. 当|PT | 0且|TF | 0时，由| PT ||TF |0，得PT TF . 2 2 2 又| PQ|| PF |，所以T为线段FQ的中点. 2 2 1 在△QFF 中，|OT | | FQ| a，所以有x2  y2  a2. 1 2 2 1 综上所述，点T的轨迹C的方程是x2  y2  a2.…………………………7分 解法二：设点T的坐标为(x,y). 当|PT |0时，点（a，0）和点（－a，0）在轨迹上. 当|PT | 0且|TF | 0时，由PT TF 0，得PT TF . 2 2 2 又| PQ|| PF |，所以T为线段FQ的中点. 2 2  xc x ,  设点Q的坐标为（x,y），则 2  y y  .   2 x2xc, 因此 ①  y2y. 由| FQ| 2a得(xc)2  y2  4a2. ② 1 将①代入②，可得x2  y2  a2. 综上所述，点T的轨迹C的方程是x2  y2  a2.……………………7分 （Ⅲ）解法一：C上存在点M（x ,y ）使S=b2的充要条件是 0 0 x2  y2  a2, ③  0 0 1  2 2c| y 0 |b2. ④ 由③得| y | a，由④得| y | b2 . 所以，当a b2 时，存在点M，使S=b2； 0 0 c c 第9页 | 共11页当 b2 时，不存在满足条件的点M.………………………11分 a c b2 当a 时，MF (cx ,y ),MF (cx ,y )， 1 0 0 2 0 0 c 由MF MF  x2 c2  y2  a2 c2 b2， 1 2 0 0 MF MF |MF ||MF |cosFMF ， 1 2 1 2 1 2 1 S  |MF ||MF |sinFMF b2，得tanFMF  2. 2 1 2 1 2 1 2 解法二：C上存在点M（x ,y ）使S=b2的充要条件是 0 0 x2  y2  a2, ③  0 0 1  2 2c| y 0 |b2. ④ b2 b4 b2 b2 由④得| y | . 上式代入③得x2 a2  (a )(a )0. 0 c 0 c2 c c 于是，当a b2 时，存在点M，使S=b2； c 当 b2 时，不存在满足条件的点M.………………………11分 a c b2 y y 当a 时，记k k  0 ,k k  0 ， c 1 F 1 M x c 2 F 2 M x c 0 0 由| F F | 2a,知FMF 90，所以 k k …………14分 1 2 1 2 tanFMF | 1 2 |2. 1 2 1k k 1 2 22．本小题考查导数概念的几何意义，函数极值、最值的判定以及灵活运用数形结合的思想 判断函数之间的大小关系.考查学生的学习能力、抽象思维能力及综合运用数学基本关 系解决问题的能力.满分12分 （Ⅰ）解：m  f(x )x f (x ).…………………………………………2分 0 0 0 （Ⅱ）证明：令h(x)  g(x) f(x),则h(x)  f (x ) f (x),h(x ) 0. 0 0 因为 f (x)递减，所以h(x)递增，因此，当x  x 时,h(x) 0； 0 当x  x 时,h(x)0.所以x 是h(x)唯一的极值点，且是极小值点，可知h(x) 0 0 的 最小值为0，因此h(x)0,即g(x) f(x).…………………………6分 （Ⅲ）解法一：0b 1，a  0是不等式成立的必要条件，以下讨论设此条件成立. x2 1 axb,即x2 ax(1b)0对任意x[0,)成立的充要条件是 1 a2(1b)2. 3 2 另一方面，由于 f(x) x3满足前述题设中关于函数 y  f(x)的条件，利用（II）的 2 第10页 | 共11页结果可知，axb 3 x3 2 的充要条件是：过点（0，b）与曲线 y 3 x3 2 相切的直线的斜率大 2 2 1 于a，该切线的方程为y(2b)  2xb. 1 于是 3 2 的充要条件是a(2b)2.…………………………10分 axb x3 2 3 2 综上，不等式x2 1 axb  x3 对任意x[0,)成立的充要条件是 2 1 1  (2b) 2 a2(1b)2. ① 1 1  显然，存在a、b使①式成立的充要条件是：不等式(2b) 2 2(1b)2. ② 2 2 2 2 有解、解不等式②得 b . ③ 4 4 因此，③式即为b的取值范围，①式即为实数在a与b所满足的关系.…………12分 （Ⅲ）解法二：0b1,a 0是不等式成立的必要条件，以下讨论设此条件成立. x2 1 axb,即x2 ax(1b)0对任意x[0,)成立的充要条件是 1 a2(1b)2.………………………………………………………………8分 3 2 3 2 令(x)  axb x3，于是axb x3对任意x[0,)成立的充要条件是 2 2 1  (x)0. 由(x)  ax 3 0得x  a3. 当0 x  a3时(x)0;当x  a3时，(x) 0，所以，当x  a3时，(x)取最 1  小值.因此(x)0成立的充要条件是(a3)0，即a (2b) 2.………………10分 3 2 综上，不等式 x2 1axb x3 对任意x[0,)成立的充要条件是 2 1 1  (2b) 2 a2(1b)2. ① 1 1  显然，存在a、b使①式成立的充要条件是：不等式(2b) 2 2(1b)2 ② 2 2 2 2 有解、解不等式②得 b . 4 4 因此，③式即为b的取值范围，①式即为实数在a与b所满足的关系.…………12分 第11页 | 共11页