文档内容
2005 年重庆高考理科数学真题及答案
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。如需改动,
用
橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束后,将试题卷和答题卡一并交回。
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概
率
第一部分(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个备选项中,
只有一项是符合题目要求的.
1.圆 关于原点(0,0)对称的圆的方程为 ( )
A. B.
C. D.
2. ( )
A. B.- C. D.-
3.若函数 是定义在R上的偶函数,在 上是减函数,且 ,则使得
的x的取值范围是 ( )
A. B. C. D.(-2,2)
4.已知A(3,1),B(6,1),C(4,3),D为线段BC的中点,则向量 与 的夹角
为 ( )
A. B. C. D.-
5.若x,y是正数,则 的最小值是 ( )
第1页 | 共11页A.3 B. C.4 D.
6.已知 、 均为锐角,若 的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
7.对于不重合的两个平面 与 ,给定下列条件:
①存在平面 ,使得 、 都垂直于 ;
②存在平面 ,使得 、 都平行于 ;
③ 内有不共线的三点到 的距离相等;
④存在异面直线l、m,使得l// ,l// ,m// ,m// ,
其中,可以判定 与 平行的条件有 ( )
A.1个 B.2个 C.3个 D.4个
8.若 n 展开式中含 项的系数与含 项的系数之比为-5,则 n 等于
( )
A.4 B.6 C.8 D.10
9.若动点( )在曲线 上变化,则 的最大值为 ( )
A. B.
C. D.2
10.如图,在体积为1的三棱锥A—BCD侧棱
AB、AC、AD上分别取点E、F、G, 使
AE : EB=AF : FC=AG : GD=2 : 1,记O为
三平面BCG、CDE、DBF的交点,则三棱
锥O—BCD的体积等于 ( )
A. B.
第2页 | 共11页C. D.
第二部分(非选择题 共100分)
二、填空题:本大题共6小题,每小题4分,共24分. 把答案填写在答题卡相应位置上.
11.集合 R| ,则 = .
12.曲线 处的切线与x轴、直线 所围成的三角形的面积为
= .
13.已知 、 均为锐角,且 = .
14. = .
15.某轻轨列车有4节车厢,现有6位乘客准备乘坐,设每一位乘客进入每节车厢是等可
能的,则这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为 .
16.连接抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号).
①菱形 ②有3条边相等的四边形 ③梯形
④平行四边形 ⑤有一组对角相等的四边形
三、解答题:本大题共6小题,共76分. 解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分13分)
若函数 的最大值为2,试确定常数a的值.
18.(本小题满分13分)
在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;
有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任
抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值 (元)的概率分布列和期望 .
19.(本小题满分13分)
已知 ,讨论函数 的极值点的个数.
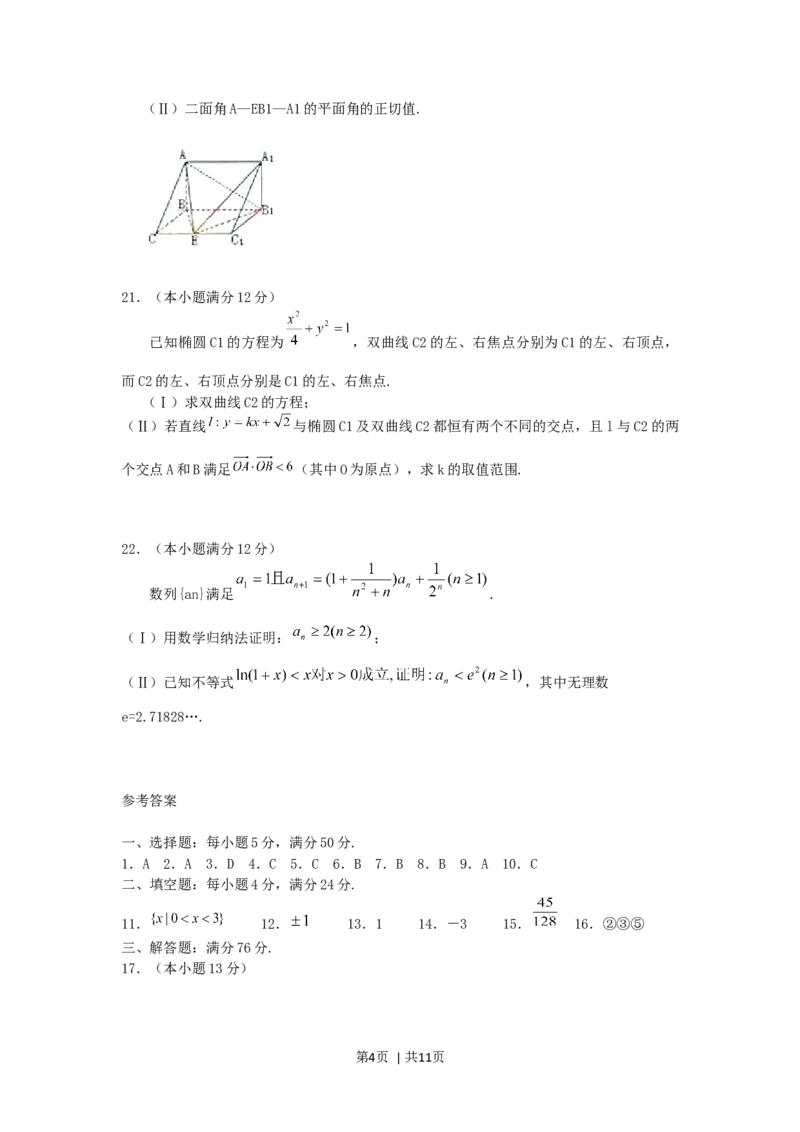
20.(本小题满分13分)
如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,
EA⊥EB1,已知AB= ,BB1=2,BC=1,∠BCC1= ,求:
(Ⅰ)异面直线AB与EB1的距离;
第3页 | 共11页(Ⅱ)二面角A—EB1—A1的平面角的正切值.
21.(本小题满分12分)
已知椭圆C1的方程为 ,双曲线C2的左、右焦点分别为C1的左、右顶点,
而C2的左、右顶点分别是C1的左、右焦点.
(Ⅰ)求双曲线C2的方程;
(Ⅱ)若直线 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两
个交点A和B满足 (其中O为原点),求k的取值范围.
22.(本小题满分12分)
数列{an}满足 .
(Ⅰ)用数学归纳法证明: ;
(Ⅱ)已知不等式 ,其中无理数
e=2.71828….
参考答案
一、选择题:每小题5分,满分50分.
1.A 2.A 3.D 4.C 5.C 6.B 7.B 8.B 9.A 10.C
二、填空题:每小题4分,满分24分.
11. 12. 13.1 14.-3 15. 16.②③⑤
三、解答题:满分76分.
17.(本小题13分)
第4页 | 共11页18.(本小题13分)
解法一:
(Ⅰ) ,即该顾客中奖的概率为 .
(Ⅱ) 的所有可能值为:0,10,20,50,60(元).
0 10 20 50 60
故 有分布列:
P
从而期望
解法二:
(Ⅰ)
(Ⅱ) 的分布列求法同解法一
由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值
=2×8=16(元).
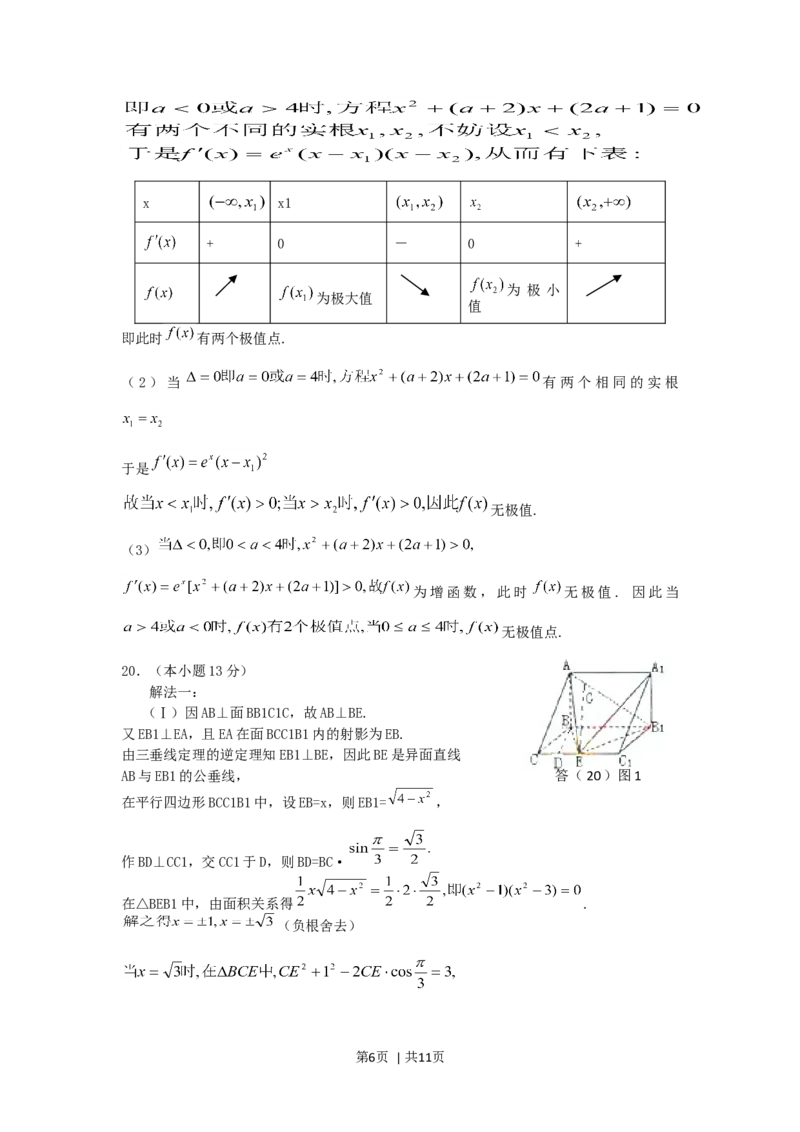
19.(本小题13分)
(1)当
第5页 | 共11页x x1
+ 0 - 0 +
为 极 小
为极大值
值
即此时 有两个极值点.
(2)当 有两个相同的实根
于是
无极值.
(3)
为增函数,此时 无极值. 因此当
无极值点.
20.(本小题13分)
解法一:
(Ⅰ)因AB⊥面BB1C1C,故AB⊥BE.
又EB1⊥EA,且EA在面BCC1B1内的射影为EB.
由三垂线定理的逆定理知EB1⊥BE,因此BE是异面直线
AB与EB1的公垂线, 答(20)图1
在平行四边形BCC1B1中,设EB=x,则EB1= ,
作BD⊥CC1,交CC1于D,则BD=BC·
在△BEB1中,由面积关系得 .
(负根舍去)
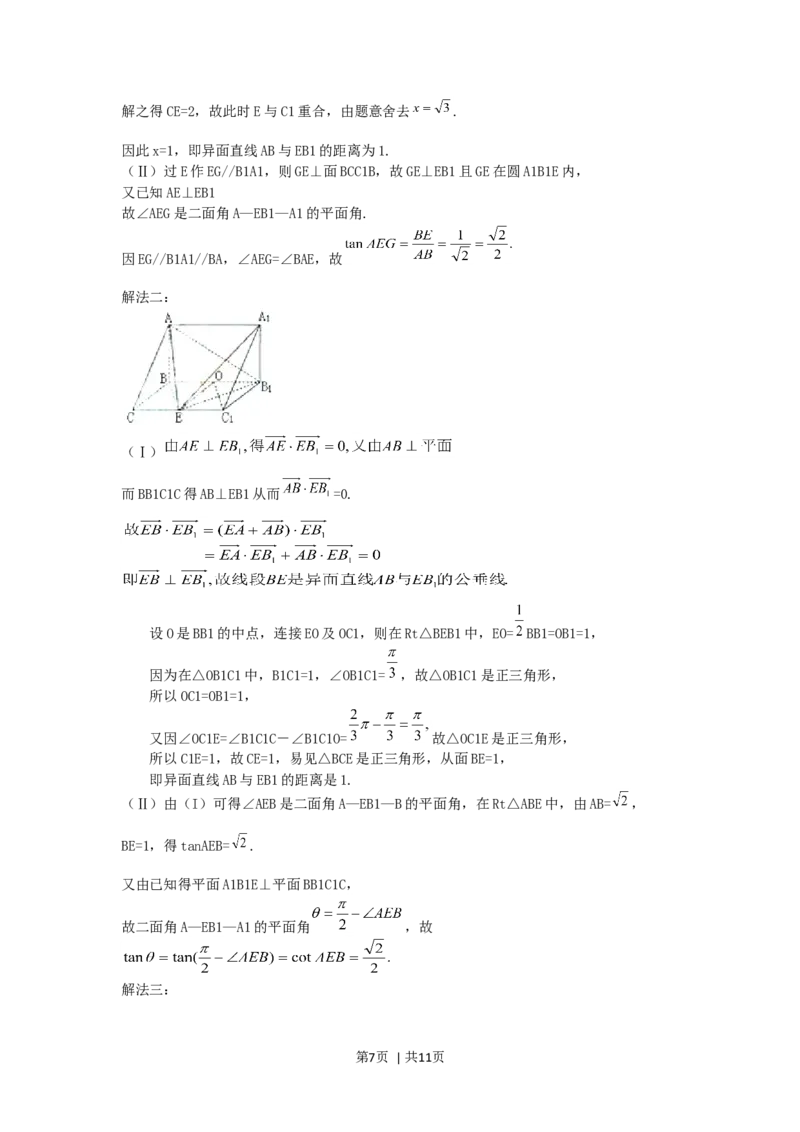
第6页 | 共11页解之得CE=2,故此时E与C1重合,由题意舍去 .
因此x=1,即异面直线AB与EB1的距离为1.
(Ⅱ)过E作EG//B1A1,则GE⊥面BCC1B,故GE⊥EB1且GE在圆A1B1E内,
又已知AE⊥EB1
故∠AEG是二面角A—EB1—A1的平面角.
因EG//B1A1//BA,∠AEG=∠BAE,故
解法二:
(Ⅰ)
而BB1C1C得AB⊥EB1从而 =0.
设O是BB1的中点,连接EO及OC1,则在Rt△BEB1中,EO= BB1=OB1=1,
因为在△OB1C1中,B1C1=1,∠OB1C1= ,故△OB1C1是正三角形,
所以OC1=OB1=1,
又因∠OC1E=∠B1C1C-∠B1C1O= 故△OC1E是正三角形,
所以C1E=1,故CE=1,易见△BCE是正三角形,从面BE=1,
即异面直线AB与EB1的距离是1.
(Ⅱ)由(I)可得∠AEB是二面角A—EB1—B的平面角,在Rt△ABE中,由AB= ,
BE=1,得tanAEB= .
又由已知得平面A1B1E⊥平面BB1C1C,
故二面角A—EB1—A1的平面角 ,故
解法三:
第7页 | 共11页(I)以B为原点, 、 分别为y、z轴建立空间直角坐标系.
由于BC=1,BB1=2,AB= ,∠BCC1= ,
在三棱柱ABC—A1B1C1中有
B(0,0,0),A(0,0, ),B1(0,2,0),
设
又AB⊥面BCC1B1,故AB⊥BE. 因此BE是异面直线AB、EB1的公垂线,
则 ,故异面直线AB、EB1的距离为1.
(II)由已知有 故二面角A—EB1—A1的平面角 的大小为向量
的夹角.
21.(本小题12分)
第8页 | 共11页解 : ( Ⅰ ) 设 双 曲 线 C2 的 方 程 为 , 则
故C2的方程为
(II)将
由直线l与椭圆C1恒有两个不同的交点得
即 ①
.
由直线l与双曲线C2恒有两个不同的交点A,B得
②
解此不等式得
③
由①、②、③得
故k的取值范围为
22.(本小题12分)
第9页 | 共11页(Ⅰ)证明:(1)当n=2时, ,不等式成立.
(2)假设当 时不等式成立,即
那么 . 这就是说,当 时不等式成立.
根据(1)、(2)可知: 成立.
(Ⅱ)证法一:
由递推公式及(Ⅰ)的结论有
两边取对数并利用已知不等式得
故
上式从1到 求和可得
即
(Ⅱ)证法二:
由数学归纳法易证 成立,故
令
取对数并利用已知不等式得
上式从2到n求和得
第10页 | 共11页因
故 成立.
第11页 | 共11页