2006年北京高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_北京

2006 年北京高考文科数学真题及答案 一、选择题（共8小题，每小题5分，满分40分） 1．（5分）设集合A{x|2x13}，B{x|3x2}，则A B等于( )  A．{x|3x1} B．{x|1x2} C．{x|x3} D．{x|x1} 2．（5分）函数y1cosx的图象( ) A．关于x轴对称 B．关于y轴对称  C．关于原点对称 D．关于直线x 对称 2 3．（5分）若a与b  c都是非零向量，则“a b  a c”是“a(b  c)”的( )   A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 4．（5分）在1，2，3，4，5这五个数字组成的没有重复数字的三位数中，各位数字之和为 奇数的共有( ) A．36个 B．24个 C．18个 D．6个 (3a1)x4a,x„1 5．（5 分）已知 f(x) 是(,)上的减函数，那么a的取值范围是( log x,x1 a ) 1 1 1 1 A．(0,1) B．(0, ) C．[ , ) D．[ ,1) 3 7 3 7 6．（5分）如果1，a，b，c，9成等比数列，那么( ) A．b3，ac9 B．b3，ac9 C．b3，ac9 D．b3，ac9 7．（5分）设A、B、C、D是空间四个不同的点，在下列命题中，不正确的是( ) A．若AC与BD共面，则AD与BC共面 B．若AC与BD是异面直线，则AD与BC是异面直线 C．若AB AC，DBDC ，则ADBC D．若AB AC，DBDC ，则ADBC 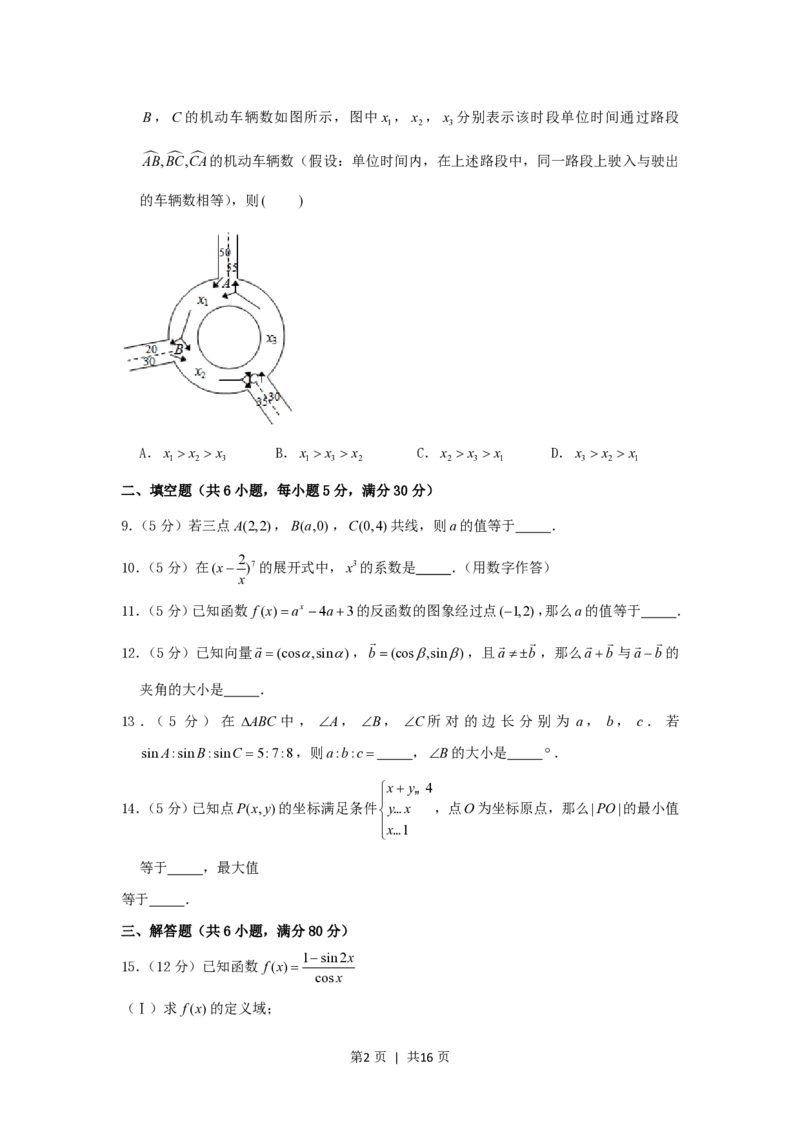8．（5分）如图为某三岔路口交通环岛的简化模型，在某高峰时段，单位时间进出路口A， 第1页 | 共16页B，C的机动车辆数如图所示，图中x ，x ，x 分别表示该时段单位时间通过路段 1 2 3 AB,BC,CA的机动车辆数（假设：单位时间内，在上述路段中，同一路段上驶入与驶出 的车辆数相等），则( ) A．x x x B．x x x C．x x x D．x x x 1 2 3 1 3 2 2 3 1 3 2 1 二、填空题（共6小题，每小题5分，满分30分） 9．（5分）若三点A(2,2)，B(a,0)，C(0,4)共线，则a的值等于 ． 2 10．（5分）在(x )7的展开式中，x3的系数是 ．（用数字作答） x 11．（5分）已知函数 f(x)ax 4a3的反函数的图象经过点(1,2)，那么a的值等于 ． 12．（5分）已知向量a(cos,sin)，b  (cos,sin)，且ab  ，那么ab  与ab  的 夹角的大小是 ． 13 ．（ 5 分 ） 在 ABC 中 ， A， B， C所 对 的 边 长 分 别 为 a， b， c． 若 sinA:sinB:sinC 5:7:8，则a:b:c ，B的大小是 ． x y„ 4  14．（5分）已知点P(x,y)的坐标满足条件y…x ，点O为坐标原点，那么|PO|的最小值  x…1 等于 ，最大值 等于 ． 三、解答题（共6小题，满分80分） 1sin2x 15．（12分）已知函数 f(x) cosx （Ⅰ）求 f(x)的定义域； 第2页 | 共16页4 （Ⅱ）设是第四象限的角，且tan ，求 f()的值． 3 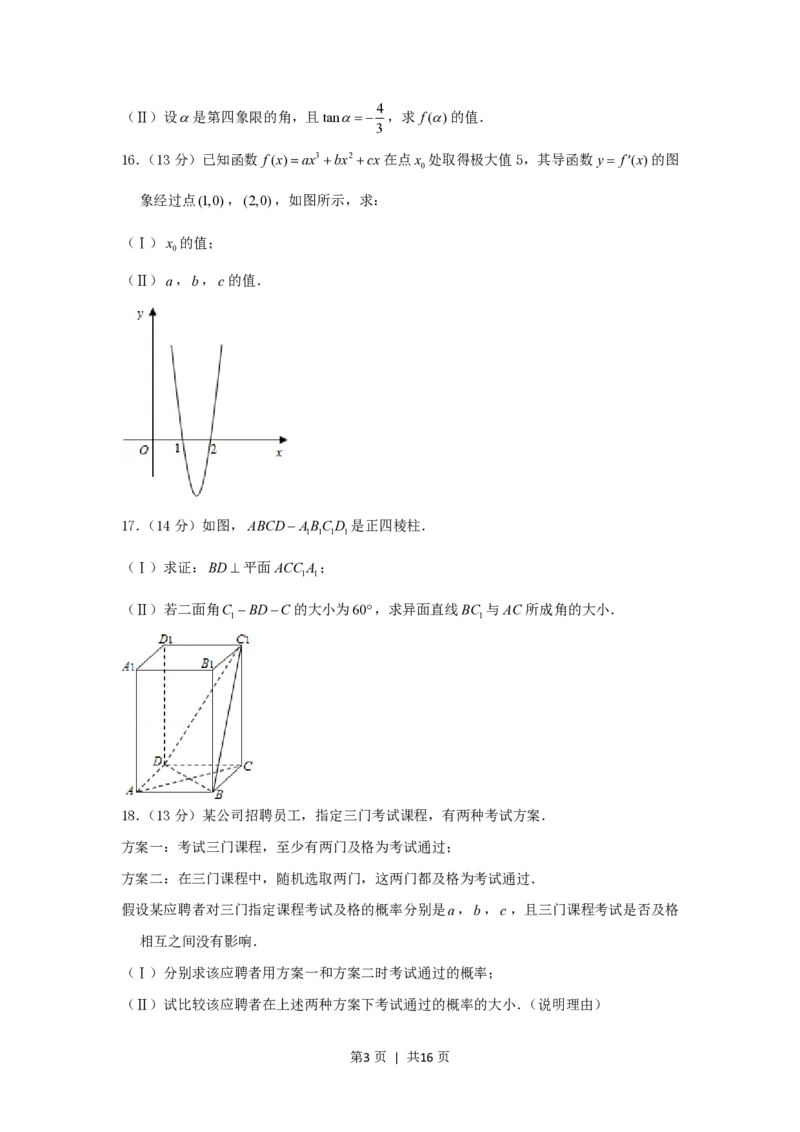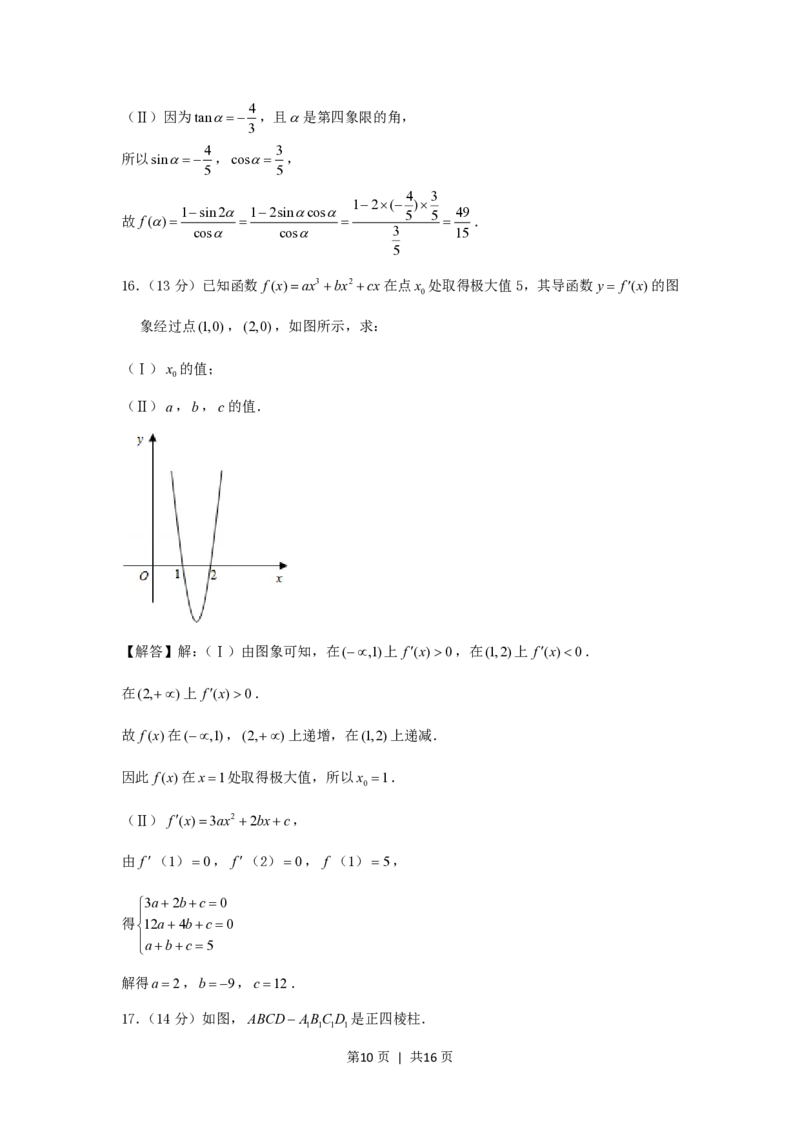16．（13分）已知函数 f(x)ax3 bx2 cx在点x 处取得极大值5，其导函数y f(x)的图 0 象经过点(1,0)，(2,0)，如图所示，求： （Ⅰ）x 的值； 0 （Ⅱ）a，b，c的值． 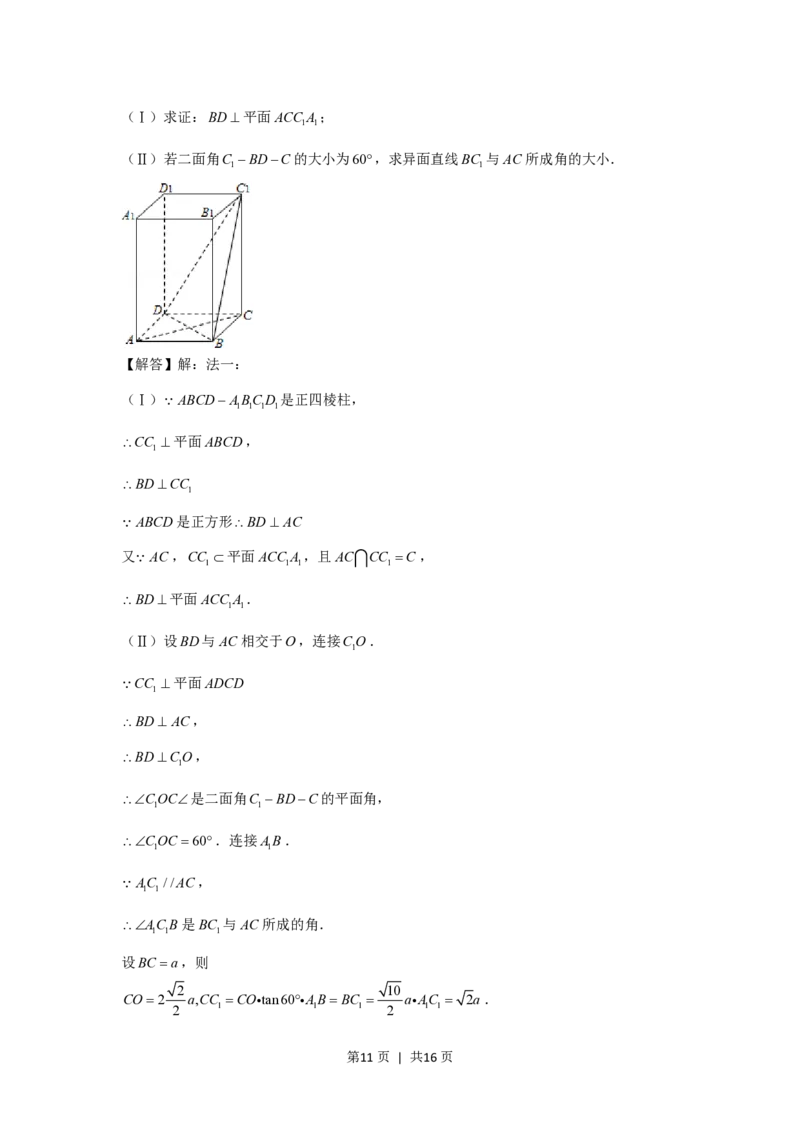17．（14分）如图，ABCDABCD 是正四棱柱． 1 1 1 1 （Ⅰ）求证：BD平面ACC A ； 1 1 （Ⅱ）若二面角C BDC的大小为60，求异面直线BC 与AC所成角的大小． 1 1 18．（13分）某公司招聘员工，指定三门考试课程，有两种考试方案． 方案一：考试三门课程，至少有两门及格为考试通过； 方案二：在三门课程中，随机选取两门，这两门都及格为考试通过． 假设某应聘者对三门指定课程考试及格的概率分别是a，b，c，且三门课程考试是否及格 相互之间没有影响． （Ⅰ）分别求该应聘者用方案一和方案二时考试通过的概率； （Ⅱ）试比较该应聘者在上述两种方案下考试通过的概率的大小．（说明理由） 第3页 | 共16页x2 y2 19．（14分）已知椭圆  1(ab0)的左、右焦点分别为F ，F ，点P在此椭圆上， a2 b2 1 2 4 14 且PF FF ，|PF | ，|PF | ． 1 1 2 1 3 2 3 （1）求椭圆的方程； （2）若直线l过圆x2  y2 4x2y0的圆心M 且交椭圆于A，B两点，且A，B关于点 M 对称，求直线l的方程． 20．（14分）设等差数列{a }的首项a 及公差d都为整数，前n项和为S ． n 1 n （Ⅰ）若a 0，S 98，求数列{a }的通项公式； 11 14 n （Ⅱ）若a…6，a 0，S „ 77，求所有可能的数列{a }的通项公式． 1 11 14 n 2006年北京高考文科数学真题参考答案 一、选择题（共8小题，每小题5分，满分40分） 1．（5分）设集合A{x|2x13}，B{x|3x2}，则A B等于( )  A．{x|3x1} B．{x|1x2} C．{x|x3} D．{x|x1} 【解答】解： A{x|2x13}{x|x1}，B{x|3x2}，  A B{x|3x1}  故选：A． 2．（5分）函数y1cosx的图象( ) A．关于x轴对称 B．关于y轴对称  C．关于原点对称 D．关于直线x 对称 2 【解答】解： 余弦函数ycosx是偶函数  函数y1cos是偶函数，故关于y轴对称， 故选：B． 3．（5分）若a与b  c都是非零向量，则“a b  a c”是“a(b  c)”的( )   A．充分而不必要条件 B．必要而不充分条件 第4页 | 共16页C．充分必要条件 D．既不充分也不必要条件 【解答】解： a b  a c    a b  a c0   a (b  c)0  a(b  c)， 由于本过程可逆， 故选：C． 4．（5分）在1，2，3，4，5这五个数字组成的没有重复数字的三位数中，各位数字之和为 奇数的共有( ) A．36个 B．24个 C．18个 D．6个 【解答】解：由题意知本题是一个分类计数问题， 各位数字之和为奇数的有两类： ①两个偶数一个奇数：有C1A3 18个； 3 3 ②三个都是奇数：有A3 6个． 3 根据分类计数原理知共有18624个． 故选：B． (3a1)x4a,x„1 5．（5 分）已知 f(x) 是(,)上的减函数，那么a的取值范围是( log x,x1 a ) 1 1 1 1 A．(0,1) B．(0, ) C．[ , ) D．[ ,1) 3 7 3 7 【解答】解：依题意，有0a1且3a10， 1 解得0a ， 3 又当x1时，(3a1)x4a7a1， 当x1时，log x0， a 1 因为 f(x)在R上单调递减，所以7a1…0解得a… 7 1 1 综上： „ a 7 3 第5页 | 共16页故选：C． 6．（5分）如果1，a，b，c，9成等比数列，那么( ) A．b3，ac9 B．b3，ac9 C．b3，ac9 D．b3，ac9 【解答】解：由等比数列的性质可得ac(1)(9)9， bb9且b与奇数项的符号相同， b3， 故选：B． 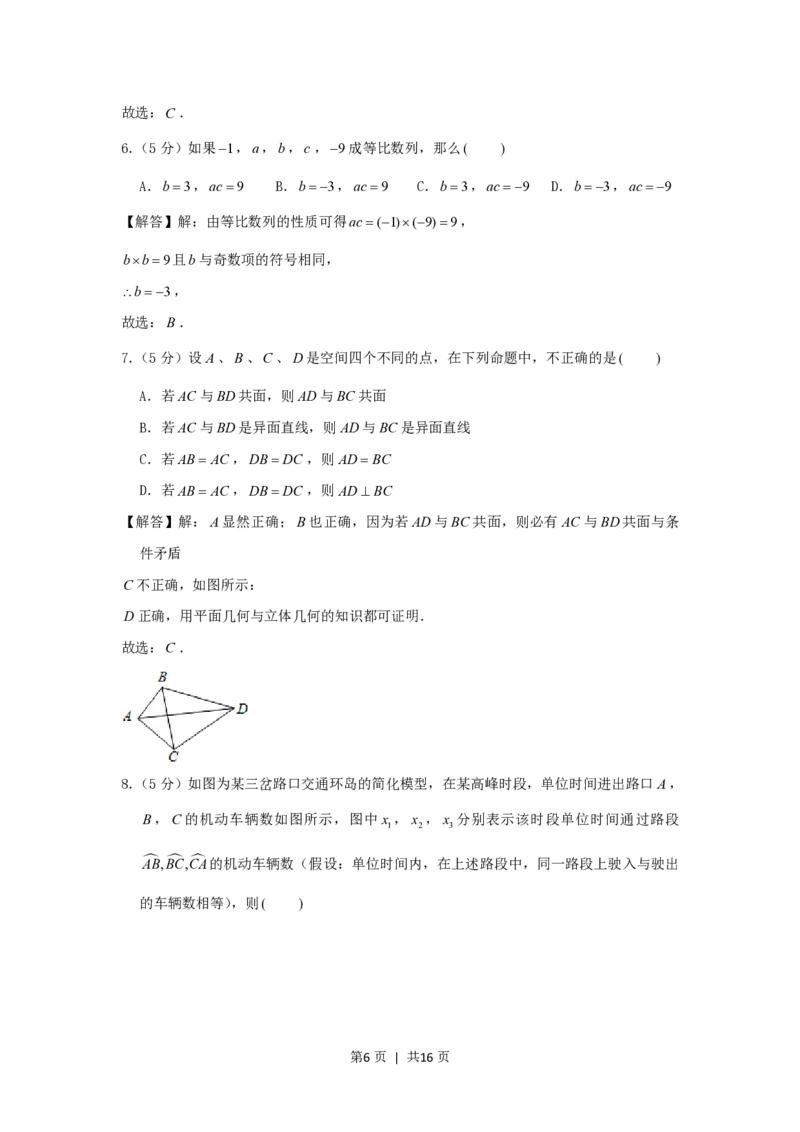7．（5分）设A、B、C、D是空间四个不同的点，在下列命题中，不正确的是( ) A．若AC与BD共面，则AD与BC共面 B．若AC与BD是异面直线，则AD与BC是异面直线 C．若AB AC，DBDC ，则ADBC D．若AB AC，DBDC ，则ADBC 【解答】解：A显然正确；B也正确，因为若AD与BC共面，则必有AC与BD共面与条 件矛盾 C不正确，如图所示： D正确，用平面几何与立体几何的知识都可证明． 故选：C． 8．（5分）如图为某三岔路口交通环岛的简化模型，在某高峰时段，单位时间进出路口A， B，C的机动车辆数如图所示，图中x ，x ，x 分别表示该时段单位时间通过路段 1 2 3 AB,BC,CA的机动车辆数（假设：单位时间内，在上述路段中，同一路段上驶入与驶出 的车辆数相等），则( ) 第6页 | 共16页A．x x x B．x x x C．x x x D．x x x 1 2 3 1 3 2 2 3 1 3 2 1 【解答】解：依题意，有x 50x 55x 5， 1 3 3 x x ， 1 3 同理，x 30x 20x 10 2 1 1 x x ， 1 2 同理，x 30x 35x 5 3 2 2 x x 3 2 故选：C． 二、填空题（共6小题，每小题5分，满分30分） 9．（5分）若三点A(2,2)，B(a,0)，C(0,4)共线，则a的值等于 4 ．   【解答】解：AB(a2,2)，AC (2,2)，   依题意，向量AB与AC共线， 故有2(a2)40， 得a4 故答案为4 2 10．（5分）在(x )7的展开式中，x3的系数是 84 ．（用数字作答） x 2 【解答】解：T Crx7r( )r (2)rCrx72r， r1 7 x 7 令72r 3， 解得r 2， 第7页 | 共16页故所求的系数为(2)2C2 84 7 故答案为84 11．（5分）已知函数 f(x)ax 4a3的反函数的图象经过点(1,2)，那么a的值等于 2 ． 【解答】解：依题意，点(1,2)在函数 f(x)ax 4a3的反函数的图象上， 则点(2,1)在函数 f(x)ax 4a3的图象上 将x2，y1，代入yax 4a3中，解得a2 故答案为：2 12．（5分）已知向量a(cos,sin)，b  (cos,sin)，且ab  ，那么ab  与ab  的  夹角的大小是 ． 2 【解答】解： ab  (coscos,sinsin)，ab  (coscos,sinsin)，  (ab  ) (ab  )(coscos)(coscos)(sinsin)(sinsin)  cos2 cos2 sin2 sin2 110 设ab  与ab  的夹角为， 则cos0，  故 ， 2  故答案为： ． 2 13 ．（ 5 分 ） 在 ABC 中 ， A， B， C所 对 的 边 长 分 别 为 a， b， c． 若 sinA:sinB:sinC 5:7:8，则a:b:c 5:7:8 ，B的大小是 ． 【解答】解：由正弦定理得sinA:sinB:sinC 5:7:8 a:b:c5:7:8 设a5k，b7k，c8k， a2 c2 b2 25k2 64k2 49k2 1 由余弦定理cosB   2ac 2 5k 8k 2    B ． 3 第8页 | 共16页 故答案为：5:7:8， 3 x y„ 4  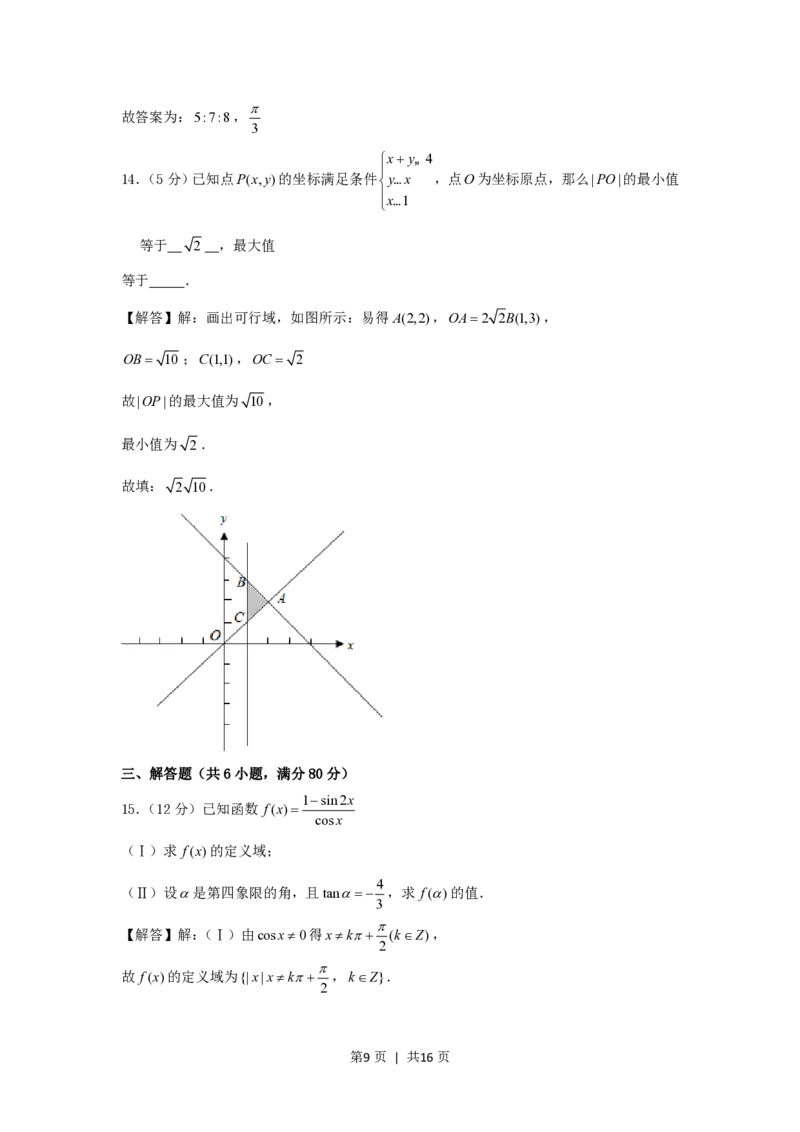14．（5分）已知点P(x,y)的坐标满足条件y…x ，点O为坐标原点，那么|PO|的最小值  x…1 等于 2 ，最大值 等于 ． 【解答】解：画出可行域，如图所示：易得A(2,2)，OA2 2B(1,3)， OB 10 ；C(1,1)，OC  2 故|OP|的最大值为 10， 最小值为 2． 故填： 2 10． 三、解答题（共6小题，满分80分） 1sin2x 15．（12分）已知函数 f(x) cosx （Ⅰ）求 f(x)的定义域； 4 （Ⅱ）设是第四象限的角，且tan ，求 f()的值． 3  【解答】解：（Ⅰ）由cosx0得xk (kZ)， 2  故 f(x)的定义域为{|x|xk ，kZ}． 2 第9页 | 共16页4 （Ⅱ）因为tan ，且是第四象限的角， 3 4 3 所以sin ，cos ， 5 5 4 3 12( ) 1sin2 12sincos 5 5 49 故 f()    ． cos cos 3 15 5 16．（13分）已知函数 f(x)ax3 bx2 cx在点x 处取得极大值5，其导函数y f(x)的图 0 象经过点(1,0)，(2,0)，如图所示，求： （Ⅰ）x 的值； 0 （Ⅱ）a，b，c的值． 【解答】解：（Ⅰ）由图象可知，在(,1)上 f(x)0，在(1,2)上 f(x)0． 在(2,)上 f(x)0． 故 f(x)在(,1)，(2,)上递增，在(1,2)上递减． 因此 f(x)在x1处取得极大值，所以x 1． 0 （Ⅱ） f(x)3ax2 2bxc， 由 f（1）0， f（2）0， f （1）5， 3a2bc0  得12a4bc0  abc5 解得a2，b9，c12． 17．（14分）如图，ABCDABCD 是正四棱柱． 1 1 1 1 第10页 | 共16页（Ⅰ）求证：BD平面ACC A ； 1 1 （Ⅱ）若二面角C BDC的大小为60，求异面直线BC 与AC所成角的大小． 1 1 【解答】解：法一： （Ⅰ） ABCDABCD 是正四棱柱，  1 1 1 1 CC 平面ABCD， 1 BDCC 1 ABCD是正方形BD AC  又 AC，CC 平面ACC A ，且AC CC C，  1 1 1  1 BD平面ACC A ． 1 1 （Ⅱ）设BD与AC相交于O，连接CO． 1 CC 平面ADCD  1 BD AC， BDCO， 1 COC是二面角C BDC的平面角， 1 1 COC 60．连接AB． 1 1 AC //AC，  1 1 ACB是BC 与AC所成的角． 1 1 1 设BC a，则 2 10 CO2 a,CC CO tan60 ABBC  a AC  2a． 2 1   1 1 2  1 1 第11页 | 共16页AC2 BC2 AB2 5 在△ABC 中，由余弦定理得cosACB 1 1 1 1  ， 1 1 1 1 2AC BC 5 1 1 1 5 ACBarccos 1 1 5 5 异面直线BC 与AC所成角的大小为arccos ． 1 5 法二： （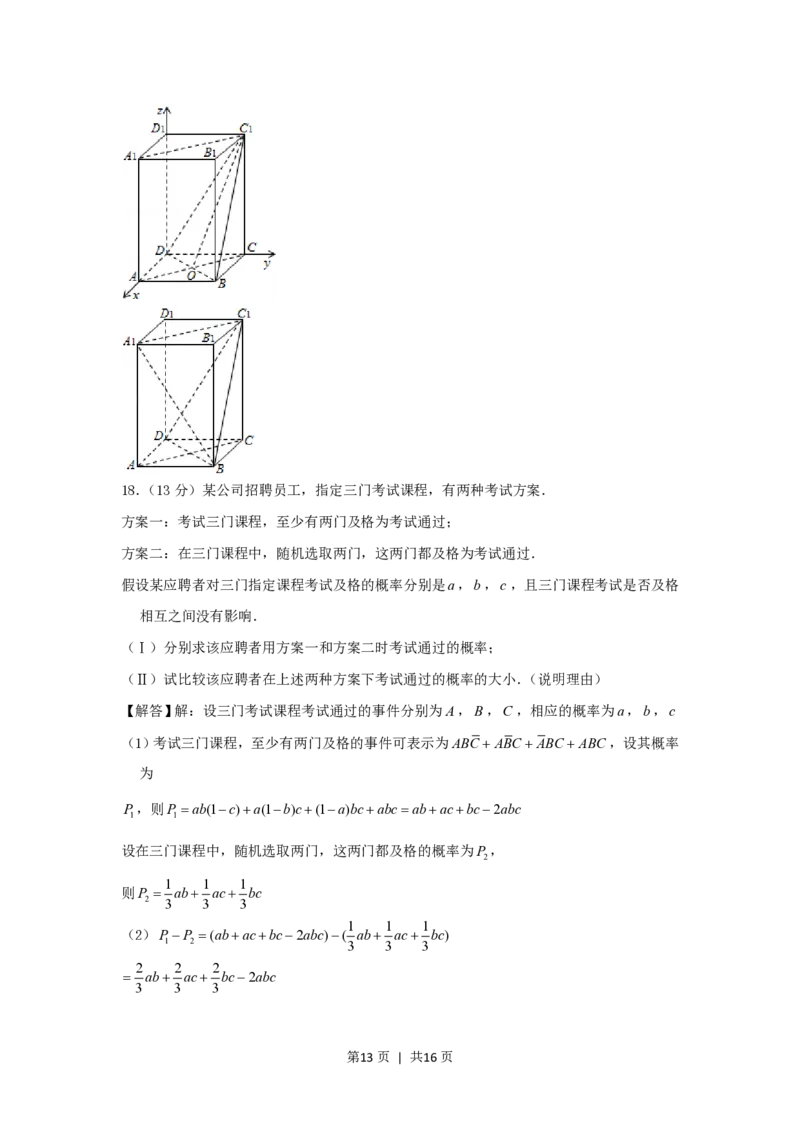Ⅰ）建立空间直角坐标系Dxyz，如图． 设ADa，DD b，则有D(0，0，0)，A(a，0，0)，B(a，a，0)，C(0，a，0)， 1 C (0，a，b)， 1        BD(a,a,0),AC (a,a,0),CC (0，0，b)，BD AC 0,BD CC 0， 1   1 BD AC，BDCC ， 1 又 AC，CC 平面ACC A ，且AC CC C，  1 1 1  1 BD平面ACC A ． 1 1 （Ⅱ）设BD与AC相交于O，连接CO， 1 a a  a a 则点O坐标为( , ,0),OC ( , ,b)， 2 2 1 2 2   BD OC 0，BDCO，又 BDCO，   1 1  COC 是二面角CBDC的平面角，COC 60， 1 1 1 CC b 6 tanCOC  1   3，b a．  1 OC 2 2 a 2   AC (a,a,0),BC (a，0，b)，  1   cos  A  C  ,  B  C   AC  BC 1  5 ， 1 |  A  C  ||  B  C  | 5  1 5 异面直线BC 与AC所成角的大小为arccos ． 1 5 第12页 | 共16页18．（13分）某公司招聘员工，指定三门考试课程，有两种考试方案． 方案一：考试三门课程，至少有两门及格为考试通过； 方案二：在三门课程中，随机选取两门，这两门都及格为考试通过． 假设某应聘者对三门指定课程考试及格的概率分别是a，b，c，且三门课程考试是否及格 相互之间没有影响． （Ⅰ）分别求该应聘者用方案一和方案二时考试通过的概率； （Ⅱ）试比较该应聘者在上述两种方案下考试通过的概率的大小．（说明理由） 【解答】解：设三门考试课程考试通过的事件分别为A，B，C，相应的概率为a，b，c （1）考试三门课程，至少有两门及格的事件可表示为ABC ABC ABC ABC，设其概率 为 P，则P ab(1c)a(1b)c(1a)bcabcabacbc2abc 1 1 设在三门课程中，随机选取两门，这两门都及格的概率为P ， 2 1 1 1 则P  ab ac bc 2 3 3 3 1 1 1 （2）P P (abacbc2abc)( ab ac bc) 1 2 3 3 3 2 2 2  ab ac bc2abc 3 3 3 第13页 | 共16页2  (abacbc3abc) 3 2  [ab(1c)ac(1b)bc(1a)]0 3 P P 即用方案一的概率大于用方案二的概率． 1 2 x2 y2 19．（14分）已知椭圆  1(ab0)的左、右焦点分别为F ，F ，点P在此椭圆上， a2 b2 1 2 4 14 且PF FF ，|PF | ，|PF | ． 1 1 2 1 3 2 3 （1）求椭圆的方程； （2）若直线l过圆x2  y2 4x2y0的圆心M 且交椭圆于A，B两点，且A，B关于点 M 对称，求直线l的方程． 【解答】解：（Ⅰ）因为点P在椭圆C上，所以2a|PF ||PF |6，a3． 1 2 在Rt△PFF 中，|FF | |PF |2 |PF |2 2 5， 1 2 1 2 2 1 故椭圆的半焦距c 5， 从而b2 a2 c2 4， x2 y2 所以椭圆C的方程为  1． 9 4 （Ⅱ）解法一： 设A，B的坐标分别为(x ，y )、(x ，y )． 1 1 2 2 已知圆的方程为(x2)2 (y1)2 5， 所以圆心M 的坐标为(2,1)． 从而可设直线l的方程为 yk(x2)1， 代入椭圆C的方程得 (49k2)x2 (36k2 18k)x36k2 36k270． 因为A，B关于点M 对称． x x 18k2 9k 所以 1 2  2． 2 49k2 8 解得k  ， 9 第14页 | 共16页8 所以直线l的方程为y (x2)1， 9 即8x9y250． （经检验，所求直线方程符合题意） （Ⅱ）解法二： 已知圆的方程为(x2)2 (y1)2 5， 所以圆心M 的坐标为(2,1)． 设A，B的坐标分别为(x ，y )，(x ，y )． 1 1 2 2 x2 y2 x 2 y 2 由题意x  x 且 1  1 1，① 2  2 1，② 1 2 9 4 9 4 (x x )(x x ) (y  y )(y  y ) 由①②得 1 2 1 2  1 2 1 2 0．③ 9 4 因为A、B关于点M 对称， 所以x x 4，y  y 2， 1 2 1 2 y  y 8 代入③得 1 2  ， x x 9 1 2 8 即直线l的斜率为 ， 9 8 所以直线l的方程为y1 (x2)， 9 即8x9y250． （经检验，所求直线方程符合题意．) 20．（14分）设等差数列{a }的首项a 及公差d都为整数，前n项和为S ． n 1 n （Ⅰ）若a 0，S 98，求数列{a }的通项公式； 11 14 n （Ⅱ）若a…6，a 0，S „ 77，求所有可能的数列{a }的通项公式． 1 11 14 n 【解答】解：（Ⅰ）由S 98得2a 13d 14， 14 1 又a a 10d 0， 11 1 解得d 2，a 20． 1 {a }的通项公式是a 222n， n n 第15页 | 共16页S „ 77 14  （Ⅱ）由a 0 11  a…6 1 2a 13d„11 1  得a 10d0 1  a…6 1 2a 13d„11 1  即2a 20d0 1  2a„ 12 1 由①②得7d 11． 11 即d  ． 7 由①③得13d„ 1 1 即d„  13 11 1 于是 d„  7 13 又dZ ，故 d 1④ 将④代入①②得10a„12． 1 又a Z ，故a 11或a 12． 1 1 1 所有可能的数列{a }的通项公式是 n a 12n和a 13n， n n 第16页 | 共16页