文档内容
2006 年山西高考理科数学真题及答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)设集合M={x|x2﹣x<0},N={x||x|<2},则( )
A.M∩N=∅ B.M∩N=M C.M∪N=M D.M∪N=R
2.(5分)已知函数y=ex的图象与函数y=f(x)的图象关于直线y=x对称,则( )
A.f(2x)=e2x(x∈R) B.f(2x)=ln2•lnx(x>0)
C.f(2x)=2ex(x∈R) D.f(2x)=lnx+ln2(x>0)
3.(5分)双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m=( )
A. B.﹣4 C.4 D.
4.(5分)如果复数(m2+i)(1+mi)是实数,则实数m=( )
A.1 B.﹣1 C. D.
5.(5分)函数 的单调增区间为( )
A. B.(kπ,(k+1)π),k∈Z
C. D.
6.(5分)△ABC的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且c=2a,
则cosB=( )
A. B. C. D.
7.(5分)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
( )
A.16π B.20π C.24π D.32π
8.(5分)抛物线y=﹣x2上的点到直线4x+3y﹣8=0距离的最小值是( )
A. B. C. D.3
9.(5 分)设平面向量 、 、 的和 + + =0.如果向量 、 、 ,满足
1 2 3 1 2 3 1 2 3
| |=2| |,且 顺时针旋转30°后与 同向,其中i=1,2,3,则( )
i i i i
A.﹣ + + =0 B. ﹣ + =0 C. + ﹣ =0 D. + + =0
1 2 3 1 2 3 1 2 3 1 2 3
10.(5分)设{a}是公差为正数的等差数列,若a+a+a=15,aaa=80,则a +a +a =( )
n 1 2 3 1 2 3 11 12 13
第1页 | 共17页A.120 B.105 C.90 D.75
11.(5分)用长度分别为2、3、4、5、6(单位:cm)的5根细木棒围成一个三角形(允许
连接,但不允许折断),能够得到的三角形的最大面积为( )
A. B. C. D.20cm2
12.(5分)设集合I={1,2,3,4,5}.选择I的两个非空子集A和B,要使B中最小的数
大于A中最大的数,则不同的选择方法共有( )
A.50种B.49种C.48种D.47种
二、填空题(共4小题,每小题4分,满分16分)
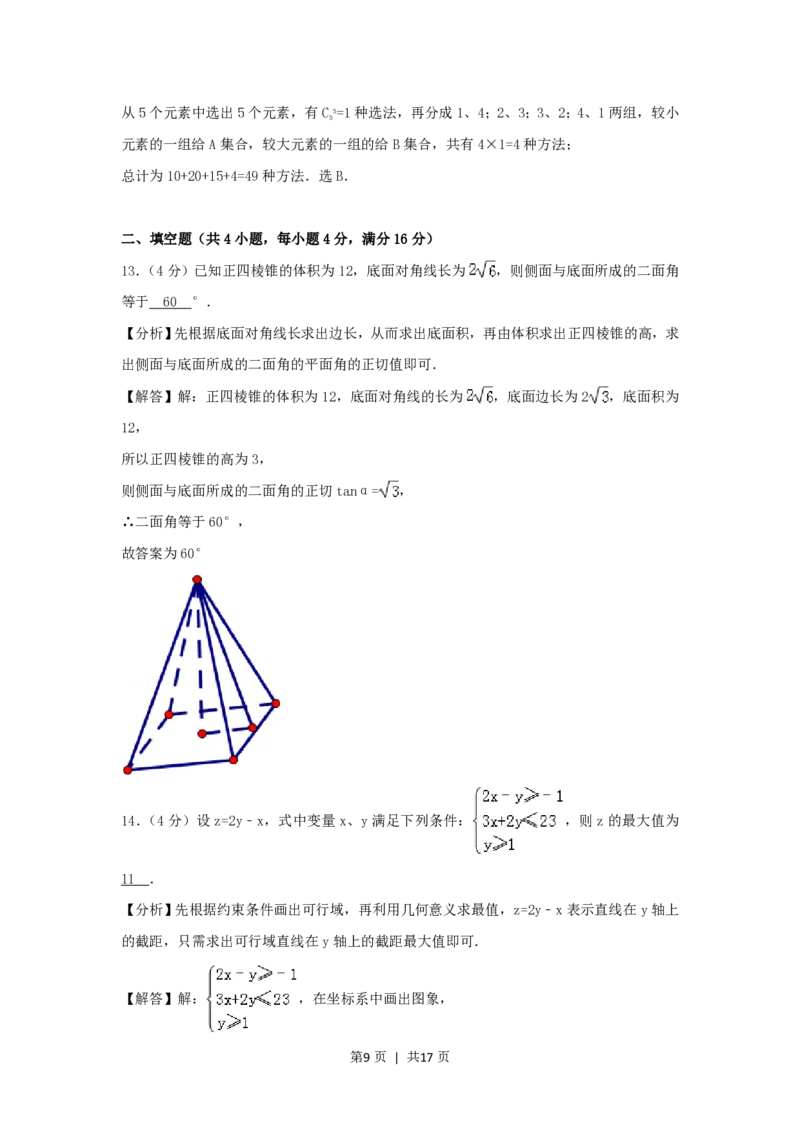
13.(4分)已知正四棱锥的体积为12,底面对角线长为 ,则侧面与底面所成的二面角
等于 °.
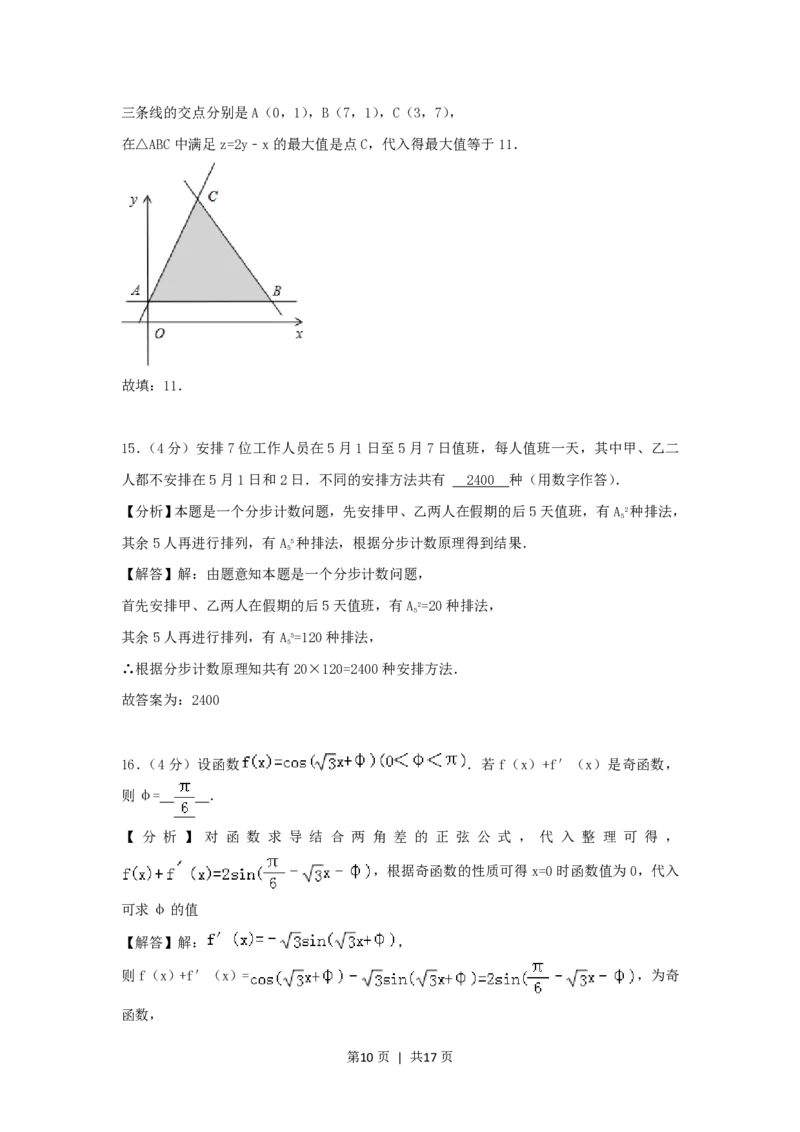
14.(4分)设z=2y﹣x,式中变量x、y满足下列条件: ,则z的最大值为 .
15.(4分)安排7位工作人员在5月1日至5月7日值班,每人值班一天,其中甲、乙二
人都不安排在5月1日和2日.不同的安排方法共有 种(用数字作答).
16.(4分)设函数 .若f(x)+f′(x)是奇函数,
则φ= .
三、解答题(共6小题,满分74分)
17.(12分)ABC的三个内角为A、B、C,求当A为何值时, 取得最大值,
并求出这个最大值.
18.(12分)A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由
4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服
用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A
有效的概率为 ,服用B有效的概率为 .
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用ξ表示这3个试验组中甲类组的个数,求ξ的分布列和数学期
望.
第2页 | 共17页19.(12分)如图,l、l 是互相垂直的异面直线,MN是它们的公垂线段.点A、B在l 上,C
1 2 1
在l 上,AM=MB=MN.
2
(Ⅰ)证明AC⊥NB;
(Ⅱ)若∠ACB=60°,求NB与平面ABC所成角的余弦值.
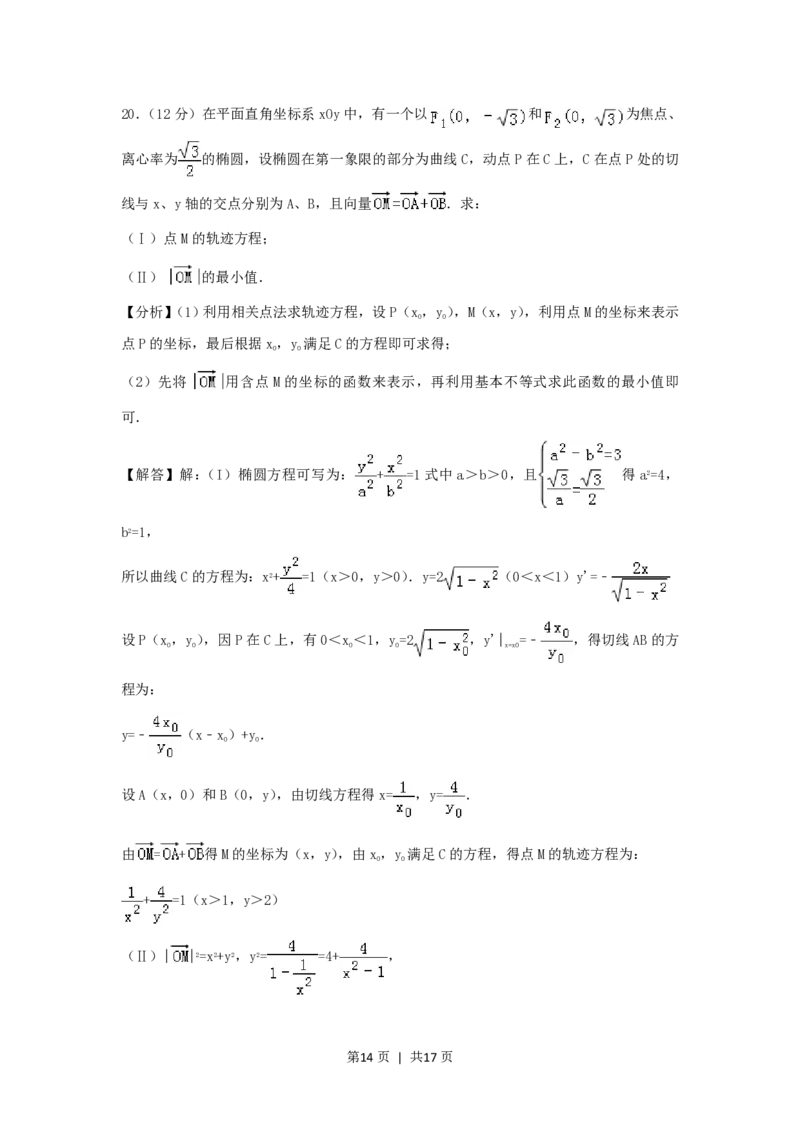
20.(12分)在平面直角坐标系xOy中,有一个以 和 为焦点、
离心率为 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切
线与x、y轴的交点分别为A、B,且向量 .求:
(Ⅰ)点M的轨迹方程;
(Ⅱ) 的最小值.
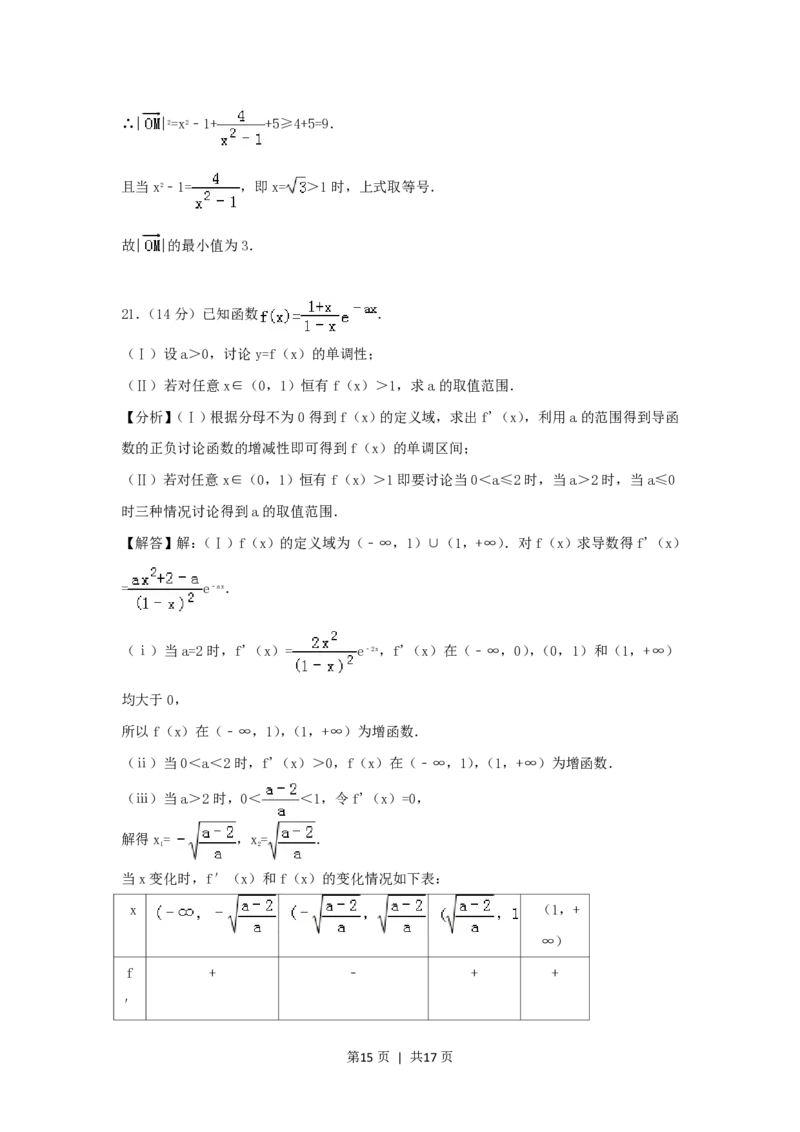
21.(14分)已知函数 .
(Ⅰ)设a>0,讨论y=f(x)的单调性;
(Ⅱ)若对任意x∈(0,1)恒有f(x)>1,求a的取值范围.
22.(12分)设数列{a}的前n项的和 ,n=1,2,3,…
n
(Ⅰ)求首项a 与通项a;
1 n
(Ⅱ)设 ,n=1,2,3,…,证明: .
2006年山西高考理科数学真题参考答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)设集合M={x|x2﹣x<0},N={x||x|<2},则( )
A.M∩N=∅ B.M∩N=M C.M∪N=M D.M∪N=R
【分析】M、N分别是二次不等式和绝对值不等式的解集,分别解出再求交集合并集.
第3页 | 共17页【解答】解:集合M={x|x2﹣x<0}={x|0<x<1},N={x||x|<2}={x|﹣2<x<2},∴M∩N=M,
故选:B.
2.(5分)已知函数y=ex的图象与函数y=f(x)的图象关于直线y=x对称,则( )
A.f(2x)=e2x(x∈R) B.f(2x)=ln2•lnx(x>0)
C.f(2x)=2ex(x∈R) D.f(2x)=lnx+ln2(x>0)
【分析】本题考查反函数的概念、互为反函数的函数图象的关系、求反函数的方法等相关知
识和方法.
根据函数y=ex的图象与函数y=f(x)的图象关于直线y=x对称可知f(x)是y=ex的反函数,
由此可得f(x)的解析式,进而获得f(2x).
【解答】解:函数y=ex的图象与函数y=f(x)的图象关于直线y=x对称,
所以f(x)是y=ex的反函数,即f(x)=lnx,
∴f(2x)=ln2x=lnx+ln2(x>0),
选D.
3.(5分)双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m=( )
A. B.﹣4 C.4 D.
【分析】由双曲线mx2+y2=1的虚轴长是实轴长的2倍,可求出该双曲线的方程,从而求出m
的值.
【解答】解:双曲线mx2+y2=1的虚轴长是实轴长的2倍,
∴m<0,且双曲线方程为 ,
∴m= ,
故选:A.
4.(5分)如果复数(m2+i)(1+mi)是实数,则实数m=( )
A.1 B.﹣1 C. D.
【分析】注意到复数a+bi(a∈R,b∈R)为实数的充要条件是b=0
【解答】解:复数(m2+i)(1+mi)=(m2﹣m)+(1+m3)i是实数,
∴1+m3=0,m=﹣1,
第4页 | 共17页选B.
5.(5分)函数 的单调增区间为( )
A. B.(kπ,(k+1)π),k∈Z
C. D.
【分析】先利用正切函数的单调性求出函数单调增时x+ 的范围i,进而求得x的范围.
【解答】解:函数 的单调增区间满足 ,
∴单调增区间为 ,
故选C
6.(5分)△ABC的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且c=2a,
则cosB=( )
A. B. C. D.
【分析】根据等比数列的性质,可得b= a,将c、b与a的关系结合余弦定理分析可得答
案.
【解答】解:△ABC中,a、b、c成等比数列,则b2=ac,
由c=2a,则b= a,
= ,
故选B.
7.(5分)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
( )
A.16π B.20π C.24π D.32π
【分析】先求正四棱柱的底面边长,然后求其对角线,就是球的直径,再求其表面积.
【解答】解:正四棱柱高为4,体积为16,底面积为4,正方形边长为2,
正四棱柱的对角线长即球的直径为2 ,
第5页 | 共17页∴球的半径为 ,球的表面积是24π,
故选C.
8.(5分)抛物线y=﹣x2上的点到直线4x+3y﹣8=0距离的最小值是( )
A. B. C. D.3
【分析】设抛物线 y=﹣x2上一点为(m,﹣m2),该点到直线 4x+3y﹣8=0 的距离为
,由此能够得到所求距离的最小值.
【解答】解:设抛物线y=﹣x2上一点为(m,﹣m2),
该点到直线4x+3y﹣8=0的距离为 ,
分析可得,当m= 时,取得最小值为 ,
故选B.
9.(5 分)设平面向量 、 、 的和 + + =0.如果向量 、 、 ,满足
1 2 3 1 2 3 1 2 3
| |=2| |,且 顺时针旋转30°后与 同向,其中i=1,2,3,则( )
i i i i
A.﹣ + + =0 B. ﹣ + =0 C. + ﹣ =0 D. + + =0
1 2 3 1 2 3 1 2 3 1 2 3
【分析】三个向量的和为零向量,在这三个向量前都乘以相同的系数,我们可以把系数提出
公因式,括号中各项的和仍是题目已知中和为零向量的三个向量,当三个向量都按相同的方
向和角度旋转时,相对关系不变.
【解答】解:向量 、 、 的和 + + =0,
1 2 3 1 2 3
向量 、 、 顺时针旋转30°后与 、 、 同向,
1 2 3 1 2 3
且| |=2| |,
i i
∴ + + =0,
1 2 3
故选D.
10.(5分)设{a}是公差为正数的等差数列,若a+a+a=15,aaa=80,则a +a +a =( )
n 1 2 3 1 2 3 11 12 13
第6页 | 共17页A.120 B.105 C.90 D.75
【分析】先由等差数列的性质求得a,再由aaa=80求得d即可.
2 1 2 3
【解答】解:{a}是公差为正数的等差数列,
n
∵a+a+a=15,aaa=80,
1 2 3 1 2 3
∴a=5,
2
∴aa=(5﹣d)(5+d)=16,
1 3
∴d=3,a =a+10d=35
12 2
∴a +a +a =105
11 12 13
故选B.
11.(5分)用长度分别为2、3、4、5、6(单位:cm)的5根细木棒围成一个三角形(允许
连接,但不允许折断),能够得到的三角形的最大面积为( )
A. B. C. D.20cm2
【分析】设三角形的三边分别为 a,b,c,令 p= ,则 p=10.海伦公式 S=
≤ = 故排除C,D,
由于等号成立的条件为10﹣a=10﹣b=10﹣c,故“=”不成立,推测当三边长相等时面积最
大,故考虑当a,b,c三边长最接近时面积最大,进而得到答案.
【解答】解:设三角形的三边分别为a,b,c,
令p= ,则p=10.由海伦公式S=
知 S=
≤ = <20<3
由于等号成立的条件为10﹣a=10﹣b=10﹣c,故“=”不成立,
∴S<20< .
3
排除C,D.
由以上不等式推测,当三边长相等时面积最大,故考虑当a,b,c三边长最接近时面积最大,
此时三边长为7,7,6,用2、5连接,3、4连接各为一边,第三边长为7组成三角形,此
第7页 | 共17页三角形面积最大,面积为 ,
故选B.
12.(5分)设集合I={1,2,3,4,5}.选择I的两个非空子集A和B,要使B中最小的数
大于A中最大的数,则不同的选择方法共有( )
A.50种B.49种C.48种D.47种
【分析】解法一,根据题意,按A、B的元素数目不同,分9种情况讨论,分别计算其选法
种数,进而相加可得答案;
解法二,根据题意,B中最小的数大于A中最大的数,则集合A、B中没有相同的元素,且
都不是空集,按A、B中元素数目这和的情况,分4种情况讨论,分别计算其选法种数,进
而相加可得答案.
【解答】解:
解法一,若集合A、B中分别有一个元素,则选法种数有C2=10种;
5
若集合A中有一个元素,集合B中有两个元素,则选法种数有C3=10种;
5
若集合A中有一个元素,集合B中有三个元素,则选法种数有C4=5种;
5
若集合A中有一个元素,集合B中有四个元素,则选法种数有C5=1种;
5
若集合A中有两个元素,集合B中有一个元素,则选法种数有C3=10种;
5
若集合A中有两个元素,集合B中有两个元素,则选法种数有C4=5种;
5
若集合A中有两个元素,集合B中有三个元素,则选法种数有C5=1种;
5
若集合A中有三个元素,集合B中有一个元素,则选法种数有C4=5种;
5
若集合A中有三个元素,集合B中有两个元素,则选法种数有C5=1种;
5
若集合A中有四个元素,集合B中有一个元素,则选法种数有C5=1种;
5
总计有49种,选B.
解法二:集合A、B中没有相同的元素,且都不是空集,
从5个元素中选出2个元素,有C2=10种选法,小的给A集合,大的给B集合;
5
从5个元素中选出3个元素,有C3=10种选法,再分成1、2两组,较小元素的一组给A集
5
合,较大元素的一组的给B集合,共有2×10=20种方法;
从5个元素中选出4个元素,有C4=5种选法,再分成1、3;2、2;3、1两组,较小元素的
5
一组给A集合,较大元素的一组的给B集合,共有3×5=15种方法;
第8页 | 共17页从5个元素中选出5个元素,有C5=1种选法,再分成1、4;2、3;3、2;4、1两组,较小
5
元素的一组给A集合,较大元素的一组的给B集合,共有4×1=4种方法;
总计为10+20+15+4=49种方法.选B.
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)已知正四棱锥的体积为12,底面对角线长为 ,则侧面与底面所成的二面角
等于 60 °.
【分析】先根据底面对角线长求出边长,从而求出底面积,再由体积求出正四棱锥的高,求
出侧面与底面所成的二面角的平面角的正切值即可.
【解答】解:正四棱锥的体积为12,底面对角线的长为 ,底面边长为2 ,底面积为
12,
所以正四棱锥的高为3,
则侧面与底面所成的二面角的正切tanα= ,
∴二面角等于60°,
故答案为60°
14.(4分)设z=2y﹣x,式中变量x、y满足下列条件: ,则z的最大值为
11 .
【分析】先根据约束条件画出可行域,再利用几何意义求最值,z=2y﹣x表示直线在y轴上
的截距,只需求出可行域直线在y轴上的截距最大值即可.
【解答】解: ,在坐标系中画出图象,
第9页 | 共17页三条线的交点分别是A(0,1),B(7,1),C(3,7),
在△ABC中满足z=2y﹣x的最大值是点C,代入得最大值等于11.
故填:11.
15.(4分)安排7位工作人员在5月1日至5月7日值班,每人值班一天,其中甲、乙二
人都不安排在5月1日和2日.不同的安排方法共有 2400 种(用数字作答).
【分析】本题是一个分步计数问题,先安排甲、乙两人在假期的后5天值班,有A2种排法,
5
其余5人再进行排列,有A5种排法,根据分步计数原理得到结果.
5
【解答】解:由题意知本题是一个分步计数问题,
首先安排甲、乙两人在假期的后5天值班,有A2=20种排法,
5
其余5人再进行排列,有A5=120种排法,
5
∴根据分步计数原理知共有20×120=2400种安排方法.
故答案为:2400
16.(4分)设函数 .若f(x)+f′(x)是奇函数,
则φ= .
【 分 析 】 对 函 数 求 导 结 合 两 角 差 的 正 弦 公 式 , 代 入 整 理 可 得 ,
,根据奇函数的性质可得x=0时函数值为0,代入
可求φ的值
【解答】解: ,
则f(x)+f′(x)= ,为奇
函数,
第10页 | 共17页令g(x)=f(x)+f′(x),即函数g(x)为奇函数,
g(0)=0⇒2sin( φ)=0,
∵0<φ<π,
∴φ= .
故答案为: .
三、解答题(共6小题,满分74分)
17.(12分)ABC的三个内角为A、B、C,求当A为何值时, 取得最大值,
并求出这个最大值.
【分析】利用三角形中内角和为π,将三角函数变成只含角A,再利用三角函数的二倍角公
式将函数化为只含角 ,利用二次函数的最值求出最大值
【解答】解:由A+B+C=π,得 = ﹣ ,
所以有cos =sin .
cosA+2cos =cosA+2sin =1﹣2sin2 +2sin
=﹣2(sin ﹣ )2+
当sin = ,即A= 时,cosA+2cos 取得最大值为
故最大值为
18.(12分)A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由
4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服
用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A
有效的概率为 ,服用B有效的概率为 .
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用ξ表示这3个试验组中甲类组的个数,求ξ的分布列和数学期
望.
【分析】(1)由题意知本题是一个独立重复试验,根据所给的两种药物对小白鼠有效的概率,
第11页 | 共17页计算出小白鼠有效的只数的概率,对两种药物有效的小白鼠进行比较,得到甲类组的概率.
(2)由题意知本试验是一个甲类组的概率不变,实验的条件不变,可以看做是一个独立重
复试验,所以变量服从二项分布,根据二项分布的性质写出分布列和期望.
【解答】解:(1)设A 表示事件“一个试验组中,服用A有效的小鼠有i只“,i=0,1,
i
2,
B 表示事件“一个试验组中,服用B有效的小鼠有i只“,i=0,1,2,
i
依题意有:P(A)=2× × = ,P(A)= × = .P(B)= × = ,
1 2 0
P(B)=2× × = ,所求概率为:
1
P=P(B•A)+P(B•A)+P(B•A)
0 1 0 2 1 2
= × + × + × =
(Ⅱ)ξ的可能值为0,1,2,3且ξ~B(3, ).
P(ξ=0)=( )3= ,
P(ξ=1)=C1× ×( )2= ,
3
P(ξ=2)=C2×( )2× = ,
3
P(ξ=3)=( )3=
∴ξ的分布列为:
ξ 0 1 2 3
P
∴数学期望Eξ=3× = .
19.(12分)如图,l、l 是互相垂直的异面直线,MN是它们的公垂线段.点A、B在l 上,
1 2 1
C在l 上,AM=MB=MN.
2
(Ⅰ)证明AC⊥NB;
(Ⅱ)若∠ACB=60°,求NB与平面ABC所成角的余弦值.
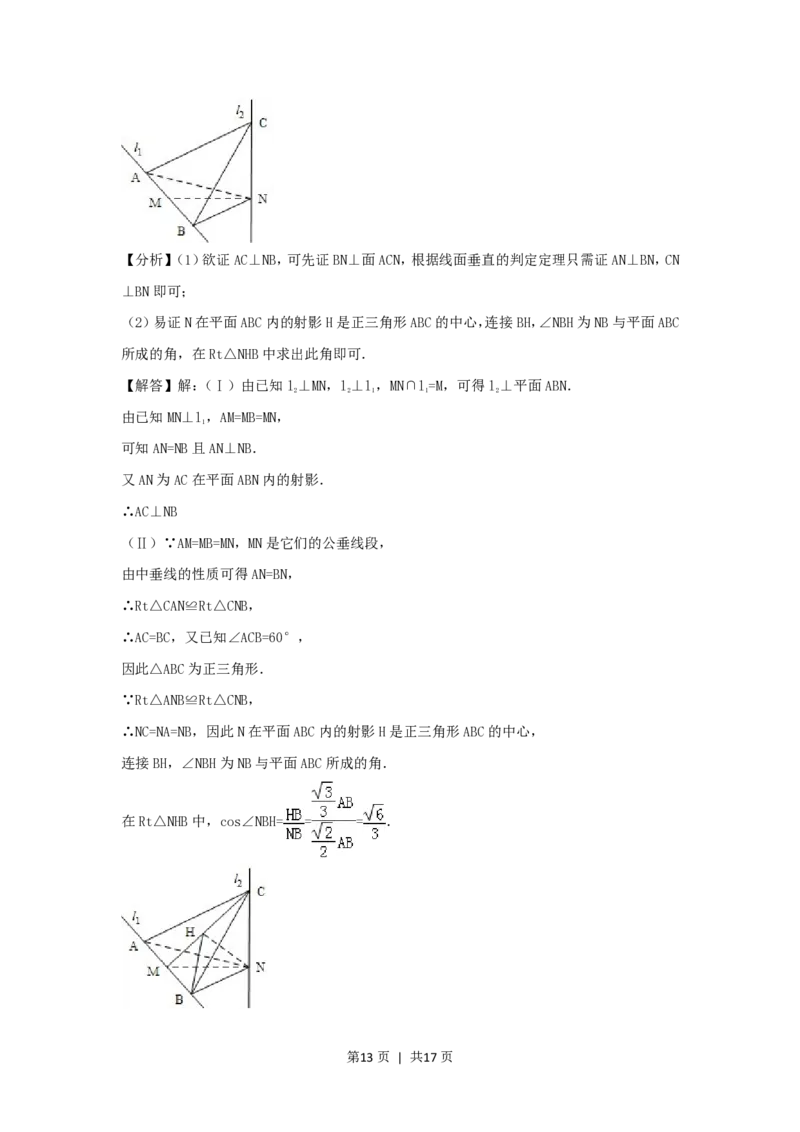
第12页 | 共17页【分析】(1)欲证AC⊥NB,可先证BN⊥面ACN,根据线面垂直的判定定理只需证AN⊥BN,CN
⊥BN即可;
(2)易证N在平面ABC内的射影H是正三角形ABC的中心,连接BH,∠NBH为NB与平面ABC
所成的角,在Rt△NHB中求出此角即可.
【解答】解:(Ⅰ)由已知l⊥MN,l⊥l,MN∩l=M,可得l⊥平面ABN.
2 2 1 1 2
由已知MN⊥l,AM=MB=MN,
1
可知AN=NB且AN⊥NB.
又AN为AC在平面ABN内的射影.
∴AC⊥NB
(Ⅱ)∵AM=MB=MN,MN是它们的公垂线段,
由中垂线的性质可得AN=BN,
∴Rt△CAN≌Rt△CNB,
∴AC=BC,又已知∠ACB=60°,
因此△ABC为正三角形.
∵Rt△ANB≌Rt△CNB,
∴NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心,
连接BH,∠NBH为NB与平面ABC所成的角.
在Rt△NHB中,cos∠NBH= = = .
第13页 | 共17页20.(12分)在平面直角坐标系xOy中,有一个以 和 为焦点、
离心率为 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切
线与x、y轴的交点分别为A、B,且向量 .求:
(Ⅰ)点M的轨迹方程;
(Ⅱ) 的最小值.
【分析】(1)利用相关点法求轨迹方程,设P(x,y),M(x,y),利用点M的坐标来表示
0 0
点P的坐标,最后根据x,y 满足C的方程即可求得;
0 0
(2)先将 用含点 M 的坐标的函数来表示,再利用基本不等式求此函数的最小值即
可.
【解答】解:(I)椭圆方程可写为: + =1式中a>b>0,且 得a2=4,
b2=1,
所以曲线C的方程为:x2+ =1(x>0,y>0).y=2 (0<x<1)y'=﹣
设P(x,y),因P在C上,有0<x<1,y=2 ,y'| =﹣ ,得切线AB的方
0 0 0 0 x=x0
程为:
y=﹣ (x﹣x)+y.
0 0
设A(x,0)和B(0,y),由切线方程得x= ,y= .
由 = + 得M的坐标为(x,y),由x,y 满足C的方程,得点M的轨迹方程为:
0 0
+ =1(x>1,y>2)
(Ⅱ)| |2=x2+y2,y2= =4+ ,
第14页 | 共17页∴| |2=x2﹣1+ +5≥4+5=9.
且当x2﹣1= ,即x= >1时,上式取等号.
故| |的最小值为3.
21.(14分)已知函数 .
(Ⅰ)设a>0,讨论y=f(x)的单调性;
(Ⅱ)若对任意x∈(0,1)恒有f(x)>1,求a的取值范围.
【分析】(Ⅰ)根据分母不为0得到f(x)的定义域,求出f'(x),利用a的范围得到导函
数的正负讨论函数的增减性即可得到f(x)的单调区间;
(Ⅱ)若对任意x∈(0,1)恒有f(x)>1即要讨论当0<a≤2时,当a>2时,当a≤0
时三种情况讨论得到a的取值范围.
【解答】解:(Ⅰ)f(x)的定义域为(﹣∞,1)∪(1,+∞).对f(x)求导数得f'(x)
= e﹣ax.
(ⅰ)当a=2时,f'(x)= e﹣2x,f'(x)在(﹣∞,0),(0,1)和(1,+∞)
均大于0,
所以f(x)在(﹣∞,1),(1,+∞)为增函数.
(ⅱ)当0<a<2时,f'(x)>0,f(x)在(﹣∞,1),(1,+∞)为增函数.
(ⅲ)当a>2时,0< <1,令f'(x)=0,
解得x= ,x= .
1 2
当x变化时,f′(x)和f(x)的变化情况如下表:
x (1,+
∞)
f + ﹣ + +
′
第15页 | 共17页(
x)
f ↑ ↓ ↑ ↑
(
x)
f(x)在(﹣∞, ),( ,1),(1,+∞)为增函数,f(x)在
( , )为减函数.
(Ⅱ)(ⅰ)当0<a≤2时,由(Ⅰ)知:对任意x∈(0,1)恒有f(x)>f(0)=1.
(ⅱ)当a>2时,取x= ∈(0,1),则由(Ⅰ)知f(x)<f(0)=1
0 0
(ⅲ)当a≤0时,对任意x∈(0,1),恒有 >1且e﹣ax≥1,得f(x)= e﹣ax≥
>1.
综上当且仅当a∈(﹣∞,2]时,对任意x∈(0,1)恒有f(x)>1.
22.(12分)设数列{a}的前n项的和 ,n=1,2,3,…
n
(Ⅰ)求首项a 与通项a;
1 n
(Ⅱ)设 ,n=1,2,3,…,证明: .
【分析】对于(Ⅰ)首先由数列{a}的前n项的和求首项a 与通项a,可先求出S ,然后
n 1 n n﹣1
有a=S﹣S ,公比为4的等比数列,从而求解;
n n n﹣1
对于(Ⅱ)已知 ,n=1,2,3,…,将a=4n﹣2n代入S= a﹣ ×2n+1+ ,n=1,2,
n n n
3,得S= ×(4n﹣2n)﹣ ×2n+1+ = ×(2n+1﹣1)(2n+1﹣2)
n
然后再利用求和公式进行求解.
【解答】解:(Ⅰ)由S= a﹣ ×2n+1+ ,n=1,2,3,①得a=S= a﹣ ×4+
n n 1 1 1
所以a=2.
1
再由①有S = a ﹣ ×2n+ ,n=2,3,4,
n﹣1 n﹣1
第16页 | 共17页将①和②相减得:a=S﹣S = (a﹣a )﹣ ×(2n+1﹣2n),n=2,3,
n n n﹣1 n n﹣1
整理得:a+2n=4(a +2n﹣1),n=2,3,
n n﹣1
因而数列{a+2n}是首项为a+2=4,公比为4的等比数列,即:a+2n=4×4n﹣1=4n,n=1,2,3,
n 1 n
因而a=4n﹣2n,n=1,2,3,
n
(Ⅱ)将a=4n﹣2n代入①得S= ×(4n﹣2n)﹣ ×2n+1+ = ×(2n+1﹣1)(2n+1﹣2)
n n
= ×(2n+1﹣1)(2n﹣1)
T= = × = ×( ﹣ )
n
所以, = ﹣ )= ×( ﹣ )< (1﹣
)
第17页 | 共17页