文档内容
浙江省台州市 2024-2025 学年高二上学期期末质量评估数学试题
第I卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在空间直角坐标系Oxyz中,点A(1,2,3)在坐标平面xOy内射影的坐标为( )
A. (0,1,2) B. (1,0,3) C. (1,2,0) D. (0,0,0)
2.已知直线l的一般式方程为x-2y+6=0,则( )
x y x y
A. 直线l的截距式方程为 + =1 B. 直线l的截距式方程为 - =1
-6 3 6 3
1 1
C. 直线l的斜截式方程为y=- x+3 D. 直线l的斜截式方程为y= x-3
2 2
x2 y2
3.已知椭圆的标准方程为 + =1,下列说法正确的是( )
4 3
A. 椭圆的长轴长为2 B. 椭圆的焦点坐标为(√7,0),(-√7,0)
C. 椭圆关于直线 对称 D. 当点 在椭圆上时,
y=x (x ,y ) |y |≤√3
0 0 0
4.设等比数列 的前 项和为 ,若S ,则S 的值为( )
{a }(n∈N* ) n S 3=3 4
n n a a
2 3
A. 1 B. 2 C. 3 D. 4
5.台州学子黄雨婷夺得巴黎奥运会10米气步枪比赛1金1银两块奖牌后,10米气步枪射击项目引起了大家
的关注.在10米气步枪比赛中,瞄准目标并不是直接用眼睛对准靶心,而是通过觇孔式瞄具来实现.这种瞄
具有前后两个觇孔(觇孔的中心分别记为点A,B),运动员需要确保靶纸上的黑色圆心(记为点C)与这两个
3 4 89
觇孔的中心对齐,以达到三圆同心的状态.若某次射击达到三圆同心,且点A(0, ),点B( , ),则点
2 5 50
第 页,共 页
1 16C的坐标为( )
9 11
A. (10, ) B. (10,5) C. (10, ) D. (10,6)
2 2
6.在四面体 中, ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ , ⃗ ⃗ ,若直线 与平面
OABC OC ABC
OA⋅OB=OA⋅OC=OB⋅OC=0 |OA|=|OC|=2
所成角为30∘,则|⃗OB|=( )
A. 1 B. √2 C. √3 D. 2
7.已知等差数列 的首项为 ,公差为 ,前 项和为 ,数列 满足: ,则下列
{a }(n∈N* ) a √2 n S {b } nb =S
n 1 n n n n
说法正确的是( )
A. ∀a ∈R,数列{S }为递增数列
1 n
B. ∃a ∈R,使得数列{b }为递减数列
1 n
C. ∃a ∈R及正整数p,q,r(10,则曲线Γ表示圆 B. 若AB=0,则曲线Γ表示抛物线
C. 若AB>0,则曲线Γ表示椭圆 D. 若AB<0,则曲线Γ表示双曲线
10.对于数列 ,若存在正整数 ,使得对于任意正整数 ,都有 ,则称数列 为周
{a }(n∈N* ) T n a =a {a }
n n+T n n
期数列.下列数列{a }中为周期数列的是( )
n
1+(-1) n 1
A. a = B. a =2,a =1-
n 2 1 n+1 a
n
{2a ,n是奇数,
C. a =2nsin nπ D. a =1 , a = 1 n
n 2 1 n+1 ,n是偶数.
a
n
11.已知正方体ABCD-A B C D 的棱长为1,M为A D 的中点,N为D C 的中点,P为平面ACB 内
1 1 1 1 1 1 1 1 1
的动点,则( )
A. MC //平面ACB
1 1
B. 平面ADD A 与平面ACB 所成角的正切值为√2
1 1 1
π
C. 若MP与BD 所成角为 ,则点P的轨迹为圆
1 3
√2+√14
D. △MPN周长的最小值为
2
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分。
12.已知双曲线 y2 的离心率为 ,则 .
x2- =1(b>0) √5 b=
b2
13.已知曲线x2+ y2=|x|+|y|,则该曲线的一条对称轴方程为 .(写出满足条件的一个方程即可)
14.用 表示两数 , 中的较大者,记 , ,若
max{a,b} a b c =max{3n-1,λ·2n-1 }(λ>0 n∈N❑ * )
n
c +c +c +c +c ≥60,则λ的取值范围是 .
1 2 3 4 5
第 页,共 页
3 16四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知直线 ,圆 .
l:x- y+4=0 C:(x-a) 2+(y-2) 2=2
(1)若直线l把圆C分成面积相等的两部分,求实数a的值;
(2)若直线l与圆C相切,求实数a的值.
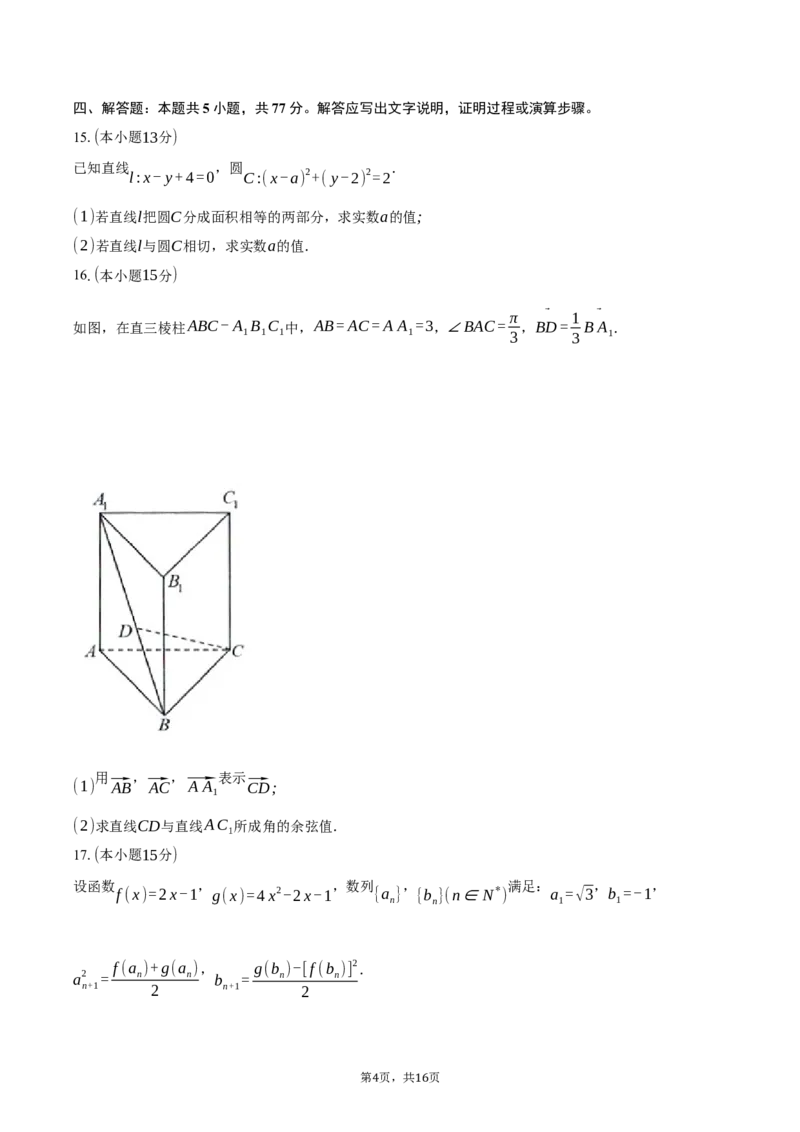
16.(本小题15分)
π ⃗ 1 ⃗
如图,在直三棱柱ABC-A B C 中,AB=AC=A A =3,∠BAC= ,BD= BA .
1 1 1 1 3 3 1
用 , , 表示
(1) ⃗AB ⃗AC ⃗A A ⃗CD;
1
(2)求直线CD与直线AC 所成角的余弦值.
1
17.(本小题15分)
设函数 , ,数列 , 满足: , ,
f(x)=2x-1 g(x)=4x2-2x-1 {a } {b }(n∈N* ) a =√3 b =-1
n n 1 1
f(a )+g(a ), g(b )-[f(b )] 2 .
a2 = n n b = n n
n+1 2 n+1 2
第 页,共 页
4 16(1)若a >0,求数列{a }的通项公式;
n n
求数列 的前 项和 .
(2) {b (a2-1)}(n∈N* ) n S
n n n
18.(本小题17分)
1
动点M(x,y)到直线y=x与直线y=-x的距离之积为 ,记点M的轨迹为曲线E.
2
(1)求曲线E的方程;
3
(2)若点A(x ,y )为曲线E与抛物线y2=2px(00,且y ≠1时,求直线AB斜率的取值范围.
0 0
19.(本小题17分)
把n元有序实数组(a ,a ,⋯,a )称为n维向量,类似平面向量与空间向量,对于n维向量
1 2 n
⃗ ,⃗ ,也可定义两个向量的加法运算和减法运算
i=(a ,a ,⋯,a ) j=(b ,b ,⋯,b )
1 2 n 1 2 n
⃗ ⃗ 数乘运算 ⃗ , 向量的长度 模
i± j=(a ±b ,a ±b ,⋯,a ±b ); λi=(λa ,λa ,⋯,λa ) λ∈R; (
1 1 2 2 n n 1 2 n
)|
⃗
i|=
√
∑
n
a i 2;
两个向量的数量积⃗
i⋅
⃗
j=|
⃗
i|·|
⃗
j|cos
⟨⃗
i,
⃗
j
⟩
=∑
n
a i b i (
⟨⃗
i,
⃗
j
⟩表示向量⃗
i
,⃗
j
的夹角,
i=1 i=1
n
|∑a b |
i i
⟨⃗ ⃗⟩ 向量⃗在向量⃗上的投影向量的模 i=1 .n维向量为我们解决数学问题提供了更为广
i, j ∈[0,π]); j i
√ n
∑a2
i
i=1
阔的思维空间.
已知⃗ ,⃗ ,求向量 , 的夹角的余弦值
(1) m=(1,2,3,4,5) n=(1,1,1,1,1) ⃗m ⃗n ;
已知 维向量 ⃗ , ⃗ , ⃗ , ⃗ ,
(2) 4 OA=(1,2,3,0) OB=(1,2,0,4) OC=(1,0,3,4) OD=(0,2,3,4)
O
⃗
P=aO
⃗
A+bO
⃗
B+cO
⃗
C+dO
⃗
D
,且 6a+7b+8c+9d=1 ,求 |⃗OP| 的最小值 ;
第 页,共 页
5 16n
|∑a |
n i
(3)a∈R(i=1,2⋯,n) ,∑ia =0 ,求 i=1 的最大值 ( 用含 n 的式子表示 ) .
i i √ n
i=1 ∑a2
i
i=1
n(n+1)(2n+1)
(注:12+22+⋯+n2=
)
6
第 页,共 页
6 16答案和解析
1.C
【解析】
在空间直角坐标系Oxyz中,点A(1,2,3)在坐标平面xOy的射影坐标是(1,2,0).
故选:C.
2.A
【解析】
因为直线l的一般式方程为x-2y+6=0,
x y
所以直线l的截距式方程为 + =1,故A正确,B错误;
-6 3
1
直线l的斜截式方程为y= x+3,故C,D错误.
2
故选A.
3.D
【解析】
x2 y2
对于A、椭圆的标准方程为 + =1,
4 3
其中a=√4=2,b=√3,则其长轴长2a=4,故A错误;
x2 y2
对于B、椭圆的标准方程为 + =1,
4 3
其中 , ,则 ,
a=2 b=√3 c=√a2-b2=1
则其焦点坐标为(1,0)、(-1,0),故B错误;
x2 y2
对于C、椭圆的标准方程为 + =1,其中a=2,b=√3,
4 3
则其焦点在x轴上,关于直线y=x不对称,故C错误;
x2 y2
对于D、椭圆的标准方程为 + =1,其中a=2,b=√3,
4 3
第 页,共 页
7 16则 的最大值为 ,则必有 ,故D正确.
y √3 |y |≤√3
0 0
故选:D.
4.D
【解析】
设等比数列{a }的公比为q,
n
当 时,满足S 3a ,则S 4a ,
q=1 3= 1=3 4= 1=4
a a a a
2 1 3 1
当 时,S a (1+q+q2) ,则 ,矛盾,
q≠1 3= 1 =3 q=1
a a q
2 1
综上,S 的值为 .
4 4
a
3
故选:D.
5.B
【解析】
根据题意可设C(10,y),
因为A,B,C三点共线,
则⃗AB=λ⃗AC,
即(4 7 ) ( 3) ( ( 3)),
, =λ 10,y- = 10λ,λ y-
5 25 2 2
4
{ 10λ= { 4
5 λ=
则 ⇒ 50 ,
( 3) 7
λ y- = y=5
2 25
第 页,共 页
8 16则点C的坐标为(10,5).
故选:B.
6.B
【解析】
由题可知OA⊥OB,OA⊥OC,OB⊥OC,
以O为原点,OA,OB,OC所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
设 ⃗ ,
|OB|=m(m>0)
则O(0,0,0),A(2,0,0),B(0,m,0),C(0,0,2),
则 ⃗ , ⃗ ,
AB=(-2,m,0) AC=(-2,0,2)
设平面ABC的法向量为⃗n=(x,y,z),
{⃗ ⃗
由 n⋅AB=0,可得{-2x+my=0,
⃗ ⃗ -2x+2z=0
n⋅AC=0
令x=m,则y=2,z=m,
所以平面 的一个法向量为⃗ ,
ABC n=(m,2,m)
直线 的一个方向向量为 ,
OC ⃗OC=(0,0,2)
已知直线OC与平面ABC所成角为30∘,
⃗ ⃗
OC⋅n 1
则有sin30∘=| |= ,
⃗ ⃗ 2
|OC||n|
即1 |m| ,化简得: ,
= 2m2+4=4m2
2 √2m2+4
第 页,共 页
9 16又因为 m>0 ,所以 m=√2 ,即|
O
⃗
B
|
=√2
.
故选:B.
7.C
【解析】
选项A,显然当 时, 为先减后增数列,故A错误;
a <-√2 {S }
1 n
n(n-1)
选项B,由题意,可得S =na + ×√2
n 1 2
√2 √2 √2 √2
=na + n2- n= n2+(a - )n,
1 2 2 2 1 2
S √2 √2
又nb =S ,可得b = n= n+a - ,
n n n n 2 1 2
√2 √2 √2 √2 √2
则b -b = (n+1)+(a - )-[ n+(a - )]= >0,
n+1 n 2 1 2 2 1 2 2
√2
所以数列{b }是公差为 的等差数列,且为递增数列,故B错误;
n 2
选项C,假设 , , 成等比数列,则 ,
a a a a2=a a
p q r q p r
因为 ,
a =a +√2(n-1)
n 1
所以有 ,
[a +√2(q-1)] 2=[a +√2(p-1)][a +√2(r-1)]
1 1 1
可得: ,
2√2a (q-1)-√2a [(p-1)+(r-1)]=2(p-1)(r-1)-2(q-1) 2
1 1
整理可得 2[(p-1)(r-1)-(q-1) 2 ],可知 不恒为 ,
a = 2q-p-r 0
1 √2(2q-p-r)
因此∃a ∈R及正整数p,q,r(1-1,故D错误.
3√2
故选:C.
8.D
【解析】
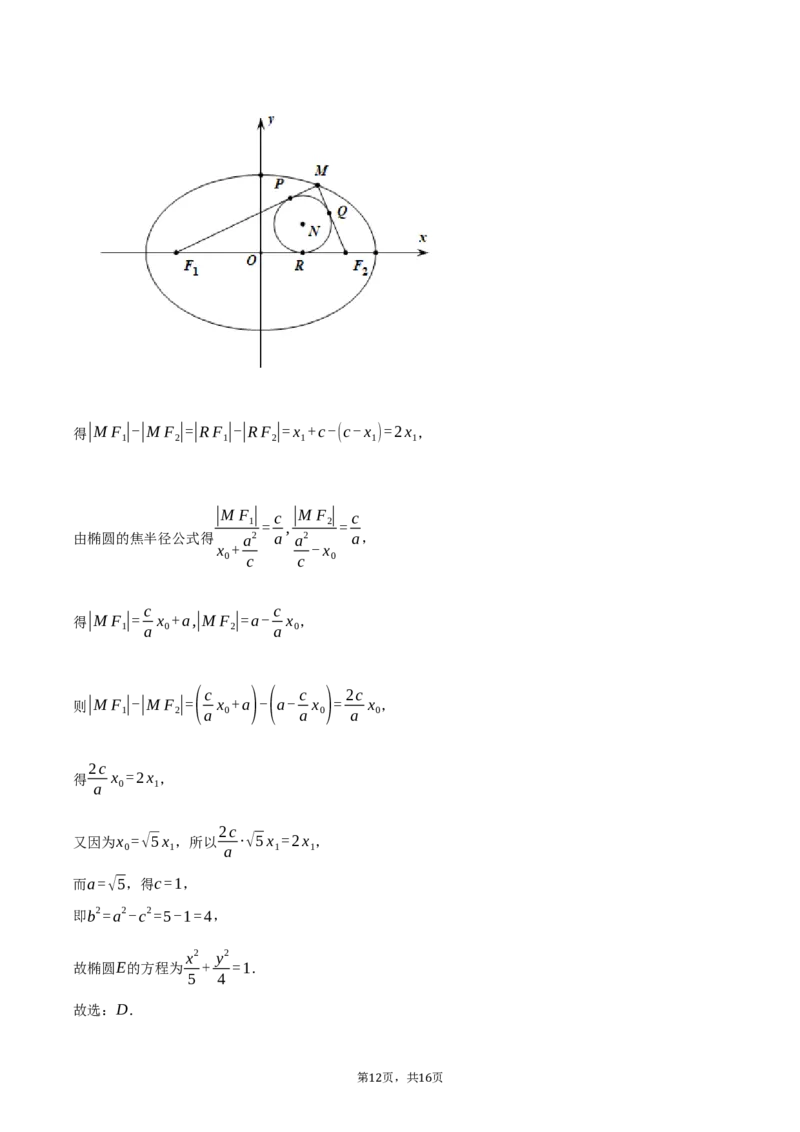
如图所示:设内切圆的切点分别为P,Q,R,
则|MP|=|MQ|,|RF |=|PF |,|RF |=|QF |,
1 1 2 2
第 页,共 页
11 16得|M F |-|M F |=|RF |-|RF |=x +c-(c-x )=2x ,
1 2 1 2 1 1 1
|M F | c |M F | c
1 = , 2 =
由椭圆的焦半径公式得 a2 a a2 a,
x + -x
0 c c 0
c c
得|M F |= x +a,|M F |=a- x ,
1 a 0 2 a 0
(c ) ( c ) 2c
则|M F |-|M F |= x +a - a- x = x ,
1 2 a 0 a 0 a 0
2c
得 x =2x ,
a 0 1
2c
又因为x =√5x ,所以 ·√5x =2x ,
0 1 a 1 1
而a=√5,得c=1,
即b2=a2-c2=5-1=4,
x2 y2
故椭圆E的方程为 + =1.
5 4
故选:D.
第 页,共 页
12 169.AD
【解析】
1
对于A、若A=B>0,则方程可化为x2+ y2= ,
A
√ 1
表示以(0,0)为圆心, 为半径的圆,故A正确;
A
对于B、若AB=0,取A=0,B=1,
则方程可化为y2=1,不表示抛物线,故B错误;
对于C、若AB>0,取A=B=-1,
则方程可化为-x2- y2=1,不表示椭圆,故C错误;
x2 y2
+ =1
对于D、若AB<0,则方程可化为 1 1 ,表示双曲线,故D正确.
A B
故选:AD.
10.ABD
【解析】
1+(-1) n 1+(-1) n+2 1+(-1) n
对于A,a = ,a = = =a ,
n 2 n+2 2 2 n
从而数列{a }是周期为2的周期数列,故A正确;
n
1 1 -1 -1
a =1- =1- = = =a
对于B, n+1 a 1 a -1 1 n-2,
n 1- n-1 1- -1
a a
n-1 n-2
从而数列{a }是周期为3的周期数列,故B正确;
n
对于C,当n为偶数时,a =0,满足a =a ,
n n n+2
当
n
为奇数时,
|a |=2n
,从而不存在正整数
T
,使得
a =a
,故C错误;
n n+T n
对于D,①当n为奇数时,a =2a ,
n+1 n
1 1 1 1
则a = = ,a =2a = ,a = =a ,
n+2 a 2a n+3 n+2 a n+4 a n
n+1 n n n+3
第 页,共 页
13 16当 为偶数时, 1 , 2 , 1 a , ,
② n a = a =2a = a = = n a =2a =a
n+1 a n+2 n+1 a n+3 a 2 n+4 n+3 n
n n n+2
由①②得数列{a }是周期为4的周期数列,故D正确.
n
故选:ABD.
11.BCD
【解析】
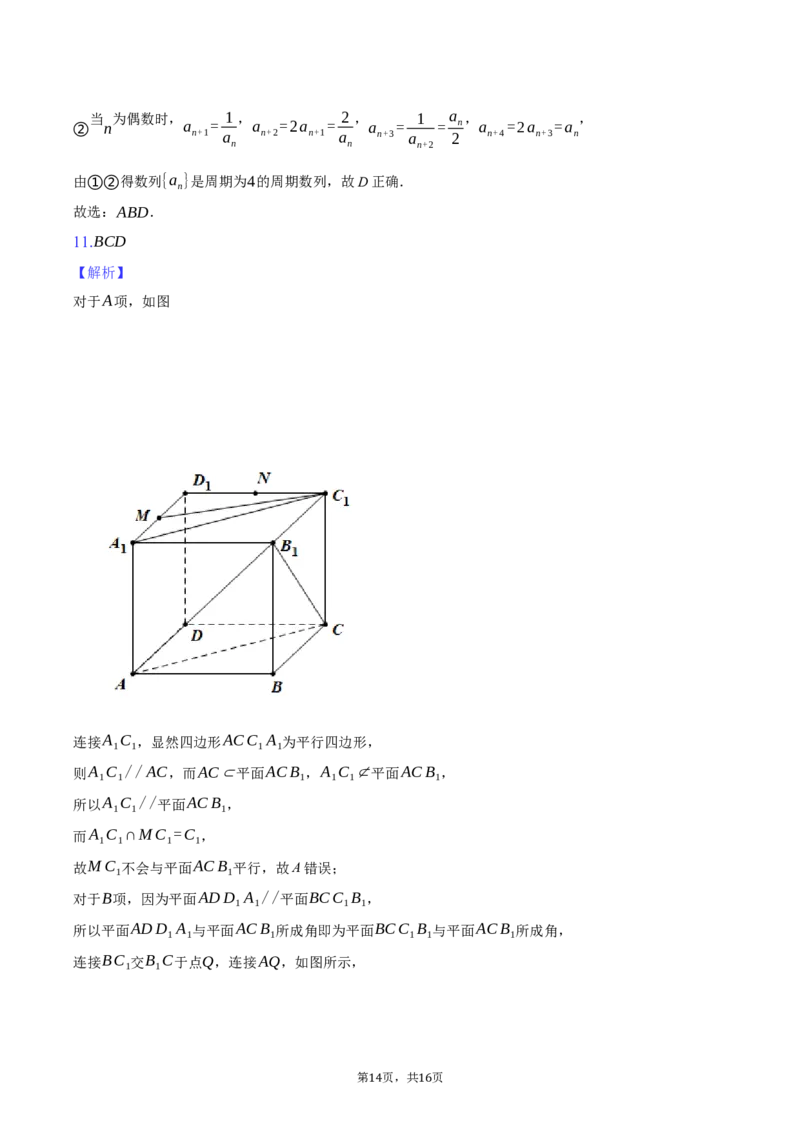
对于A项,如图
连接A C ,显然四边形ACC A 为平行四边形,
1 1 1 1
则A C //AC,而AC⊂平面ACB ,A C ⊄平面ACB ,
1 1 1 1 1 1
所以A C //平面ACB ,
1 1 1
而A C ∩MC =C ,
1 1 1 1
故MC 不会与平面ACB 平行,故A错误;
1 1
对于B项,因为平面ADD A //平面BCC B ,
1 1 1 1
所以平面ADD A 与平面ACB 所成角即为平面BCC B 与平面ACB 所成角,
1 1 1 1 1 1
连接BC 交B C于点Q,连接AQ,如图所示,
1 1
第 页,共 页
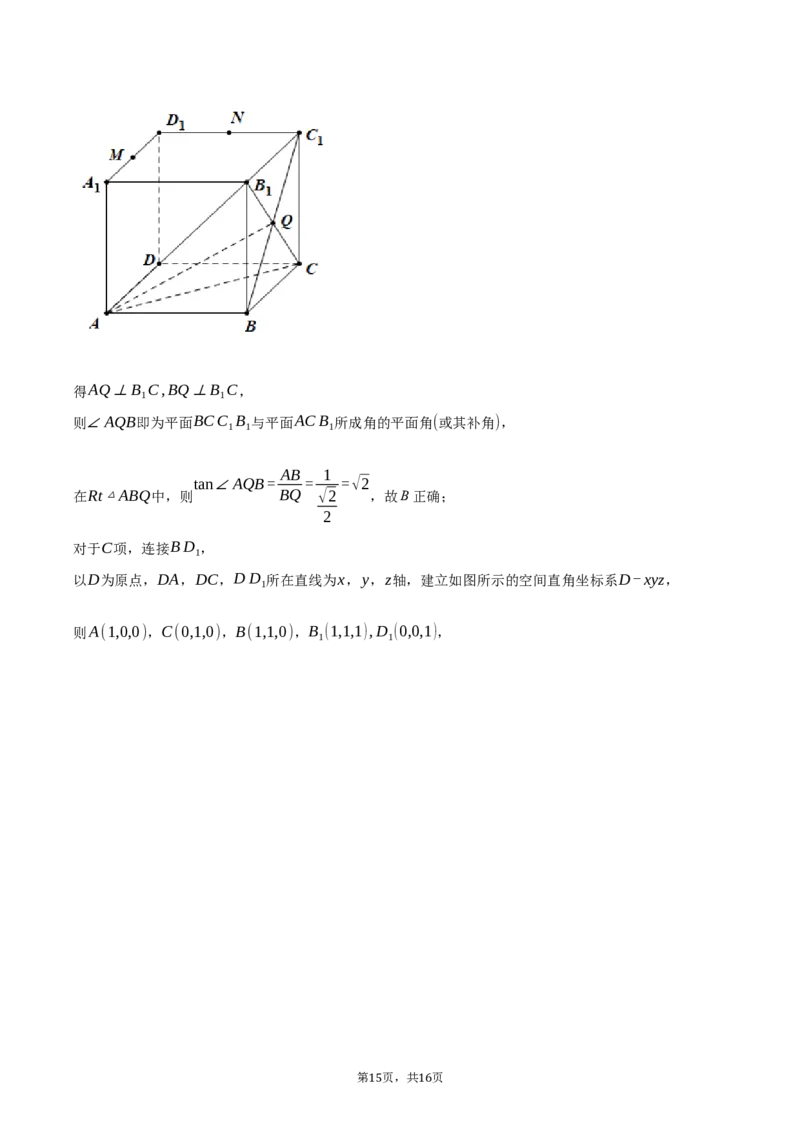
14 16得AQ⊥B C,BQ⊥B C,
1 1
则∠AQB即为平面BCC B 与平面ACB 所成角的平面角(或其补角),
1 1 1
AB 1
tan∠AQB= = =√2
在Rt△ABQ中,则 BQ √2 ,故B正确;
2
对于C项,连接BD ,
1
以D为原点,DA,DC,DD 所在直线为x,y,z轴,建立如图所示的空间直角坐标系D-xyz,
1
则A(1,0,0),C(0,1,0),B(1,1,0),B (1,1,1),D (0,0,1),
1 1
第 页,共 页
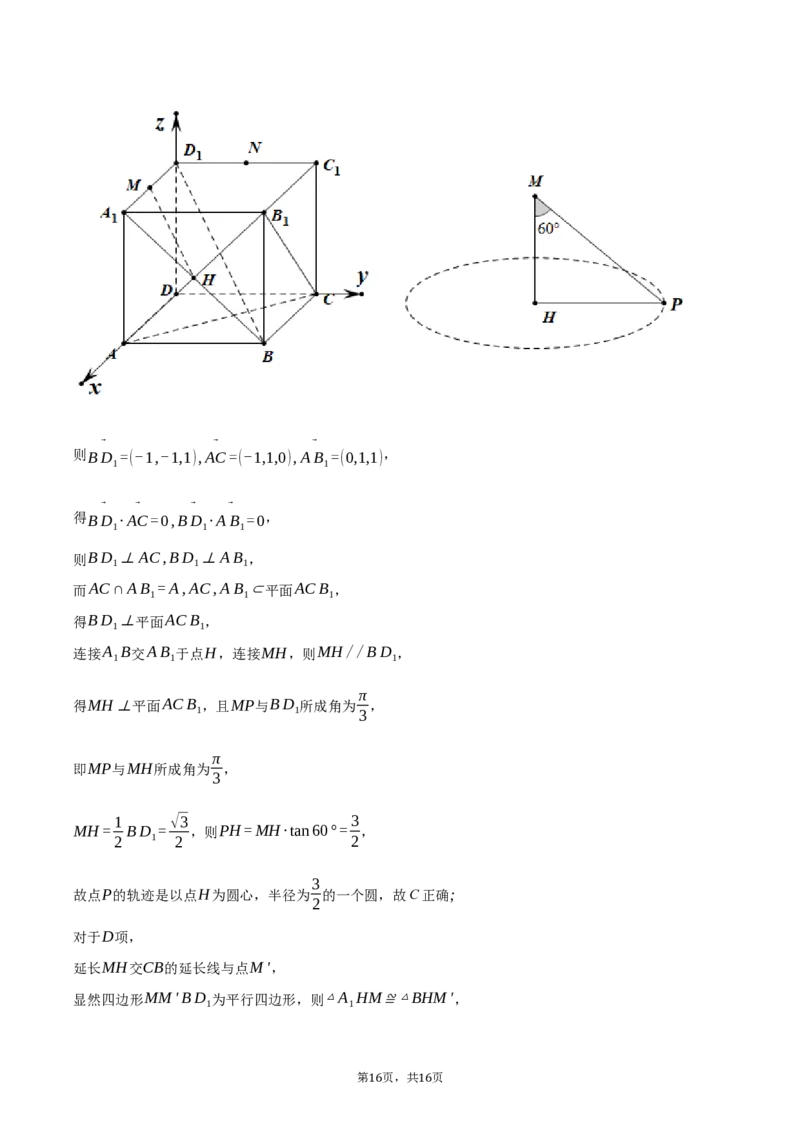
15 16⃗ ⃗ ⃗
则BD =(-1,-1,1),AC=(-1,1,0),AB =(0,1,1),
1 1
⃗ ⃗ ⃗ ⃗
得BD ·AC=0,BD ·AB =0,
1 1 1
则BD ⊥AC,BD ⊥AB ,
1 1 1
而AC∩AB =A,AC,AB ⊂平面ACB ,
1 1 1
得BD ⊥平面ACB ,
1 1
连接A B交AB 于点H,连接MH,则MH//BD ,
1 1 1
π
得MH⊥平面ACB ,且MP与BD 所成角为 ,
1 1 3
π
即MP与MH所成角为 ,
3
1 √3 3
MH= BD = ,则PH=MH·tan60°= ,
2 1 2 2
3
故点P的轨迹是以点H为圆心,半径为 的一个圆,故C正确;
2
对于D项,
延长MH交CB的延长线与点M',
显然四边形MM'BD 为平行四边形,则△A HM≌△BHM',
1 1
第 页,共 页
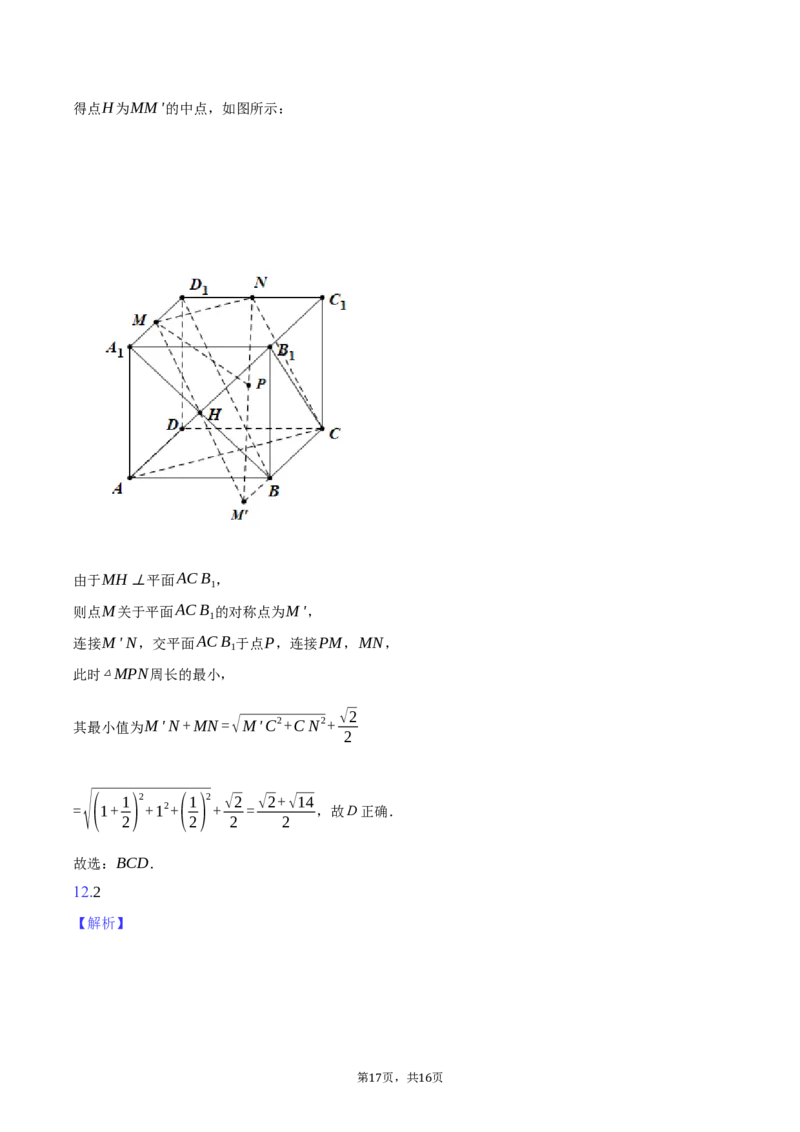
16 16得点H为MM'的中点,如图所示:
由于MH⊥平面ACB ,
1
则点M关于平面ACB 的对称点为M',
1
连接M'N,交平面ACB 于点P,连接PM,MN,
1
此时△MPN周长的最小,
√2
其最小值为M'N+MN=√M'C2+CN2+
2
= √ ( 1+ 1) 2 +12+ (1) 2 + √2 = √2+√14 ,故D正确.
2 2 2 2
故选:BCD.
12.2
【解析】
第 页,共 页
17 16由双曲线方程可知 a=1,又离心率为√5,
可得 c2 a2+b2,
e2= =
a2 a2
代入可得 b2=4,
则 b=2.
故答案为:2.
13.x=0(答案不唯一,y=-x,y=x,y=0均可)
【解析】
因为曲线x2+ y2=|x|+|y|,
则 也成立,
(-x) 2+ y2=|-x|+|y|
故若点(x,y)在曲线x2+ y2=|x|+|y|上,(-x,y)也在曲线上,
故该曲线的一条对称轴方程为x=0.
故答案为:x=0(答案不唯一,y=-x,y=x,y=0均可).
15
14.[ ,+∞)
8
【解析】
1 1
由题意可知:c =max{2,λ}= max{16,8λ},c =max{5,2λ}= max{20,8λ},
1 8 2 4
1
c =max{8,4λ}= max{16,8λ},c =max{11,8λ},c =max{14,16λ}=2max{7,8λ},
3 2 4 5
7
当0<8λ⩽7,即0<λ⩽ 时,
8
c +c +c +c +c =2+5+8+11+14=40<60,
1 2 3 4 5
不满足题意;
7 11
当7<8λ⩽11,即 <λ⩽ 时,
8 8
c +c +c +c +c =2+5+8+11+16λ⩾60,
1 2 3 4 5
13
解得λ⩾ ,则λ∈⌀;
8
第 页,共 页
18 1611 16
当11<8λ⩽16,即 <λ⩽ 时,
8 8
c +c +c +c +c =2+5+8+8λ+16λ⩾60,
1 2 3 4 5
15 15 16
解得λ⩾ ,所以 ⩽λ⩽ ;
8 8 8
16 20
当16<8λ⩽20,即 <λ⩽ 时,
8 8
c +c +c +c +c =λ+5+4λ+8λ+16λ⩾60,
1 2 3 4 5
55 55 20
解得λ⩾ ,所以 ⩽λ⩽ ;
29 29 8
20
当8λ>20,即λ> 时,
8
20
c +c +c +c +c =λ+2λ+4λ+8λ+16λ=31λ>31× >62>60,满足条件.
1 2 3 4 5 8
15
综上,λ的取值范围是[ ,+∞).
8
15
故答案为:[ ,+∞).
8
15.解:(1)由题意得,圆心(a,2)在直线l上,即a+2=0,即a=-2;
(2)圆C的半径为√2,
|a+2|
圆心到直线l的距离d= =√2,
√2
解得a=0或a=-4.
⃗ ⃗ ⃗ ⃗ 1 ⃗
16.解:(1)CD=CB+BD=CB+ BA
3 1
⃗ ⃗ 1 ⃗ ⃗
=AB-AC+ (A A -AB)
3 1
2 ⃗ ⃗ 1 ⃗
= AB-AC+ A A ;
3 3 1
(2)设直线CD与直线AC 所成角为θ,
1
第 页,共 页
19 16| ⃗ | 2 ⃗ ⃗ 1 ⃗
且 CD =| AB-AC+ A A |
3 3 1
√ 2 ⃗ ⃗ 1 ⃗ √4 ⃗ ⃗ 1 ⃗ 4 ⃗ ⃗ 4 ⃗ ⃗ 2 ⃗ ⃗
= ( AB-AC+ A A ) 2= AB2+AC2+ A A 2- AB·AC+ AB·A A - AC·A A
3 3 1 9 9 1 3 9 1 3 1
=2√2,
⃗ ,
|AC |=3√2
1
⃗ ⃗ 2 ⃗ ⃗ 1 ⃗ ⃗ ⃗
CD⋅AC =( AB-AC+ A A )⋅(AC+A A )=-3,
1 3 3 1 1
⃗ ⃗
所以 CD·AC 1,
cosθ=| 1 |=
⃗ ⃗ 4
|CD||AC |
1
1
所以直线CD与直线AC 所成角的余弦值为 .
1 4
17.解: 2a -1+4a2-2a -1 ,
(1)a2 = n n n =2a2-1
n+1 2 n
得 ,又 ,
a2 -1=2(a2-1) a2-1=2
n+1 n 1
所以数列 是以 为首项, 为公比的等比数列,
{a2-1} 2 2
n
所以 ,
a2-1=2×2n-1
n
则 ,
a2=2n+1
n
因为 ,所以 的通项公式为
a >0 {a } a =√2n+1;
n n n
第 页,共 页
20 16g(b )-[f(b )] 2 ,
(2)b = n n =b -1
n+1 2 n
所以数列{b }是以-1为首项,-1为公差的等差数列,
n
b =-1+(n-1)×(-1)=-n,
n
,
b (a2-1)=-n⋅2n
n n
,
S =-1×2-2×22-3×23-···-n×2n
n
,
2S =-1×22-2×23-3×24-···-n×2n+1
n
两式相减得 ,
-S =-2-22-23-···-2n+n×2n+1
n
所以 ,
S =2+22+23+⋯+2n-n×2n+1=(1-n)⋅2n+1-2
n
故 .
S =(1-n)⋅2n+1-2
n
|x- y| |x+ y| 1
18.解:(1)由题意得 . = ,
√2 √2 2
化简得|x2- y2|=1,故曲线E的方程为:x2- y2=1或y2-x2=1;
由 可知, 或 ,
(2)① (1) x2- y2=1 y2-x2=1
0 0 0 0
{y2-x2=1 x2+1
当 y2-x2=1 时,由 0 0 ,得 p= 0 ,
0 0 y2=2px 2x
0 0 0
3
因为p≤ 时,x 无解(舍去);
4 0
{x2- y2=1 x2-1
当 x2- y2=1 时,由 0 0 ,得 p= 0 ,
0 0 y2=2px 2x
0 0 0
第 页,共 页
21 163
由00,
AB t t
√ 1 1
当t∈[-2,0)时,k =- 2( ) 2-3( )+1≤-√3,
AB t t
所以直线AB的斜率取值范围为(-∞,-√3]⋃(0,+∞).
19.解: ⃗ ⃗ ,
(1)m⋅n=1+2+3+4+5=15
⃗ , ⃗ ,
|m|=√12+22+32+42+52=√55 |n|=√5
⃗ ⃗
⟨⃗ ⃗⟩ m·n 15 3√11
所以cos m,n = = = ,
|⃗| ⃗ √55×√5 11
m ·|n|
3√11
所以向量⃗m,⃗n的夹角的余弦值为 ;
11
由 ⃗ ⃗ ⃗ ⃗ ⃗
(2)
OP=aOA+bOB+cOC+dOD
=(a+b+c,2a+2b+2d,3a+3c+3d,4b+4c+4d);
设⃗ ,
k=(1,1,1,1)
则有⃗ ⃗ ,
k⋅OP=(a+b+c)+(2a+2b+2d)+(3a+3c+3d)+(4b+4c+4d)=6a+7b+8c+9d=1
第 页,共 页
22 16由⃗ ⃗ |⃗| | ⃗ | ⟨⃗ ⃗ ⟩ |⃗| | ⃗ |,
k⋅OP= k ⋅OP cos k,OP ⩽ k ⋅OP
得 ⃗ ,
2|OP|≥1
1
故|⃗OP|的最小值为 ;
2
1 13 7 -11
当且仅当a= ,b= ,c= ,d= 时取等;
9 144 144 144
解法 设⃗ ,⃗ ,⃗ ,
(3) 1: n =(a ,a ,···,a ) n =(1,1,···,1) n =(1,2,···,n)
1 1 2 n 2 3
n
|∑a | |⃗ ⃗|
i n ·n
i=1 = 1 2 ,表示向量 ⃗n 在 ⃗n 上投影向量的模.
√ n ⃗ 2 1
∑a2 |n
1
|
i
i=1
下求该投影向量模的最大值,
设以⃗为法向量的“平面”为 ,
α
n
3
因为 n ⃗ ⋅n ⃗ =0 ,所以 ⃗n 1 在“平面” α 内,
3 1
设⃗n 与“平面”α夹角为θ,
2
向量⃗n
2
在⃗n
1
上投影向量模的最大值为⃗n
2
在“平面”α投影|
n
⃗|
cosθ
,
2
⃗ ⃗
⟨⃗ ⃗ ⟩ n ·n
故 sinθ=|cos n ,n |= 2 3
2 3 |⃗||⃗|
n · n
2 3
1+2+···+n √6√ n+1 ,
= =
√12+12+···+12-√12+22+···+n2 2 2n+1
第 页,共 页
23 163n+3 n-1
cos2θ=1- = ,
4n+2 4n+2
所以|⃗| √ n-1 √n(n-1),
n cosθ=√n =
2 4n+2 4n+2
n
|∑a |
i
故 i=1 的最大值为√n(n-1),
√ n 4n+2
∑a2
i
i=1
n n n
解法 因为 ,所以 对任意 恒成立,
2: ∑ia =0 ∑a =∑(1-ci)a c∈R
i i i
i=1 i=1 i=1
3
取c= ,
2n+1
由 n n √ n √ n ,
|∑a |=|∑(1-ci)a |≤ ∑(1-ci) 2 ⋅ ∑a2
i i i
i=1 i=1 i=1 i=1
n
|∑a |
1 √ n √ n(n+1) [n(n+1)(n+1)] √n(n-1)
得 i=1 ≤ ∑(1-ci) 2= n-2c +c2 = ,
√ n i=1 2 6 4n+2
∑a2
2
i=1
3
当且仅当a =1- i时取等号,
i 2n+1
n
∑a
1
故 i=1 的最大值为√n(n-1).
√ n 4n+2
∑a2
i
i=1
第 页,共 页
24 16