文档内容
http://t.cn/Ri466E4
江苏省泰州市兴化市城东镇湖北小学五年级(下)期中数学复
习卷(1)
一、填空.
1.报警的电话号码是 ,急救的电话号码是 .你所读学校地的
邮政编码是 .
2.桃树有x棵,梨树的棵数是桃树的4倍,用含有x的式子表示梨树的棵数是
棵.
3.苹果有Y个,梨比苹果少2个,梨有 个.
4.五个连续的自然数的中间数是a,这五个数的和为 .
5.如果a、b是两个连续的自然数(且a、b都不为0),则他们的最大公因数是
,最小公倍数是 ;如果a、b是两个非零的自然数,且a是b的倍数,则他们
的最大公因数是 ,最小公倍数是 .
6.x÷8=y,x和y的最大公因数是 ,最小公倍数是 .
7.两个素数的最小公倍数是51,这两个素数分别是 和 .
8.三个连续的奇数和是33,这三个数分别为为 .
9.甲袋有a千克大米,乙袋有b千克大米.如果从甲袋倒出8千克装入乙袋,那么两袋的
大米同样重.原来甲袋比乙袋多 千克.
10.6、12、18、24…既是2的倍数,又是3的倍数,它们是2和3的 .
11.6和9的公倍数中最小的一个是18,18就是6和9的 .
12.一个两位数既是3的倍数,也是5的倍数,而且是偶数,这个数最小是 ,
最大是 .
13.把一张长24cm、宽16cm的长方形纸剪成同样大小、面积尽可能大的正方形,且纸没
有 剩余.剪出的正方形的边长最大是 cm.最少能剪 个.
二、准确判断.
14.方程包含等式,等式只是方程一部分. .
15.两个数的最大公因数,一定是这两个数的最小公倍数的因数. .
16.含有未知数的式子叫做方程. .(判断对错)
17.4和11是44的公因数. .(判断对错)
18.一个数的最大因数和最小倍数都等于它本身. .(判断对错)
19.所有非0的自然数的公因数是1. (判断对错)
20.9和17没有公因数. .(判断对错)
21.两个数的乘积一定是这两个数的最小公倍数. .(正确判断)
22.两个数的公因数的个数是有限的,公倍数的个数是无限的. .(判断对
错)
23.等式的两边同时除以同一个数,所得的结果仍然是等式. .(判断对
错)
三、精心选择
24.17和21的( )是1.
A.倍数B.公因数 C.最大公因数 D.最小公倍数
教育 1http://t.cn/Ri466E4
25.在下面的四个数中,( )既有因数2,又有因数3.
A.1 B.23 C.24 D.15
26.用长6厘米,宽4厘米的长方形可拼成边长是( )厘米的正方形.
A.9 B.12 C.15 D.16
27.a=3b,a,b都是大于0自然数,则a,b的最小公倍数是( )
A.a B.b C.3 D.1
28.有一个比20小的数,它既是3的倍数,又是4的倍数,这个数是( )
A.18 B.16 C.12 D.15
四、看图列方程并解答.
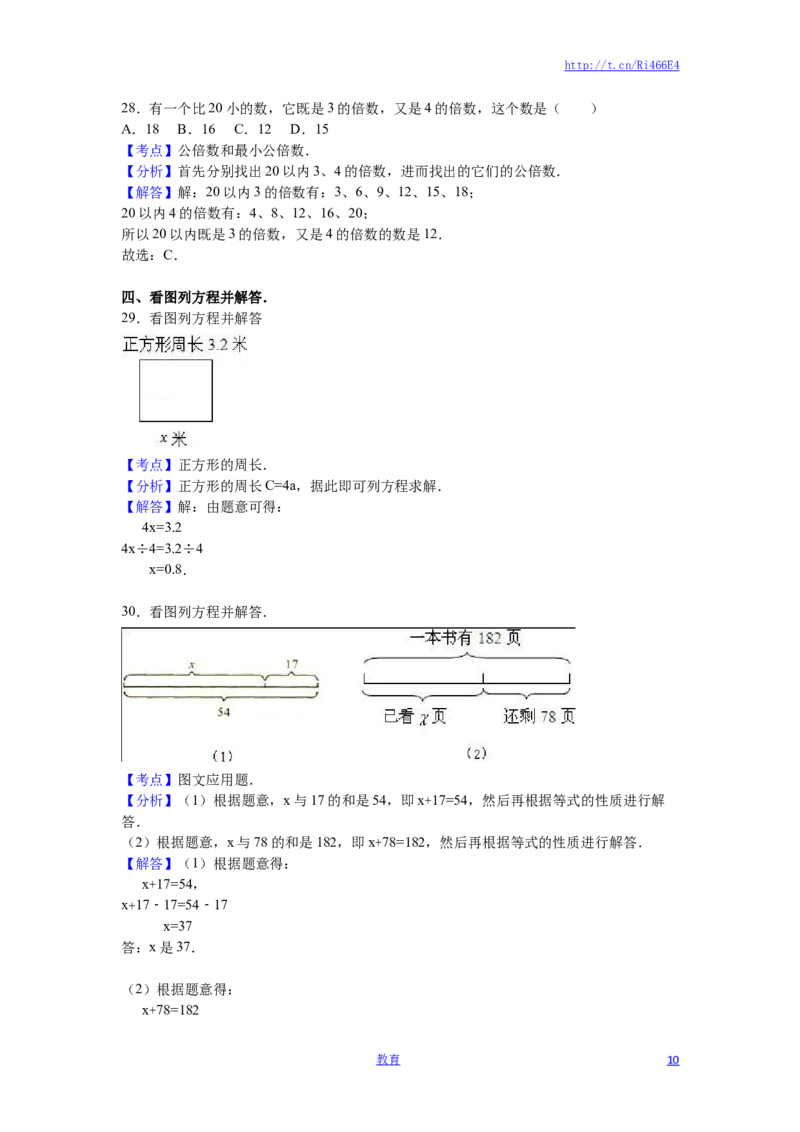
29.看图列方程并解答
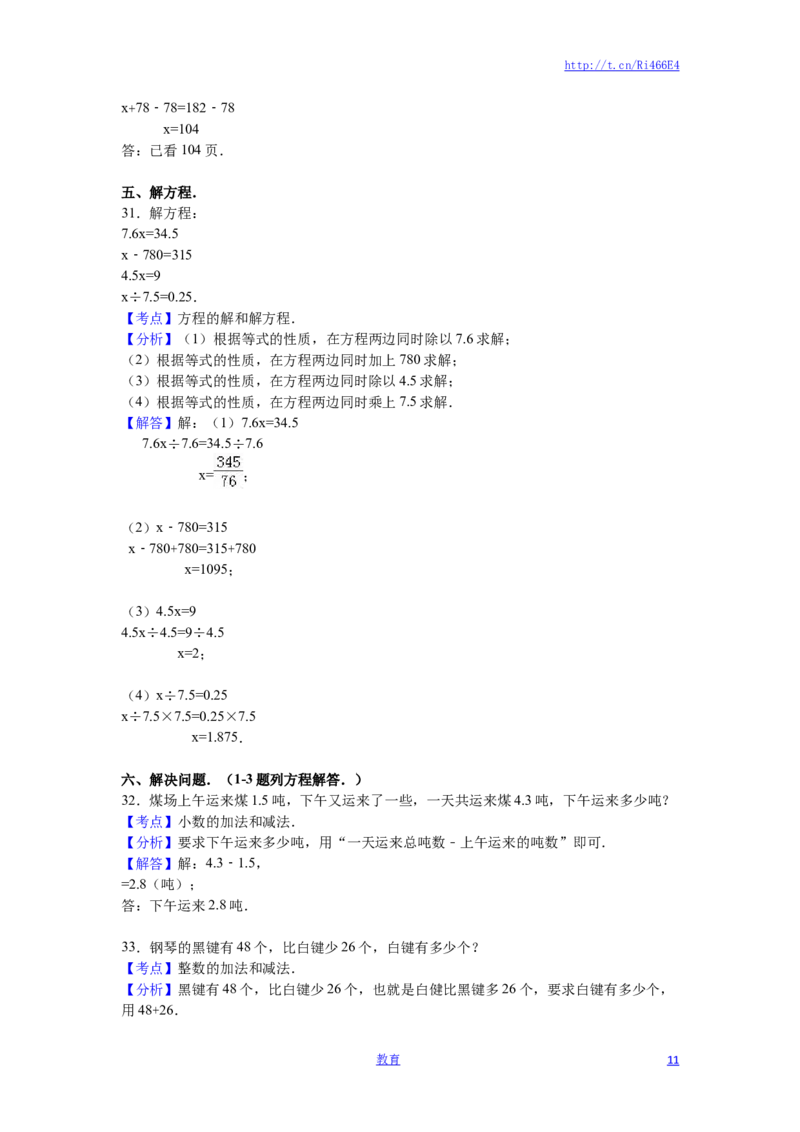
30.看图列方程并解答.
五、解方程.
31.解方程:
7.6x=34.5
x﹣780=315
4.5x=9
x÷7.5=0.25.
六、解决问题.(1-3题列方程解答.)
32.煤场上午运来煤1.5吨,下午又运来了一些,一天共运来煤4.3吨,下午运来多少吨?
33.钢琴的黑键有48个,比白键少26个,白键有多少个?
34.一艘轮船从甲港开往乙港,4小时到达终点,已知两港之间的水路长128千米,这艘
轮船每小时行多少千米?
35.1路和2路公共汽车早上7时同时从起始站发车,1路车每隔6分发一辆车,2路车每
隔7分发一辆车.这两路车第二次同时发车的时间是多少?
36.把40本故事书和24本科技书分别分给一个组的同学,结果正好分完,你知道这个组
最多有几位同学吗.
37.小朋友做游戏,分成8人一组,或6人一组都正好,做游戏的小朋友至少有多少个?
教育 2http://t.cn/Ri466E4
38.有两根绳子,一根长16米,另一根长20米.现在要把它们剪成同样长的小段,每段
长要尽可能长,且没有剩余.每段绳子长多少米?二根绳子一共可以剪成几段?
39.小明每4天去一次学校图书馆借书,小红每6天去一次学校图书馆借书.如果他们两
人,4月1日同时去图书馆借书,那么他们下一次是几月几日又同时去借书?
40.用红花48朵,黄花60朵做花束,如果每束花里的红花朵数都相等,每束花里的黄花
朵数也都相等,最多可以做几束花?每个花束里红花最多有几朵?黄花最多几朵?
41.把一张长12cm、宽8cm的长方形纸剪成同样大小、面积尽可能大的正方形,且纸没有
剩余,剪出的正方形的边长是多少?这样可以剪多少个?
教育 3http://t.cn/Ri466E4
江苏省泰州市兴化市城东镇湖北小学五年级(下)期中
数学复习卷(1)
参考答案与试题解析
一、填空.
1.报警的电话号码是 11 0 ,急救的电话号码是 12 0 .你所读学校地的 邮政编码是
273311 .
【考点】数字编码.
【分析】报警的电话号码是:110,急救的电话号码是:120.根据邮政编码的编号方法,
以及实际情况,找出所在地的邮政编码.
【解答】解:报警的电话号码是:110,急救的电话号码是:120.
所读学校地的 邮政编码是273311.
故答案为:110,120,273311.
2.桃树有x棵,梨树的棵数是桃树的4倍,用含有x的式子表示梨树的棵数是 4 x 棵.
【考点】用字母表示数.
【分析】本题是一个用字母表示数的题.用含有字母的式子表示梨树的棵树,就是求X棵
的4倍是多少,用乘法计算.
【解答】解:梨树的棵树:X×4=4X(棵).
答:梨树的棵树是4X棵.
故答案为:4X.
3.苹果有Y个,梨比苹果少2个,梨有 Y﹣ 2 个.
【考点】用字母表示数.
【分析】根据“梨比苹果少2个,”知道梨的个数=苹果的个数﹣2,由此即可得出答案.
【解答】解:因为,梨的个数=苹果的个数﹣2,
所以,梨有:Y﹣2,
答:梨有Y﹣2个,
故答案为:Y﹣2.
4.五个连续的自然数的中间数是a,这五个数的和为 5 a .
【考点】用字母表示数;整数的认识.
【分析】根据自然数的意义知道,每相邻的两个自然数相差1,所以五个连续的自然数的
中间数是a,那么a前面的两个数为a﹣1,a﹣1﹣1,它后面的两个数是a+1,a+1+1,由此
把五个数加起来就是五个数的和;或根据自然数的意义与平均数的意义知道,a就是此五
个数的平均数,由此用5直接乘a就是五个数的和.
【解答】解:(1)因为五个连续的自然数的中间数是a,
那么a前面的两个数为a﹣1,a﹣1﹣1,
它后面的两个数是a+1,a+1+1,
所以五个数的和为:a﹣1+a﹣1﹣1+a+a+1+a+1+1=5a;
或:5×a=5a;
教育 4http://t.cn/Ri466E4
故答案为:5a.
5.如果a、b是两个连续的自然数(且a、b都不为0),则他们的最大公因数是 1 ,最
小公倍数是 a b ;如果a、b是两个非零的自然数,且a是b的倍数,则他们的最大公因
数是 b ,最小公倍数是 a .
【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【分析】(1)相邻的两个自然数是互质数,根据互质数的意义得:最大公因数是1,最小
公倍数是它们的乘积;
(2)a、b是两个非零的自然数,且a是b的倍数,成倍数关系的两个非0自然数,它们的
最大公因数是较小的那个数,小公倍数是较大的那个数;据此解答.
【解答】解:(1)由分析知:ab的最大公约数是1,最小公倍数是ab;
(2)因为a、b是两个非零的自然数,a和b成倍数关系,则它们的最大公约数是b,最小
公倍数是a;
故答案为:1,ab,b,a.
6.x÷8=y,x和y的最大公因数是 y ,最小公倍数是 x .
【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【分析】由题意得出x÷y=8,根据“两个非0的自然数成倍数关系,较小的那个数为两个
数的最大公因数,较大的那个数为两个数的最小公倍数”进行解答即可.
【解答】解:因为自然数x是自然数y的8倍,
所以x和y的最大公因数是y;最小公倍数是x.
故答案为:y,x.
7.两个素数的最小公倍数是51,这两个素数分别是 3 和 1 7 .
【考点】求几个数的最小公倍数的方法;合数与质数.
【分析】两个数互质,则最小公倍数是这两个数的乘积;任意两个素数,都是互质数,所
以它们的最小公倍数就是它们的乘积;由此可以得出两个素数最小公倍数是51,这两个数
是3和17.
【解答】解:任意两个素数,都是互质数,所以它们的最小公倍数就是它们的乘积,
3×17=51,3和17都是质数,所以这两个数数3和17;
故答案为:3,17.
8.三个连续的奇数和是33,这三个数分别为为 9 , 1 1 , 1 3 . .
【考点】奇数与偶数的初步认识.
【分析】每相邻的两个奇数之间的差为2,因此可设这三个连续奇数中的第一个奇数为x,
则中间的奇数为x+2,第三个奇数为x+4,又三个连续奇数的和是33,据此可得等量关系
式:x+(x+2)+(x+4)=33,解此方程后即得三个连续奇数中的第一个奇数.
【解答】解:设这三个连续奇数中的第一个奇数为x,可得方程:
x+(x+2)+(x+4)=33
x+6=33
3x=27
x=9
则这三个连续的奇数为:9,9+2,9+4,即9,11,13.
故答案为:9,11,13.
教育 5http://t.cn/Ri466E4
9.甲袋有a千克大米,乙袋有b千克大米.如果从甲袋倒出8千克装入乙袋,那么两袋的
大米同样重.原来甲袋比乙袋多 1 6 千克.
【考点】用字母表示数.
【分析】从甲袋倒出8千克装入乙袋,那么现在甲袋就有a﹣8千克,乙袋就有b+8千克,
根据二者相等找出a、b之间的关系.
【解答】解:a﹣8=b+8,
a﹣b=16;
即原来甲比乙多16千克.
故答案为:16.
10.6、12、18、24…既是2的倍数,又是3的倍数,它们是2和3的 公倍数 .
【考点】2、3、5的倍数特征.
【分析】既是2的倍数,又是3的倍数的数是2和3的公倍数,据此解答即可.
【解答】解:6、12、18、24…既是2的倍数,又是3的倍数,它们是2和3的公倍数.
故答案为:公倍数.
11.6和9的公倍数中最小的一个是18,18就是6和9的 最小公倍数 .
【考点】公倍数和最小公倍数.
【分析】根据求一个的倍数的方法,进行列举,明确两个数公有的倍数是它们的公倍数,
其中最小的一个,是它们的最小公倍数;由此解答即可.
【解答】解:6的倍数有6,12,18,24,30,36,42,48…;
9的倍数有9,18,27,36,45,54,…;
其中6和9的公倍数有18,36,54,72,…;
其中最小的公倍数是18.
故答案为:最小公倍数.
12.一个两位数既是3的倍数,也是5的倍数,而且是偶数,这个数最小是 3 0 ,最大
是 9 0 .
【考点】找一个数的倍数的方法.
【分析】先根据能被5整除的数的特征,又因为是偶数,能判断出个位数是0,进而根据
能被3整除的数的特征,推断出这个数十位上的数最小是3,最大是9,继而得出结论.
【解答】解:由分析知:这个数最小是30,最大是90;
故答案为:30,90.
13.把一张长24cm、宽16cm的长方形纸剪成同样大小、面积尽可能大的正方形,且纸没
有 剩余.剪出的正方形的边长最大是 8 cm.最少能剪 6 个.
【考点】图形的拼组.
【分析】根据题意“把一张长24cm、宽16cm的长方形纸剪成同样大小、面积尽可能大的
正方形,且纸没有剩余”,可以求出24和16的最大公因数,就是每个正方形的边长;用
24和16分别除以正方形边长,得到的数相乘就是最少可以裁成的正方形个数,因此得解.
【解答】解:24=2×2×2×3,
16=2×2×2×2,
所以24和16的最大公因数是:2×2×2=8
教育 6http://t.cn/Ri466E4
(24÷8)×(16÷8)
=3×2
=6(个)
答:剪出的正方形的边长最大是8厘米,最少剪6个.
故答案为:8,6.
二、准确判断.
14.方程包含等式,等式只是方程一部分. 错误 .
【考点】方程与等式的关系.
【分析】方程是指含有未知数的等式.所以等式包含方程,方程只是等式的一部分.
【解答】解:等式包含方程,方程只是等式的一部分;不能说成方程包含等式,等式只是
方程一部分.
故判断为:错误.
15.两个数的最大公因数,一定是这两个数的最小公倍数的因数. √ .
【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【分析】根据最大公约数和最小公倍数的意义可知;最大公因数是两个数的公有的质因数
的乘积,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积,可以举例证明,
据此解答.
【解答】解:最大公因数是两个数的公有的质因数的乘积,最小公倍数是两个数公有的质
因数和各自独有的质因数的乘积,
例如:4=2×2,6=2×3,4和6的最大公因数是 2,最小公倍数是2×2×3=12,2是12的
因数,
所以两个数的最大公因数,一定是这两个数的最小公倍数的因数的说法是正确的;
故答案为:√.
16.含有未知数的式子叫做方程. × .(判断对错)
【考点】方程的意义.
【分析】根据方程的意义,首先是等式,再就是含有未知数,举例子进一步说明可得出答
案.
【解答】解:例如4x+6是含有未知数的式子,4+5=9是等式,可它们都不是方程,而
5+x=9就是方程.
故答案为:×.
17.4和11是44的公因数. × .(判断对错)
【考点】因数、公因数和最大公因数.
【分析】根据公因数的含义:两个数公有的因数,是它们的公因数,一个数不存在公因数
说法;由此判断即可.
【解答】解:两个数公有的因数,是它们的公因数,一个数不存在公因数说法,
所以本题说法错误;
故答案为:×.
18.一个数的最大因数和最小倍数都等于它本身. 正确 .(判断对错)
【考点】因数和倍数的意义.
教育 7http://t.cn/Ri466E4
【分析】一个数的因数是有限的,最小是1,最大是它本身,如12的因数有1、2、3、4、
6、12,一个数的倍数是无限的,最小是它本身,如12的倍数有12、24、36…据此解答.
【解答】解:一个数的最大因数和最小倍数都等于它本身正确;
故答案为:正确
19.所有非0的自然数的公因数是1. √ (判断对错)
【考点】因数、公因数和最大公因数;自然数的认识.
【分析】根据公因数的意义可知:公因数是几个数公有的因数,1是所有非0自然数的公
因数,据此解答.
【解答】解:所有非0的自然数的公因数是1,说法正确.
故答案为:√.
20.9和17没有公因数. × .(判断对错)
【考点】因数、公因数和最大公因数.
【分析】根据互质数的特征,可得9和17是互质数,它们的公因数只有1,不是它们没有
公因数,据此判断即可.
【解答】解:根据互质数的特征,可得9和17是互质数,
它们的公因数只有1,不是它们没有公因数,
所以题中说法不正确.
故答案为:×.
21.两个数的乘积一定是这两个数的最小公倍数. × .(正确判断)
【考点】求几个数的最小公倍数的方法.
【分析】求两数的最小公倍数,要看两个数之间的关系:两个数互质,则最小公倍数是这
两个数的乘积;两个数为倍数关系,则最小公倍数为较大的数;两个数有公约数的,最小
公倍数是两个数公有质因数与独有质因数的连乘积;由此选择情况解决问题.
【解答】解:两个数是互质数,这两个数的最小公倍数是它们的乘积.
如果两个数不互质,如2和4,它们的最小公倍数是4,而不是2×4=8;所以两个数的乘
积一定是这两个数的最小公倍数是错误的;
故答案为:×.
22.两个数的公因数的个数是有限的,公倍数的个数是无限的. √ .(判断对错)
【考点】公倍数和最小公倍数.
【分析】一个数的因数的个数是有限的,最小的是1,最大的是它本身;一个数的倍数的
个数是无限的最小的倍数是它本身,没有最大的倍数;由此解答.
【解答】解:因为一个数的因数的个数是有限的,所以两个数的公因数的个数也是有限的;
因为一个数的倍数的个数是无限的,所以两个数的公倍数的个数也是无限的,只有最小公
倍数,没有最大公倍数;
因此,两个数的公因数的个数是有限的,而两个数的公倍数的个数是无限的.说法正确.
故答案为:√.
23.等式的两边同时除以同一个数,所得的结果仍然是等式. 错误 .(判断对错)
【考点】等式的意义.
教育 8http://t.cn/Ri466E4
【分析】根据等式的性质,可知:等式两边同时乘或除以一个相同的数(0除外),等式
仍然成立.
【解答】解:等式两边同时乘或除以一个相同的数(0除外),等式仍然成立;
需要限制相同的这个数,必须得0除外,因为0做除以无意义;
故答案为:错误.
三、精心选择
24.17和21的( )是1.
A.倍数B.公因数 C.最大公因数 D.最小公倍数
【考点】因数、公因数和最大公因数.
【分析】根据互质数的含义:公因数只有1的两个数叫做互质数;据此依次分析、即可得
出结论.
【解答】解:17和21是互质数,它们的公因数是1.
故选:B.
25.在下面的四个数中,( )既有因数2,又有因数3.
A.1 B.23 C.24 D.15
【考点】2、3、5的倍数特征.
【分析】这个数既有因数2,又有因数3,即这个数能同时被2与3整除,能同时被2与3
整除数的特征是:数的末位是偶数且各位数相加的和能被3整除,据此选择即可.
【解答】解:根据能同时被2与3整除数的特征可知,
24有因数2,又有因数3.
故选:C.
26.用长6厘米,宽4厘米的长方形可拼成边长是( )厘米的正方形.
A.9 B.12 C.15 D.16
【考点】公因数和公倍数应用题.
【分析】要求出正方形的边长最小是多少厘米,只有求6和4的最小公倍数,即可得解.
【解答】解:6=2×3
4=2×2
所以6和4的最小公倍数是2×3×2=12
答:用长6厘米,宽4厘米的长方形可拼成边长是12厘米的正方形.
故选:B.
27.a=3b,a,b都是大于0自然数,则a,b的最小公倍数是( )
A.a B.b C.3 D.1
【考点】求几个数的最小公倍数的方法.
【分析】求两数的最小公倍数,要看两个数之间的关系:两个数互质,则最小公倍数是这
两个数的乘积;两个数为倍数关系,则最小公倍数为较大的数;两个数有公约数的,最小
公倍数是两个数公有质因数与独有质因数的连乘积;由此选择情况解决问题.
【解答】解:由a=3b可知,数a是数b的3倍,属于倍数关系,a>b,
所以a和b的最小公倍数是 a;
故选:A.
教育 9http://t.cn/Ri466E4
28.有一个比20小的数,它既是3的倍数,又是4的倍数,这个数是( )
A.18 B.16 C.12 D.15
【考点】公倍数和最小公倍数.
【分析】首先分别找出20以内3、4的倍数,进而找出的它们的公倍数.
【解答】解:20以内3的倍数有:3、6、9、12、15、18;
20以内4的倍数有:4、8、12、16、20;
所以20以内既是3的倍数,又是4的倍数的数是12.
故选:C.
四、看图列方程并解答.
29.看图列方程并解答
【考点】正方形的周长.
【分析】正方形的周长C=4a,据此即可列方程求解.
【解答】解:由题意可得:
4x=3.2
4x÷4=3.2÷4
x=0.8.
30.看图列方程并解答.
【考点】图文应用题.
【分析】(1)根据题意,x与17的和是54,即x+17=54,然后再根据等式的性质进行解
答.
(2)根据题意,x与78的和是182,即x+78=182,然后再根据等式的性质进行解答.
【解答】(1)根据题意得:
x+17=54,
x+17﹣17=54﹣17
x=37
答:x是37.
(2)根据题意得:
x+78=182
教育 10http://t.cn/Ri466E4
x+78﹣78=182﹣78
x=104
答:已看104页.
五、解方程.
31.解方程:
7.6x=34.5
x﹣780=315
4.5x=9
x÷7.5=0.25.
【考点】方程的解和解方程.
【分析】(1)根据等式的性质,在方程两边同时除以7.6求解;
(2)根据等式的性质,在方程两边同时加上780求解;
(3)根据等式的性质,在方程两边同时除以4.5求解;
(4)根据等式的性质,在方程两边同时乘上7.5求解.
【解答】解:(1)7.6x=34.5
7.6x÷7.6=34.5÷7.6
x= ;
(2)x﹣780=315
x﹣780+780=315+780
x=1095;
(3)4.5x=9
4.5x÷4.5=9÷4.5
x=2;
(4)x÷7.5=0.25
x÷7.5×7.5=0.25×7.5
x=1.875.
六、解决问题.(1-3题列方程解答.)
32.煤场上午运来煤1.5吨,下午又运来了一些,一天共运来煤4.3吨,下午运来多少吨?
【考点】小数的加法和减法.
【分析】要求下午运来多少吨,用“一天运来总吨数﹣上午运来的吨数”即可.
【解答】解:4.3﹣1.5,
=2.8(吨);
答:下午运来2.8吨.
33.钢琴的黑键有48个,比白键少26个,白键有多少个?
【考点】整数的加法和减法.
【分析】黑键有48个,比白键少26个,也就是白健比黑键多26个,要求白键有多少个,
用48+26.
教育 11http://t.cn/Ri466E4
【解答】解:48+26=74(个).
答:白键有74个.
34.一艘轮船从甲港开往乙港,4小时到达终点,已知两港之间的水路长128千米,这艘
轮船每小时行多少千米?
【考点】简单的行程问题.
【分析】已知路程和时间,根据路程÷时间=速度,列式解答即可.
【解答】解:128÷4=32(千米);
答:这艘轮船每小时行32千米.
35.1路和2路公共汽车早上7时同时从起始站发车,1路车每隔6分发一辆车,2路车每
隔7分发一辆车.这两路车第二次同时发车的时间是多少?
【考点】公因数和公倍数应用题.
【分析】1路车每6分钟发车一次,那么1路车的发车间隔时间就是6的倍数;
2路车每7分钟发车一次,那么2路车的发车间隔时间就是7的倍数;
两辆车同时发车的间隔是6和7的公倍数,最少的间隔时间就是6和7的最小公倍数;求
出这个间隔时间,然后从7时推算即可.
【解答】解:6和7的最小公倍数就是:6×7=42;
两辆车每两次同时发车的间隔是42分钟;
从7时再过42分就是7时42分.
答:这两路车第二次同时发车的时间是7时42分.
36.把40本故事书和24本科技书分别分给一个组的同学,结果正好分完,你知道这个组
最多有几位同学吗.
【考点】公因数和公倍数应用题.
【分析】根据题意,也就是求40与24的最大公因数,即是这个组的最多人数;先把40和
24分别分解质因数,进而找出它们公有的质因数,再把公有的质因数相乘即可.
【解答】解:因为40=2×2×2×5,
24=2×2×2×3,
所以40和24的最大公因数是:2×2×2=8;
答:这个组最多有8位同学.
37.小朋友做游戏,分成8人一组,或6人一组都正好,做游戏的小朋友至少有多少个?
【考点】公因数和公倍数应用题.
【分析】由题意可知,做游戏的小朋友一定是6、8的公倍数,先求出6、8的最小公倍数,
由于数量最少,最小公倍数就是做游戏的小朋友的最少数,由此得解.
【解答】解:因为6=2×3
8=2×2×2
6、8的最小公倍数是24,
所以做游戏的小朋友至少有24个.
38.有两根绳子,一根长16米,另一根长20米.现在要把它们剪成同样长的小段,每段
长要尽可能长,且没有剩余.每段绳子长多少米?二根绳子一共可以剪成几段?
【考点】公因数和公倍数应用题.
教育 12http://t.cn/Ri466E4
【分析】根据题意,可计算出16与20的最大公因数,即是每段绳子最长的长度,然后再
用16除以最大公约数加上20除以最大公因数的商,即是一共剪成的段数,列式解答即可
得到答案.
【解答】解:16=2×2×2×2
20=2×2×5
所以16与20最大公因数是2×2=4.
即每小段最长是4米,
16÷4+20÷4
=4+5
=9(段);
答:每小段最长是4米,一共可以剪成9段.
39.小明每4天去一次学校图书馆借书,小红每6天去一次学校图书馆借书.如果他们两
人,4月1日同时去图书馆借书,那么他们下一次是几月几日又同时去借书?
【考点】公因数和公倍数应用题.
【分析】根据小明4天去一次学校图书馆,小红6天去一次学校图书馆借书,要求他们再
过多少天又同时去借书,只要求出4、6的最小公倍数即可,用4月1日加上再经过的天数
即可得解.
【解答】解:因为4=2×2,6=2×3,
所以4、6的最小公倍数是:2×2×3=12,
即他们再过12天又同时去借书,4月1日再过12天就是4月13日.
答:他们下一次是4月13日又同时去借书.
40.用红花48朵,黄花60朵做花束,如果每束花里的红花朵数都相等,每束花里的黄花
朵数也都相等,最多可以做几束花?每个花束里红花最多有几朵?黄花最多几朵?
【考点】公因数和公倍数应用题.
【分析】把这些花分成相同的若干束,就是分得的红花和黄花的数量,既是60的因数也是
48的因数,即是60和48的公因数,要求最多就是求60和48的最大公因数,因此求出60
和48的最大公因数就是最多可以分成几束,然后用红花和黄花的数量分别除以它们的最大
公因数,就是每束里红花、黄花各几朵.
【解答】解:48=2×2×2×2×3,
60=2×2×3×5,
所以48和60的最大公因数是:2×2×3=12;
每束里红花的朵数:48÷12=4(朵)
黄花朵数:60÷12=5(朵).
答:最多能扎12束,每束里4朵红花、5朵黄花.
41.把一张长12cm、宽8cm的长方形纸剪成同样大小、面积尽可能大的正方形,且纸没有
剩余,剪出的正方形的边长是多少?这样可以剪多少个?
【考点】公因数和公倍数应用题.
【分析】根据题意知道,要使面积尽可能大,纸没有剩余,也就是求8和12的最大公约数,
所裁正方形的个数就是8和12独有的质因数的积;12=2×2×3,8=2×2×2,8与12的最
大公约数4,由此可以分成边长是4cm的正方形有2×3个.
【解答】解:因为,8=2×2×2,12=2×2×3,
教育 13http://t.cn/Ri466E4
8与12的最大公约数是:2×2=4,
则可以分成边长是4cm的正方形,
所裁正方形的个数就是8和12独有的质因数的积,
即,2×3=6(个);
答:剪出的正方形的边长是4厘米,这样可以剪6个.
教育 14http://t.cn/Ri466E4
2016年8月25日
教育 15