文档内容
2020 成都中考数学答案与解析
A卷(共100分)
第I卷(选择题,共30分)
一.选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有
一项符合题目要求,答案涂在答题卡上)
1.-2的绝对值是( )
A.-2 B.1 C.2 D.
2.如图所示的几何体是由四个大小相同的小立方块搭成,其左视图是( )
3.2020年6月23日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利
进入预定轨道,它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统
全面建成.该卫星距离地面约为36000千米,将数据36000用科学记数法表示为( )
A.3.6×103 B.3.6×104 C.3.6×105 D.36×104
4.在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2) C.(5,2) D.(3,4)
5.下列计算正确的是( )
A. B. C. D.
6.成都市国家历史文化名城,区域内的都江堰、武侯祠、杜甫草堂、金沙遗址、青羊宫都有深厚的文化底蕴.某班同学分组到以上五个地方进行研学旅行,人数分别为:12,5,11,5,7
(单位:人)这组数据的众数和中位数分别是( )
A.5人,7人 B.5人,11人 C.5人,12人 D.7人,11人
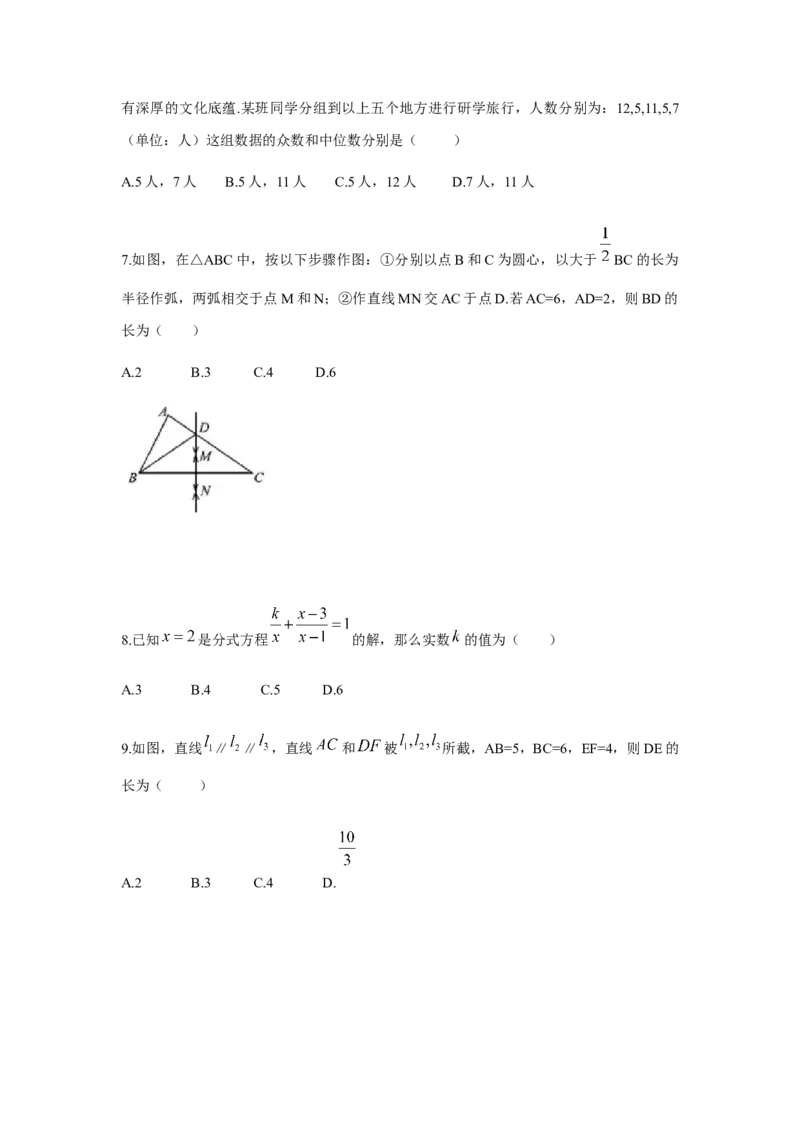
7.如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于 BC的长为
半径作弧,两弧相交于点M和N;②作直线MN交AC于点D.若AC=6,AD=2,则BD的
长为( )
A.2 B.3 C.4 D.6
8.已知 是分式方程 的解,那么实数 的值为( )
A.3 B.4 C.5 D.6
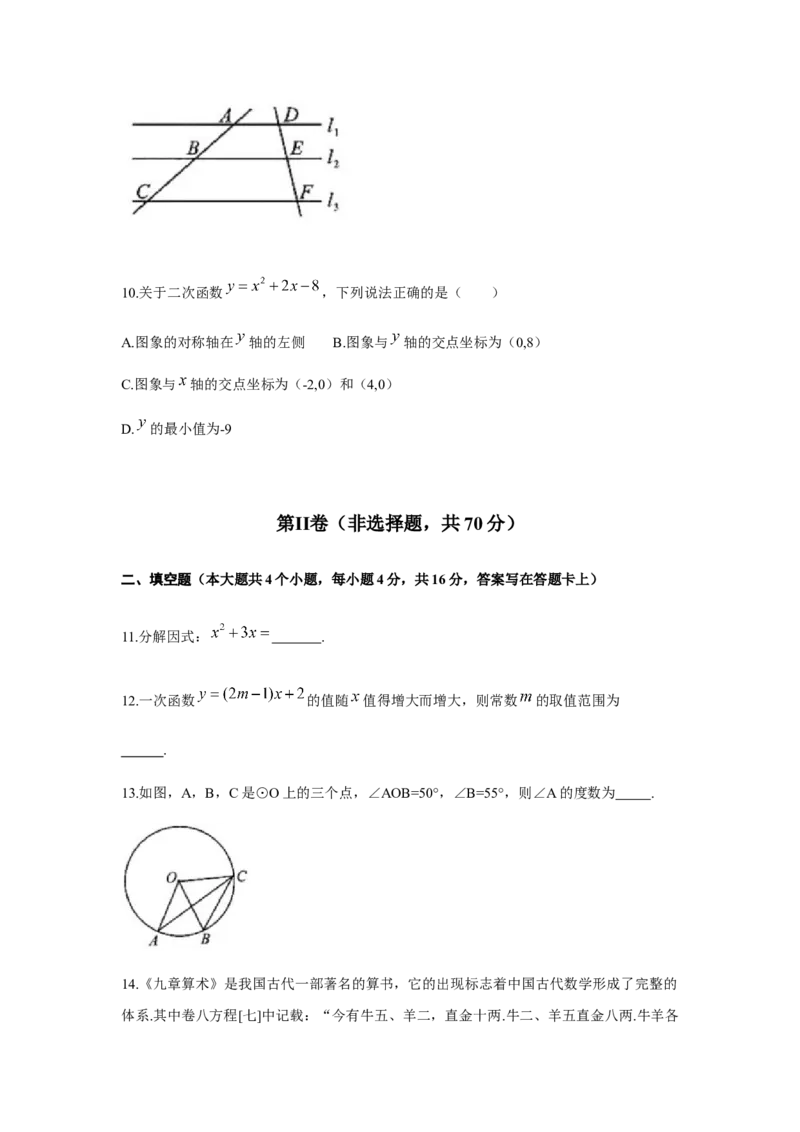
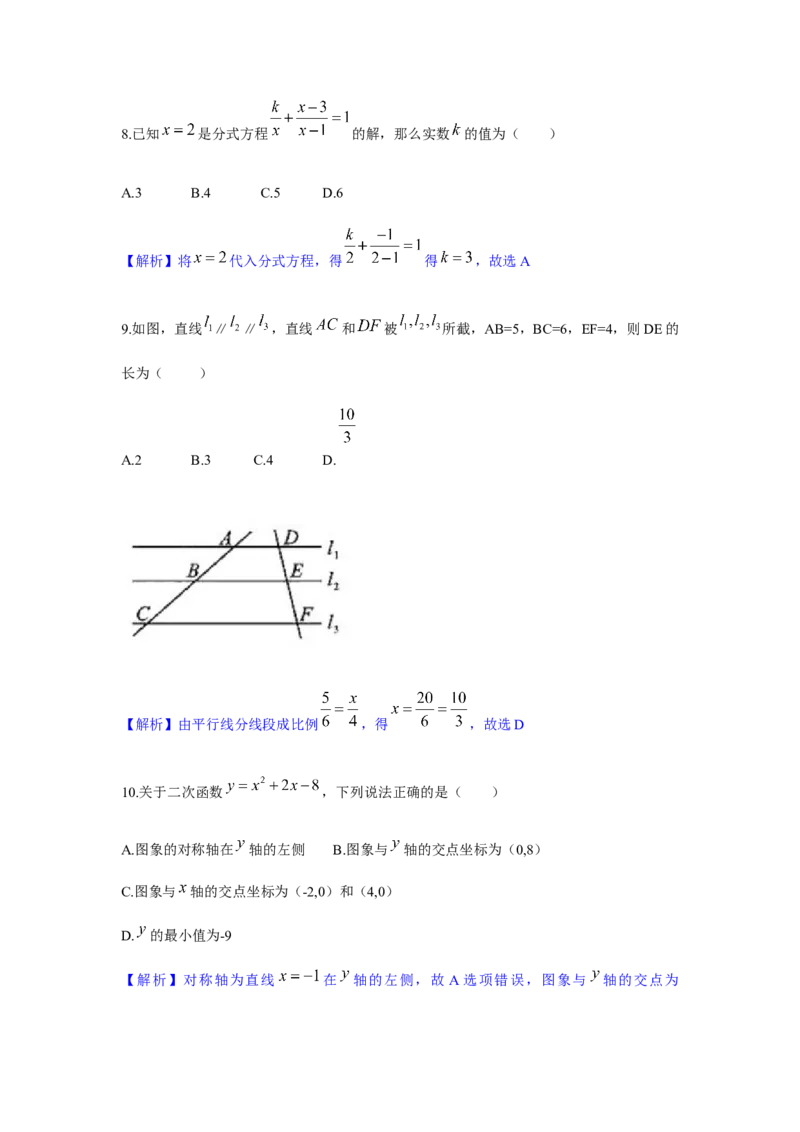
9.如图,直线 ∥ ∥ ,直线 和 被 所截,AB=5,BC=6,EF=4,则DE的
长为( )
A.2 B.3 C.4 D.10.关于二次函数 ,下列说法正确的是( )
A.图象的对称轴在 轴的左侧 B.图象与 轴的交点坐标为(0,8)
C.图象与 轴的交点坐标为(-2,0)和(4,0)
D. 的最小值为-9
第II卷(非选择题,共70分)
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)
11.分解因式: .
12.一次函数 的值随 值得增大而增大,则常数 的取值范围为
.
13.如图,A,B,C是⊙O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为 .
14.《九章算术》是我国古代一部著名的算书,它的出现标志着中国古代数学形成了完整的
体系.其中卷八方程[七]中记载:“今有牛五、羊二,直金十两.牛二、羊五直金八两.牛羊各直金几何?”题目大意是:5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、
每只羊各值金多少两?设1头牛值金 两,1只羊值金 两,则可列方程组为 .
三.解答题(本大题共6个小题,共54分,解答过程写在答题卡上)
15.(本小题满分12分,每题6分)
(1)计算: . (2)解不等式组:
16.(本小题满分6分)
先化简,再求值 ,其中 .
17.(本小题满分8分)
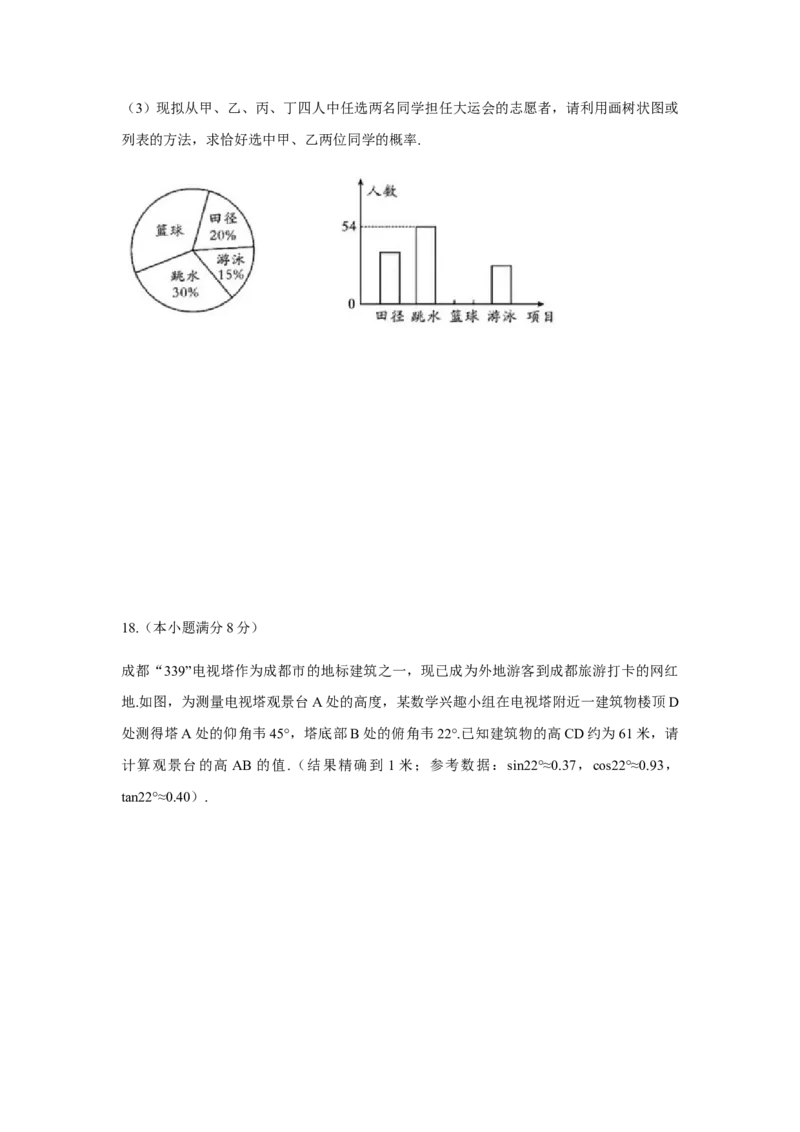
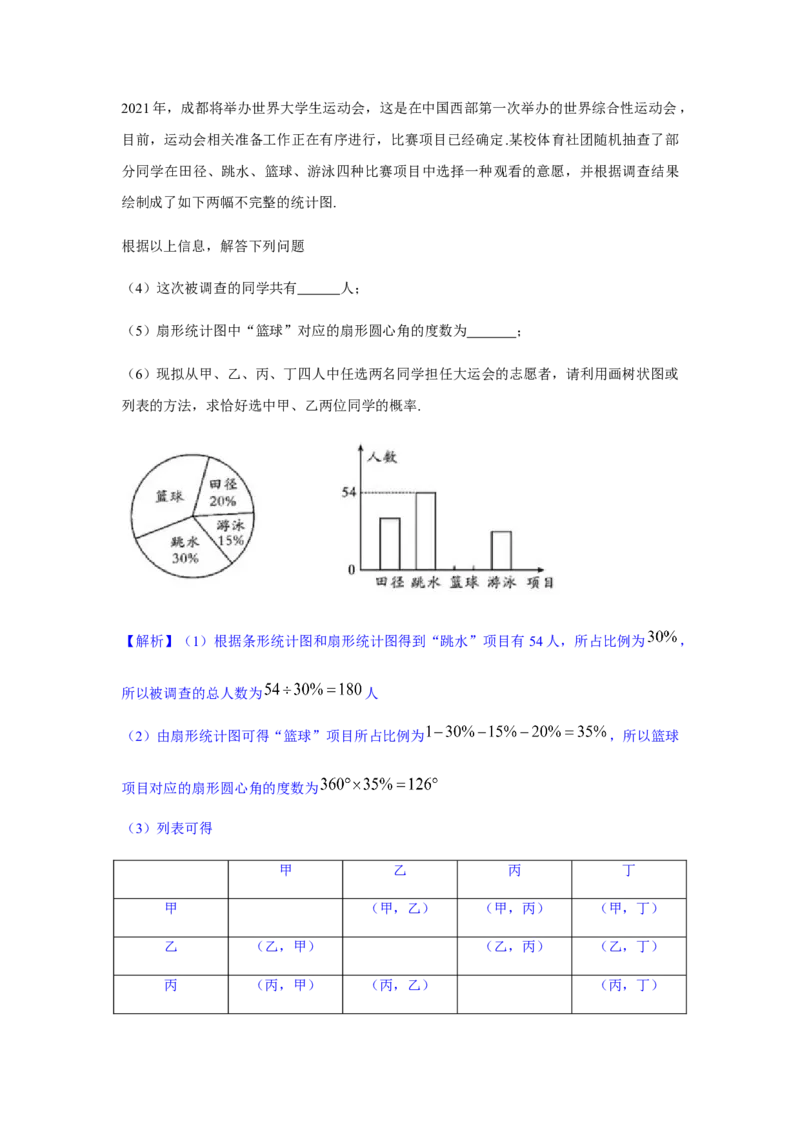
2021年,成都将举办世界大学生运动会,这是在中国西部第一次举办的世界综合性运动会,
目前,运动会相关准备工作正在有序进行,比赛项目已经确定.某校体育社团随机抽查了部
分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果
绘制成了如下两幅不完整的统计图.
根据以上信息,解答下列问题
(1)这次被调查的同学共有 人;
(2)扇形统计图中“篮球”对应的扇形圆心角的度数为 ;(3)现拟从甲、乙、丙、丁四人中任选两名同学担任大运会的志愿者,请利用画树状图或
列表的方法,求恰好选中甲、乙两位同学的概率.
18.(本小题满分8分)
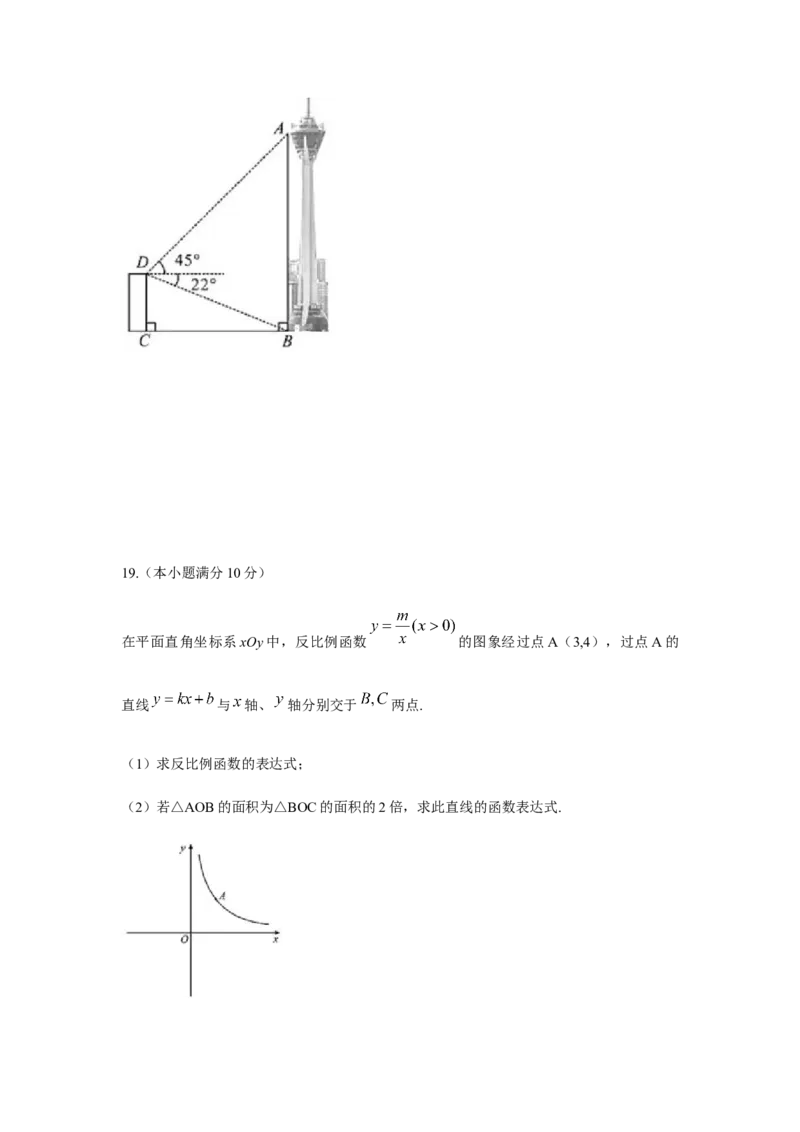
成都“339”电视塔作为成都市的地标建筑之一,现已成为外地游客到成都旅游打卡的网红
地.如图,为测量电视塔观景台A处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶D
处测得塔A处的仰角韦45°,塔底部B处的俯角韦22°.已知建筑物的高CD约为61米,请
计算观景台的高 AB 的值.(结果精确到 1 米;参考数据:sin22°≈0.37,cos22°≈0.93,
tan22°≈0.40).19.(本小题满分10分)
在平面直角坐标系xOy中,反比例函数 的图象经过点A(3,4),过点A的
直线 与 轴、 轴分别交于 两点.
(1)求反比例函数的表达式;
(2)若△AOB的面积为△BOC的面积的2倍,求此直线的函数表达式.20.(本小题满分10分)
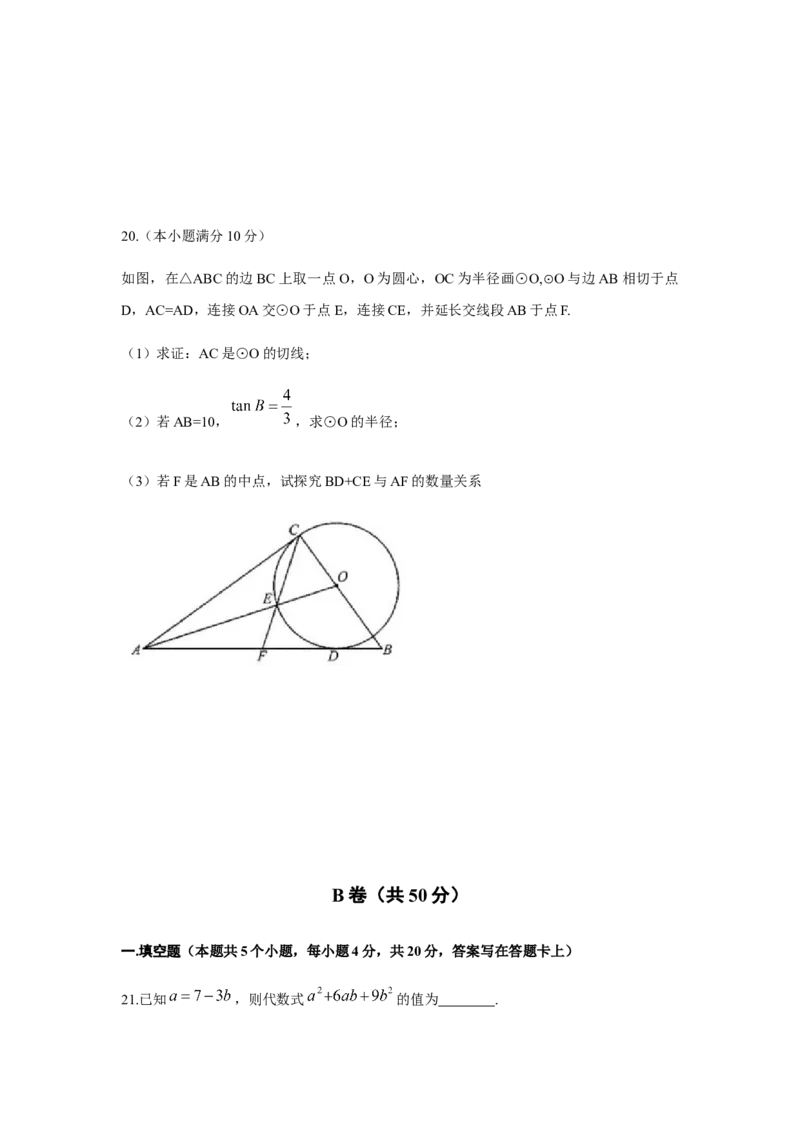
如图,在△ABC的边BC上取一点O,O为圆心,OC为半径画⊙O,⊙O与边AB相切于点
D,AC=AD,连接OA交⊙O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是⊙O的切线;
(2)若AB=10, ,求⊙O的半径;
(3)若F是AB的中点,试探究BD+CE与AF的数量关系
B卷(共50分)
一.填空题(本题共5个小题,每小题4分,共20分,答案写在答题卡上)
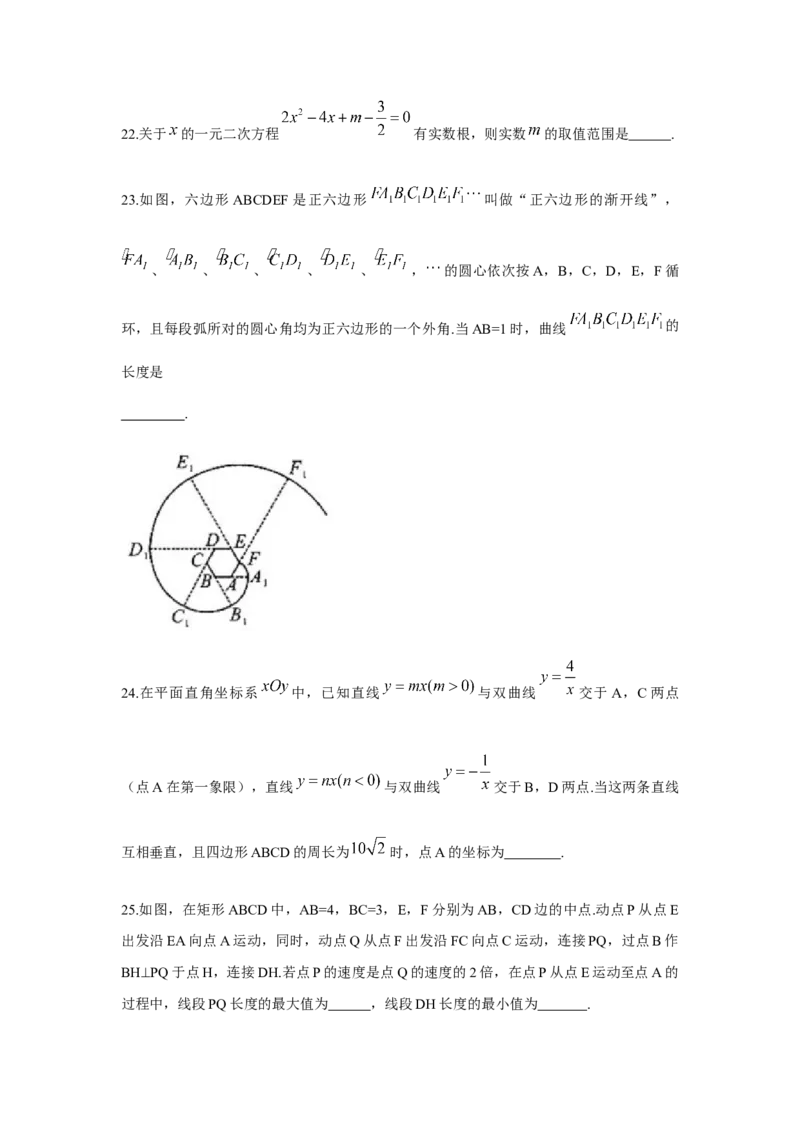
21.已知 ,则代数式 的值为 .22.关于 的一元二次方程 有实数根,则实数 的取值范围是 .
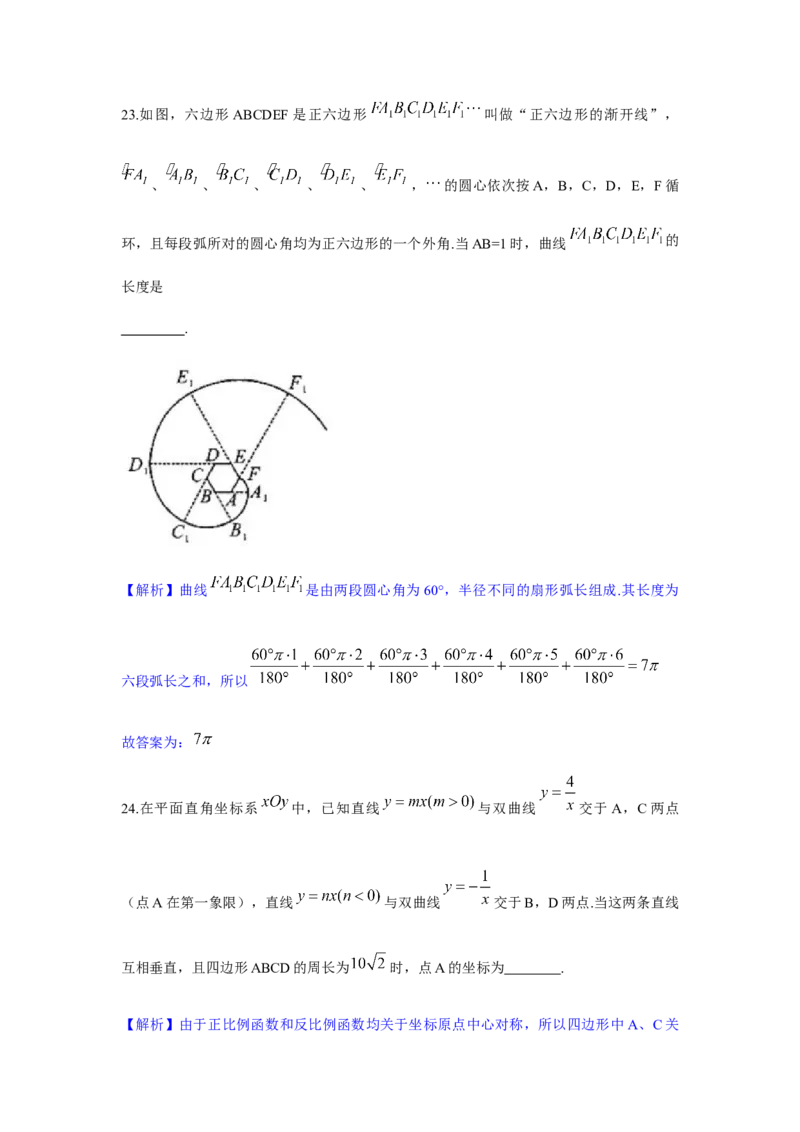
23.如图,六边形 ABCDEF是正六边形 叫做“正六边形的渐开线”,
、 、 、 、 、 , 的圆心依次按A,B,C,D,E,F循
环,且每段弧所对的圆心角均为正六边形的一个外角.当AB=1时,曲线 的
长度是
.
24.在平面直角坐标系 中,已知直线 与双曲线 交于A,C两点
(点A在第一象限),直线 与双曲线 交于B,D两点.当这两条直线
互相垂直,且四边形ABCD的周长为 时,点A的坐标为 .
25.如图,在矩形ABCD中,AB=4,BC=3,E,F分别为AB,CD边的中点.动点P从点E
出发沿EA向点A运动,同时,动点Q从点F出发沿FC向点C运动,连接PQ,过点B作
BH⊥PQ于点H,连接DH.若点P的速度是点Q的速度的2倍,在点P从点E运动至点A的
过程中,线段PQ长度的最大值为 ,线段DH长度的最小值为 .二.解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
26.(本小题满分8分)
在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利
润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本价为10元/件,拟采取线上和线
下两种方式进行销售.调查发现,线下的月销量 (单位:件)与线下售价 (单位:元/件,
)满足一次函数的关系,部分数据如下表:
(元/件) 12 13 14 15 16
(件) 1200 1100 1000 900 900
(1)求 与 的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当 为多
少时,线上和线下月利润总和达到最大?并求出此时的最大利润.27.(本小题满分10分)
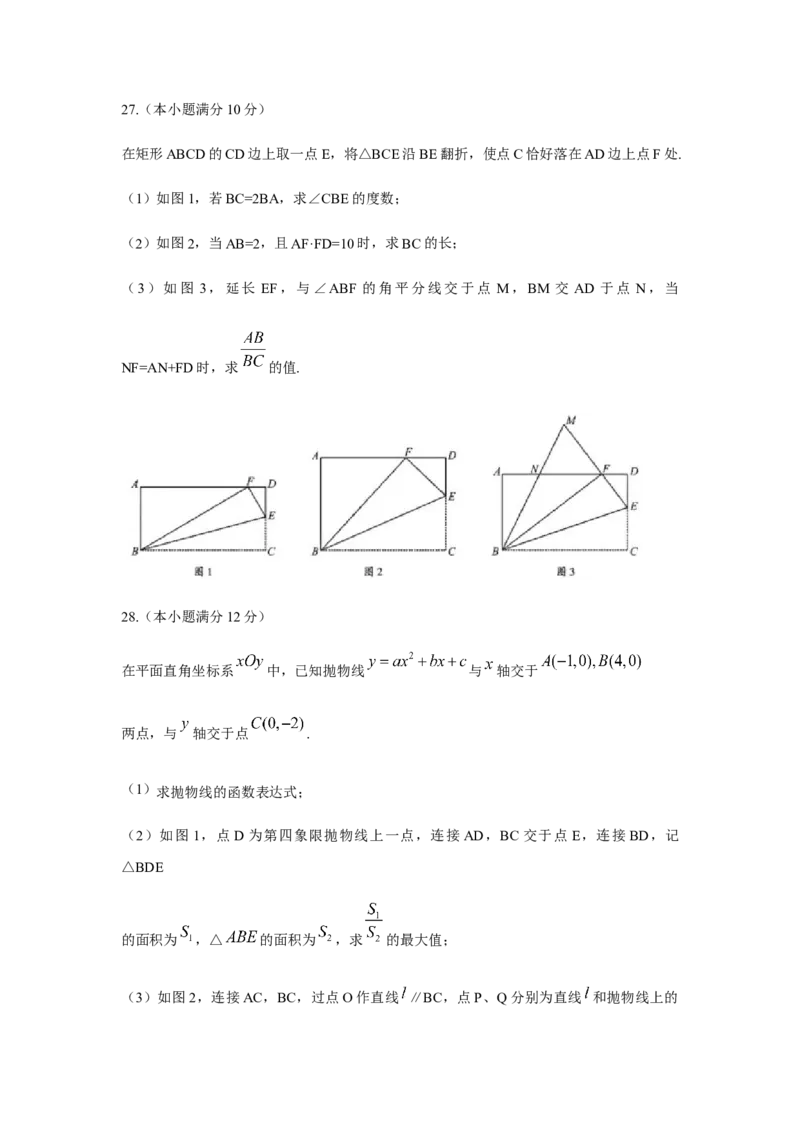
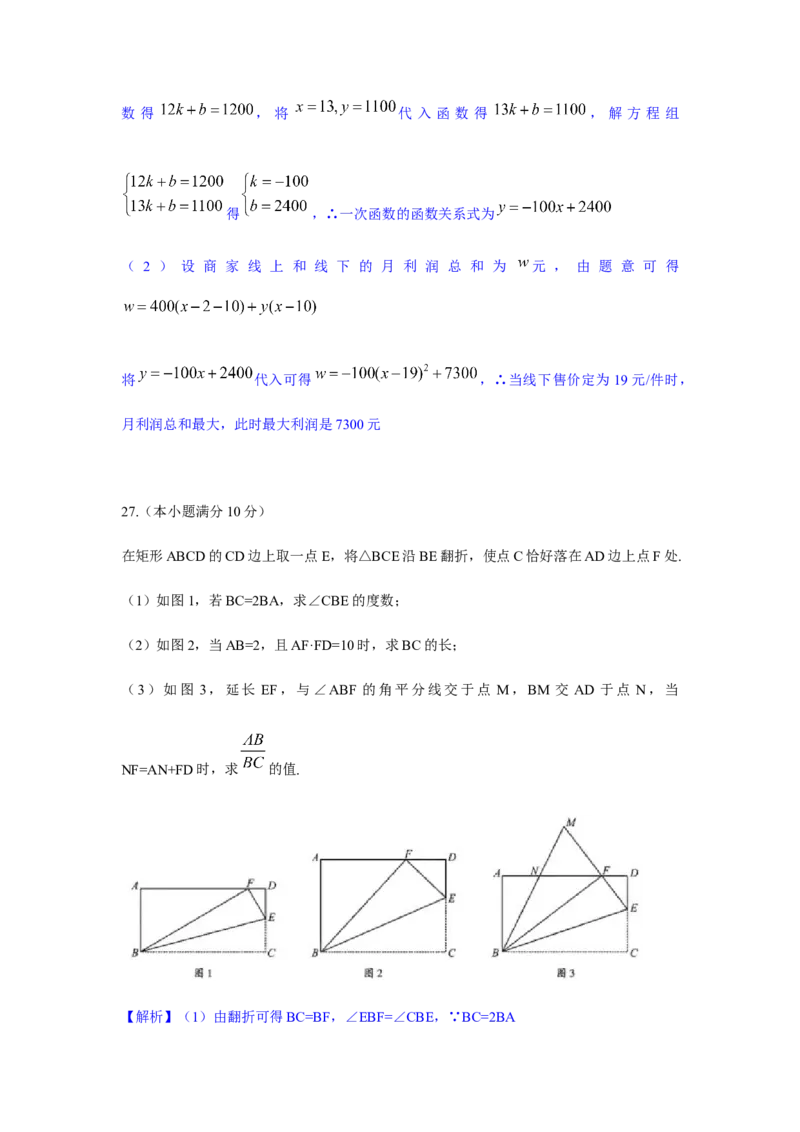
在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
(1)如图1,若BC=2BA,求∠CBE的度数;
(2)如图2,当AB=2,且AF·FD=10时,求BC的长;
(3)如图 3,延长 EF,与∠ABF 的角平分线交于点 M,BM 交 AD 于点 N,当
NF=AN+FD时,求 的值.
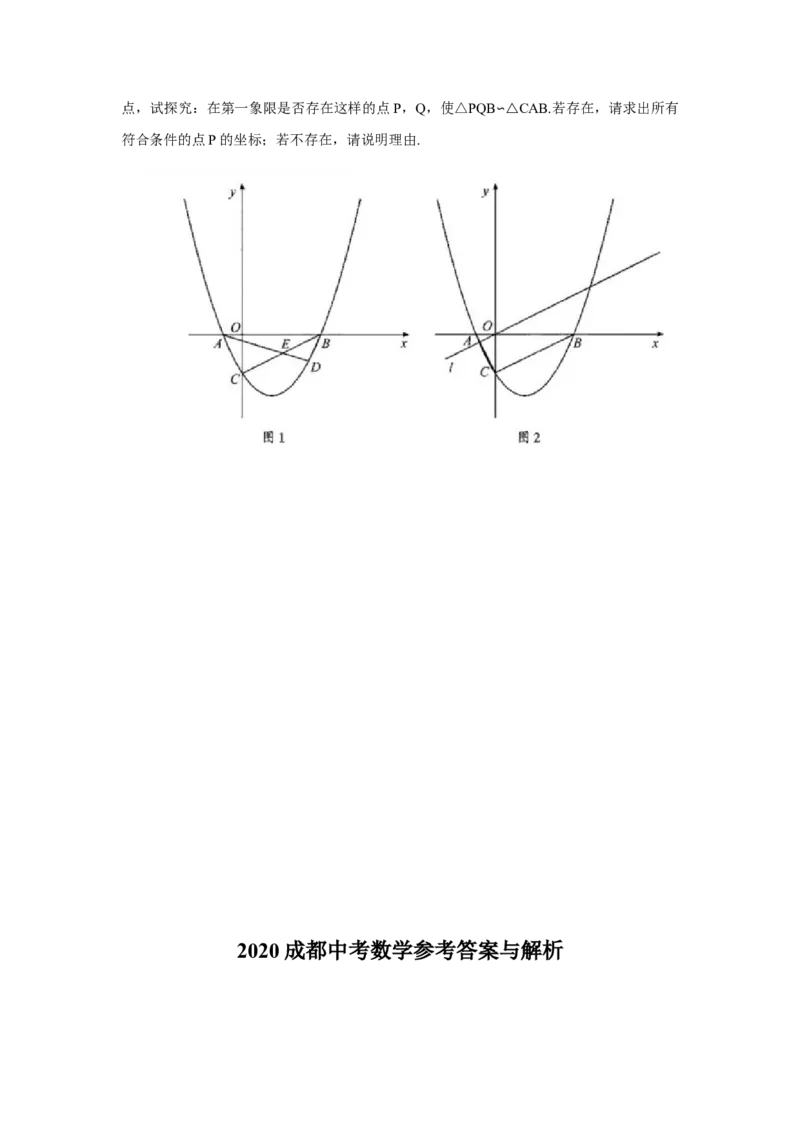
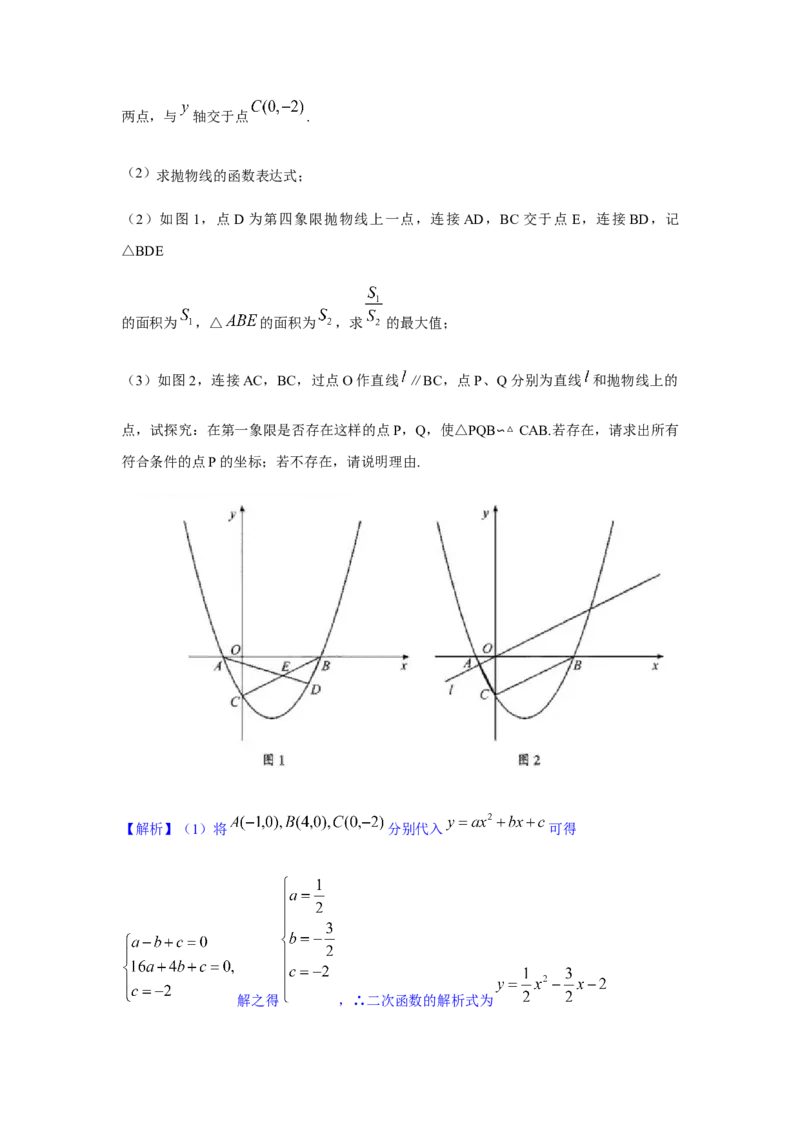
28.(本小题满分12分)
在平面直角坐标系 中,已知抛物线 与 轴交于
两点,与 轴交于点 .
(1)求抛物线的函数表达式;
(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,连接BD,记
△BDE
的面积为 ,△ 的面积为 ,求 的最大值;
(3)如图2,连接AC,BC,过点O作直线 ∥BC,点P、Q分别为直线 和抛物线上的点,试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB.若存在,请求出所有
符合条件的点P的坐标;若不存在,请说明理由.
2020 成都中考数学参考答案与解析A卷(共100分)
第I卷(选择题,共30分)
一.选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有
一项符合题目要求,答案涂在答题卡上)
1.-2的绝对值是( )
A.-2 B.1 C.2 D.
【解析】根据负数的绝对值是它的相反数可知,答案为C
2.如图所示的几何体是由四个大小相同的小立方块搭成,其左视图是( )
【解析】根据左视图为从左往右观看几何体,故应选D
3.2020年6月23日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利
进入预定轨道,它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统
全面建成.该卫星距离地面约为36000千米,将数据36000用科学记数法表示为( )
A.3.6×103 B.3.6×104 C.3.6×105 D.36×104
【解析】科学记数法为 ,其中 可得答案为B
4.在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2) C.(5,2) D.(3,4)【解析】点的平移规律为左减右加,上加下减,所以答案为A
5.下列计算正确的是( )
B. C. D.
A.
【解析】A选项
和 不是同类项,不能直接相加,B选项,同底指数幂相乘,底数不
变,指数应相加,所以正确结果为 ,D选项应是 ,故正确答案为C
6.成都市国家历史文化名城,区域内的都江堰、武侯祠、杜甫草堂、金沙遗址、青羊宫都
有深厚的文化底蕴.某班同学分组到以上五个地方进行研学旅行,人数分别为:12,5,11,5,7
(单位:人)这组数据的众数和中位数分别是( )
A.5人,7人 B.5人,11人 C.5人,12人 D.7人,11人
【解析】将数据按从小到大顺序排列号为 ,所以众数是5,中位数是7,故答
案为A
7.如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于 BC的长为
半径作弧,两弧相交于点M和N;②作直线MN交AC于点D.若AC=6,AD=2,则BD的
长为( )
A.2 B.3 C.4 D.6
【解析】由题意可得,按步骤作图的结果是:DN为线段BC的垂直平分线,∴DC=BD,
又∵AC=6,AD=2,∴CD=BD=4,故选C8.已知 是分式方程 的解,那么实数 的值为( )
A.3 B.4 C.5 D.6
【解析】将 代入分式方程,得 得 ,故选A
9.如图,直线 ∥ ∥ ,直线 和 被 所截,AB=5,BC=6,EF=4,则DE的
长为( )
A.2 B.3 C.4 D.
【解析】由平行线分线段成比例 ,得 ,故选D
10.关于二次函数 ,下列说法正确的是( )
A.图象的对称轴在 轴的左侧 B.图象与 轴的交点坐标为(0,8)
C.图象与 轴的交点坐标为(-2,0)和(4,0)
D. 的最小值为-9
【解析】对称轴为直线 在 轴的左侧,故 A 选项错误,图象与 轴的交点为,故选项B错误, 的解为 ,∴ 与
轴交点坐标为(2,0)和(-4,0),故选项C错误,D选项配方可得 ,所以
的最小值为-9,故答案为D
第II卷(非选择题,共70分)
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)
11.分解因式: .
【解析】提公因式即可得到答案,故答案为
12.一次函数 的值随 值得增大而增大,则常数 的取值范围为
.
【解析】由一次函数 的增减性可知, 随 的增大而增大时, ,所以
,解之得 ,∴本题答案为
13.如图,A,B,C是⊙O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为 .
【 解 析 】 ∵ OB=OC=r , ∴ ∠ B=∠OCB=55° , ∴ ∠ BOC=180°-∠B-∠OCB=70° ,
∴∠AOC=∠AOB+∠BOC=50°+70°=120°,∵OA=OC,∴∠OAC=∠OCA=30°,本题答案为
30°14.《九章算术》是我国古代一部著名的算书,它的出现标志着中国古代数学形成了完整的
体系.其中卷八方程[七]中记载:“今有牛五、羊二,直金十两.牛二、羊五直金八两.牛羊各
直金几何?”题目大意是:5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、
每只羊各值金多少两?设1头牛值金 两,1只羊值金 两,则可列方程组为 .
【解析】依题意可得
三.解答题(本大题共6个小题,共54分,解答过程写在答题卡上)
15.(本小题满分12分,每题6分)
(1)计算: . (2)解不等式组:
【解析】(1) ; (2)解不等式①得 ;解不等式②得
= =3 ; 所以不等式组的解集为
16.(本小题满分6分)
先化简,再求值 ,其中 .
【解析】原式=
将 代入 =
17.(本小题满分8分)2021年,成都将举办世界大学生运动会,这是在中国西部第一次举办的世界综合性运动会,
目前,运动会相关准备工作正在有序进行,比赛项目已经确定.某校体育社团随机抽查了部
分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果
绘制成了如下两幅不完整的统计图.
根据以上信息,解答下列问题
(4)这次被调查的同学共有 人;
(5)扇形统计图中“篮球”对应的扇形圆心角的度数为 ;
(6)现拟从甲、乙、丙、丁四人中任选两名同学担任大运会的志愿者,请利用画树状图或
列表的方法,求恰好选中甲、乙两位同学的概率.
【解析】(1)根据条形统计图和扇形统计图得到“跳水”项目有54人,所占比例为 ,
所以被调查的总人数为 人
(2)由扇形统计图可得“篮球”项目所占比例为 ,所以篮球
项目对应的扇形圆心角的度数为
(3)列表可得
甲 乙 丙 丁
甲 (甲,乙) (甲,丙) (甲,丁)
乙 (乙,甲) (乙,丙) (乙,丁)
丙 (丙,甲) (丙,乙) (丙,丁)丁 (丁,甲) (丁,乙) (丁,丙)
由表格可得,甲,乙,丙,丁四人中任选两名同学担任大运会志愿者总的情况有 12种,恰
好是甲,乙两位同学的情况有2种,∴恰好选中甲、乙两位同学的概率为
18.(本小题满分8分)
成都“339”电视塔作为成都市的地标建筑之一,现已成为外地游客到成都旅游打卡的网红
地.如图,为测量电视塔观景台A处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶D
处测得塔A处的仰角韦45°,塔底部B处的俯角韦22°.已知建筑物的高CD约为61米,请
计算观景台的高 AB 的值.(结果精确到 1 米;参考数据:sin22°≈0.37,cos22°≈0.93,
tan22°≈0.40).
【解析】
过D作DE⊥AB于E
在Rt△BDE中tan∠BDE=
∴ 米∵△ADE是等腰直角三角形,
∴AE=DE=152.5米,
∵∠DCB=∠CBE=∠BED=90°
∴四边形BCDE是矩形
∴DC=BE=61米
∴AB=AE+BE=213.5米≈214米
答:观景台AB的高度约为214米.
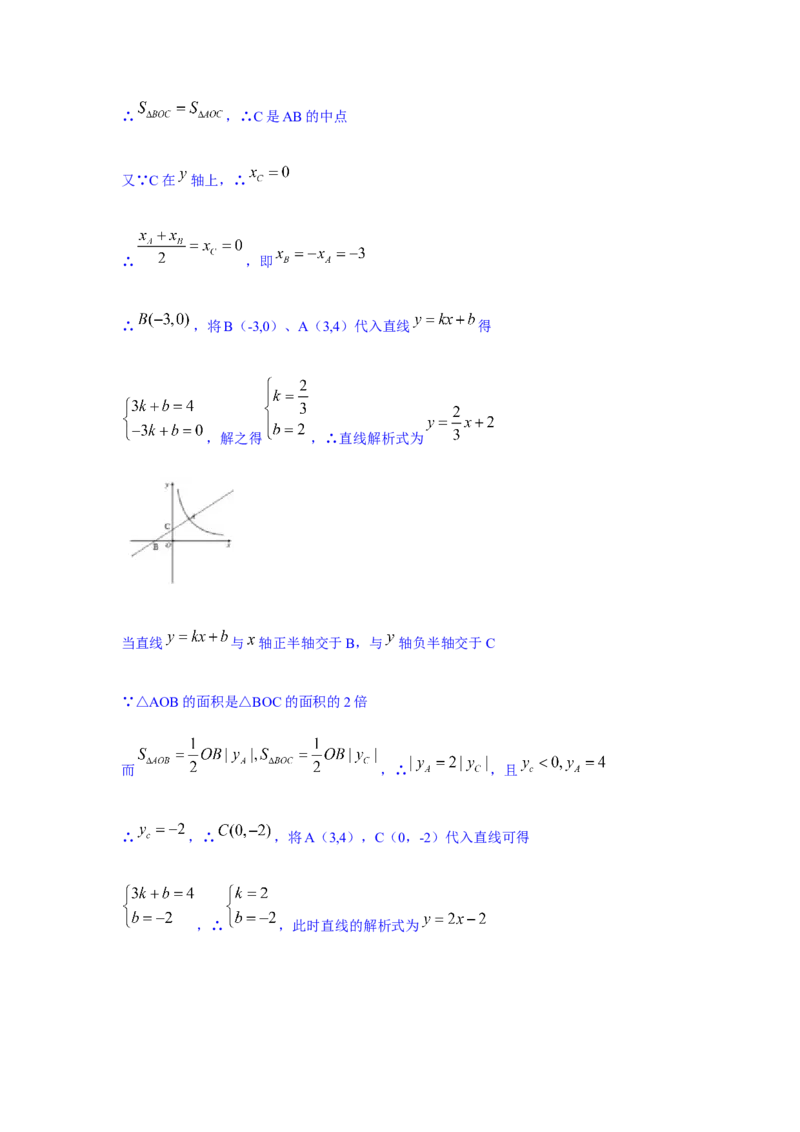
19.(本小题满分10分)
在平面直角坐标系xOy中,反比例函数 的图象经过点A(3,4),过点A的
直线 与 轴、 轴分别交于 两点.
(1)求反比例函数的表达式;
(2)若△AOB的面积为△BOC的面积的2倍,求此直线的函数表达式.
【解析】(1)将A(3,4)代入 得 ,∴反比例函数的表达式为
(2)当直线 与 轴负半轴交于B,与 轴正半轴交于C
∵△AOB的面积是△BOC的面积的2倍∴ ,∴C是AB的中点
又∵C在 轴上,∴
∴ ,即
∴ ,将B(-3,0)、A(3,4)代入直线 得
,解之得 ,∴直线解析式为
当直线 与 轴正半轴交于B,与 轴负半轴交于C
∵△AOB的面积是△BOC的面积的2倍
而 ,∴ ,且
∴ ,∴ ,将A(3,4),C(0,-2)代入直线可得
,∴ ,此时直线的解析式为综上所述:直线的函数表达式为 或
20.(本小题满分10分)
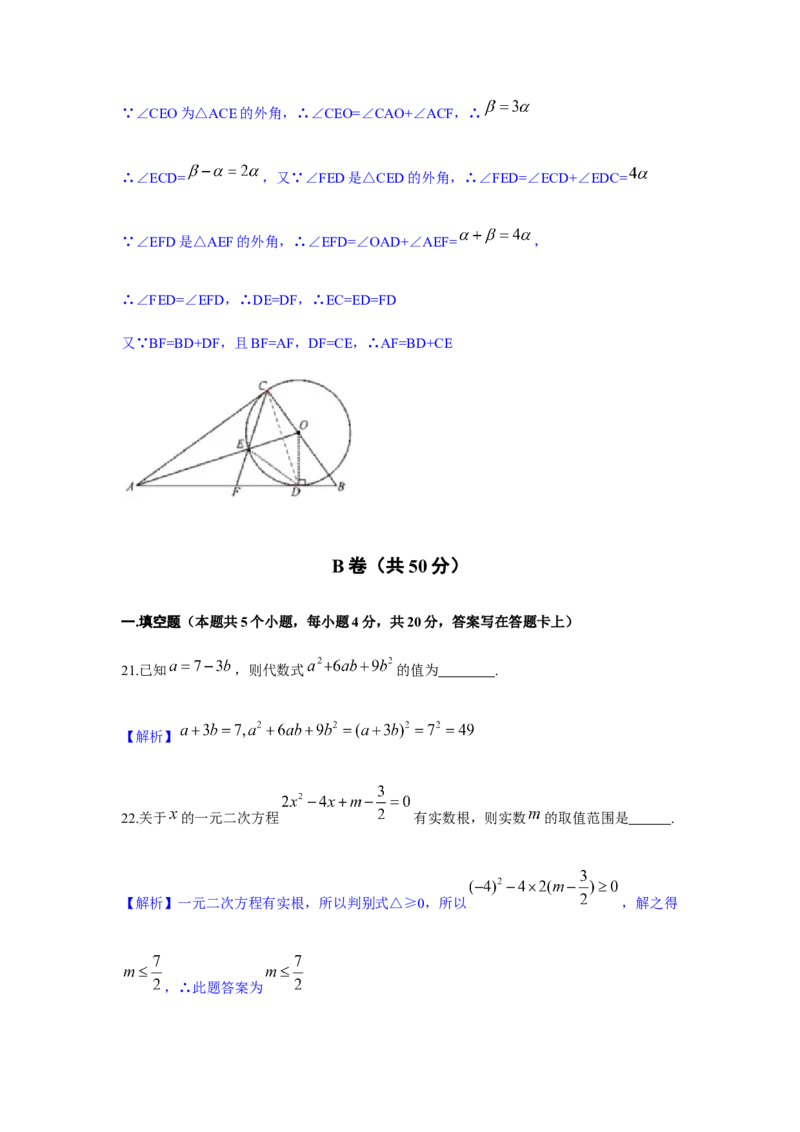
如图,在△ABC的边BC上取一点O,O为圆心,OC为半径画⊙O,⊙O与边AB相切于点
D,AC=AD,连接OA交⊙O于点E,连接CE,并延长交线段AB于点F.
(1)求证:AC是⊙O的切线;
(2)若AB=10, ,求⊙O的半径;
(3)若F是AB的中点,试探究BD+CE与AF的数量关系
【解析】(1)证明:连接OD,∵⊙O与AB相切,∴∠ADO=90°
在△AOC和△AOD中
∴△AOC≌△AOD(SSS),∴∠ADO=∠ACO=90°,∴OC⊥AC∵OC为⊙O的半径,∴AC是⊙O的切线.
(2)设OD= ,∵在Rt△OBD中, ,∴ ,
∴ ,∴BC=OB+OC=
在Rt△ACB中, ,∴ ,∴
又∵AB=10,∴ ,∴ ,∴ ,即⊙O的半径是
(3)探究关系结果: ,理由如下:
连接ED,CD,∵AC,AD为⊙O的切线,∴AO平分∠COD和∠CAD,∴∠COE=∠DOE
且∠COE及∠DOE均为圆心角,∴CE=DE,∴∠ECD=∠EDC.
在△OCE和△ODE中
∴△OCE≌△ODE(SSS),∴∠CEO=∠DEO
设∠CAO= ,∠CEO=
∵AC=AD,且OA平分∠CAD,∴OA⊥CD,
∴∠CAO+∠ACD=90°,又∵∠ACD+∠OCD=90°,∴∠OCD=
∴∠ECD= ,又∵∠AEF和∠CEO互为对顶角,∴∠AEF=∠CEO=
在Rt△ACB中,因为C是斜边AB中点,∴BF=AF=CF,∴∠CAF=∠ACF=∵∠CEO为△ACE的外角,∴∠CEO=∠CAO+∠ACF,∴
∴∠ECD= ,又∵∠FED是△CED的外角,∴∠FED=∠ECD+∠EDC=
∵∠EFD是△AEF的外角,∴∠EFD=∠OAD+∠AEF= ,
∴∠FED=∠EFD,∴DE=DF,∴EC=ED=FD
又∵BF=BD+DF,且BF=AF,DF=CE,∴AF=BD+CE
B卷(共50分)
一.填空题(本题共5个小题,每小题4分,共20分,答案写在答题卡上)
21.已知 ,则代数式 的值为 .
【解析】
22.关于 的一元二次方程 有实数根,则实数 的取值范围是 .
【解析】一元二次方程有实根,所以判别式△≥0,所以 ,解之得
,∴此题答案为23.如图,六边形 ABCDEF是正六边形 叫做“正六边形的渐开线”,
、 、 、 、 、 , 的圆心依次按A,B,C,D,E,F循
环,且每段弧所对的圆心角均为正六边形的一个外角.当AB=1时,曲线 的
长度是
.
【解析】曲线 是由两段圆心角为60°,半径不同的扇形弧长组成.其长度为
六段弧长之和,所以
故答案为:
24.在平面直角坐标系 中,已知直线 与双曲线 交于A,C两点
(点A在第一象限),直线 与双曲线 交于B,D两点.当这两条直线
互相垂直,且四边形ABCD的周长为 时,点A的坐标为 .
【解析】由于正比例函数和反比例函数均关于坐标原点中心对称,所以四边形中A、C关于O对称,B、D关于O中心对称,所以对角线 AC、BD被坐标原点平分,即四边形
ABCD是平行四边形,当AC⊥BD时,可得四边形ABCD为菱形.由四边形周长为 ,
可得四边形边长 ,将直线 代入反比例函数 得 ,∴
,代入反比例函数得 ,∵AC⊥BD,∴ ,即 ,将直
线 代入反比例函数 得 ,∴ ,∴ ,∴
∴ , 在 Rt△ AOD 中 , , ∴
整理得 ,∴ 或2,当 时, ,当 时,
,∴A的坐标为 或
25.如图,在矩形ABCD中,AB=4,BC=3,E,F分别为AB,CD边的中点.动点P从点E
出发沿EA向点A运动,同时,动点Q从点F出发沿FC向点C运动,连接PQ,过点B作
BH⊥PQ于点H,连接DH.若点P的速度是点Q的速度的2倍,在点P从点E运动至点A的
过程中,线段PQ长度的最大值为 ,线段DH长度的最小值为 .【解析】∵P由E往A运动,Q由F往C运动,且点P的速度是点Q的速度的2倍,所以
当 P 与 A 重合时,Q 在 FC 中点时,线段 PQ 取得最大值,过 Q 作 QN⊥AB 于 N,则
AN=QN=3 , 此 时 线 段 , 连 接 DE , HE , 则
,所以 ,当D、H、E三点共线时DH取得最
小值,此时HE= ,故DH最小值为
二.解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
26.(本小题满分8分)
在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利
润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本价为10元/件,拟采取线上和线
下两种方式进行销售.调查发现,线下的月销量 (单位:件)与线下售价 (单位:元/件,
)满足一次函数的关系,部分数据如下表:
(元/件) 12 13 14 15 16
(件) 1200 1100 1000 900 900
(3)求 与 的函数关系式;
(4)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当 为多
少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
【解析】(1)设一次函数的函数关系式为 ,将 代入函数 得 , 将 代 入 函 数 得 , 解 方 程 组
得 ,∴一次函数的函数关系式为
( 2 ) 设 商 家 线 上 和 线 下 的 月 利 润 总 和 为 元 , 由 题 意 可 得
将 代入可得 ,∴当线下售价定为19元/件时,
月利润总和最大,此时最大利润是7300元
27.(本小题满分10分)
在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
(1)如图1,若BC=2BA,求∠CBE的度数;
(2)如图2,当AB=2,且AF·FD=10时,求BC的长;
(3)如图 3,延长 EF,与∠ABF 的角平分线交于点 M,BM 交 AD 于点 N,当
NF=AN+FD时,求 的值.
【解析】(1)由翻折可得BC=BF,∠EBF=∠CBE,∵BC=2BA∴在Rt△ABF中,sin∠AFB= ,∴∠AFB=30°
∵在矩形ABCD中,AD∥BC,∴∠AFB=∠CBF=30°
∴∠CBE= ∠CBF=15°
(2)在矩形ABCD中,有∠A=∠D=∠C=90°,由翻折性质可知∠C=∠BFE=90°.
∵在Rt△ABF中,有∠AFB+∠ABF=90°,根据平角定义可得∠AFB+∠BFE+∠EFD=180°
∴∠ABF=∠EFD,又∵∠A=∠D=90°,∴△FAB∽△EDF
∴ ,∴ ,∵ ,AB=5,解得ED=2
CE=CD-ED=5-2=3,由翻折性质可知EF=CE=3,
在Rt△EFD中, ;
∵ ,∴ ,∴
由矩形ABCD性质可得,BC=AD=
(3)作 ⊥ 于G,
在△FNG和△FBA中 ∴△FNG∽△FBA,∴
,
∵NF=AN+FD且NF+AN+FD=AD,∴2NF=AD,即∵AD=BC,BC=BF,∴ ,∴
设 , 则 , , ∴ , ∴
∵BM平分∠ABF,N在BM上,且NA⊥AB,NG⊥BF,∴NA=NG=
在Rt△NGF中, ,∴ ,整理可得
解得 ,负值舍掉,∴ ,∴
在Rt△BAN和Rt△BGN中 ,∴Rt△BAN≌Rt△BGN(HL),
,∴
∴
28.(本小题满分12分)
在平面直角坐标系 中,已知抛物线 与 轴交于两点,与 轴交于点 .
(2)求抛物线的函数表达式;
(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,连接BD,记
△BDE
的面积为 ,△ 的面积为 ,求 的最大值;
(3)如图2,连接AC,BC,过点O作直线 ∥BC,点P、Q分别为直线 和抛物线上的
点,试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△ CAB.若存在,请求出所有
符合条件的点P的坐标;若不存在,请说明理由.
【解析】(1)将 分别代入 可得
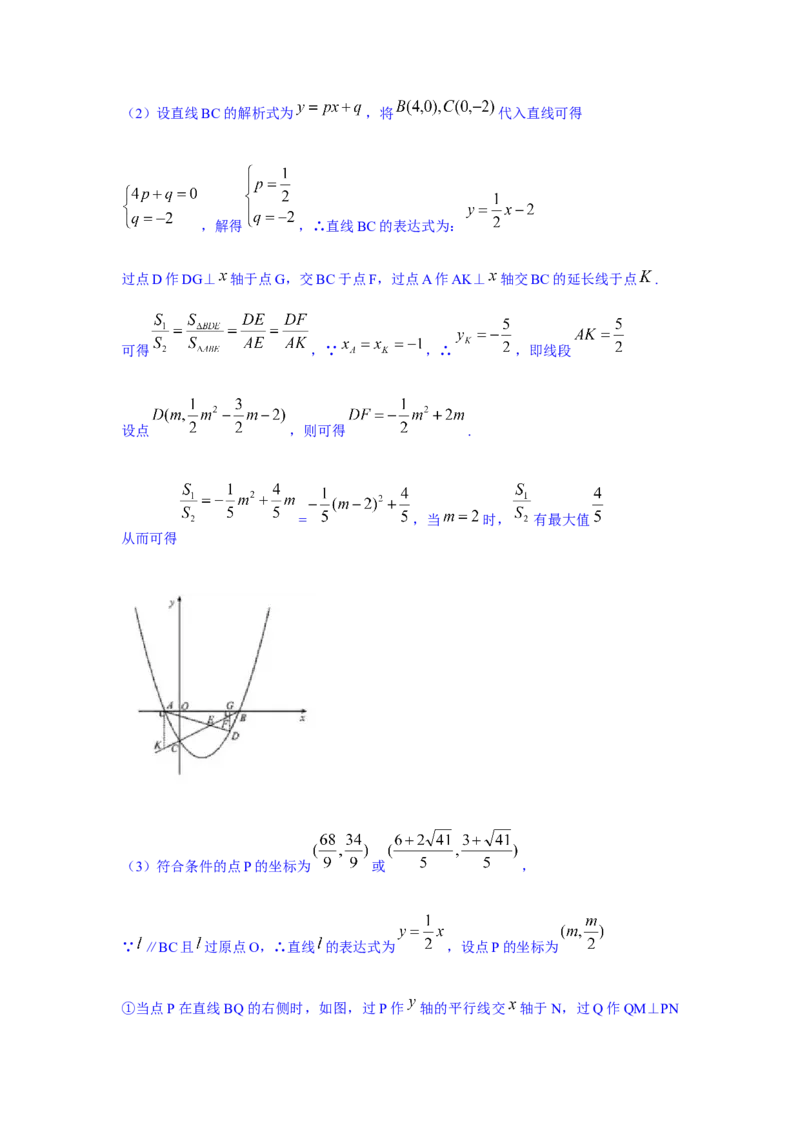
解之得 ,∴二次函数的解析式为(2)设直线BC的解析式为 ,将 代入直线可得
,解得 ,∴直线BC的表达式为:
过点D作DG⊥ 轴于点G,交BC于点F,过点A作AK⊥ 轴交BC的延长线于点 .
可得 ,∵ ,∴ ,即线段
设点 ,则可得 .
= ,当 时, 有最大值
从而可得
(3)符合条件的点P的坐标为 或 ,
∵ ∥BC且 过原点O,∴直线 的表达式为 ,设点P的坐标为
①当点P在直线BQ的右侧时,如图,过P作 轴的平行线交 轴于N,过Q作QM⊥PN于M.
∵△PQB∽△CAB,∴∠BPQ=∠BCA
在 Rt△ AOC 中 , , 在 Rt△ BOC 中 ,
∵AB=5,∴ ,即∠ACB=90°
∴∠BPQ=90°,∴∠MPQ+∠BPN=90°,∵∠BPN+∠PBN=90°,∴∠PBN=∠QPM
∴△QPM∽△PBN,∴
又∵△PQB∽△CAB,∴
∴ ,∵ ,
∴ ,
∴ ,∴
∵Q在抛物线上,∴ ,且 ,∴
∴此时P的坐标为
②当点P在直线BQ左侧时.由①的方法可得点Q的坐标为 ,此时P点坐标为