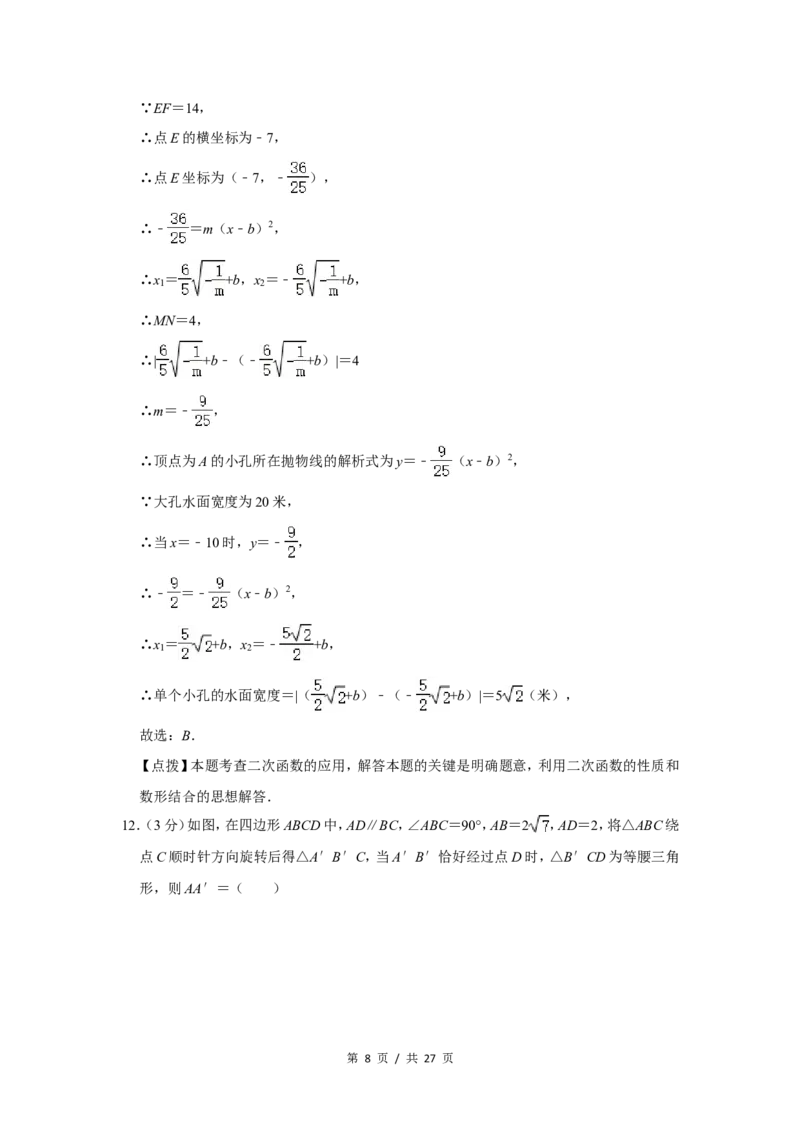文档内容
2020年四川省绵阳市中考数学试卷(教师版)
一、选择题:本大题共12小题,每小题3分,共36分.每小题只有一个选项符合题目要求.
1.(3分)﹣3的相反数是( )
A.﹣3 B.﹣ C. D.3
【微点】相反数.
【思路】根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.
【解析】解:﹣3的相反数是3,
故选:D.
【点拨】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号:一
个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义
与倒数的意义混淆.
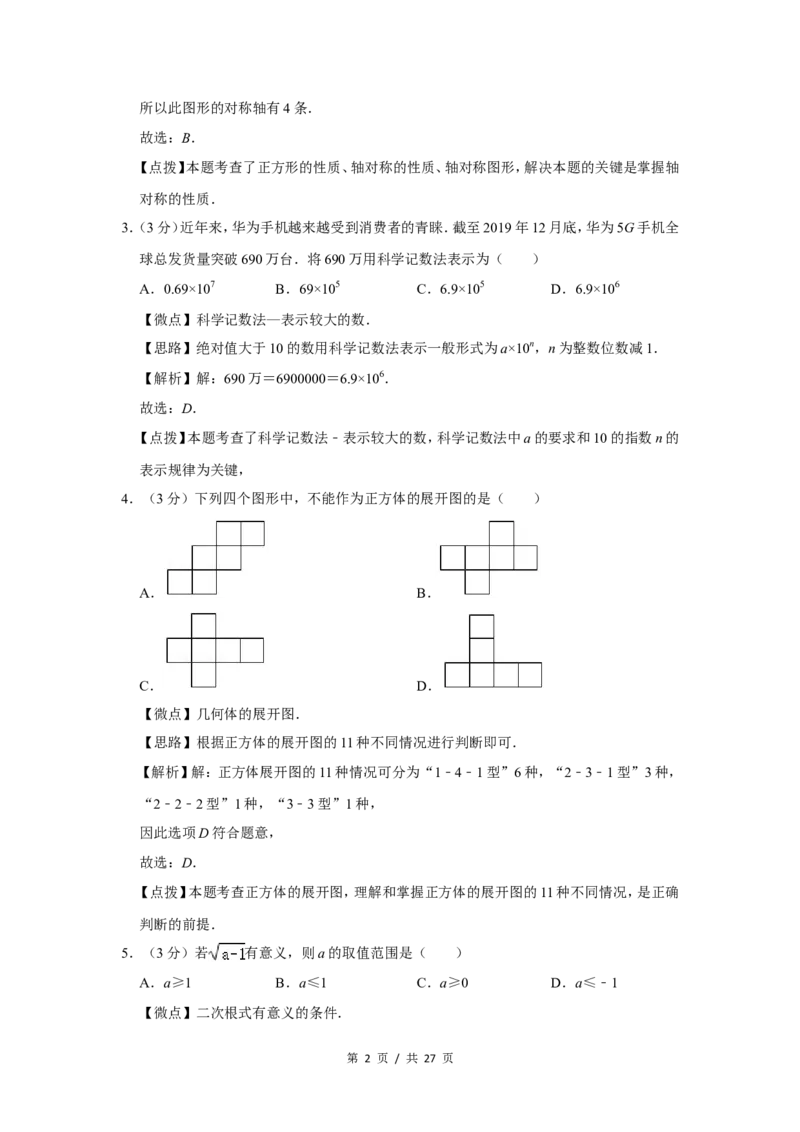
2.(3分)如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴
有( )
A.2条 B.4条 C.6条 D.8条
【微点】正方形的性质;轴对称的性质;轴对称图形.
【思路】根据轴对称的性质即可画出对称轴进而可得此图形的对称轴的条数.
【解析】解:如图,
因为以正方形的边长为直径,在正方形内画半圆得到的图形,
第 1 页 / 共 27 页所以此图形的对称轴有4条.
故选:B.
【点拨】本题考查了正方形的性质、轴对称的性质、轴对称图形,解决本题的关键是掌握轴
对称的性质.
3.(3分)近年来,华为手机越来越受到消费者的青睐.截至2019年12月底,华为5G手机全
球总发货量突破690万台.将690万用科学记数法表示为( )
A.0.69×107 B.69×105 C.6.9×105 D.6.9×106
【微点】科学记数法—表示较大的数.
【思路】绝对值大于10的数用科学记数法表示一般形式为a×10n,n为整数位数减1.
【解析】解:690万=6900000=6.9×106.
故选:D.
【点拨】本题考查了科学记数法﹣表示较大的数,科学记数法中a的要求和10的指数n的
表示规律为关键,
4.(3分)下列四个图形中,不能作为正方体的展开图的是( )
A. B.
C. D.
【微点】几何体的展开图.
【思路】根据正方体的展开图的11种不同情况进行判断即可.
【解析】解:正方体展开图的11种情况可分为“1﹣4﹣1型”6种,“2﹣3﹣1型”3种,
“2﹣2﹣2型”1种,“3﹣3型”1种,
因此选项D符合题意,
故选:D.
【点拨】本题考查正方体的展开图,理解和掌握正方体的展开图的11种不同情况,是正确
判断的前提.
5.(3分)若 有意义,则a的取值范围是( )
A.a≥1 B.a≤1 C.a≥0 D.a≤﹣1
【微点】二次根式有意义的条件.
第 2 页 / 共 27 页【思路】直接利用二次根式有意义的条件分析得出答案.
【解析】解:若 有意义,则a﹣1≥0,
解得:a≥1.
故选:A.
【点拨】此题主要考查了二次根式有意义的条件,正确把握二次根式的定义是解题关键.
6.(3分)《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、
羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还
差3钱,问合伙人数、羊价各是多少?此问题中羊价为( )
A.160钱 B.155钱 C.150钱 D.145钱
【微点】二元一次方程组的应用.
【思路】设共有x人合伙买羊,羊价为y钱,根据“若每人出5钱,还差45钱;若每人出7
钱,还差3钱”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
【解析】解:设共有x人合伙买羊,羊价为y钱,
依题意,得: ,
解得: .
故选:C.
【点拨】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是
解题的关键.
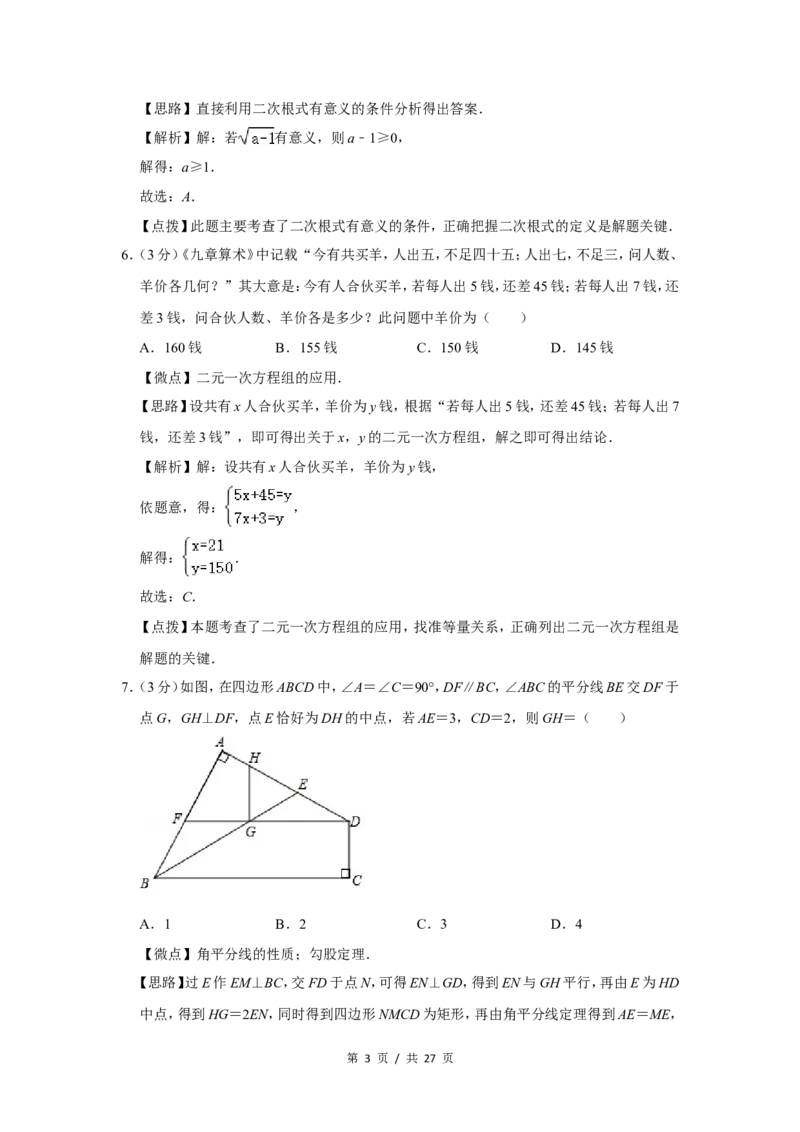
7.(3分)如图,在四边形ABCD中,∠A=∠C=90°,DF∥BC,∠ABC的平分线BE交DF于
点G,GH⊥DF,点E恰好为DH的中点,若AE=3,CD=2,则GH=( )
A.1 B.2 C.3 D.4
【微点】角平分线的性质;勾股定理.
【思路】过E作EM⊥BC,交FD于点N,可得EN⊥GD,得到EN与GH平行,再由E为HD
中点,得到HG=2EN,同时得到四边形NMCD为矩形,再由角平分线定理得到AE=ME,
第 3 页 / 共 27 页进而求出EN的长,得到HG的长.
【解析】解:过E作EM⊥BC,交FD于点N,
∵DF∥BC,
∴EN⊥DF,
∴EN∥HG,
∴ = ,
∵E为HD中点,
∴ = ,
∴ = ,即HG=2EN,
∴∠DNM=∠NMC=∠C=90°,
∴四边形NMCD为矩形,
∴MN=DC=2,
∵BE平分∠ABC,EA⊥AB,EM⊥BC,
∴EM=AE=3,
∴EN=EM﹣MN=3﹣2=1,
则HG=2EN=2.
故选:B.
【点拨】此题考查了勾股定理,矩形的判定与性质,角平分线定理,以及平行线分线段成比
例,熟练掌握定理及性质是解本题的关键.
8.(3分)将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为
( )
A. B. C. D.
【微点】列表法与树状图法.
第 4 页 / 共 27 页【思路】根据题意画出树状图得出所有等可能的情况数,找出恰有一个篮子为空的情况数,
然后根据概率公式即可得出答案.
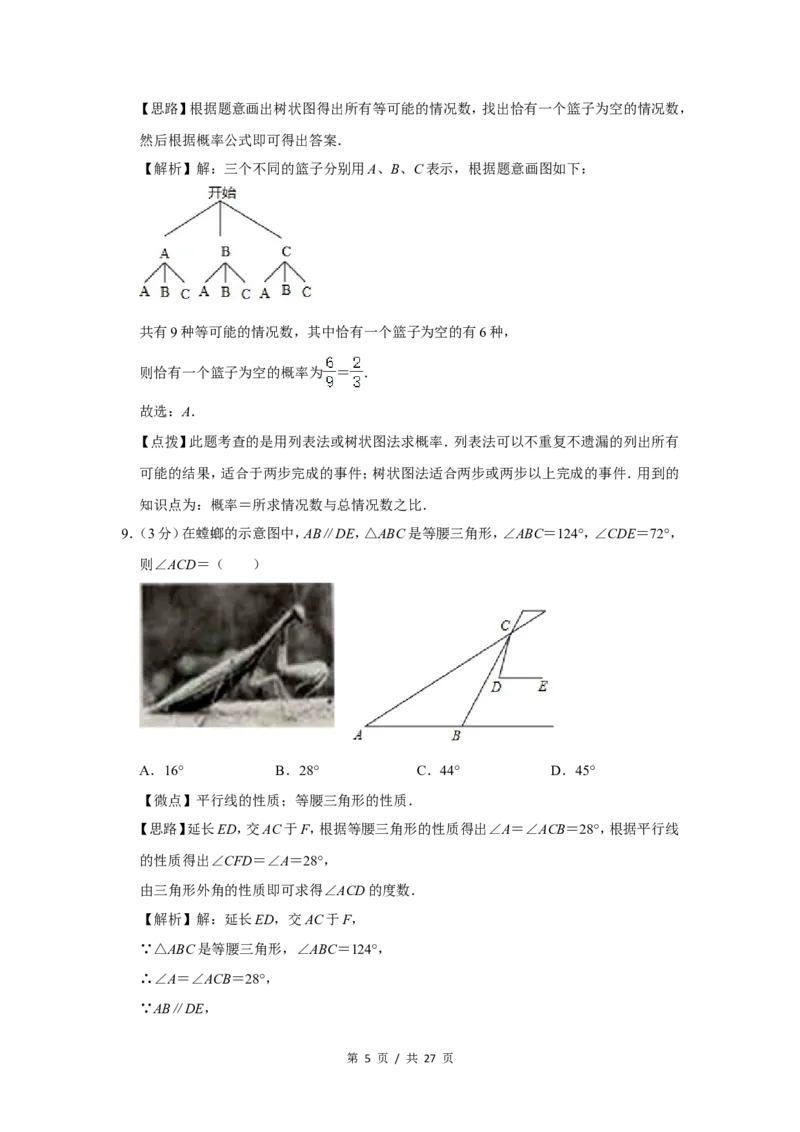
【解析】解:三个不同的篮子分别用A、B、C表示,根据题意画图如下:
共有9种等可能的情况数,其中恰有一个篮子为空的有6种,
则恰有一个篮子为空的概率为 = .
故选:A.
【点拨】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有
可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的
知识点为:概率=所求情况数与总情况数之比.
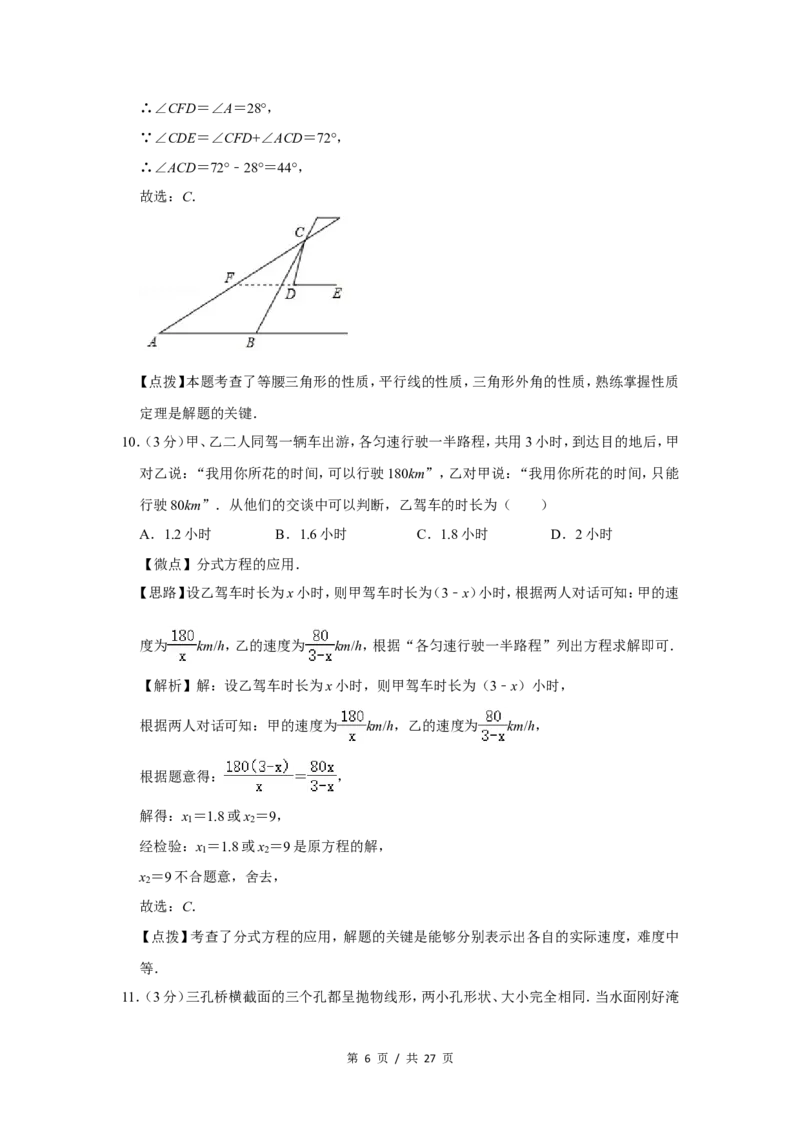
9.(3分)在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,
则∠ACD=( )
A.16° B.28° C.44° D.45°
【微点】平行线的性质;等腰三角形的性质.
【思路】延长ED,交AC于F,根据等腰三角形的性质得出∠A=∠ACB=28°,根据平行线
的性质得出∠CFD=∠A=28°,
由三角形外角的性质即可求得∠ACD的度数.
【解析】解:延长ED,交AC于F,
∵△ABC是等腰三角形,∠ABC=124°,
∴∠A=∠ACB=28°,
∵AB∥DE,
第 5 页 / 共 27 页∴∠CFD=∠A=28°,
∵∠CDE=∠CFD+∠ACD=72°,
∴∠ACD=72°﹣28°=44°,
故选:C.
【点拨】本题考查了等腰三角形的性质,平行线的性质,三角形外角的性质,熟练掌握性质
定理是解题的关键.
10.(3分)甲、乙二人同驾一辆车出游,各匀速行驶一半路程,共用3小时,到达目的地后,甲
对乙说:“我用你所花的时间,可以行驶180km”,乙对甲说:“我用你所花的时间,只能
行驶80km”.从他们的交谈中可以判断,乙驾车的时长为( )
A.1.2小时 B.1.6小时 C.1.8小时 D.2小时
【微点】分式方程的应用.
【思路】设乙驾车时长为x小时,则甲驾车时长为(3﹣x)小时,根据两人对话可知:甲的速
度为 km/h,乙的速度为 km/h,根据“各匀速行驶一半路程”列出方程求解即可.
【解析】解:设乙驾车时长为x小时,则甲驾车时长为(3﹣x)小时,
根据两人对话可知:甲的速度为 km/h,乙的速度为 km/h,
根据题意得: = ,
解得:x =1.8或x =9,
1 2
经检验:x =1.8或x =9是原方程的解,
1 2
x =9不合题意,舍去,
2
故选:C.
【点拨】考查了分式方程的应用,解题的关键是能够分别表示出各自的实际速度,难度中
等.
11.(3分)三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹
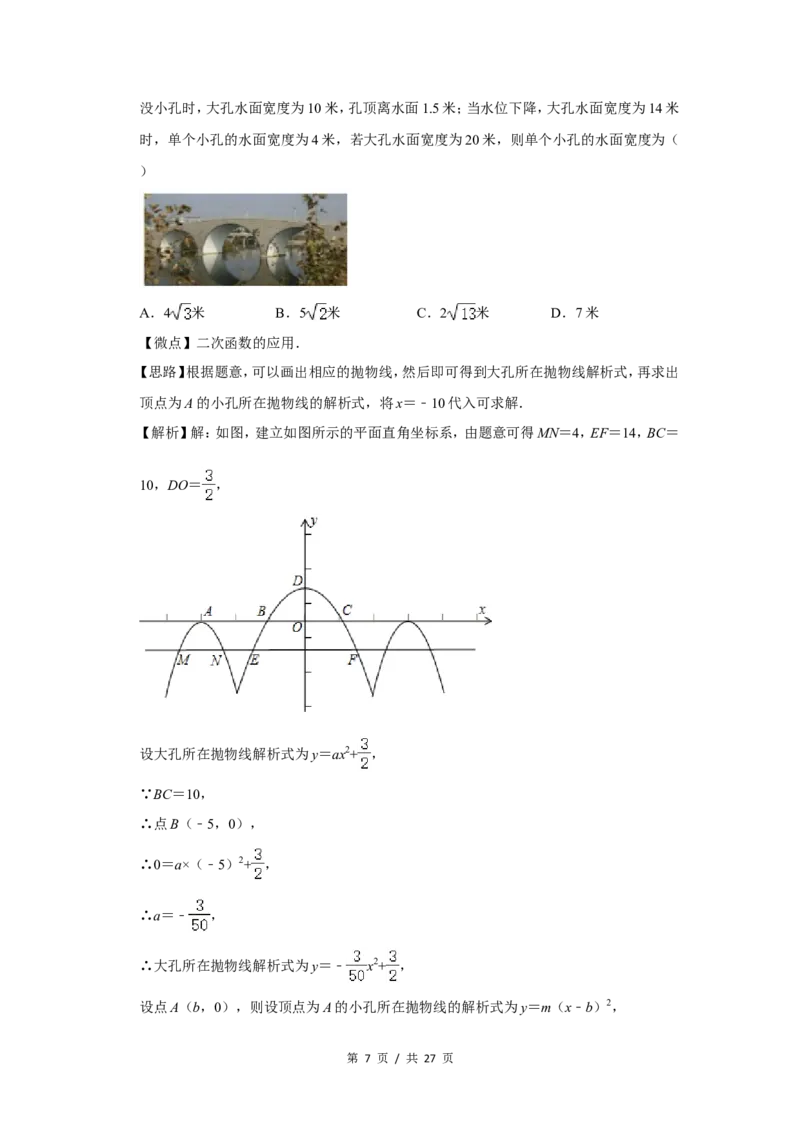
第 6 页 / 共 27 页没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米
时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为(
)
A.4 米 B.5 米 C.2 米 D.7米
【微点】二次函数的应用.
【思路】根据题意,可以画出相应的抛物线,然后即可得到大孔所在抛物线解析式,再求出
顶点为A的小孔所在抛物线的解析式,将x=﹣10代入可求解.
【解析】解:如图,建立如图所示的平面直角坐标系,由题意可得MN=4,EF=14,BC=
10,DO= ,
设大孔所在抛物线解析式为y=ax2+ ,
∵BC=10,
∴点B(﹣5,0),
∴0=a×(﹣5)2+ ,
∴a=﹣ ,
∴大孔所在抛物线解析式为y=﹣ x2+ ,
设点A(b,0),则设顶点为A的小孔所在抛物线的解析式为y=m(x﹣b)2,
第 7 页 / 共 27 页∵EF=14,
∴点E的横坐标为﹣7,
∴点E坐标为(﹣7,﹣ ),
∴﹣ =m(x﹣b)2,
∴x = +b,x =﹣ +b,
1 2
∴MN=4,
∴| +b﹣(﹣ +b)|=4
∴m=﹣ ,
∴顶点为A的小孔所在抛物线的解析式为y=﹣ (x﹣b)2,
∵大孔水面宽度为20米,
∴当x=﹣10时,y=﹣ ,
∴﹣ =﹣ (x﹣b)2,
∴x = +b,x =﹣ +b,
1 2
∴单个小孔的水面宽度=|( +b)﹣(﹣ +b)|=5 (米),
故选:B.
【点拨】本题考查二次函数的应用,解答本题的关键是明确题意,利用二次函数的性质和
数形结合的思想解答.
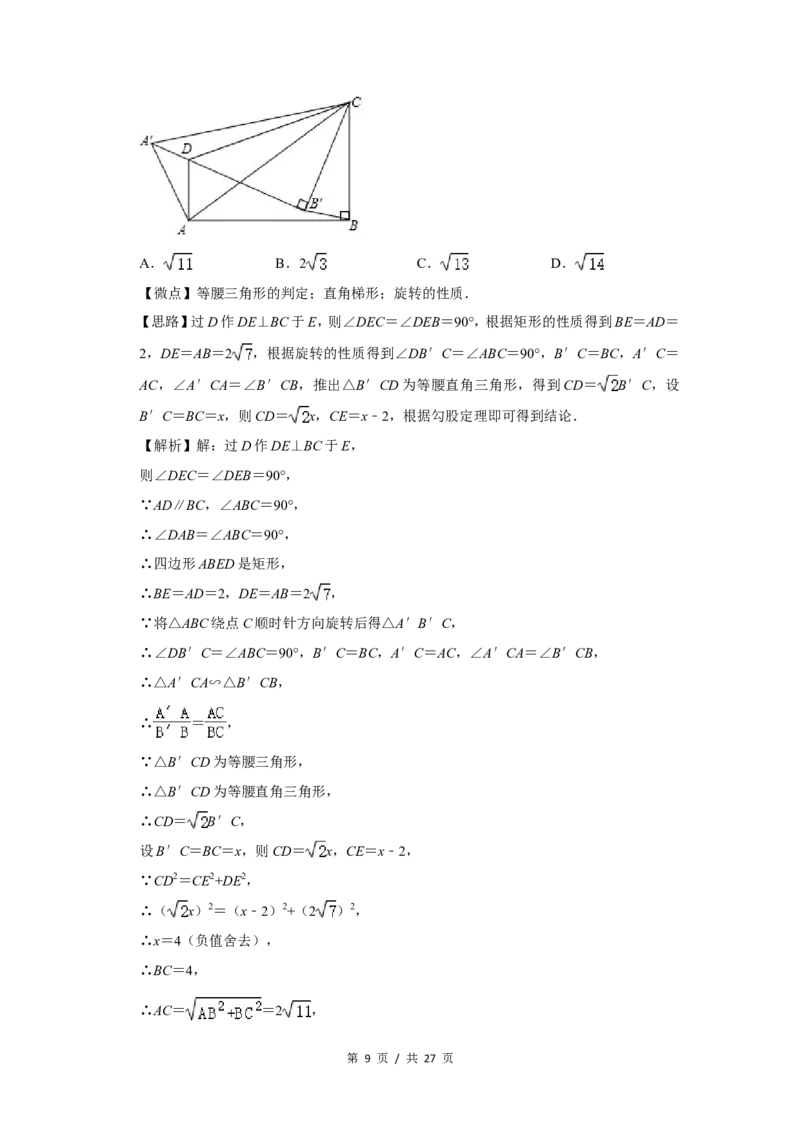
12.(3分)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=2 ,AD=2,将△ABC绕
点C顺时针方向旋转后得△A′B′C,当A′B′恰好经过点D时,△B′CD为等腰三角
形,则AA′=( )
第 8 页 / 共 27 页A. B.2 C. D.
【微点】等腰三角形的判定;直角梯形;旋转的性质.
【思路】过D作DE⊥BC于E,则∠DEC=∠DEB=90°,根据矩形的性质得到BE=AD=
2,DE=AB=2 ,根据旋转的性质得到∠DB′C=∠ABC=90°,B′C=BC,A′C=
AC,∠A′CA=∠B′CB,推出△B′CD为等腰直角三角形,得到CD= B′C,设
B′C=BC=x,则CD= x,CE=x﹣2,根据勾股定理即可得到结论.
【解析】解:过D作DE⊥BC于E,
则∠DEC=∠DEB=90°,
∵AD∥BC,∠ABC=90°,
∴∠DAB=∠ABC=90°,
∴四边形ABED是矩形,
∴BE=AD=2,DE=AB=2 ,
∵将△ABC绕点C顺时针方向旋转后得△A′B′C,
∴∠DB′C=∠ABC=90°,B′C=BC,A′C=AC,∠A′CA=∠B′CB,
∴△A′CA∽△B′CB,
∴ = ,
∵△B′CD为等腰三角形,
∴△B′CD为等腰直角三角形,
∴CD= B′C,
设B′C=BC=x,则CD= x,CE=x﹣2,
∵CD2=CE2+DE2,
∴( x)2=(x﹣2)2+(2 )2,
∴x=4(负值舍去),
∴BC=4,
∴AC= =2 ,
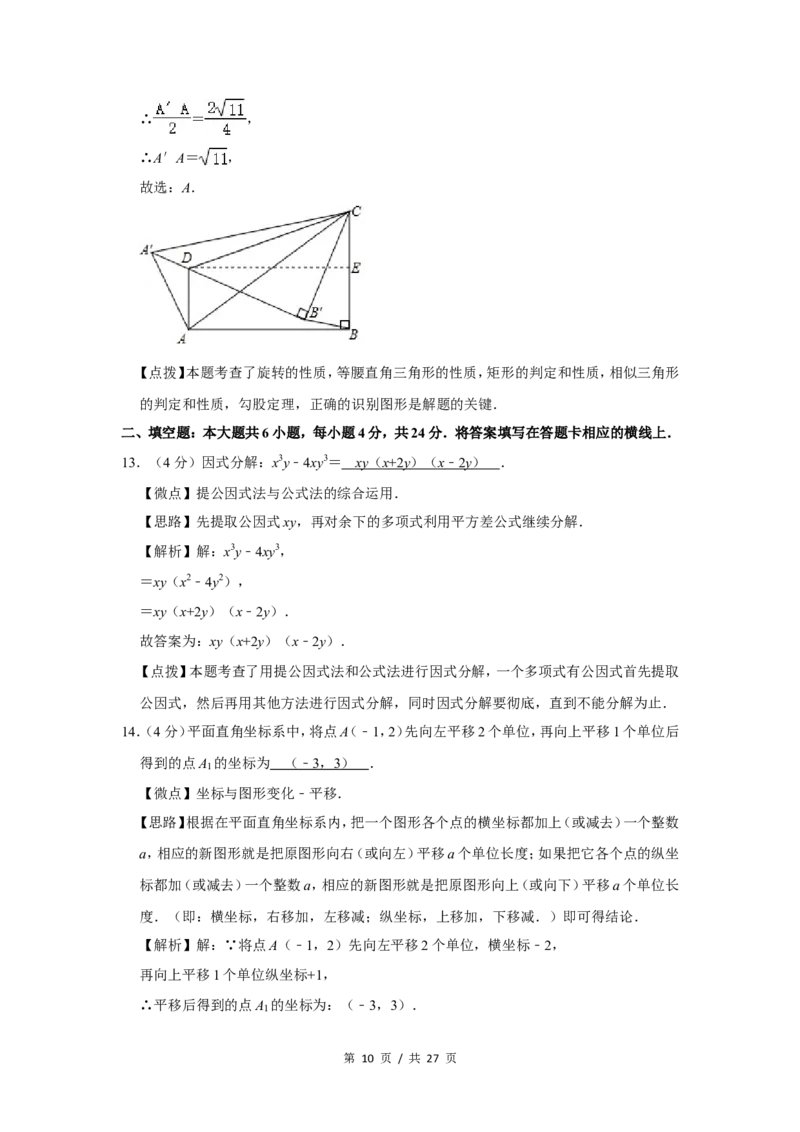
第 9 页 / 共 27 页∴ = ,
∴A′A= ,
故选:A.
【点拨】本题考查了旋转的性质,等腰直角三角形的性质,矩形的判定和性质,相似三角形
的判定和性质,勾股定理,正确的识别图形是解题的关键.
二、填空题:本大题共6小题,每小题4分,共24分.将答案填写在答题卡相应的横线上.
13.(4分)因式分解:x3y﹣4xy3= x y ( x + 2 y )( x ﹣ 2 y ) .
【微点】提公因式法与公式法的综合运用.
【思路】先提取公因式xy,再对余下的多项式利用平方差公式继续分解.
【解析】解:x3y﹣4xy3,
=xy(x2﹣4y2),
=xy(x+2y)(x﹣2y).
故答案为:xy(x+2y)(x﹣2y).
【点拨】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取
公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
14.(4分)平面直角坐标系中,将点A(﹣1,2)先向左平移2个单位,再向上平移1个单位后
得到的点A 的坐标为 (﹣ 3 , 3 ) .
1
【微点】坐标与图形变化﹣平移.
【思路】根据在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数
a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐
标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长
度.(即:横坐标,右移加,左移减;纵坐标,上移加,下移减.)即可得结论.
【解析】解:∵将点A(﹣1,2)先向左平移2个单位,横坐标﹣2,
再向上平移1个单位纵坐标+1,
∴平移后得到的点A 的坐标为:(﹣3,3).
1
第 10 页 / 共 27 页故答案为:(﹣3,3).
【点拨】本题考查了坐标与图形变化﹣平移,解决本题的关键是掌握平移定义.
15.(4分)若多项式xy|m﹣n|+(n﹣2)x2y2+1是关于x,y的三次多项式,则mn= 0 或 8 .
【微点】多项式.
【思路】直接利用多项式的次数确定方法得出答案.
【解析】解:∵多项式xy|m﹣n|+(n﹣2)x2y2+1是关于x,y的三次多项式,
∴n﹣2=0,1+|m﹣n|=3,
∴n=2,|m﹣n|=2,
∴m﹣n=2或n﹣m=2,
∴m=4或m=0,
∴mn=0或8.
故答案为:0或8.
【点拨】此题主要考查了多项式,正确掌握多项式的次数确定方法是解题关键.
16.(4分)我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种
火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1
万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过
100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是 12 5 万元.
(利润=销售额﹣种植成本)
【微点】一元一次不等式组的应用;一次函数的应用.
【思路】设甲种火龙果种植x亩,乙种火龙果种植(100﹣x)亩,此项目获得利润w,根据题
意列出不等式求出x的范围,然后根据题意列出w与x的函数关系即可求出答案.
【解析】解:设甲种火龙果种植x亩,乙种火龙果种植(100﹣x)亩,此项目获得利润w,
甲、乙两种火龙果每亩利润为1.1万元,1.4万元,
由题意可知: ,
解得:50≤x≤60,
此项目获得利润w=1.1x+1.4(100﹣x)=140﹣0.3x,
当x=50时,
w的最大值为140﹣15=125万元.
【点拨】本题考查一次函数,解题的关键是根据题意给出的等量关系列出函数关系式,本
题属于中等题型.
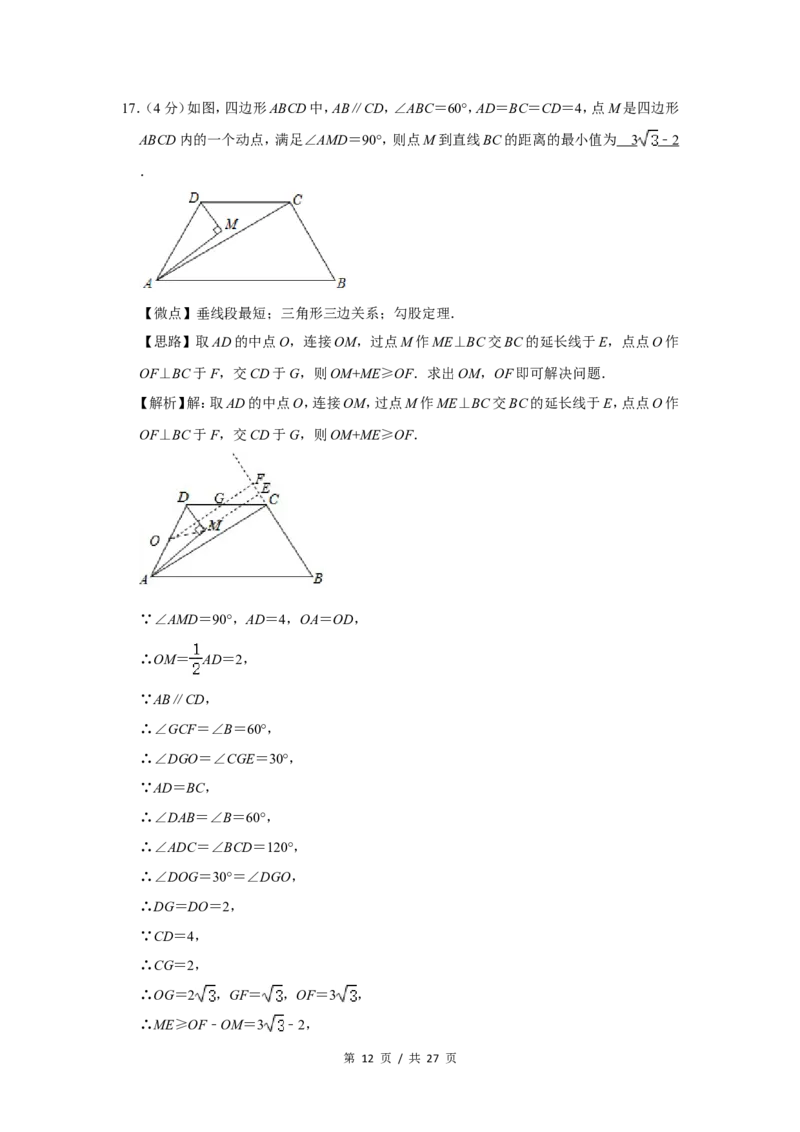
第 11 页 / 共 27 页17.(4分)如图,四边形ABCD中,AB∥CD,∠ABC=60°,AD=BC=CD=4,点M是四边形
ABCD内的一个动点,满足∠AMD=90°,则点M到直线BC的距离的最小值为 3 ﹣ 2
.
【微点】垂线段最短;三角形三边关系;勾股定理.
【思路】取AD的中点O,连接OM,过点M作ME⊥BC交BC的延长线于E,点点O作
OF⊥BC于F,交CD于G,则OM+ME≥OF.求出OM,OF即可解决问题.
【解析】解:取AD的中点O,连接OM,过点M作ME⊥BC交BC的延长线于E,点点O作
OF⊥BC于F,交CD于G,则OM+ME≥OF.
∵∠AMD=90°,AD=4,OA=OD,
∴OM= AD=2,
∵AB∥CD,
∴∠GCF=∠B=60°,
∴∠DGO=∠CGE=30°,
∵AD=BC,
∴∠DAB=∠B=60°,
∴∠ADC=∠BCD=120°,
∴∠DOG=30°=∠DGO,
∴DG=DO=2,
∵CD=4,
∴CG=2,
∴OG=2 ,GF= ,OF=3 ,
∴ME≥OF﹣OM=3 ﹣2,
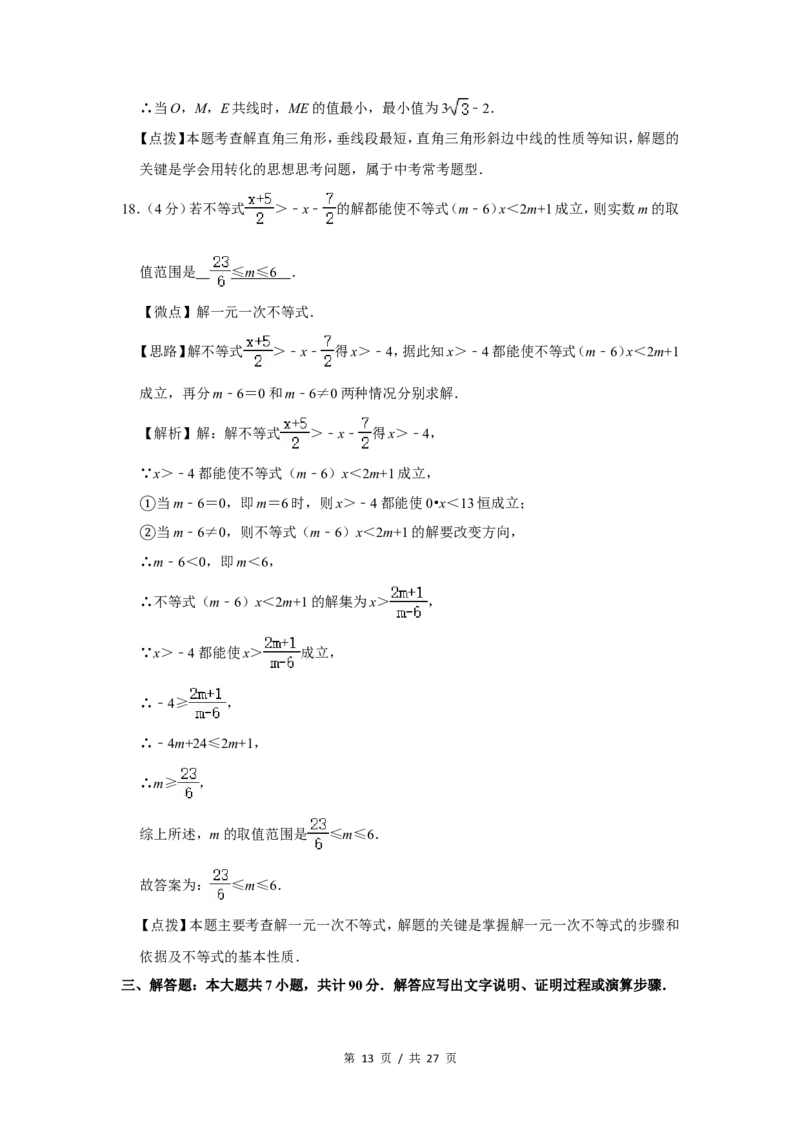
第 12 页 / 共 27 页∴当O,M,E共线时,ME的值最小,最小值为3 ﹣2.
【点拨】本题考查解直角三角形,垂线段最短,直角三角形斜边中线的性质等知识,解题的
关键是学会用转化的思想思考问题,属于中考常考题型.
18.(4分)若不等式 >﹣x﹣ 的解都能使不等式(m﹣6)x<2m+1成立,则实数m的取
值范围是 ≤ m ≤ 6 .
【微点】解一元一次不等式.
【思路】解不等式 >﹣x﹣ 得x>﹣4,据此知x>﹣4都能使不等式(m﹣6)x<2m+1
成立,再分m﹣6=0和m﹣6≠0两种情况分别求解.
【解析】解:解不等式 >﹣x﹣ 得x>﹣4,
∵x>﹣4都能使不等式(m﹣6)x<2m+1成立,
当m﹣6=0,即m=6时,则x>﹣4都能使0•x<13恒成立;
①当m﹣6≠0,则不等式(m﹣6)x<2m+1的解要改变方向,
②∴m﹣6<0,即m<6,
∴不等式(m﹣6)x<2m+1的解集为x> ,
∵x>﹣4都能使x> 成立,
∴﹣4≥ ,
∴﹣4m+24≤2m+1,
∴m≥ ,
综上所述,m的取值范围是 ≤m≤6.
故答案为: ≤m≤6.
【点拨】本题主要考查解一元一次不等式,解题的关键是掌握解一元一次不等式的步骤和
依据及不等式的基本性质.
三、解答题:本大题共7小题,共计90分.解答应写出文字说明、证明过程或演算步骤.
第 13 页 / 共 27 页19.(16分)(1)计算:| ﹣3|+2 cos60°﹣ × ﹣(﹣ )0.
(2)先化简,再求值:(x+2+ )÷ ,其中x= ﹣1.
【微点】分式的化简求值;零指数幂;分母有理化;二次根式的混合运算;特殊角的三角函
数值.
【思路】(1)先去绝对值符号、代入三角函数值、化简二次根式、计算零指数幂,再计算乘法,
最后计算加减可得;
(2)先根据分式的混合运算顺序和运算法则化简原式,再将x的值代入计算可得.
【解析】解:(1)原式=3﹣ +2 × ﹣ ×2 ﹣1
=3﹣ + ﹣2﹣1
=0;
(2)原式=( + )÷
= •
= ,
当x= ﹣1时,
原式=
=
=1﹣ .
【点拨】本题主要考查实数的混合运算与分式的化简求值,解题的关键是掌握绝对值性质、
二次根式的性质、零指数幂的规定、熟记三角函数值及分式的混合运算顺序和运算法则.
20.(12分)4月23日是“世界读书日”,甲、乙两个书店在这一天举行了购书优惠活动.
甲书店:所有书籍按标价8折出售;
乙书店:一次购书中标价总额不超过100元的按原价计费,超过100元后的部分打6折.
(1)以x(单位:元)表示标价总额,y(单位:元)表示应支付金额,分别就两家书店的优惠
方式,求y关于x的函数解析式;
(2)“世界读书日”这一天,如何选择这两家书店去购书更省钱?
第 14 页 / 共 27 页【微点】一元一次不等式的应用;一次函数的应用.
【思路】(1)根据题意给出的等量关系即可求出答案.
(2)先求出两书店所需费用相同时的书本数量,从而可判断哪家书店省钱.
【解析】解:(1)甲书店:y=0.8x,
乙书店:y= .
(2)令0.8x=0.6x+40,
解得:x=200,
当x<200时,选择甲书店更省钱,
当x=200,甲乙书店所需费用相同,
当x>200,选择乙书店更省钱.
【点拨】本题考查一次函数的应用,解题的关键是正确找出题中的等量关系,本题属于基
础题型.
21.(12分)为助力新冠肺炎疫情后经济的复苏,天天快餐公司积极投入到复工复产中.现有
A、B两家农副产品加工厂到该公司推销鸡腿,两家鸡腿的价格相同,品质相近.该公司决
定通过检查质量来确定选购哪家的鸡腿.检察人员从两家分别抽取100个鸡腿,然后再从
中随机各抽取10个,记录它们的质量(单位:克)如表:
A加工厂 74 75 75 75 73 77 78 72 76 75
B加工厂 78 74 78 73 74 75 74 74 75 75
(1)根据表中数据,求A加工厂的10个鸡腿质量的中位数、众数、平均数;
(2)估计B加工厂这100个鸡腿中,质量为75克的鸡腿有多少个?
(3)根据鸡腿质量的稳定性,该快餐公司应选购哪家加工厂的鸡腿?
【微点】用样本估计总体;算术平均数;中位数;众数;方差.
【思路】(1)根据中位数、众数和平均数的计算公式分别进行解答即可;
(2)用总数乘以质量为75克的鸡腿所占的百分比即可;
(3)根据方差的定义,方差越小数据越稳定即可得出答案.
【解析】解:(1)把这些数从小到大排列,最中间的数是第5和第6个数的平均数,
则中位数是 =75(克);
因为75出现了4次,出现的次数最多,
所以众数是75克;
第 15 页 / 共 27 页平均数是: (74+75+75+75+73+77+78+72+76+75)=75(克);
(2)根据题意得:
100× =30(个),
答:质量为75克的鸡腿有30个;
(3)选B加工厂的鸡腿.
A的方差是: ([ 74﹣75)2+4×(75﹣75)2+(76﹣75)2+(73﹣75)2+(72﹣75)2+(77﹣75)
2+(78﹣75)2]=2.8;
B的平均数是: (78+74+78+73+74+75+74+74+75+75)=75,
B的方差是: [2×(78﹣75)2+4×(74﹣75)2+(73﹣75)2+3×(75﹣75)2]=2.6;
∵A、B平均值一样,B的方差比A的方差小,B更稳定,
∴选B加工厂的鸡腿.
【点拨】本题考查了方差、平均数、中位数、众数,熟悉计算公式和意义是解题的关键.
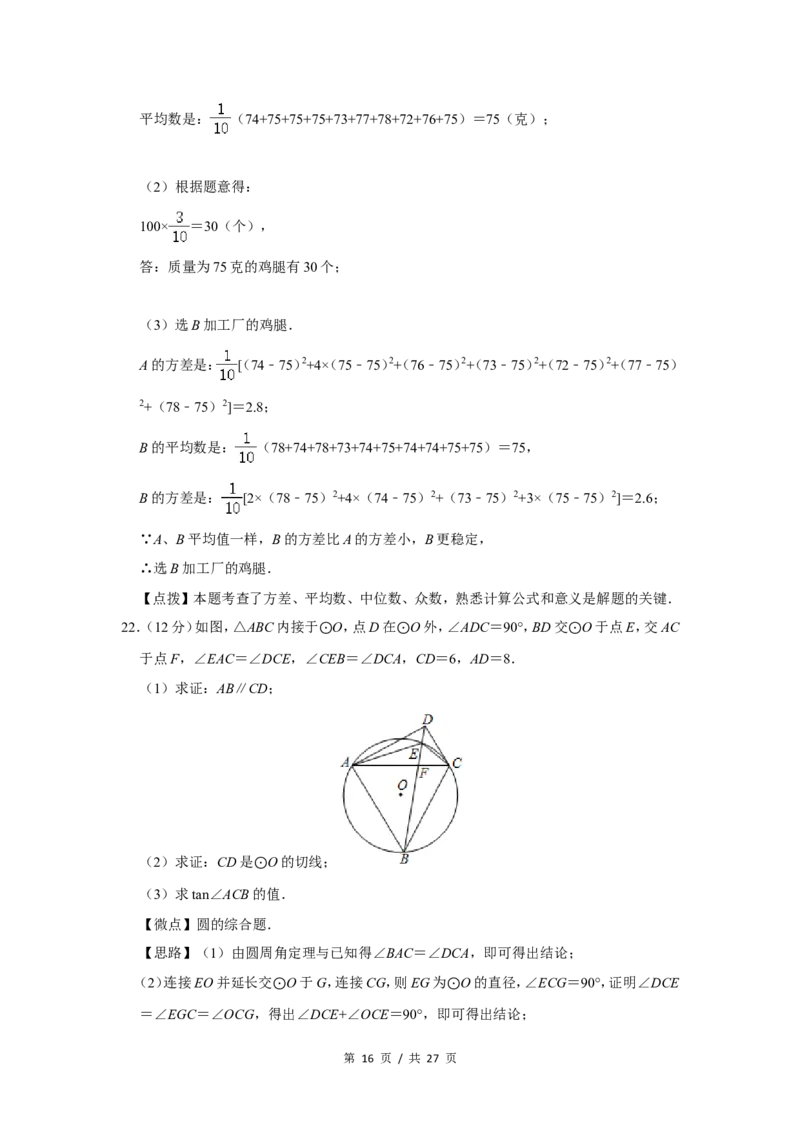
22.(12分)如图,△ABC内接于 O,点D在 O外,∠ADC=90°,BD交 O于点E,交AC
于点F,∠EAC=∠DCE,∠C⊙EB=∠DCA⊙,CD=6,AD=8. ⊙
(1)求证:AB∥CD;
(2)求证:CD是 O的切线;
(3)求tan∠ACB的⊙值.
【微点】圆的综合题.
【思路】(1)由圆周角定理与已知得∠BAC=∠DCA,即可得出结论;
(2)连接EO并延长交 O于G,连接CG,则EG为 O的直径,∠ECG=90°,证明∠DCE
=∠EGC=∠OCG,得⊙出∠DCE+∠OCE=90°,即⊙可得出结论;
第 16 页 / 共 27 页(3)由三角函数定义求出cos∠ACD= ,证出∠ABC=∠ACD=∠CAB,求出BC=AC=
10,AB=12,过点B作BG⊥AC于C,设GC=x,则AG=10﹣x,由勾股定理得出方程,解
方程得GC= ,由勾股定理求出BG= ,由三角函数定义即可得答案.
【解析】(1)证明:∵∠BAC=∠CEB,∠CEB=∠DCA,
∴∠BAC=∠DCA,
∴AB∥CD;
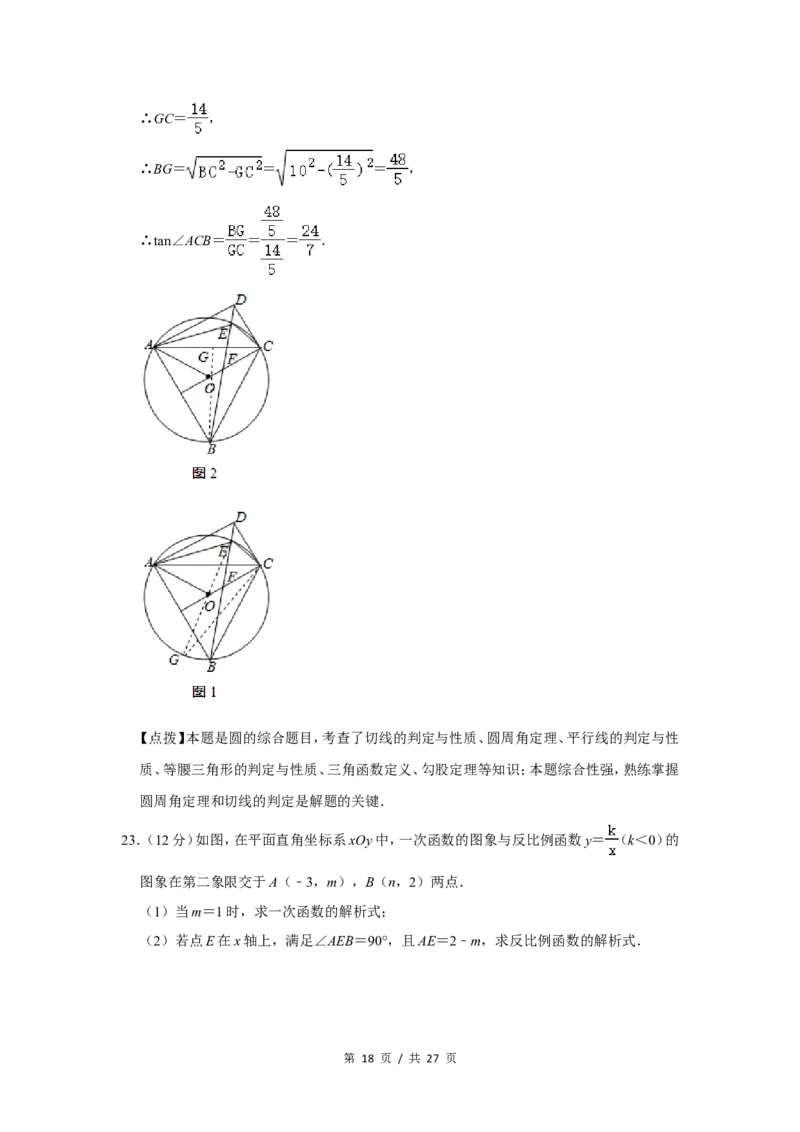
(2)证明:连接EO并延长交 O于G,连接CG,如图1所示:
则EG为 O的直径, ⊙
∴∠ECG⊙=90°,
∵OC=OG,
∴∠OCG=∠EGC,
∵∠EAC=∠EGC,∠EAC=∠DCE,
∴∠DCE=∠EGC=∠OCG,
∵∠OCG+∠OCE=∠ECG=90°,
∴∠DCE+∠OCE=90°,即∠DCO=90°,
∵OC是 O的半径,
∴CD是⊙O的切线;
⊙
(3)解:在Rt△ADC中,由勾股定理得:AC= = =10,
∴cos∠ACD= = = ,
∵CD是 O的切线,AB∥CD,
∴∠ABC⊙=∠ACD=∠CAB,
∴BC=AC=10,AB=2BC•cos∠ABC=2×10× =12,
过点B作BG⊥AC于C,如图2所示:
设GC=x,则AG=10﹣x,
由勾股定理得:AB2﹣AG2=BG2=BC2﹣GC2,
即:122﹣(10﹣x)2=102﹣x2,
解得:x= ,
第 17 页 / 共 27 页∴GC= ,
∴BG= = = ,
∴tan∠ACB= = = .
【点拨】本题是圆的综合题目,考查了切线的判定与性质、圆周角定理、平行线的判定与性
质、等腰三角形的判定与性质、三角函数定义、勾股定理等知识;本题综合性强,熟练掌握
圆周角定理和切线的判定是解题的关键.
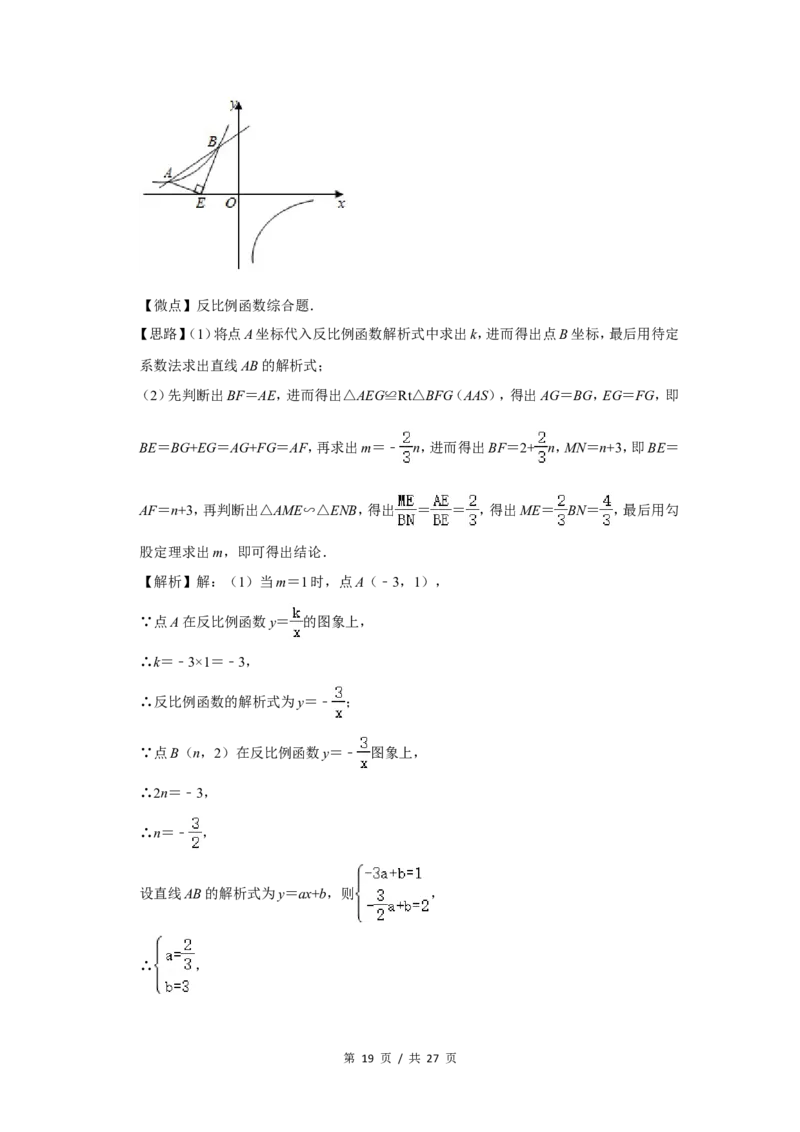
23.(12分)如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数y= (k<0)的
图象在第二象限交于A(﹣3,m),B(n,2)两点.
(1)当m=1时,求一次函数的解析式;
(2)若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,求反比例函数的解析式.
第 18 页 / 共 27 页【微点】反比例函数综合题.
【思路】(1)将点A坐标代入反比例函数解析式中求出k,进而得出点B坐标,最后用待定
系数法求出直线AB的解析式;
(2)先判断出BF=AE,进而得出△AEG≌Rt△BFG(AAS),得出AG=BG,EG=FG,即
BE=BG+EG=AG+FG=AF,再求出m=﹣ n,进而得出BF=2+ n,MN=n+3,即BE=
AF=n+3,再判断出△AME∽△ENB,得出 = = ,得出ME= BN= ,最后用勾
股定理求出m,即可得出结论.
【解析】解:(1)当m=1时,点A(﹣3,1),
∵点A在反比例函数y= 的图象上,
∴k=﹣3×1=﹣3,
∴反比例函数的解析式为y=﹣ ;
∵点B(n,2)在反比例函数y=﹣ 图象上,
∴2n=﹣3,
∴n=﹣ ,
设直线AB的解析式为y=ax+b,则 ,
∴ ,
第 19 页 / 共 27 页∴直线AB的解析式为y= x+3;
(2)如图,过点A作AM⊥x轴于M,过点B作BN⊥x轴于N,过点A作AF⊥BN于F,交
BE于G,
则四边形AMNF是矩形,
∴FN=AM,AF=MN,
∵A(﹣3,m),B(n,2),
∴BF=2﹣m,
∵AE=2﹣m,
∴BF=AE,
在△AEG和△BFG中, ,
∴△AEG≌Rt△BFG(AAS),
∴AG=BG,EG=FG,
∴BE=BG+EG=AG+FG=AF,
∵点A(﹣3,m),B(n,2)在反比例函数y= 的图象上,
∴k=﹣3m=2n,
∴m=﹣ n,
∴BF=BN﹣FN=BN﹣AM=2﹣m=2+ n,MN=n﹣(﹣3)=n+3,
∴BE=AF=n+3,
∵∠AEM+∠MAE=90°,∠AEM+∠BEN=90°,
∴∠MAE=∠NEB,
∵∠AME=∠ENB=90°,
∴△AME∽△ENB,
∴ = = = = ,
∴ME= BN= ,
第 20 页 / 共 27 页在Rt△AME中,AM=m,AE=2﹣m,根据勾股定理得,AM2+ME2=AE2,
∴m2+( )2=(2﹣m)2,
∴m= ,
∴k=﹣3m=﹣ ,
∴反比例函数的解析式为y=﹣ .
【点拨】此题是反比例函数综合题,主要考查了待定系数法,勾股定理,矩形的判定和性质,
全等三角形的判定和性质,构造出△AEG≌△BFG(AAS)是解本题的关键.
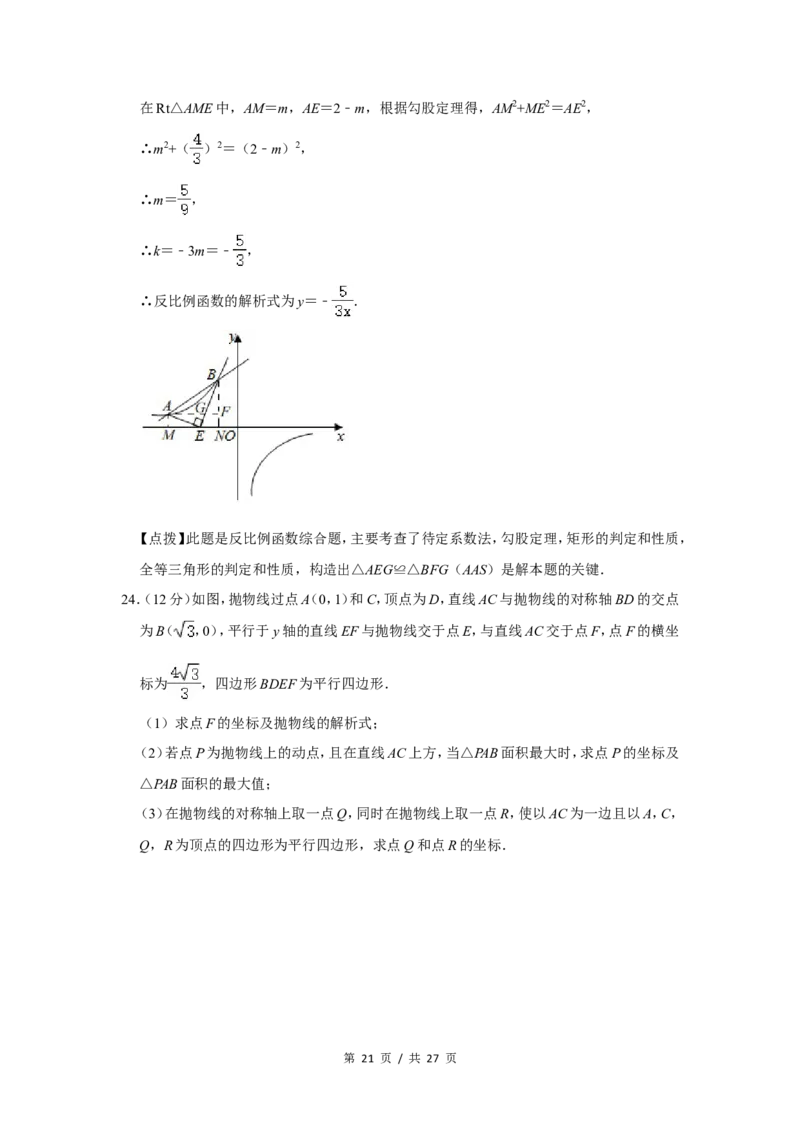
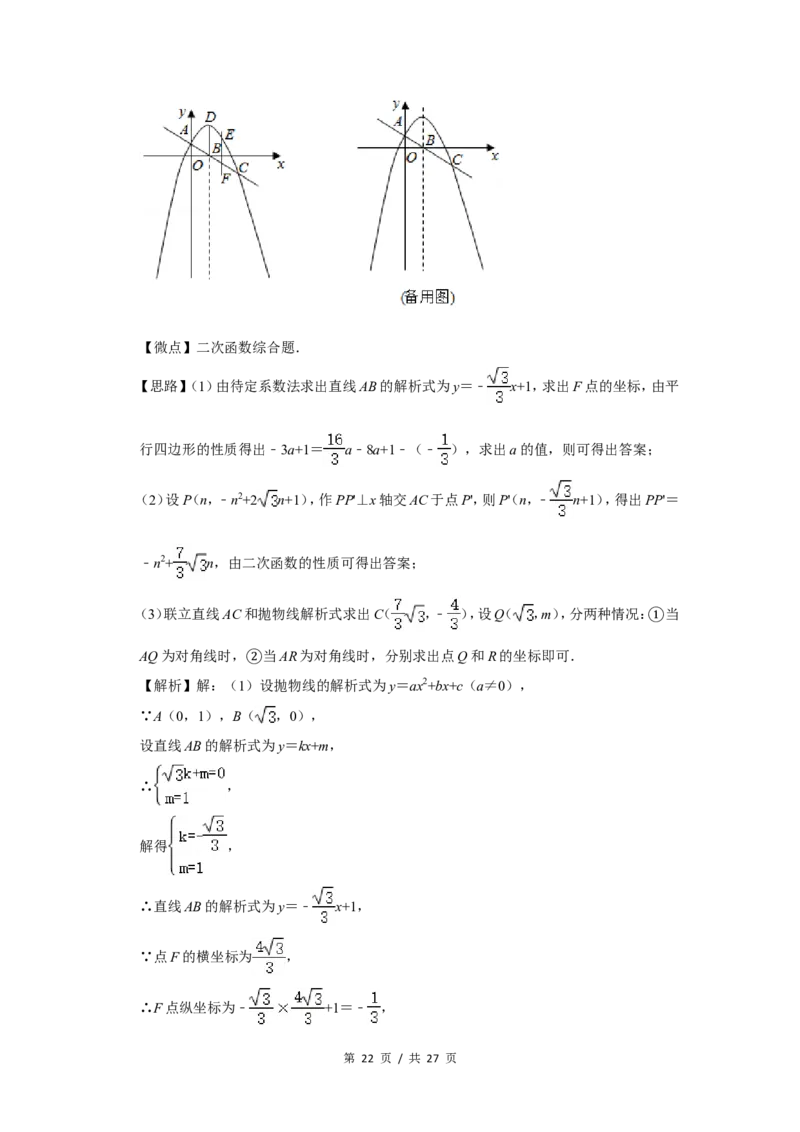
24.(12分)如图,抛物线过点A(0,1)和C,顶点为D,直线AC与抛物线的对称轴BD的交点
为B( ,0),平行于y轴的直线EF与抛物线交于点E,与直线AC交于点F,点F的横坐
标为 ,四边形BDEF为平行四边形.
(1)求点F的坐标及抛物线的解析式;
(2)若点P为抛物线上的动点,且在直线AC上方,当△PAB面积最大时,求点P的坐标及
△PAB面积的最大值;
(3)在抛物线的对称轴上取一点Q,同时在抛物线上取一点R,使以AC为一边且以A,C,
Q,R为顶点的四边形为平行四边形,求点Q和点R的坐标.
第 21 页 / 共 27 页【微点】二次函数综合题.
【思路】(1)由待定系数法求出直线AB的解析式为y=﹣ x+1,求出F点的坐标,由平
行四边形的性质得出﹣3a+1= a﹣8a+1﹣(﹣ ),求出a的值,则可得出答案;
(2)设P(n,﹣n2+2 n+1),作PP'⊥x轴交AC于点P',则P(' n,﹣ n+1),得出PP'=
﹣n2+ n,由二次函数的性质可得出答案;
(3)联立直线AC和抛物线解析式求出C( ,﹣ ),设Q( ,m),分两种情况: 当
①
AQ为对角线时, 当AR为对角线时,分别求出点Q和R的坐标即可.
【解析】解:(1)②设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(0,1),B( ,0),
设直线AB的解析式为y=kx+m,
∴ ,
解得 ,
∴直线AB的解析式为y=﹣ x+1,
∵点F的横坐标为 ,
∴F点纵坐标为﹣ +1=﹣ ,
第 22 页 / 共 27 页∴F点的坐标为( ,﹣ ),
又∵点A在抛物线上,
∴c=1,
对称轴为:x=﹣ ,
∴b=﹣2 a,
∴解析式化为:y=ax2﹣2 ax+1,
∵四边形DBFE为平行四边形.
∴BD=EF,
∴﹣3a+1= a﹣8a+1﹣(﹣ ),
解得a=﹣1,
∴抛物线的解析式为y=﹣x2+2 x+1;
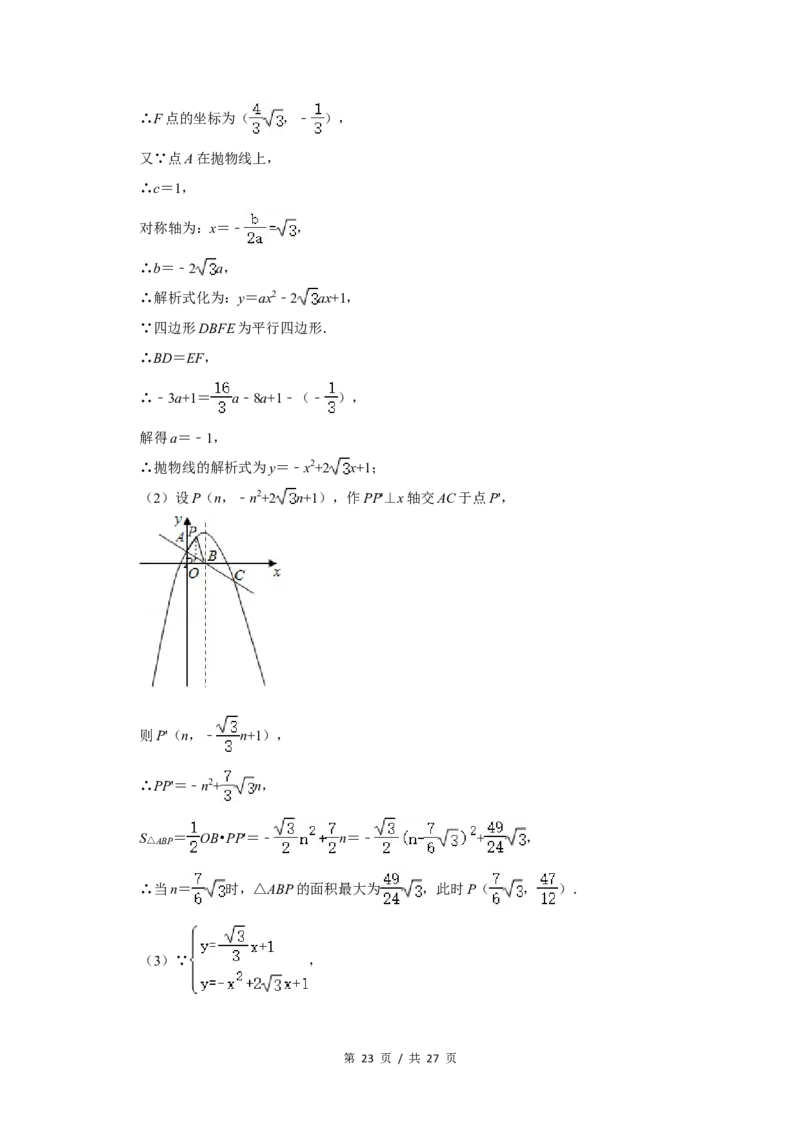
(2)设P(n,﹣n2+2 n+1),作PP'⊥x轴交AC于点P',
则P'(n,﹣ n+1),
∴PP'=﹣n2+ n,
S△ABP = OB•PP'=﹣ n=﹣ + ,
∴当n= 时,△ABP的面积最大为 ,此时P( , ).
(3)∵ ,
第 23 页 / 共 27 页∴x=0或x= ,
∴C( ,﹣ ),
设Q( ,m),
当AQ为对角线时,
①
∴R(﹣ ),
∵R在抛物线y= +4上,
∴m+ =﹣ +4,
解得m=﹣ ,
∴Q ,R ;
当AR为对角线时,
②
∴R( ),
∵R在抛物线y= +4上,
∴m﹣ +4,
解得m=﹣10,
∴Q( ,﹣10),R( ).
综上所述,Q ,R ;或Q( ,﹣10),R( ).
【点拨】本题是二次函数综合题,考查了待定系数法,二次函数的性质,二次函数图象上点
的坐标特征,平行四边形的性质等知识,熟练掌握二次函数的性质及方程思想,分类讨论
思想是解题的关键.
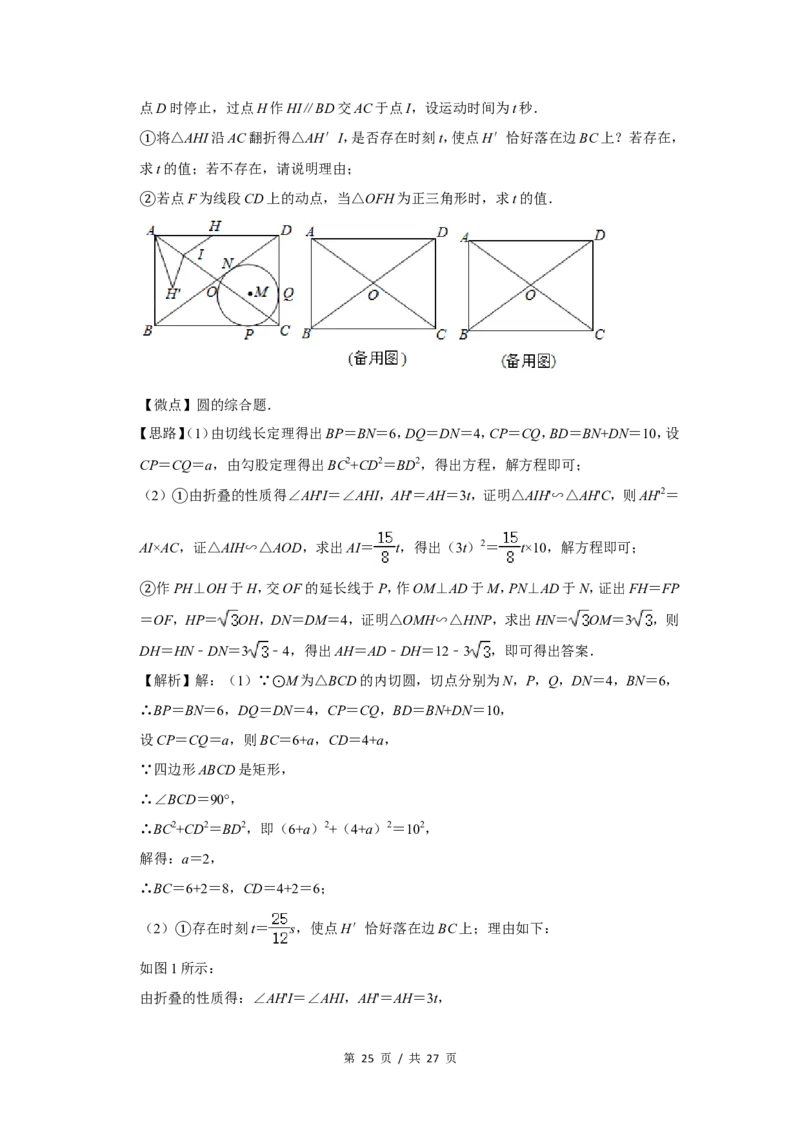
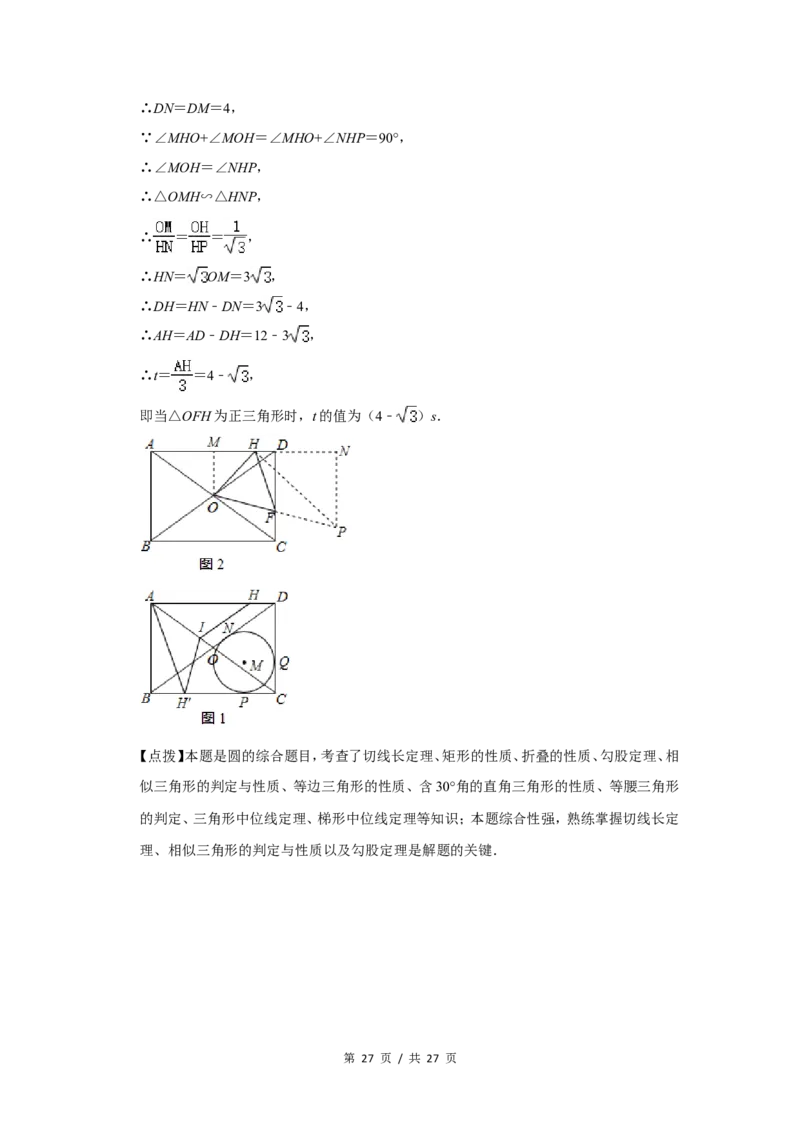
25.(14分)如图,在矩形ABCD中,对角线相交于点O, M为△BCD的内切圆,切点分别为
N,P,Q,DN=4,BN=6. ⊙
(1)求BC,CD;
(2)点H从点A出发,沿线段AD向点D以每秒3个单位长度的速度运动,当点H运动到
第 24 页 / 共 27 页点D时停止,过点H作HI∥BD交AC于点I,设运动时间为t秒.
将△AHI沿AC翻折得△AH′I,是否存在时刻t,使点H′恰好落在边BC上?若存在,
①求t的值;若不存在,请说明理由;
若点F为线段CD上的动点,当△OFH为正三角形时,求t的值.
②
【微点】圆的综合题.
【思路】(1)由切线长定理得出BP=BN=6,DQ=DN=4,CP=CQ,BD=BN+DN=10,设
CP=CQ=a,由勾股定理得出BC2+CD2=BD2,得出方程,解方程即可;
(2) 由折叠的性质得∠AH'I=∠AHI,AH'=AH=3t,证明△AIH'∽△AH'C,则AH'2=
①
AI×AC,证△AIH∽△AOD,求出AI= t,得出(3t)2= t×10,解方程即可;
作PH⊥OH于H,交OF的延长线于P,作OM⊥AD于M,PN⊥AD于N,证出FH=FP
②=OF,HP= OH,DN=DM=4,证明△OMH∽△HNP,求出HN= OM=3 ,则
DH=HN﹣DN=3 ﹣4,得出AH=AD﹣DH=12﹣3 ,即可得出答案.
【解析】解:(1)∵ M为△BCD的内切圆,切点分别为N,P,Q,DN=4,BN=6,
∴BP=BN=6,DQ=⊙DN=4,CP=CQ,BD=BN+DN=10,
设CP=CQ=a,则BC=6+a,CD=4+a,
∵四边形ABCD是矩形,
∴∠BCD=90°,
∴BC2+CD2=BD2,即(6+a)2+(4+a)2=102,
解得:a=2,
∴BC=6+2=8,CD=4+2=6;
(2) 存在时刻t= s,使点H′恰好落在边BC上;理由如下:
①
如图1所示:
由折叠的性质得:∠AH'I=∠AHI,AH'=AH=3t,
第 25 页 / 共 27 页∵四边形ABCD是矩形,
∴AD=BC=8,AD∥BC,∠BCD=90°,OA=OC= AC,OB=OD= BD,AC=BD,
∴AC=BD= = =10,OA=OD=5,
∴∠ADO=∠OAD,
∵HI∥BD,
∴∠AHI=∠ADO,
∴∠AH'I=∠AHI=∠ADO=∠OAD=∠ACH',
∴△AIH'∽△AH'C,
∴ = ,
∴AH'2=AI×AC,
∵HI∥BD,
∴△AIH∽△AOD,
∴ = ,即 = ,
解得:AI= t,
∴(3t)2= t×10,
解得:t= ,
即存在时刻t= s,使点H′恰好落在边BC上;
作PH⊥OH于H,交OF的延长线于P,作OM⊥AD于M,PN⊥AD于N,如图2所示:
②则OM∥CD∥PN,∠OMH=∠HNP=90°,OM是△ACD的中位线,
∴OM= CD=3,
∵△OFH是等边三角形,
∴OF=FH,∠OHF=∠HOF=60°,
∴∠FHP=∠HPO=30°,
∴FH=FP=OF,HP= OH,
∴DF是梯形OMNP的中位线,
第 26 页 / 共 27 页∴DN=DM=4,
∵∠MHO+∠MOH=∠MHO+∠NHP=90°,
∴∠MOH=∠NHP,
∴△OMH∽△HNP,
∴ = = ,
∴HN= OM=3 ,
∴DH=HN﹣DN=3 ﹣4,
∴AH=AD﹣DH=12﹣3 ,
∴t= =4﹣ ,
即当△OFH为正三角形时,t的值为(4﹣ )s.
【点拨】本题是圆的综合题目,考查了切线长定理、矩形的性质、折叠的性质、勾股定理、相
似三角形的判定与性质、等边三角形的性质、含30°角的直角三角形的性质、等腰三角形
的判定、三角形中位线定理、梯形中位线定理等知识;本题综合性强,熟练掌握切线长定
理、相似三角形的判定与性质以及勾股定理是解题的关键.
第 27 页 / 共 27 页