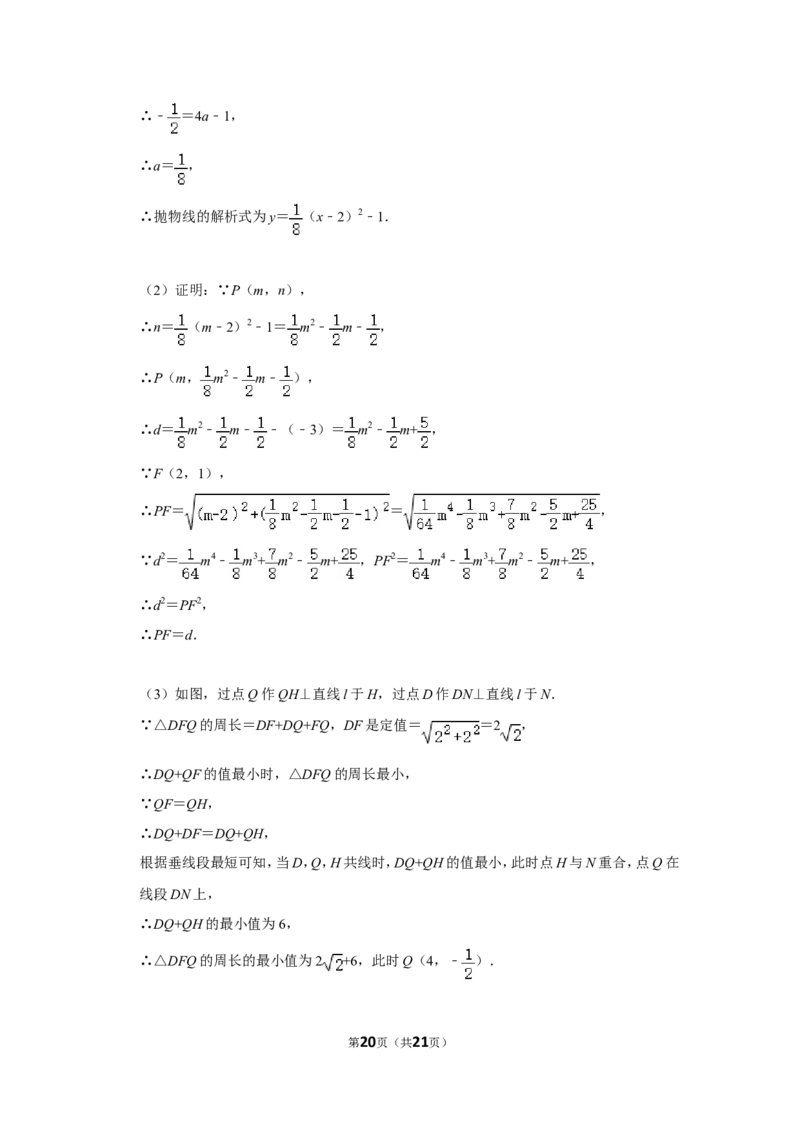文档内容
2020年山东省滨州市中考数学试卷
一、选择题:本大题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的选
项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑.每小题涂对得3分,满分36分.
1.(3分)下列各式正确的是( )
A.﹣|﹣5|=5 B.﹣(﹣5)=﹣5 C.|﹣5|=﹣5 D.﹣(﹣5)=5
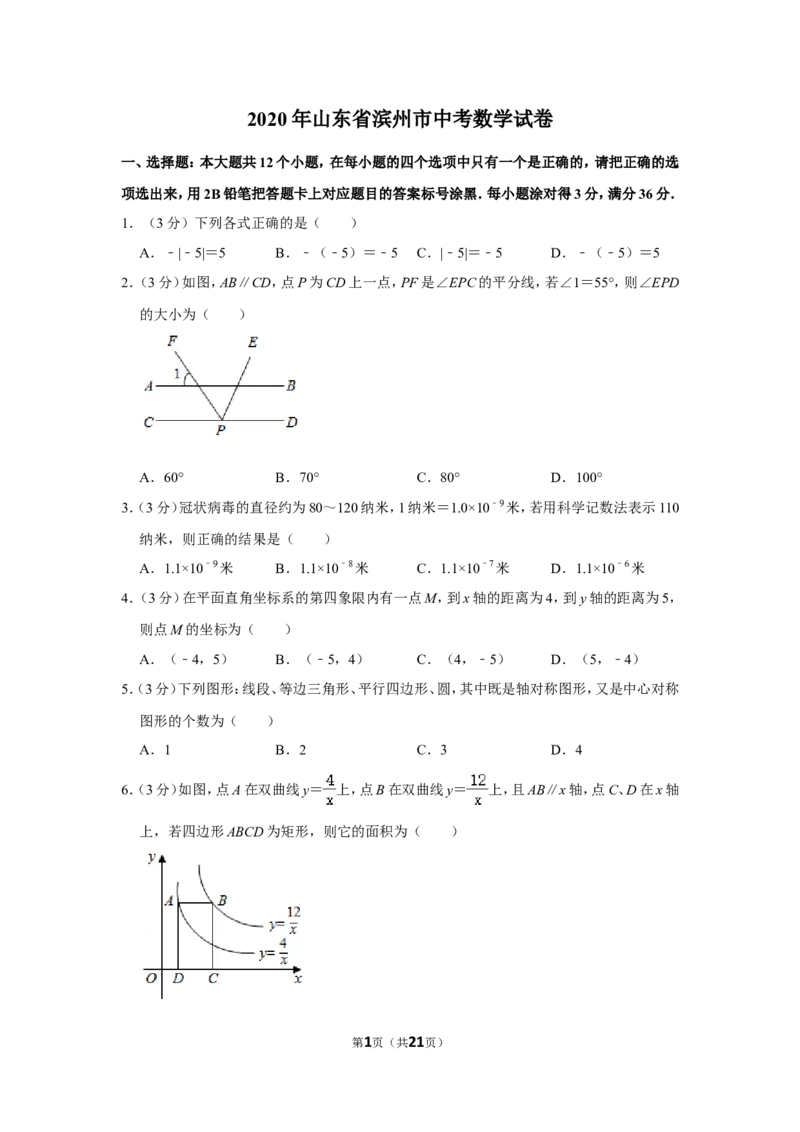
2.(3分)如图,AB∥CD,点P为CD上一点,PF是∠EPC的平分线,若∠1=55°,则∠EPD
的大小为( )
A.60° B.70° C.80° D.100°
3.(3分)冠状病毒的直径约为80~120纳米,1纳米=1.0×10﹣9米,若用科学记数法表示110
纳米,则正确的结果是( )
A.1.1×10﹣9米 B.1.1×10﹣8米 C.1.1×10﹣7米 D.1.1×10﹣6米
4.(3分)在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,
则点M的坐标为( )
A.(﹣4,5) B.(﹣5,4) C.(4,﹣5) D.(5,﹣4)
5.(3分)下列图形:线段、等边三角形、平行四边形、圆,其中既是轴对称图形,又是中心对称
图形的个数为( )
A.1 B.2 C.3 D.4
6.(3分)如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥x轴,点C、D在x轴
上,若四边形ABCD为矩形,则它的面积为( )
第1页(共21页)A.4 B.6 C.8 D.12
7.(3分)下列命题是假命题的是( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线相等的菱形是正方形
D.对角线互相垂直且平分的四边形是正方形
8.(3分)已知一组数据:5,4,3,4,9,关于这组数据的下列描述:
平均数是5, 中位数是4, 众数是4, 方差是4.4,
①其中正确的个数②为( ) ③ ④
A.1 B.2 C.3 D.4
9.(3分)在 O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6 ⊙ B.9 C.12 D.15
10.(3分)对于任意实数k,关于x的方程 x2﹣(k+5)x+k2+2k+25=0的根的情况为( )
A.有两个相等的实数根 B.没有实数根
C.有两个不相等的实数根 D.无法判定
11.(3分)对称轴为直线x=1的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)如图所示,小明
同学得出了以下结论: abc<0, b2>4ac, 4a+2b+c>0, 3a+c>0, a+b≤m
(am+b)(m为任意实数①), 当x<②﹣1时,y随x③的增大而增大.其④中结论正确⑤的个数为(
) ⑥
A.3 B.4 C.5 D.6
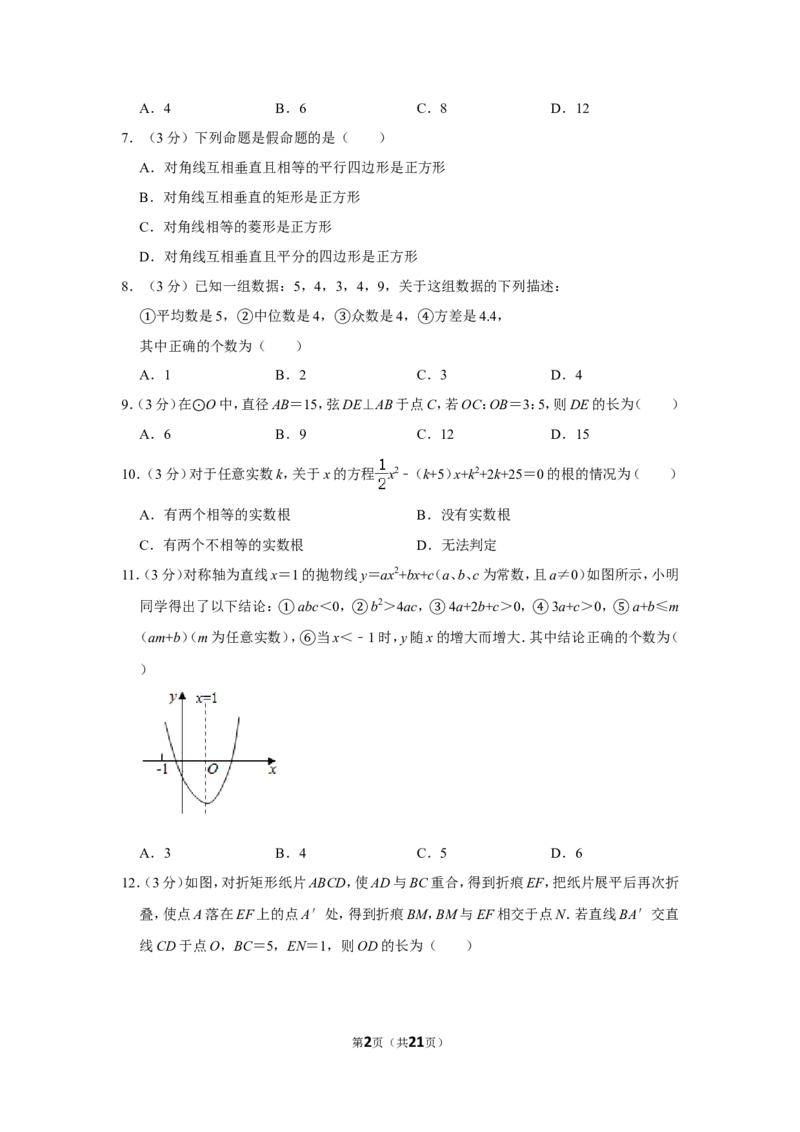
12.(3分)如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折
叠,使点A落在EF上的点A′处,得到折痕BM,BM与EF相交于点N.若直线BA′交直
线CD于点O,BC=5,EN=1,则OD的长为( )
第2页(共21页)A. B. C. D.
二、填空题:本大题共8个小题.每小题5分,满分40分.
13.(5分)若二次根式 在实数范围内有意义,则x的取值范围为 .
14.(5分)在等腰△ABC中,AB=AC,∠B=50°,则∠A的大小为 .
15.(5分)若正比例函数y=2x的图象与某反比例函数的图象有一个交点的纵坐标是2,则该
反比例函数的解析式为 .
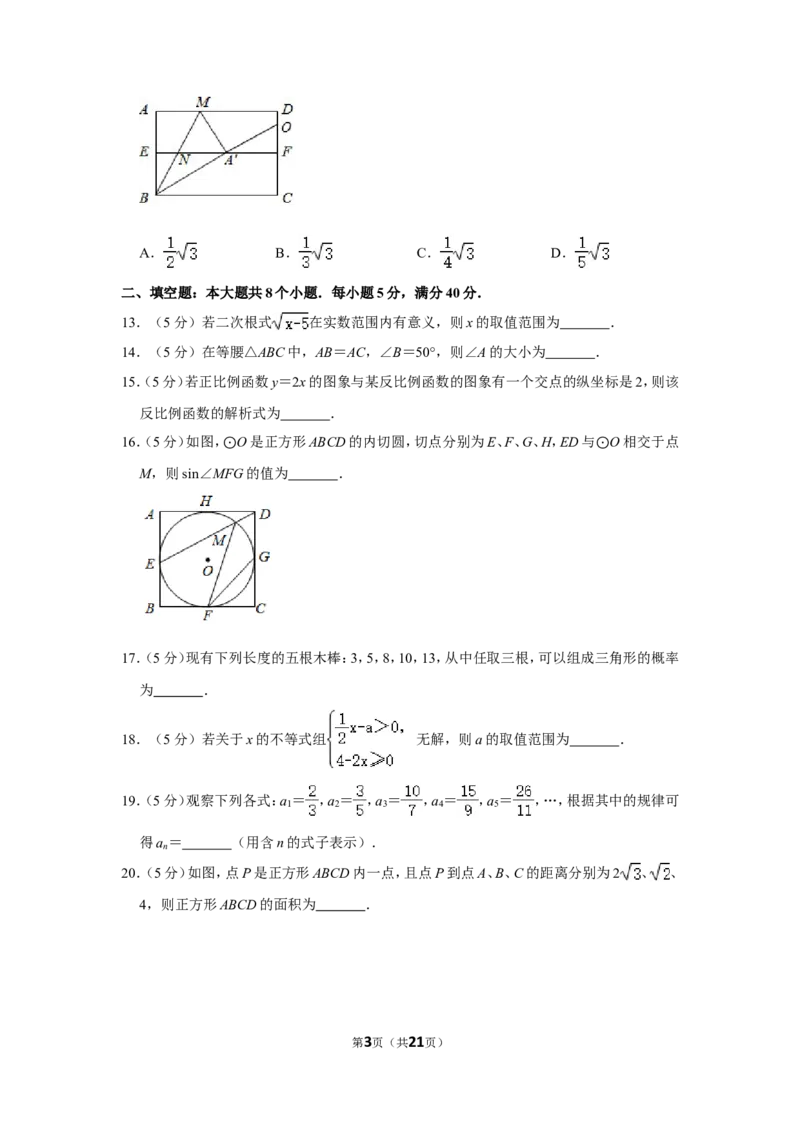
16.(5分)如图, O是正方形ABCD的内切圆,切点分别为E、F、G、H,ED与 O相交于点
M,则sin∠M⊙FG的值为 . ⊙
17.(5分)现有下列长度的五根木棒:3,5,8,10,13,从中任取三根,可以组成三角形的概率
为 .
18.(5分)若关于x的不等式组 无解,则a的取值范围为 .
19.(5分)观察下列各式:a = ,a = ,a = ,a = ,a = ,…,根据其中的规律可
1 2 3 4 5
得a = (用含n的式子表示).
n
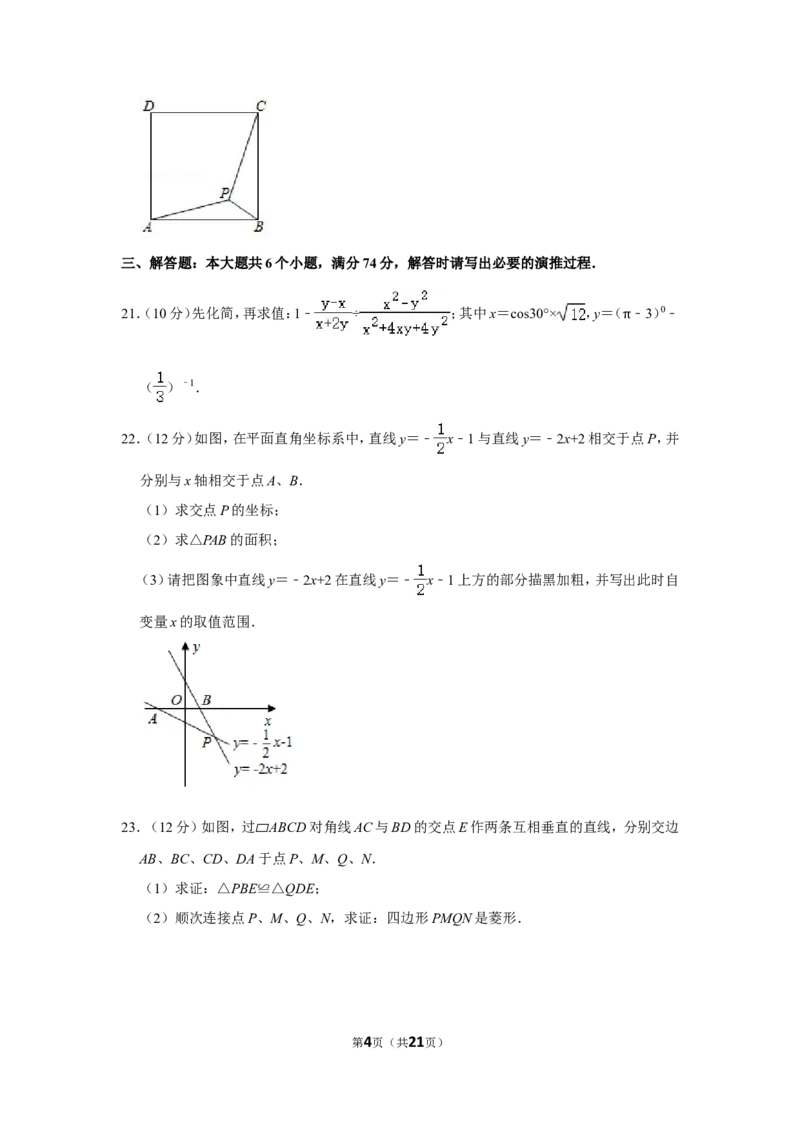
20.(5分)如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为2 、 、
4,则正方形ABCD的面积为 .
第3页(共21页)三、解答题:本大题共6个小题,满分74分,解答时请写出必要的演推过程.
21.(10分)先化简,再求值:1﹣ ÷ ;其中x=cos30°× ,y=( ﹣3)0﹣
π
( )﹣1.
22.(12分)如图,在平面直角坐标系中,直线y=﹣ x﹣1与直线y=﹣2x+2相交于点P,并
分别与x轴相交于点A、B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y=﹣2x+2在直线y=﹣ x﹣1上方的部分描黑加粗,并写出此时自
变量x的取值范围.
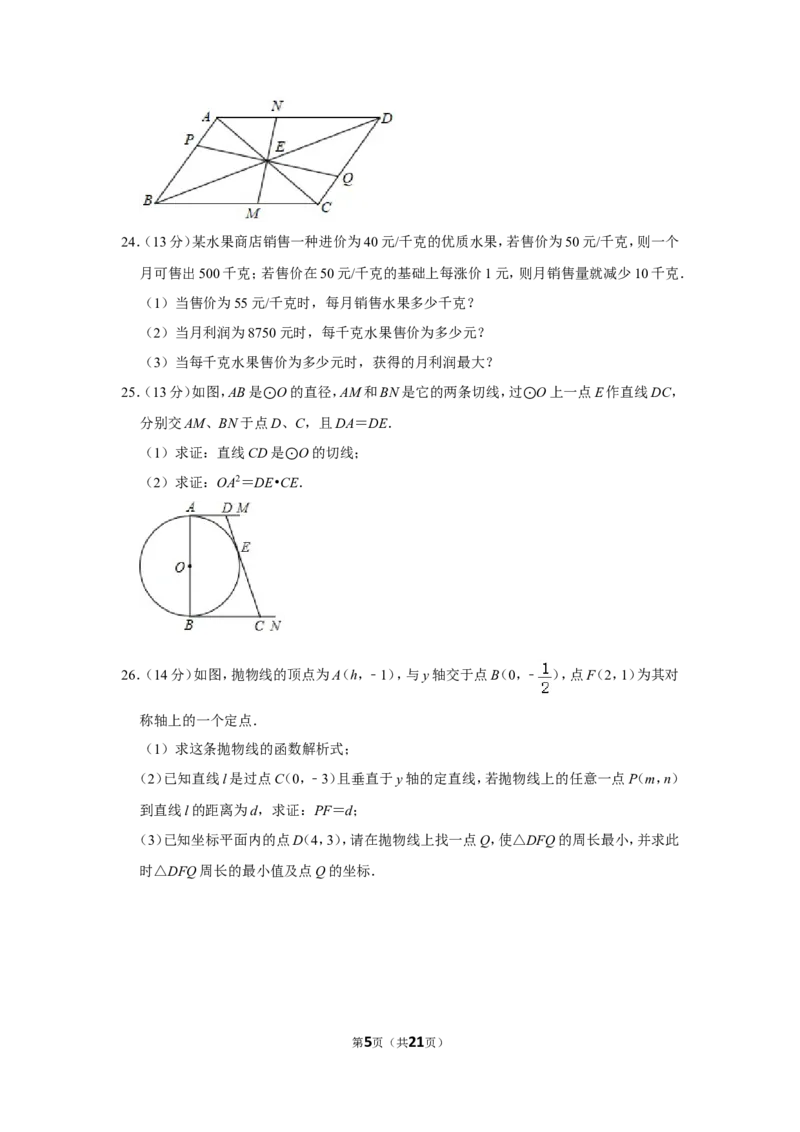
23.(12分)如图,过 ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边
AB、BC、CD、DA▱于点P、M、Q、N.
(1)求证:△PBE≌△QDE;
(2)顺次连接点P、M、Q、N,求证:四边形PMQN是菱形.
第4页(共21页)24.(13分)某水果商店销售一种进价为40元/千克的优质水果,若售价为50元/千克,则一个
月可售出500千克;若售价在50元/千克的基础上每涨价1元,则月销售量就减少10千克.
(1)当售价为55元/千克时,每月销售水果多少千克?
(2)当月利润为8750元时,每千克水果售价为多少元?
(3)当每千克水果售价为多少元时,获得的月利润最大?
25.(13分)如图,AB是 O的直径,AM和BN是它的两条切线,过 O上一点E作直线DC,
分别交AM、BN于点⊙D、C,且DA=DE. ⊙
(1)求证:直线CD是 O的切线;
(2)求证:OA2=DE•C⊙E.
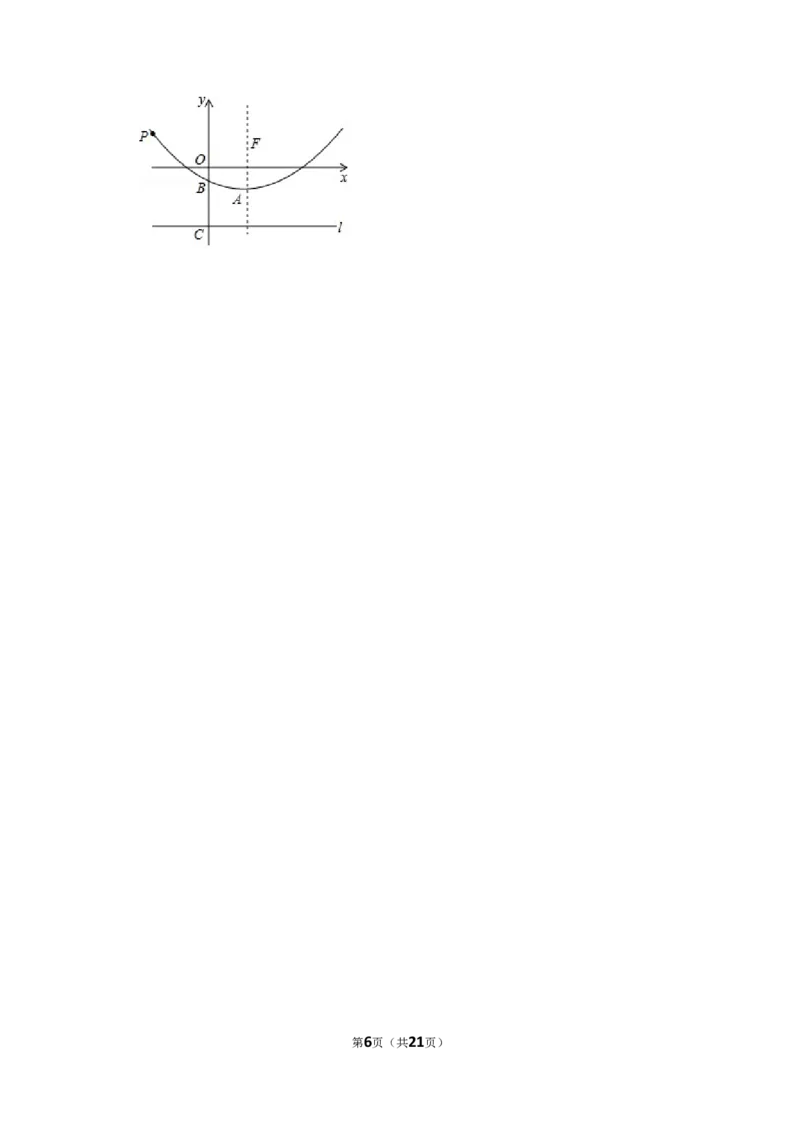
26.(14分)如图,抛物线的顶点为A(h,﹣1),与y轴交于点B(0,﹣ ),点F(2,1)为其对
称轴上的一个定点.
(1)求这条抛物线的函数解析式;
(2)已知直线l是过点C(0,﹣3)且垂直于y轴的定直线,若抛物线上的任意一点P(m,n)
到直线l的距离为d,求证:PF=d;
(3)已知坐标平面内的点D(4,3),请在抛物线上找一点Q,使△DFQ的周长最小,并求此
时△DFQ周长的最小值及点Q的坐标.
第5页(共21页)第6页(共21页)2020年山东省滨州市中考数学试卷
参考答案与试题解析
一、选择题:本大题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的选
项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑.每小题涂对得3分,满分36分.
1.【分析】根据绝对值的性质和相反数的定义对各选项分析判断即可.
【解答】解:A、∵﹣|﹣5|=﹣5,
∴选项A不符合题意;
B、∵﹣(﹣5)=5,
∴选项B不符合题意;
C、∵|﹣5|=5,
∴选项C不符合题意;
D、∵﹣(﹣5)=5,
∴选项D符合题意.
故选:D.
【点评】此题主要考查相反数的定义以及绝对值的含义和求法,解答此题的关键是要明确
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
2.【分析】根据平行线和角平分线的定义即可得到结论.
【解答】解:∵AB∥CD,
∴∠1=∠CPF=55°,
∵PF是∠EPC的平分线,
∴∠CPE=2∠CPF=110°,
∴∠EPD=180°﹣110°=70°,
故选:B.
【点评】本题考查了平行线的性质以及角平分线的定义,熟练掌握平行线的性质是解题的
关键.
3.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数
的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零
的数字前面的0的个数所决定.
【解答】解:110纳米=110×10﹣9米=1.1×10﹣7米.
第7页(共21页)故选:C.
【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为
由原数左边起第一个不为零的数字前面的0的个数所决定.
4.【分析】直接利用点的坐标特点进而分析得出答案.
【解答】解:∵在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距
离为5,
∴点M的纵坐标为:﹣4,横坐标为:5,
即点M的坐标为:(5,﹣4).
故选:D.
【点评】此题主要考查了点的坐标,正确掌握第四象限点的坐标特点是解题关键.
5.【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:线段是轴对称图形,也是中心对称图形;
等边三角形是轴对称图形,不是中心对称图形;
平行四边形不是轴对称图形,是中心对称图形;
圆是轴对称图形,也是中心对称图形;
则既是轴对称图形又是中心对称图形的有2个.
故选:B.
【点评】此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对
称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身
重合.
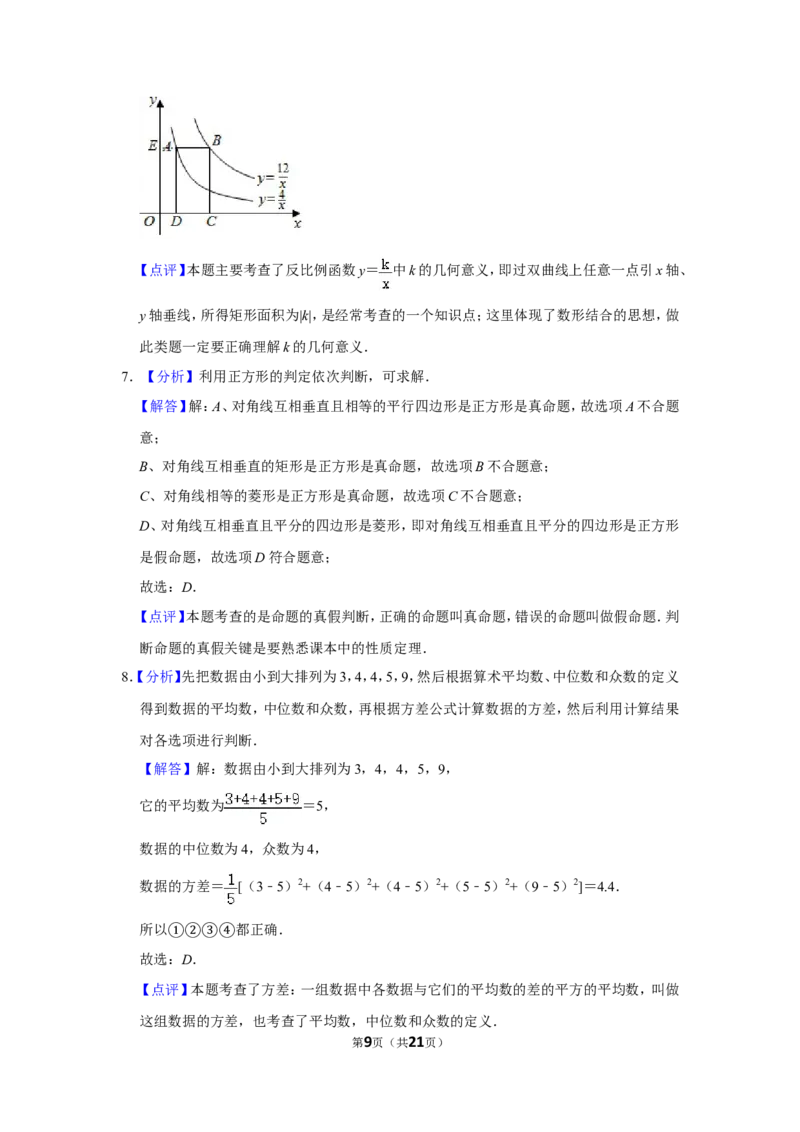
6.【分析】根据双曲线上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的矩形的面
积S的关系S=|k|即可判断.
【解答】解:延长BA交y轴于E,则BE⊥y轴,
∵点A在双曲线y= 上,
∴四边形AEOD的面积为4,
∵点B在双曲线线y= 上,且AB∥x轴,
∴四边形BEOC的面积为12,
∴矩形ABCD的面积为12﹣4=8.
故选:C.
第8页(共21页)【点评】本题主要考查了反比例函数y= 中k的几何意义,即过双曲线上任意一点引x轴、
y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做
此类题一定要正确理解k的几何意义.
7.【分析】利用正方形的判定依次判断,可求解.
【解答】解:A、对角线互相垂直且相等的平行四边形是正方形是真命题,故选项A不合题
意;
B、对角线互相垂直的矩形是正方形是真命题,故选项B不合题意;
C、对角线相等的菱形是正方形是真命题,故选项C不合题意;
D、对角线互相垂直且平分的四边形是菱形,即对角线互相垂直且平分的四边形是正方形
是假命题,故选项D符合题意;
故选:D.
【点评】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判
断命题的真假关键是要熟悉课本中的性质定理.
8.【分析】先把数据由小到大排列为3,4,4,5,9,然后根据算术平均数、中位数和众数的定义
得到数据的平均数,中位数和众数,再根据方差公式计算数据的方差,然后利用计算结果
对各选项进行判断.
【解答】解:数据由小到大排列为3,4,4,5,9,
它的平均数为 =5,
数据的中位数为4,众数为4,
数据的方差= [(3﹣5)2+(4﹣5)2+(4﹣5)2+(5﹣5)2+(9﹣5)2]=4.4.
所以 都正确.
故选①:D②.③④
【点评】本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做
这组数据的方差,也考查了平均数,中位数和众数的定义.
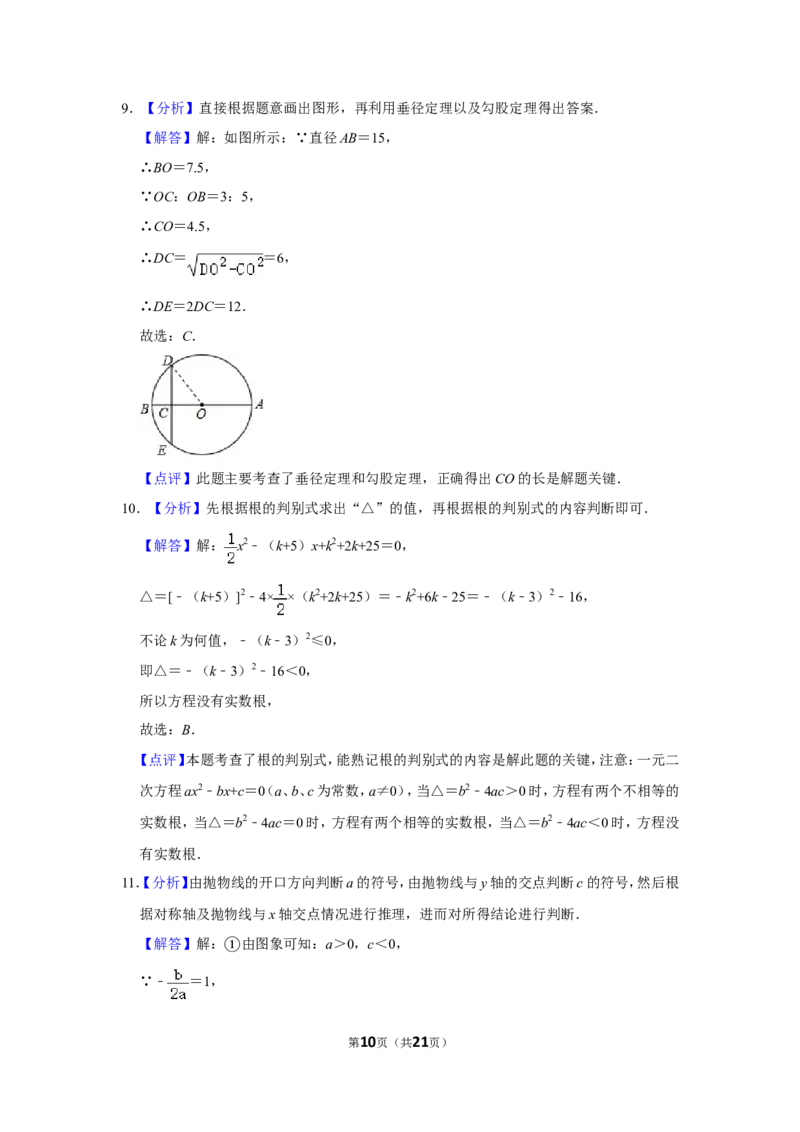
第9页(共21页)9.【分析】直接根据题意画出图形,再利用垂径定理以及勾股定理得出答案.
【解答】解:如图所示:∵直径AB=15,
∴BO=7.5,
∵OC:OB=3:5,
∴CO=4.5,
∴DC= =6,
∴DE=2DC=12.
故选:C.
【点评】此题主要考查了垂径定理和勾股定理,正确得出CO的长是解题关键.
10.【分析】先根据根的判别式求出“△”的值,再根据根的判别式的内容判断即可.
【解答】解: x2﹣(k+5)x+k2+2k+25=0,
△=[﹣(k+5)]2﹣4× ×(k2+2k+25)=﹣k2+6k﹣25=﹣(k﹣3)2﹣16,
不论k为何值,﹣(k﹣3)2≤0,
即△=﹣(k﹣3)2﹣16<0,
所以方程没有实数根,
故选:B.
【点评】本题考查了根的判别式,能熟记根的判别式的内容是解此题的关键,注意:一元二
次方程ax2﹣bx+c=0(a、b、c为常数,a≠0),当△=b2﹣4ac>0时,方程有两个不相等的
实数根,当△=b2﹣4ac=0时,方程有两个相等的实数根,当△=b2﹣4ac<0时,方程没
有实数根.
11.【分析】由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根
据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】解: 由图象可知:a>0,c<0,
①
∵﹣ =1,
第10页(共21页)∴b=﹣2a<0,
∴abc>0,故 错误;
∵抛物线与①x轴有两个交点,
②∴b2﹣4ac>0,
∴b2>4ac,故 正确;
当x=2时,②y=4a+2b+c<0,故 错误;
③当x=﹣1时,y=a﹣b+c=a﹣(③﹣2a)+c>0,
④∴3a+c>0,故 正确;
当x=1时,④y取到值最小,此时,y=a+b+c,
⑤而当x=m时,y=am2+bm+c,
所以a+b+c≤am2+bm+c,
故a+b≤am2+bm,即a+b≤m(am+b),故 正确,
当x<﹣1时,y随x的增大而减小,故 ⑤错误,
⑥故选:A. ⑥
【点评】本题考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物
线开口方向、对称轴和抛物线与y轴的交点确定.
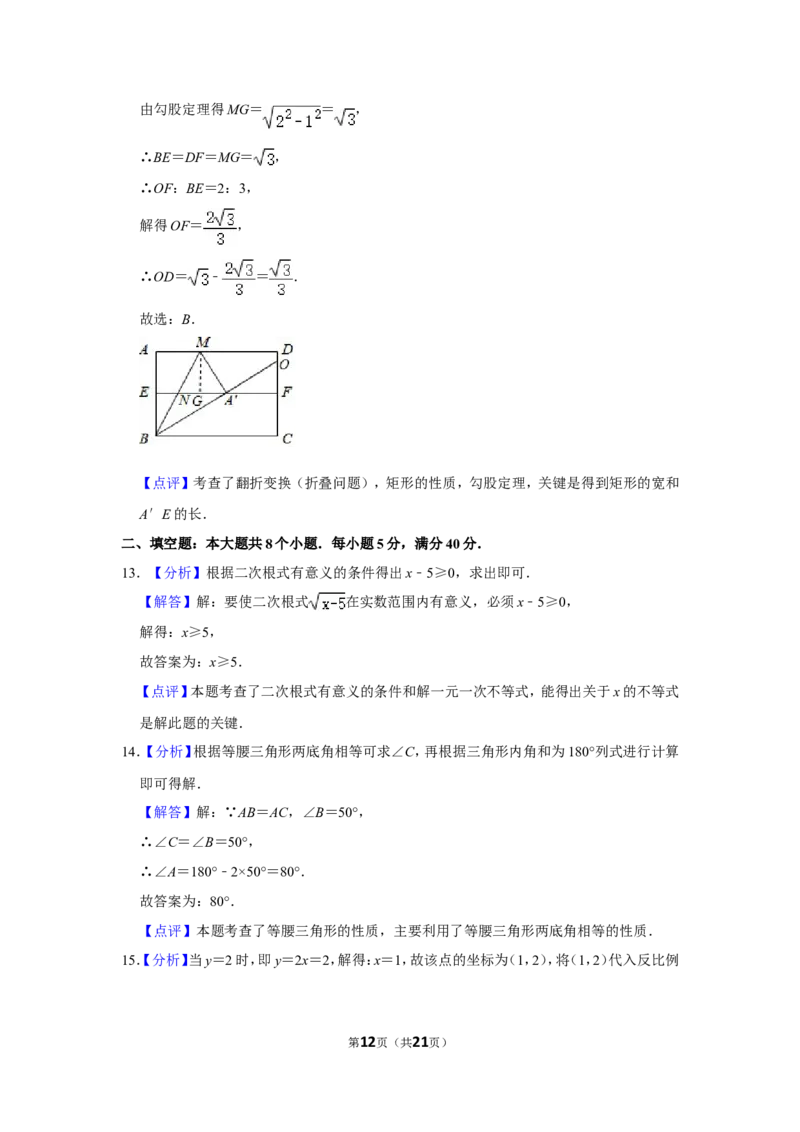
12.【分析】根据中位线定理可得AM=2,根据折叠的性质和等腰三角形的性质可得A′M=
A′N=2,过M点作MG⊥EF于G,可求A′G,根据勾股定理可求MG,进一步得到BE,
再根据平行线分线段成比例可求OF,从而得到OD.
【解答】解:∵EN=1,
∴由中位线定理得AM=2,
由折叠的性质可得A′M=2,
∵AD∥EF,
∴∠AMB=∠A′NM,
∵∠AMB=∠A′MB,
∴∠A′NM=∠A′MB,
∴A′N=2,
∴A′E=3,A′F=2
过M点作MG⊥EF于G,
∴NG=EN=1,
∴A′G=1,
第11页(共21页)由勾股定理得MG= = ,
∴BE=DF=MG= ,
∴OF:BE=2:3,
解得OF= ,
∴OD= ﹣ = .
故选:B.
【点评】考查了翻折变换(折叠问题),矩形的性质,勾股定理,关键是得到矩形的宽和
A′E的长.
二、填空题:本大题共8个小题.每小题5分,满分40分.
13.【分析】根据二次根式有意义的条件得出x﹣5≥0,求出即可.
【解答】解:要使二次根式 在实数范围内有意义,必须x﹣5≥0,
解得:x≥5,
故答案为:x≥5.
【点评】本题考查了二次根式有意义的条件和解一元一次不等式,能得出关于x的不等式
是解此题的关键.
14.【分析】根据等腰三角形两底角相等可求∠C,再根据三角形内角和为180°列式进行计算
即可得解.
【解答】解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∴∠A=180°﹣2×50°=80°.
故答案为:80°.
【点评】本题考查了等腰三角形的性质,主要利用了等腰三角形两底角相等的性质.
15.【分析】当y=2时,即y=2x=2,解得:x=1,故该点的坐标为(1,2),将(1,2)代入反比例
第12页(共21页)函数表达式y= ,即可求解.
【解答】解:当y=2时,即y=2x=2,解得:x=1,
故该点的坐标为(1,2),
将(1,2)代入反比例函数表达式y= 并解得:k=2,
故答案为:y= .
【点评】本题考查的是反比例函数与一次函数的交点问题,解题的关键是通过正比例函数
确定交点的坐标,进而求解.
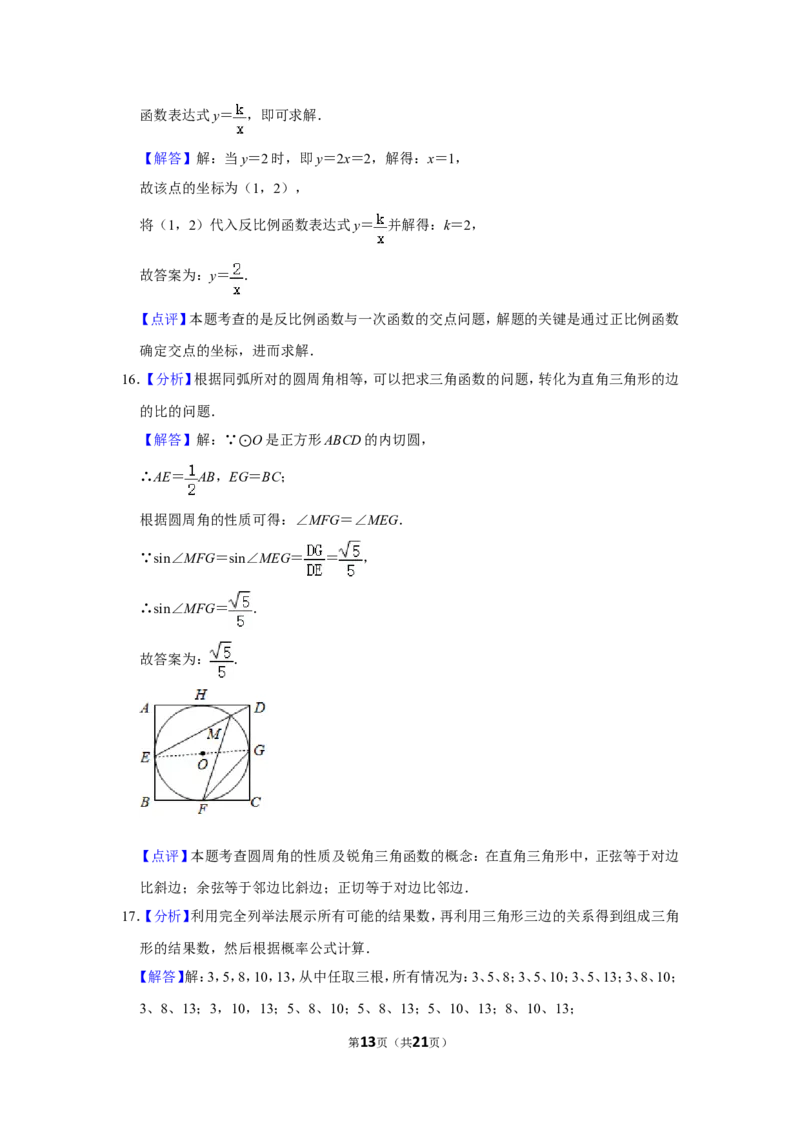
16.【分析】根据同弧所对的圆周角相等,可以把求三角函数的问题,转化为直角三角形的边
的比的问题.
【解答】解:∵ O是正方形ABCD的内切圆,
∴AE= AB,EG ⊙=BC;
根据圆周角的性质可得:∠MFG=∠MEG.
∵sin∠MFG=sin∠MEG= = ,
∴sin∠MFG= .
故答案为: .
【点评】本题考查圆周角的性质及锐角三角函数的概念:在直角三角形中,正弦等于对边
比斜边;余弦等于邻边比斜边;正切等于对边比邻边.
17.【分析】利用完全列举法展示所有可能的结果数,再利用三角形三边的关系得到组成三角
形的结果数,然后根据概率公式计算.
【解答】解:3,5,8,10,13,从中任取三根,所有情况为:3、5、8;3、5、10;3、5、13;3、8、10;
3、8、13;3,10,13;5、8、10;5、8、13;5、10、13;8、10、13;
第13页(共21页)共有10种等可能的结果数,其中可以组成三角形的结果数为 4,所以可以组成三角形的
概率= = .
故答案为 .
【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,
再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概
率.也考查了三角形三边的关系.
18.【分析】分别求出每一个不等式的解集,根据口诀:大大小小无解了可得答案.
【解答】解:解不等式 x﹣a>0,得:x>2a,
解不等式4﹣2x≥0,得:x≤2,
∵不等式组无解,
∴2a≥2,
解得a≥1,
故答案为:a≥1.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知
“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
19.【分析】观察发现,每一项都是一个分数,分母依次为3、5、7,…,那么第n项的分母是
2n+1;分子依次为2,3,10,15,26,…,变化规律为:奇数项的分子是n2+1,偶数项的分子
是n2﹣1,即第n项的分子是n2+(﹣1)n+1;依此即可求解.
【解答】解:由分析可得a = .
n
故答案为: .
【点评】本题考查学生通过观察、归纳、抽象出数列的规律的能力,要求学生首先分析题意,
找到规律,并进行推导得出答案.
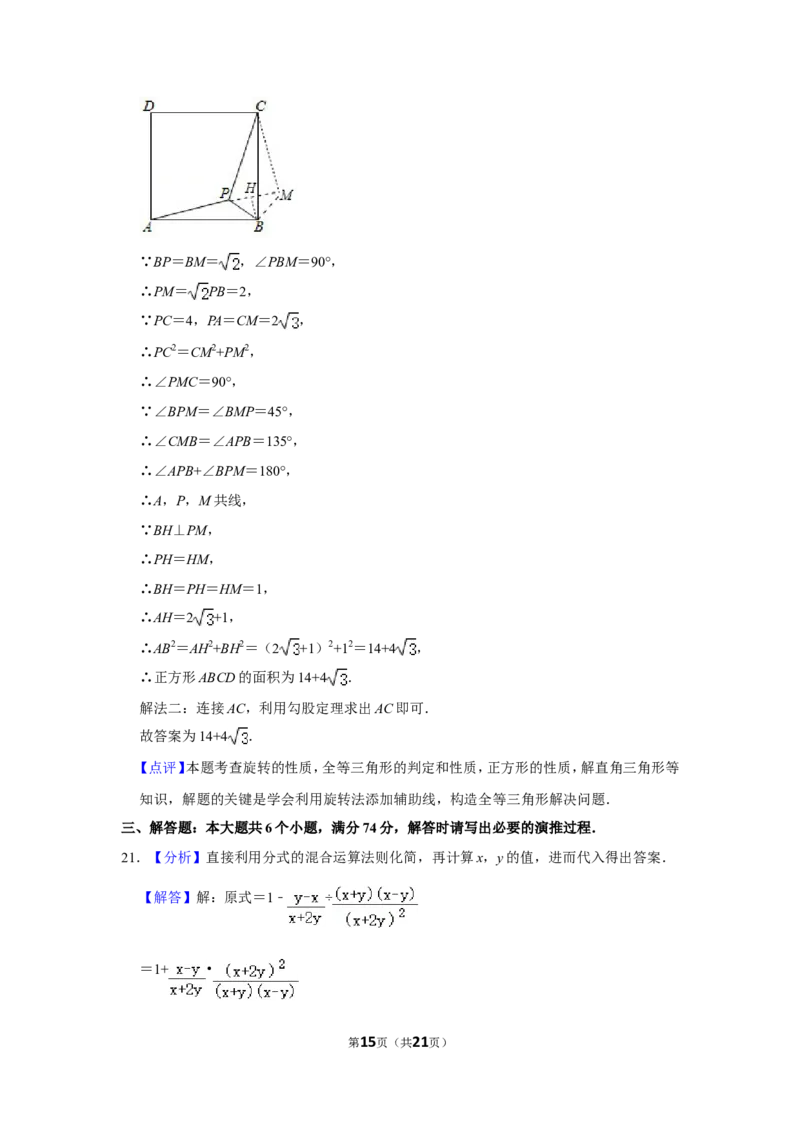
20.【分析】如图,将△ABP绕点B顺时针旋转90°得到△CBM,连接PM,过点B作BH⊥PM
于H.首先证明∠PMC=90°,推出∠CMB=∠APB=135°,推出A,P,M共线,利用勾股定
理求出AB2即可.
【解答】解:如图,将△ABP绕点B顺时针旋转90°得到△CBM,连接PM,过点B作
BH⊥PM于H.
第14页(共21页)∵BP=BM= ,∠PBM=90°,
∴PM= PB=2,
∵PC=4,PA=CM=2 ,
∴PC2=CM2+PM2,
∴∠PMC=90°,
∵∠BPM=∠BMP=45°,
∴∠CMB=∠APB=135°,
∴∠APB+∠BPM=180°,
∴A,P,M共线,
∵BH⊥PM,
∴PH=HM,
∴BH=PH=HM=1,
∴AH=2 +1,
∴AB2=AH2+BH2=(2 +1)2+12=14+4 ,
∴正方形ABCD的面积为14+4 .
解法二:连接AC,利用勾股定理求出AC即可.
故答案为14+4 .
【点评】本题考查旋转的性质,全等三角形的判定和性质,正方形的性质,解直角三角形等
知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题.
三、解答题:本大题共6个小题,满分74分,解答时请写出必要的演推过程.
21.【分析】直接利用分式的混合运算法则化简,再计算x,y的值,进而代入得出答案.
【解答】解:原式=1﹣ ÷
=1+ •
第15页(共21页)=1+
=
= ,
∵x=cos30°× = ×2 =3,y=( ﹣3)0﹣( )﹣1=1﹣3=﹣2,
π
∴原式= =0.
【点评】此题主要考查了分式的化简求值,正确进行分式的混合运算是解题关键.
22.【分析】(1)解析式联立,解方程组即可求得交点P的坐标;
(2)求得A、B的坐标,然后根据三角形面积公式求得即可;
(3)根据图象求得即可.
【解答】解:(1)由 解得 ,
∴P(2,﹣2);
(2)直线y=﹣ x﹣1与直线y=﹣2x+2中,令y=0,则﹣ x﹣1=0与﹣2x+2=0,
解得x=﹣2与x=1,
∴A(﹣2,0),B(1,0),
∴AB=3,
∴S△PAB = = =3;
(3)如图所示:
自变量x的取值范围是x<2.
【点评】本题考查了两条直线平行或相交问题,两条直线的交点坐标是两条直线的解析式
第16页(共21页)构成的方程组的解.
23.【分析】(1)由ASA证△PBE≌△QDE即可;
(2)由全等三角形的性质得出EP=EQ,同理△BME≌△DNE(ASA),得出EM=EN,证出
四边形PMQN是平行四边形,由对角线PQ⊥MN,即可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴EB=ED,AB∥CD,
∴∠EBP=∠EDQ,
在△PBE和△QDE中, ,
∴△PBE≌△QDE(ASA);
(2)证明:如图所示:
∵△PBE≌△QDE,
∴EP=EQ,
同理:△BME≌△DNE(ASA),
∴EM=EN,
∴四边形PMQN是平行四边形,
∵PQ⊥MN,
∴四边形PMQN是菱形.
【点评】本题考查了平行四边形的判定与性质,菱形的判定,全等三角形的判定与性质;熟
练掌握菱形的判定和平行四边形的判定与性质,证明三角形全等是解题的关键.
24.【分析】(1)由月销售量=500﹣(销售单价﹣50)×10,可求解;
(2)设每千克水果售价为x元,由利润=每千克的利润×销售的数量,可列方程,即可求解;
(3)设每千克水果售价为m元,获得的月利润为y元,由利润=每千克的利润×销售的数
量,可得y与x的关系式,由二次函数的性质可求解.
【解答】解:(1)当售价为55元/千克时,每月销售水果=500﹣10×(55﹣50)=450千克;
(2)设每千克水果售价为x元,
第17页(共21页)由题意可得:8750=(x﹣40)[500﹣10(x﹣50)],
解得:x =65,x =75,
1 2
答:每千克水果售价为65元或75元;
(3)设每千克水果售价为m元,获得的月利润为y元,
由题意可得:y=(m﹣40)[500﹣10(m﹣50)]=﹣10(m﹣70)2+9000,
∴当m=70时,y有最大值为9000元,
答:当每千克水果售价为70元时,获得的月利润最大值为9000元.
【点评】本题主要考查二次函数的应用,解题的关键是熟练掌握销售问题中关于销售总利
润的相等关系,并据此列出函数解析式及熟练掌握二次函数的性质.
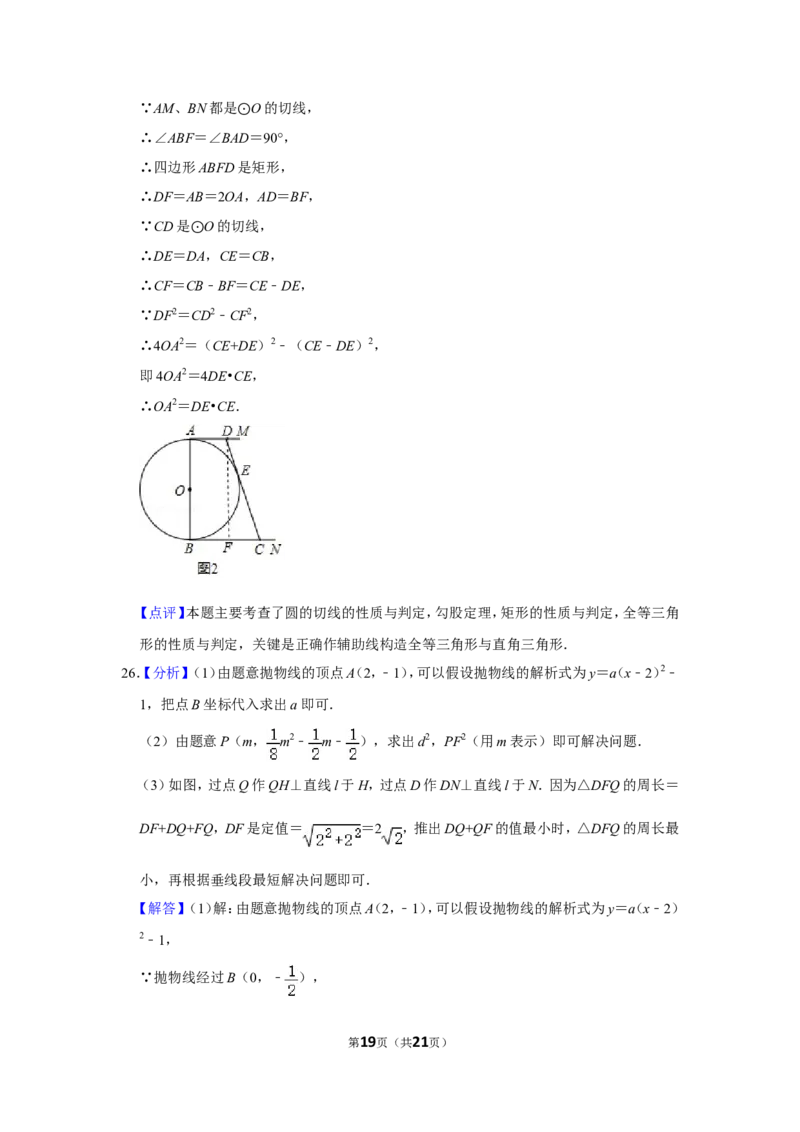
25.【分析】(1)连接OD,OE,证明△OAD≌△OED,得∠OAD=∠OED=90°,进而得CD是
切线;
(2)过D作DF⊥BC于点F,得四边形ABFD为矩形,得DF=2OA,再证明CF=CE﹣
DE,进而根据勾股定理得结论.
【解答】解:(1)连接OD,OE,如图1,
在△OAD和△OED中,
,
∴△OAD≌△OED(SSS),
∴∠OAD=∠OED,
∵AM是 O的切线,
∴∠OAD⊙=90°,
∴∠OED=90°,
∴直线CD是 O的切线;
⊙
(2)过D作DF⊥BC于点F,如图2,则∠DFB=∠DFC=90°,
第18页(共21页)∵AM、BN都是 O的切线,
∴∠ABF=∠BA⊙D=90°,
∴四边形ABFD是矩形,
∴DF=AB=2OA,AD=BF,
∵CD是 O的切线,
∴DE=D⊙A,CE=CB,
∴CF=CB﹣BF=CE﹣DE,
∵DF2=CD2﹣CF2,
∴4OA2=(CE+DE)2﹣(CE﹣DE)2,
即4OA2=4DE•CE,
∴OA2=DE•CE.
【点评】本题主要考查了圆的切线的性质与判定,勾股定理,矩形的性质与判定,全等三角
形的性质与判定,关键是正确作辅助线构造全等三角形与直角三角形.
26.【分析】(1)由题意抛物线的顶点A(2,﹣1),可以假设抛物线的解析式为y=a(x﹣2)2﹣
1,把点B坐标代入求出a即可.
(2)由题意P(m, m2﹣ m﹣ ),求出d2,PF2(用m表示)即可解决问题.
(3)如图,过点Q作QH⊥直线l于H,过点D作DN⊥直线l于N.因为△DFQ的周长=
DF+DQ+FQ,DF是定值= =2 ,推出DQ+QF的值最小时,△DFQ的周长最
小,再根据垂线段最短解决问题即可.
【解答】(1)解:由题意抛物线的顶点A(2,﹣1),可以假设抛物线的解析式为y=a(x﹣2)
2﹣1,
∵抛物线经过B(0,﹣ ),
第19页(共21页)∴﹣ =4a﹣1,
∴a= ,
∴抛物线的解析式为y= (x﹣2)2﹣1.
(2)证明:∵P(m,n),
∴n= (m﹣2)2﹣1= m2﹣ m﹣ ,
∴P(m, m2﹣ m﹣ ),
∴d= m2﹣ m﹣ ﹣(﹣3)= m2﹣ m+ ,
∵F(2,1),
∴PF= = ,
∵d2= m4﹣ m3+ m2﹣ m+ ,PF2= m4﹣ m3+ m2﹣ m+ ,
∴d2=PF2,
∴PF=d.
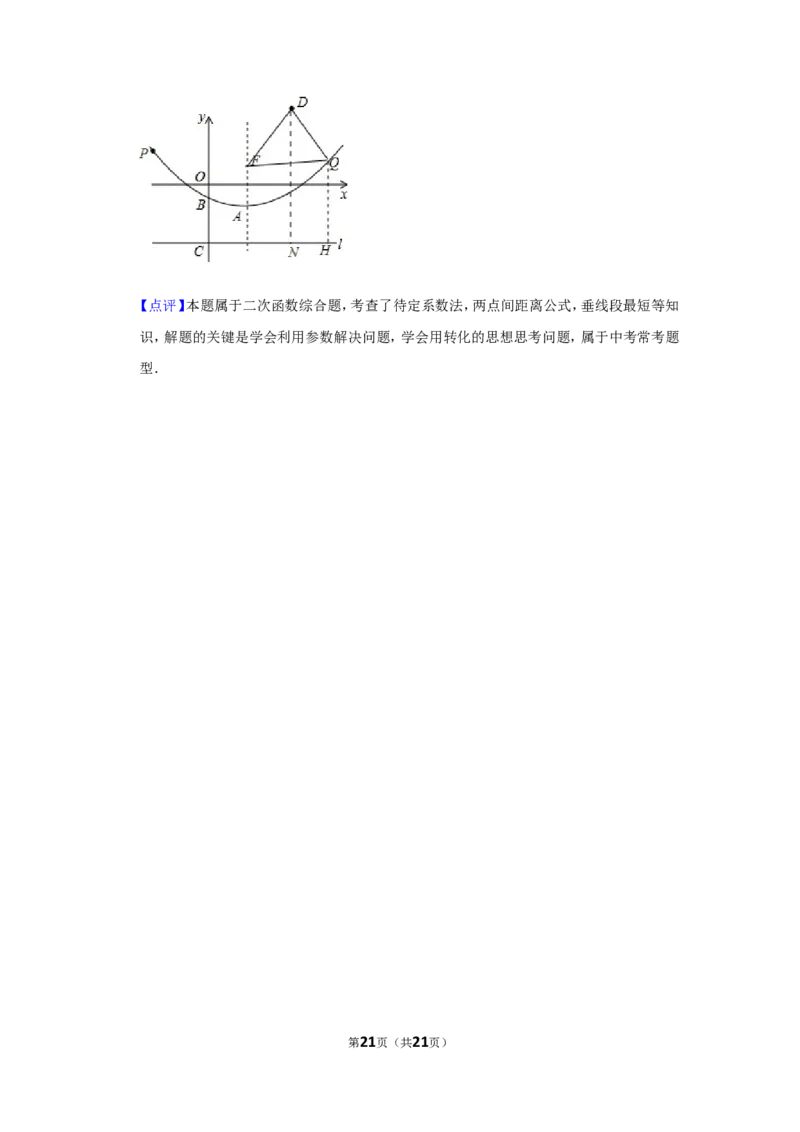
(3)如图,过点Q作QH⊥直线l于H,过点D作DN⊥直线l于N.
∵△DFQ的周长=DF+DQ+FQ,DF是定值= =2 ,
∴DQ+QF的值最小时,△DFQ的周长最小,
∵QF=QH,
∴DQ+DF=DQ+QH,
根据垂线段最短可知,当D,Q,H共线时,DQ+QH的值最小,此时点H与N重合,点Q在
线段DN上,
∴DQ+QH的最小值为6,
∴△DFQ的周长的最小值为2 +6,此时Q(4,﹣ ).
第20页(共21页)【点评】本题属于二次函数综合题,考查了待定系数法,两点间距离公式,垂线段最短等知
识,解题的关键是学会利用参数解决问题,学会用转化的思想思考问题,属于中考常考题
型.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/8/12 15:50:39;用户:18366185883;邮箱:18366185883;学号:22597006
第21页(共21页)