文档内容
2020 年年广广西西贵贵港港市市中中考考数数学学试试卷卷
1. −2的相反数是( )
A. −2 B. − 1 C. 2 D. 1
2 2
2. 若式子√(cid:1)+ 1在实数范围内有意义,则实数x的取值范围是( )
A. (cid:1) < −1 B. (cid:1) ≥ −1 C. (cid:1) ≥ 0 D. (cid:1) ≥ 1
3. 目前世界上刻度最小的标尺是钻石标尺,它的最小刻度为0.2(cid:2)(cid:3)( 其中1(cid:2)(cid:3) =
10−9 (cid:3)),用科学记数法表示这个最小刻度(单位: (cid:3)),结果是( )
A. 2 × 10−8 (cid:3) B. 2 × 10−9 (cid:3) C. 2 × 10−10 (cid:3) D. 2 × 10−11 (cid:3)
4. 数据2,6,5,0,1,6,8的中位数和众数分别是( )
A. 0和 6 B. 0和 8 C. 5和 8 D. 5和 6
5. 下列运算正确的是( )
A. 2(cid:4) + 3(cid:5) = 5(cid:4)(cid:5) B. 5(cid:4) 2 − 3(cid:4) = 2(cid:4)
C. ((cid:4)(cid:5) 3)2 = (cid:4) 2 (cid:5) 6 D. ((cid:4) + 2)2 = (cid:4) 2 + 4
6. 一元二次方程 (cid:1) 2 − (cid:1) − 3 = 0的根的情况为( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 只有一个实数根 D. 没有实数根
7. 如果 (cid:4) < (cid:5) , (cid:6) < 0,那么下列不等式中不成立的是( )
A. (cid:4) + (cid:6) < (cid:5) + (cid:6) B. (cid:4)(cid:6) > (cid:5)(cid:6) C. (cid:4)(cid:6) + 1 > (cid:5)(cid:6) + 1 D. (cid:4)(cid:6) 2 > (cid:5)(cid:6) 2
8. 下列命题中真命题是( )
6
A. √4的算术平方根是2 B. 数据 2,0,3,2,3的方差是
5
C. 正六边形的内角和为360° D. 对角线互相垂直的四边形是菱形
9. 如图,点A,B,C均在⊙ (cid:7) 上,若∠ (cid:8)(cid:9)(cid:10)= 130°,则∠ (cid:11) 的度
数为( )
A. 100°
B. 110°
C. 120°
D. 130°
10. 如图,在△ (cid:8)(cid:10)(cid:9) 中,点D在 AB边上,若 (cid:10)(cid:9)= 3, (cid:10)(cid:12)= 2,
且∠ (cid:10)(cid:9)(cid:12)= ∠ (cid:8) ,则线段AD的长为( )
第1 页,共26 页A. 2
5
B.
2
C. 3
9
D.
2
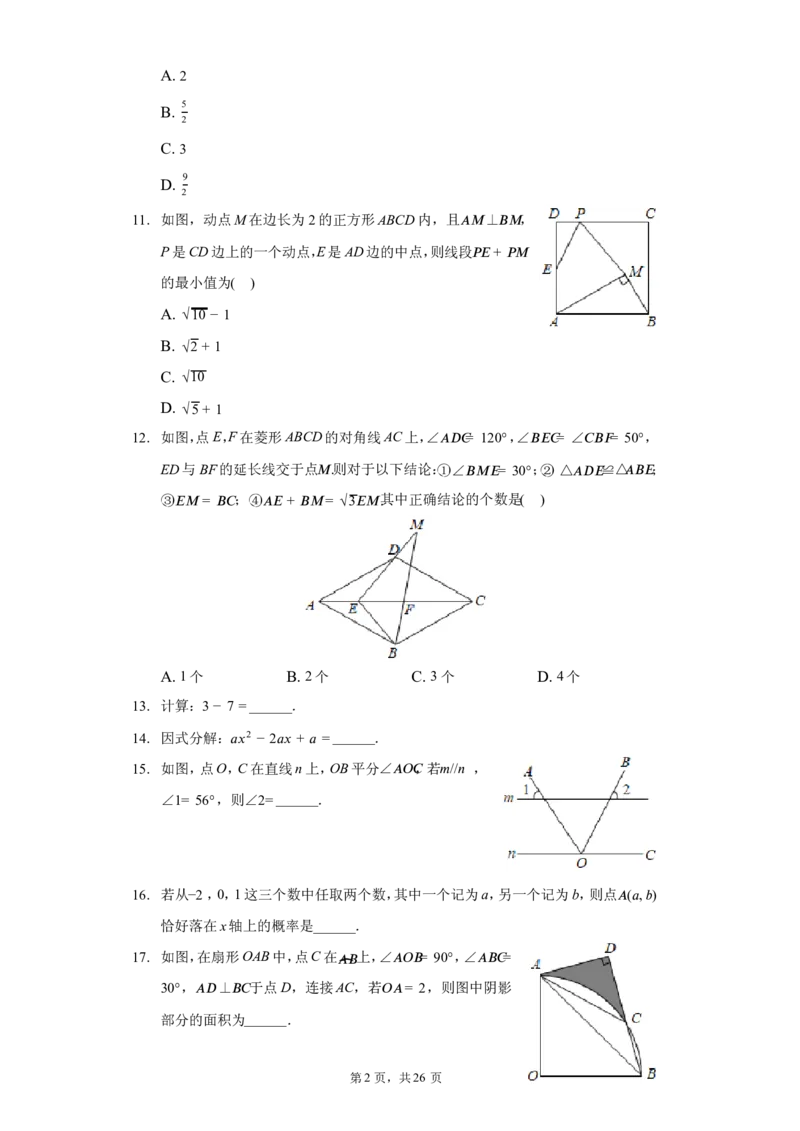
11. 如图,动点M在边长为 2的正方形ABCD内,且 (cid:8)(cid:13) ⊥ (cid:10)(cid:13) ,
P是CD边上的一个动点,E是 AD边的中点,则线段 (cid:14)(cid:15)+ (cid:14)(cid:13)
的最小值为( )
A. √10 − 1
B. √2 + 1
C. √10
D. √5 + 1
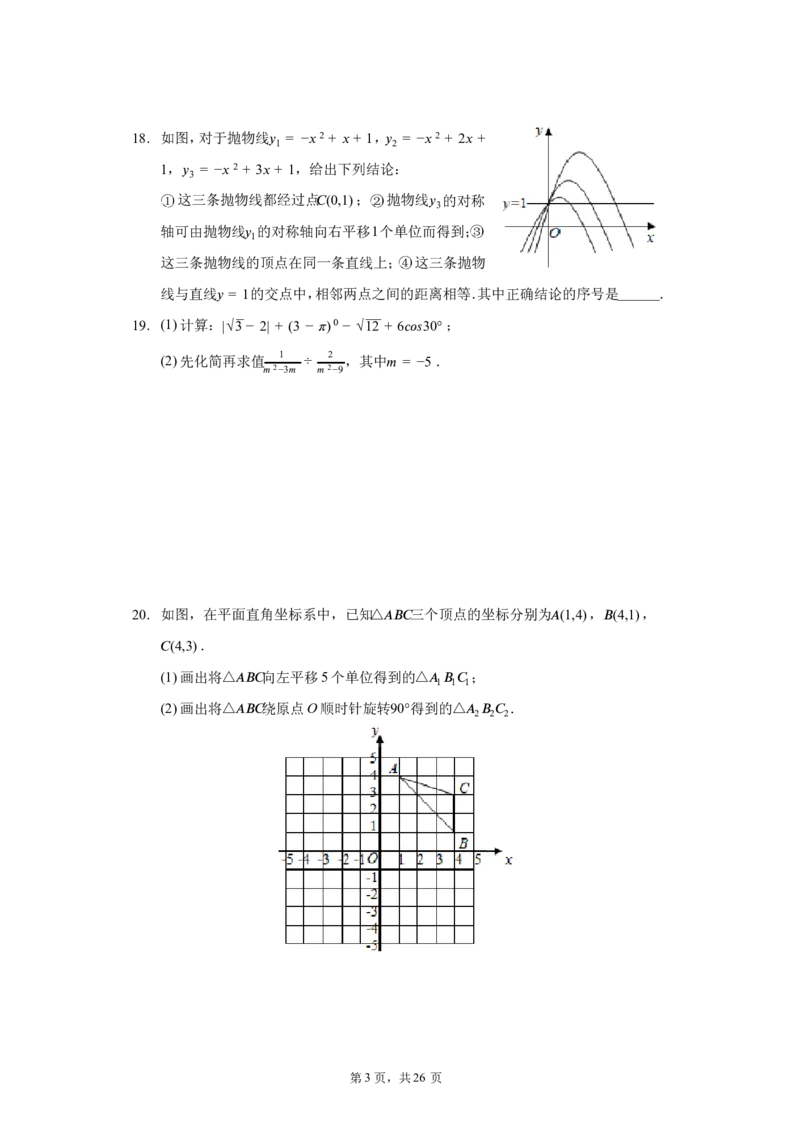
12. 如图,点 E,F在菱形 ABCD的对角线AC上,∠ (cid:8)(cid:12)(cid:9)= 120°,∠ (cid:10)(cid:15)(cid:9)= ∠ (cid:9)(cid:10)(cid:16)= 50°,
ED与 BF的延长线交于点 (cid:13).则对于以下结论:①∠ (cid:10)(cid:13)(cid:15)= 30°;② △ (cid:8)(cid:12)(cid:15) ≌△ (cid:8)(cid:10)(cid:15) ;
③ (cid:15)(cid:13)= (cid:10)(cid:9) ;④ (cid:8)(cid:15) + (cid:10)(cid:13)= √3(cid:15)(cid:13).其中正确结论的个数是( )
A. 1个 B. 2个 C. 3 个 D. 4个
13. 计算:3 − 7 =______.
14. 因式分解: (cid:4)(cid:1) 2 − 2(cid:4)(cid:1) + (cid:4) =______.
15. 如图,点O,C在直线n上,OB平分∠ (cid:8)(cid:7)(cid:9) ,若 (cid:3)//(cid:2) ,
∠1= 56°,则∠2=______.
16. 若从−2 ,0,1这三个数中任取两个数,其中一个记为a,另一个记为b,则点 (cid:8)((cid:4),(cid:5))
恰好落在x轴上的概率是______.
17. 如图,在扇形OAB中,点C在 (cid:8)⏜(cid:10) 上,∠ (cid:8)(cid:7)(cid:10)= 90°,∠ (cid:8)(cid:10)(cid:9)=
30°, (cid:8)(cid:12) ⊥ (cid:10)(cid:9) 于点 D,连接AC,若 (cid:7)(cid:8)= 2,则图中阴影
部分的面积为______.
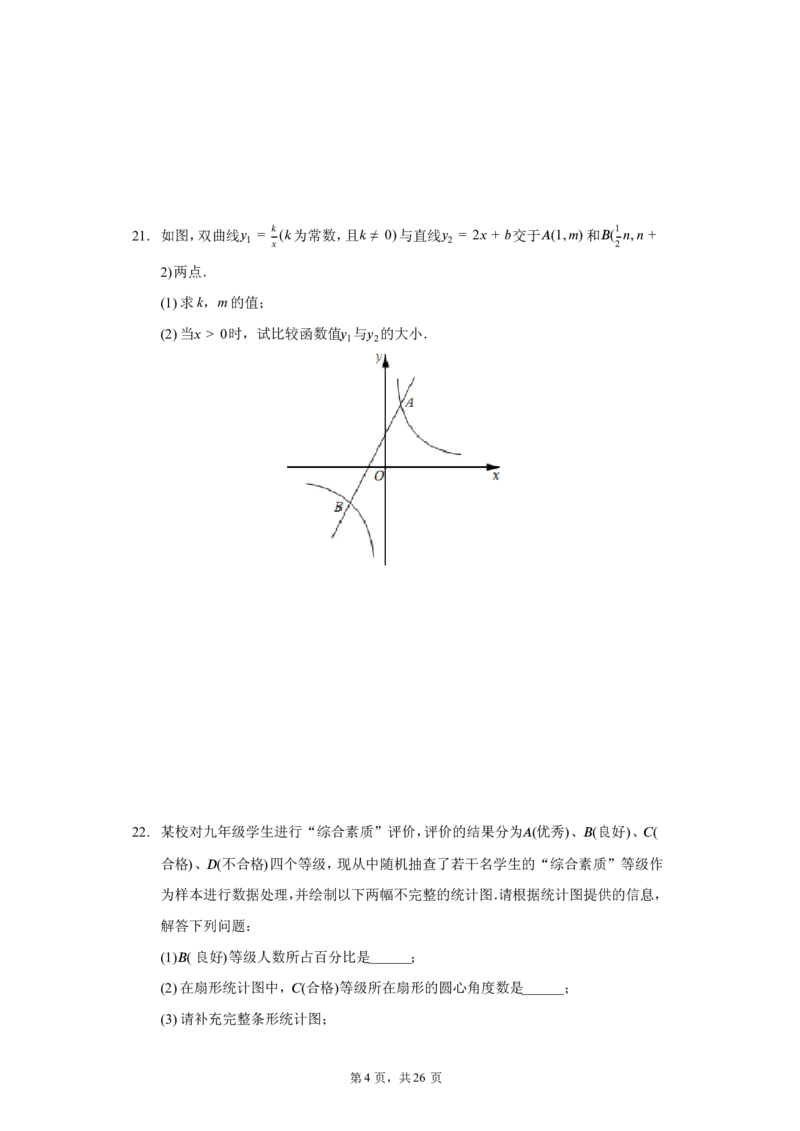
第2 页,共26 页18. 如图,对于抛物线 (cid:18) = −(cid:1) 2 + (cid:1)+ 1, (cid:18) = −(cid:1) 2 + 2(cid:1) +
1 2
1, (cid:18) = −(cid:1) 2 + 3(cid:1) + 1,给出下列结论:
3
①这三条抛物线都经过点 (cid:9)(0,1);②抛物线
(cid:18)
的对称
3
轴可由抛物线 的对称轴向右平移1个单位而得到;③
(cid:18)1
这三条抛物线的顶点在同一条直线上;④这三条抛物
线与直线 (cid:18) = 1的交点中,相邻两点之间的距离相等.其中正确结论的序号是______.
19. (1)计算:|√3 − 2| + (3 − (cid:19))0 − √12 + 6(cid:6)(cid:20)(cid:21)30°;
1 2
(2)先化简再求值 ÷ ,其中 (cid:3) = −5 .
(cid:3)
2−3(cid:3)
(cid:3)
2−9
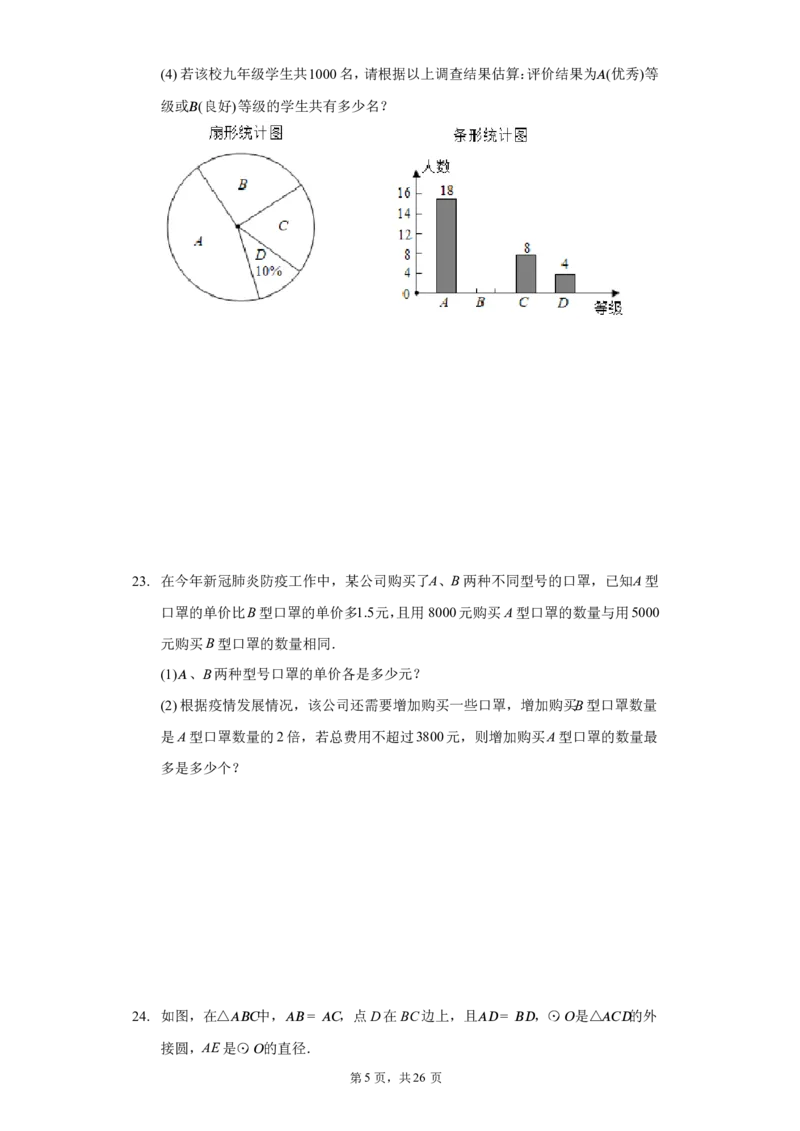
20. 如图,在平面直角坐标系中,已知△ (cid:8)(cid:10)(cid:9) 三个顶点的坐标分别为 (cid:8)(1,4), (cid:10)(4,1),
(cid:9)(4,3).
(1)画出将△
(cid:8)(cid:10)(cid:9)
向左平移5个单位得到的△
(cid:8) (cid:10) (cid:9)
;
1 1 1
(2)画出将△
(cid:8)(cid:10)(cid:9)
绕原点O顺时针旋转90°得到的△
(cid:8) (cid:10) (cid:9)
.
2 2 2
第3 页,共26 页21. 如图,双曲线 (cid:18) = (cid:22)((cid:22) 为常数,且 (cid:22) ≠ 0)与直线 (cid:18) = 2(cid:1) + (cid:5) 交于 (cid:8)(1,(cid:3))和 (cid:10)( 1 (cid:2),(cid:2) +
1 (cid:1) 2 2
2)两点.
(1)求k,m的值;
(2)当 (cid:1) > 0时,试比较函数值 (cid:18)1 与 (cid:18)2 的大小.
22. 某校对九年级学生进行“综合素质”评价,评价的结果分为 (cid:8)(优秀)、 (cid:10)(良好)、 (cid:9)(
合格)、 (cid:12)(不合格)四个等级,现从中随机抽查了若干名学生的“综合素质”等级作
为样本进行数据处理,并绘制以下两幅不完整的统计图.请根据统计图提供的信息,
解答下列问题:
(1)(cid:10)(良好)等级人数所占百分比是______;
(2)在扇形统计图中, (cid:9)(合格)等级所在扇形的圆心角度数是______;
(3)请补充完整条形统计图;
第4 页,共26 页(4)若该校九年级学生共1000名,请根据以上调查结果估算:评价结果为 (cid:8)(优秀)等
级或 (cid:10)(良好)等级的学生共有多少名?
23. 在今年新冠肺炎防疫工作中,某公司购买了A、B两种不同型号的口罩,已知A型
口罩的单价比B型口罩的单价多1.5元,且用 8000元购买 A型口罩的数量与用5000
元购买B型口罩的数量相同.
(1)(cid:8) 、B两种型号口罩的单价各是多少元?
(2)根据疫情发展情况,该公司还需要增加购买一些口罩,增加购买B型口罩数量
是A型口罩数量的2倍,若总费用不超过3800元,则增加购买A型口罩的数量最
多是多少个?
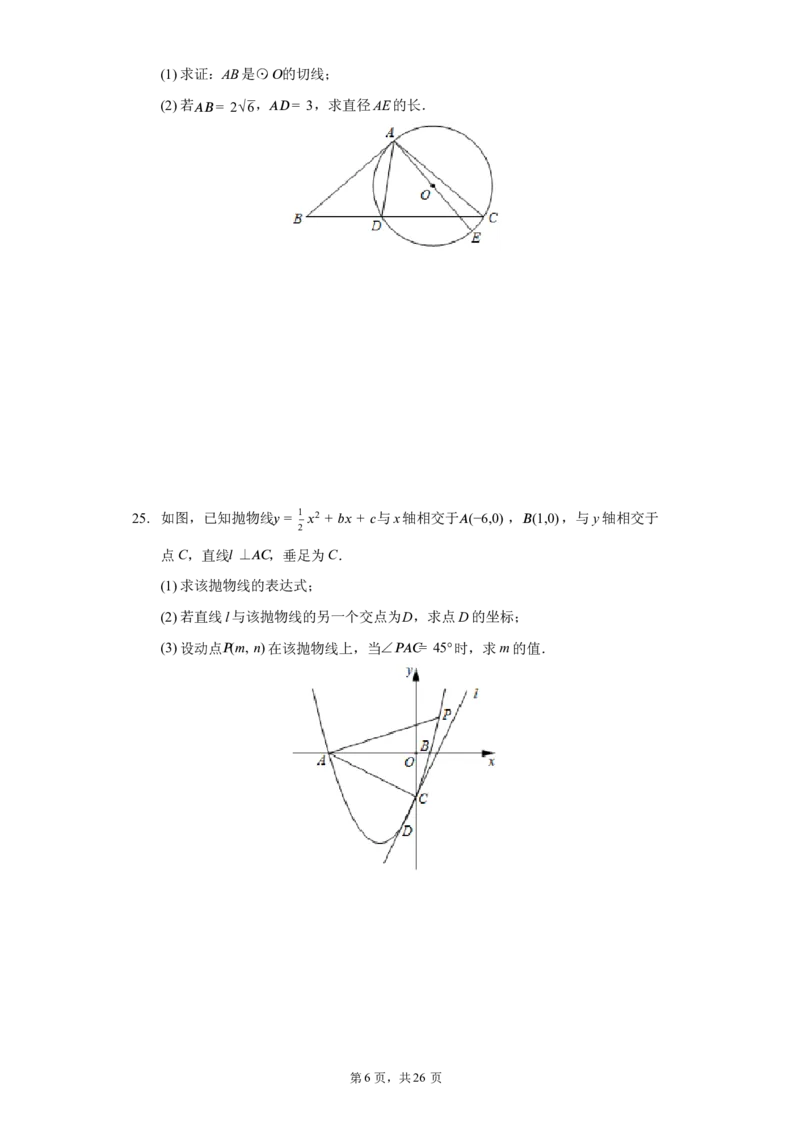
24. 如图,在△ (cid:8)(cid:10)(cid:9) 中, (cid:8)(cid:10)= (cid:8)(cid:9) ,点 D在 BC边上,且 (cid:8)(cid:12)= (cid:10)(cid:12) ,⊙ (cid:7) 是△ (cid:8)(cid:9)(cid:12) 的外
接圆,AE是⊙ 的直径.
(cid:7)
第5 页,共26 页(1)求证:AB是⊙
(cid:7)
的切线;
(2)若 (cid:8)(cid:10)= 2√6, (cid:8)(cid:12)= 3,求直径AE的长.
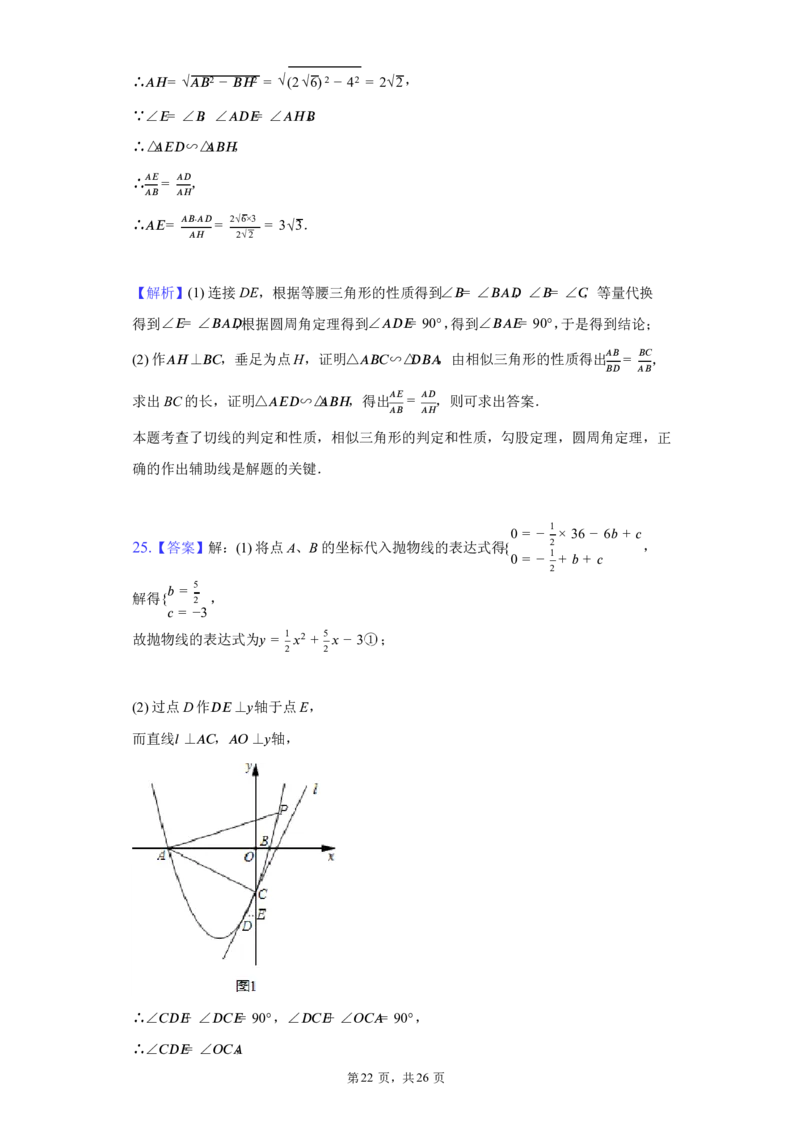
25. 如图,已知抛物线 (cid:18) = 1 (cid:1) 2 + (cid:5)(cid:1) + (cid:6) 与x轴相交于 (cid:8)(−6,0) , (cid:10)(1,0),与 y轴相交于
2
点 C,直线
(cid:23)
⊥
(cid:8)(cid:9)
,垂足为C.
(1)求该抛物线的表达式;
(2)若直线l与该抛物线的另一个交点为D,求点D的坐标;
(3)设动点 (cid:14)((cid:3), (cid:2))在该抛物线上,当∠ (cid:14)(cid:8)(cid:9)= 45°时,求m的值.
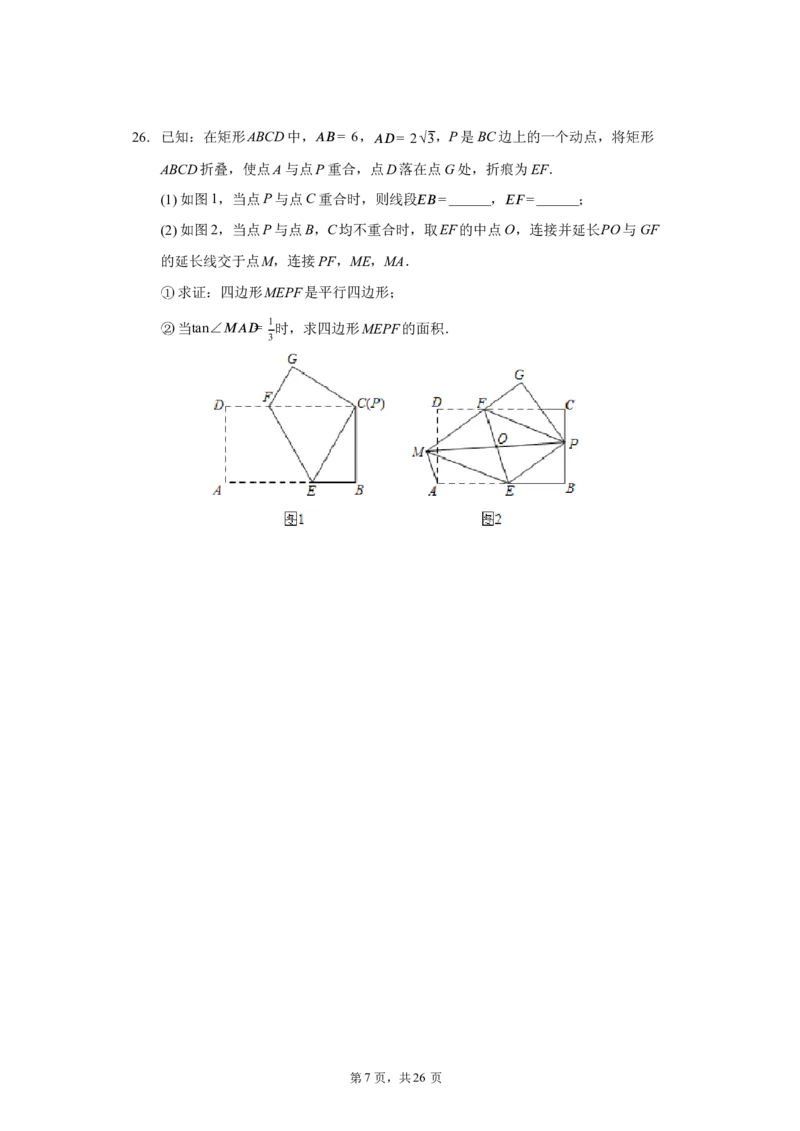
第6 页,共26 页26. 已知:在矩形ABCD中, (cid:8)(cid:10)= 6, (cid:8)(cid:12)= 2√3,P是 BC边上的一个动点,将矩形
ABCD折叠,使点A与点P重合,点D落在点G处,折痕为EF.
(1)如图1,当点P与点C重合时,则线段 (cid:15)(cid:10)=______, (cid:15)(cid:16)=______;
(2)如图2,当点P与点B,C均不重合时,取EF的中点O,连接并延长PO与 GF
的延长线交于点M,连接PF,ME,MA.
①求证:四边形MEPF是平行四边形;
②当tan∠ (cid:13)(cid:8)(cid:12)= 1 时,求四边形MEPF的面积.
3
第7 页,共26 页答案和解析
1.【答案】C
【解析】解:−2的相反数是2,
故选:C.
根据只有符号不同的两个数互为相反数,可得答案.
本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.
2.【答案】B
【解析】解:∵式子√(cid:1)+ 1在实数范围内有意义,
∴ (cid:1)+ 1 ≥ 0,
解得: (cid:1) ≥ −1 ,
故选:B.
根据二次根式有意义的条件得出不等式,求出不等式的解集即可.
本题考查了二次根式有意义的条件和解一元一次不等式,能根据二次根式有意义的条件
得出不等式是解此题的关键,注意:√(cid:4) 中 (cid:4) ≥ 0.
3.【答案】C
【解析】解:0.2(cid:2)(cid:3) = 0.2 × 10−9 (cid:3) = 2 × 10−10 (cid:3).
故选:C.
绝对值小于1的正数也可以利用科学记数法表示,一般形式为 (cid:4) × 10−(cid:2) ,与较大数的科
学记数法不同的是其所使用的是负整数指数幂,指数 n由原数左边起第一个不为零的数
字前面的0的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为 (cid:4) × 10−(cid:2) ,其中1 ≤ |(cid:4)| < 10,n 为由
原数左边起第一个不为零的数字前面的0的个数所决定.
4.【答案】D
【解析】解:从小到大排列此数据为:0,1,2,5,6,6,8数据,6 出现了2次最多
为众数,
第8 页,共26 页处在中间位置的数为5,故中位数为5.
所以本题这组数据的中位数是5,众数是6.
故选:D.
找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为
中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
本题主要考查众数与中位数的定义,中位数是将一组数据从小到大(或从大到小)重新排
列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数
的概念掌握得不好,不把数据按要求重新排列,就会出错.一组数据中出现次数最多的
数据叫做众数.
5.【答案】C
【解析】解:A、2a与 3b不是同类项,所以不能合并,故本选项不合题意;
B、5(cid:4) 2与−3(cid:4) 不是同类项,所以不能合并,故本选项不合题意;
C、((cid:4)(cid:5) 3)2 = (cid:4) 2 (cid:5) 6,故本选项符合题意;
D、((cid:4) + 2)2 = (cid:4) 2 + 4(cid:4) + 4,故本选项不合题意;
故选:C.
分别根据合并同类项法则,幂的乘方与积的乘方运算法则以及完全平方公式逐一判断即
可.
本题主要考查了合并同类项,幂的乘方与积的乘方以及完全平方公式,熟记相关运算法
则是解答本题的关键.
6.【答案】B
【解析】解:∵△=(−1) 2 − 4 × 1 × (−3) = 13 > 0,
∴该方程有两个不相等的实数根.
故选:B.
根据方程的系数结合根的判别式,可得出△=13 > 0,进而可找出该方程有两个不相等
的实数根.
本题考查了根的判别式,牢记“当△>0时,方程有两个不相等的实数根”是解题的关
键.
第9 页,共26 页7.【答案】D
【解析】解:A、由 (cid:4) < (cid:5) , (cid:6) < 0得到: (cid:4) + (cid:6) < (cid:5) + (cid:6) ,原变形正确,故此选项不符合
题意;
B、由 (cid:4) < (cid:5) , (cid:6) < 0得到: (cid:4)(cid:6) > (cid:5)(cid:6) ,原变形正确,故此选项不符合题意;
C、由 (cid:4) < (cid:5) , (cid:6) < 0得到: (cid:4)(cid:6) + 1 > (cid:5)(cid:6) + 1,原变形正确,故此选项不符合题意;
D、由 (cid:4) < (cid:5) , (cid:6) < 0得到: (cid:4)(cid:6) 2 < (cid:5)(cid:6) 2,原变形错误,故此选项符合题意.
故选:D.
根据不等式的性质解答即可.
本题考查了不等式的性质,解题的关键是明确不等式的性质是不等式变形的主要依
据.要认真弄清不等式的性质与等式的性质的异同,特别是在不等式两边同乘以(或除
以)同一个数时,不仅要考虑这个数是否等于0,而且必须先确定这个数是正数还是负数,
如果是负数,不等号的方向必须改变.
8.【答案】B
【解析】解:A、√4 = 2的算术平方根是√2,原命题是假命题,不符合题意;
B、数据2,0,3,2,3的方差= 1 [2 × (2 − 2)2 + (0 − 2)2 + 2 × (3 − 2)2]= 6 ,是真命
5 5
题,符合题意;
C、正六边形的内角和为720°,原命题是假命题,不符合题意;
D、对角线互相平分且垂直的四边形是菱形,原命题是假命题,不符合题意;
故选:B.
根据算术平方根、方差、正多边形以及菱形的判定判断即可.
本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真
即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只
需举出一个反例即可.
9.【答案】A
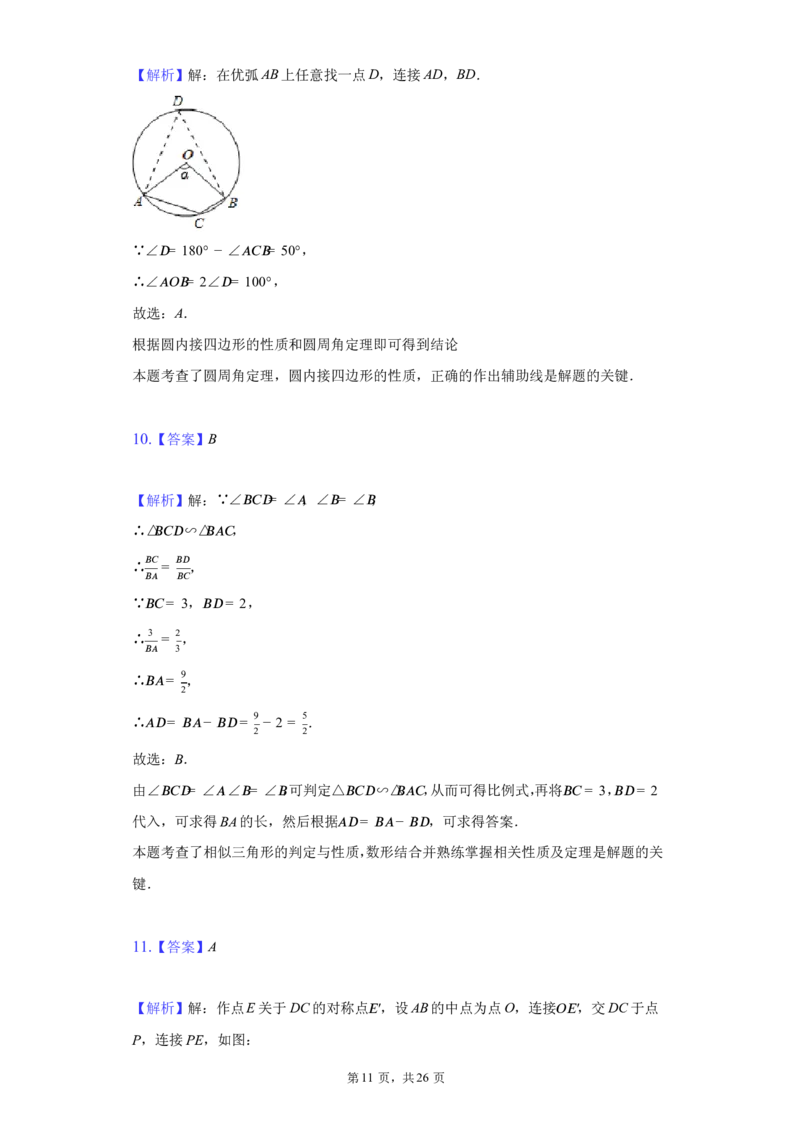
第10 页,共26 页【解析】解:在优弧AB上任意找一点D,连接AD,BD.
∵∠ (cid:12)= 180° − ∠ (cid:8)(cid:9)(cid:10)= 50°,
∴∠ (cid:8)(cid:7)(cid:10)= 2∠ (cid:12)= 100°,
故选:A.
根据圆内接四边形的性质和圆周角定理即可得到结论
本题考查了圆周角定理,圆内接四边形的性质,正确的作出辅助线是解题的关键.
10.【答案】B
【解析】解:∵∠ (cid:10)(cid:9)(cid:12)= ∠ (cid:8) ,∠ (cid:10)= ∠ (cid:10) ,
∴△ ∽△ ,
(cid:10)(cid:9)(cid:12) (cid:10)(cid:8)(cid:9)
∴(cid:10)(cid:9) = (cid:10)(cid:12),
(cid:10)(cid:8) (cid:10)(cid:9)
∵ (cid:10)(cid:9)= 3, (cid:10)(cid:12)= 2,
∴3
=
2
,
(cid:10)(cid:8) 3
∴ (cid:10)(cid:8)= 9 ,
2
∴ (cid:8)(cid:12)= (cid:10)(cid:8)− (cid:10)(cid:12)= 9 − 2 = 5 .
2 2
故选:B.
由∠ (cid:10)(cid:9)(cid:12)= ∠ (cid:8) ,∠ (cid:10)= ∠ (cid:10) ,可判定△ (cid:10)(cid:9)(cid:12) ∽△ (cid:10)(cid:8)(cid:9) ,从而可得比例式,再将 (cid:10)(cid:9)= 3, (cid:10)(cid:12)= 2
代入,可求得BA的长,然后根据 (cid:8)(cid:12)= (cid:10)(cid:8)− (cid:10)(cid:12) ,可求得答案.
本题考查了相似三角形的判定与性质,数形结合并熟练掌握相关性质及定理是解题的关
键.
11.【答案】A
【解析】解:作点E关于 DC的对称点 (cid:15)′,设AB的中点为点O,连接 (cid:7)(cid:15)′,交DC于点
P,连接PE,如图:
第11 页,共26 页∵动点 M在边长为2的正方形ABCD内,且 ⊥ ,
(cid:8)(cid:13) (cid:10)(cid:13)
1
∴点 M在以 AB为直径的圆上, (cid:7)(cid:13)= (cid:8)(cid:10)= 1,
2
∵正方形 ABCD的边长为2,
∴ (cid:8)(cid:12)= (cid:8)(cid:10)= 2,∠ (cid:12)(cid:8)(cid:10)= 90°,
∵
(cid:15)
是 AD的中点,
∴ (cid:12)(cid:15)= 1 (cid:8)(cid:12)= 1 × 2 = 1,
2 2
∵点 E与点 (cid:15)′关于 DC对称,
∴ (cid:12)(cid:15)′= (cid:12)(cid:15)= 1, (cid:14)(cid:15) = (cid:14)(cid:15)′,
∴ (cid:8)(cid:15)′= (cid:8)(cid:12)+ (cid:12)(cid:15)′= 2 + 1 = 3,
在 (cid:24)(cid:25) △ (cid:8)(cid:7)(cid:15)′中, (cid:7)(cid:15)′= √(cid:8)(cid:15)′2 + (cid:8)(cid:7) 2 = √32 + 12 = √10,
∴线段 (cid:14)(cid:15)+ (cid:14)(cid:13) 的最小值为:
(cid:14)(cid:15)+ (cid:14)(cid:13)
= (cid:14)(cid:15)′+ (cid:14)(cid:13)
= (cid:13)(cid:15) ′
= (cid:7)(cid:15)′− (cid:7)(cid:13)
= √10 − 1.
故选:A.
作点 E关于DC的对称点 (cid:15)′,设AB的中点为点O,连接 (cid:7)(cid:15)′,交DC于点 P,连接 PE,
由轴对称的性质及90°的圆周角所对的弦是直径,可知线段 (cid:14)(cid:15)+ (cid:14)(cid:13) 的最小值为 (cid:7)(cid:15)′的值
减去以 AB为直径的圆的半径OM,根据正方形的性质及勾股定理计算即可.
本题考查了轴对称−最短路线问题、圆周角定理的推论、正方形的性质及勾股定理等知
识点,数形结合并熟练掌握相关性质及定理是解题的关键.
12.【答案】D
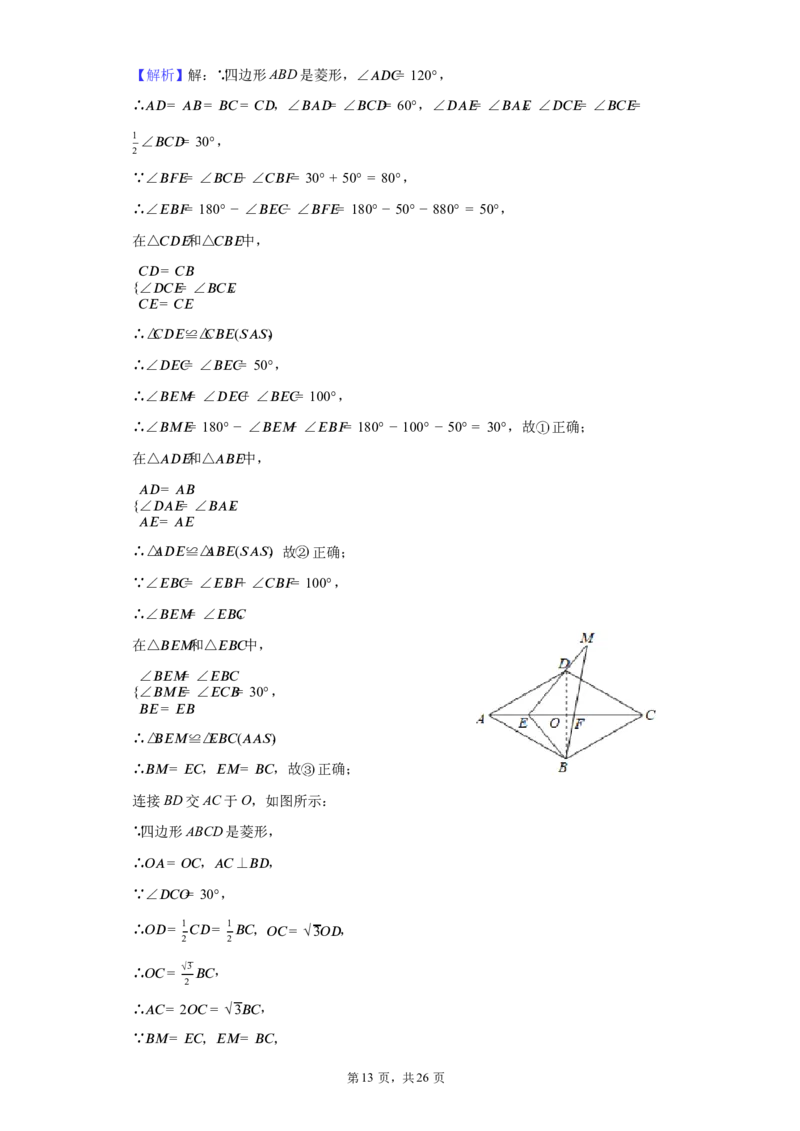
第12 页,共26 页【解析】解:∵四边形ABD是菱形,∠ (cid:8)(cid:12)(cid:9)= 120°,
∴ (cid:8)(cid:12)= (cid:8)(cid:10)= (cid:10)(cid:9)= (cid:9)(cid:12) ,∠ (cid:10)(cid:8)(cid:12)= ∠ (cid:10)(cid:9)(cid:12)= 60°,∠ (cid:12)(cid:8)(cid:15)= ∠ (cid:10)(cid:8)(cid:15) ,∠ (cid:12)(cid:9)(cid:15)= ∠ (cid:10)(cid:9)(cid:15)=
1∠ (cid:10)(cid:9)(cid:12)= 30°,
2
∵∠ (cid:10)(cid:16)(cid:15)= ∠ (cid:10)(cid:9)(cid:15)+ ∠ (cid:9)(cid:10)(cid:16)= 30° + 50° = 80°,
∴∠ (cid:15)(cid:10)(cid:16)= 180° − ∠ (cid:10)(cid:15)(cid:9)− ∠ (cid:10)(cid:16)(cid:15)= 180° − 50° − 880° = 50°,
在△ 和△ 中,
(cid:9)(cid:12)(cid:15) (cid:9)(cid:10)(cid:15)
(cid:9)(cid:12)= (cid:9)(cid:10)
{∠ (cid:12)(cid:9)(cid:15)= ∠ (cid:10)(cid:9)(cid:15) ,
(cid:9)(cid:15)= (cid:9)(cid:15)
∴△ (cid:9)(cid:12)(cid:15) ≌△ (cid:9)(cid:10)(cid:15)((cid:26)(cid:8)(cid:26) ,)
∴∠ (cid:12)(cid:15)(cid:9)= ∠ (cid:10)(cid:15)(cid:9)= 50°,
∴∠ (cid:10)(cid:15)(cid:13)= ∠ (cid:12)(cid:15)(cid:9)+ ∠ (cid:10)(cid:15)(cid:9)= 100°,
∴∠ (cid:10)(cid:13)(cid:15)= 180° − ∠ (cid:10)(cid:15)(cid:13)− ∠ (cid:15)(cid:10)(cid:16)= 180° − 100° − 50° = 30°,故①正确;
在△ 和△ 中,
(cid:8)(cid:12)(cid:15) (cid:8)(cid:10)(cid:15)
(cid:8)(cid:12)= (cid:8)(cid:10)
{∠ (cid:12)(cid:8)(cid:15)= ∠ (cid:10)(cid:8)(cid:15) ,
(cid:8)(cid:15)= (cid:8)(cid:15)
∴△ (cid:8)(cid:12)(cid:15) ≌△ (cid:8)(cid:10)(cid:15)((cid:26)(cid:8)(cid:26) ,) 故②正确;
∵∠ (cid:15)(cid:10)(cid:9)= ∠ (cid:15)(cid:10)(cid:16)+ ∠ (cid:9)(cid:10)(cid:16)= 100°,
∴∠ (cid:10)(cid:15)(cid:13)= ∠ (cid:15)(cid:10)(cid:9) ,
在△ 和△ 中,
(cid:10)(cid:15)(cid:13) (cid:15)(cid:10)(cid:9)
∠ (cid:10)(cid:15)(cid:13)= ∠ (cid:15)(cid:10)(cid:9)
{∠ (cid:10)(cid:13)(cid:15)= ∠ (cid:15)(cid:9)(cid:10)= 30°,
(cid:10)(cid:15)= (cid:15)(cid:10)
∴△
(cid:10)(cid:15)(cid:13)
≌△ (cid:15)(cid:10)(cid:9)((cid:8)(cid:8)(cid:26)),
∴ (cid:10)(cid:13)= (cid:15)(cid:9) , (cid:15)(cid:13)= (cid:10)(cid:9) ,故③正确;
连接 BD交 AC于 O,如图所示:
∵四边形 ABCD是菱形,
∴ (cid:7)(cid:8)= (cid:7)(cid:9) , (cid:8)(cid:9) ⊥ (cid:10)(cid:12) ,
∵∠ (cid:12)(cid:9)(cid:7)= 30°,
∴ (cid:7)(cid:12)= 1 (cid:9)(cid:12)= 1 (cid:10)(cid:9) , (cid:7)(cid:9)= √3(cid:7)(cid:12) ,
2 2
∴ (cid:7)(cid:9)= √3 (cid:10)(cid:9) ,
2
∴ (cid:8)(cid:9)= 2(cid:7)(cid:9)= √3(cid:10)(cid:9) ,
∵ (cid:10)(cid:13)= (cid:15)(cid:9) , (cid:15)(cid:13)= (cid:10)(cid:9) ,
第13 页,共26 页∴ (cid:8)(cid:15)+ (cid:10)(cid:13)= (cid:8)(cid:15)+ (cid:15)(cid:9)= (cid:8)(cid:9)= √3(cid:10)(cid:9) = √3(cid:15)(cid:13) ,故④正确,
正确结论的个数是4个,
故选:D.
先由菱形的性质得 (cid:8)(cid:12)= (cid:8)(cid:10)= (cid:10)(cid:9)= (cid:9)(cid:12) ,∠ (cid:10)(cid:8)(cid:12)= ∠ (cid:10)(cid:9)(cid:12)= 60°,∠ (cid:12)(cid:8)(cid:15)= ∠ (cid:10)(cid:8)(cid:15) ,
∠ (cid:12)(cid:9)(cid:15)= ∠ (cid:10)(cid:9)(cid:15)= 30°,再由三角形的外角性质得∠ (cid:10)(cid:16)(cid:15)= 80°,则∠ (cid:15)(cid:10)(cid:16)= 50°,然后证
△ (cid:9)(cid:12)(cid:15) ≌△ (cid:9)(cid:10)(cid:15)((cid:26)(cid:8)(cid:26) ,) 得∠ (cid:12)(cid:15)(cid:9)= ∠ (cid:10)(cid:15)(cid:9)= 50°,进而得出①正确;由SAS证△ (cid:8)(cid:12)(cid:15) ≌△
(cid:8)(cid:10)(cid:15) ,得②正确;证出△ (cid:10)(cid:15)(cid:13) ≌△ (cid:15)(cid:10)(cid:9)((cid:8)(cid:8)(cid:26) ,) 得 (cid:10)(cid:13)= (cid:15)(cid:9) , (cid:15)(cid:13)= (cid:10)(cid:9) ,③正确;连接
1 1
BD交AC于O,由菱形的性质得 (cid:8)(cid:9) ⊥ (cid:10)(cid:12) ,再由直角三角形的性质得 (cid:7)(cid:12)= (cid:9)(cid:12)= (cid:10)(cid:9) ,
2 2
(cid:7)(cid:9)= √3(cid:7)(cid:12) ,则 (cid:7)(cid:9)= √3 (cid:10)(cid:9) ,进而得出④正确即可.
2
本题考查了菱形的性质、全等三角形的判定与性质、直角三角形的性质等知识;熟练掌
握菱形的性质,证明三角形全等是解题的关键.
13.【答案】−4
【解析】解:3 − 7 = 3 + (−7) = −4 .
故答案为:−4 .
减去一个数,等于加上这个数的相反数,据此计算即可.
本题主要考查了有理数的减法,熟记运算法则是解答本题的关键.
14.【答案】 (cid:4)((cid:1) − 1)2
【解析】解: (cid:4)(cid:1) 2 − 2(cid:4)(cid:1) + (cid:4)
= (cid:4)((cid:1) 2 − 2(cid:1) + 1)
= (cid:4)((cid:1) − 1)2.
故答案为: (cid:4)((cid:1) − 1)2.
直接提取公因式a,再利用完全平方公式分解因式.
此题主要考查了提取公因式法、公式法分解因式,正确运用乘法公式是解题关键.
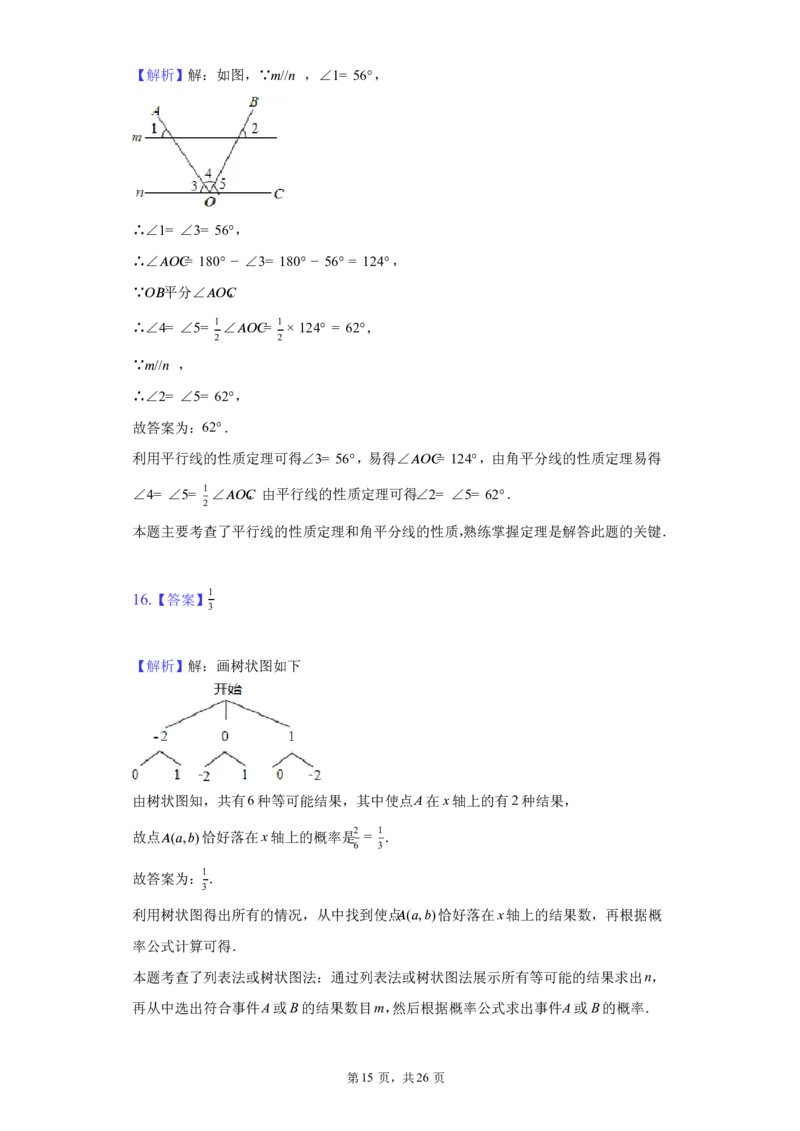
15.【答案】62°
第14 页,共26 页【解析】解:如图,∵ (cid:3)//(cid:2) ,∠1= 56°,
∴∠1= ∠3= 56°,
∴∠ (cid:8)(cid:7)(cid:9)= 180° − ∠3= 180° − 56° = 124°,
∵ 平分∠ ,
(cid:7)(cid:10) (cid:8)(cid:7)(cid:9)
∴∠4= ∠5= 1∠ (cid:8)(cid:7)(cid:9)= 1 × 124° = 62°,
2 2
∵ (cid:3)//(cid:2) ,
∴∠2= ∠5= 62°,
故答案为:62°.
利用平行线的性质定理可得∠3= 56°,易得∠ (cid:8)(cid:7)(cid:9)= 124°,由角平分线的性质定理易得
∠4= ∠5= 1∠
(cid:8)(cid:7)(cid:9)
,由平行线的性质定理可得∠2= ∠5= 62°.
2
本题主要考查了平行线的性质定理和角平分线的性质,熟练掌握定理是解答此题的关键.
1
16.【答案】
3
【解析】解:画树状图如下
由树状图知,共有6种等可能结果,其中使点A在 x轴上的有2种结果,
2 1
故点 (cid:8)((cid:4),(cid:5))恰好落在x轴上的概率是 = .
6 3
1
故答案为: .
3
利用树状图得出所有的情况,从中找到使点 (cid:8)((cid:4),(cid:5))恰好落在x轴上的结果数,再根据概
率公式计算可得.
本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,
再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或 B的概率.
第15 页,共26 页2
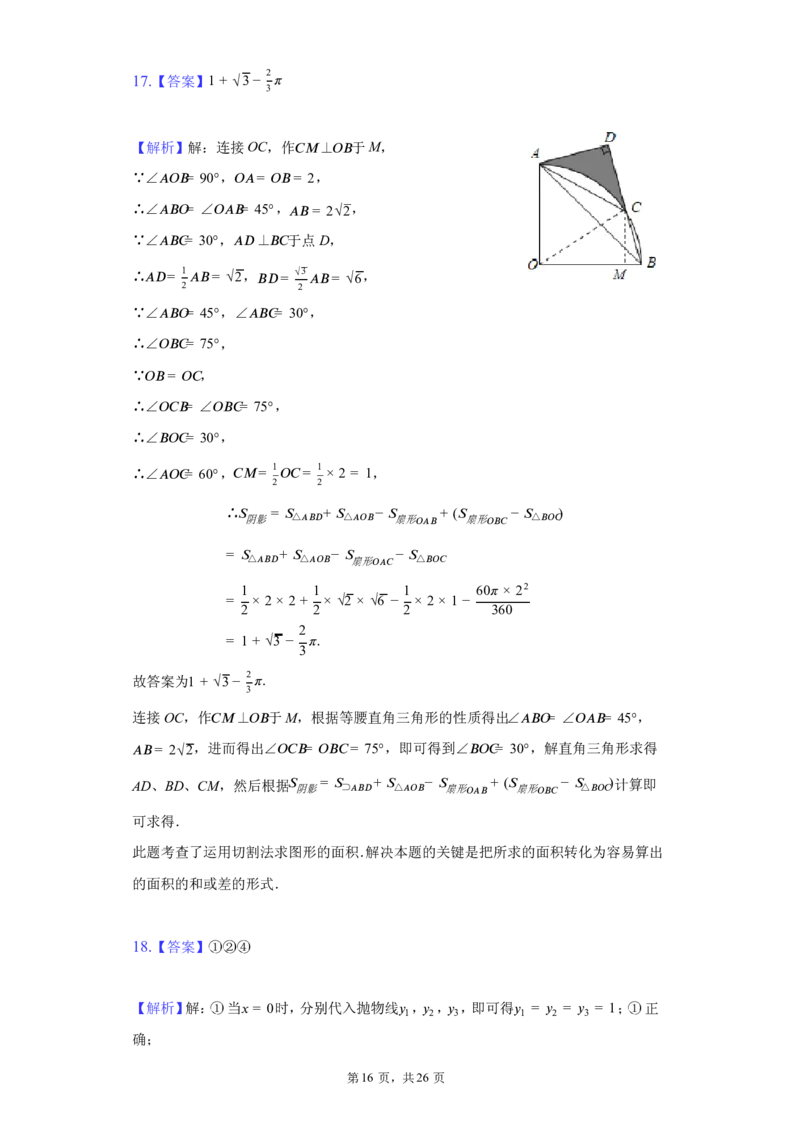
17.【答案】1 + √3 − (cid:19)
3
【解析】解:连接OC,作 ⊥ 于 M,
(cid:9)(cid:13) (cid:7)(cid:10)
∵∠ (cid:8)(cid:7)(cid:10)= 90°, (cid:7)(cid:8)= (cid:7)(cid:10)= 2,
∴∠ (cid:8)(cid:10)(cid:7)= ∠ (cid:7)(cid:8)(cid:10)= 45°, (cid:8)(cid:10)= 2√2,
∵∠ (cid:8)(cid:10)(cid:9)= 30°, (cid:8)(cid:12) ⊥ (cid:10)(cid:9) 于点 D,
∴ (cid:8)(cid:12)= 1 (cid:8)(cid:10)= √2, (cid:10)(cid:12)= √3 (cid:8)(cid:10)= √6,
2 2
∵∠ (cid:8)(cid:10)(cid:7)= 45°,∠ (cid:8)(cid:10)(cid:9)= 30°,
∴∠ (cid:7)(cid:10)(cid:9)= 75°,
∵ (cid:7)(cid:10)= (cid:7)(cid:9) ,
∴∠ (cid:7)(cid:9)(cid:10)= ∠ (cid:7)(cid:10)(cid:9)= 75°,
∴∠ (cid:10)(cid:7)(cid:9)= 30°,
1 1
∴∠ (cid:8)(cid:7)(cid:9)= 60°, (cid:9)(cid:13)= (cid:7)(cid:9)= × 2 = 1,
2 2
∴ (cid:26)
阴影
= (cid:26)△(cid:8)(cid:10)(cid:12) + (cid:26)△(cid:8)(cid:7)(cid:10) − (cid:26)
扇形
(cid:7)(cid:8)(cid:10)
+ ((cid:26)
扇形
(cid:7)(cid:10)(cid:9)
− (cid:26)△(cid:10)(cid:7)(cid:9) )
= (cid:26)△(cid:8)(cid:10)(cid:12) + (cid:26)△(cid:8)(cid:7)(cid:10) − (cid:26)
扇形
(cid:7)(cid:8)(cid:9)
− (cid:26)△(cid:10)(cid:7)(cid:9)
1 1 1 60(cid:19) × 22
= × 2 × 2 + × √2 × √6 − × 2 × 1 −
2 2 2 360
2
= 1 + √3 − (cid:19).
3
2
故答案为1 + √3 − (cid:19).
3
连接 OC,作 (cid:9)(cid:13) ⊥ (cid:7)(cid:10) 于 M,根据等腰直角三角形的性质得出∠ (cid:8)(cid:10)(cid:7)= ∠ (cid:7)(cid:8)(cid:10)= 45°,
(cid:8)(cid:10)= 2√2,进而得出∠ (cid:7)(cid:9)(cid:10)= (cid:7)(cid:10)(cid:9)= 75°,即可得到∠ (cid:10)(cid:7)(cid:9)= 30°,解直角三角形求得
AD、BD、CM,然后根据(cid:26)
阴影
= (cid:26)
⊃(cid:8)(cid:10)(cid:12)
+ (cid:26)△(cid:8)(cid:7)(cid:10) − (cid:26)
扇形
(cid:7)(cid:8)(cid:10)
+ ((cid:26)
扇形
(cid:7)(cid:10)(cid:9)
− (cid:26)△(cid:10)(cid:7)(cid:9) )计算即
可求得.
此题考查了运用切割法求图形的面积.解决本题的关键是把所求的面积转化为容易算出
的面积的和或差的形式.
18.【答案】①②④
【解析】解:①当 (cid:1) = 0时,分别代入抛物线 (cid:18)1 , (cid:18)2 , (cid:18)3 ,即可得 (cid:18)1 = (cid:18) 2 = (cid:18) 3 = 1;①正
确;
第16 页,共26 页1 3
② (cid:18)1 = −(cid:1) 2 + (cid:1)+ 1, (cid:18) 3 = −(cid:1) 2 + 3(cid:1) + 1的对称轴分别为直线 (cid:1) = 2 , (cid:1) = 2 ,
1 3
由 (cid:1) = 向右平移1个单位得到 (cid:1) = ,②正确;
2 2
③ (cid:18) = −(cid:1) 2 + (cid:1)+ 1 = −((cid:1) − 1 )2 + 5 ,顶点坐标( 1 , 5 ),
1
2 4 2 4
(cid:18)2 = −(cid:1) 2 + 2(cid:1) + 1 = −((cid:1) − 1)2 + 2,顶点坐标为(1,2);
(cid:18) = −(cid:1) 2 + 3(cid:1) + 1 = −((cid:1) − 3 )2 + 13 ,顶点坐标为( 3 , 13 ),
3 2 4 2 4
∴顶点不在同一条直线上,③错误;
④当 (cid:18) = 1时,则−(cid:1) 2 + (cid:1)+ 1 = 1,
∴ (cid:1) = 0或 (cid:1) = 1;
−(cid:1) 2 + 2(cid:1) + 1 = 1,
∴ (cid:1) = 0或 (cid:1) = 2;
−(cid:1) 2 + 3(cid:1) + 1 = 1,
∴ (cid:1) = 0或 (cid:1) = 3;
∴相邻两点之间的距离都是1,④正确;
故答案为①②④ .
①当 (cid:1) = 0时,分别代入抛物线 (cid:18) 1 , (cid:18)2 , (cid:18)3 ,得 (cid:18)1 = (cid:18) 2 = (cid:18) 3 = 1,即可判断;
② (cid:18)
1
= −(cid:1) 2 + (cid:1)+ 1, (cid:18)3 = −(cid:1) 2 + 3(cid:1) + 1的对称轴分别为直线 (cid:1) = 1
2
, (cid:1) = 3
2
,即可判断;
③求得顶点坐标即可判断;
④当 (cid:18) = 1时,则−(cid:1) 2 − (cid:1) + 1 = 1,可得 (cid:1) = 0或 (cid:1) = −1 ;−(cid:1) 2 − 2(cid:1) + 1 = 1,可得 (cid:1) = 0
或 (cid:1) = −2 ;−(cid:1) 2 − 3(cid:1) + 1 = 1,可得 (cid:1) = 0或 (cid:1) = −3,即可判断,
本题考查了二次函数的图象与几何变换,二次函数图象上点的坐标特征,二次函数的性
质,熟练掌握二次函数的性质是解题的关键.
19.【答案】解:(1)原式= 2 − √3 + 1 − 2√3 + 6 × √3
2
= 2 − √3 + 1 − 2√3 + 3√3
= 3;
1 2
(2) ÷
(cid:3)2 − 3(cid:3) (cid:3)2 − 9
1 ((cid:3) + 3)((cid:3) − 3)
= ·
(cid:3)((cid:3) − 3) 2
=
(cid:3)+3
,
2(cid:3)
第17 页,共26 页−5+3 1
当 (cid:3) = −5 时,原式= = .
2×(−5) 5
【解析】(1)先根据绝对值,零指数幂,算术平方根,特殊角的三角函数值进行计算,
再求出答案即可;
(2)把除法变成乘法,算乘法,再求出答案即可.
本题考查了绝对值,零指数幂,算术平方根,特殊角的三角函数值,实数的混合运算和
分式的混合运算与求值等知识点,能求出每一部分的值是解(1)的关键,能根据分式的
乘法和除法法则进行化简是解(2)的关键.
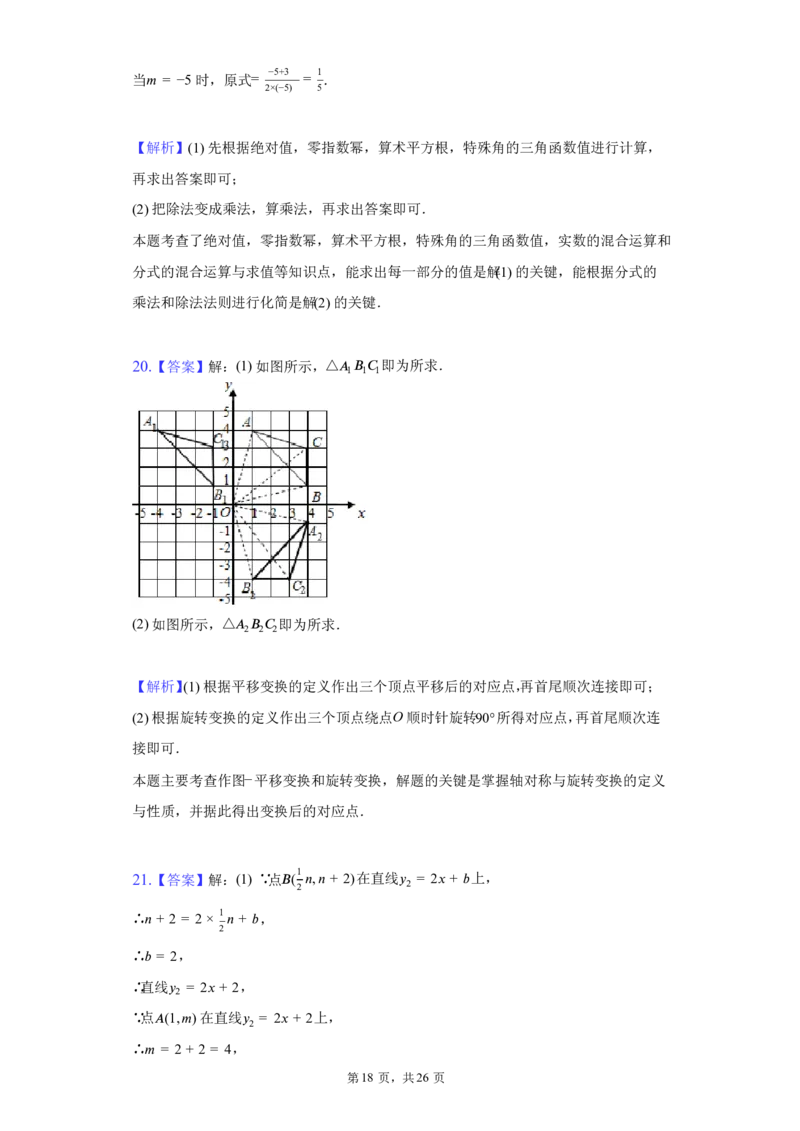
20.【答案】解:(1)如图所示,△
(cid:8)1 (cid:10) 1 (cid:9) 1
即为所求.
(2)如图所示,△
(cid:8) (cid:10) (cid:9)
即为所求.
2 2 2
【解析】(1)根据平移变换的定义作出三个顶点平移后的对应点,再首尾顺次连接即可;
(2)根据旋转变换的定义作出三个顶点绕点O顺时针旋转90°所得对应点,再首尾顺次连
接即可.
本题主要考查作图−平移变换和旋转变换,解题的关键是掌握轴对称与旋转变换的定义
与性质,并据此得出变换后的对应点.
21.【答案】解:(1) ∵点 (cid:10)( 1
2
(cid:2),(cid:2) + 2)在直线 (cid:18)
2
= 2(cid:1) + (cid:5) 上,
∴ (cid:2) + 2 = 2 × 1 (cid:2) + (cid:5) ,
2
∴ (cid:5) = 2,
∴直线 (cid:18)2 = 2(cid:1) + 2,
∵点 (cid:8)(1,(cid:3))在直线 (cid:18) = 2(cid:1) + 2上,
2
∴ (cid:3) = 2 + 2 = 4,
第18 页,共26 页∴ (cid:8)(1,4),
∵双曲线 (cid:18)1 = (cid:22) ((cid:22) 为常数,且 (cid:22) ≠ 0)与直线 (cid:18)
2
= 2(cid:1) + (cid:5) 交于 (cid:8)(1,4),
(cid:1)
∴ (cid:22) = 1 × 4 = 4;
(2)由图象可知,当0 < (cid:1) < 1时, (cid:18) > (cid:18) ;
1 2
当 (cid:1) = 1时, (cid:18)1 = (cid:18) 2 = 4;
当 (cid:1) < 1时, (cid:18)1 < (cid:18) 2 .
1
【解析】(1)把点 (cid:10)( (cid:2),(cid:2) + 2)代入 (cid:18) = 2(cid:1) + (cid:5) ,即可求得b,再把 (cid:8)(1,(cid:3))代入直线解析
2 2
式即可求得m,然后根据待定系数法即可求得k;
(2)根据图象结合A的坐标即可求得.
本题考查了反比例函数和一次函数的交点问题,以及用待定系数法求反比例函数和一次
函数的解析式,是基础知识要熟练掌握.
22.【答案】25% 72°
【解析】解:(1) ∵被调查的人数为4 ÷ 10% = 40(人),
∴ (cid:10) 等级人数为40 − (18 + 8 + 4) = 10(人),
则 (cid:10)(良好)等级人数所占百分比是 10 × 100% = 25%,
40
故答案为:25%;
(2)在扇形统计图中, (cid:9)(合格)等级所在扇形的圆心角度数是360° × 8 = 72°,
40
故答案为:72°;
(3)补全条形统计图如下:
(4)估计评价结果为 (cid:8)(优秀)等级或 (cid:10)(良好)等级的学生共有1000 × 18+10 = 700(人).
40
(1)先根据D等级人数及其所占百分比求出被调查的总人数,再由四个等级人数之和等
第19 页,共26 页于总人数求出B等级人数,最后用B等级人数除以总人数可得答案;
(2)用360°乘以C等级人数所占比例可得答案;
(3)根据(1)中计算结果可补全条形图;
(4)用总人数乘以样本中A、B等级人数和所占比例即可.
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得
到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,扇形统
计图直接反映部分占总体的百分比大小.
23.【答案】解:(1)设 A型口罩的单价为x元,则B型口罩的单价为((cid:1) − 1.5)元,
8000 5000
根据题意,得: = .
(cid:1) (cid:1)−1.5
解方程,得: (cid:1) = 4.
经检验: (cid:1) = 4是原方程的根,且符合题意.
所以 (cid:1)− 1.5 = 2.5.
答:A型口罩的单价为4元,则B型口罩的单价为2.5元;
(2)设增加购买A型口罩的数量是m个,
根据题意,得:2.5 × 2(cid:3) + 4(cid:3) ≤ 3800.
2
解不等式,得: (cid:3) ≤ 422 .
9
因为 m为正整数,所以正整数m的最大值为422.
答:增加购买A型口罩的数量最多是422个.
【解析】(1)设A型口罩的单价为x元,则 B型口罩的单价为((cid:1) − 1.5)元,根据“用8000
元购买A型口罩的数量与用5000元购买B型口罩的数量相同”列出方程并解答;
(2)设增加购买A型口罩的数量是m个,根据“增加购买B型口罩数量是A型口罩数量
的 2倍,若总费用不超过3800元”列出不等式.
本题主要考查了分式方程的应用和一元一次不等式的应用,分析题意,找到关键描述语,
找到合适的数量关系是解决问题的关键.
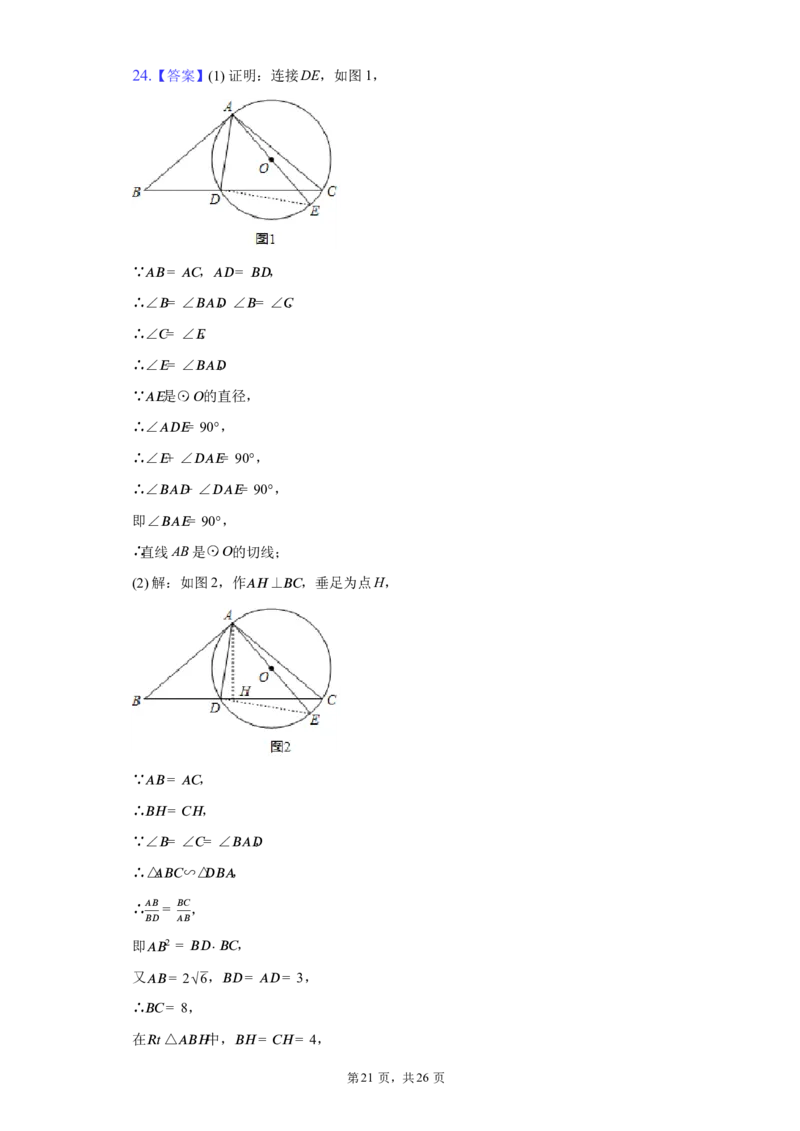
第20 页,共26 页24.【答案】(1)证明:连接DE,如图 1,
∵ (cid:8)(cid:10)= (cid:8)(cid:9) , (cid:8)(cid:12)= (cid:10)(cid:12) ,
∴∠ (cid:10)= ∠ (cid:10)(cid:8)(cid:12) ,∠ (cid:10)= ∠ (cid:9) ,
∴∠ (cid:9)= ∠ (cid:15) ,
∴∠ (cid:15)= ∠ (cid:10)(cid:8)(cid:12) ,
∵ 是⊙ 的直径,
(cid:8)(cid:15) (cid:7)
∴∠ (cid:8)(cid:12)(cid:15)= 90°,
∴∠ (cid:15)+ ∠ (cid:12)(cid:8)(cid:15)= 90°,
∴∠ (cid:10)(cid:8)(cid:12)+ ∠ (cid:12)(cid:8)(cid:15)= 90°,
即∠ (cid:10)(cid:8)(cid:15)= 90°,
∴直线 AB是⊙
(cid:7)
的切线;
(2)解:如图2,作
(cid:8)(cid:27)
⊥
(cid:10)(cid:9)
,垂足为点H,
∵ (cid:8)(cid:10)= (cid:8)(cid:9) ,
∴ (cid:10)(cid:27)= (cid:9)(cid:27) ,
∵∠ (cid:10)= ∠ (cid:9)= ∠ (cid:10)(cid:8)(cid:12) ,
∴△ ∽△ ,
(cid:8)(cid:10)(cid:9) (cid:12)(cid:10)(cid:8)
∴(cid:8)(cid:10) = (cid:10)(cid:9),
(cid:10)(cid:12) (cid:8)(cid:10)
即 (cid:8)(cid:10) 2 = (cid:10)(cid:12)· (cid:10)(cid:9) ,
又 (cid:8)(cid:10)= 2√6, (cid:10)(cid:12)= (cid:8)(cid:12)= 3,
∴ (cid:10)(cid:9)= 8,
在 (cid:24)(cid:25) △ (cid:8)(cid:10)(cid:27) 中, (cid:10)(cid:27)= (cid:9)(cid:27)= 4,
第21 页,共26 页∴ (cid:8)(cid:27)= √(cid:8)(cid:10) 2 − (cid:10)(cid:27) 2 = √(2√6)2 − 42 = 2√2,
∵∠ (cid:15)= ∠ (cid:10) ,∠ (cid:8)(cid:12)(cid:15)= ∠ (cid:8)(cid:27)(cid:10) ,
∴△ ∽△ ,
(cid:8)(cid:15)(cid:12) (cid:8)(cid:10)(cid:27)
∴(cid:8)(cid:15)= (cid:8)(cid:12),
(cid:8)(cid:10) (cid:8)(cid:27)
∴ (cid:8)(cid:15)= (cid:8)(cid:10)·(cid:8)(cid:12)= 2√6×3 = 3√3.
(cid:8)(cid:27) 2√2
【解析】(1)连接 DE,根据等腰三角形的性质得到∠ (cid:10)= ∠ (cid:10)(cid:8)(cid:12) ,∠ (cid:10)= ∠ (cid:9) ,等量代换
得到∠ (cid:15)= ∠ (cid:10)(cid:8)(cid:12) ,根据圆周角定理得到∠ (cid:8)(cid:12)(cid:15)= 90°,得到∠ (cid:10)(cid:8)(cid:15)= 90°,于是得到结论;
(2)作 (cid:8)(cid:27) ⊥ (cid:10)(cid:9) ,垂足为点H,证明△ (cid:8)(cid:10)(cid:9) ∽△ (cid:12)(cid:10)(cid:8) ,由相似三角形的性质得出(cid:8)(cid:10) = (cid:10)(cid:9),
(cid:10)(cid:12) (cid:8)(cid:10)
求出 BC的长,证明△
(cid:8)(cid:15)(cid:12)
∽△
(cid:8)(cid:10)(cid:27)
,得出(cid:8)(cid:15) = (cid:8)(cid:12),则可求出答案.
(cid:8)(cid:10) (cid:8)(cid:27)
本题考查了切线的判定和性质,相似三角形的判定和性质,勾股定理,圆周角定理,正
确的作出辅助线是解题的关键.
1
0 = − × 36 − 6(cid:5) + (cid:6)
25.【答案】解:(1)将点 A、B的坐标代入抛物线的表达式得{ 2 ,
1
0 = − + (cid:5) + (cid:6)
2
5
解得{ (cid:5) =
2
,
(cid:6) = −3
故抛物线的表达式为 (cid:18) = 1 (cid:1) 2 + 5 (cid:1) − 3①;
2 2
(2)过点 D作
(cid:12)(cid:15)
⊥
(cid:18)
轴于点E,
而直线 ⊥ , ⊥ 轴,
(cid:23) (cid:8)(cid:9) (cid:8)(cid:7) (cid:18)
∴∠ (cid:9)(cid:12)(cid:15)+ ∠ (cid:12)(cid:9)(cid:15)= 90°,∠ (cid:12)(cid:9)(cid:15)+ ∠ (cid:7)(cid:9)(cid:8)= 90°,
∴∠ (cid:9)(cid:12)(cid:15)= ∠ (cid:7)(cid:9)(cid:8) ,
第22 页,共26 页∵∠ (cid:8)(cid:7)(cid:9)= ∠ (cid:9)(cid:15)(cid:12)= 90°,
∴△
(cid:9)(cid:15)(cid:12)
∽△
(cid:8)(cid:7)(cid:9)
,则(cid:12)(cid:15)= (cid:9)(cid:15),
(cid:7)(cid:9) (cid:8)(cid:7)
而点 A、C的坐标分别为(−6,0) 、(0,−3) ,则 (cid:8)(cid:7)= 6, (cid:7)(cid:9)= 3,设点 (cid:12)((cid:1), 1 (cid:1) 2 + 5 (cid:1) − 3),
2 2
则 (cid:12)(cid:15)= −(cid:1) , (cid:9)(cid:15)= − 1 (cid:1) 2 − 5 (cid:1) ,
2 2
则−(cid:1) = − 1 2 (cid:1) 2− 5 2 (cid:1),解得 (cid:1) = 0(舍去)或−1 ,
3 6
当 (cid:1) = −1 时, (cid:18) = 1 (cid:1) 2 + 5 (cid:1)− 3 = −5 ,
2 2
故点 D的坐标为(−1, −5) ;
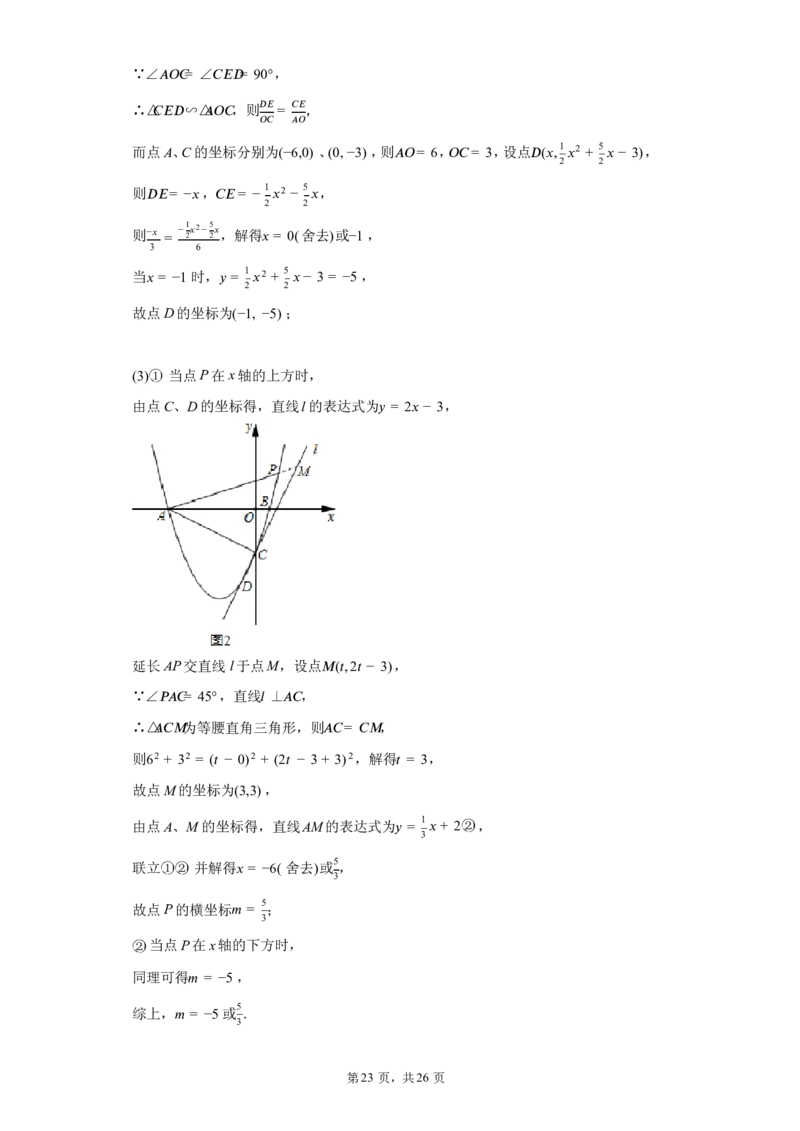
(3)① 当点P在 x轴的上方时,
由点 C、D的坐标得,直线l的表达式为 (cid:18) = 2(cid:1) − 3,
延长 AP交直线 l于点M,设点 (cid:13)((cid:25),2(cid:25) − 3),
∵∠ (cid:14)(cid:8)(cid:9)= 45°,直线 (cid:23) ⊥ (cid:8)(cid:9) ,
∴△ (cid:8)(cid:9)(cid:13) 为等腰直角三角形,则 (cid:8)(cid:9)= (cid:9)(cid:13) ,
则62 + 32 = ((cid:25) − 0)2 + (2(cid:25) − 3 + 3)2,解得 (cid:25) = 3,
故点 M的坐标为(3,3),
由点 A、M的坐标得,直线AM的表达式为 (cid:18) = 1 (cid:1)+ 2②,
3
5
联立①② 并解得 (cid:1) = −6( 舍去)或 ,
3
5
故点 P的横坐标 (cid:3) = ;
3
②当点 P在 x轴的下方时,
同理可得 (cid:3) = −5 ,
5
综上, (cid:3) = −5 或 .
3
第23 页,共26 页【解析】(1)用待定系数法即可求解;
(2)证明△
(cid:9)(cid:15)(cid:12)
∽△
(cid:8)(cid:7)(cid:9)
,则(cid:12)(cid:15)= (cid:9)(cid:15),即−(cid:1)
=
− 1
2
(cid:1) 2− 5
2
(cid:1),即可求解;
(cid:7)(cid:9) (cid:8)(cid:7) 3 6
(3)① 当点P在 x轴的上方时,证明△ (cid:8)(cid:9)(cid:13) 为等腰直角三角形,利用 (cid:8)(cid:9)= (cid:9)(cid:13) ,即可求
解;②当点P在 x轴的下方时,同理可解.
本题是二次函数综合题,主要考查了一次函数的性质、等腰直角三角形的性质、三角形
相似等,其中(3),要注意分类求解,避免遗漏.
26.【答案】2 4
【解析】解:(1) ∵将矩形ABCD折叠,使点A与点 P重合,点D落在点G处,
∴ (cid:8)(cid:15)= (cid:9)(cid:15) ,∠ (cid:8)(cid:15)(cid:16)= ∠ (cid:9)(cid:15)(cid:16) ,
∵ (cid:9)(cid:15) 2 = (cid:10)(cid:15) 2 + (cid:10)(cid:9) 2,
∴(6 − (cid:10)(cid:15))2 = (cid:10)(cid:15) 2 + 12,
∴ (cid:10)(cid:15)= 2,
∴ (cid:9)(cid:15)= 4,
∵cos∠ (cid:9)(cid:15)(cid:10)= (cid:10)(cid:15)= 1 ,
(cid:9)(cid:15) 2
∴∠ (cid:9)(cid:15)(cid:10)= 60°,
∴∠ (cid:8)(cid:15)(cid:16)= ∠ (cid:16)(cid:15)(cid:9)= 60°,
∵ (cid:8)(cid:10)//(cid:12)(cid:9) ,
∴∠ (cid:8)(cid:15)(cid:16)= ∠ (cid:9)(cid:16)(cid:15)= 60°,
∴△ 是等边三角形,
(cid:9)(cid:15)(cid:16)
∴ (cid:15)(cid:16)= (cid:9)(cid:15)= 4,
故答案为:2,4;
(2)① ∵将矩形 ABCD折叠,
∴ (cid:16)(cid:28)//(cid:15)(cid:14) ,
∴∠ (cid:13)(cid:16)(cid:7)= ∠ (cid:14)(cid:15)(cid:7) ,
∵点 O是EF的中点,
∴ (cid:15)(cid:7)= (cid:16)(cid:7) ,
又∵∠ (cid:15)(cid:7)(cid:14)= ∠ (cid:16)(cid:7)(cid:13) ,
∴△ (cid:15)(cid:7)(cid:14) ≌△ (cid:16)(cid:7)(cid:13)((cid:8)(cid:8)(cid:26) ,)
∴ (cid:16)(cid:13)= (cid:14)(cid:15) ,
第24 页,共26 页又∵ (cid:13)(cid:16)//(cid:14)(cid:15) ,
∴四边形 MEPF是平行四边形;
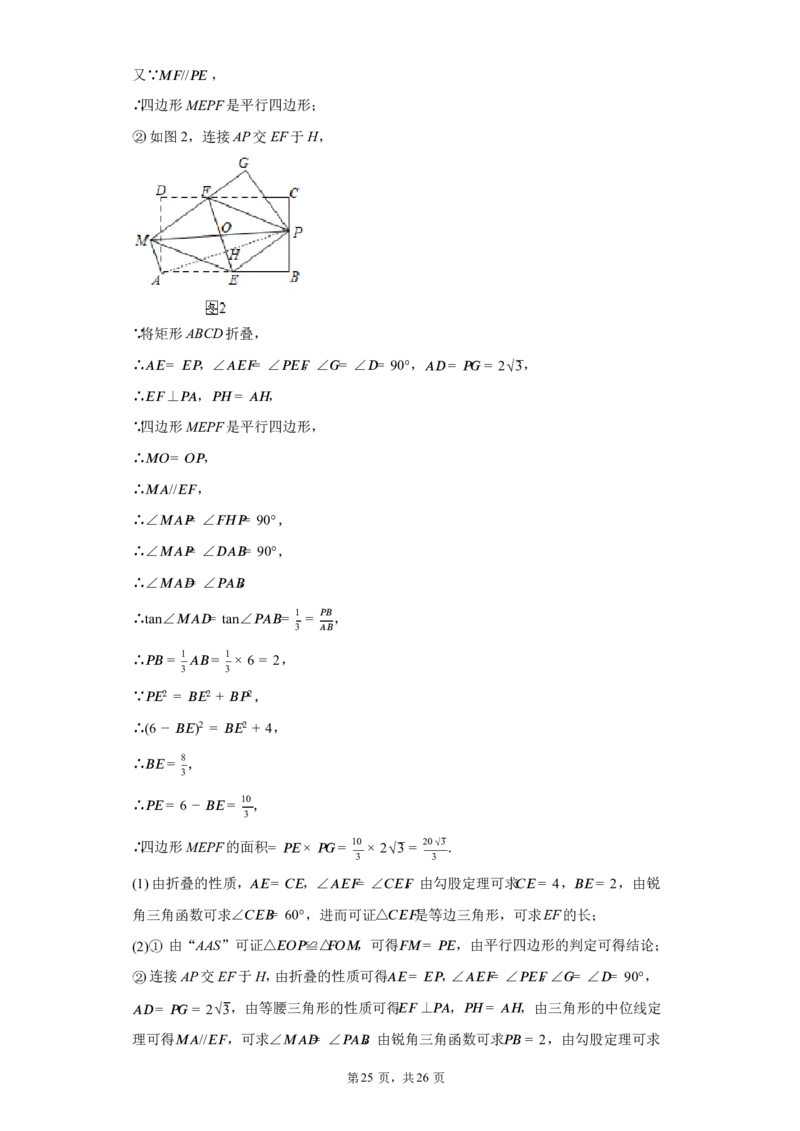
②如图 2,连接AP交 EF于 H,
∵将矩形 ABCD折叠,
∴ (cid:8)(cid:15)= (cid:15)(cid:14) ,∠ (cid:8)(cid:15)(cid:16)= ∠ (cid:14)(cid:15)(cid:16) ,∠ (cid:28)= ∠ (cid:12)= 90°, (cid:8)(cid:12)= (cid:14)(cid:28)= 2√3,
∴ (cid:15)(cid:16) ⊥ (cid:14)(cid:8) , (cid:14)(cid:27)= (cid:8)(cid:27) ,
∵四边形 MEPF是平行四边形,
∴ (cid:13)(cid:7)= (cid:7)(cid:14) ,
∴ (cid:13)(cid:8)//(cid:15)(cid:16) ,
∴∠ (cid:13)(cid:8)(cid:14)= ∠ (cid:16)(cid:27)(cid:14)= 90°,
∴∠ (cid:13)(cid:8)(cid:14)= ∠ (cid:12)(cid:8)(cid:10)= 90°,
∴∠ (cid:13)(cid:8)(cid:12)= ∠ (cid:14)(cid:8)(cid:10) ,
∴tan∠ (cid:13)(cid:8)(cid:12)= tan∠ (cid:14)(cid:8)(cid:10)= 1 = (cid:14)(cid:10),
3 (cid:8)(cid:10)
∴ (cid:14)(cid:10) = 1 (cid:8)(cid:10)= 1 × 6 = 2,
3 3
∵ (cid:14)(cid:15) 2 = (cid:10)(cid:15) 2 + (cid:10)(cid:14) 2,
∴(6 − (cid:10)(cid:15))2 = (cid:10)(cid:15) 2 + 4,
∴ (cid:10)(cid:15)= 8 ,
3
∴ (cid:14)(cid:15)= 6 − (cid:10)(cid:15)= 10 ,
3
∴四边形 MEPF的面积= (cid:14)(cid:15)× (cid:14)(cid:28)= 10 × 2√3 = 20√3.
3 3
(1)由折叠的性质, (cid:8)(cid:15)= (cid:9)(cid:15) ,∠ (cid:8)(cid:15)(cid:16)= ∠ (cid:9)(cid:15)(cid:16) ,由勾股定理可求 (cid:9)(cid:15)= 4, (cid:10)(cid:15)= 2,由锐
角三角函数可求∠ (cid:9)(cid:15)(cid:10)= 60°,进而可证△ (cid:9)(cid:15)(cid:16) 是等边三角形,可求EF的长;
(2)① 由“AAS”可证△ (cid:15)(cid:7)(cid:14) ≌△ (cid:16)(cid:7)(cid:13) ,可得 (cid:16)(cid:13)= (cid:14)(cid:15) ,由平行四边形的判定可得结论;
②连接 AP交 EF于 H,由折叠的性质可得 (cid:8)(cid:15)= (cid:15)(cid:14) ,∠ (cid:8)(cid:15)(cid:16)= ∠ (cid:14)(cid:15)(cid:16) ,∠ (cid:28)= ∠ (cid:12)= 90°,
(cid:8)(cid:12)= (cid:14)(cid:28)= 2√3,由等腰三角形的性质可得 (cid:15)(cid:16) ⊥ (cid:14)(cid:8) , (cid:14)(cid:27)= (cid:8)(cid:27) ,由三角形的中位线定
理可得 (cid:13)(cid:8)//(cid:15)(cid:16) ,可求∠ (cid:13)(cid:8)(cid:12)= ∠ (cid:14)(cid:8)(cid:10) ,由锐角三角函数可求 (cid:14)(cid:10) = 2,由勾股定理可求
第25 页,共26 页PE的长,即可求解.
本题是四边形综合题,考查了矩形的性质,折叠的性质,平行四边形的判定和性质,勾
股定理,全等三角形的判定和性质,锐角三角函数等知识,灵活运用这些性质进行推理
是本题关键.
第26 页,共26 页