文档内容
2020年湖南省娄底市中考数学试卷
一、选择题(本大题共12小题,每小题3分,满分36分,每小题给出的四个选项中,只有一个
选项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方
框里)
1.(3分)﹣2020的倒数是( )
A.﹣2020 B.2020 C. D.﹣
2.(3分)下列运算正确的是( )
A.a2•a3=a6 B.(a+b)2=a2+b2
C.(﹣2a)3=﹣8a3 D.a2+a2=a4
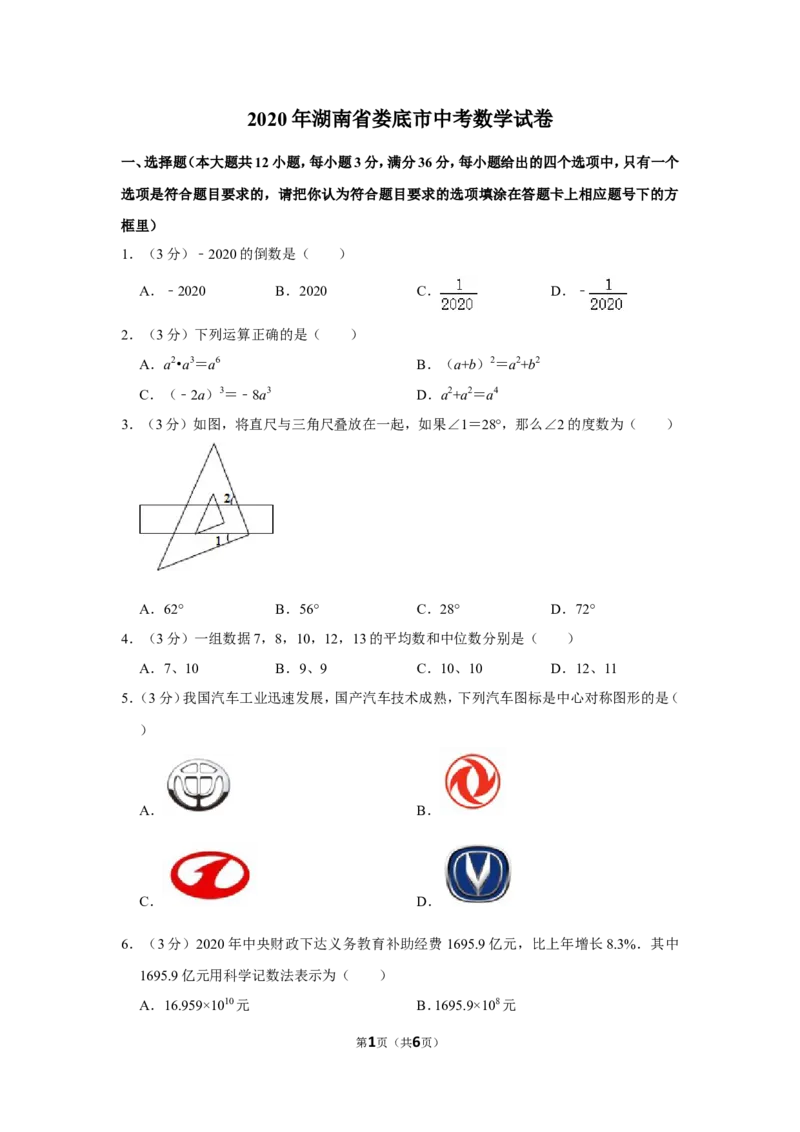
3.(3分)如图,将直尺与三角尺叠放在一起,如果∠1=28°,那么∠2的度数为( )
A.62° B.56° C.28° D.72°
4.(3分)一组数据7,8,10,12,13的平均数和中位数分别是( )
A.7、10 B.9、9 C.10、10 D.12、11
5.(3分)我国汽车工业迅速发展,国产汽车技术成熟,下列汽车图标是中心对称图形的是(
)
A. B.
C. D.
6.(3分)2020年中央财政下达义务教育补助经费1695.9亿元,比上年增长8.3%.其中
1695.9亿元用科学记数法表示为( )
A.16.959×1010元 B.1695.9×108元
第1页(共6页)C.1.6959×1010元 D.1.6959×1011元
7.(3分)正多边形的一个外角为60°,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
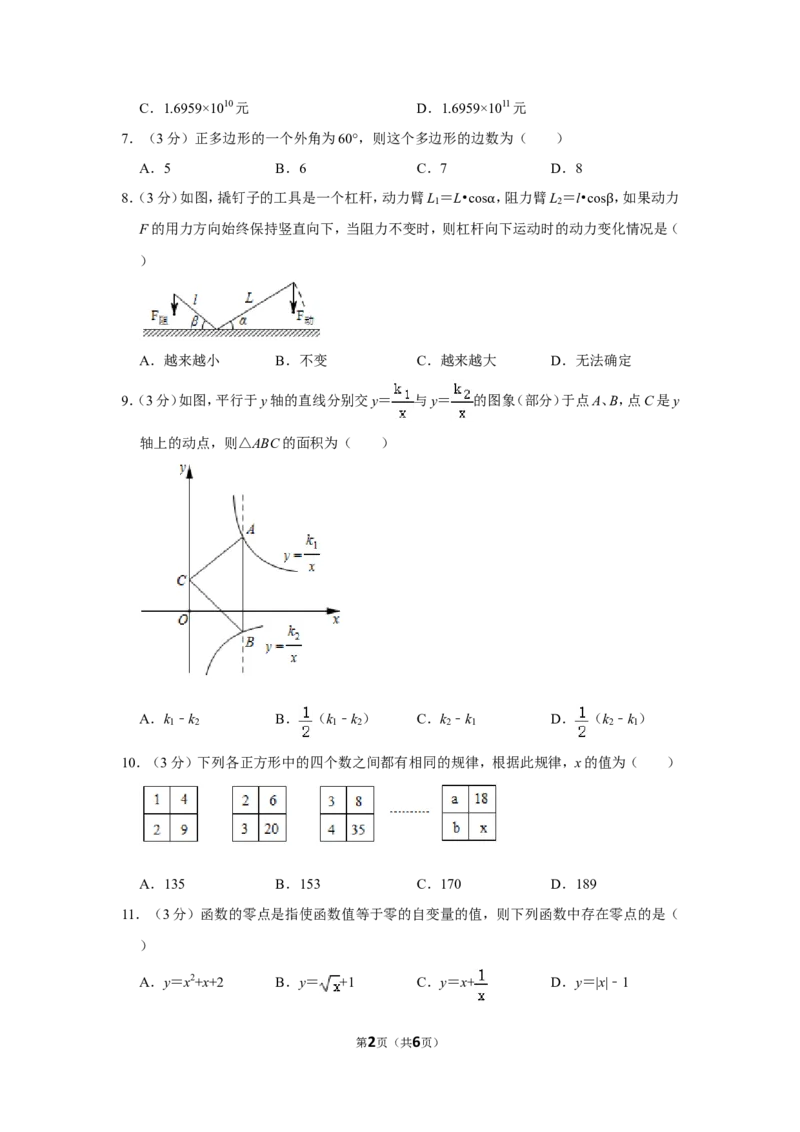
8.(3分)如图,撬钉子的工具是一个杠杆,动力臂L =L•cos ,阻力臂L =l•cos ,如果动力
1 2
F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向α下运动时的动力变β化情况是(
)
A.越来越小 B.不变 C.越来越大 D.无法确定
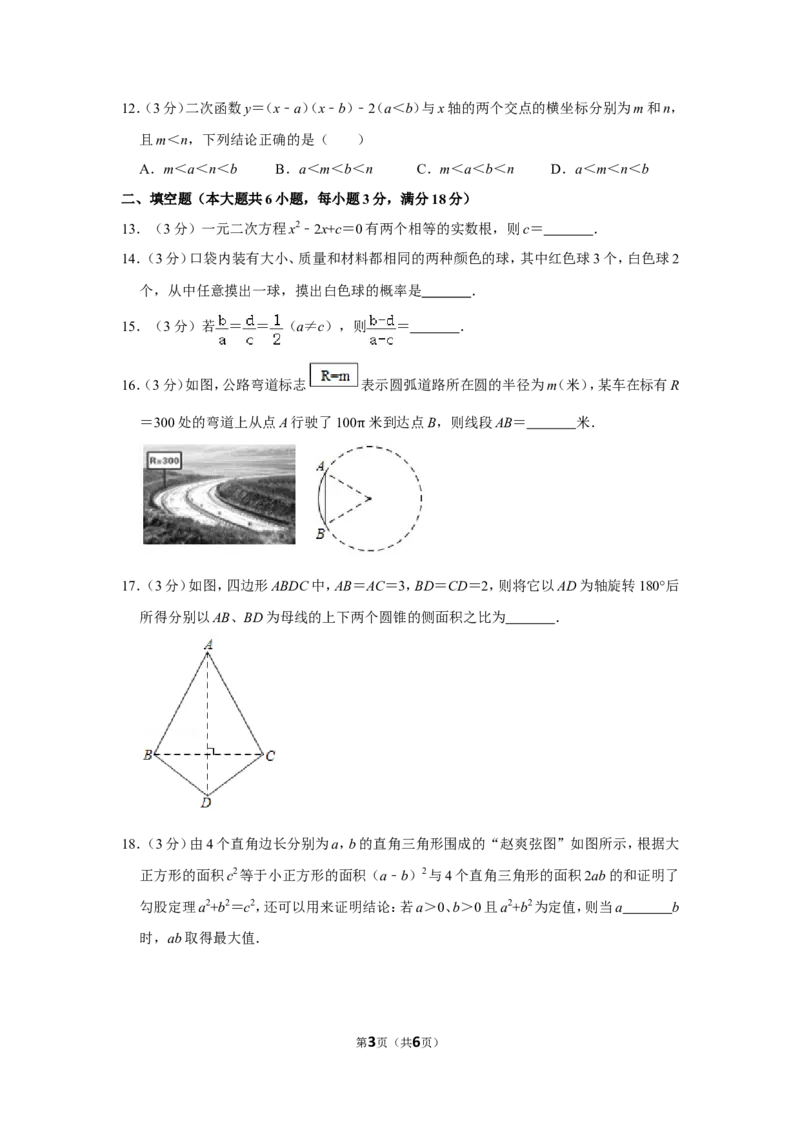
9.(3分)如图,平行于y轴的直线分别交y= 与y= 的图象(部分)于点A、B,点C是y
轴上的动点,则△ABC的面积为( )
A.k ﹣k B. (k ﹣k ) C.k ﹣k D. (k ﹣k )
1 2 1 2 2 1 2 1
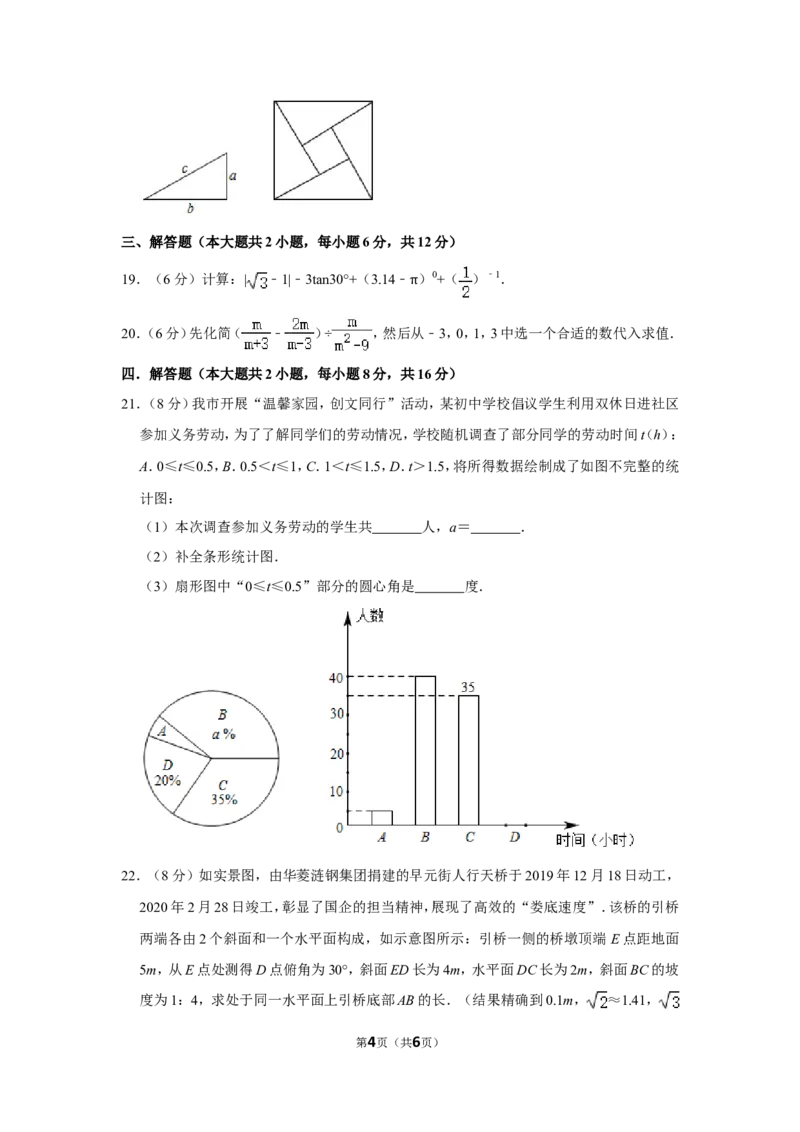
10.(3分)下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为( )
A.135 B.153 C.170 D.189
11.(3分)函数的零点是指使函数值等于零的自变量的值,则下列函数中存在零点的是(
)
A.y=x2+x+2 B.y= +1 C.y=x+ D.y=|x|﹣1
第2页(共6页)12.(3分)二次函数y=(x﹣a)(x﹣b)﹣2(a<b)与x轴的两个交点的横坐标分别为m和n,
且m<n,下列结论正确的是( )
A.m<a<n<b B.a<m<b<n C.m<a<b<n D.a<m<n<b
二、填空题(本大题共6小题,每小题3分,满分18分)
13.(3分)一元二次方程x2﹣2x+c=0有两个相等的实数根,则c= .
14.(3分)口袋内装有大小、质量和材料都相同的两种颜色的球,其中红色球3个,白色球2
个,从中任意摸出一球,摸出白色球的概率是 .
15.(3分)若 = = (a≠c),则 = .
16.(3分)如图,公路弯道标志 表示圆弧道路所在圆的半径为m(米),某车在标有R
=300处的弯道上从点A行驶了100 米到达点B,则线段AB= 米.
π
17.(3分)如图,四边形ABDC中,AB=AC=3,BD=CD=2,则将它以AD为轴旋转180°后
所得分别以AB、BD为母线的上下两个圆锥的侧面积之比为 .
18.(3分)由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示,根据大
正方形的面积c2等于小正方形的面积(a﹣b)2与4个直角三角形的面积2ab的和证明了
勾股定理a2+b2=c2,还可以用来证明结论:若a>0、b>0且a2+b2为定值,则当a b
时,ab取得最大值.
第3页(共6页)三、解答题(本大题共2小题,每小题6分,共12分)
19.(6分)计算:| ﹣1|﹣3tan30°+(3.14﹣ )0+( )﹣1.
π
20.(6分)先化简( ﹣ )÷ ,然后从﹣3,0,1,3中选一个合适的数代入求值.
四.解答题(本大题共2小题,每小题8分,共16分)
21.(8分)我市开展“温馨家园,创文同行”活动,某初中学校倡议学生利用双休日进社区
参加义务劳动,为了了解同学们的劳动情况,学校随机调查了部分同学的劳动时间(t h):
A.0≤t≤0.5,B.0.5<t≤1,C.1<t≤1.5,D.t>1.5,将所得数据绘制成了如图不完整的统
计图:
(1)本次调查参加义务劳动的学生共 人,a= .
(2)补全条形统计图.
(3)扇形图中“0≤t≤0.5”部分的圆心角是 度.
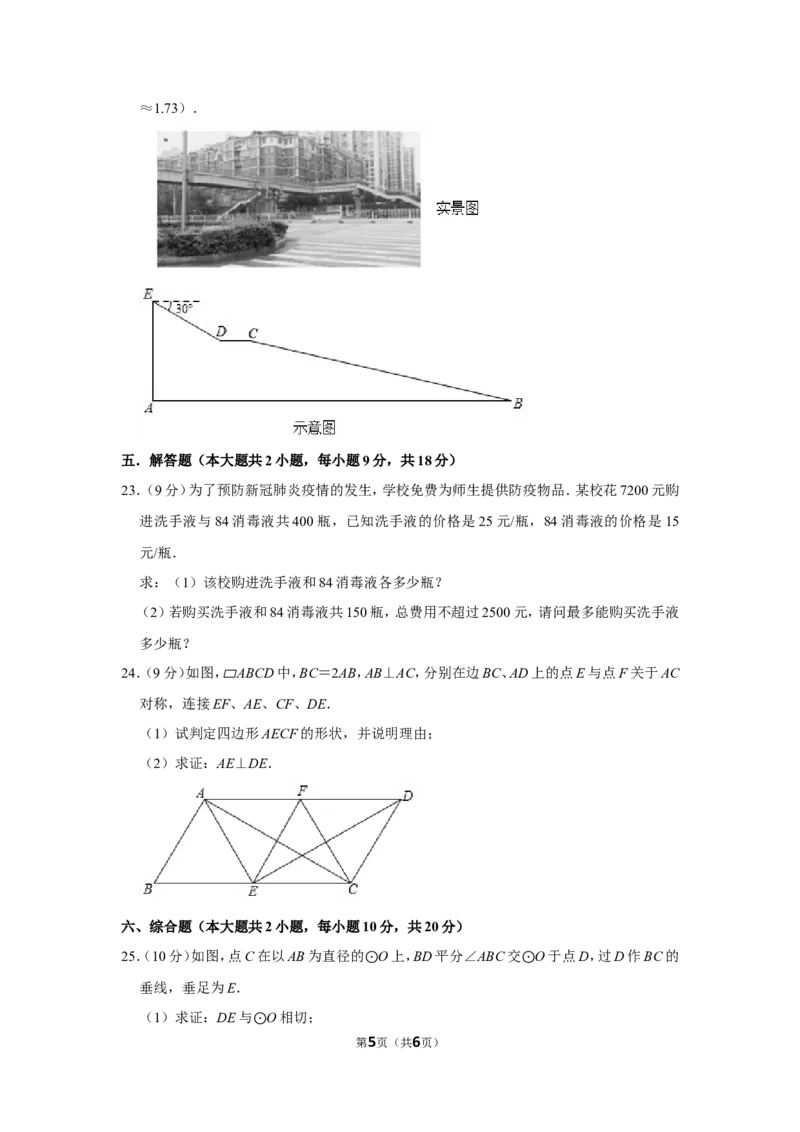
22.(8分)如实景图,由华菱涟钢集团捐建的早元街人行天桥于2019年12月18日动工,
2020年2月28日竣工,彰显了国企的担当精神,展现了高效的“娄底速度”.该桥的引桥
两端各由2个斜面和一个水平面构成,如示意图所示:引桥一侧的桥墩顶端 E点距地面
5m,从E点处测得D点俯角为30°,斜面ED长为4m,水平面DC长为2m,斜面BC的坡
度为1:4,求处于同一水平面上引桥底部AB的长.(结果精确到0.1m, ≈1.41,
第4页(共6页)≈1.73).
五.解答题(本大题共2小题,每小题9分,共18分)
23.(9分)为了预防新冠肺炎疫情的发生,学校免费为师生提供防疫物品.某校花7200元购
进洗手液与84消毒液共400瓶,已知洗手液的价格是25元/瓶,84消毒液的价格是15
元/瓶.
求:(1)该校购进洗手液和84消毒液各多少瓶?
(2)若购买洗手液和84消毒液共150瓶,总费用不超过2500元,请问最多能购买洗手液
多少瓶?
24.(9分)如图, ABCD中,BC=2AB,AB⊥AC,分别在边BC、AD上的点E与点F关于AC
对称,连接EF▱、AE、CF、DE.
(1)试判定四边形AECF的形状,并说明理由;
(2)求证:AE⊥DE.
六、综合题(本大题共2小题,每小题10分,共20分)
25.(10分)如图,点C在以AB为直径的 O上,BD平分∠ABC交 O于点D,过D作BC的
垂线,垂足为E. ⊙ ⊙
(1)求证:DE与 O相切;
第5页(共6页)
⊙(2)若AB=5,BE=4,求BD的长;
(3)请用线段AB、BE表示CE的长,并说明理由.
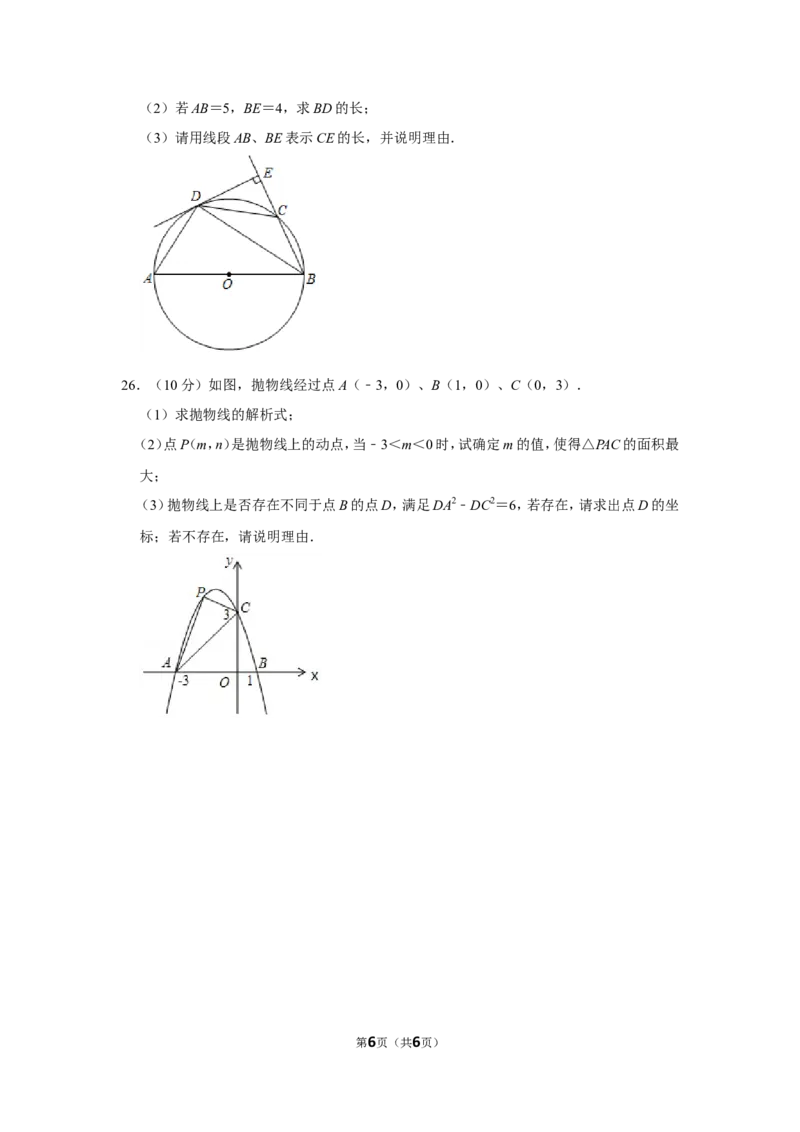
26.(10分)如图,抛物线经过点A(﹣3,0)、B(1,0)、C(0,3).
(1)求抛物线的解析式;
(2)点P(m,n)是抛物线上的动点,当﹣3<m<0时,试确定m的值,使得△PAC的面积最
大;
(3)抛物线上是否存在不同于点B的点D,满足DA2﹣DC2=6,若存在,请求出点D的坐
标;若不存在,请说明理由.
第6页(共6页)