文档内容
【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
2020年辽宁省铁岭市、葫芦岛市中考数学试卷
参考答案与试题解析
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.(3分)﹣ 的绝对值是( )
A. B.﹣ C.3 D.﹣3
【分析】依据绝对值的性质求解即可.
【解答】解:|﹣ |= .
故选:A.
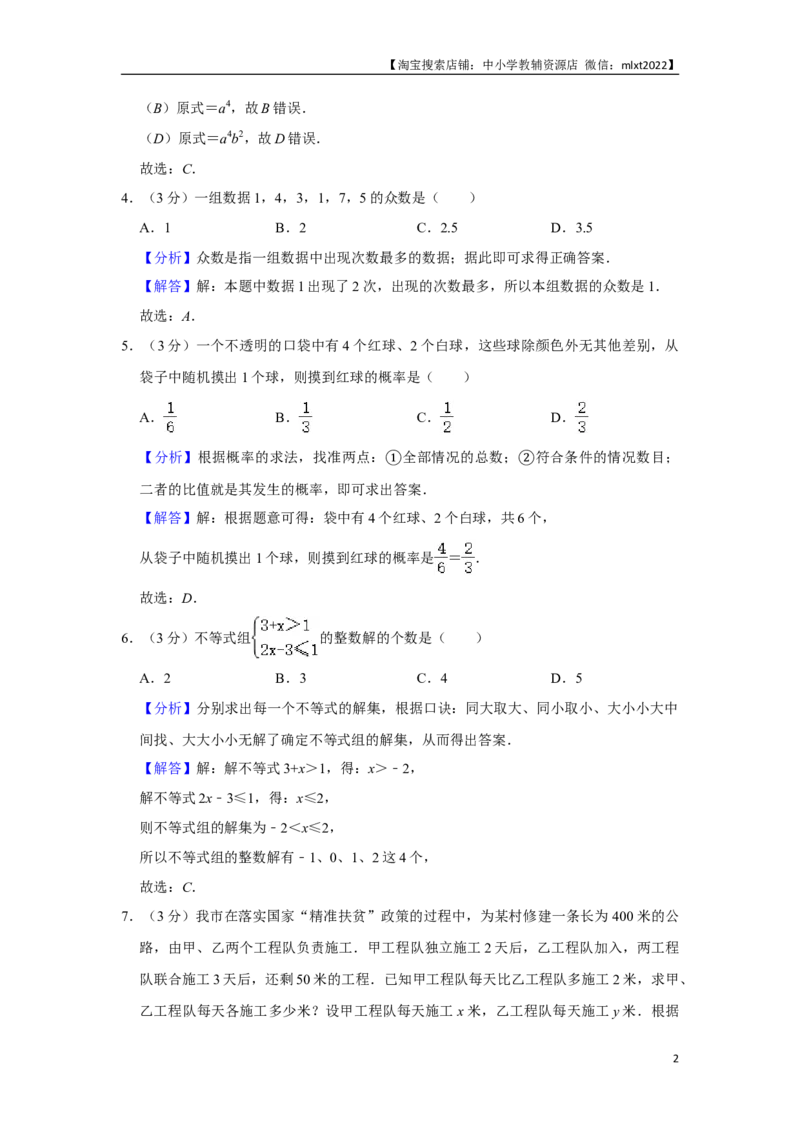
2.(3分)如图是由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
A. B. C. D.
【分析】根据从上面看得到的图形是俯视图,可得答案.
【解答】解:从上面看,底层左边是一个小正方形,上层是两个小正方形.
故选:B.
3.(3分)下列运算正确的是( )
A.a2•a3=a6 B.a8÷a4=a2
C.5a﹣3a=2a D.(﹣ab2)2=﹣a2b4
【分析】根据整式的运算法则即可求出答案.
【解答】解:(A)原式=a5,故A错误.
1【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
(B)原式=a4,故B错误.
(D)原式=a4b2,故D错误.
故选:C.
4.(3分)一组数据1,4,3,1,7,5的众数是( )
A.1 B.2 C.2.5 D.3.5
【分析】众数是指一组数据中出现次数最多的数据;据此即可求得正确答案.
【解答】解:本题中数据1出现了2次,出现的次数最多,所以本组数据的众数是1.
故选:A.
5.(3分)一个不透明的口袋中有4个红球、2个白球,这些球除颜色外无其他差别,从
袋子中随机摸出1个球,则摸到红球的概率是( )
A. B. C. D.
【分析】根据概率的求法,找准两点: 全部情况的总数; 符合条件的情况数目;
二者的比值就是其发生的概率,即可求出①答案. ②
【解答】解:根据题意可得:袋中有4个红球、2个白球,共6个,
从袋子中随机摸出1个球,则摸到红球的概率是 = .
故选:D.
6.(3分)不等式组 的整数解的个数是( )
A.2 B.3 C.4 D.5
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中
间找、大大小小无解了确定不等式组的解集,从而得出答案.
【解答】解:解不等式3+x>1,得:x>﹣2,
解不等式2x﹣3≤1,得:x≤2,
则不等式组的解集为﹣2<x≤2,
所以不等式组的整数解有﹣1、0、1、2这4个,
故选:C.
7.(3分)我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为 400米的公
路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入,两工程
队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、
乙工程队每天各施工多少米?设甲工程队每天施工x米,乙工程队每天施工y米.根据
2【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
题意,所列方程组正确的是( )
A.
B.
C.
D.
【分析】根据甲工程队独立施工2天后,乙工程队加入,两工程队联合施工3天后,还
剩50米的工程和甲工程队每天比乙工程队多施工 2米,可以列出相应的二元一次方程
组,本题得以解决.
【解答】解:由题意可得,
,
故选:D.
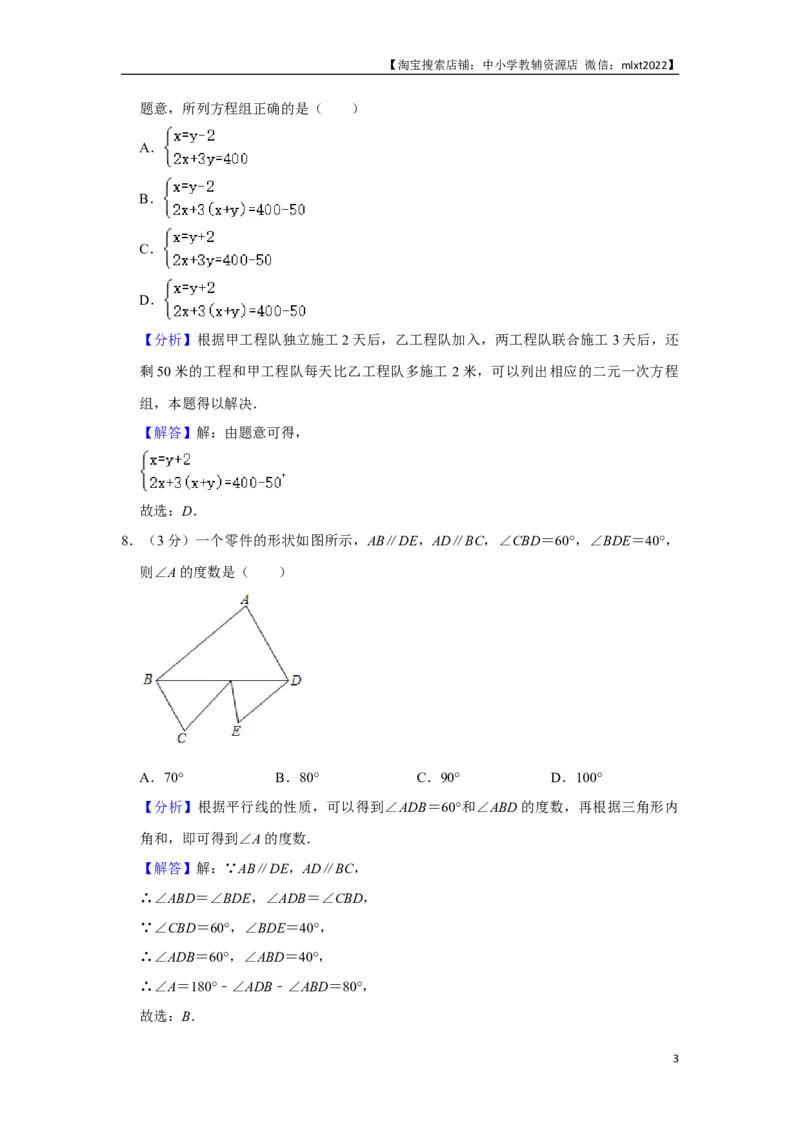
8.(3分)一个零件的形状如图所示,AB∥DE,AD∥BC,∠CBD=60°,∠BDE=40°,
则∠A的度数是( )
A.70° B.80° C.90° D.100°
【分析】根据平行线的性质,可以得到∠ADB=60°和∠ABD的度数,再根据三角形内
角和,即可得到∠A的度数.
【解答】解:∵AB∥DE,AD∥BC,
∴∠ABD=∠BDE,∠ADB=∠CBD,
∵∠CBD=60°,∠BDE=40°,
∴∠ADB=60°,∠ABD=40°,
∴∠A=180°﹣∠ADB﹣∠ABD=80°,
故选:B.
3【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
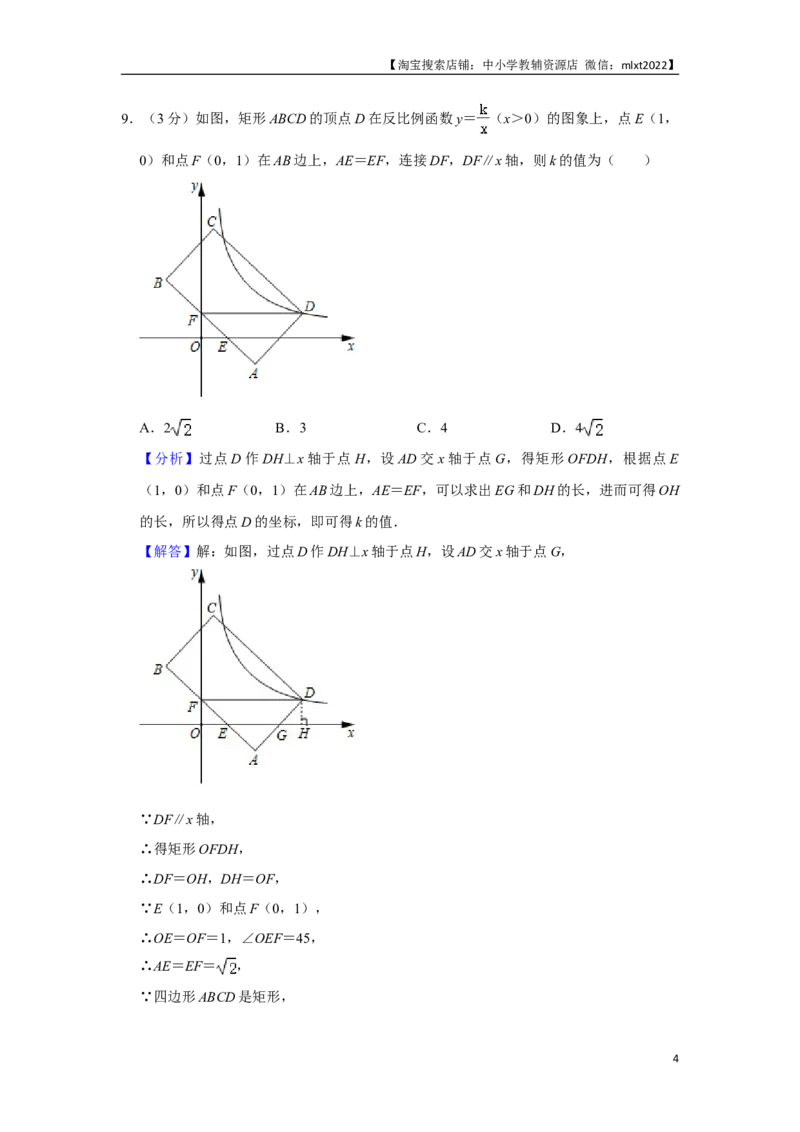
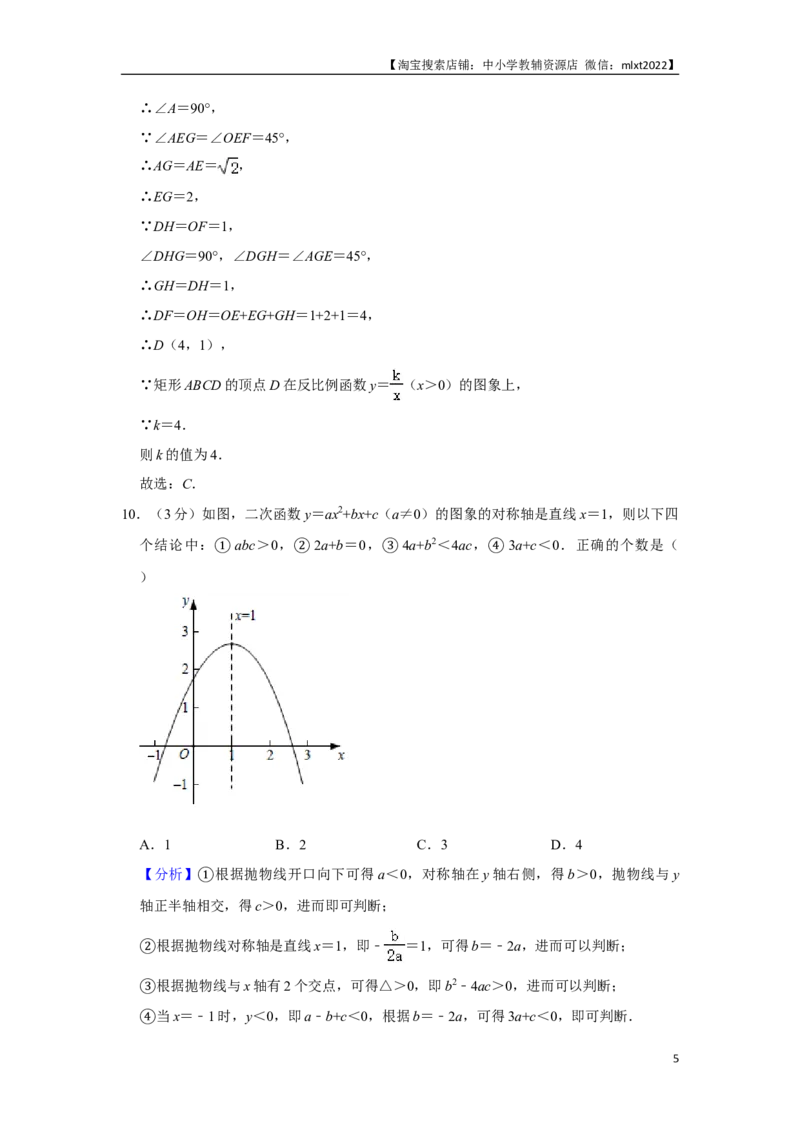
9.(3分)如图,矩形ABCD的顶点D在反比例函数y= (x>0)的图象上,点E(1,
0)和点F(0,1)在AB边上,AE=EF,连接DF,DF∥x轴,则k的值为( )
A.2 B.3 C.4 D.4
【分析】过点D作DH⊥x轴于点H,设AD交x轴于点G,得矩形OFDH,根据点E
(1,0)和点F(0,1)在AB边上,AE=EF,可以求出EG和DH的长,进而可得OH
的长,所以得点D的坐标,即可得k的值.
【解答】解:如图,过点D作DH⊥x轴于点H,设AD交x轴于点G,
∵DF∥x轴,
∴得矩形OFDH,
∴DF=OH,DH=OF,
∵E(1,0)和点F(0,1),
∴OE=OF=1,∠OEF=45,
∴AE=EF= ,
∵四边形ABCD是矩形,
4【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∴∠A=90°,
∵∠AEG=∠OEF=45°,
∴AG=AE= ,
∴EG=2,
∵DH=OF=1,
∠DHG=90°,∠DGH=∠AGE=45°,
∴GH=DH=1,
∴DF=OH=OE+EG+GH=1+2+1=4,
∴D(4,1),
∵矩形ABCD的顶点D在反比例函数y= (x>0)的图象上,
∵k=4.
则k的值为4.
故选:C.
10.(3分)如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,则以下四
个结论中: abc>0, 2a+b=0, 4a+b2<4ac, 3a+c<0.正确的个数是(
) ① ② ③ ④
A.1 B.2 C.3 D.4
【分析】 根据抛物线开口向下可得a<0,对称轴在y轴右侧,得b>0,抛物线与y
轴正半轴相①交,得c>0,进而即可判断;
根据抛物线对称轴是直线x=1,即﹣ =1,可得b=﹣2a,进而可以判断;
②
根据抛物线与x轴有2个交点,可得△>0,即b2﹣4ac>0,进而可以判断;
③当x=﹣1时,y<0,即a﹣b+c<0,根据b=﹣2a,可得3a+c<0,即可判断.
④
5【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
【解答】解: 根据抛物线开口向下可知:
a<0, ①
因为对称轴在y轴右侧,
所以b>0,
因为抛物线与y轴正半轴相交,
所以c>0,
所以abc<0,
所以 错误;
因①为抛物线对称轴是直线x=1,
②
即﹣ =1,
所以b=﹣2a,
所以b+2a=0,
所以 正确;
因②为抛物线与x轴有2个交点,
③所以△>0,
即b2﹣4ac>0,
所以b2﹣4ac+4a>4a,
所以4a+b2>4ac+4a,
所以 错误;
当③x=﹣1时,y<0,
④即a﹣b+c<0,
因为b=﹣2a,
所以3a+c<0,
所以 正确.
所以④正确的个数是 2个.
故选:B. ②④
二、填空题(本题共8小题,每小题3分,共24分)
11.(3分)伴随“互联网+”时代的来临,预计到2025年,我国各类网络互助平台的实
际参与人数将达到450000000,将数据450000000用科学记数法表示为 4.5×1 0 8 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的
值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相
6【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将数据450000000用科学记数法表示为4.5×108.
故答案为:4.5×108.
12.(3分)分解因式:ab2﹣9a= a ( b + 3 )( b ﹣ 3 ) .
【分析】根据提公因式,平方差公式,可得答案.
【解答】解:原式=a(b2﹣9)
=a(b+3)(b﹣3),
故答案为:a(b+3)(b﹣3).
13.(3分)甲、乙两人参加“环保知识”竞赛,经过6轮比赛,他们的平均成绩都是97
分.如果甲、乙两人比赛成绩的方差分别为s甲 2=6.67,s乙 2=2.50,则这6次比赛成绩
比较稳定的是 乙 .(填“甲”或“乙”)
【分析】根据方差的意义求解可得.
【解答】解:∵s甲 2=6.67,s乙 2=2.50,
∴s甲 2=>s乙 2,
∴这6次比赛成绩比较稳定的是乙,
故答案为:乙.
14.(3分)关于x的一元二次方程x2﹣2x﹣k=0有两个不相等的实数根,则k的取值范围
是 k >﹣ 1 .
【分析】根据判别式的意义得到△=(﹣2)2+4k>0,然后解不等式即可.
【解答】解:∵关于x的一元二次方程x2﹣2x﹣k=0有两个不相等的实数根,
∴△=(﹣2)2+4k>0,
解得k>﹣1.
故答案为:k>﹣1.
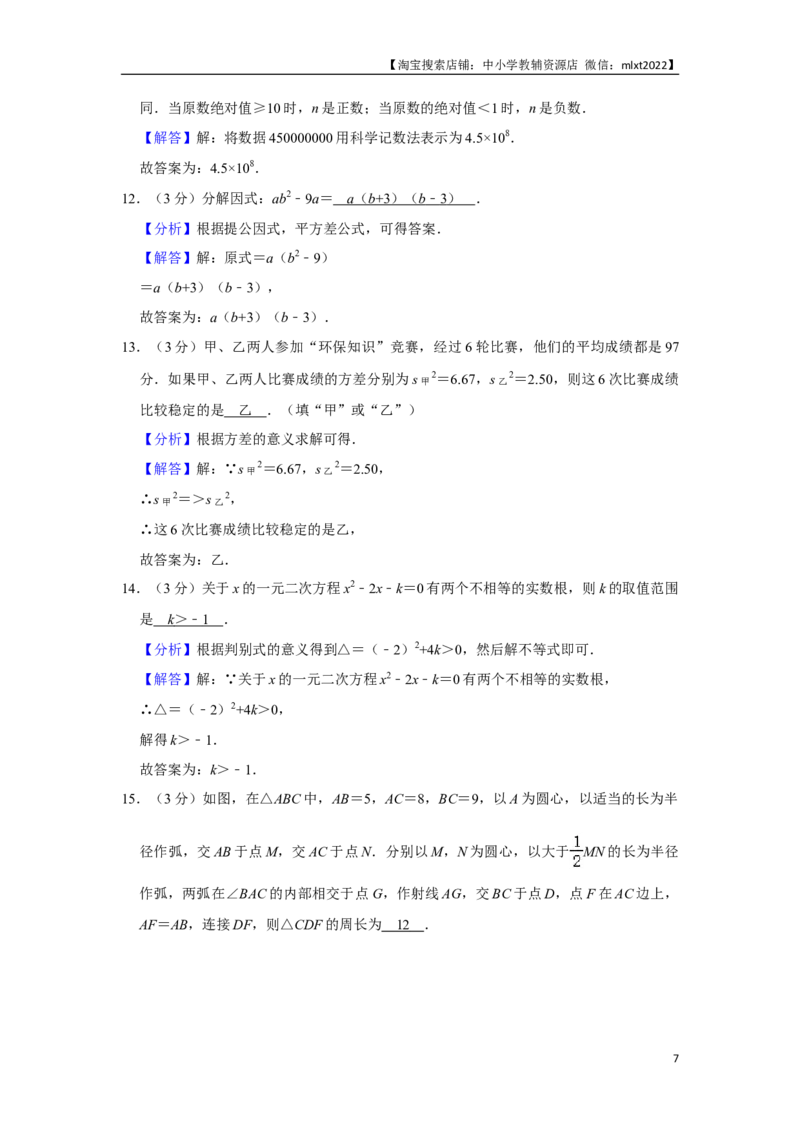
15.(3分)如图,在△ABC中,AB=5,AC=8,BC=9,以A为圆心,以适当的长为半
径作弧,交AB于点M,交AC于点N.分别以M,N为圆心,以大于 MN的长为半径
作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,
AF=AB,连接DF,则△CDF的周长为 1 2 .
7【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
【分析】直接利用基本作图方法结合全等三角形的判定与性质进而得出BD=DF,即可
得出答案.
【解答】解:∵AB=5,AC=8,AF=AB,
∴FC=AC﹣AF=8﹣5=3,
由作图方法可得:AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△AFD中
,
∴△ABD≌△AFD(SAS),
∴BD=DF,
∴△DFC的周长为:DF+FC+DC=BD+DC+FC=BC+FC=9+3=12.
故答案为:12.
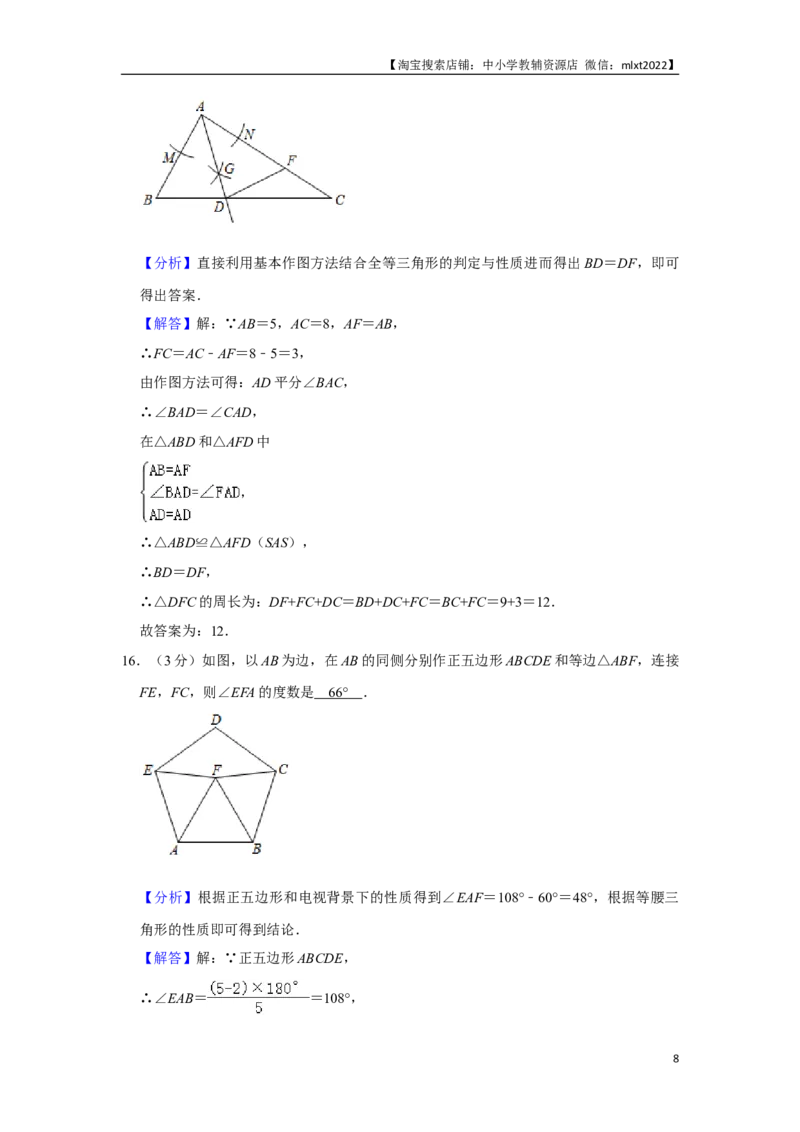
16.(3分)如图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接
FE,FC,则∠EFA的度数是 66 ° .
【分析】根据正五边形和电视背景下的性质得到∠EAF=108°﹣60°=48°,根据等腰三
角形的性质即可得到结论.
【解答】解:∵正五边形ABCDE,
∴∠EAB= =108°,
8【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∵△ABF是等边三角形,
∴∠FAB=60°,
∴∠EAF=108°﹣60°=48°,
∵AE=AF,
∴∠AE=∠AFE= (180°﹣48°)=66°,
故答案为:66°.
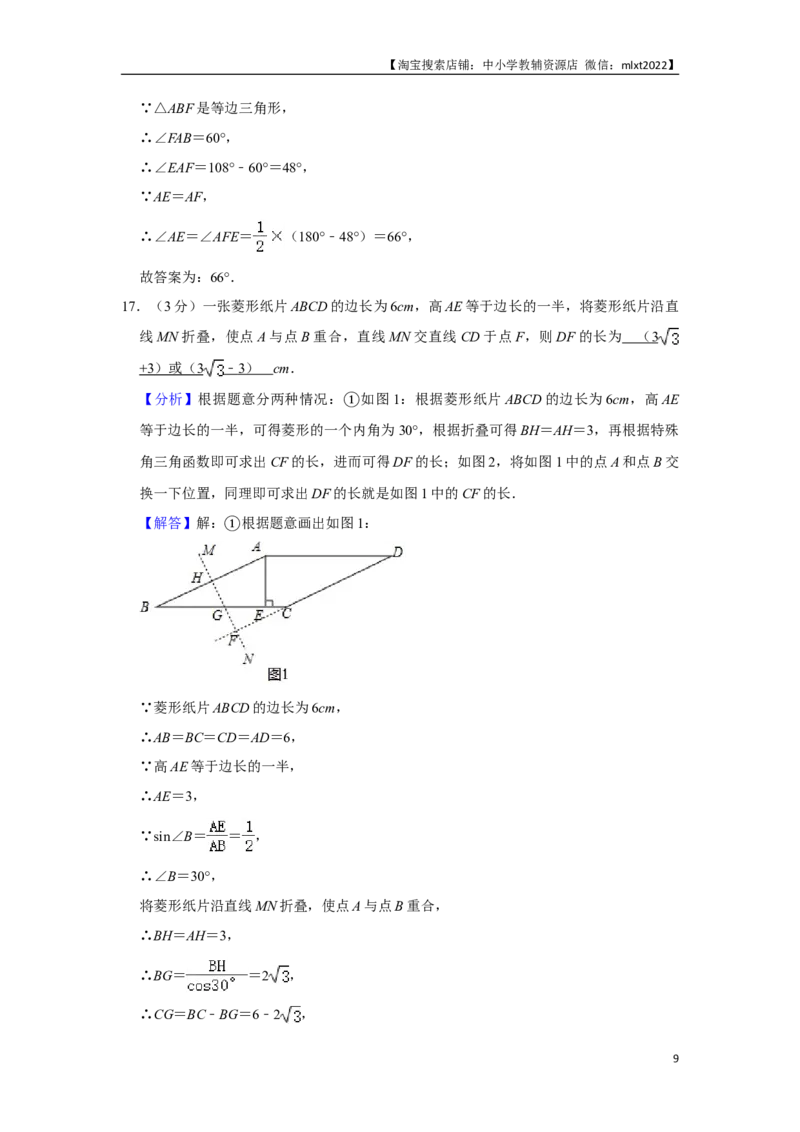
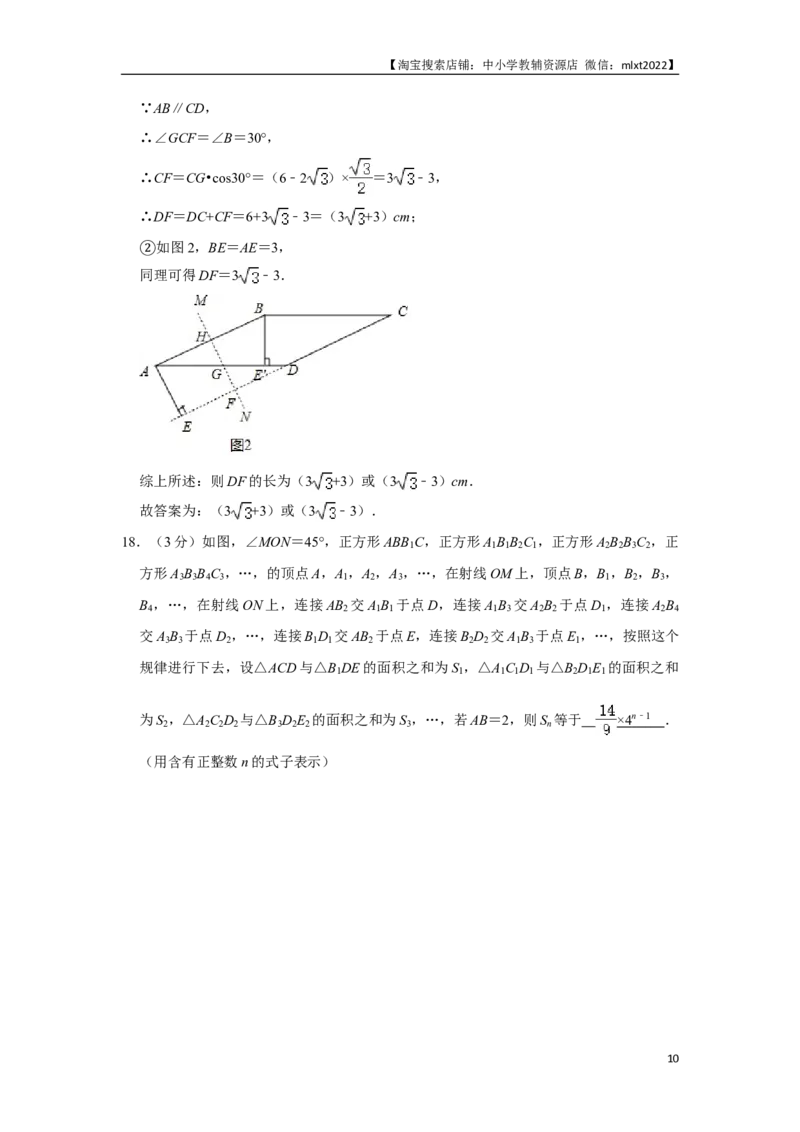
17.(3分)一张菱形纸片ABCD的边长为6cm,高AE等于边长的一半,将菱形纸片沿直
线MN折叠,使点A与点B重合,直线MN交直线CD于点F,则DF的长为 ( 3
+3 )或( 3 ﹣ 3 ) cm.
【分析】根据题意分两种情况: 如图1:根据菱形纸片ABCD的边长为6cm,高AE
等于边长的一半,可得菱形的一个①内角为30°,根据折叠可得BH=AH=3,再根据特殊
角三角函数即可求出CF的长,进而可得DF的长;如图2,将如图1中的点A和点B交
换一下位置,同理即可求出DF的长就是如图1中的CF的长.
【解答】解: 根据题意画出如图1:
①
∵菱形纸片ABCD的边长为6cm,
∴AB=BC=CD=AD=6,
∵高AE等于边长的一半,
∴AE=3,
∵sin∠B= = ,
∴∠B=30°,
将菱形纸片沿直线MN折叠,使点A与点B重合,
∴BH=AH=3,
∴BG= =2 ,
∴CG=BC﹣BG=6﹣2 ,
9【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∵AB∥CD,
∴∠GCF=∠B=30°,
∴CF=CG•cos30°=(6﹣2 )× =3 ﹣3,
∴DF=DC+CF=6+3 ﹣3=(3 +3)cm;
如图2,BE=AE=3,
②
同理可得DF=3 ﹣3.
综上所述:则DF的长为(3 +3)或(3 ﹣3)cm.
故答案为:(3 +3)或(3 ﹣3).
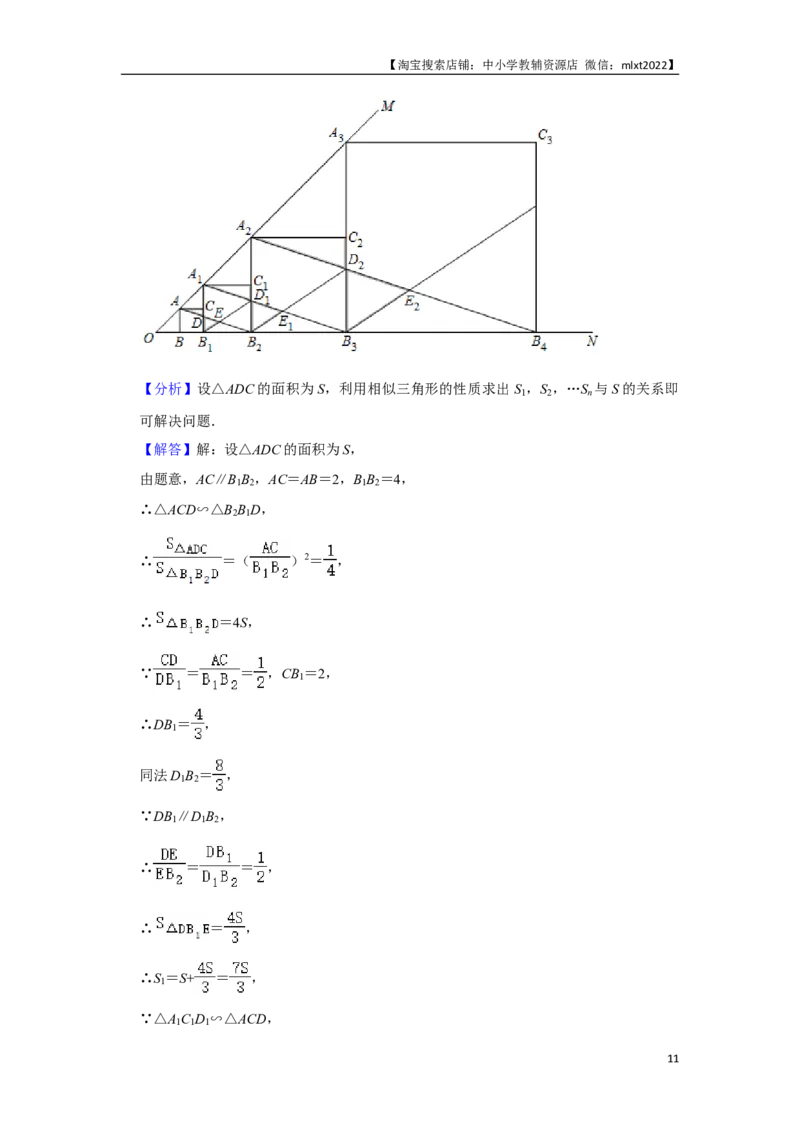
18.(3分)如图,∠MON=45°,正方形ABB C,正方形A B B C ,正方形A B B C ,正
1 1 1 2 1 2 2 3 2
方形A B B C ,…,的顶点A,A ,A ,A ,…,在射线OM上,顶点B,B ,B ,B ,
3 3 4 3 1 2 3 1 2 3
B ,…,在射线ON上,连接AB 交A B 于点D,连接A B 交A B 于点D ,连接A B
4 2 1 1 1 3 2 2 1 2 4
交A B 于点D ,…,连接B D 交AB 于点E,连接B D 交A B 于点E ,…,按照这个
3 3 2 1 1 2 2 2 1 3 1
规律进行下去,设△ACD与△B DE的面积之和为S ,△A C D 与△B D E 的面积之和
1 1 1 1 1 2 1 1
为S ,△A C D 与△B D E 的面积之和为S ,…,若AB=2,则S 等于 ×4 n ﹣ 1 .
2 2 2 2 3 2 2 3 n
(用含有正整数n的式子表示)
10【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
【分析】设△ADC的面积为S,利用相似三角形的性质求出S ,S ,…S 与S的关系即
1 2 n
可解决问题.
【解答】解:设△ADC的面积为S,
由题意,AC∥B B ,AC=AB=2,B B =4,
1 2 1 2
∴△ACD∽△B B D,
2 1
∴ =( )2= ,
∴ =4S,
∵ = = ,CB =2,
1
∴DB = ,
1
同法D B = ,
1 2
∵DB ∥D B ,
1 1 2
∴ = = ,
∴ = ,
∴S =S+ = ,
1
∵△A C D ∽△ACD,
1 1 1
11【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∴ =( )2= ,
∴ =4S,
同法可得, = ,
∴S =4S+ = = ×4,
2
…
S = ×4n﹣1,
n
∵S= ×2× = ,
∴S = ×4n﹣1.
n
故答案为: .
三、解答题(第19题10分,第20题12分,共22分)
19.(10分)先化简,再求值:(x﹣1﹣ )÷ ,其中x=3.
【分析】根据分式的减法和除法可以化简题目中的式子,然后将x的值代入化简后的式
子即可解答本题.
【解答】解:(x﹣1﹣ )÷
=
=
= ,
当x=3时,原式= .
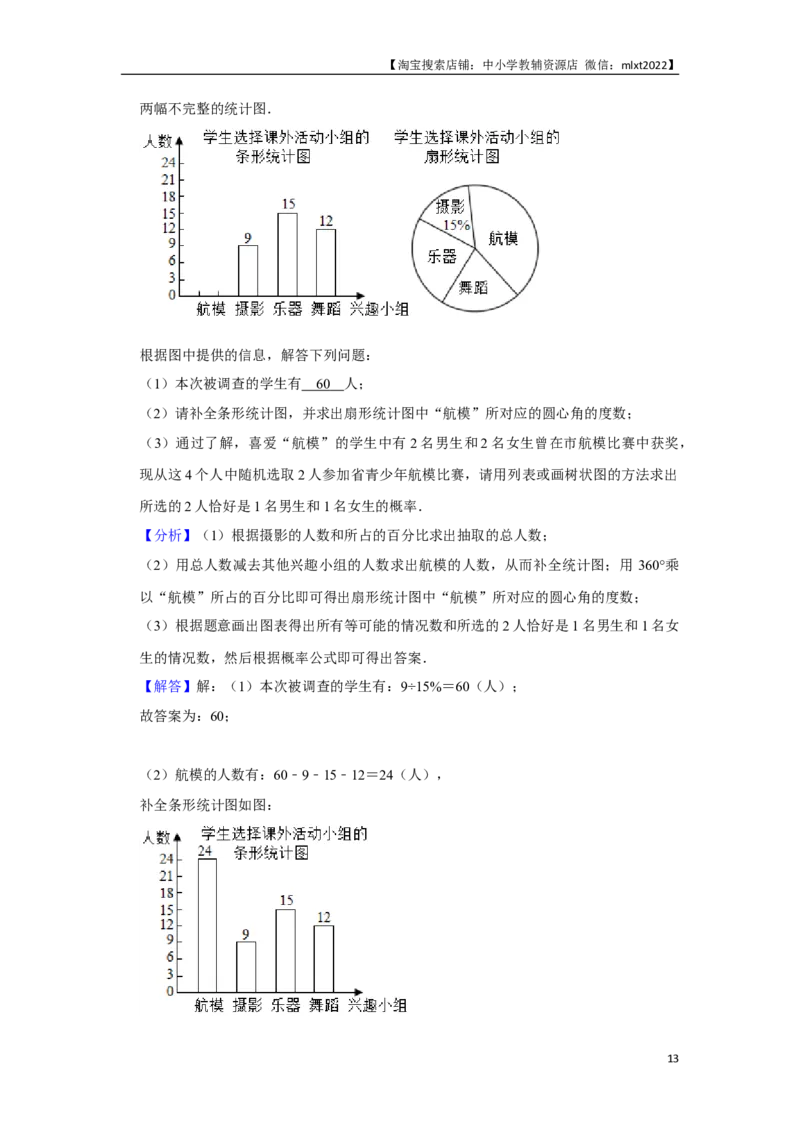
20.(12分)某校计划组建航模、摄影、乐器、舞蹈四个课外活动小组,要求每名同学必
须参加,并且只能选择其中一个小组.为了解学生对四个课外活动小组的选择情况,学
校从全体学生中随机抽取部分学生进行问卷调查,并把此次调查结果整理并绘制成如图
12【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
两幅不完整的统计图.
根据图中提供的信息,解答下列问题:
(1)本次被调查的学生有 6 0 人;
(2)请补全条形统计图,并求出扇形统计图中“航模”所对应的圆心角的度数;
(3)通过了解,喜爱“航模”的学生中有2名男生和2名女生曾在市航模比赛中获奖,
现从这4个人中随机选取2人参加省青少年航模比赛,请用列表或画树状图的方法求出
所选的2人恰好是1名男生和1名女生的概率.
【分析】(1)根据摄影的人数和所占的百分比求出抽取的总人数;
(2)用总人数减去其他兴趣小组的人数求出航模的人数,从而补全统计图;用 360°乘
以“航模”所占的百分比即可得出扇形统计图中“航模”所对应的圆心角的度数;
(3)根据题意画出图表得出所有等可能的情况数和所选的2人恰好是1名男生和1名女
生的情况数,然后根据概率公式即可得出答案.
【解答】解:(1)本次被调查的学生有:9÷15%=60(人);
故答案为:60;
(2)航模的人数有:60﹣9﹣15﹣12=24(人),
补全条形统计图如图:
13【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
“航模”所对应的圆心角的度数是:360°× =144°;
(3)设两名男生分别为男1,男2,两名女生分别为女1,女2,列表如下:
男1 男2 女1 女2
男1 (男2,男1) (女1,男1) (女2,男1)
男2 (男1,男2) (女1,男2) (女2,男2)
女1 (男1,女1) (男2,女1) (女2,女1)
女2 (男1,女2) (男2,女2) (女1,女2)
由表格可以看出,所有可能出现的结果有12种,并且它们出现的可能性相等,其中恰
好是1名男生和1名女生的情况有8种.
则所选的2人恰好是1名男生和1名女生的概率是 = .
四、解答题(第21题12分,第22题12分,共24分)
21.(12分)某中学为了创设“书香校园”,准备购买A,B两种书架,用于放置图书.
在购买时发现,A种书架的单价比B种书架的单价多20元,用600元购买A种书架的个
数与用480元购买B种书架的个数相同.
(1)求A,B两种书架的单价各是多少元?
(2)学校准备购买A,B两种书架共15个,且购买的总费用不超过1400元,求最多可
以购买多少个A种书架?
【分析】(1)设B种书架的单价为x元,则A种书架的单价为(x+20)元,根据数量
=总价÷单价结合用600元购买A种书架的个数与用480元购买B种书架的个数相同,
即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设准备购买m个A种书架,则购买B种书架(15﹣m)个,根据题意列出不等式
并解答.
【解答】解:(1)设B种书架的单价为x元,根据题意,得 .
解得x=80.
经检验:x=80是原分式方程的解.
∴x+20=100.
答:购买A种书架需要100元,B种书架需要80元.
14【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
(2)设准备购买m个A种书架,根据题意,得100m+80(15﹣m)≤1400.
解得m≤10.
答:最多可购买10个A种书架.
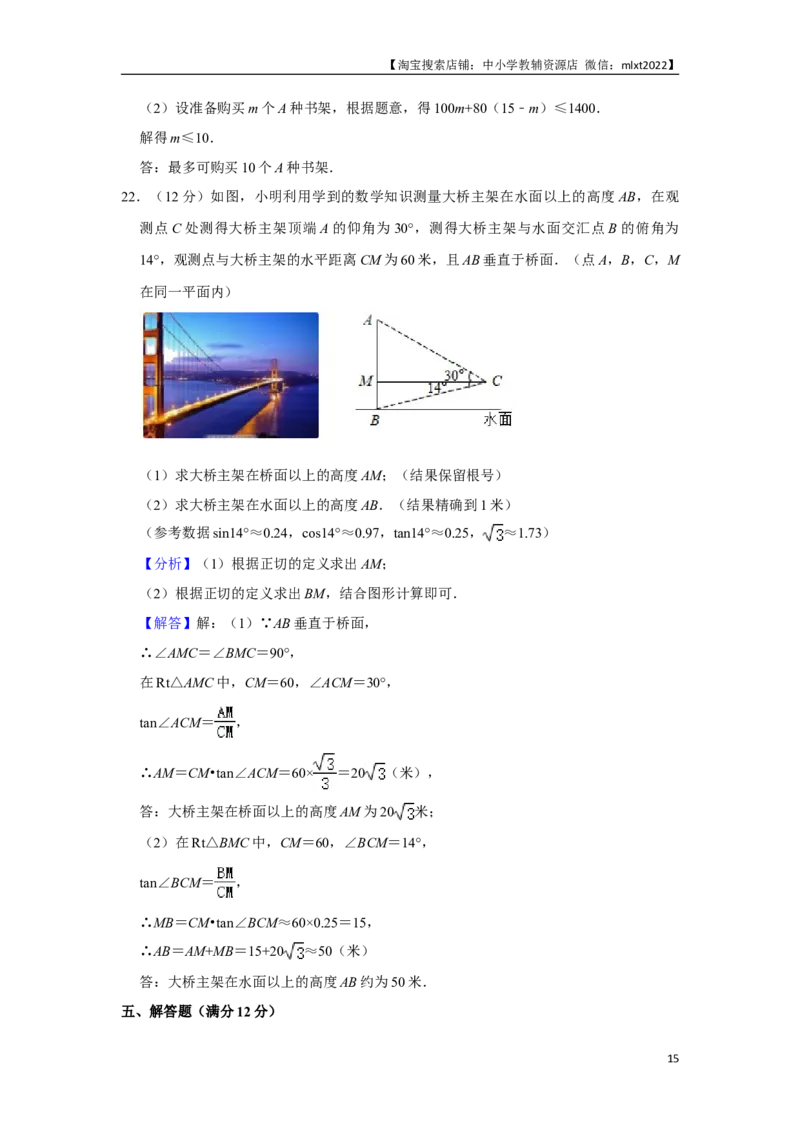
22.(12分)如图,小明利用学到的数学知识测量大桥主架在水面以上的高度AB,在观
测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为
14°,观测点与大桥主架的水平距离CM为60米,且AB垂直于桥面.(点A,B,C,M
在同一平面内)
(1)求大桥主架在桥面以上的高度AM;(结果保留根号)
(2)求大桥主架在水面以上的高度AB.(结果精确到1米)
(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25, ≈1.73)
【分析】(1)根据正切的定义求出AM;
(2)根据正切的定义求出BM,结合图形计算即可.
【解答】解:(1)∵AB垂直于桥面,
∴∠AMC=∠BMC=90°,
在Rt△AMC中,CM=60,∠ACM=30°,
tan∠ACM= ,
∴AM=CM•tan∠ACM=60× =20 (米),
答:大桥主架在桥面以上的高度AM为20 米;
(2)在Rt△BMC中,CM=60,∠BCM=14°,
tan∠BCM= ,
∴MB=CM•tan∠BCM≈60×0.25=15,
∴AB=AM+MB=15+20 ≈50(米)
答:大桥主架在水面以上的高度AB约为50米.
五、解答题(满分12分)
15【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
23.(12分)小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网
店在试销售期间发现,每周销售数量y(本)与销售单价x(元)之间满足一次函数关
系,三对对应值如下表:
销售单价x(元) 12 14 16
每周的销售量y(本) 500 400 300
(1)求y与x之间的函数关系式;
(2)通过与其他网店对比,小红将这款笔记本的单价定为 x元(12≤x≤15,且x为整
数),设每周销售该款笔记本所获利润为w元,当销售单价定为多少元时每周所获利润
最大,最大利润是多少元?
【分析】(1)根据题意和表格中的数据,可以求得y与x之间的函数关系式;
(2)根据题意,可以得到w与x的函数关系式,然后根据二次函数的性质,可以解答
本题.
【解答】解:(1)设y与x之间的函数关系式是y=kx+b(k≠0),
,得 ,
即y与x之间的函数关系式为y=﹣50x+1100;
(2)由题意可得,
w=(x﹣10)y=(x﹣10)(﹣50x+1100)=﹣50(x﹣16)2+1800,
∵a=﹣50<0
∴w有最大值
∴当x<16时,w随x的增大而增大,
∵12≤x≤15,x为整数,
∴当x=15时,w有最大值,
∴w=﹣50(15﹣16)2+1800=1750,
答:销售单价为15元时,每周获利最大,最大利润是1750元.
六、解答题(满分12分)
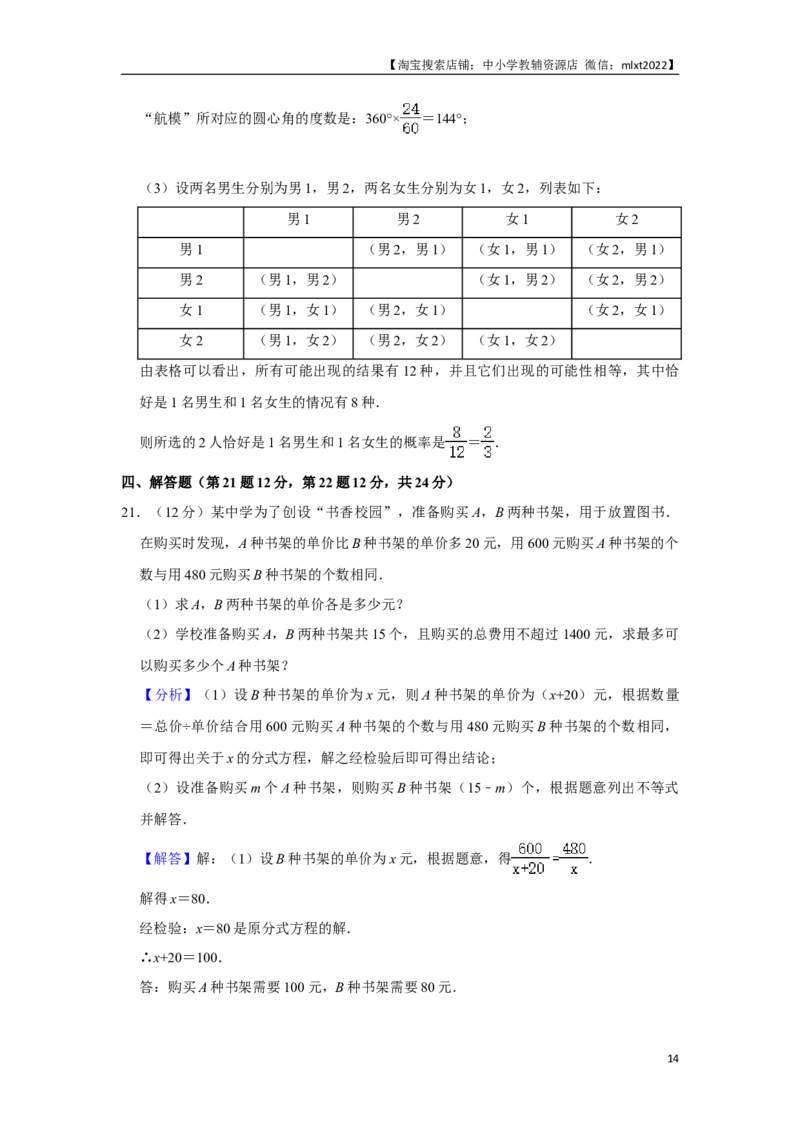
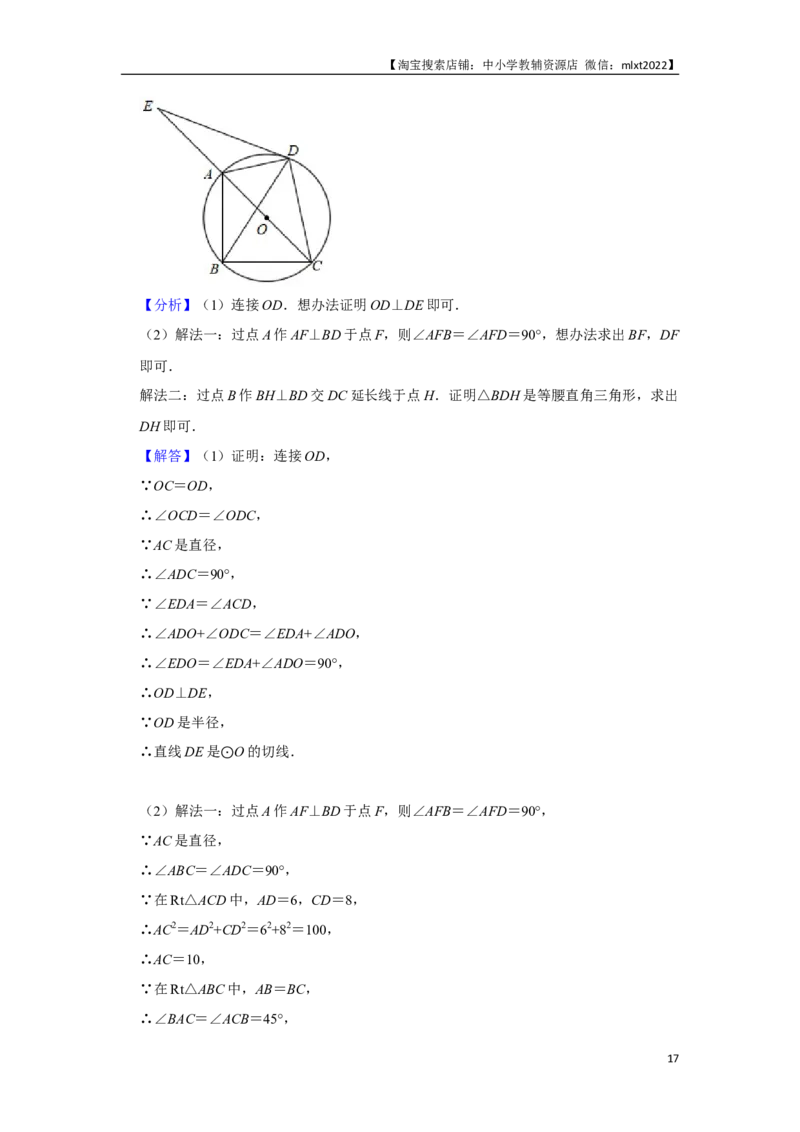
24.(12分)如图,四边形ABCD内接于 O,AC是直径,AB=BC,连接BD,过点D的
直线与CA的延长线相交于点E,且∠E⊙DA=∠ACD.
(1)求证:直线DE是 O的切线;
(2)若AD=6,CD=8⊙,求BD的长.
16【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
【分析】(1)连接OD.想办法证明OD⊥DE即可.
(2)解法一:过点A作AF⊥BD于点F,则∠AFB=∠AFD=90°,想办法求出BF,DF
即可.
解法二:过点B作BH⊥BD交DC延长线于点H.证明△BDH是等腰直角三角形,求出
DH即可.
【解答】(1)证明:连接OD,
∵OC=OD,
∴∠OCD=∠ODC,
∵AC是直径,
∴∠ADC=90°,
∵∠EDA=∠ACD,
∴∠ADO+∠ODC=∠EDA+∠ADO,
∴∠EDO=∠EDA+∠ADO=90°,
∴OD⊥DE,
∵OD是半径,
∴直线DE是 O的切线.
⊙
(2)解法一:过点A作AF⊥BD于点F,则∠AFB=∠AFD=90°,
∵AC是直径,
∴∠ABC=∠ADC=90°,
∵在Rt△ACD中,AD=6,CD=8,
∴AC2=AD2+CD2=62+82=100,
∴AC=10,
∵在Rt△ABC中,AB=BC,
∴∠BAC=∠ACB=45°,
17【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∵ ,
∴ ,
∵∠ADB=∠ACB=45°,
∵在Rt△ADF中,AD=6,
∵ ,
∴ ,
∴ ,
∵在Rt△ABF中,
∴ ,
∴ ,
∴ .
解法二:过点B作BH⊥BD交DC延长线于点H.
∴∠DBH=90°,
∵AC是直径,
∴∠ABC=90°,
∵∠ABD=90°﹣∠DBC∠CBH=90°﹣∠DBC,
∴∠ABD=∠CBH,
∵四边形ABCD内接于 O,
∴∠BAD+∠BCD=180°⊙,
∵∠BCD+∠BCH=180°,
∴∠BAD=∠BCH,
∵AB=CB,
∴△ABD≌△CBH(ASA),
∴AD=CH,BD=BH,
∵AD=6,CD=8,
∴DH=CD+CH=14,
在Rt△BDH中,∵BD2=DH2﹣BH2=98,
∴ .
18【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
七、解答题(满分12分)
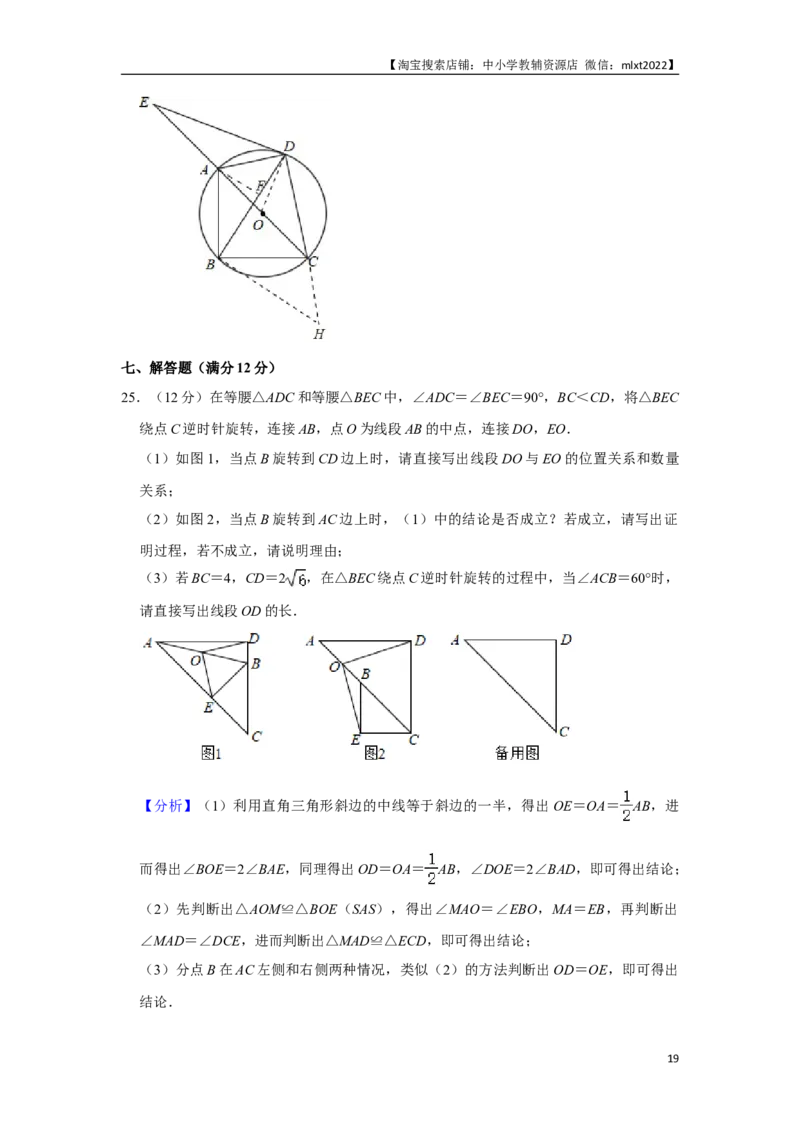
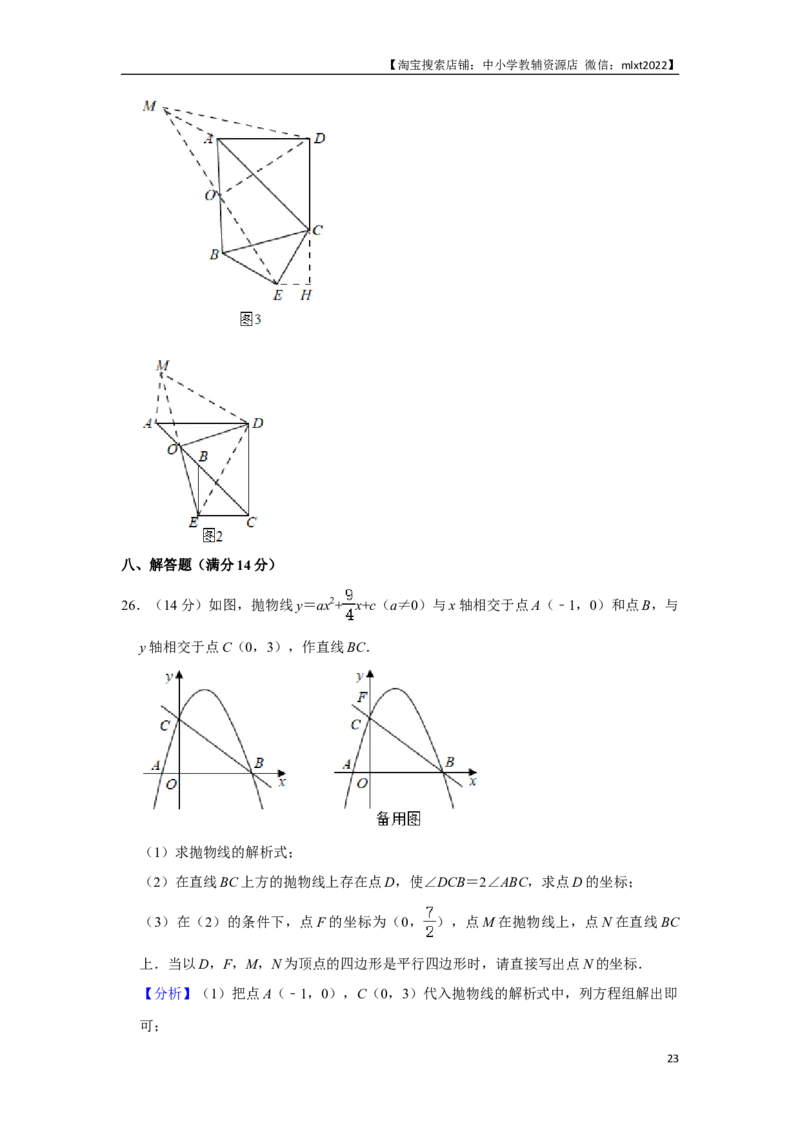
25.(12分)在等腰△ADC和等腰△BEC中,∠ADC=∠BEC=90°,BC<CD,将△BEC
绕点C逆时针旋转,连接AB,点O为线段AB的中点,连接DO,EO.
(1)如图1,当点B旋转到CD边上时,请直接写出线段DO与EO的位置关系和数量
关系;
(2)如图2,当点B旋转到AC边上时,(1)中的结论是否成立?若成立,请写出证
明过程,若不成立,请说明理由;
(3)若BC=4,CD=2 ,在△BEC绕点C逆时针旋转的过程中,当∠ACB=60°时,
请直接写出线段OD的长.
【分析】(1)利用直角三角形斜边的中线等于斜边的一半,得出OE=OA= AB,进
而得出∠BOE=2∠BAE,同理得出OD=OA= AB,∠DOE=2∠BAD,即可得出结论;
(2)先判断出△AOM≌△BOE(SAS),得出∠MAO=∠EBO,MA=EB,再判断出
∠MAD=∠DCE,进而判断出△MAD≌△ECD,即可得出结论;
(3)分点B在AC左侧和右侧两种情况,类似(2)的方法判断出OD=OE,即可得出
结论.
19【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
【解答】解:(1)DO⊥EO,DO=EO;
理由:当点B旋转到CD边上时,点E必在边AC上,
∴∠AEB=∠CEB=90°,
在Rt△ABE中,点O是AB的中点,
∴OE=OA= AB,
∴∠BOE=2∠BAE,
在Rt△ABD中,点O是AB的中点,
∴OD=OA= AB,
∴∠DOE=2∠BAD,
∴OD=OE,
∵等腰△ADC,且∠ADC=90°,
∴∠DAC=45°,
∴∠DOE=∠BOE+DOE=2∠BAE+2∠BAD=2(∠BAE+∠DAE)=2∠DAC=90°,
∴OD⊥OE;
(2)仍然成立,
理由:如图1,延长ED到点M,使得OM=OE,连接AM,DM,DE,
∵O是AB的中点,
∴OA=OB,
∵∠AOM=∠BOE,
∴△AOM≌△BOE(SAS),
∴∠MAO=∠EBO,MA=EB,
∵△ACD和△CBE是等腰三角形,∠ADC=∠CEB=90°,
∴∠CAD=∠ACD=∠EBC=∠BCE=45°,
∵∠OBE=180°﹣∠EBC=135°,
∴∠MAO=135°,
∴∠MAD=∠MAO﹣∠DAC=90°,
∵∠DCE=∠DCA+∠BCE=90°,
∴∠MAD=∠DCE,
∵MA=EB,EB=EC,
20【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∴MA=EC,
∵AD=DC,
∴△MAD≌△ECD,
∴MD=ED,∠ADM=∠CDE,
∵∠CDE+∠ADE=90°,
∴∠ADM+∠ADE=90°,
∴∠MDE=90°,
∵MO=EO,MD=DE,
∴ ,OD⊥ME,
∵ ,
∴OD=OE,OD⊥OE;
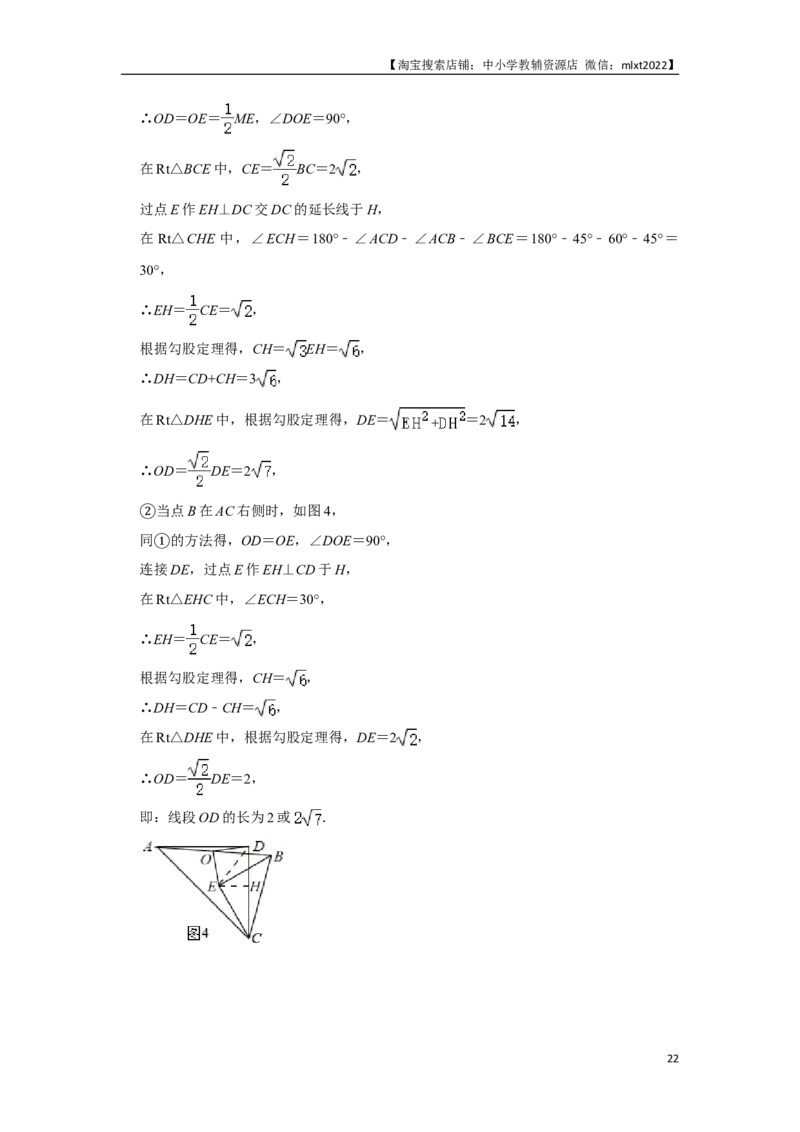
(3) 当点B在AC左侧时,如图3,
延长E①D到点M,使得OM=OE,连接AM,DM,DE,
同(2)的方法得,△OBE≌△OAM(SAS),
∴∠OBE=∠OAM,OM=OE,BE=AM,
∵BE=CE,
∴AM=CE,
在四边形ABECD中,∠ADC+∠DCE+∠BEC+∠OBE+∠BAD=540°,
∵∠ADC=∠BEC=90°,
∴∠DCE=540°﹣90°﹣90°﹣∠OBE﹣∠BAD=360°﹣∠OBE=360°﹣∠OAM﹣
∠BAD,
∵∠DAM+∠OAM+∠BAD=360°,
∴∠DAM=360°﹣∠OAM﹣∠BAD,
∴∠DAM=∠DCE,
∵AD=CD,
∴△DAM≌△DCE(SAS),
∴DM=DE,∠ADM=∠CDE,
∴∠EDM=∠ADM+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∵OM=OE,
21【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∴OD=OE= ME,∠DOE=90°,
在Rt△BCE中,CE= BC=2 ,
过点E作EH⊥DC交DC的延长线于H,
在 Rt△CHE 中,∠ECH=180°﹣∠ACD﹣∠ACB﹣∠BCE=180°﹣45°﹣60°﹣45°=
30°,
∴EH= CE= ,
根据勾股定理得,CH= EH= ,
∴DH=CD+CH=3 ,
在Rt△DHE中,根据勾股定理得,DE= =2 ,
∴OD= DE=2 ,
当点B在AC右侧时,如图4,
②同 的方法得,OD=OE,∠DOE=90°,
连①接DE,过点E作EH⊥CD于H,
在Rt△EHC中,∠ECH=30°,
∴EH= CE= ,
根据勾股定理得,CH= ,
∴DH=CD﹣CH= ,
在Rt△DHE中,根据勾股定理得,DE=2 ,
∴OD= DE=2,
即:线段OD的长为2或 .
22【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
八、解答题(满分14分)
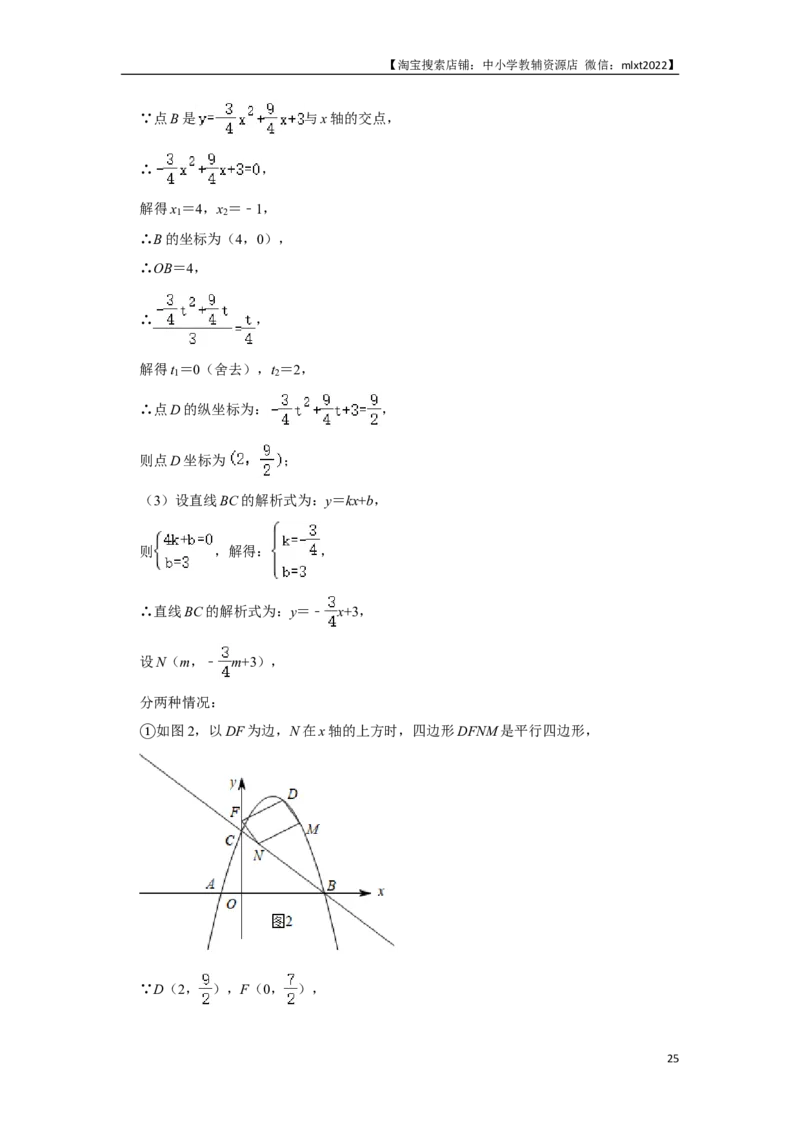
26.(14分)如图,抛物线y=ax2+ x+c(a≠0)与x轴相交于点A(﹣1,0)和点B,与
y轴相交于点C(0,3),作直线BC.
(1)求抛物线的解析式;
(2)在直线BC上方的抛物线上存在点D,使∠DCB=2∠ABC,求点D的坐标;
(3)在(2)的条件下,点F的坐标为(0, ),点M在抛物线上,点N在直线BC
上.当以D,F,M,N为顶点的四边形是平行四边形时,请直接写出点N的坐标.
【分析】(1)把点A(﹣1,0),C(0,3)代入抛物线的解析式中,列方程组解出即
可;
23【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
(2)如图1,作辅助线,构建相似三角形,证明△DCH∽△CBO,则 ,设点D
的横坐标为t,则 ,列关于t的方程解出可得结论;
(3)利用待定系数法求直线BC的解析式为:y=﹣ x+3,设N(m,﹣ m+3),当
以D,F,M,N为顶点的四边形是平行四边形时,存在两种情况:如图2和图3,分别
画图,根据平移的性质可表示M的坐标,代入抛物线的解析式列方程可解答.
【解答】解:(1)∵抛物线 经过点A(﹣1,0),C(0,3),
∴ ,解得: ,
∴抛物线的解析式为: ;
(2)如图1,过点C作CE∥x轴交抛物线于点E,则∠ECB=∠ABC,
过点D作DH⊥CE于点H,则∠DHC=90°,
∵∠DCB=∠DCH+∠ECB=2∠ABC,
∴∠DCH=∠ABC,
∵∠DHC=∠COB=90°,
∴△DCH∽△CBO,
∴ ,
设点D的横坐标为t,则 ,
∵C(0,3),
∴ ,
24【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∵点B是 与x轴的交点,
∴ ,
解得x =4,x =﹣1,
1 2
∴B的坐标为(4,0),
∴OB=4,
∴ ,
解得t =0(舍去),t =2,
1 2
∴点D的纵坐标为: ,
则点D坐标为 ;
(3)设直线BC的解析式为:y=kx+b,
则 ,解得: ,
∴直线BC的解析式为:y=﹣ x+3,
设N(m,﹣ m+3),
分两种情况:
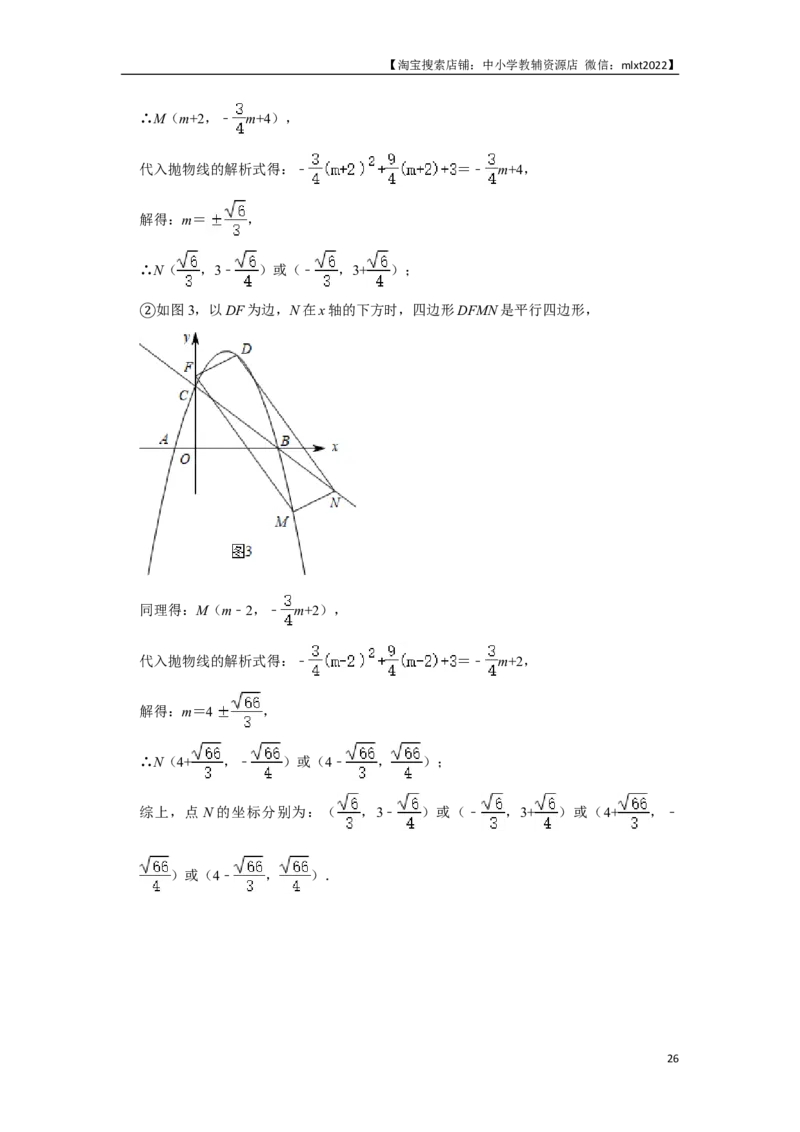
如图2,以DF为边,N在x轴的上方时,四边形DFNM是平行四边形,
①
∵D(2, ),F(0, ),
25【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
∴M(m+2,﹣ m+4),
代入抛物线的解析式得:﹣ =﹣ m+4,
解得:m= ,
∴N( ,3﹣ )或(﹣ ,3+ );
如图3,以DF为边,N在x轴的下方时,四边形DFMN是平行四边形,
②
同理得:M(m﹣2,﹣ m+2),
代入抛物线的解析式得:﹣ =﹣ m+2,
解得:m=4 ,
∴N(4+ ,﹣ )或(4﹣ , );
综上,点 N的坐标分别为:( ,3﹣ )或(﹣ ,3+ )或(4+ ,﹣
)或(4﹣ , ).
26