文档内容
2021年贵州省毕节市中考数学试卷
一、选择题(本题15小题,每小题3分,共45分)
1.(3分)(2021•毕节市)下列各数中,为无理数的是
A. B. C.0 D.
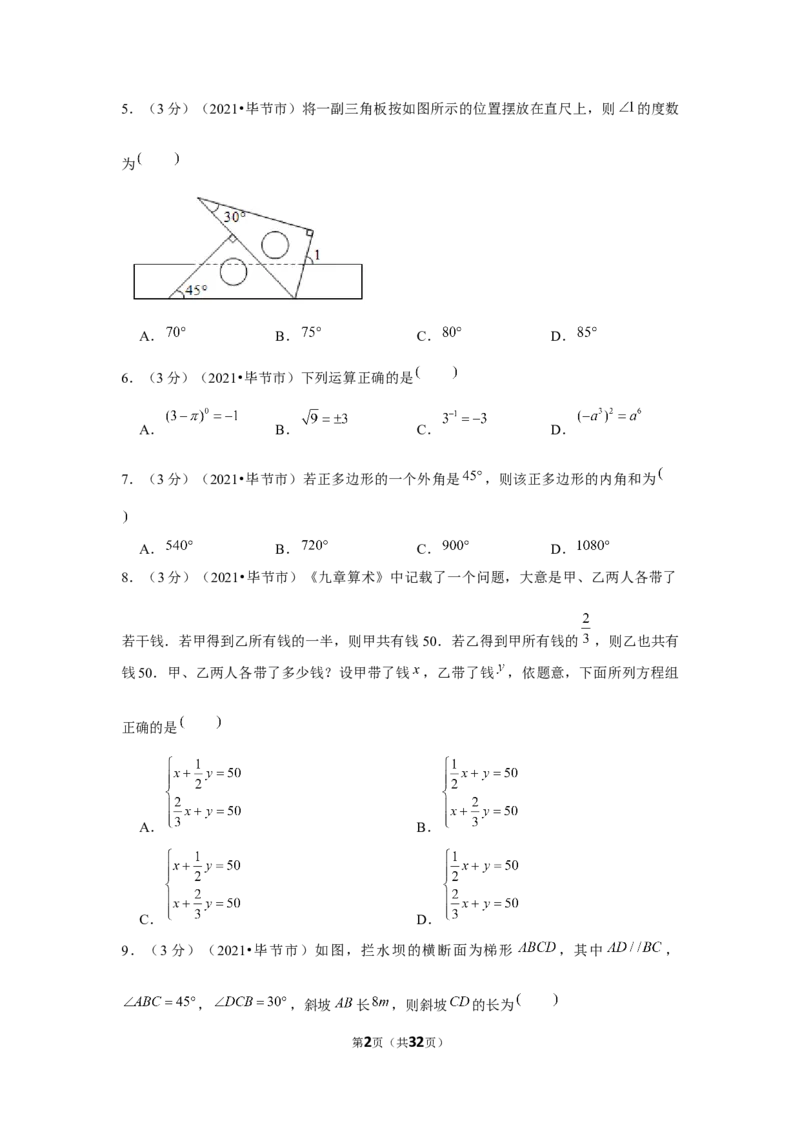
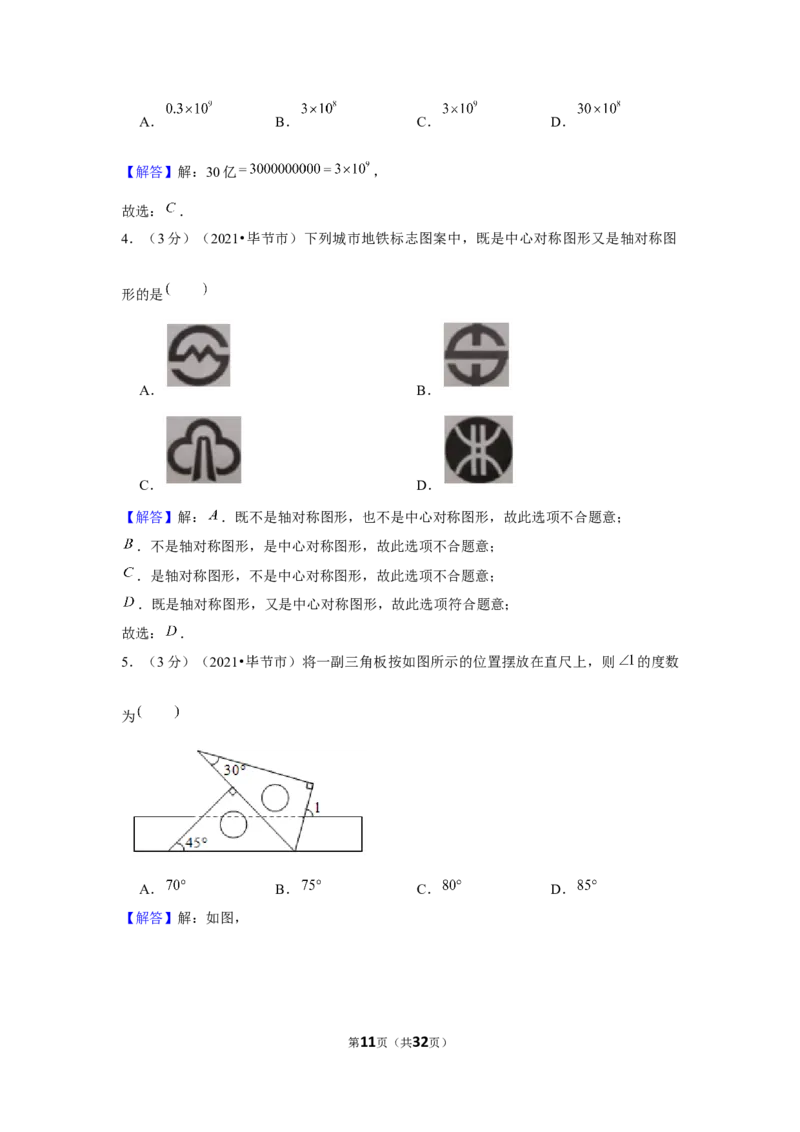
2.(3分)(2021•毕节市)如图所示的几何体,其左视图是
A. B. C. D.
3.(3分)(2021•毕节市)6月6日是全国“放鱼日”为促进渔业绿色发展,今年“放鱼
日”当天,全国同步举办增殖放流200余场,放流各类水生生物苗种近30亿尾.数30亿
用科学记数法表示为
A. B. C. D.
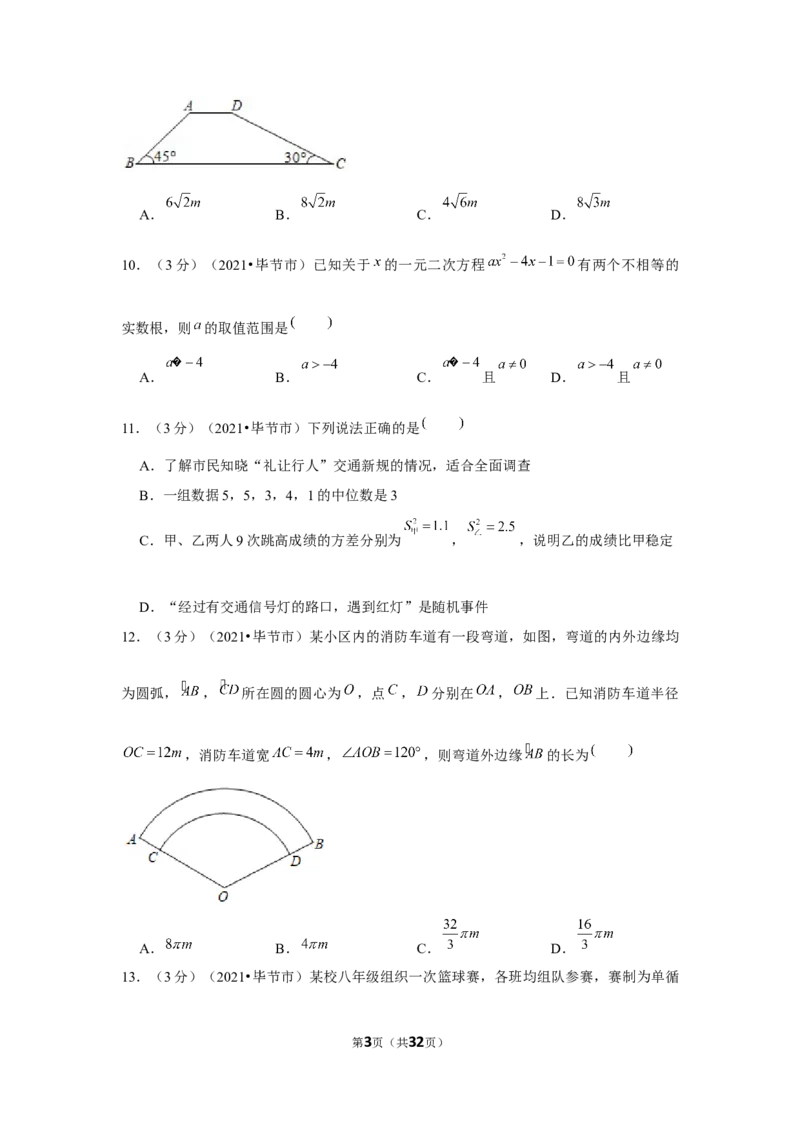
4.(3分)(2021•毕节市)下列城市地铁标志图案中,既是中心对称图形又是轴对称图
形的是
A. B.
C. D.
第1页(共32页)5.(3分)(2021•毕节市)将一副三角板按如图所示的位置摆放在直尺上,则 的度数
为
A. B. C. D.
6.(3分)(2021•毕节市)下列运算正确的是
A. B. C. D.
7.(3分)(2021•毕节市)若正多边形的一个外角是 ,则该正多边形的内角和为
A. B. C. D.
8.(3分)(2021•毕节市)《九章算术》中记载了一个问题,大意是甲、乙两人各带了
若干钱.若甲得到乙所有钱的一半,则甲共有钱50.若乙得到甲所有钱的 ,则乙也共有
钱50.甲、乙两人各带了多少钱?设甲带了钱 ,乙带了钱 ,依题意,下面所列方程组
正确的是
A. B.
C. D.
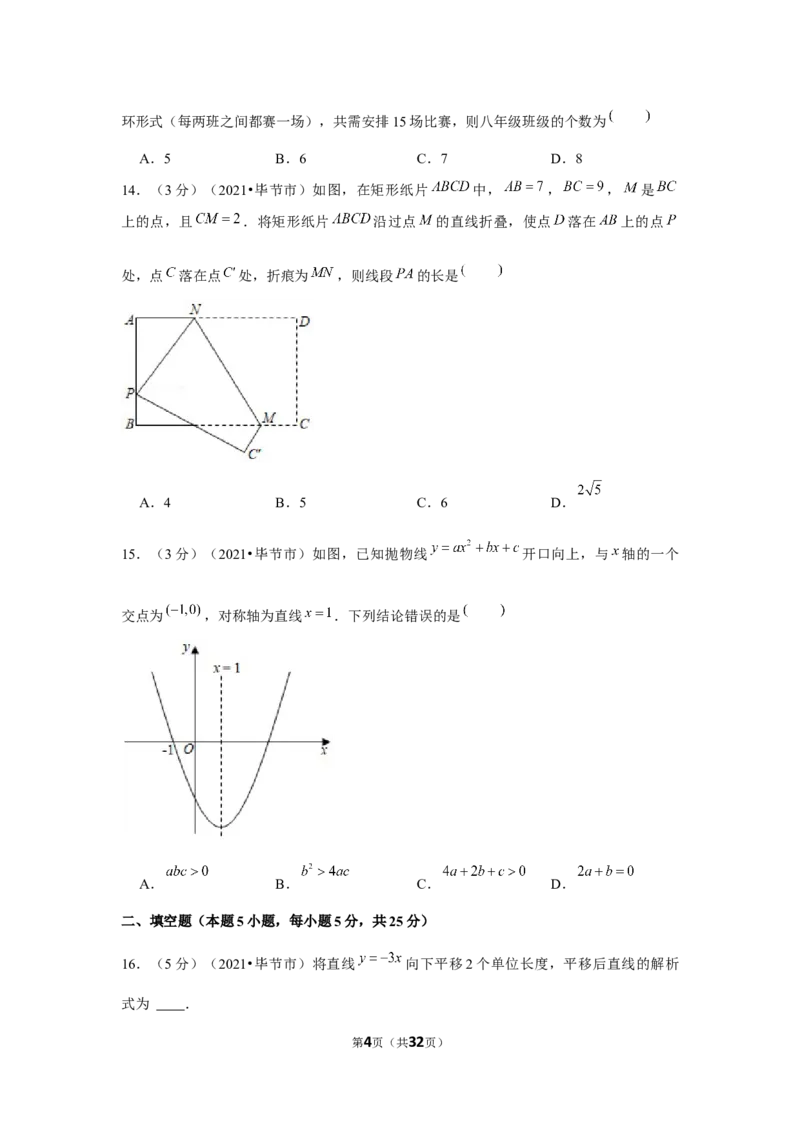
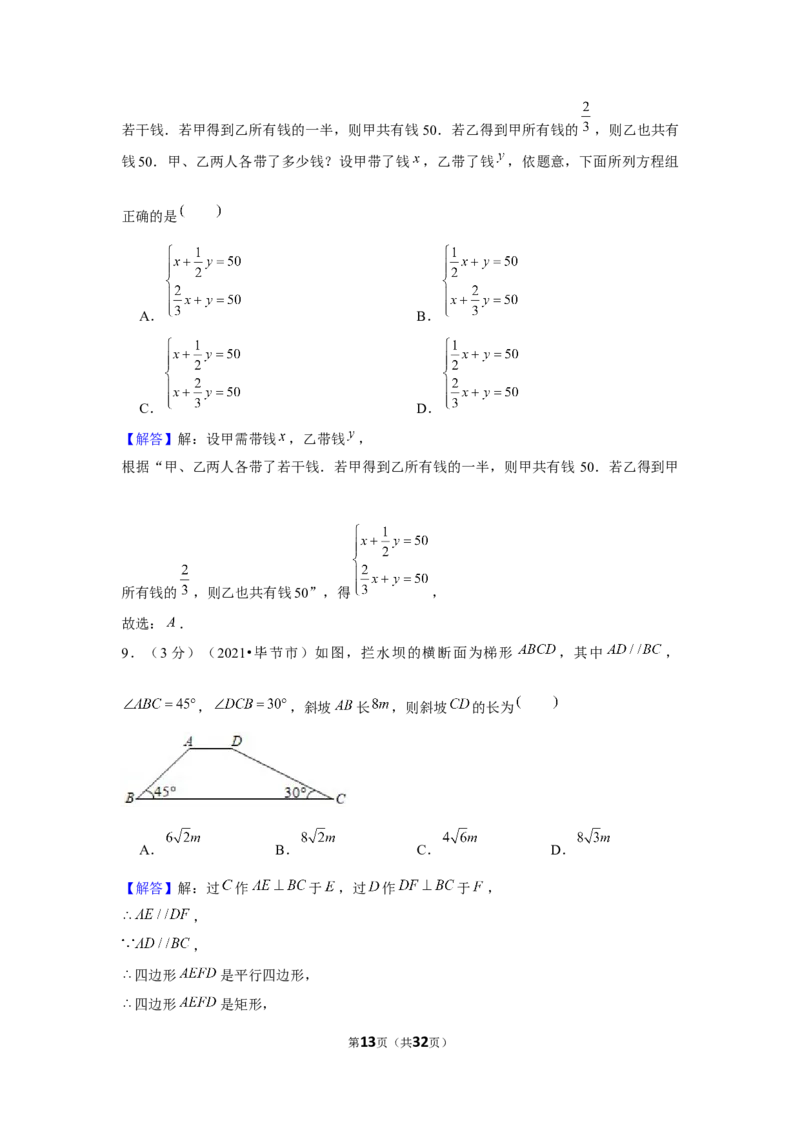
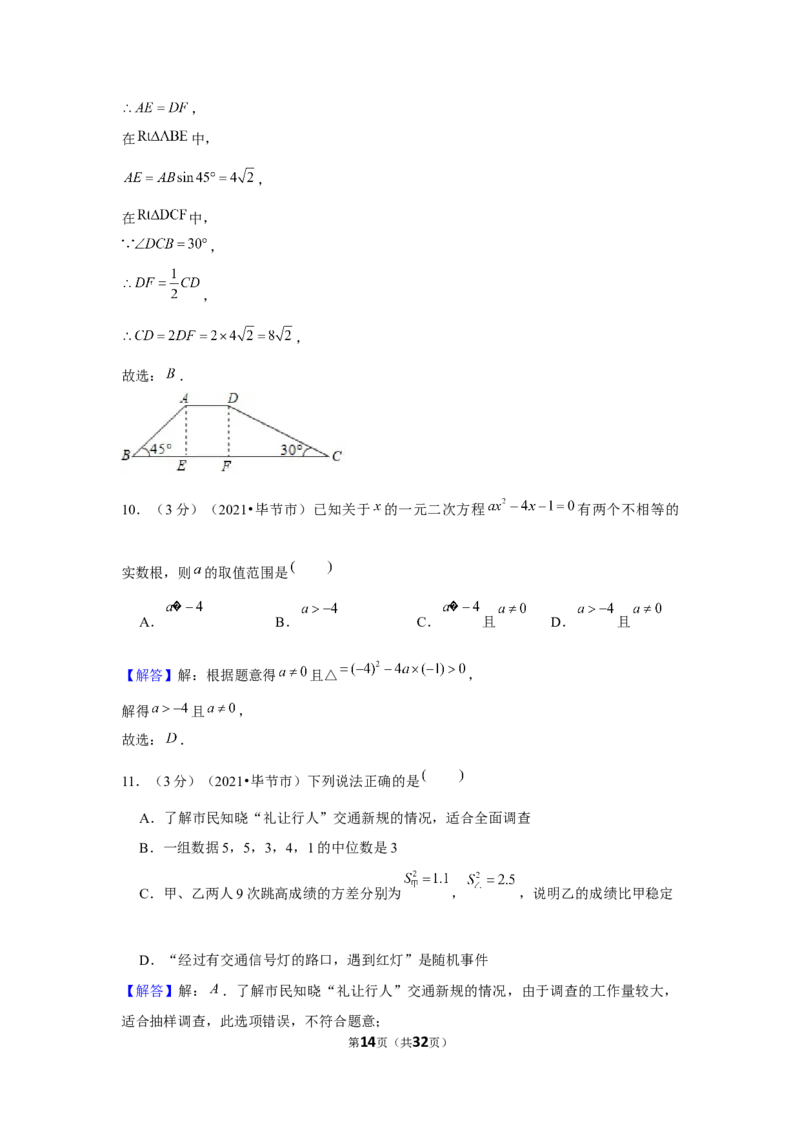
9.(3分)(2021•毕节市)如图,拦水坝的横断面为梯形 ,其中 ,
, ,斜坡 长 ,则斜坡 的长为
第2页(共32页)A. B. C. D.
10.(3分)(2021•毕节市)已知关于 的一元二次方程 有两个不相等的
实数根,则 的取值范围是
A. B. C. 且 D. 且
11.(3分)(2021•毕节市)下列说法正确的是
A.了解市民知晓“礼让行人”交通新规的情况,适合全面调查
B.一组数据5,5,3,4,1的中位数是3
C.甲、乙两人9次跳高成绩的方差分别为 , ,说明乙的成绩比甲稳定
D.“经过有交通信号灯的路口,遇到红灯”是随机事件
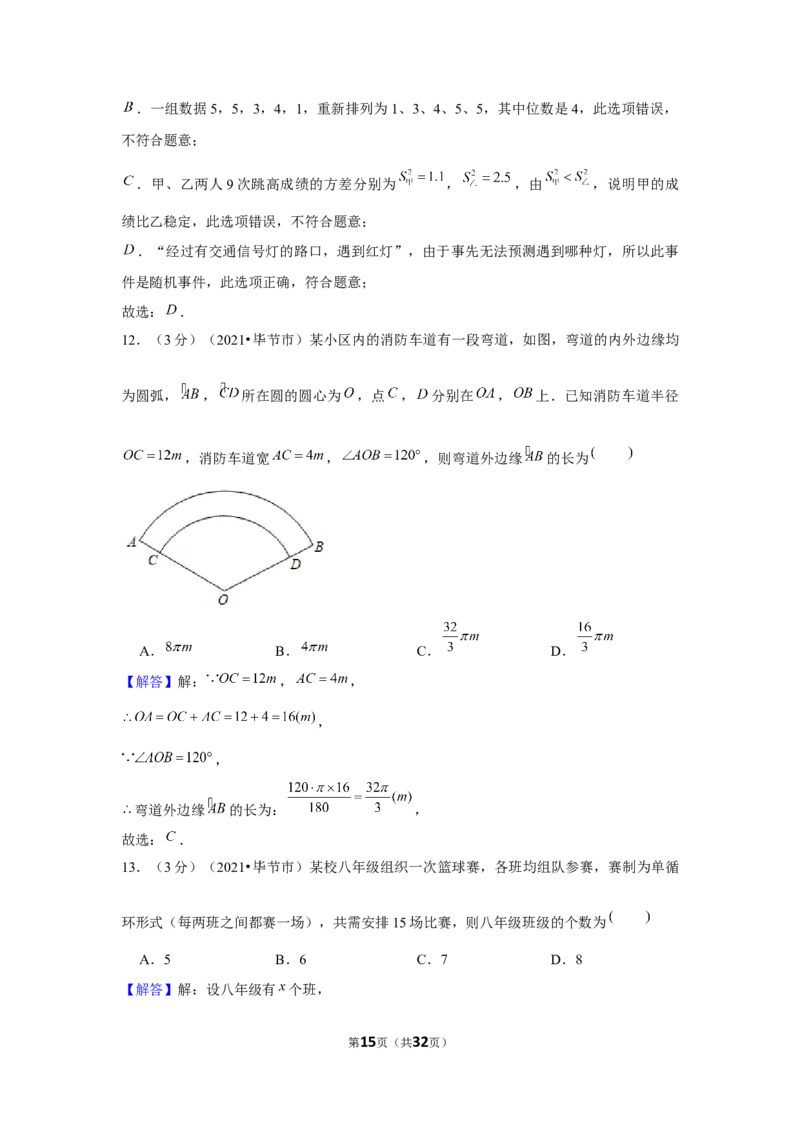
12.(3分)(2021•毕节市)某小区内的消防车道有一段弯道,如图,弯道的内外边缘均
为圆弧, , 所在圆的圆心为 ,点 , 分别在 , 上.已知消防车道半径
,消防车道宽 , ,则弯道外边缘 的长为
A. B. C. D.
13.(3分)(2021•毕节市)某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循
第3页(共32页)环形式(每两班之间都赛一场),共需安排15场比赛,则八年级班级的个数为
A.5 B.6 C.7 D.8
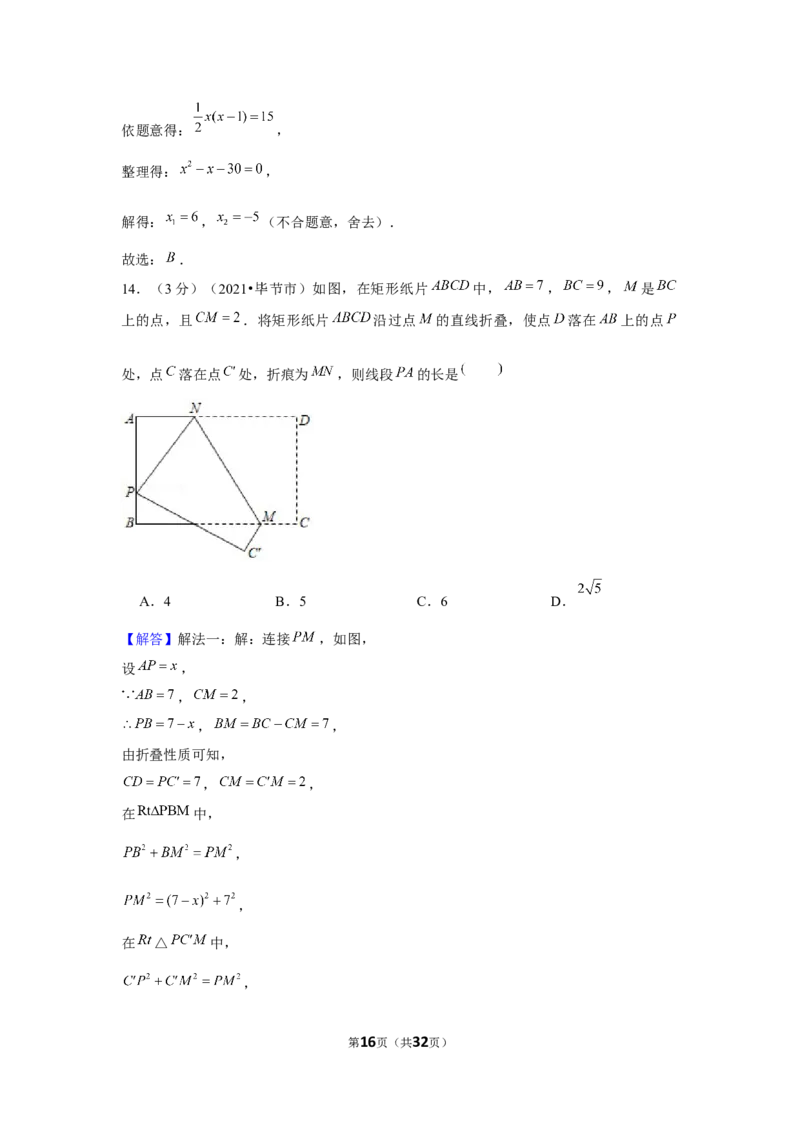
14.(3分)(2021•毕节市)如图,在矩形纸片 中, , , 是
上的点,且 .将矩形纸片 沿过点 的直线折叠,使点 落在 上的点
处,点 落在点 处,折痕为 ,则线段 的长是
A.4 B.5 C.6 D.
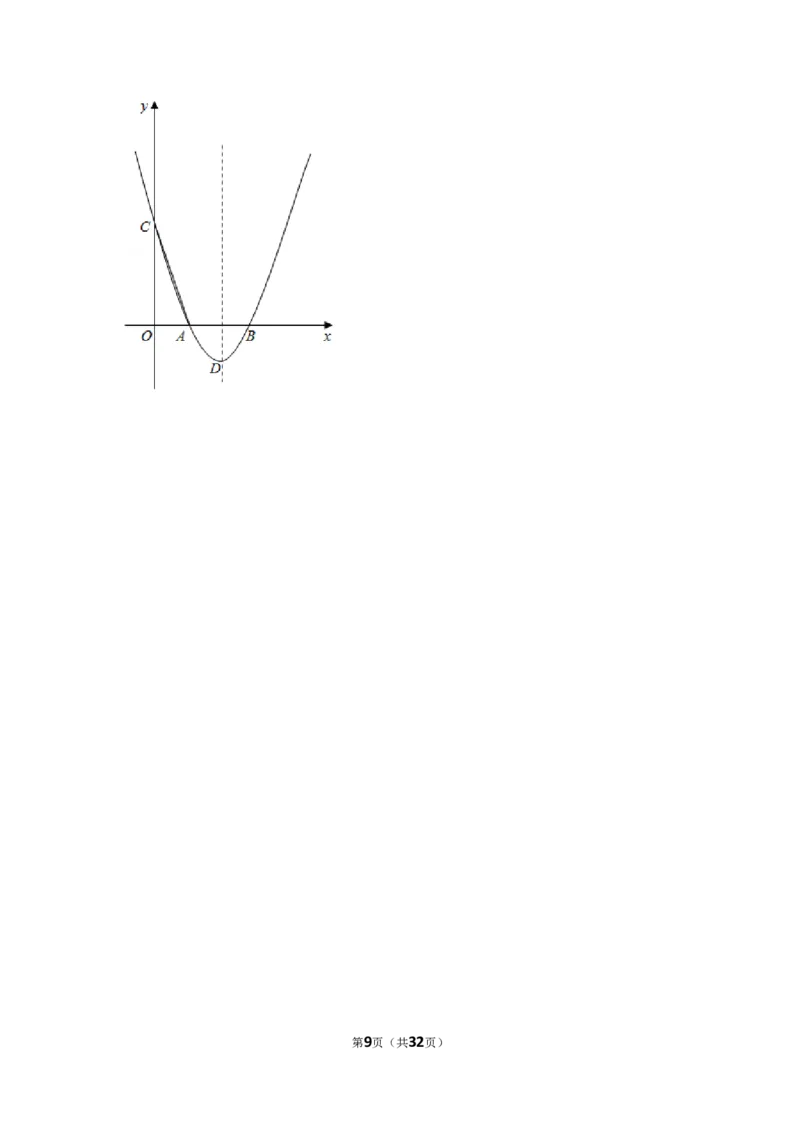
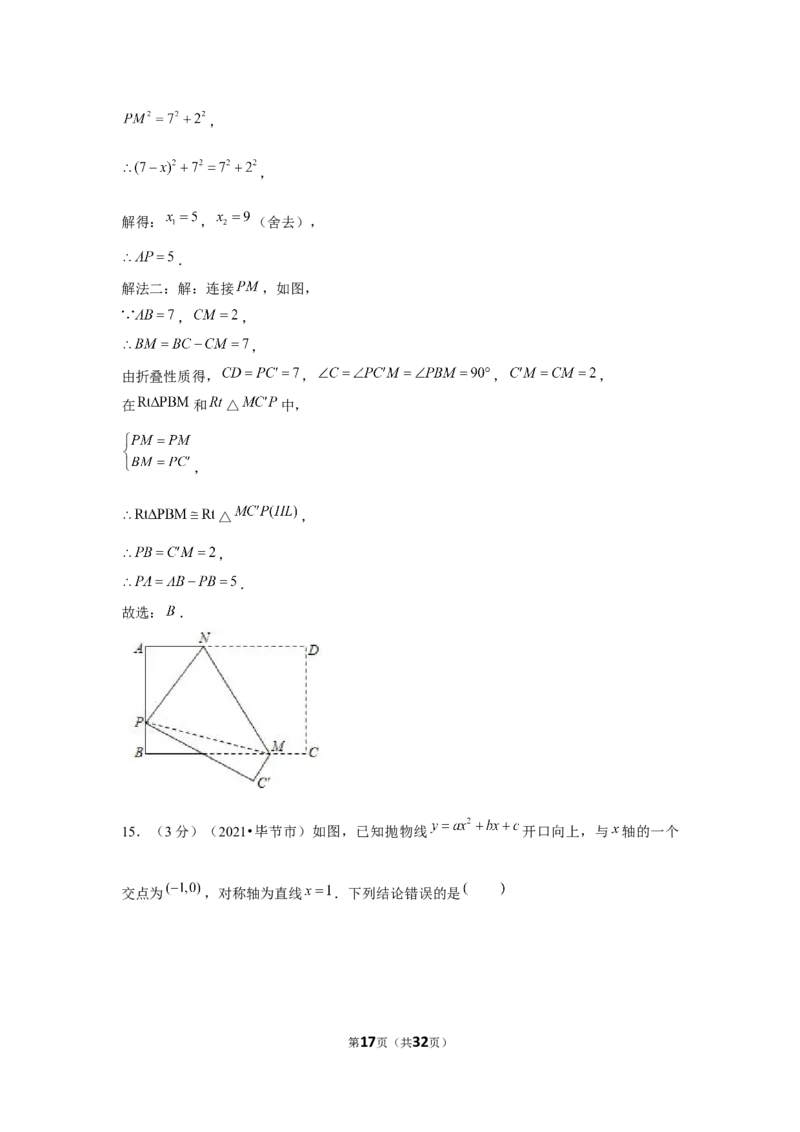
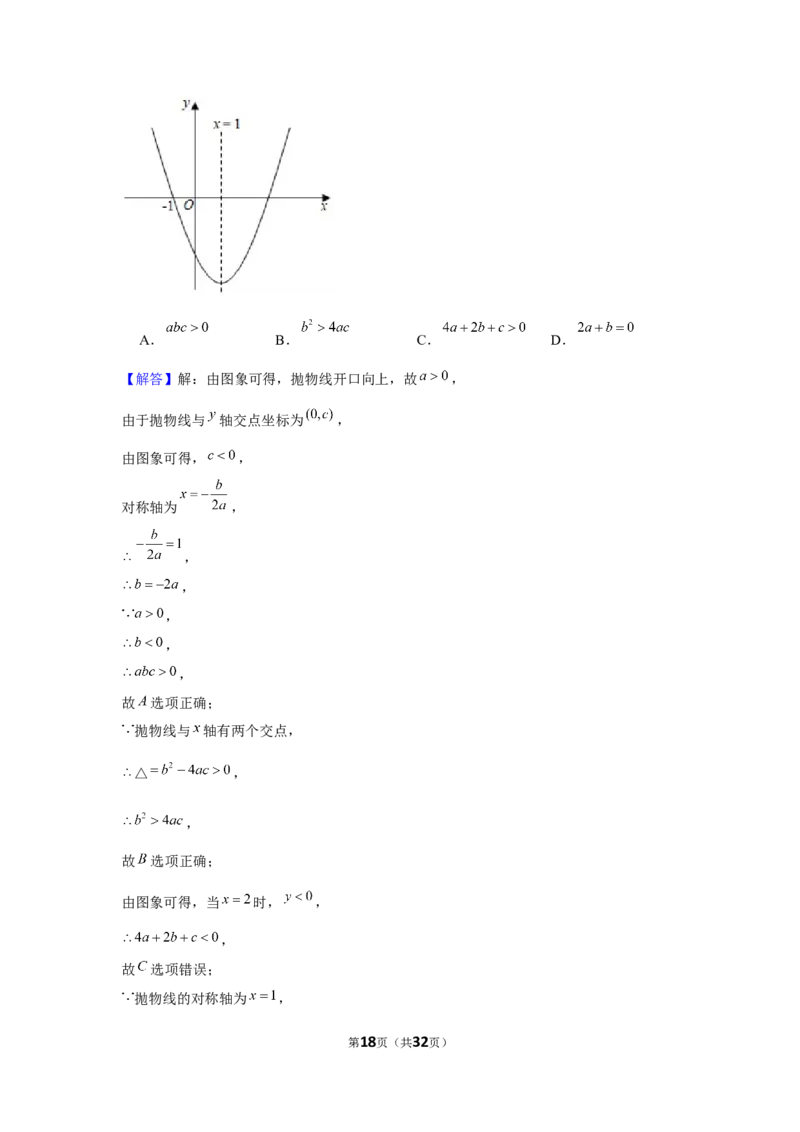
15.(3分)(2021•毕节市)如图,已知抛物线 开口向上,与 轴的一个
交点为 ,对称轴为直线 .下列结论错误的是
A. B. C. D.
二、填空题(本题5小题,每小题5分,共25分)
16.(5分)(2021•毕节市)将直线 向下平移2个单位长度,平移后直线的解析
式为 .
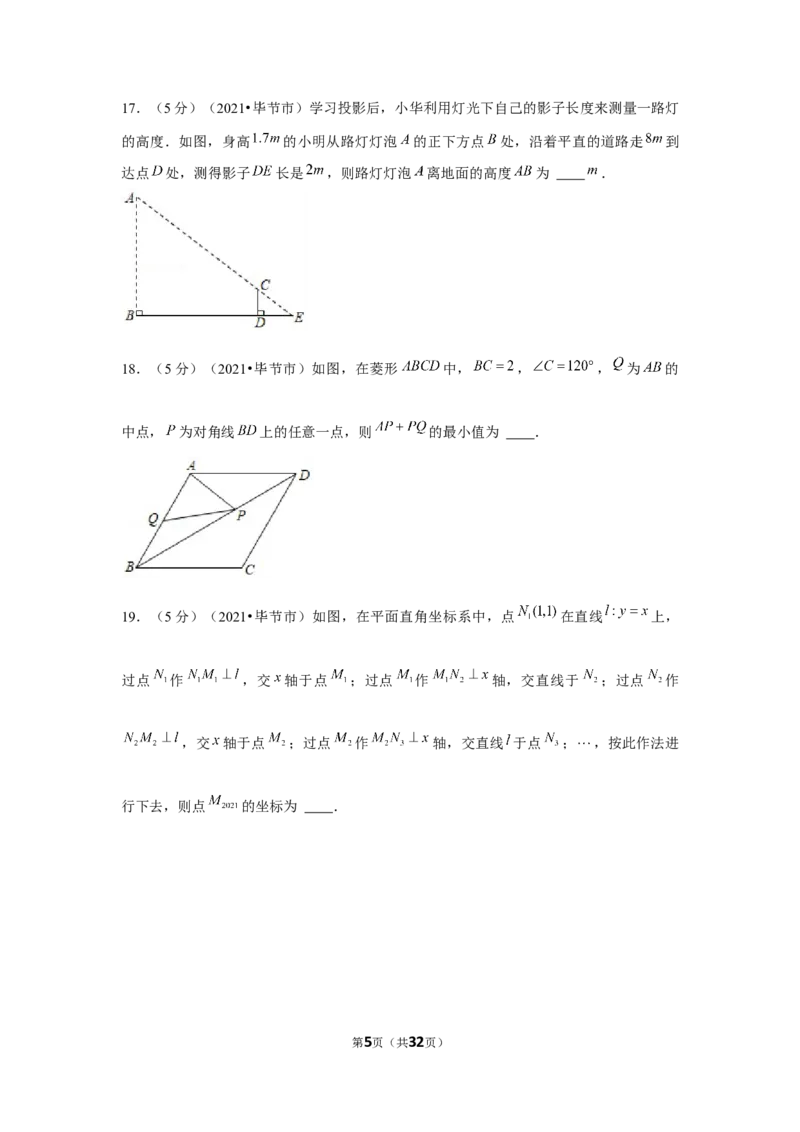
第4页(共32页)17.(5分)(2021•毕节市)学习投影后,小华利用灯光下自己的影子长度来测量一路灯
的高度.如图,身高 的小明从路灯灯泡 的正下方点 处,沿着平直的道路走 到
达点 处,测得影子 长是 ,则路灯灯泡 离地面的高度 为 .
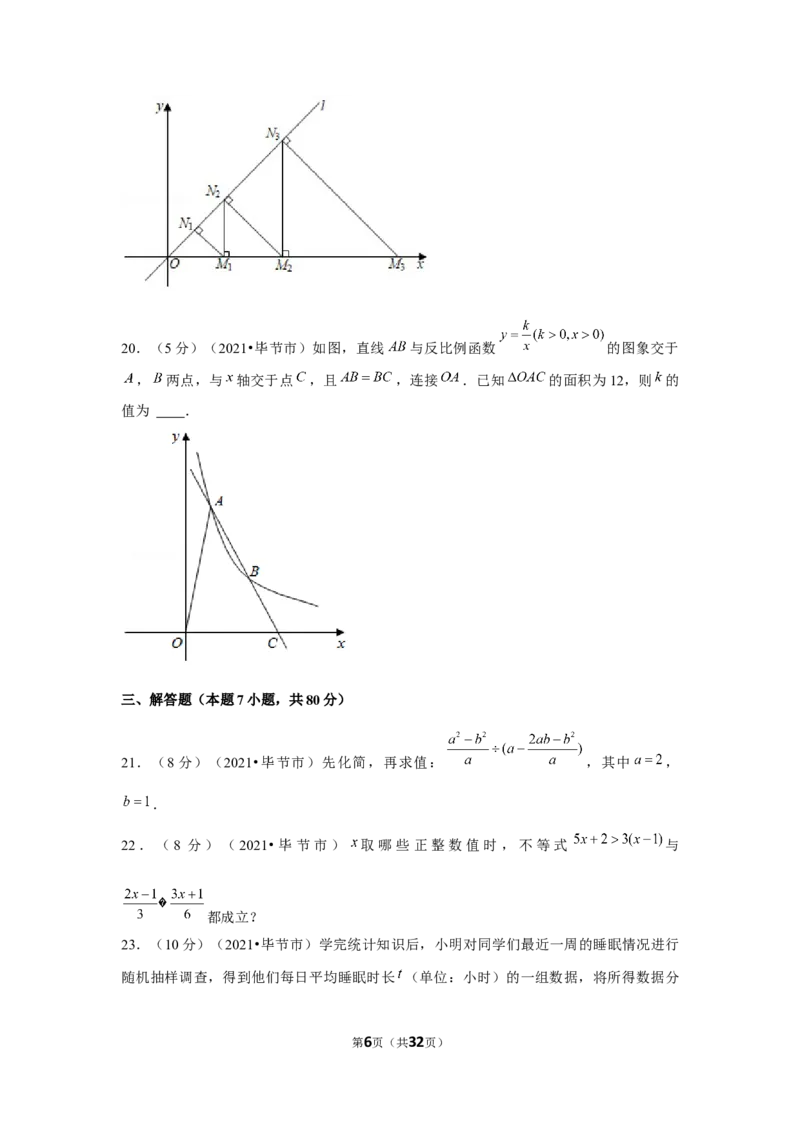
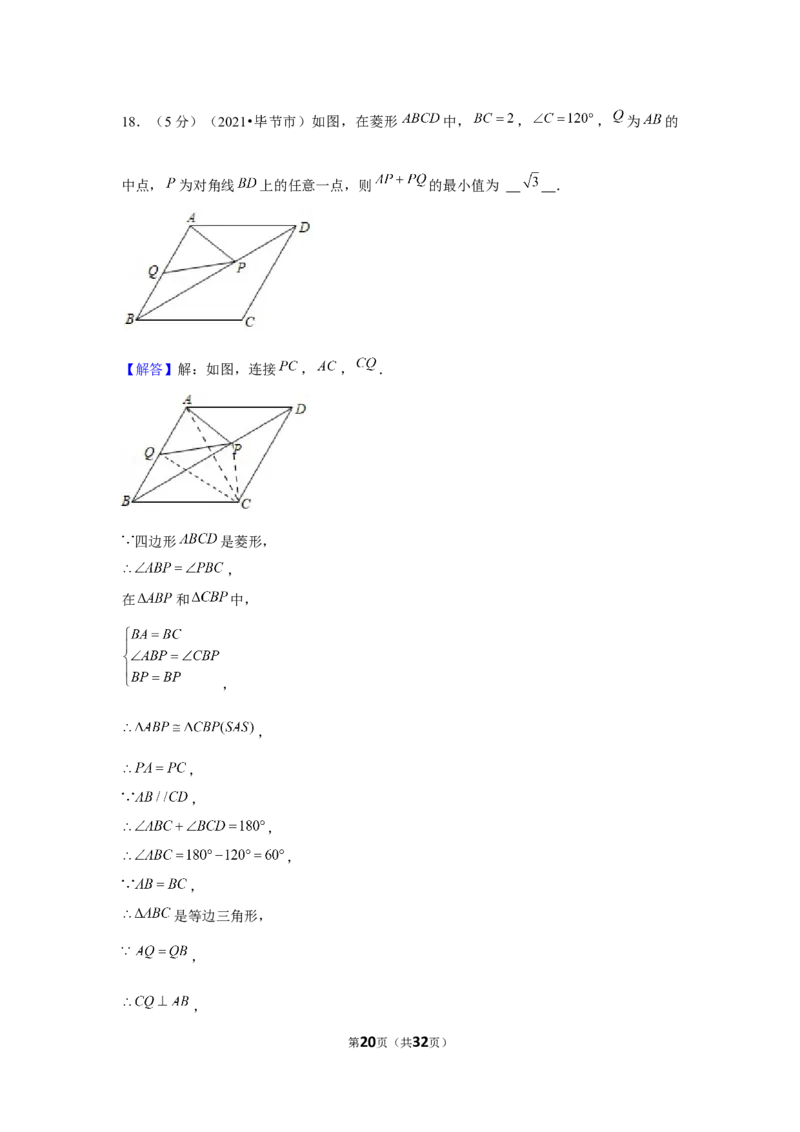
18.(5分)(2021•毕节市)如图,在菱形 中, , , 为 的
中点, 为对角线 上的任意一点,则 的最小值为 .
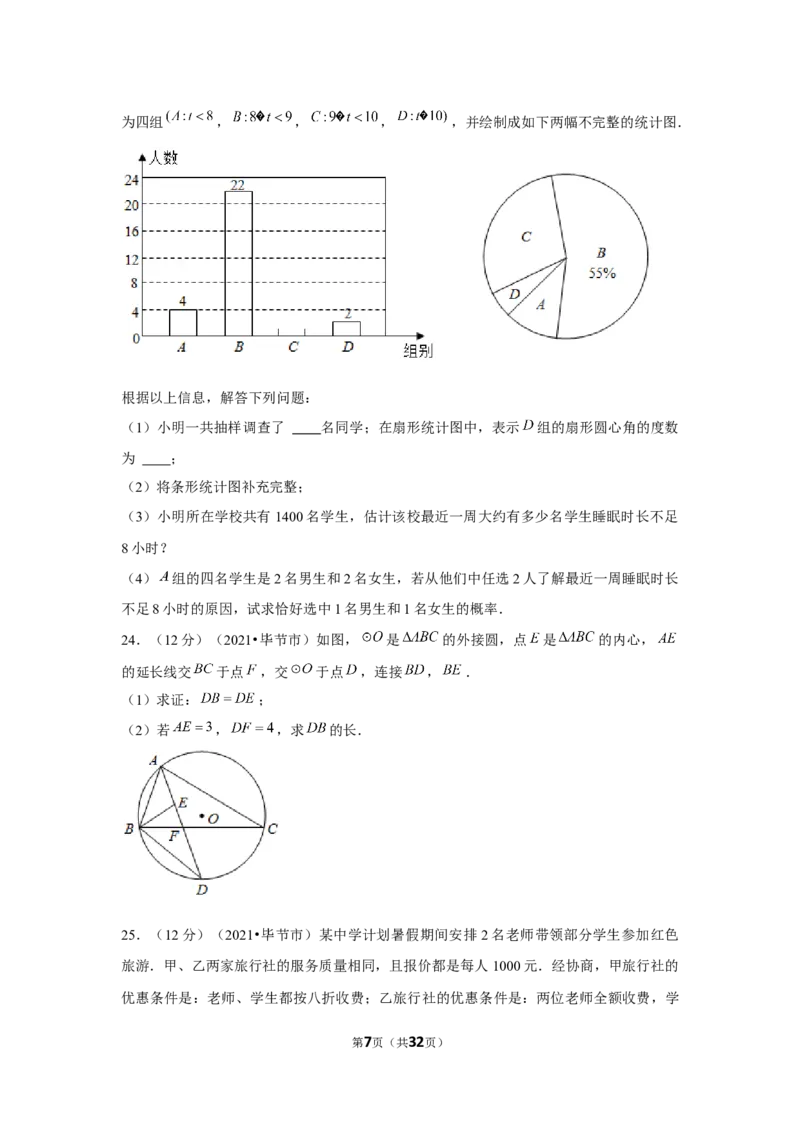
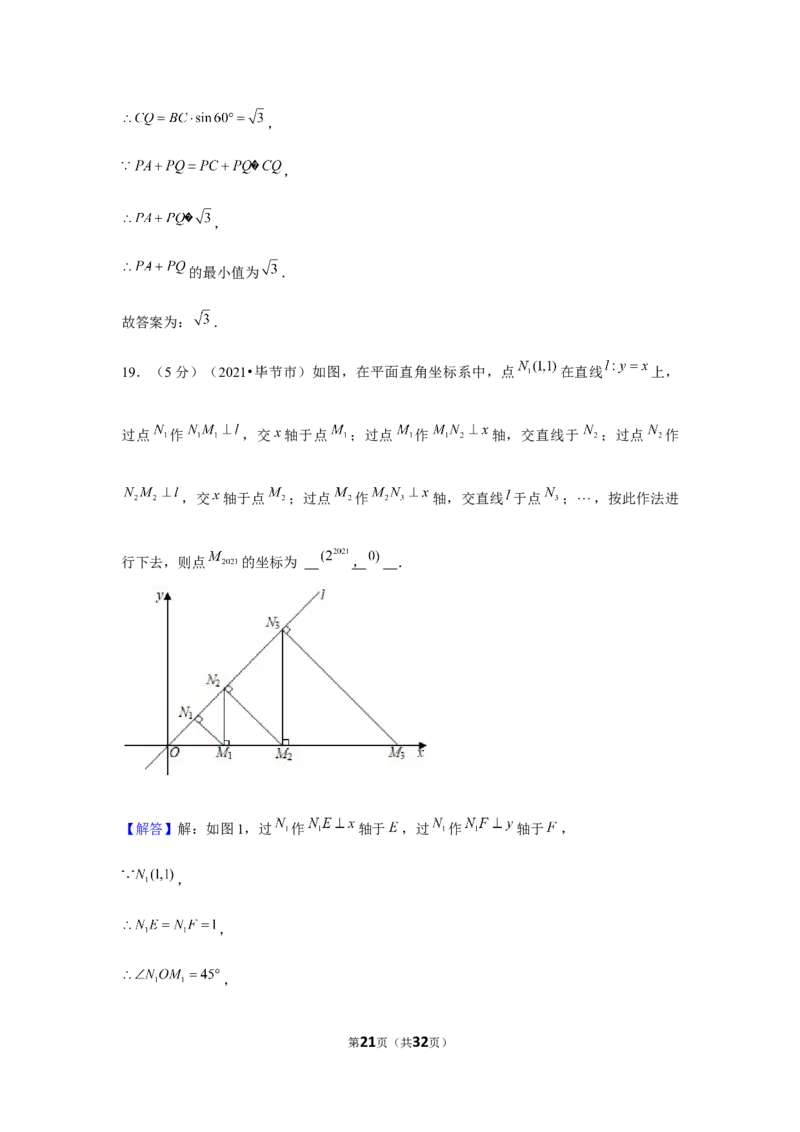
19.(5分)(2021•毕节市)如图,在平面直角坐标系中,点 在直线 上,
过点 作 ,交 轴于点 ;过点 作 轴,交直线于 ;过点 作
,交 轴于点 ;过点 作 轴,交直线 于点 ; ,按此作法进
行下去,则点 的坐标为 .
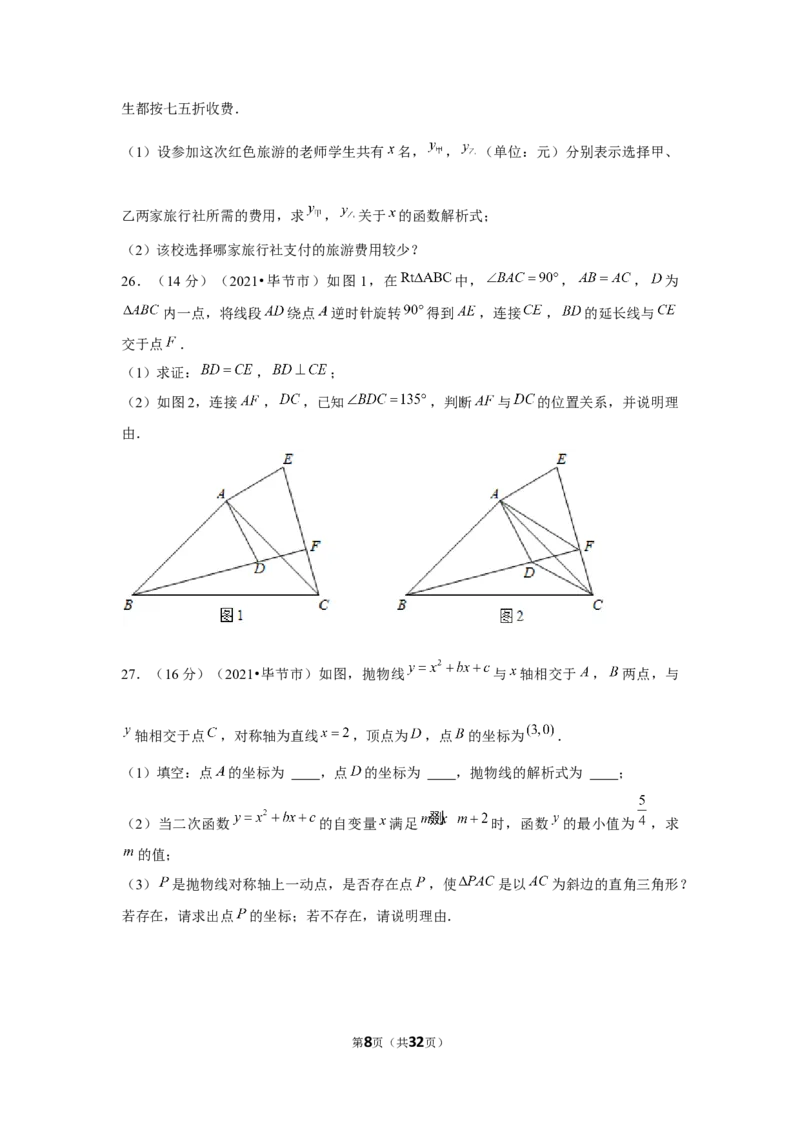
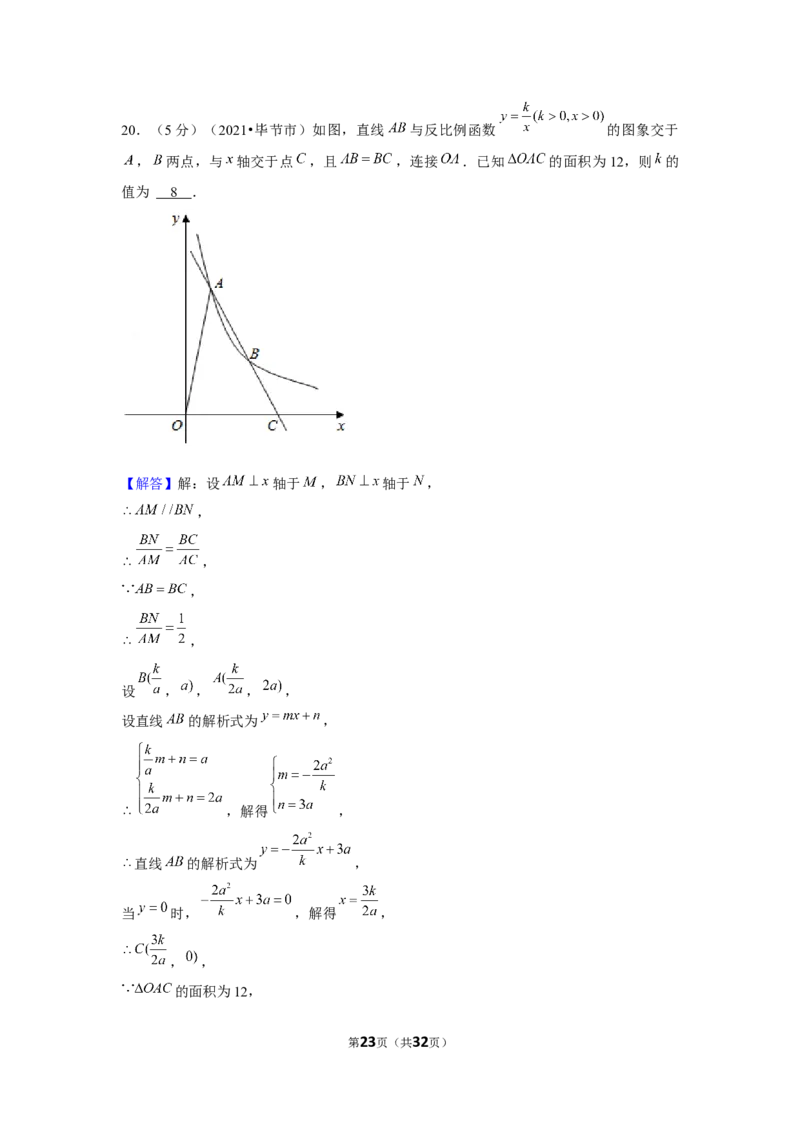
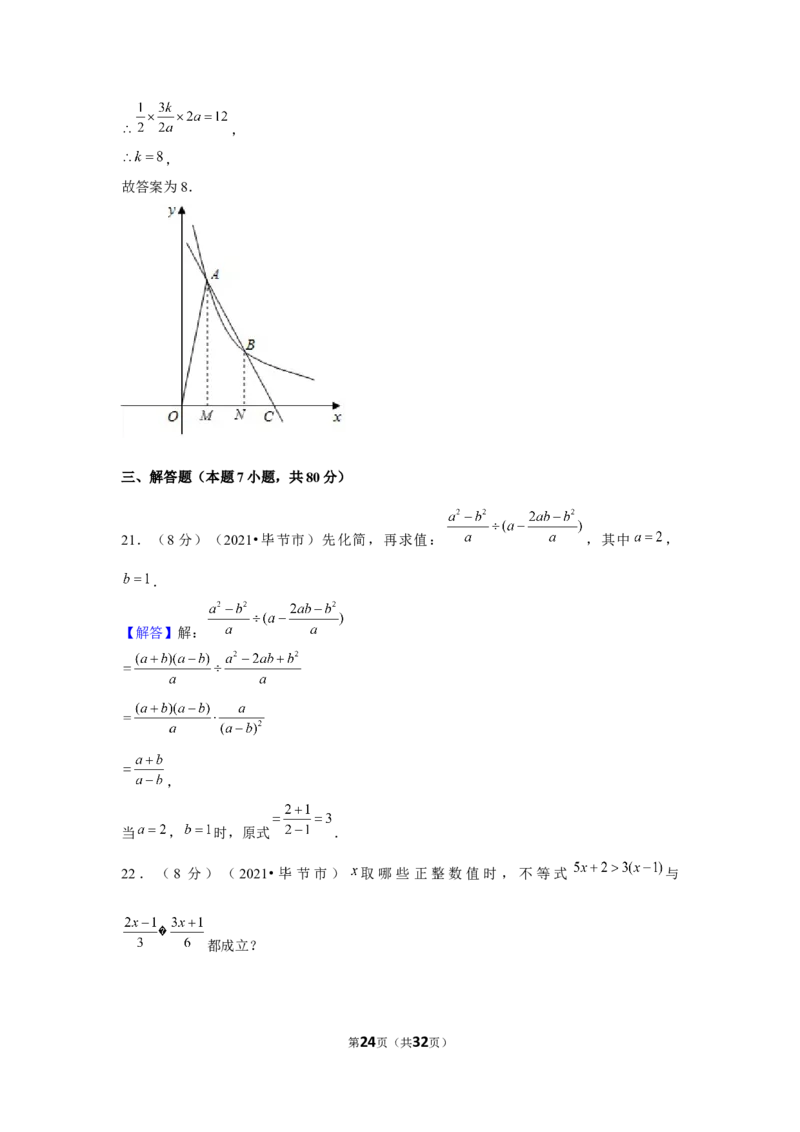
第5页(共32页)20.(5分)(2021•毕节市)如图,直线 与反比例函数 的图象交于
, 两点,与 轴交于点 ,且 ,连接 .已知 的面积为12,则 的
值为 .
三、解答题(本题7小题,共80分)
21.(8分)(2021•毕节市)先化简,再求值: ,其中 ,
.
22.(8 分)(2021•毕节市) 取哪些正整数值时,不等式 与
都成立?
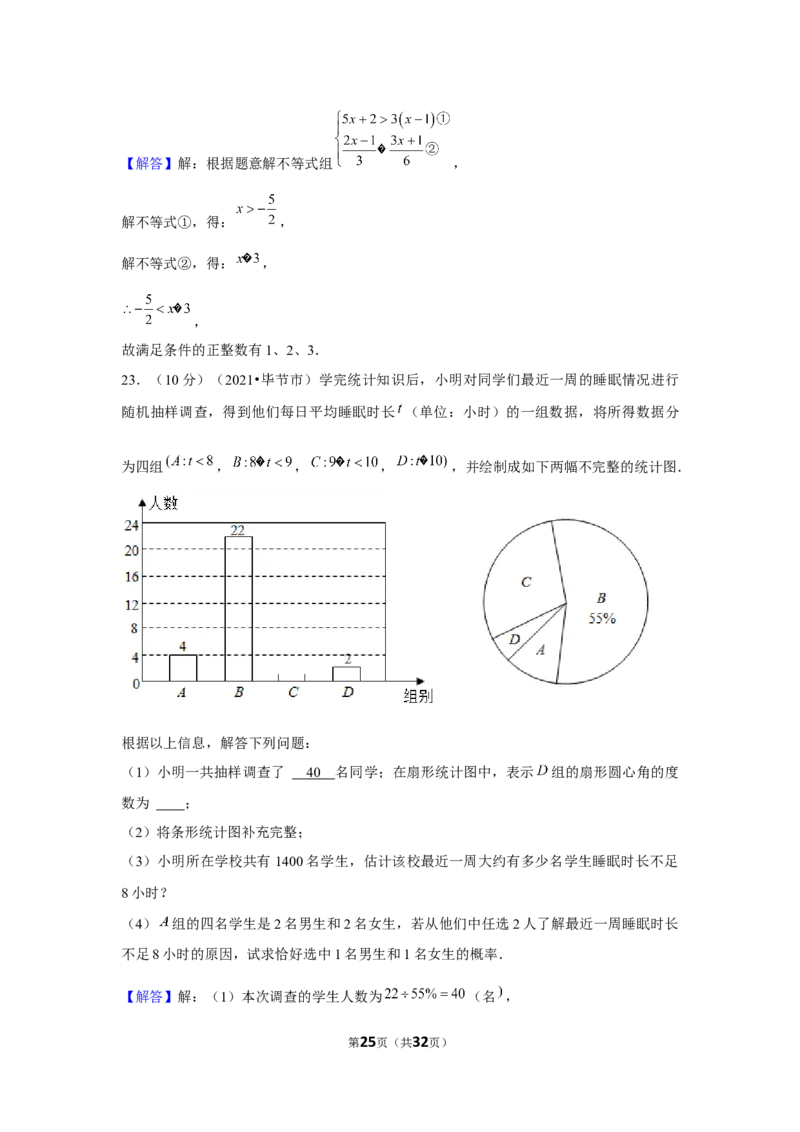
23.(10分)(2021•毕节市)学完统计知识后,小明对同学们最近一周的睡眠情况进行
随机抽样调查,得到他们每日平均睡眠时长 (单位:小时)的一组数据,将所得数据分
第6页(共32页)为四组 , , , ,并绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)小明一共抽样调查了 名同学;在扇形统计图中,表示 组的扇形圆心角的度数
为 ;
(2)将条形统计图补充完整;
(3)小明所在学校共有1400名学生,估计该校最近一周大约有多少名学生睡眠时长不足
8小时?
(4) 组的四名学生是2名男生和2名女生,若从他们中任选2人了解最近一周睡眠时长
不足8小时的原因,试求恰好选中1名男生和1名女生的概率.
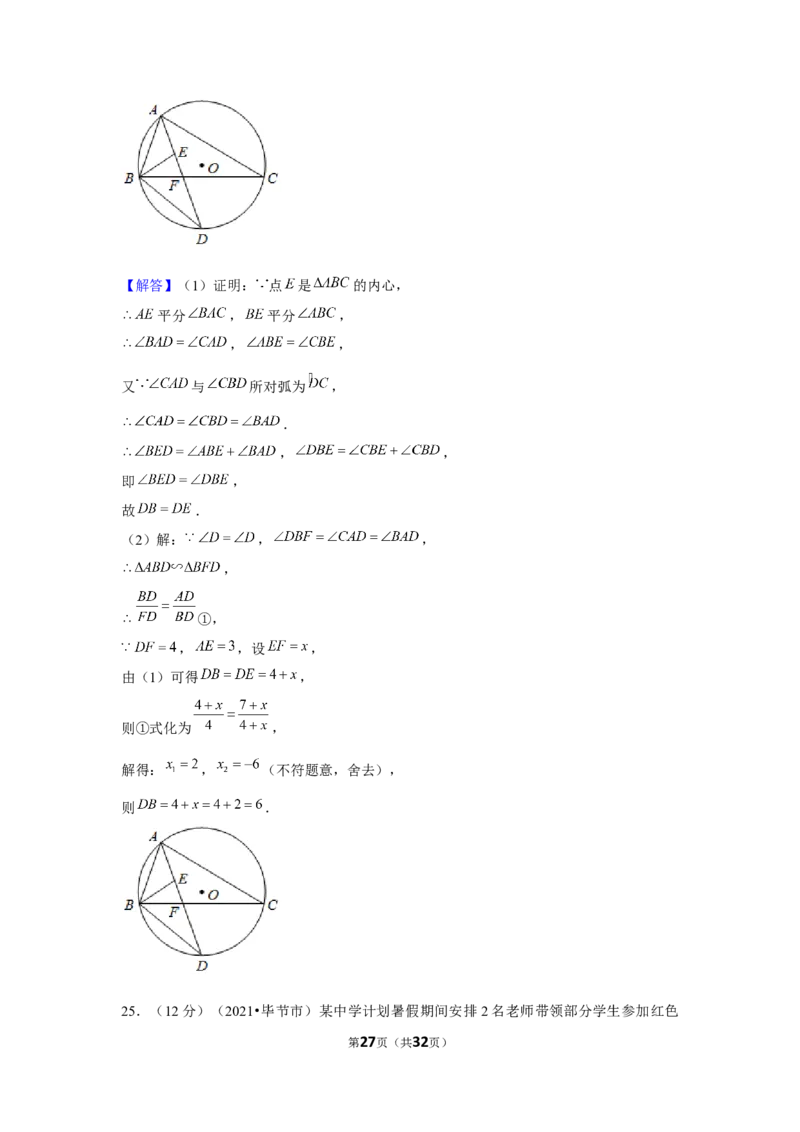
24.(12分)(2021•毕节市)如图, 是 的外接圆,点 是 的内心,
的延长线交 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)若 , ,求 的长.
25.(12分)(2021•毕节市)某中学计划暑假期间安排2名老师带领部分学生参加红色
旅游.甲、乙两家旅行社的服务质量相同,且报价都是每人 1000元.经协商,甲旅行社的
优惠条件是:老师、学生都按八折收费;乙旅行社的优惠条件是:两位老师全额收费,学
第7页(共32页)生都按七五折收费.
(1)设参加这次红色旅游的老师学生共有 名, , (单位:元)分别表示选择甲、
乙两家旅行社所需的费用,求 , 关于 的函数解析式;
(2)该校选择哪家旅行社支付的旅游费用较少?
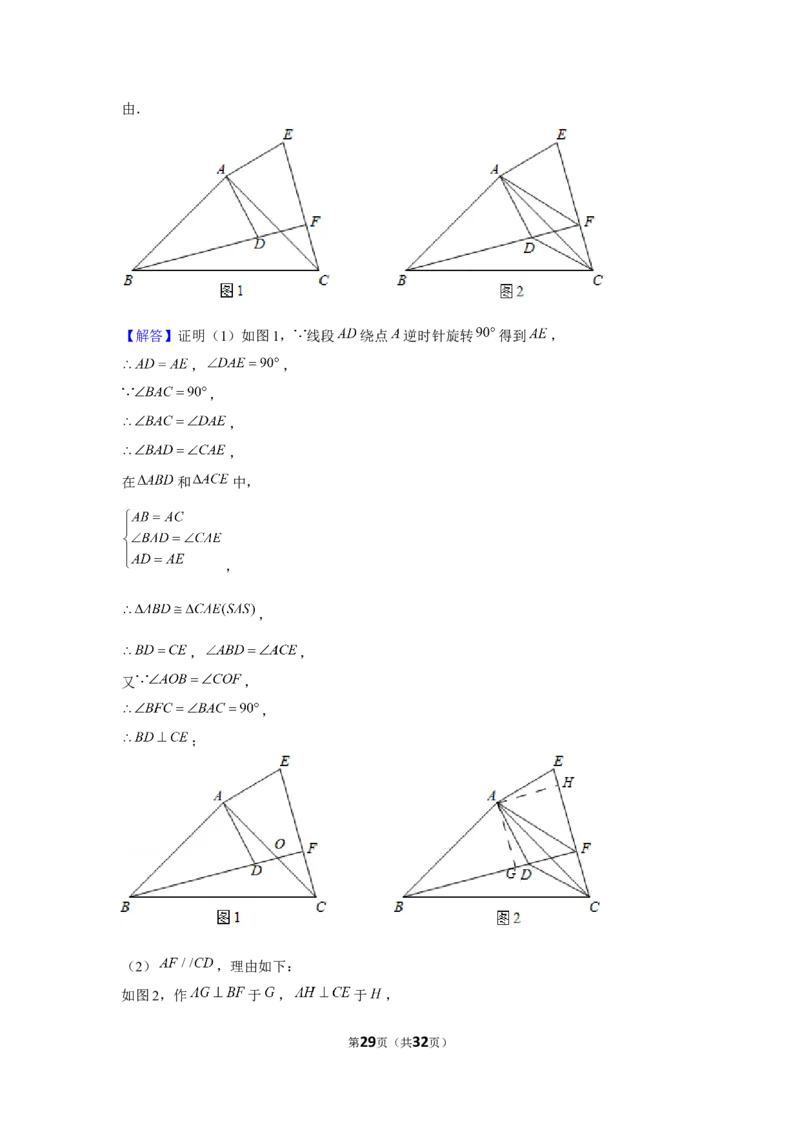
26.(14分)(2021•毕节市)如图 1,在 中, , , 为
内一点,将线段 绕点 逆时针旋转 得到 ,连接 , 的延长线与
交于点 .
(1)求证: , ;
(2)如图2,连接 , ,已知 ,判断 与 的位置关系,并说明理
由.
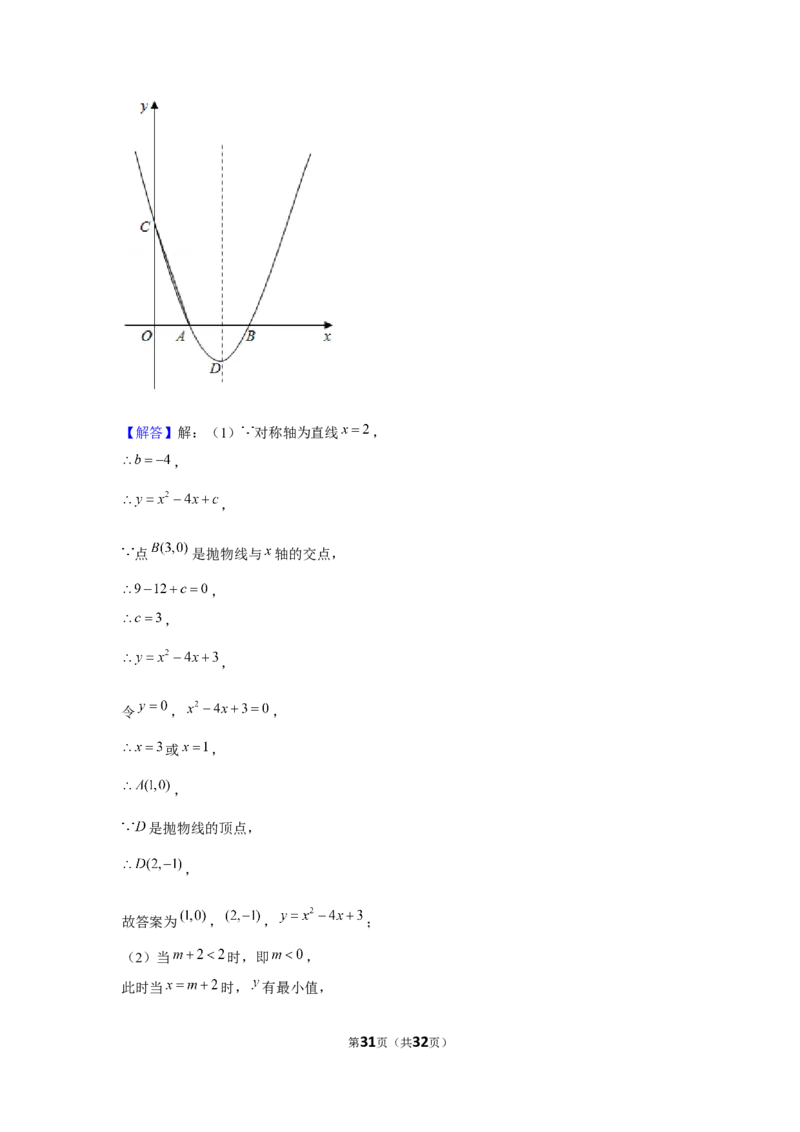
27.(16分)(2021•毕节市)如图,抛物线 与 轴相交于 , 两点,与
轴相交于点 ,对称轴为直线 ,顶点为 ,点 的坐标为 .
(1)填空:点 的坐标为 ,点 的坐标为 ,抛物线的解析式为 ;
(2)当二次函数 的自变量 满足 时,函数 的最小值为 ,求
的值;
(3) 是抛物线对称轴上一动点,是否存在点 ,使 是以 为斜边的直角三角形?
若存在,请求出点 的坐标;若不存在,请说明理由.
第8页(共32页)第9页(共32页)2021年贵州省毕节市中考数学试卷
参考答案与试题解析
一、选择题(本题15小题,每小题3分,共45分)
1.(3分)(2021•毕节市)下列各数中,为无理数的是
A. B. C.0 D.
【解答】解: . 是无理数,故本选项符合题意;
. 是有理数,不是无理数,故本选项不符合题意;
.0是有理数,不是无理数,故本选项不符合题意;
. 是有理数,不是无理数,故本选项不符合题意;
故选: .
2.(3分)(2021•毕节市)如图所示的几何体,其左视图是
A. B. C. D.
【解答】解:这个几何体的左视图为:
故选: .
3.(3分)(2021•毕节市)6月6日是全国“放鱼日”为促进渔业绿色发展,今年“放鱼
日”当天,全国同步举办增殖放流200余场,放流各类水生生物苗种近30亿尾.数30亿
用科学记数法表示为
第10页(共32页)A. B. C. D.
【解答】解:30亿 ,
故选: .
4.(3分)(2021•毕节市)下列城市地铁标志图案中,既是中心对称图形又是轴对称图
形的是
A. B.
C. D.
【解答】解: .既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
.不是轴对称图形,是中心对称图形,故此选项不合题意;
.是轴对称图形,不是中心对称图形,故此选项不合题意;
.既是轴对称图形,又是中心对称图形,故此选项符合题意;
故选: .
5.(3分)(2021•毕节市)将一副三角板按如图所示的位置摆放在直尺上,则 的度数
为
A. B. C. D.
【解答】解:如图,
第11页(共32页),
,
,
,
故选: .
6.(3分)(2021•毕节市)下列运算正确的是
A. B. C. D.
【解答】解: . ,故本选项不符合题意;
. ,故本选项不符合题意;
. ,故本选项不符合题意;
. ,故本选项符合题意;
故选: .
7.(3分)(2021•毕节市)若正多边形的一个外角是 ,则该正多边形的内角和为
A. B. C. D.
【解答】解:正多边形的边数为: ,
这个多边形是正八边形,
该多边形的内角和为 .
故选: .
8.(3分)(2021•毕节市)《九章算术》中记载了一个问题,大意是甲、乙两人各带了
第12页(共32页)若干钱.若甲得到乙所有钱的一半,则甲共有钱50.若乙得到甲所有钱的 ,则乙也共有
钱50.甲、乙两人各带了多少钱?设甲带了钱 ,乙带了钱 ,依题意,下面所列方程组
正确的是
A. B.
C. D.
【解答】解:设甲需带钱 ,乙带钱 ,
根据“甲、乙两人各带了若干钱.若甲得到乙所有钱的一半,则甲共有钱 50.若乙得到甲
所有钱的 ,则乙也共有钱50”,得 ,
故选: .
9.(3分)(2021•毕节市)如图,拦水坝的横断面为梯形 ,其中 ,
, ,斜坡 长 ,则斜坡 的长为
A. B. C. D.
【解答】解:过 作 于 ,过 作 于 ,
,
,
四边形 是平行四边形,
四边形 是矩形,
第13页(共32页),
在 中,
,
在 中,
,
,
,
故选: .
10.(3分)(2021•毕节市)已知关于 的一元二次方程 有两个不相等的
实数根,则 的取值范围是
A. B. C. 且 D. 且
【解答】解:根据题意得 且△ ,
解得 且 ,
故选: .
11.(3分)(2021•毕节市)下列说法正确的是
A.了解市民知晓“礼让行人”交通新规的情况,适合全面调查
B.一组数据5,5,3,4,1的中位数是3
C.甲、乙两人9次跳高成绩的方差分别为 , ,说明乙的成绩比甲稳定
D.“经过有交通信号灯的路口,遇到红灯”是随机事件
【解答】解: .了解市民知晓“礼让行人”交通新规的情况,由于调查的工作量较大,
适合抽样调查,此选项错误,不符合题意;
第14页(共32页).一组数据5,5,3,4,1,重新排列为1、3、4、5、5,其中位数是4,此选项错误,
不符合题意;
.甲、乙两人9次跳高成绩的方差分别为 , ,由 ,说明甲的成
绩比乙稳定,此选项错误,不符合题意;
.“经过有交通信号灯的路口,遇到红灯”,由于事先无法预测遇到哪种灯,所以此事
件是随机事件,此选项正确,符合题意;
故选: .
12.(3分)(2021•毕节市)某小区内的消防车道有一段弯道,如图,弯道的内外边缘均
为圆弧, , 所在圆的圆心为 ,点 , 分别在 , 上.已知消防车道半径
,消防车道宽 , ,则弯道外边缘 的长为
A. B. C. D.
【解答】解: , ,
,
,
弯道外边缘 的长为: ,
故选: .
13.(3分)(2021•毕节市)某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循
环形式(每两班之间都赛一场),共需安排15场比赛,则八年级班级的个数为
A.5 B.6 C.7 D.8
【解答】解:设八年级有 个班,
第15页(共32页)依题意得: ,
整理得: ,
解得: , (不合题意,舍去).
故选: .
14.(3分)(2021•毕节市)如图,在矩形纸片 中, , , 是
上的点,且 .将矩形纸片 沿过点 的直线折叠,使点 落在 上的点
处,点 落在点 处,折痕为 ,则线段 的长是
A.4 B.5 C.6 D.
【解答】解法一:解:连接 ,如图,
设 ,
, ,
, ,
由折叠性质可知,
, ,
在 中,
,
,
在 △ 中,
,
第16页(共32页),
,
解得: , (舍去),
.
解法二:解:连接 ,如图,
, ,
,
由折叠性质得, , , ,
在 和 △ 中,
,
△ ,
,
.
故选: .
15.(3分)(2021•毕节市)如图,已知抛物线 开口向上,与 轴的一个
交点为 ,对称轴为直线 .下列结论错误的是
第17页(共32页)A. B. C. D.
【解答】解:由图象可得,抛物线开口向上,故 ,
由于抛物线与 轴交点坐标为 ,
由图象可得, ,
对称轴为 ,
,
,
,
,
,
故 选项正确;
抛物线与 轴有两个交点,
△ ,
,
故 选项正确;
由图象可得,当 时, ,
,
故 选项错误;
抛物线的对称轴为 ,
第18页(共32页),
,
故 选项正确,
故选: .
二、填空题(本题5小题,每小题5分,共25分)
16.(5分)(2021•毕节市)将直线 向下平移2个单位长度,平移后直线的解析
式为 .
【解答】解:由题意得:平移后的解析式为: .
故答案为: .
17.(5分)(2021•毕节市)学习投影后,小华利用灯光下自己的影子长度来测量一路灯
的高度.如图,身高 的小明从路灯灯泡 的正下方点 处,沿着平直的道路走 到
达点 处,测得影子 长是 ,则路灯灯泡 离地面的高度 为 8. 5 .
【解答】解: , ,
,
,
,
,
解得: ,
答:路灯灯泡 离地面的高度 为8.5米,
故答案为:8.5.
第19页(共32页)18.(5分)(2021•毕节市)如图,在菱形 中, , , 为 的
中点, 为对角线 上的任意一点,则 的最小值为 .
【解答】解:如图,连接 , , .
四边形 是菱形,
,
在 和 中,
,
,
,
,
,
,
,
是等边三角形,
,
,
第20页(共32页),
,
,
的最小值为 .
故答案为: .
19.(5分)(2021•毕节市)如图,在平面直角坐标系中,点 在直线 上,
过点 作 ,交 轴于点 ;过点 作 轴,交直线于 ;过点 作
,交 轴于点 ;过点 作 轴,交直线 于点 ; ,按此作法进
行下去,则点 的坐标为 , .
【解答】解:如图1,过 作 轴于 ,过 作 轴于 ,
,
,
,
第21页(共32页),
△ 是等腰直角三角形,
,
,
,
同理,△ 是等腰直角三角形,
,
,
同理, ,
,
,
, ,
依次类推,故 , ,
故答案为: , .
第22页(共32页)20.(5分)(2021•毕节市)如图,直线 与反比例函数 的图象交于
, 两点,与 轴交于点 ,且 ,连接 .已知 的面积为12,则 的
值为 8 .
【解答】解:设 轴于 , 轴于 ,
,
,
,
,
设 , , , ,
设直线 的解析式为 ,
,解得 ,
直线 的解析式为 ,
当 时, ,解得 ,
, ,
的面积为12,
第23页(共32页),
,
故答案为8.
三、解答题(本题7小题,共80分)
21.(8分)(2021•毕节市)先化简,再求值: ,其中 ,
.
【解答】解:
,
当 , 时,原式 .
22.(8 分)(2021•毕节市) 取哪些正整数值时,不等式 与
都成立?
第24页(共32页)【解答】解:根据题意解不等式组 ,
解不等式①,得: ,
解不等式②,得: ,
,
故满足条件的正整数有1、2、3.
23.(10分)(2021•毕节市)学完统计知识后,小明对同学们最近一周的睡眠情况进行
随机抽样调查,得到他们每日平均睡眠时长 (单位:小时)的一组数据,将所得数据分
为四组 , , , ,并绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)小明一共抽样调查了 4 0 名同学;在扇形统计图中,表示 组的扇形圆心角的度
数为 ;
(2)将条形统计图补充完整;
(3)小明所在学校共有1400名学生,估计该校最近一周大约有多少名学生睡眠时长不足
8小时?
(4) 组的四名学生是2名男生和2名女生,若从他们中任选2人了解最近一周睡眠时长
不足8小时的原因,试求恰好选中1名男生和1名女生的概率.
【解答】解:(1)本次调查的学生人数为 (名 ,
第25页(共32页)表示 组的扇形圆心角的度数为 ,
故答案为:40、 ;
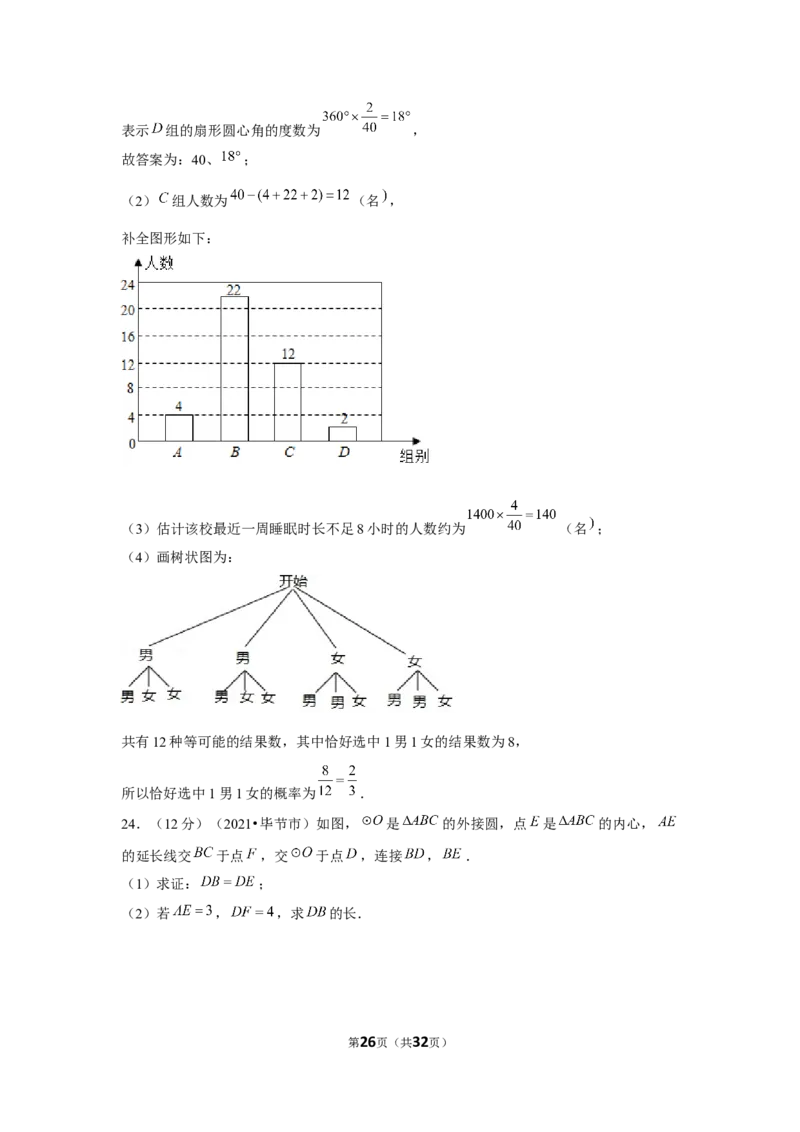
(2) 组人数为 (名 ,
补全图形如下:
(3)估计该校最近一周睡眠时长不足8小时的人数约为 (名 ;
(4)画树状图为:
共有12种等可能的结果数,其中恰好选中1男1女的结果数为8,
所以恰好选中1男1女的概率为 .
24.(12分)(2021•毕节市)如图, 是 的外接圆,点 是 的内心,
的延长线交 于点 ,交 于点 ,连接 , .
(1)求证: ;
(2)若 , ,求 的长.
第26页(共32页)【解答】(1)证明: 点 是 的内心,
平分 , 平分 ,
, ,
又 与 所对弧为 ,
.
, ,
即 ,
故 .
(2)解: , ,
,
①,
, ,设 ,
由(1)可得 ,
则①式化为 ,
解得: , (不符题意,舍去),
则 .
25.(12分)(2021•毕节市)某中学计划暑假期间安排2名老师带领部分学生参加红色
第27页(共32页)旅游.甲、乙两家旅行社的服务质量相同,且报价都是每人 1000元.经协商,甲旅行社的
优惠条件是:老师、学生都按八折收费;乙旅行社的优惠条件是:两位老师全额收费,学
生都按七五折收费.
(1)设参加这次红色旅游的老师学生共有 名, , (单位:元)分别表示选择甲、
乙两家旅行社所需的费用,求 , 关于 的函数解析式;
(2)该校选择哪家旅行社支付的旅游费用较少?
【解答】解:(1) ,
;
(2)① ,
,
解得 ,
② ,
,
解得 ,
③ ,
,
解得 ,
答:当老师学生数超10人时,选择乙旅行社支付的旅游费用较少;当老师学生数为10人
时,两旅行社支付的旅游费用相同;当老师学生数少于 10人时,选择甲旅行社支付的旅游
费用较少.
26.(14分)(2021•毕节市)如图 1,在 中, , , 为
内一点,将线段 绕点 逆时针旋转 得到 ,连接 , 的延长线与
交于点 .
(1)求证: , ;
(2)如图2,连接 , ,已知 ,判断 与 的位置关系,并说明理
第28页(共32页)由.
【解答】证明(1)如图1, 线段 绕点 逆时针旋转 得到 ,
, ,
,
,
,
在 和 中,
,
,
, ,
又 ,
,
;
(2) ,理由如下:
如图2,作 于 , 于 ,
第29页(共32页)由(1)知 ,
, ,
,
又 , ,
平分 ,
又 ,
,
,
,
,
.
27.(16分)(2021•毕节市)如图,抛物线 与 轴相交于 , 两点,与
轴相交于点 ,对称轴为直线 ,顶点为 ,点 的坐标为 .
(1)填空:点 的坐标为 ,点 的坐标为 ,抛物线的解析式为 ;
(2)当二次函数 的自变量 满足 时,函数 的最小值为 ,求
的值;
(3) 是抛物线对称轴上一动点,是否存在点 ,使 是以 为斜边的直角三角形?
若存在,请求出点 的坐标;若不存在,请说明理由.
第30页(共32页)【解答】解:(1) 对称轴为直线 ,
,
,
点 是抛物线与 轴的交点,
,
,
,
令 , ,
或 ,
,
是抛物线的顶点,
,
故答案为 , , ;
(2)当 时,即 ,
此时当 时, 有最小值,
第31页(共32页)则 ,
解得 ,
;
当 时,此时当 时, 有最小值,
则 ,
解得 或 ,
;
当 时,此时当 时, 有最小值为 ,与题意不符;
综上所述: 的值为 或 ;
(3)存在,理由如下:
, ,
, 的中点为 , ,
设 ,
是以 为斜边的直角三角形,
,
,
或 ,
或 ,
使 是以 为斜边的直角三角形时, 点坐标为 或 .
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/9/13 17:15:16;用户:初中数学61;邮箱:ydyd61@xyh.com;学号:36810736
第32页(共32页)