文档内容
2023 年高考考前押题密卷(北京卷)
数 学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写
在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、先选择题共10小题,每小题4分,分。在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知集合A={x∣x2−4x≤0,x∈Z},B={x∣−1≤x<4},则A∩B=( )
A.[−1,4] B.[0,4) C.{0,1,2,3,4} D.{0,1,2,3}
【答案】D
【分析】利用二次不等式的解法解出集合A,然后计算集合的交集.
【详解】由A={x∣x2−4x≤0,x∈Z}={0,1,2,3,4},
B={x∣−1≤x<4},
所以A∩B={0,1,2,3},
故选:D.
2.若z=1−i,则|z2−2z+i|=( )
A.5 B.❑√5 C.❑√3 D.3
【答案】B
【分析】由题意求z2−2z+i,进而可求其模长.
【详解】∵z=1−i,则z2−2z+i=(z−1) 2−1+i=(−i) 2−1+i=−2+i,
则|z2−2z+i|=❑√(−2) 2+12=❑√5.
故选:B.
3.已知抛物线y2=4x的焦点为F,点P在该抛物线上,且P的横坐标为4,则|PF|=( )
A.2 B.3 C.4 D.5
【答案】D
【分析】直接根据抛物线焦半径公式计算得到答案.
【详解】抛物线y2=4x的准线方程为x=−1,
因为点P在抛物线y2=4x上,P的横坐标为4,抛物线y2=4x的焦点为F,
学科网(北京)股份有限公司所以|PF|等于点P到直线x=−1的距离,
所以|PF|=4+1=5,
故选:D.
4.(1+x+x2)(1−x) 6的展开式中x2的系数为( )
A.9 B.10 C.24 D.25
【答案】B
【分析】首先求出(1−x) 6的通项T =(−1) rCrxr,再根据通项求解即可.
r+1 6
【详解】(1−x) 6的通项T =Cr(−x) r=(−1) rCrxr,
r+1 6 6
令r=2,T =(−1) 2C2x2=15x2,令r=1,T =−C1x=−6x,令r=0,T =1,
3 6 2 6 1
展开式中x2的系数为15x2−6x2+x2=10x2
.
所以(1+x+x2)(1−x) 6的展开式中x2的系数为10.
故选:B
5.已知的f(x)=sinx+❑√3cosx图象向左平移φ个单位长度后,得到函数g(x)的图象,且g(x)的图象关
于y轴对称,则|φ|的最小值为( )
π π π 5π
A. B. C. D.
12 6 3 12
【答案】B
π
【分析】化简f(x)=2sin(x+ ),根据三角函数图象的平移变换可得g(x)的表达式,结合其性质,求
3
得φ的表达式,即可求得答案.
π
【详解】由题意可得f(x)=sinx+❑√3cosx=2sin(x+ ),
3
π
故g(x)=2sin(x+φ+ ),由于g(x)的图象关于y轴对称,
3
π π π
则g(x)为偶函数,故φ+ = +kπ,k∈Z ,即φ= +kπ,k∈Z
,
3 2 6
π
故|φ|的最小值为 ,
6
故选:B
6.已知a>1,b>1,a3b=100,则log 10+3log 10的最小值为( )
a b
A.4 B.6 C.8 D.12
【答案】B
【分析】条件等式两边取对数后,得3lga+lgb=2,再结合换底公式,以及基本不等式“1”的妙用,即可
求解.
【详解】因为a3b=100,所以lga3b=2,即3lga+lgb=2,
学科网(北京)股份有限公司1 3 1( 1 3 ) 1( lgb 9lga)
所以log 10+3log 10= + = + ⋅(3lga+lgb)= 6+ +
a b lga lgb 2 lga lgb 2 lga lgb
1( √lgb 9lga)
≥ 6+2❑ ⋅ =6,
2 lga lgb
1
当且仅当lgb=3lga,即 a=103,b=10时等号成立,
所以log 10+3log 10的最小值为6.
a b
故选:B.
7.定义:|⃗a×⃗b|=|⃗a||⃗b|sinθ,其中θ为向量⃗a与⃗b的夹角.若|⃗a|=2,|⃗b|=5,⃗a⋅⃗b=−6,则|⃗a×⃗b|等于
( )
A.6 B.−6 C.−8 D.8
【答案】D
【分析】由向量数量积定义可构造方程求得cosθ,由此可得sinθ,根据|⃗a×⃗b|=|⃗a||⃗b|sinθ可求得结果.
3 4
【详解】∵⃗a⋅⃗b=|⃗a||⃗b|cosθ=10cosθ=−6,∴cosθ=− ,又θ∈[0,π],∴sinθ= ,
5 5
4
∴|⃗a×⃗b|=|⃗a||⃗b|sinθ=10sinθ=10× =8.
5
故选:D.
8.已知正实数x,y,z满足log x=log y=log z≠0,则( )
2 3 5
A.x>y>z
B.x0时,g(k)=kt在(0,+∞)上单调递增,故2t<3t<5t,即x3t>5t,即x>y>z;
故AB不一定正确;
假设x、y、z成等比数列,则y2=xz⇒(3t) 2 =2t ⋅5t ⇒9t=10t,
则t=0,与已知矛盾,故C错误;
学科网(北京)股份有限公司(2) t (3) t
令f (t)= + −1,由指数函数的性质可知f (t)在R上单调递减,
5 5
(2) t (3) t
注意到f (1)=0,故f (t)只有一个零点,即 + =1只有一个解t=1,
5 5
所以x+ y=z只有一组解x=2,y=3,z=5,故D正确.
故选:D
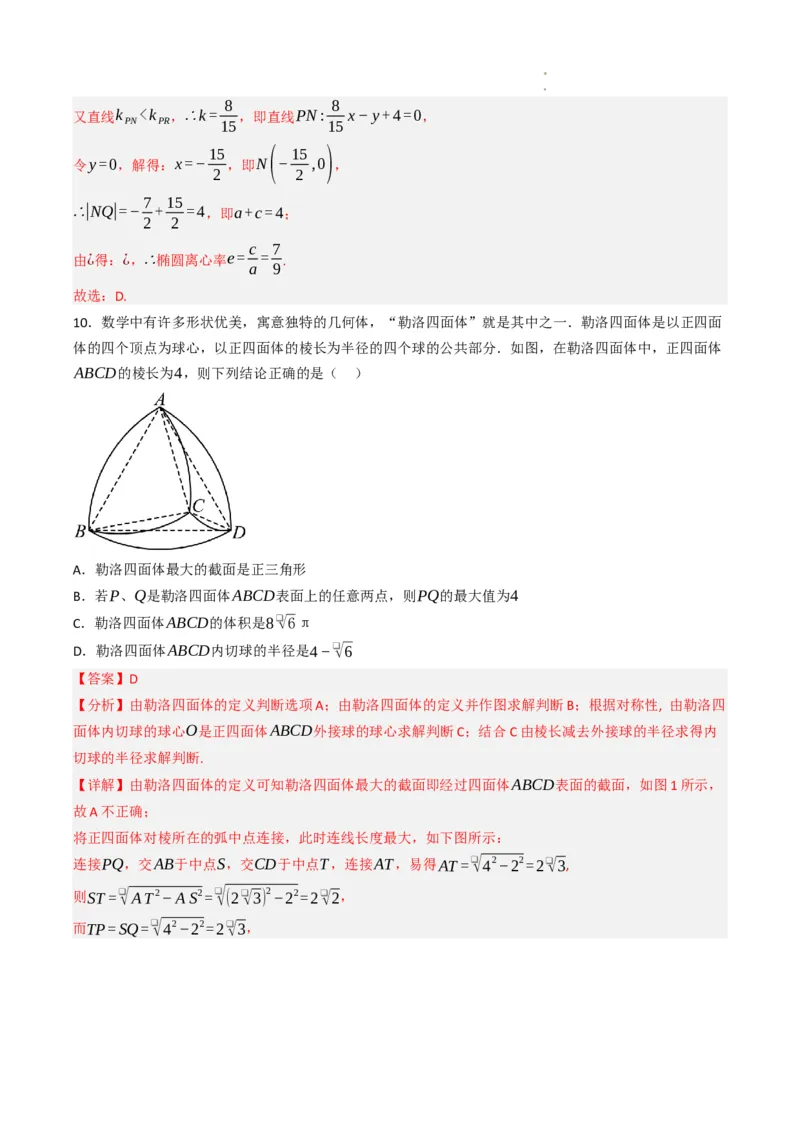
9.如图所示,当篮球放在桌面并被斜上方一个灯泡P(当成质点)发出的光线照射后,在桌面上留下的影
子是椭圆,且篮球与桌面的接触点是椭圆的右焦点.若篮球的半径为1个单位长度,灯泡与桌面的距离为4
个单位长度,灯泡垂直照射在平面上的点为A,椭圆的右顶点到A点的距离为3个单位长度,则此时椭圆的
离心率e等于( )
2 3 4 7
A. B. C. D.
3 4 5 9
【答案】D
【分析】以A为坐标原点建立平面直角坐标系,根据直线与圆相切可构造方程求得Q点坐标和N点坐标,
确定|NQ|=a+c,|QR|=a−c的值,由此可构造方程组求得a,c,进而得到离心率.
【详解】以A为坐标原点,可建立如图所示平面直角坐标系,
由题意知:|NQ|=a+c,|QR|=a−c,P(0,4),R(−3,0),
x y
则直线PR:− + =1,即4x−3 y+12=0,
3 4
设Q(n,0)(n<−3),则M(n,1),
|4n+9| 7
∴点M到直线PR的距离d = =1,解得:n=− ,
1 5 2
7 1 1
∴|QR|=−3+ = ,即a−c= ;
2 2 2
设直线PN:y=kx+4(k>0),即kx−y+4=0,
| 7 |
3− k 8 4
∴点M到直线PN的距离 |nk+3| 2 ,解得:k= 或k= ,
d = = =1 15 3
2 ❑√k2+1 ❑√k2+1
学科网(北京)股份有限公司8 8
又直线k 4,
故勒洛四面体表面上两点间的距离可能大于4,故B错误,
如图2,由对称性可知勒洛四面体内切球的球心O是正四面体ABCD外接球的球心,
连接BO并延长交勒洛四面体的曲面于点E,则OE就是勒洛四面体内切球的半径.
如图3, 在正四面体ABCD中,M为△BCD的中心,O是正四面体ABCD外接球的球心,
连接BM、BO、AM,由正四面体的性质可知O在AM上.
因为AB=4, 所以BM=
2
×❑√42−22=
4❑√3
,则AM=❑
√
42−
(4❑√3) 2
=
4❑√6
.
3 3 3 3
因为BO2=BM2+OM2=(AM−OM) 2,
即BO2= (4❑√3) 2 +OM2= (4❑√6 −OM ) 2 ,解得BO=❑√6,
3 3
4 4
则正四面体ABCD外接球的体积是 πR3= π×(❑√6) 3=8❑√6π,
3 3
而勒洛四面体ABCD的体积小于其外接球的体积,C错误;
因为BE=AB=4,所以OE=4−❑√6
,
所以,勒洛四面体ABCD内切球的半径是4−❑√6,则 D正确.
故选:D.
【点睛】关键点睛:解决与球有关的内切或外接问题时,关键是确定球心的位置,再利用球的截面小圆性
质求解.
学科网(北京)股份有限公司第Ⅱ卷
二、填空题共5个小题,每小题5分,共25分。
1
11.已知函数y=f(x)满足:当−2≤x≤2时,f(x)=− x2+1,且f(x)=f(x+4)对任意x∈R都成立,
4
则方程16f(x)=4|x|+1的实根个数是______.
【答案】4
【分析】根据给定条件,探讨函数y=f(x)的性质,变形给定方程,转化成求两个函数图象的公共点个数
作答
1
【详解】依题意,函数y=f (x)是以4为周期的偶函数,当−2≤x≤2时,f(x)=− x2+1,
4
1 1
则当2≤x≤6时,f(x)=− (x−4) 2+1=− x2+2x−3,
4 4
1 1
方程16f(x)=4|x|+1⇔f(x)= |x|+ ,
4 16
1 1
因此原方程的实根就是函数y=f(x)与函数y= |x|+ 的图象的交点的横坐标,
4 16
1 1
在同一坐标系内作出函数y=f(x)与y= |x|+ 的图象,如图,
4 16
观察图象知,当0≤x≤2时,两函数图象只有一个交点,
当2≤x≤6时,由¿得¿,即当2≤x≤6时,两函数图象只有一个公共点,
1 1
于是当x≥0时,函数y=f(x)与y= |x|+ 的图象有2个公共点,
4 16
1 1
又函数y=f(x)与y= |x|+ 均为偶函数,则当x<0时,两个函数图象有2个公共点,
4 16
1 1
所以函数y=f(x)与y= |x|+ 的图象有4个公共点,即原方程有4个根.
4 16
故答案为:4
【点睛】方法点睛:函数零点个数判断方法:(1)直接法:直接求出f(x)=0的解;(2)图象法:作出函数f(x)
的图象,观察与x轴公共点个数或者将函数变形为易于作图的两个函数,作出这两个函数的图象,观察它
们的公共点个数.
学科网(北京)股份有限公司12.“民生”供电公司为了分析“康居”小区的用电量y(单位kw⋅h)与气温x(单位:℃)之间的关系,
随机统计了4天的用电量与当天的气温,这两者之间的对应关系见下表:
气温x 18 13 10 −1
用电量y 24 34 38 64
若上表中的数据可用回归方程y=−2x+b(b∈R)来预测,则当气温为−4℃时该小区相应的用电量约为
______kw⋅h.
【答案】68
【分析】求出样本中心点,再根据线性回归方程必过样本中心点求出b,再将x=−4代入即可得解.
18+13+10−1 24+34+38+64
【详解】x= =10,y= =40,
4 4
则40=−2×10+b,解得b=60,
所以y=−2x+60,
当x=−4时,y=68,
即当气温为−4℃时该小区相应的用电量约为68 kw⋅h.
故答案为:68.
13.△ABC的内角A,B,C的对边分别为a,b,c,若3bcosC+3ccosB=5asin A,且A为锐角,则当
a2 a
取得最小值时, 的值为___________.
bc 2b+c
❑√10
【答案】
15
【分析】根据正弦定理将表达式边化角变形,结合正弦和角公式即可求得sinA,结合同角三角函数关系式
a2
求得cosA,代入余弦定理表示出a2,代入 中由基本不等式即可求得最小值,并求得取最小值时b,c关
bc
a
系,进而求得 的值.
2b+c
【详解】由正弦定理将3bcosC+3ccosB=5asinA变形可得
3sinBcosC+3sinCcosB=5sin2A,
即3sin(B+C)=5sin2A,
3
由sin(B+C)=sin A>0可得sin A= ,
5
4
而A是锐角,所以cosA= ,
5
8
则由余弦定理可得a2=b2+c2−2bccosA=b2+c2− bc,
5
学科网(北京)股份有限公司8
b2+c2− bc 2bc 8 2
则a2 5 b2+c2 8 ≥ − = ,
= = − bc 5 5
bc bc bc 5
a2 2
当且仅当b=c时, 取得最小值 ,
bc 5
2 ❑√10
故a2= b2 ,故a= b,
5 5
a ❑√10
所以 = .
2b+c 15
❑√10
故答案为:
15
14.已知抛物线C:y2=2px,O为坐标原点,过抛物线的焦点F的直线与抛物线交于A,B两点(点A在
第一象限),且AF=6,直线AO交抛物线的准线于点C,△AOF与△ACB的面积之比为4:9,则p的值为
________.
【答案】4
【分析】首先证明△AOF∽△ACB,求出|AB|=9,则y =−2y ,再利用证明的结论y ⋅y =−p2 ,得
A B A B
到A(p,❑√2p),利用焦点弦公式求出p值即可.
【详解】设A(x ,y ),B(x ,y ),则y2 =2px ,
A A B B A A
p
设直线AB的方程为x− =ty,联立抛物线方程有
2
y2−2pty−p2=0,Δ=4 p2t2+4 p2>0,y ⋅y =−p2 ,
A B
−p2 y
则y = ,直线AO的方程为y= A x,
B y x
A A
y −p −py❑❑ −p2
p y = A ⋅ = A = = y
令x=− ,则 C x 2 y 2 y B,则OF//CB,
2 A A A
p
则△AOF∽△ACB得
S
△AOF =
(AF) 2
=
4
,
S AB 9
△ACB
∴|AB|=9,∴|BF|=3,y =−2y ,又y ⋅y =−p2 ,
A B A B
学科网(北京)股份有限公司p
则y =❑√2p,∴点A(p,❑√2p),AF=p+ =6,解得p=4.
A 2
故答案为:4.
15.冬季两项是冬奥会的项目之一,是把越野滑雪和射击两种不同特点的竞赛项目结合在一起进行的运动,
其中冬季两项男子个人赛,选手需要携带枪支和20发子弹,每滑行4千米射击1次,共射击4次,每次5
发子弹,若每有1发子弹没命中,则被罚时1分钟,总用时最少者获胜.已知某男选手在一次比赛中共被罚
时3分钟,假设其射击时每发子弹命中的概率都相同,且每发子弹是否命中相互独立,记事件A为其在前
两次射击中没有被罚时,事件B为其在第4次射击中被罚时2分钟,那么P¿___________.
1
【答案】
3
【分析】事件B为前3次中有一次中1发未中,第4次射击中有2发未中,事件AB是第3次有1发未中,
第4次有2发未中,然后利用利用条件概率求解.
C1C1C2 C1C2
【详解】解:由题意得P(B)= 3 5 5 ,P(AB)= 5 5 ,
C3 C3
20 20
P(AB)
C1C2 C1C1C2
1
∴P( A|B)= = 5 5 ÷ 3 5 5 = ,
P(B) C3 C3 3
20 20
1
故答案为:
3
三、解答题共6小题,共85分。解答应写出文字说明,盐酸步骤或证明过程。
16.如图,AC为圆O的直径,PA垂直于圆O所在的平面,B为圆周上不与点A,C重合的点,连接
PB,PC,AB,BC,作AS⊥PC于点S,AN⊥PB于点N.
(1)求证:∠ASN是二面角A−PC−B的平面角;
(2)若∠ACB=30∘,∠PCA=45∘,求二面角A−PC−B的正弦值.
【答案】(1)证明见解析
❑√10
(2)
5
【分析】(1)利用线面垂直的判定定理和性质定理结合二面角的平面角的定义证明;
(2)利用空间向量的坐标运算,利用法向量求二面角的正弦值.
学科网(北京)股份有限公司【详解】(1)因为PA垂直于圆O所在的平面,即PA⊥平面ABC,
BC⊂平面ABC,所以PA⊥BC,
又因为AC为圆O的直径,所以BC⊥AB,
PA∩AB=A,PA,AB⊂平面PAB,
所以BC⊥平面PAB,AN⊂平面PAB,所以BC⊥AN,
又因为AN⊥PB,BC∩PB=B,BC,PB⊂平面PBC,
所以AN⊥平面PBC,PC⊂平面PBC,所以AN⊥PC,
又因为AS⊥PC,AS∩AN=A,AS,AN⊂平面ASN,
所以PC⊥平面ASN,SN⊂平面ASN,
所以∠ASN是二面角A−PC−B的平面角.
(2)设AC=2a,因为∠ACB=30∘,∠PCA=45∘,
所以AB=a,PA=2a,BC=❑√3a,
过点B作AP的平行线为z轴,并以BC,BA为x,y轴建系如图,
则A(0,a,0),B(0,0,0),C(❑√3a,0,0),P(0,a,2a),
设平面APC的法向量为⃗m=(x,y,z),
⃗AP=(0,0,2a),⃗AC=(❑√3a,−a,0),
所以¿令x=1,则y=❑√3,z=0,
所以⃗m=(1,❑√3,0),
设平面PBC的法向量为⃗n=(x ,y ,z ),
1 1 1
⃗BC=(❑√3a,0,0),⃗BP=(0,a,2a),
所以¿令y =2,则x =0,z =−1,
1 1 1
所以⃗n=(0,2,−1),
设二面角A−PC−B的大小为θ,
|⃗m⋅⃗n| 2❑√3 ❑√15
则cosθ=|cos⟨⃗m,⃗n⟩|= = = ,
|⃗m|⋅|⃗n| 2×❑√5 5
❑√10
所以sinθ=❑√1−cos2θ=
.
5
学科网(北京)股份有限公司1
17.△ABC的内角A,B,C的对边分别为a,b,c,sinB= ,且______.
3
(1)求△ABC的面积;
❑√2
(2)若sin AsinC= ,求b.
3
在①a2−b2+c2=2,②⃗AB⋅⃗BC=−1这两个条件中任选一个,补充在横线中,并解答.
注:如果选择多个条件分别解答,按第一个解答计分.
❑√2
【答案】(1)
8
1
(2)
2
【分析】(1)若选①则根据余弦定理得accosB=1,且cosB>0,于是利用平方公式得cosB,即可得ac
的值,再根据面积公式即可得△ABC的面积;若选②根据向量数量积定义得⃗AB⋅⃗BC =−accosB,且
cosB>0,于是利用平方公式得cosB,即可得ac的值,再根据面积公式即可得△ABC的面积;
(2)由正弦定理得即可求得b的值.
a2+c2−b2
【详解】(1)若选①a2−b2+c2=2,由余弦定理得cosB= ,整理得accosB=1,则cosB>0,
2ac
又sinB=
1
,则cosB=❑
√
1−
(1) 2
=
2❑√2
,ac=
1
=
3❑√2
,则S =
1
acsinB=
❑√2
;
3 3 3 cosB 4 △ABC 2 8
若选②⃗AB⋅⃗BC=−1<0,则cosB>0,又sinB=
1
,则cosB=❑
√
1−
(1) 2
=
2❑√2
,
3 3 3
1 3❑√2 1 ❑√2
又⃗AB⋅⃗BC =−accosB,得ac= = ,则S = acsinB= ;
cosB 4 △ABC 2 8
3❑√2
b a c b2 a c ac 4 9
(2)由正弦定理得: = = ,则 = ⋅ = = = ,则
sinB sinA sinC sin2B sin A sinC sin AsinC ❑√2 4
3
b 3 3 1
= ,b= sinB= .
sinB 2 2 2
18.某县城为活跃经济,特举办传统文化民俗节,小张弄了一个套小白兔的摊位,设x表示第i天的平均
i
气温,y表示第i天参与活动的人数,i=1,2,⋯,20,根据统计,计算得到如下一些统计量的值:
i
20 20 20
∑(x −x) 2=80,∑(y −y) 2=9000,∑(x −x)(y −y)=800.
i i i i
i=1 i=1 i=1
(1)根据所给数据,用相关系数r(精确到0.01)判断是否可用线性回归模型拟合y与x的关系;
3
(2)现有两个家庭参与套圈,A家庭3位成员每轮每人套住小白兔的概率都为 ,B家庭3位成员每轮每人
10
学科网(北京)股份有限公司1 1 1
套住小白兔的概率分别为 , , ,每个家庭的3位成员均玩一次套圈为一轮,每轮每人收费20元,每个
3 4 6
小白免价值40元,且每人是否套住相互独立,以每个家庭的盈利的期望为决策依据,问:一轮结束后,哪
个家庭损失较大?
n
∑ x y −nx y
i i
附:相关系数r= i=1
.
√ n n
❑∑(x −x) 2∑(y −y) 2
i i
i=1 i=1
【答案】(1)可用线性回归模型拟合y与x的关系.
(2)B家庭的损失较大
【分析】(1)计算相关系数r,若|r|接近1,则可用线性回归模型拟合y与x的关系.
(2)A家庭符合二项分布,直接用公式求期望,B家庭先根据题意列出分布列再求期望.
【详解】(1)由题可知
20 20
∑ x y −20x y ∑(x −x)(y −y)
i i i i 800 2❑√2
r= i=1 = i=1 = = ≈0.94,
√ 20 20 √ 20 20 ❑√80×9000 3
❑∑(x −x) 2∑(y −y) 2 ❑∑(x −x) 2∑(y −y) 2
i i i i
i=1 i=1 i=1 i=1
故可用线性回归模型拟合y与x的关系.
( 3 )
(2)设A家庭中套中小白兔的人数为X ,则X ~B 3, ,
1 1 10
3 9
所以E(X )=3× = .
1 10 10
设A家庭的盈利为X 元,则X =40X −60,
2 2 1
所以E(X )=40E(X )−60=−24.
2 1
设B家庭中套中小白兔的人数为Y ,
1
则Y 的所有可能取值为0,1,2,3,
1
2 3 5 5
P(Y =0)= × × = ,
1 3 4 6 12
1 3 5 2 1 5 2 3 1 31
P(Y =1)= × × + × × + × × = ,
1 3 4 6 3 4 6 3 4 6 72
1 1 5 1 3 1 2 1 1 5
P(Y =2)= × × + × × + × × = ,
1 3 4 6 3 4 6 3 4 6 36
1 1 1 1
P(Y =3)= × × = ,
1 3 4 6 72
5 31 5 1 3
所以E(Y )=0× +1× +2× +3× = .
1 12 72 36 72 4
学科网(北京)股份有限公司设B家庭的盈利为Y 元,则Y =40Y −60,
2 2 1
3
所以E(Y )=40E(Y )−60=40× −60=−30.
2 1 4
因为−24>−30,所以B家庭的损失较大
❑√2 x2 y2
19.已知离心率为 的椭圆C: + =1(a>b>0)的左焦点为F,左、右顶点分别为A 、A ,上顶点为
2 a2 b2 1 2
B,且△A BF的外接圆半径大小为❑√3.
1
(1)求椭圆C方程;
(2)设斜率存在的直线l交椭圆C于P,Q两点(P,Q位于x轴的两侧),记直线A P、A P、A Q、A Q的
1 2 2 1
5
斜率分别为k 、k 、k 、k ,若k +k = (k +k ),求△A PQ面积的取值范围.
1 2 3 4 1 4 3 2 3 2
x2 y2
【答案】(1) + =1
4 2
( 5 )
(2) 0, ❑√30
8
【分析】(1)根据椭圆离心率确定椭圆中a,b,c的关系,再结合正弦定理的推论确定外接圆半径与边角关
系即可得c的值,从而求得椭圆方程;
(2)由题可设直线l:x=ty+m(t≠0),P(x ,y ),Q(x ,y ),联立直线与椭圆即可得交点坐标关系,根
1 1 2 2
1 1 5 3
据斜率的计算式可得k k =− ,k k =− ,再由已知等式k +k = (k +k )确定k k =− ,由坐标
1 2 2 3 4 2 1 4 3 2 3 2 3 10
关系进行转化可求得m的值,求解△A PQ面积的表达式,结合函数性质即可得△A PQ面积的取值范围.
2 2
❑√2
【详解】(1)根据椭圆C的离心率为 知a=❑√2c,所以b=❑√a2−c2=c,如图,则|OF|=|OB|=c
2
3π
则在△A BF中,可得∠BF A = ,|A B|=❑√|OA | 2+|OB| 2=❑√3c,
1 1 4 1 1
|A B| ❑√3c
1 = =❑√6c=2×❑√3
由正弦定理得sin∠BF A ❑√2 ,
1
2
解得c=❑√2,所以a=2,b=❑√2,
x2 y2
所以椭圆C的方程为 + =1.
4 2
学科网(北京)股份有限公司(2)由条件知直线l的斜率不为0,
设直线l:x=ty+m(t≠0),P(x ,y ),Q(x ,y ),
1 1 2 2
联立¿,得(t2+2)y2+2mty+m2−4=0,Δ>0得2t2+4>m2
2mt m2−4
于是y + y =− ,y y = ,
1 2 t2+2 1 2 t2+2
x2 y2
因为A (−2,0),A (2,0),P(x ,y )代入椭圆方程得 1+ 1=1,
1 2 1 1
4 2
(
x2
)
2 1− 1
所以 y y y2 4 1,
k k = 1 ⋅ 1 = 1 = =−
1 2 x +2 x −2 x2−4 x2−4 2
1 1 1 1
1 1 1
同理k k =− ,于是k =− ,k =− ,
3 4 2 1 2k 4 2k
2 3
5 1 1 5
因为k +k = (k +k ),所以− − = (k +k ),
1 4 3 2 3 2k 2k 3 2 3
2 3
k +k 5
即− 2 3= (k +k ).
2k k 3 2 3
2 3
3
又直线l的斜率存在,所以k +k ≠0,于是k k =− ,
2 3 2 3 10
y y 3
所以 1 ⋅ 2 =− ,即10 y y +3(x −2)(x −2)=0,
x −2 x −2 10 1 2 1 2
1 2
又x =t y +m,x =t y +m,
1 1 2 2
所以10 y y +3(t y +m−2)(t y +m−2)=0,
1 2 1 2
整理得(3t2+10)y y +3t(m−2)(y + y )+3(m−2) 2=0,
1 2 1 2
所以(3t2+10) (m2−4) +3t(m−2) ( − 2mt ) +3(m−2) 2=0,
t2+4 t2+2
化简整理得(m−2)(2m+1)=0,
m2−4
又P、Q位于x轴的两侧,所以y y = <0,解得−2❑√30,t2= ,
16
5 16λ 20
S = ⋅ =
于是 △A 2 PQ 4 λ2+2 2,
λ+
λ
20
y=
又函数 2在(❑√30,+∞)上单调递减,
λ+
λ
( 5 )
所以△A PQ面积的取值范围为 0, ❑√30 .
2 8
【点睛】关键点点睛:本题考查了直线与椭圆相交的坐标关系,利用坐标运算解决直线斜率关系及面积关
系.解决本题的关键是确定直线直线A P、A P、A Q、A Q之间的斜率关系,结合椭圆上的任意一点与
1 2 2 1
左右顶点之间的斜率关系,可将四个斜率值简化为两个斜率关系,即可减少位置数,从而利用坐标运算及
坐标关系确定所设直线过定点,于是简化所求面积表达式中的变量个数从而可结合函数关系确定取值范围,
得以解决问题.
20.已知函数f (x)=e2x−ax+2.
(1)若f (x)在点(0,f (0))处的切线方程为 ,求实数a的值;
x
(2)设g(x)=x−3ln ,在(1)的条件下,若满足f (m)=g(n)(m≥0,n≥3),求证:n≤3e2m.
3
【答案】(1)a=2
(2)证明见解析
【分析】(1)根据导数的几何意义以及切线的方程进行求解.
(2)f (m)=g(n)等价于e2m−2m+2=2
(n
−ln
n)
+
n
−ln
n
,结合:当x≥1时,x−lnx≥1,得
3 3 3 3
e2m−2m+2≥2+ n −ln n ,即e2m−2m≥e ln n 3−ln n ,令ℎ(x)=ex−x,则ℎ(2m)≥ℎ ( ln n) ,结合
3 3 3 3
ℎ(x)的单调性即可证得结论.
【详解】(1)f'(x)=2e2x−a,f (0)=3,即切点为(0,3),
学科网(北京)股份有限公司该点处的斜率k=f'(0)=2−a.
则2−a=0,故a=2.
(2)由(1)知f (x)=e2x−2x+2.
n
则f
(m)=g(n)等价于e2m−2m+2=n−3ln
,
3
故e2m−2m+2=2
(n
−ln
n)
+
n
−ln
n
3 3 3 3
1 x−1
设t(x)=x−lnx,x≥1,则t'(x)=1− = ,所以当x≥1时,t'(x)≥0,
x x
所以t(x)=x−lnx在1,+∞)上单调递增,所以t(x)≥t(1)=1,
即当x≥1时,x−lnx≥1,
n n n
因为 ≥1,所以 −ln ≥1,当且仅当n=3时取等号,
3 3 3
n n ln n n
所以e2m−2m+2≥2+ −ln ,即e2m−2m≥e 3−ln .
3 3 3
令ℎ(x)=ex−x,则ℎ '(x)=ex−1,
当x∈(0,+∞),ℎ '(x)>0,则ℎ(x)=ex−x在(0,+∞)上为增函数.
n
因为n≥3,所以ln ≥0,又2m≥0,
3
ln n n ( n)
由于e2m−2m≥e 3−ln ,即ℎ(2m)≥ℎ ln ,
3 3
n
则2m≥ln ,即n≤3e2m.
3
【点睛】方法点睛:利用导数证明不等式常见类型及解题策略:
(1)构造差函数ℎ(x)=f(x)−g(x),根据差函数导函数符号,确定差函数单调性,利用单调性得不等
量关系,进而证明不等式;
(2)根据条件,寻找目标函数,一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放
缩、等量代换将多元函数转化为一元函数.
a +a +⋯+a
21.已知数列{a },设m = 1 2 n(n∈N∗),若{a }满足性质Ω:存在常数c,使得对于任意两
n n n n
两不等的正整数i、j、k,都有(i− j)m +(j−k)m +(k−i)m =c,则称数列{a }为“梦想数列”.
k i j n
(1)若b =2n(n∈N∗),判断数列{b }是否为“梦想数列”,并说明理由;
n n
(2)若c =2n−1(n∈N∗),判断数列{c }是否为“梦想数列”,并说明理由;
n n
(3)判断“梦想数列”{a }是否为等差数列,并说明理由.
n
【答案】(1){b }不是“梦想数列”,理由见解析
n
(2){c }是“梦想数列”,理由见解析
n
学科网(北京)股份有限公司(3)“梦想数列”{a }是等差数列,理由见解析
n
【分析】(1)分析条件(i− j)m +(j−k)m +(k−i)m =c,可得c=0,对于数列{b },取两两不等的正整
k i j n
数i=1、j=2、k=3,验证不满足(i− j)m +(j−k)m +(k−i)m =0,则不是“梦想数列”;
k i j
(2)由数列{c }的通项公式可求m ,从而验证满足(i− j)m +( j−k)m +(k−i)m =c,所以是“梦想数
n n k i j
列”;
(3)先验证i=1,j=2,k=3时,a 、a 、a 成等差数列,再令i=1,j=2,k=n(n≥3),得数列{a }的前n
1 2 3 n
项和S 的表达式,从而求得数列{a }的通项公式,得证.
n n
【详解】(1)(i− j)m +(j−k)m +(k−i)m =c
k i j
(j−i)m +(i−k)m +(k− j)m =c,所以,c=0
k j i
14
当b =2n 时,m =2,m =3,m =
n 1 2 3 3
14 26
(1−2)· +(2−3)⋅2+(3−1)⋅3= ≠0所以,{b }不是“梦想数列”
3 3 n
(2)a =2i−1,a =2 j−1,a =2k−1,
i j k
n(a +a )
1 n
a +a +⋯+a S 2 n2,
m = 1 2 n= n= =
n n n n n
k2 i2 j2
(i− j) +(j−k) +(k−i) =0所以,{c }是“梦想数列”
k i j n
a +a +a a a +a
(3)①令i=1,j=2,k=3,(1−2) 1 2 3+(2−3) 1+(3−1) 1 2=0
3 1 2
所以,a +a =2a ,即:a 、a 、a 成等差数列,
1 3 2 1 2 3
②令i=1,j=2,k=n(n≥3),
S S
(1−2) n+(2−n)a +(n−1) 2=0,
n 1 2
化简为:2S +(n2−3n)a −n(n−1)a =0,
n 1 2
2S +(n2−n−2)a −n(n+1)a =0
n+1 1 2
两式相减得:2a +2na −2a −2na =0⇒a =a +nd
n+1 1 1 2 n+1 1
所以,a =a +(n−1)d(n≥4),当n=1,2,3时也成立.
n 1
综上可得,“梦想数列”{a }是等差数列.
n
学科网(北京)股份有限公司学科网(北京)股份有限公司