文档内容
四川省内江市2018年中考数学真题试题
一、选择题(本大题共12小题,每小题3分,共36分)
1.(3分)﹣3的绝对值是( )
A.﹣3 B.3 C. D.
2.(3分)小时候我们用肥皂水吹泡泡,其泡沫的厚度约0.000326毫米,用科学记数法表示
为( )
A.3.26×10﹣4毫米 B.0.326×10﹣4毫米
C.3.26×10﹣4厘米 D.32.6×10﹣4厘米
3.(3分)如图是正方体的表面展开图,则与“前”字相对的字是( )
A.认 B.真 C.复 D.习
4.(3分)下列计算正确的是( )
A.a+a=a2B.(2a)3=6a3C.(a﹣1)2=a2﹣1 D.a3÷a=a2
5.(3分)已知函数y= ,则自变量x的取值范围是( )
A.﹣1<x<1 B.x≥﹣1且x≠1 C.x≥﹣1 D.x≠1
6.(3分)已知: ﹣ = ,则 的值是( )
A. B.﹣ C.3 D.﹣3
7.(3分)已知⊙O 的半径为3cm,⊙O 的半径为2cm,圆心距OO=4cm,则⊙O 与⊙O 的位置
1 2 1 2 1 2
关系是( )
A.外高 B.外切 C.相交 D.内切
8.(3分)已知△ABC与△ABC 相似,且相似比为1:3,则△ABC与△ABC 的面积比为( )
1 1 1 1 1 1
A.1:1 B.1:3 C.1:6 D.1:9
9.(3分)为了了解内江市2018年中考数学学科各分数段成绩分布情况,从中抽取400名考
生的中考数学成绩进行统计分析,在这个问题中,样本是指( )
A.400
1B.被抽取的400名考生
C.被抽取的400名考生的中考数学成绩
D.内江市2018年中考数学成绩
10.(3分)如图,在物理课上,小明用弹簧秤将铁块A悬于盛有水的水槽中,然后匀速向上提
起,直至铁块完全露出水面一定高度,则如图能反映弹簧秤的读数y(单位:N)与铁块被提起
的高度x(单位:cm)之间的函数关系的大致图是( )
A. B. C. D.
11.(3分)如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知
∠BDC=62°,则∠DFE的度数为( )
A.31° B.28° C.62° D.56°
12.(3分)如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,
1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A′B′C′关于点P成中
心对称,则点A′的坐标为( )
2A.(﹣4,﹣5)B.(﹣5,﹣4)C.(﹣3,﹣4)D.(﹣4,﹣3)
二、填空题(本大题共4小题,每小题5分,共20分)
13.(5分)分解因式:a3b﹣ab3= .
14.(5分)有五张卡片(形状、大小、质地都相同),上面分别画有下列图形:
①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆.
将卡片背面朝上洗匀,从中抽取一张,正面图形一定满足既是轴对称图形,又是中心对称图
形的概率是 .
15.(5分)关于x的一元二次方程x2+4x﹣k=0有实数根,则k的取值范围是 .
16.(5分)已知,A、B、C、D是反比例函数y= (x>0)图象上四个整数点(横、纵坐标均为整
数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形(如图)的边长为半径作
四分之一圆周的两条弧,组成四个橄榄形(阴影部分),则这四个橄榄形的面积总和是
(用含π的代数式表示).
三、解答题(本大题共5小题,共44分)
17.(7分)计算: ﹣|﹣ |+(﹣2 )2﹣(π﹣3.14)0×( )﹣2.
18.(9分)如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC上的点,AE=CF,并且
∠AED=∠CFD.
求证:(1)△AED≌△CFD;
(2)四边形ABCD是菱形.
319.(9分)为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个
水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下
(成绩得分均为整数):
组别 成绩分组 频数 频率
1 47.5~59.5 2 0.05
2 59.5~71.5 4 0.10
3 71.5~83.5 a 0.2
4 83.5~95.5 10 0.25
5 95.5~107.5 b c
6 107.5~120 6 0.15
合计 40 1.00
根据表中提供的信息解答下列问题:
(1)频数分布表中的a= ,b= ,c= ;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,
预计优秀的人数约为 ,72分及以上为及格,预计及格的人数约为 ,及格的百
分比约为 ;
(3)补充完整频数分布直方图.
20.(9分)如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹
角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯
B的仰角分别为α和β,且tanα=6,tanβ= ,求灯杆AB的长度.
421.(10分)某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号
手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每
部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A
型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
四、填空题(本大题共4小题,每小题6分,共24分)
22.(6分)已知关于x的方程ax2+bx+1=0的两根为x=1,x=2,则方程a(x+1)2+b(x+1)+1=0
1 2
的两根之和为 .
23.(6分)如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O的半径r=2,直线AB
不垂直于直线l,过点A,B分别作直线l的垂线,垂足分别为点D,C,则四边形ABCD的面积的
最大值为 .
24.(6分)已知△ABC的三边a,b,c,满足a+b2+|c﹣6|+28=4 +10b,则△ABC的外接圆
半径= .
25.(6分)如图,直线y=﹣x+1与两坐标轴分别交于A,B两点,将线段OA分成n等份,分点分
别为P,P,P,…,P ,过每个分点作x轴的垂线分别交直线AB于点T,T,T,…,T ,用
1 2 3 n﹣1 1 2 3 n﹣1
S,S,S,…,S 分别表示Rt△TOP,Rt△TPP,…,Rt△T P P 的面积,则S+S+S+…
1 2 3 n﹣1 1 1 2 1 2 n﹣1 n﹣2 n﹣1 1 2 3
+S = .
n﹣1
5五、解答题(本大题共3小题,每小题12分,共36分)
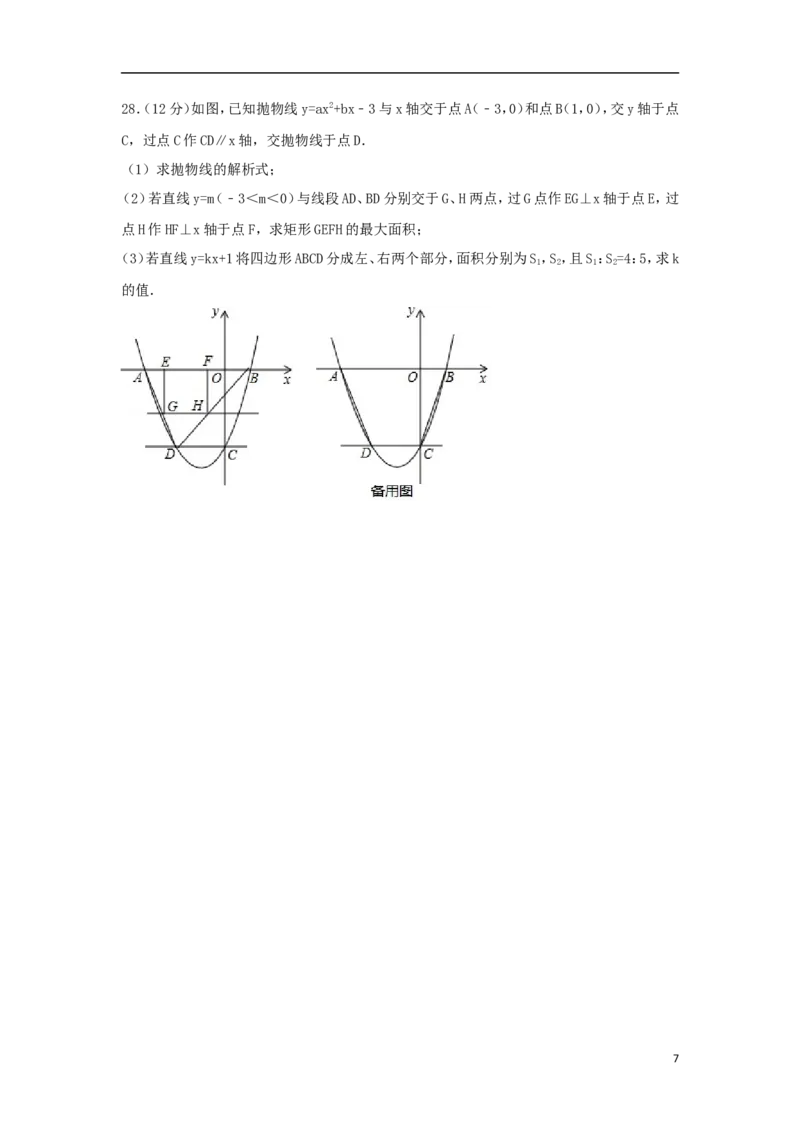
26.(12分)如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作
OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CD•OE;
(3)若tanC= ,DE= ,求AD的长.
27.(12分)对于三个数a,b,c,用M{a,b,c}表示这三个数的中位数,用max{a,b,c}表示这
三个数中最大数,例如:M{﹣2,﹣1,0}=﹣1,max{﹣2,﹣1,0}=0,max{﹣2,﹣1,a}=
解决问题:
(1)填空:M{sin45°,cos60°,tan60°}= ,如果max{3,5﹣3x,2x﹣6}=3,则x的取
值范围为 ;
(2)如果2•M{2,x+2,x+4}=max{2,x+2,x+4},求x的值;
(3)如果M{9,x2,3x﹣2}=max{9,x2,3x﹣2},求x的值.
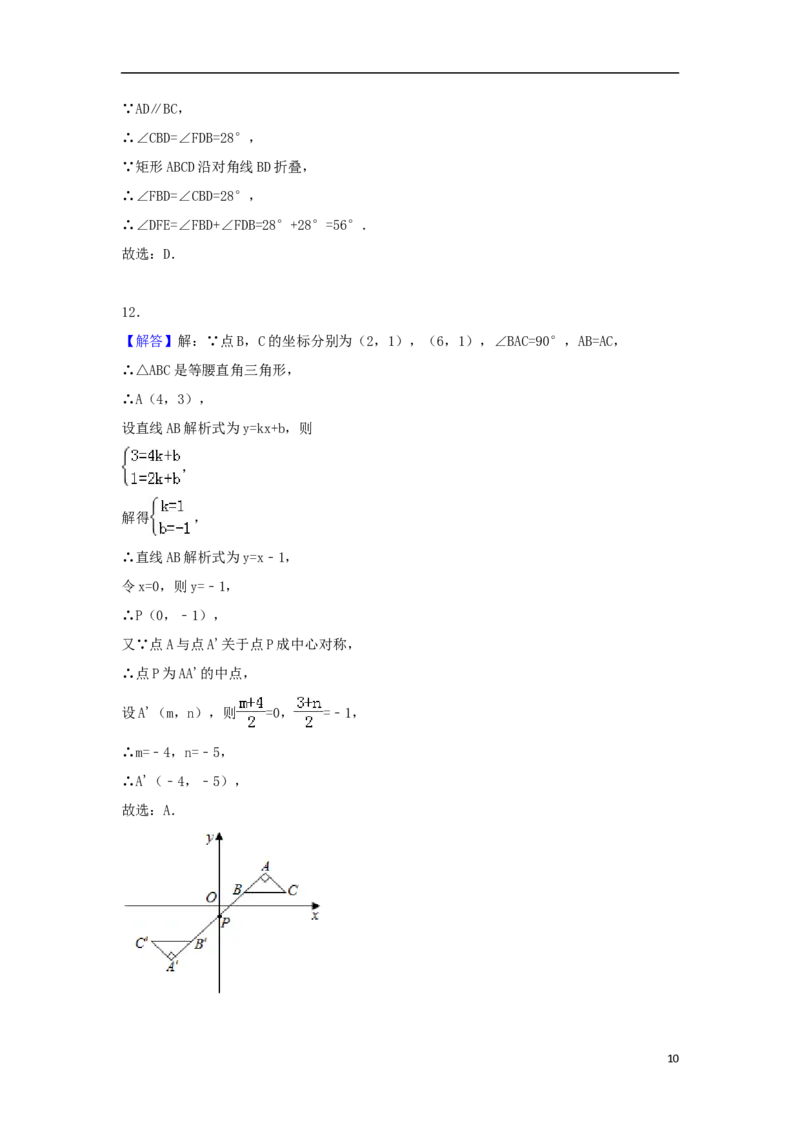
628.(12分)如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点
C,过点C作CD∥x轴,交抛物线于点D.
(1)求抛物线的解析式;
(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过
点H作HF⊥x轴于点F,求矩形GEFH的最大面积;
(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S,S,且S:S=4:5,求k
1 2 1 2
的值.
7参考答案与试题解析
一、选择题(本大题共12小题,每小题3分,共36分)
1.
【解答】解:|﹣3|=3.
故﹣3的绝对值是3.
故选:B.
2.
【解答】解:0.000326毫米,用科学记数法表示为3.26×10﹣4毫米.
故选:A.
3.
【解答】解:由图形可知,与“前”字相对的字是“真”.
故选:B.
4.
【解答】解:A,a+a=2a≠a2,故该选项错误;
B,(2a)3=8a3≠6a3,故该选项错误
C,(a﹣1)2=a2﹣2a+1≠a2﹣1,故该选项错误;
D,a3÷a=a2,故该选项正确,
故选:D.
5.
【解答】解:根据题意得: ,
解得:x≥﹣1且x≠1.
故选:B.
6.
【解答】解:∵ ﹣ = ,
∴ = ,
8则 =3,
故选:C.
7.
【解答】解:∵⊙O 的半径为3cm,⊙O 的半径为2cm,圆心距OO 为4cm,
1 2 1 2
又∵2+3=5,3﹣2=1,1<4<5,
∴⊙O 与⊙O 的位置关系是相交.
1 2
故选:C.
8.
【解答】解:已知△ABC与△ABC 相似,且相似比为1:3,
1 1 1
则△ABC与△ABC 的面积比为1:9,
1 1 1
故选:D.
9.
【解答】解:为了了解内江市2018年中考数学学科各分数段成绩分布情况,从中抽取400名
考生的中考数学成绩进行统计分析,
在这个问题中,样本是指被抽取的400名考生的中考数学成绩.
故选:C.
10.
【解答】解:露出水面前排开水的体积不变,受到的浮力不变,根据称重法可知y不变;
铁块开始露出水面到完全露出水面时,排开水的体积逐渐变小,根据阿基米德原理可知受到
的浮力变小,根据称重法可知y变大;
铁块完全露出水面后一定高度,不再受浮力的作用,弹簧秤的读数为铁块的重力,故y不变.
故选:C.
11.
【解答】解:∵四边形ABCD为矩形,
∴AD∥BC,∠ADC=90°,
∵∠FDB=90°﹣∠BDC=90°﹣62°=28°,
9∵AD∥BC,
∴∠CBD=∠FDB=28°,
∵矩形ABCD沿对角线BD折叠,
∴∠FBD=∠CBD=28°,
∴∠DFE=∠FBD+∠FDB=28°+28°=56°.
故选:D.
12.
【解答】解:∵点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴A(4,3),
设直线AB解析式为y=kx+b,则
,
解得 ,
∴直线AB解析式为y=x﹣1,
令x=0,则y=﹣1,
∴P(0,﹣1),
又∵点A与点A'关于点P成中心对称,
∴点P为AA'的中点,
设A'(m,n),则 =0, =﹣1,
∴m=﹣4,n=﹣5,
∴A'(﹣4,﹣5),
故选:A.
10二、填空题(本大题共4小题,每小题5分,共20分)
13.
【解答】解:a3b﹣ab3,
=ab(a2﹣b2),
=ab(a+b)(a﹣b).
14.
【解答】解:∵五张卡片①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆中,既是轴对
称图形,又是中心对称图形的①⑤,
∴从中抽取一张,正面图形一定满足既是轴对称图形,又是中心对称图形的概率是: .
故答案为: .
15.
【解答】解:∵关于x的一元二次方程x2+4x﹣k=0有实数根,
∴△=42﹣4×1×(﹣k)=16+4k≥0,
解得:k≥﹣4.
故答案为:k≥﹣4.
16.
【解答】解:∵A、B、C、D、E是反比例函数y= (x>0)图象上五个整数点,
∴x=1,y=8;
x=2,y=4;
x=4,y=2;
x=8,y=1;
∴一个顶点是A、D的正方形的边长为1,橄榄形的面积为:
2 ;
一个顶点是B、C的正方形的边长为2,橄榄形的面积为:
11=2(π﹣2);
∴这四个橄榄形的面积总和是:(π﹣2)+2×2(π﹣2)=5π﹣10.
故答案为:5π﹣10.
三、解答题(本大题共5小题,共44分)
17.
【解答】解:原式=2 ﹣ +12﹣1×4
= +8.
18.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C.
在△AED与△CFD中,
∴△AED≌△CFD(ASA);
(2)由(1)知,△AED≌△CFD,则AD=CD.
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
19.
【解答】解:(1)∵被调查的总人数为2÷0.05=40人,
∴a=40×0.2=8,b=40﹣(2+4+8+10+6)=10,c=10÷40=0.25,
故答案为:8、10、0.25;
(2)∵全区八年级学生总人数为200×40=8000人,
∴ 预 计 优 秀 的 人 数 约 为 8000×0.15=1200 人 , 预 计 及 格 的 人 数 约 为 8000×
12(0.2+0.25+0.25+0.15)=6800人,及格的百分比约为 ×100%=85%,
故答案为:1200人、6800人、85%;
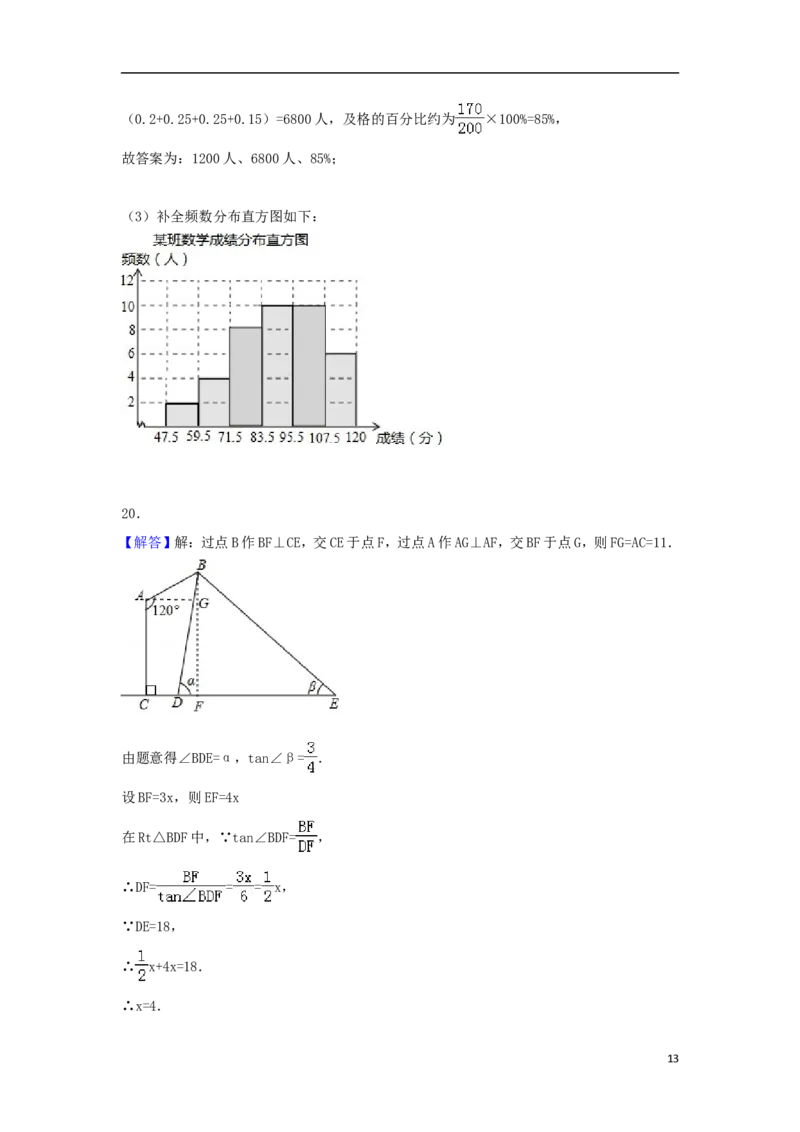
(3)补全频数分布直方图如下:
20.
【解答】解:过点B作BF⊥CE,交CE于点F,过点A作AG⊥AF,交BF于点G,则FG=AC=11.
由题意得∠BDE=α,tan∠β= .
设BF=3x,则EF=4x
在Rt△BDF中,∵tan∠BDF= ,
∴DF= = = x,
∵DE=18,
∴ x+4x=18.
∴x=4.
13∴BF=12,
∴BG=BF﹣GF=12﹣11=1,
∵∠BAC=120°,
∴∠BAG=∠BAC﹣∠CAG=120°﹣90°=30°.
∴AB=2BG=2,
答:灯杆AB的长度为2米.
21.
【解答】解:(1)设A、B两种型号的手机每部进价各是x元、y元,
根据题意得: ,
解得: ,
答:A、B两种型号的手机每部进价各是2000元、1500元;
(2)①设A种型号的手机购进a部,则B种型号的手机购进(40﹣a)部,
根据题意得: ,
解得: ≤a≤30,
∵a为解集内的正整数,
∴a=27,28,29,30,
∴有4种购机方案:
方案一:A种型号的手机购进27部,则B种型号的手机购进13部;
方案二:A种型号的手机购进28部,则B种型号的手机购进12部;
方案三:A种型号的手机购进29部,则B种型号的手机购进11部;
方案四:A种型号的手机购进30部,则B种型号的手机购进10部;
②设A种型号的手机购进a部时,获得的利润为w元.
根据题意,得w=500a+600(40﹣a)=﹣100a+24000,
∵﹣10<0,
∴w随a的增大而减小,
∴当a=27时,能获得最大利润.此时w=﹣100×27+24000=21700(元).
14因此,购进A种型号的手机27部,购进B种型号的手机13部时,获利最大.
答:购进A种型号的手机27部,购进B种型号的手机13部时获利最大.
四、填空题(本大题共4小题,每小题6分,共24分)
22.
【解答】解:设x+1=t,方程a(x+1)2+b(x+1)+1=0的两根分别是x,x,
3 4
∴at2+bt+1=0,
由题意可知:t=1,t=2,
1 2
∴t+t=3,
1 2
∴x+x+2=3
3 4
故答案为:1
23.
【解答】解:∵OE⊥l,AD⊥l,BC⊥l,
而OA=OB,
∴OE为直角梯形ADCB的中位线,
∴OE= (AD+BC),
∴S = (AD+BC)•CD=OE•CD=3CD,
四边形ABCD
当CD=AB=4时,CD最大,S 最大,最大值为12.
四边形ABCD
24.
【解答】解:∵a+b2+|c﹣6|+28=4 +10b,
∴(a﹣1﹣4 +4)+(b2﹣10b+25)+|c﹣6|=0,
∴( ﹣2)2+(b﹣5)2+|c﹣6|=0,
∴ ,b﹣5=0,c﹣6=0,
解得,a=5,b=5,c=6,
∴AC=BC=5,AB=6,
作CD⊥AB于点D,
则AD=3,CD=4,
设△ABC的外接圆的半径为r,
则OC=r,OD=4﹣r,OA=r,
15∴32+(4﹣r)2=r2,
解得,r= ,
故答案为: .
25.
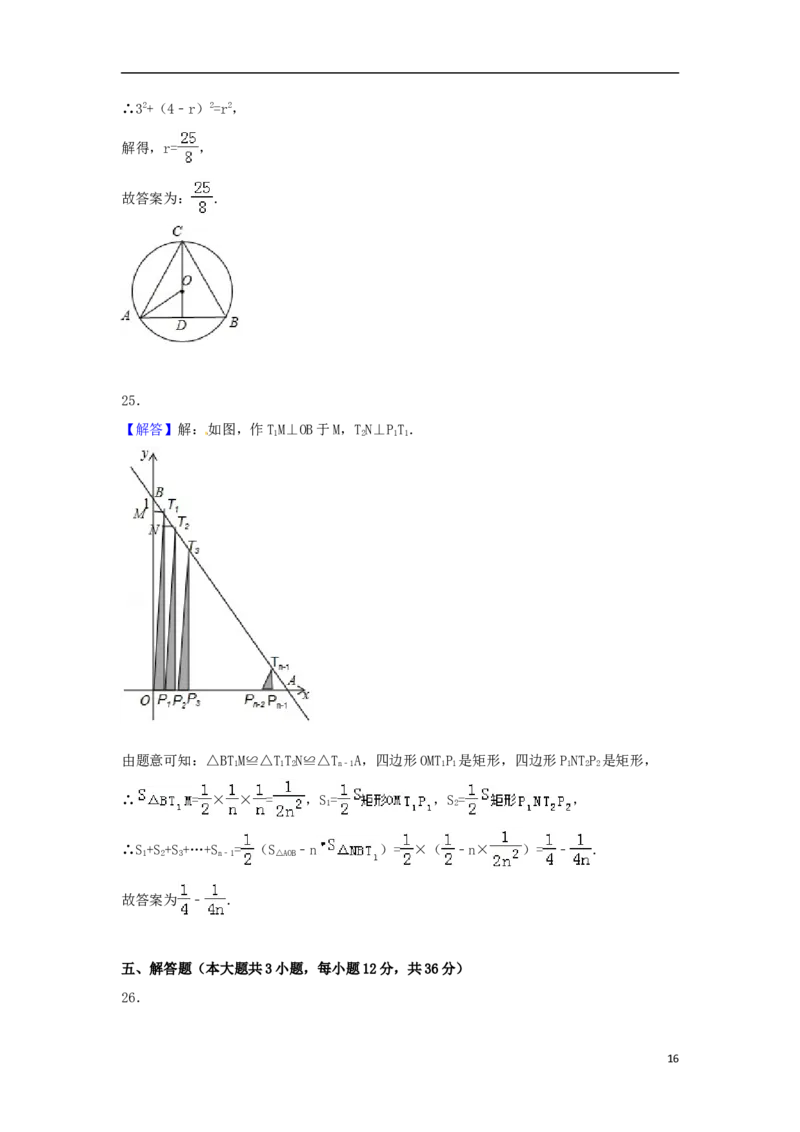
【解答】解:如图,作TM⊥OB于M,TN⊥PT.
1 2 1 1
由题意可知:△BTM≌△TTN≌△T A,四边形OMTP 是矩形,四边形PNTP 是矩形,
1 1 2 n﹣1 1 1 1 2 2
∴ = × × = ,S= ,S= ,
1 2
∴S+S+S+…+S = (S ﹣n )= ×( ﹣n× )= ﹣ .
1 2 3 n﹣1 △AOB
故答案为 ﹣ .
五、解答题(本大题共3小题,每小题12分,共36分)
26.
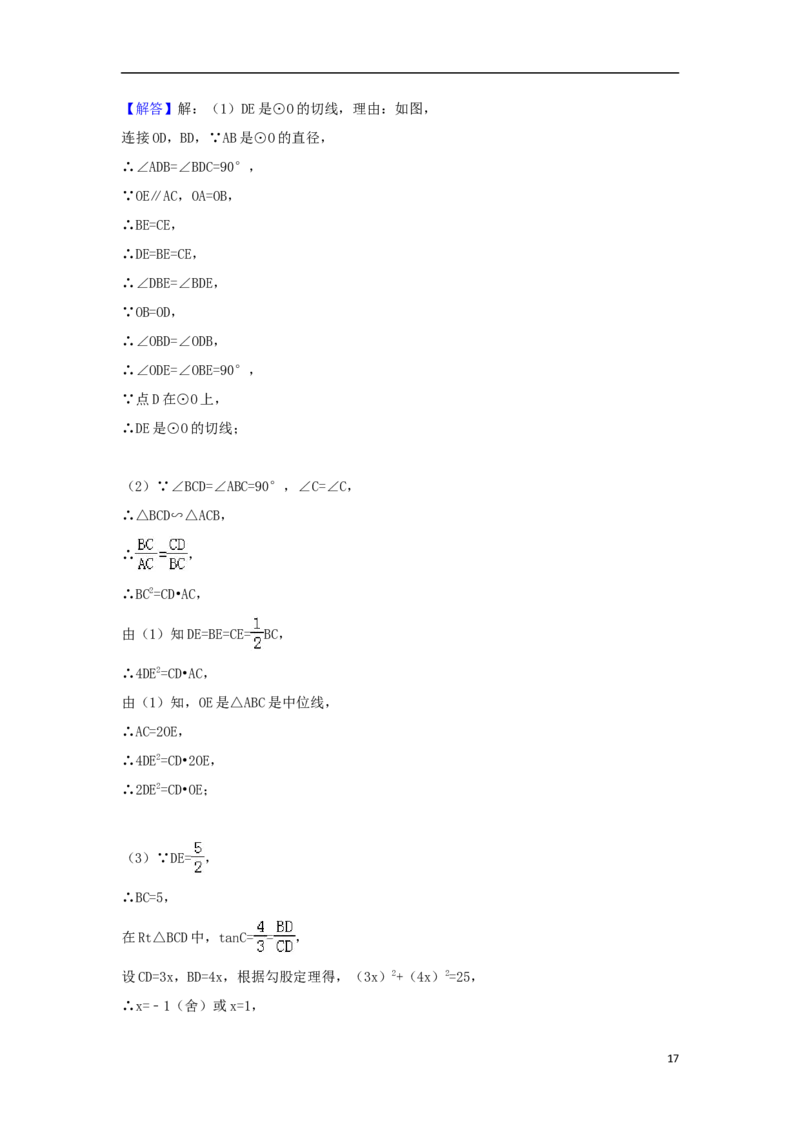
16【解答】解:(1)DE是⊙O的切线,理由:如图,
连接OD,BD,∵AB是⊙O的直径,
∴∠ADB=∠BDC=90°,
∵OE∥AC,OA=OB,
∴BE=CE,
∴DE=BE=CE,
∴∠DBE=∠BDE,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODE=∠OBE=90°,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)∵∠BCD=∠ABC=90°,∠C=∠C,
∴△BCD∽△ACB,
∴ ,
∴BC2=CD•AC,
由(1)知DE=BE=CE= BC,
∴4DE2=CD•AC,
由(1)知,OE是△ABC是中位线,
∴AC=2OE,
∴4DE2=CD•2OE,
∴2DE2=CD•OE;
(3)∵DE= ,
∴BC=5,
在Rt△BCD中,tanC= = ,
设CD=3x,BD=4x,根据勾股定理得,(3x)2+(4x)2=25,
∴x=﹣1(舍)或x=1,
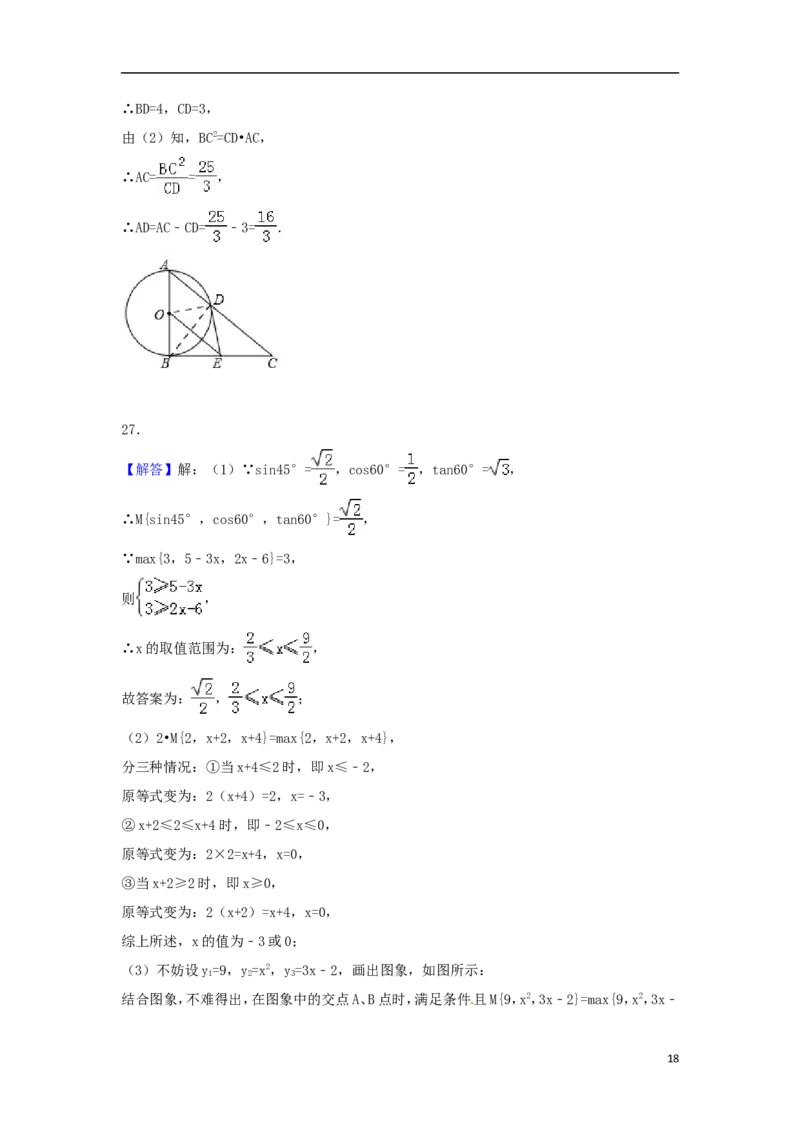
17∴BD=4,CD=3,
由(2)知,BC2=CD•AC,
∴AC= = ,
∴AD=AC﹣CD= ﹣3= .
27.
【解答】解:(1)∵sin45°= ,cos60°= ,tan60°= ,
∴M{sin45°,cos60°,tan60°}= ,
∵max{3,5﹣3x,2x﹣6}=3,
则 ,
∴x的取值范围为: ,
故答案为: , ;
(2)2•M{2,x+2,x+4}=max{2,x+2,x+4},
分三种情况:①当x+4≤2时,即x≤﹣2,
原等式变为:2(x+4)=2,x=﹣3,
②x+2≤2≤x+4时,即﹣2≤x≤0,
原等式变为:2×2=x+4,x=0,
③当x+2≥2时,即x≥0,
原等式变为:2(x+2)=x+4,x=0,
综上所述,x的值为﹣3或0;
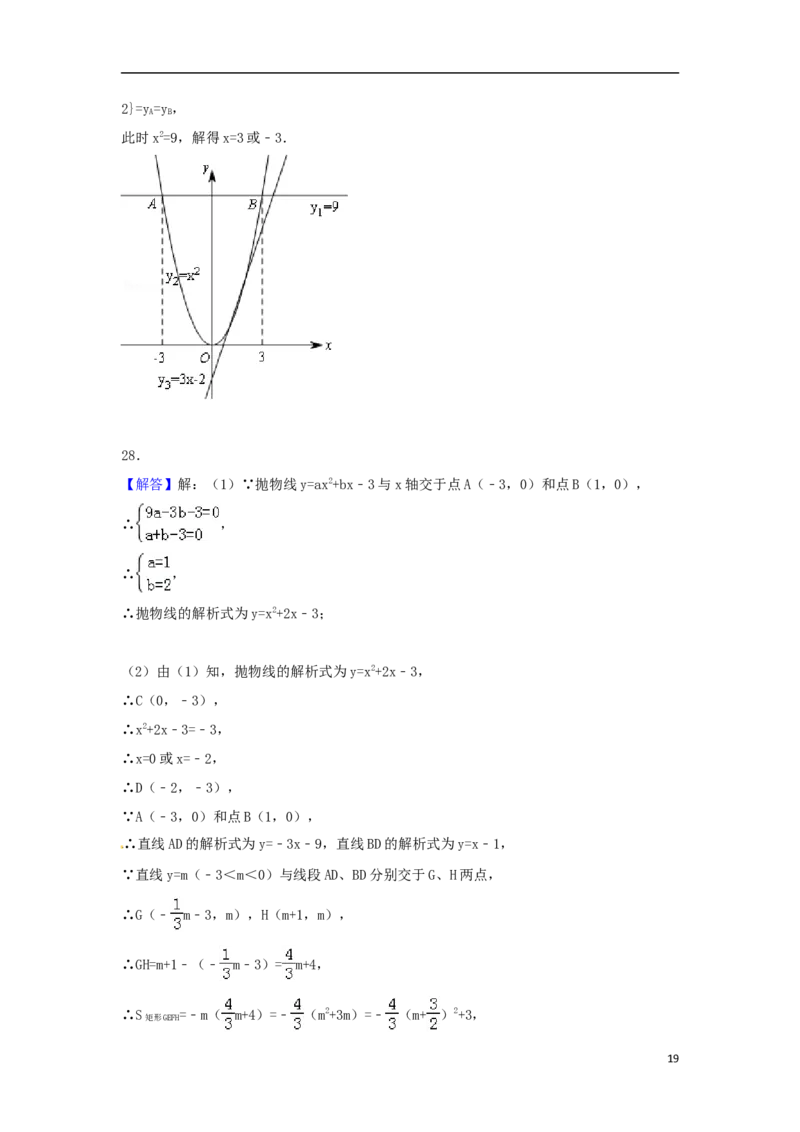
(3)不妨设y=9,y=x2,y=3x﹣2,画出图象,如图所示:
1 2 3
结合图象,不难得出,在图象中的交点A、B点时,满足条件且M{9,x2,3x﹣2}=max{9,x2,3x﹣
182}=y=y,
A B
此时x2=9,解得x=3或﹣3.
28.
【解答】解:(1)∵抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),
∴ ,
∴ ,
∴抛物线的解析式为y=x2+2x﹣3;
(2)由(1)知,抛物线的解析式为y=x2+2x﹣3,
∴C(0,﹣3),
∴x2+2x﹣3=﹣3,
∴x=0或x=﹣2,
∴D(﹣2,﹣3),
∵A(﹣3,0)和点B(1,0),
∴直线AD的解析式为y=﹣3x﹣9,直线BD的解析式为y=x﹣1,
∵直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,
∴G(﹣ m﹣3,m),H(m+1,m),
∴GH=m+1﹣(﹣ m﹣3)= m+4,
∴S =﹣m( m+4)=﹣ (m2+3m)=﹣ (m+ )2+3,
矩形GEFH
19∴m=﹣ ,矩形GEFH的最大面积为3.
(3)∵A(﹣3,0),B(1,0),
∴AB=4,
∵C(0,﹣3),D(﹣2,﹣3),
∴CD=2,
∴S = ×3(4+2)=9,
四边形ABCD
∵S:S=4:5,
1 2
∴S=4,
1
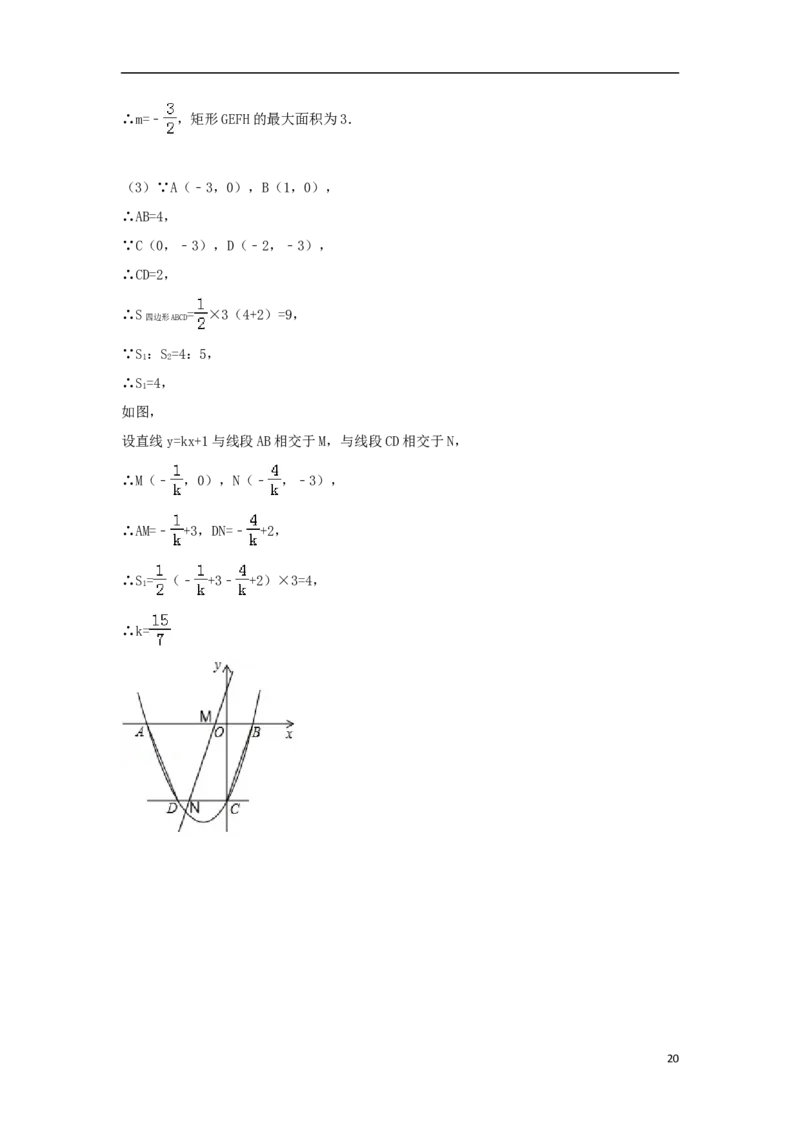
如图,
设直线y=kx+1与线段AB相交于M,与线段CD相交于N,
∴M(﹣ ,0),N(﹣ ,﹣3),
∴AM=﹣ +3,DN=﹣ +2,
∴S= (﹣ +3﹣ +2)×3=4,
1
∴k=
20