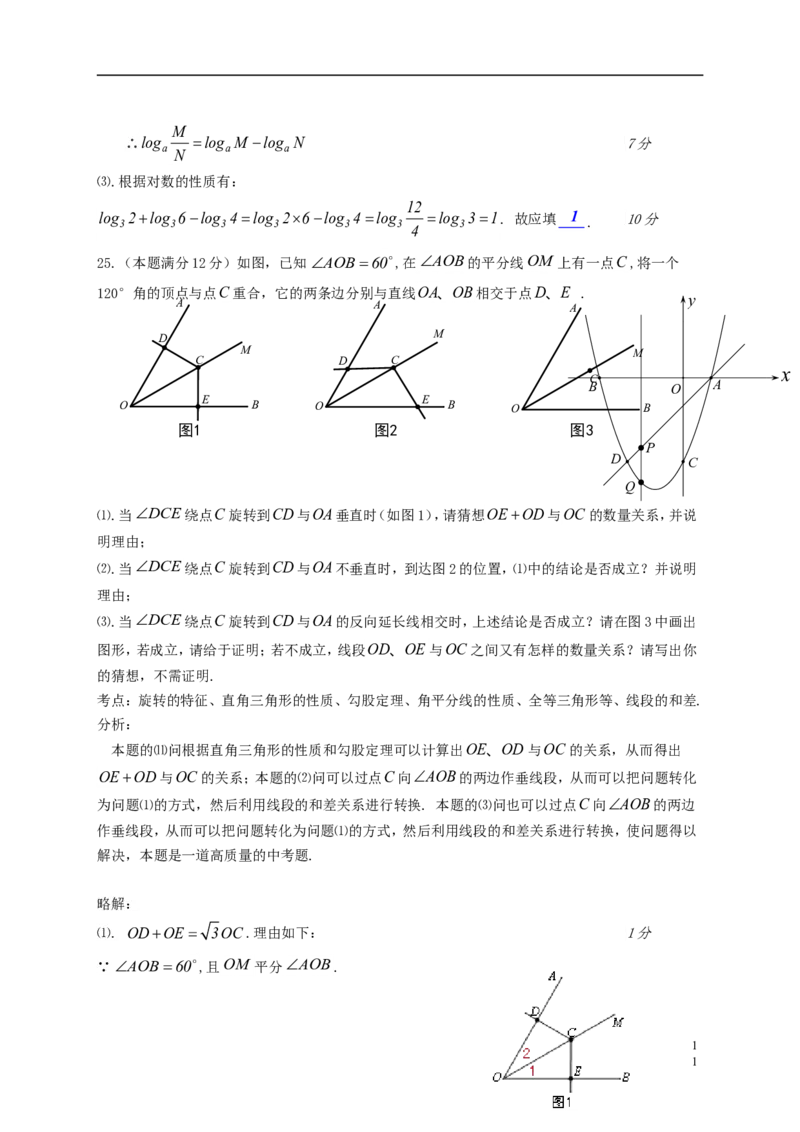四川省自贡市2018年中考数学真题试题（含答案）_中考真题_2.数学中考真题2015-2024年_2018年全国中考数学258份

四川省自贡市2018年中考数学真题试题 一.选择题（共12个小题，每小题4分，共48分；在每题给出的四个选项中，只有一项是符合题目要 求的） 1.计算31的结果是 （ ） A.2 B.4 C.4 D.2 考点：有理数的加减运算. 分析：根有理数的加减运算法则计算312. 故选A. 2.下列计算正确的是 （ ） A.ab2 a2 b2 B.x2y 3xy C. 18 3 2 0 D.  a32 a6 考点：整式的运算、二次根式的加减运算. 分析：计算 18 3 2 3 2 3 2 0. 故选C. 3.2017年我市用于资助贫困学生的助学金总额是445800000元，将445800000用科学记数法表示 为 （ ） A.44.58107 B.4.458108 C.4.458109 D.0.44581010 考点：科学记数法. 分析：445800000 4.458100000000 4.458108. 故选B. 4.在平面内，将一个直角三角板按如图所示摆放在一组平行线上；若155，则2 的度数是 （ ） 1 A.50° B.45° C.40° D.35° 2 考点：平行线的性质、互余角. 分析： 根据平行线的性质可得：13,24 ∵3+4=90,155 ∴49055 35 3 4 ∴235 故选D. 5.下面几何体的主视图是 （ ） 考点：几何体的三视图. 分析：几何体的三视图是从正面、左面和从上面看几何体得到的平面图形，主视图是从正面几何体 A B C D 得到的平面图形，本题从正面看几何体得到的是 . 故选B. 16.如图，在⊿ABC中，点D、E 分别是AB、AC 的中点，若⊿ADE 的面积 A 为4，则是⊿ABC的面积为 （ ） D E A. 8 B. 12 C. 14 D. 16 B C 考点：三角形的中位线定理、相似三角形的性质等. 分析：本题关键是抓住点D、E 分别是AB、AC 的中点，根据三角形的中位线定理可以推出 1 DE∥BC 且DE  BC ；∵DE∥BC ∴⊿ADE ∽⊿ABC ∴S ⊿ADE :S ⊿ABC= 2 DE:BC2 1:4 ；又∵⊿ADE 的面积为4 ∴⊿ABC的面积为16. 故选D. 7.在一次数学测试后，随机抽取九年级（3）班5名学生的成绩（单位：分）如下：80、98、98、83、91，关 于这组数据的说法错误的是 （ ） A.众数是98 B.平均数是90 C.中位数是91 D.方差是56 考点：平均数、中位数、众数以及方差. 分析：本可以先确定平均数、中位数、众数分别为90、91、98 .所以用“排除法”就可以得出答案， 1 直接计算S2  80902 91902 55.6 ，D是错误的 . 故选D. 5  8.回顾初中阶段函数的学习过程，从函数解析式到函数图象，再利用函数图象研究函数的性质，这 种研究方法主要体现的数学思想是 （ ） A.数形结合 B.类比 C.演绎 D.公理化 考点：函数的表示法、函数的图象及其性质. 分析：函数的解析式和函数的图象都是函数的不同表示方法，从“函数解析式到函数图象”是数形 结合起来研究函数的性质，所以体现的是“数形结合”的数学思想. 故选A. 9.如图，若⊿ABC内接于半径为R的⊙O ,且A60,连接OB、OC，则 A 边BC的长为 （ ） O 3 2 B C A. 2R B. R C. R D. 3R 2 2 考点：圆周角定理、垂径定理、等腰三角形性质以及勾股定理等. 分析：本题可以可以根据垂径定理把问题转化在直角三角形，然后再利用勾股定理能使问题可以获 得解决. 略解：过⊙O的圆心O 作OE  BC 于点D .由垂径定理可得BC 2CD . ∵弧BC  BC ∴BOC 2A260 120 1 ∵OBOC,OD BC ∴DOC  BOC 60 2 2∴OCD9060 30 1 1 在Rt ⊿ODC中，OD OC  R 2 2 2 1  3 根据勾股定理计算：CD OC2 OD2  R2  R  R   2  2 1 ∴BC 2CD2 3R 3R. 故选D. 2 6 10.从1、2、3、6这四个数中任取两数，分别记为 m、n ，那么点 m, n 在函数 y  图象的概 x 率是 （ ） 1 1 1 1 A. B. C. D. 2 3 4 8 考点：概率、函数的图象及其性质. 6 分析：要使点 m, n 在函数 y  的图象上，则需满足mn6 .利用列举法（列表法或画树状图） x 列举所有等可能的总数，再找出满足mn6 的情况数，根据“概率”的计算公式可使问题得以解 1 2 3 6 决. 略解： 2 3 6 1 3 6 1 2 6 1 2 3 画出树状图为： 4 1 所有等可能的总数为12种，要关注的mn6 的情况数有4种；P  . 故选B. 12 3 11.已知圆锥的侧面积是8cm2，若圆锥底面半径为Rcm ，母线长为lcm ，则R关于l的函数 图象大致是 （ ） R R R R l l l l O O O O A B C D 考点：圆锥的侧面展开图、扇形的面积、反比例函数的图象及其性质. 分析：圆锥的侧面展开图是一个扇形，扇形的弧长为底圆的周长2R ，扇形的半径为圆锥的母线 1 8 长lcm .根据扇形的面积公式有：8  l2R 即R l 0 ；根据反比例函数的图象及 2 l 其性质，选择支A符合；故选A. 312.如图，在边长为 a 正方形ABCD 中，把边 BC绕点B逆时针旋转60°，得到线段BM ,连接 AM 并延长交CD于N ,连接MC ,则⊿MNC 的面积为 A D （ ） M N 31 2 1 A. a2 B. a2 2 2 B C 31 2 1 C. a2 D. a2 4 4 考点：正方形的性质、等腰、等边三角形的性质、勾股定理以及三角形的面积等. 分析： 本题用正方的面积来减去其它三个三角形的面积来得到⊿MNC 的面积比较麻烦.若我们抓住要 正方形的性质、等腰、等边三角形的性质计算出在⊿MNC 的3、4是特殊角，再通过添加边 MC 的高线，把问题先转化到直角三角形中后可以逐一解决. 略解：过N 作NE MC 于点E. 如图根据正方形的性质、等腰、等边三角形的性质可以得到： MC  BC MB  AB a ，19060 30,49060 30. 1  容易计算出2 18030 75 2 ∴3180BMC21806075 45 ∴MNE 9045 45 ∴NE ME 若设NE  x，则ME  x .∵在Rt ⊿NEC中，430 ∴NC 2NE 2x 根据勾股定理有EC  NC2 NE2  2x2 x2  3x2  3x 31 31 ∴MECE  x 3x 即x 3xa，解得：x a 即NE  a 2 2 1 1 31 31 ∴S⊿MNC = MCDE  a a a2 . 故选C. 2 2 2 4 点评： 本题求⊿MNC 的面积抓住图形是由特殊四边形和特殊三角形搭建起来的所以，比较容易通过找 出求⊿MNC 内角中的特殊角作为突破口，然后通过作高线转化在直角三角形中解决问题，是一道 高质量的中考题！ 二.填空题(共6个小题，每题4分，共24分) 13. 分解因式：ax2 2axyay2= . 考点：因式分解. 分析：本题先提取公因式，再根据完全平方公式分解因式 4略解：ax2 2axyay2 a  x2 2xy y2 ax y2 . 故应填： ax y2 . 1 2 14.化简  的结果是 . x1 x2 1 考点：分式的运算. 分析：先通分，再加减，最后化简. 1 2 x1 2 1 1 略解： x1  x2 1  x1x1  x1x1  x1 . 故应填： x1 . 15.若函数 y  x2 2xm的图象与x轴有且只有一个交点，则m的值为 . 考点：二次函数的图象及其性质、二次综合问题. 分析：二次函数 y  x2 2xm的图象与x轴有且只有一个交点，这个交点就是二次函数图象的顶 点；当令y 0时，对于方程 x2 2xm0有两个相等的实数根，即△ = 0，可保证图象与x轴有 且只有一个交点.所以22 41m0 ，解得:m1. 故应填 1 . 16.六一儿童节，某幼儿园用100元钱给小朋友买了甲、乙两种不同的玩具共30个，单价分别为2元 和4元，则该幼儿园购买了甲、乙两种玩具分别为 、 个. 考点：列方程（组）解应用题. 分析：本题可以总费用和总个数建立方程则解决问题. x y 30 略解：设该幼儿园购买了甲、乙两种玩具分别为x个和 y 个，根据题意列： 2x4y 100 x10 解得： ；经检验，符合题意. 故应填 10 、 20 . y 20 17.观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2018个图形共有 个○. 第1个 第2个 第3个 第4个 C 考点：寻找规律、求代数式的值. 分析： 观察图形的排列：第一个图（31个○开始，第二个图（321）个○ …… P A B 后面每个图在前面一个图形的基础上增加3个○，故第n个图形是3n1 ； F E D 5故当n2018时。3n13201816055 .故应填 6055 . 18.如图，在⊿ABC中，AC  BC 2,AB1,将它沿AB翻折得到⊿ABD,则 四边形ADBC 的形状是 形，点P、E、F 分别为线段AB、AD、DB的 任意点，则PEPF的最小值是 . 考点：菱形、轴对称、等腰三角形的性质，两点之间线段最短，垂线段最短，勾股定理，菱形面积等 分析： 翻折前后两个部分就是成轴对称的.再加上AC  BC，可以推出AC  BC  DA DB,所以四边 形ADBC 的形状是菱形. 关于求PEPF的最小值： 方法一.本题关键是E、F 不是定点，而是动点；仍然可以先作E关于线段BC的对称点E' , 连 接E'F ,再将E'、F 移动使E'F  BD，因为“垂线段最短”.再根据轴对称的性质可得到 PEPF  PE'PF  E'F ；实际上此时的点P恰好是AB的中点. E'F就是菱形一边上的高， 可把E'F平移成等腰⊿ABC腰上的高来解决.见下面的分析流程图组图I. 见下面组图1最后一个图，过B作BM  AC于M ,连接AP ；∵AC  BC，P是AB的中点 ；∴ 1 1 1 CP AB;在Rt ⊿ABC中有BP AB 1 , BC 2 ∴CP BC2 BP2 2 2 2 1 2 15 15 1 1  22    ；根据面积公式可知S ⊿ABC = BCCP ACBM   2 4 2 2 2 15 15 15 ∴ 1 2BM , 解得BM  ；易证E'F  BM ∴PEPF  E'F  . 故应 2 4 4 15 填 . 4 方法二.大家都知道从等腰三角形底边上的任何一点向该三角形两腰作垂线段，两垂线段的和是个 恒值，且等于等腰三角形一腰上的高.所以直接过点P向菱形的两邻边边垂线段，因为“垂线段最 短”，所以PE与PF 之和便最小，然后也把PE、PF转化成等腰三角形一腰的高的高来解决，见下 面流程组图2，同样可以PEPF  BM （计算略）.两种方法的计算量是一样的. C C C C C E' M M A P F B A E E' P F B A E E' P F B A E P F B A E P F B E D D D D D 6 组图1 组图2点评： 本题三个点都是动点，可以把其中一个点作为定点切入思考，有两条思路；一是除了要注意利用 轴对称知识、“两点之间，线段最短.”，其次还结合“垂线段最短”来求出最小值，就是在变化中 寻找“不变”的部分.本题是一道高质量的中考题. 三. 解答题(共8个题，共78分) 1 1 19.（本题满分8分） 计算：  2    2cos45. 2 考点：实数的混合运算. 分析：先计算乘方、绝对值、特殊角的三角函数值，再乘除，最后加减. 2 略解：原式 = 2 22 5分 2 = 2 2 2 =2 8分  3x51  j   20.（本题满分8分）解不等式组： ，并在数轴上表示其解集. 13x  4xk  3 考点：解不等式组、在数轴上表示不等式的解集. 分析：先解每个不等式，然后求出它们的公共部分，表示在数轴上要注意弧（折线）的方向和起始位置 的标记是实心点还是空心圆圈. 略解：解不等式①得：x2 ；解不等式②得：x1 4分 所以不等式组的解集为：1 x2 6分 在数轴上表示出来为： 8分 0 1 2 21.（本题满分8分） 某校研究学生的课余爱好情况吧，采取抽样调查的方法，从阅读、运动、娱乐、 上网等四个方面调查了若干名学生的兴趣爱好，并将调查结果绘制成下面两幅不完整的统计图，请 你根据图中提供的信息解答下列问题： 7娱乐 阅读 20％ 上网 运动 10％ 40％ ⑴.在这次调查中，一共调查了 名学生； ⑵.补全条形统计图； ⑶.若该校共有1500名，估计爱好运动的学生有 人； ⑷.在全校同学中随机选取一名学生参加演讲比赛，用频率估计概率，则选出的恰好是爱好阅读的 学生的概率是 . 考点：统计图、样本估计总体、用频率估计概率. 分析：⑴.结合统计图能读出运动或娱乐的人数和所占总数的百分比，可以计算出总人数；⑵.根据总 人数和扇形图反映出的阅读和上网的百分比可以计算出相应的人数，以此可以补全条形图；⑶.样本 爱好运动的40%可以估计总体爱好运动也占40%，以此可计算出该校爱好运动的人数；⑷.根据扇形 图可以计算出样本中阅读所占的百分比，从而估计出在总体中的频率，以此得出概率的近似值. 略解： ⑴.4040%100 .故因填写 10 0 ； 2分 ⑵.上网的人数为：10010%10 （人） 阅读的人数为：10040201030（人） 补全条形图（见右面） 5分 ⑶.150040%600 .故因填写 60 0 ； 7分 3 3 ⑷.样本中阅读频率为301000.3 ，故概率为 . 故应填 . 8分 10 10 3 22.（本题满分8分）如图，在⊿ABC中， BC 12,tanA ,B 30；求 AC 和 AB的长. 4 C 考点：三角函数、直角三角形的性质、勾股定理等. 分析：本题关键爱是把问题转化在直角三角形中，当我们过点C A B 作出边AB的高后，可以问题转化在两个直角三角形中，利用高作为桥梁使问题获得解决. 略解： 过点C作CD AB于点D,则ADC CDB90 . 1分 81 1 在Rt ⊿DBC 中,B30 ,BC 12cm ∴DC  BC  126cm 3分 2 2 根据勾股定理可求BD 122 62 6 3cm . CD 3 6 3 在Rt ⊿DBC 中, tanA  ,即  ，解得：AD8 AD 4 AD 4   ∴AB BDDC  6 38 cm 6分 根据勾股定理可求AC  82 62  100 10cm . 8分 C 23.（本题满分10分）如图，在⊿ABC中，ACB 90. ⑴.作出经过点B,圆心O在斜边AB上且与边AC相切于点E的⊙O； A B （要求：用尺规作图，保留作图痕迹，不写作法和证明） ⑵.设⑴中所作的⊙O与边AB交于异于点B的另外一点D,若⊙O的直径为5，BC 4；求DE 的长.（如果用尺规作图画不出图形，可画出草图完成⑵问） 考点：尺规作图、圆的相关性质、垂径定理、圆周角定理及其推论、勾股定理以及圆的切线的性质和判 定等. 分析： 本题的⑴问可以先画出草图逆推；关键是抓住既要过点B，又要切点点落在边AC上，换句话说 要达到OE OB，同时要求OE  AC于E，通过作角的平分线以及作平行线找交点确定圆心的办 法来解决. 本题的⑵问“求DE的长”可以化归在Rt ⊿DEB来解决，关键是C求出BE的长度，而 E 这个可以通过⊿EBC ∽⊿EDB来获得解决. 略解： 1 2 ⑴.尺规作图：.如图所示. 4分 A D O B ⑵. 如图所示. ∵DB 为⊙O 的直径 ∴DEB90 5分 又 ∵ACB 90. ∴DEBACB DB BE ∵BE平分ABC ∴12 ∴⊿EDB∽⊿EBC ∴  7分 BE BC 5 BE ∵BD5,BC 4 ∴  ∴BE2 20 . 8分 BE 4 ∵DEB90 9∴DE2 BE2  BD2 即DE2 2052 ; 解得DE  5 10分 点评： 本题主要⑴问作图要进行逆向思考，才能找出作图的突破口，最好先画出草图进行逆推. 24.（本题满分10分）阅读以下材料： 对数的创始人是苏格兰数学家纳皮尔（J.Nplcr,1550 – 1617年），纳皮尔发明对数是在指数书 写方式之前，直到18世纪瑞士数学家欧拉（Evlcr,1707 – 1783年）才发现指数与对数之间的联系. 对数的定义：一般地，若ax  Na0,a1 ，那么x叫做以a为底N 的对数，记作：xlog N . a 比如指数式24 16可以转化为4log 16 ，对数式2log 25可以转化为52 25. 2 5 我们根据对数的定义可得到对数的一个性质： log M Nlog M log N a0,a1,M 0,N 0 ；理由如下： a a a 设log M m,log N n ，则M am,N an a a ∴M N aman amn ，由对数的定义得mnlog M N a 又∵mnlog M log N a a ∴logM NlogM logN 解决以下问题： ⑴.将指数43 64 转化为对数式 ； M ⑵.证明log log M log N a 0,a 1,M 0,N 0 a a a N ⑶.拓展运用：计算log 2log 6log 4 = . 3 3 3 考点：阅读运用、对数的定义、对数式与指数式的相互转化、对数性质的证明与运用. 分析：本题的⑴问直接根据对数的定义以及对数式与指数式的相互转化可以解决问题；本题的⑵问 可以参照材料中的“积的对数”的证明来“商的对数”；本题的⑶问是对对数性质的逆运用. 略解： ⑴. 根据对数的定义43 64 转化为对数式3log 4 64. 故应填 3log 4 64 . 2分 M ⑵. log log M log N a 0,a 1,M 0,N 0 .理由如下： a a a N 设log M m,log N n ，则M am,N an a a M M ∴ am an amn ，由对数的定义得mnlog a N N 又∵mnlog M log N a a 1 0M ∴log log M log N 7分 a a a N ⑶.根据对数的性质有： 12 log 3 2log 3 6log 3 4log 3 26log 3 4 log 3 log 3 31. 故应填 1 . 10分 4 25.（本题满分12分）如图，已知AOB 60,在AOB的平分线OM 上有一点C,将一个 120°角的顶点与点C重合，它的两条边分别与直线OA、OB相交于点D、E . y A A A M D M M C D C x C B O A E E O B O B O B 图1 图2 图3 P D C Q ⑴.当DCE绕点C旋转到CD与OA垂直时（如图1），请猜想OEOD与OC的数量关系，并说 明理由； ⑵.当DCE绕点C旋转到CD与OA不垂直时，到达图2的位置，⑴中的结论是否成立？并说明 理由； ⑶.当DCE绕点C旋转到CD与OA的反向延长线相交时，上述结论是否成立？请在图3中画出 图形，若成立，请给于证明；若不成立，线段OD、OE 与OC之间又有怎样的数量关系？请写出你 的猜想，不需证明. 考点：旋转的特征、直角三角形的性质、勾股定理、角平分线的性质、全等三角形等、线段的和差. 分析： 本题的⑾问根据直角三角形的性质和勾股定理可以计算出OE、OD与OC的关系，从而得出 OEOD与OC的关系；本题的⑵问可以过点C向AOB的两边作垂线段，从而可以把问题转化 为问题⑴的方式，然后利用线段的和差关系进行转换. 本题的⑶问也可以过点C向AOB的两边 作垂线段，从而可以把问题转化为问题⑴的方式，然后利用线段的和差关系进行转换，使问题得以 解决，本题是一道高质量的中考题. 略解： ⑴. ODOE  3OC.理由如下： 1分 ∵AOB 60,且OM 平分AOB. 1 11 1 ∴12 AOB 60 30 2 2 ∵DCE绕点C旋转到CD与OA垂直 ∴ODC OEC 90 1 1 ∴DC  OC,EC  OC 2 2 2 1  在 Rt ⊿ODC中根据勾股定理有：OD2 CD2 OC2 ,OD2   OC  OC2 . 2  3 3 解得：OD OC ;同理可得：OE  OC 2 2 3 3 ∴ODOE  OC OC  3OC. 即ODOE  3OC. 4分 2 2 ⑵. ⑴中的结论仍然成立.理由如下： 5分 过点C向AOB的两边作CG OA,CH OB ，垂足分别为G、H . ∴OGC OHC 90 参照⑴的方法同理可证：OGOH  3OC . 根据旋转的特征可以得到:DCE GCH ,即4DCH 3DCH ∴34 ∵OM 平分AOB,CG OA,CH OB ∴CG CH ∴⊿CGD≌⊿CHE ∴DG  EH 图2 ∴OGOH ODDGOEEH ODOE ∵OGOH  3OC ∴ODOE  3OC 8分 ⑶. ⑴中的结论不成立. 猜想：线段OD、OE 与OC之间的数量关系是OEOD 3OC. 9分 理由如下： 过点C向AOB的两边作CPOA,CQOB ，垂足分别为G、H .射线CD交OA反向延长射 线于D. ∴OGC OHC 90 A 参照⑴的方法同理可证：OPOQ 3OC. M P 1 C 2 5 O Q B E D 图3根据旋转的特征可以得到:DCE GCH ,即PCD5QCE5 ∴PCDQCE ∵OM 平分AOB,CPOA,CQOB ∴CPCQ ∴⊿CPD≌⊿CQE ∴PDQB ∴OPOQ PDODOEQE OEOD （OE OD ） ∵OPOQ 3OC ∴OEOD 3OC 12分 故线段OD、OE 与OC之间的数量关系是OEOD 3OC. 点评： 本题的三个图形首先要旋转过程中旋转角度不变，其次注意两点：其一.过点C向两边作垂线段后， 都存在一对全等的直角三角形；其二.要注意利用线段和差进行式子的转换. 26.（本题满分14分） 如图，抛物线 y ax2 bx3过 A1, 0、B3, 0 ，直线 AD交抛物线于点 D,点D的横 坐标为2 ，点Pm,n 是线段AD上的动点. ⑴.求直线 AD及抛物线的解析式； ⑵.过点 P的直线垂直于x轴，交抛物线于点Q ,求线段PQ 的长度l与m的关系式，m为何值时， PQ最长？ ⑶.在平面内是否存在整点（横、纵坐标都为整数）R,使得P、Q、D、R为顶点的四边形是平行 四边形？若存在，直接写出点R的坐标；若不存在，说明理由. 考点：待定系数法求函数解析式、函数的图象及其性质、二次函数求最值得问题、平行四边的判定、整 点问题、分类讨论思想等. 分析： 本题的⑾问先由抛物线 y ax2 bx3过 A1, 0、B3, 0 利用待定系数法可以求出抛物 线的解析式，利用抛物线可以求出点D的的纵坐标，再求出直线 AD的解析式.本题的⑵问是一个 二次函数最值应用问题，关键是用纵坐标之差的绝对值表示出线段的长度，同时要注意分类讨论思 想的应用. .本题的⑶问要先假设存在，由于点D是个定点，同时是个整点，根据两个函数解析式的 特征，所以点P、Q 也应为整点才能确保点R才可能为整点，所以本题应确定P的坐标变化范围， 从中找出P、Q整点坐标，然后进行分类讨论其存在的可能性. 1 3略解： ⑴.∵抛物线 y ax2 bx3过 A1, 0、B3, 0 ab30 a1 ∴ 解得: 所以 y  x2 2x3 2分 9a3b30 b2 ∵点D的横坐标为2 ∴当x2 时， y 22 2234433 ∴D2,3 设直线AD 的解析式为y kxb ∵A1,0、D2,3 kb0 k 1 ∴ 解得 所以 y  x1 4分 2kb3 b1 ⑵. ∵点Pm,n ，过点 P的直线垂直于x轴，交抛物线于点Q. ∴点P和点Q的横坐标相等. 5分 当xm时代入 y  x1得： y m1；则点Pm,m1 . 当xm时代入 y  x2 2x3得： y m2 2m3.则点Q  m, m2 2m3  . ∴PQ m1  m2 2m3  即l  m1  m2 2m3  ①.当m1m2 2m3时，l m1  m2 2m3  ；整理l m2 m2 1 1 ∵a10 ∴当 m  时，l有最大值；即此时线段PQ最长. 21 2 ②.当m1m2 2m3时，l   m2 2m3  m1 ；整理l m2 m2 ∵a10 ∴l此时有最小值；不合本问题意，舍去. 1 综上所述：当m 时，线段PQ最长. 10分 2 ⑶.在平面内存在整点（横、纵坐标都为整数）R,使得P、Q、D、R为顶点的四边形是平行四边 形. 整点R坐标分别为： 2,1、2,5、0,3、2,1 . 14分 因为Pm,n 是线段AD上的动点，计算出A1,0、D2,3 ，从而确定点P横纵坐标的变化 范围进行整点坐标的分类讨论（根据解析式和点D的坐标，点P、Q 也应为整点）. ①.当P 1,2 时，Q 1,4 ；以P、D、Q 作为定点，能使点R与它们构成平行四边（分别以 1 1 1 1 1 4PQ 为边和对角线讨论）的R整点坐标情况有：R 2,1、R 2,5、R 0,3 （见分析示 1 2 3 意图①）. ②.当P 0,1 时，Q 0,3 ；以P、D、Q 作为定点，能使点R与它们构成平行四边（分别以 2 1 2 2 PQ 为边和对角线讨论）的R整点坐标情况有：R 2,1、R 2,5、R 2,1 （见分析示 4 5 6 意图②）. 注：当P点与A、D 重合时，点Q点也同时会相应的与A、D 重合时，该四边形不存在. 综上所述，满足条件的整点R的坐标有 2,1、2,5、0,3、2,1 . 点评： 本题主要⑴问求出点的坐标后，用待定系数法可以求出两个函数的解析式，比较简单！在函数的 相关题型中，求“最值”问题，常通过建立二次函数的模型来解；本题⑵问就是抓住长度等于 P、Q纵坐标之差的绝对值建立二次函数来解决，注意讨论.本题以P、Q、D、R为顶点的四边 形顶点有3个动点，是本问的难点所在，结合解析式和其中一个顶点是定点且为整点，把动点中的 P、Q 也视为“定点”，在此基础上讨论就比较容易破题了. 1 5