文档内容
绵阳市 2021 年高中阶段学校招生暨初中学业水平考试数学
本试卷分试题卷和答题卡两部分,试题卷共6页,答题卡共6页,考试时间120
分钟.
注意事项:
1.答题前,考生务必将自己的姓名、准考证号用0.5毫米的黑色墨迹签字笔填
写在答题卡上,并认真核对条形码上的姓名、准考证号、考点、考场号.
2.选择题答案使用2B铅笔填涂在答题卡对应题目标号的位置上,非选择题答
案使用0.5毫米的黑色墨迹签字笔书写在答题卡的对应框内.超出答题区域书
写的答案无效;在草稿纸、试题卷上答题无效.
3.考试结束后,将试题卷和答题卡一并交回.
第Ⅰ卷(选择题)
一、选择题:本大题共12个小题,每个小题只有一个选项符合题目要求.
1. 整式 的系数是( )
A. -3 B. 3 C. D.
【答案】A
【解析】
【分析】根据单项式的系数的定义求解即可.
【详解】解: 的系数为-3,
故选A.
【点睛】本题主要考查了单项式的系数,解题的关键在于能够熟练掌握单项式的系数的定
义.
2. 计算 的结果是( )
A. 6 B. C. D.
【答案】D
【解析】
【分析】由题意化简为最简二次根式后依据二次根式的乘法运算法则进行运算即可得出答
案.
【详解】解:
故选:D.
【点睛】本题考查二次根式的乘法运算,熟练掌握二次根式的乘法运算法则是解题的关键.3. 下列图形中,轴对称图形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
【分析】根据轴对称图形的定义:如果一个平面图形沿一条直线折叠,直线两旁的部分能
够互相重合,这个图形就叫做轴对称图形进行判断即可.
【详解】解:第一个图形不是轴对称图形;第二个图形是轴对称图形;第三个图形是轴对
称图形;第四个图形不是轴对称图形;
故选B.
【点睛】本题主要考查了轴对称图形,解题的关键在于能够熟练掌握轴对称图形的定义.
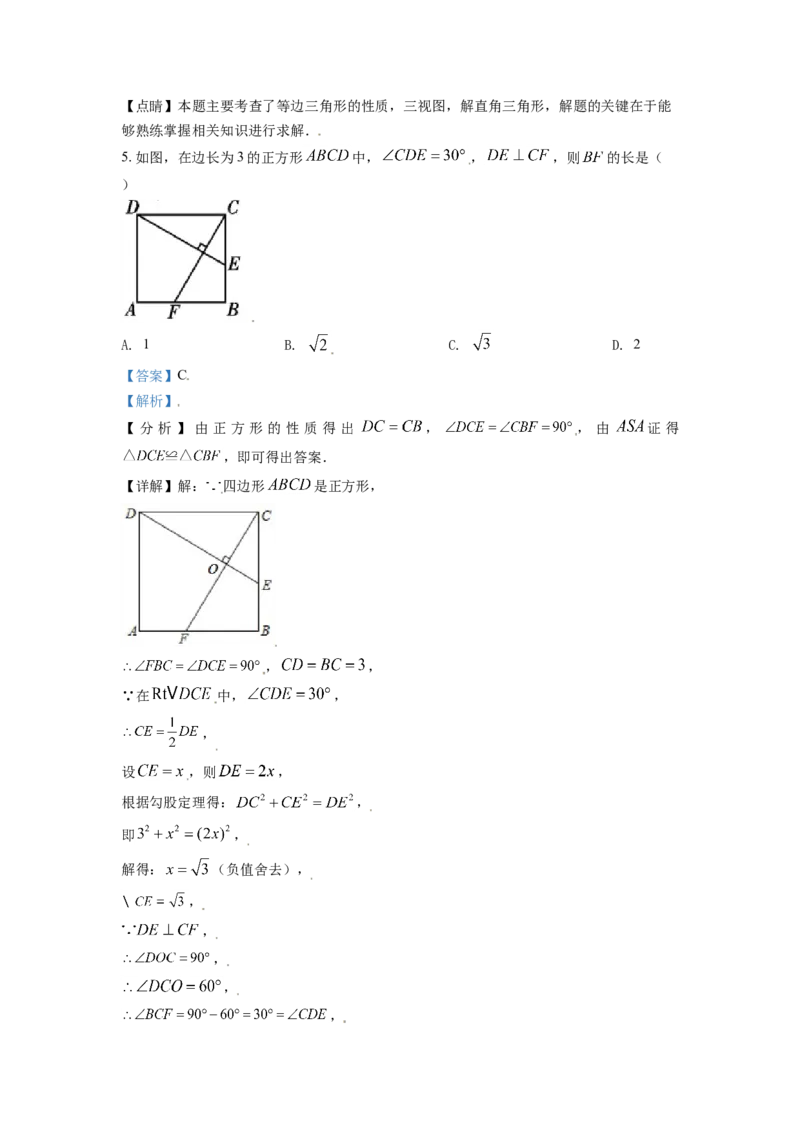
4. 如图,圆锥的左视图是边长为2的等边三角形,则此圆锥的高是( )
.
A 2 B. 3 C. D.
【答案】D
【解析】
【分析】如图所示,等边三角形ABC,BC边上的高AD即为所求.
【详解】解:如图所示等边三角形ABC,AD是BC边上的高,
由题意可知AD的长即为所求,AB=2,∠B=60°,
∴ ,
故选D.【点睛】本题主要考查了等边三角形的性质,三视图,解直角三角形,解题的关键在于能
够熟练掌握相关知识进行求解.
5. 如图,在边长为3的正方形 中, , ,则 的长是(
)
A. 1 B. C. D. 2
【答案】C
【解析】
【 分 析 】 由 正 方 形 的 性 质 得 出 , , 由 证 得
,即可得出答案.
【详解】解: 四边形 是正方形,
, ,
∵在 中, ,
,
设 ,则 ,
根据勾股定理得: ,
即 ,
解得: (负值舍去),
,
,
,
,
,, ,
,
.
故选: .
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,含 角的直
角三角形的性质等知识,证明 是解题的关键.
6. 近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派
送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,那么该分
派站现有包裹( )
A. 60件 B. 66件 C. 68件 D. 72件
【答案】B
【解析】
【分析】设该分派站有x个快递员,根据“若每个快递员派送10件,还剩6件;若每个快
递员派送12件,还差6件”,即可得出关于x的一元一次方程,解之即可得出x的值,再将
其代入(10x+6)中即可求出该分派站现有包裹数.
【详解】解:设该分派站有x个快递员,
依题意得:10x+6=12x−6,
解得:x=6,
∴10x+6=10×6+6=66,
即该分派站现有包裹66件.
故选:B.
【点睛】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题
的关键.
7. 下列数中,在 与 之间的是( )
A. 3 B. 4 C. 5 D. 6
【答案】C
【解析】
【分析】根据 , , , ,
,即可得出结果.
【详解】 , ,
,
又 , ,
,,
故选:C.
【点睛】本题考查了估算无理数 的大小,立方根,解决本题的关键是用有理数逼近无理数,
求无理数的近似值.
8. 某同学连续7天测得体温(单位: )分别是:36.5、36.3、36.7、36.5、36.7、37.1、
37.1,关于这一组数据,下列说法正确的是( )
A. 众数是36.3 B. 中位数是36.6 C. 方差是0.08 D. 方差是
0.09
【答案】C
【解析】
【分析】根据方差,众数,中位数的定义进行逐一求解判断即可.
【详解】解:把这组数据从小到大排列:36.3、36.5、36.5、36.7、36.7、37.1、37.1,
∴处在最中间的数是36.7,
∴中位数是36.7,故B不符合题意;
∵36.5,36.7,37.1都出现了两次,出现的次数最多,
∴众数为36.5,36.7,37.1,故A不符合题意;
∴ ,
∴
,
故C符合题意,D不符合题意,
故选C.
【点睛】本题主要考查了方差,众数,中位数的定义,解题的关键在于能够熟记定义.
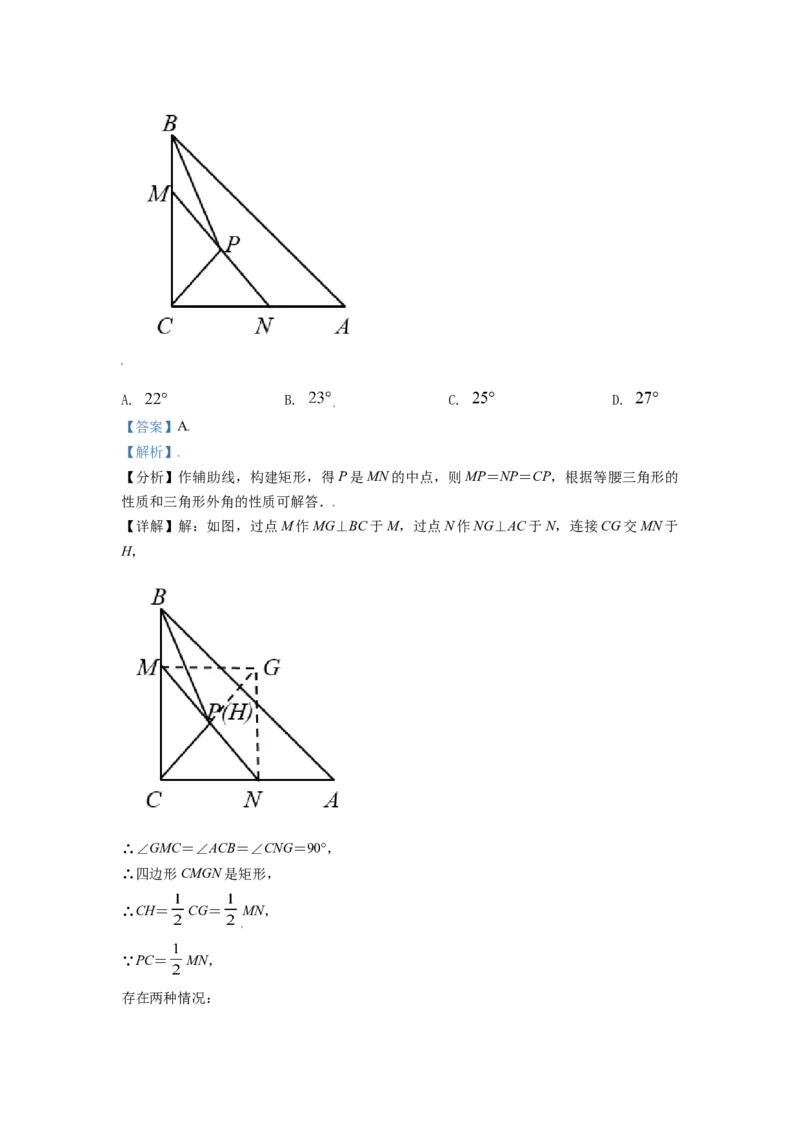
9. 如图,在等腰直角 中, , 、 分别为 、 上的点,
, 为 上的点,且 , ,则 ( )A. B. C. D.
【答案】A
【解析】
【分析】作辅助线,构建矩形,得P是MN的中点,则MP=NP=CP,根据等腰三角形的
性质和三角形外角的性质可解答.
【详解】解:如图,过点M作MG⊥BC于M,过点N作NG⊥AC于N,连接CG交MN于
H,
∴∠GMC=∠ACB=∠CNG=90°,
∴四边形CMGN是矩形,
∴CH= CG= MN,
∵PC= MN,
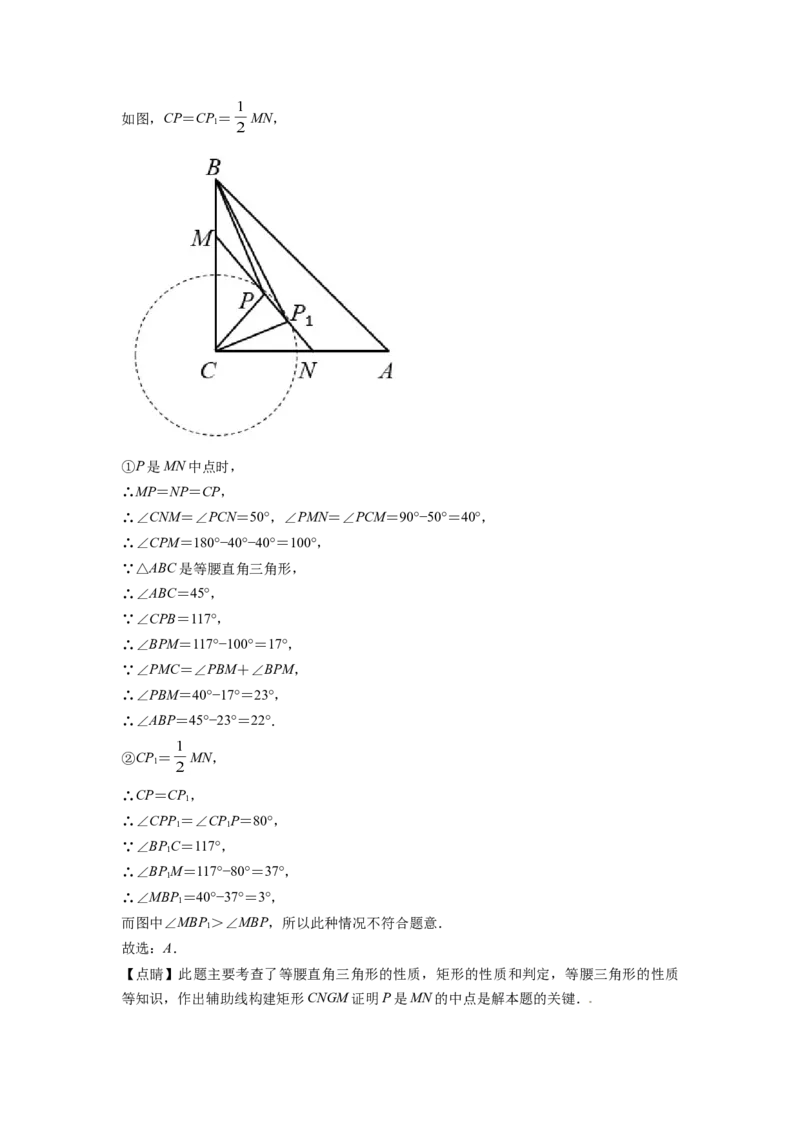
存在两种情况:如图,CP=CP = MN,
1
①P是MN中点时,
∴MP=NP=CP,
∴∠CNM=∠PCN=50°,∠PMN=∠PCM=90°−50°=40°,
∴∠CPM=180°−40°−40°=100°,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
∵∠CPB=117°,
∴∠BPM=117°−100°=17°,
∵∠PMC=∠PBM+∠BPM,
∴∠PBM=40°−17°=23°,
∴∠ABP=45°−23°=22°.
②CP = MN,
1
∴CP=CP ,
1
∴∠CPP=∠CP P=80°,
1 1
∵∠BPC=117°,
1
∴∠BPM=117°−80°=37°,
1
∴∠MBP =40°−37°=3°,
1
而图中∠MBP >∠MBP,所以此种情况不符合题意.
1
故选:A.
【点睛】此题主要考查了等腰直角三角形的性质,矩形的性质和判定,等腰三角形的性质
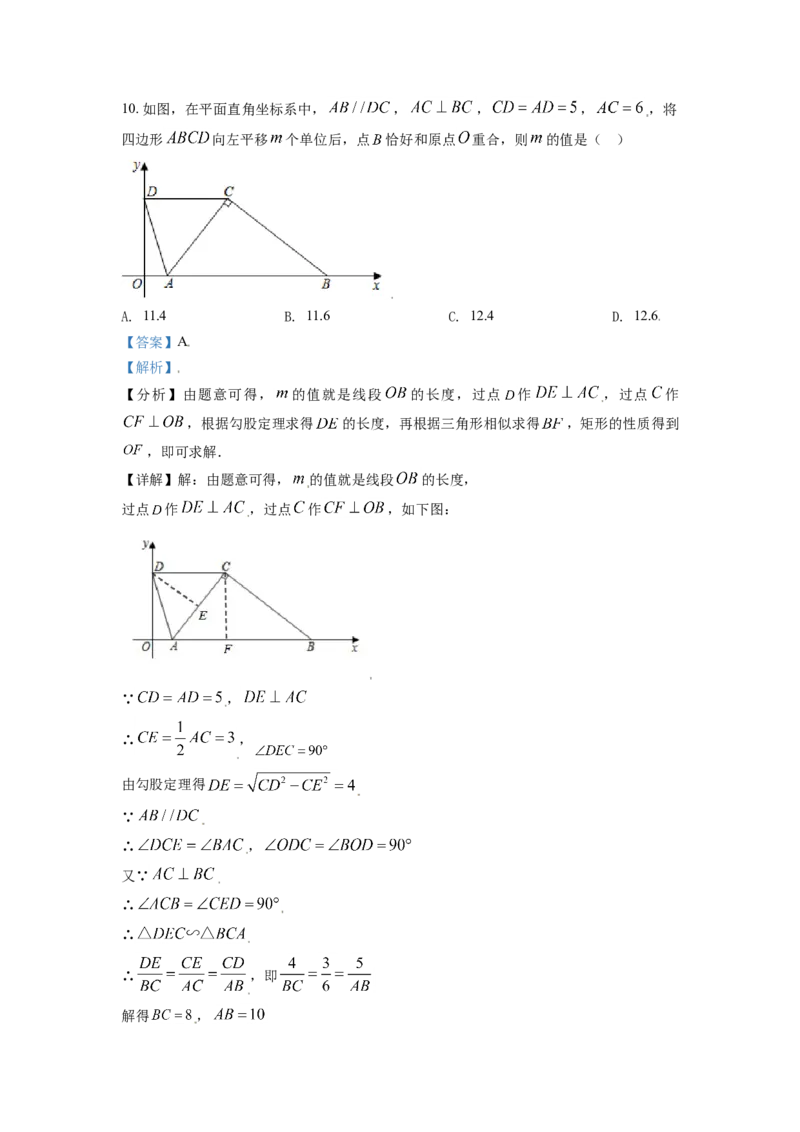
等知识,作出辅助线构建矩形CNGM证明P是MN的中点是解本题的关键.10. 如图,在平面直角坐标系中, , , , ,将
四边形 向左平移 个单位后,点 恰好和原点 重合,则 的值是( )
A. 11.4 B. 11.6 C. 12.4 D. 12.6
【答案】A
【解析】
【分析】由题意可得, 的值就是线段 的长度,过点 作 ,过点 作
,根据勾股定理求得 的长度,再根据三角形相似求得 ,矩形的性质得到
,即可求解.
【详解】解:由题意可得, 的值就是线段 的长度,
过点 作 ,过点 作 ,如下图:
∵ ,
∴ ,
由勾股定理得
∵
∴ ,
又∵
∴
∴
∴ ,即
解得 ,∵
∴
∴
∴ ,即
解得
由题意可知四边形 为矩形,∴
故选A
【点睛】此题考查了相似三角形的判定与性质,图形的平移,矩形的判定与性质,勾股定
理等,熟练掌握相关基本性质是解题的关键.
11. 关于 的方程 有两个不相等的实根 、 ,若 ,则
的最大值是( )
A. 1 B. C. D. 2
【答案】D
【解析】
【分析】根据一元二次方程根与系数的关系,求得两根之和和两根之积,再根据两根关系
求得系数的关系,代入代数式,配方法化简求值即可.
【详解】解:由方程 有两个不相等的实根 、
可得, , ,
∵ ,可得 , ,即
化简得
则
故 最大值为
故选D
【点睛】此题考查了一元二次方程根与系数的关系,涉及了配方法求解代数式的最大值,
根据一元二次方程根与系数的关系得到系数的关系是解题的关键.
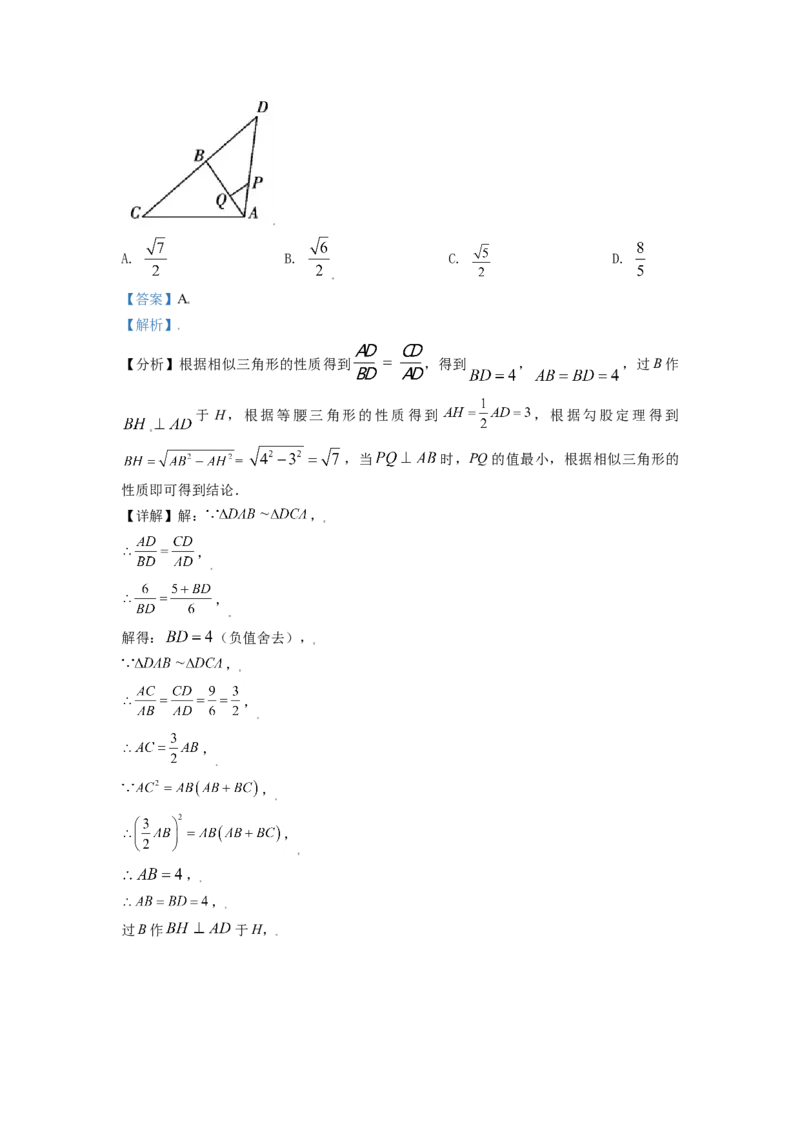
12. 如图,在 中, , , ,且
,若 ,点 是线段 上的动点,则 的最小值是( )A. B. C. D.
【答案】A
【解析】
【分析】根据相似三角形的性质得到 ,得到 , ,过B作
于 H,根据等腰三角形的性质得到 ,根据勾股定理得到
,当 时,PQ的值最小,根据相似三角形的
性质即可得到结论.
【详解】解: ,
,
,
解得: (负值舍去),
,
,
,
,
,
,
,
过B作 于H,,
,
,
,
当 时,PQ的值最小,
,
,
,
,
故选:A.
【点睛】本题考查了相似三角形的判定和性质,勾股定理,等腰三角形的判定和性质,正
确的作出辅助线构造相似三角形是解题的关键.
第Ⅱ卷(非选择题)
二、填空题:本大题共6个小题,将答案填写在答题卡相应的横线上.
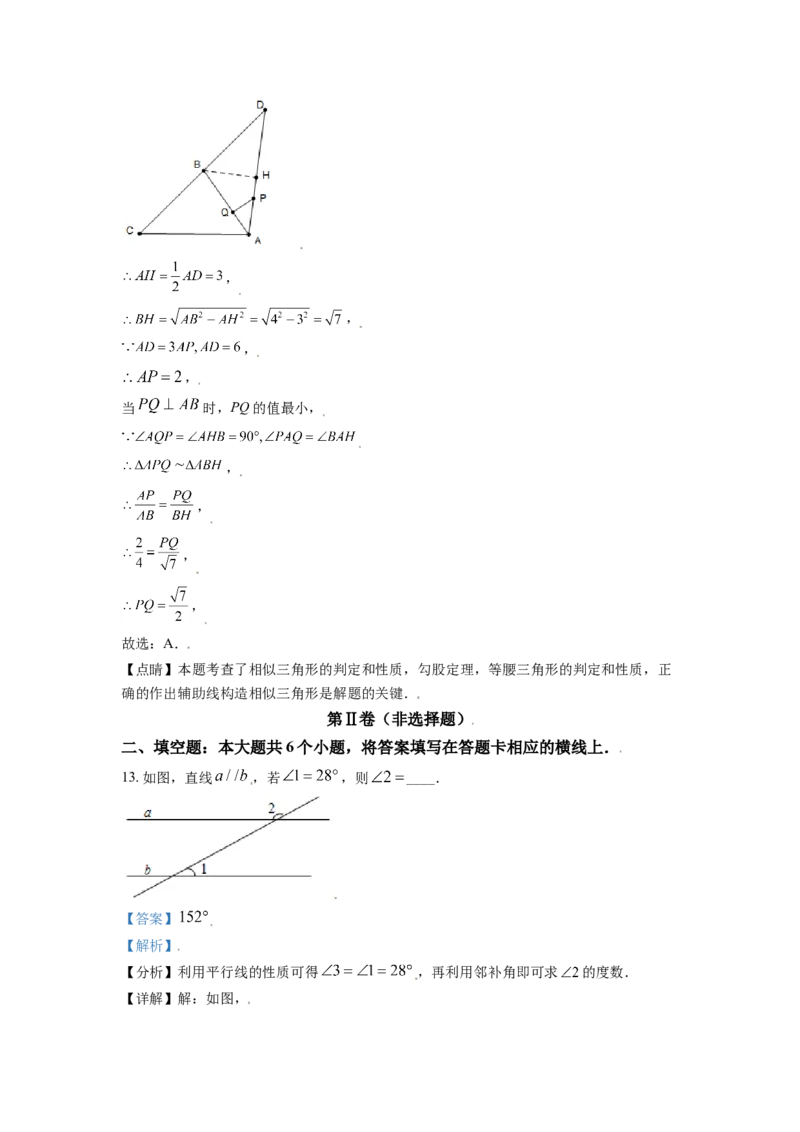
13. 如图,直线 ,若 ,则 ____.
【答案】
【解析】
【分析】利用平行线的性质可得 ,再利用邻补角即可求 的度数.
【详解】解:如图,, ,
,
.
故答案为: .
【点睛】本题主要考查平行线的性质,解答的关键是结合图形分析清楚角与角之间的关系.
14. 据统计,截止2021年3月,中国共产党党员人数超过9100万.数字91000000用科学
记数法表示为__.
【答案】
【解析】
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a| 10,n为整数.确定n的值时,
要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原
数绝对值≥1时,n是正数;当原数的绝对值小于1时,n是负数.
【详解】解:用科学记数法表示:
故答案为: .
【点睛】本题考查了科学记数法,掌握科学记数法的形式是关键.
15. 若 , ,则 _____.
【答案】0
【解析】
【分析】先求出 ,再求 的平方,然后再开方即可求出 .
【详解】解: ,
,
,
∵ ,
,
,,
,
故答案为:0.
【点睛】本题考查了完全平方公式的应用,等式的灵活变形是本题的关键.
16. 端午节是中国传统节日,人们有吃粽子的习俗.某商场从6月12日起开始打折促销,
肉粽六折,白粽七折,打折前购买4盒肉粽和5盒白粽需350元,打折后购买5盒肉粽和
10盒白粽需360元.轩轩同学想在今天中考结束后,为敬老院送肉粽和白粽各5盒,则他
6月13日购买的花费比在打折前购买节省_____元.
【答案】145
【解析】
【分析】设打折前每盒肉粽的价格为x元,每盒白粽的价格为y元,根据“打折前购买4
盒肉粽和5盒白粽需350元,打折后购买5盒肉粽和10盒白粽需360元”,即可得出关于
x,y的二元一次方程组,解之即可得出肉粽和白粽的单价,再利用节省的钱数=打折前购
买的总费用-打折后购买的总费用,即可求出节省的钱数.
【详解】解:设打折前每盒肉粽的价格为x元,每盒白粽的价格为y元,
依题意得: , 解得: ,
∴5x+5y-(0.6×5x+0.7×5y)=5×50+5×30-(0.6×5×50+0.7×5×30)=145.
故答案为:145.
【点睛】本题主要考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程
组是解题的关键.
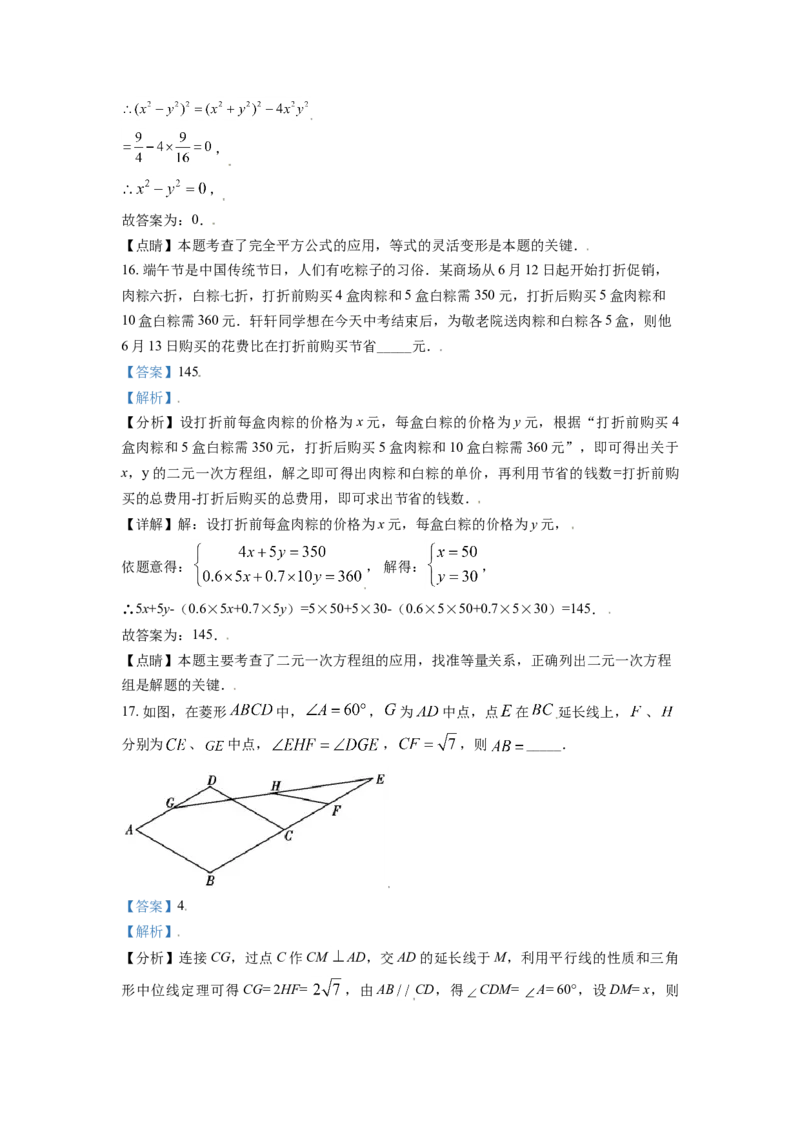
17. 如图,在菱形 中, , 为 中点,点 在 延长线上, 、
分别为 、 中点, , ,则 _____.
【答案】4
【解析】
【分析】连接CG,过点C作CM AD,交AD的延长线于M,利用平行线的性质和三角
形中位线定理可得CG= 2HF= ,由AB CD,得 CDM= A= 60°,设DM= x,则CD= 2x , CM= x , 在 Rt△CMG 中 , 借 助 勾 股 定 理 得
,即可求出x的值,从而解决问题.
【详解】如图,连接CG,过点C作CM AD,交AD的延长线于M,
F、H分别为CE、GE中点,
FH是△CEG的中位线,
HF= CG,
四边形ABCD是菱形,
AD BC,AB CD,
DGE = E,
EHF= DGE,
E= EHF,
HF = EF = CF,
CG= 2HF = ,
AB CD,
CDM= A = 60°,
设DM= x,则CD= 2x,CM= x,
点G为AD的中点,
DG= x,GM=2x,
在Rt△CMG中,由勾股定理得:
,
x=2,
AB = CD= 2x= 4.
故答案为:4.
【点睛】本题主要考查了菱形的性质,三角形的中位线定理,勾股定理等知识,有一定综
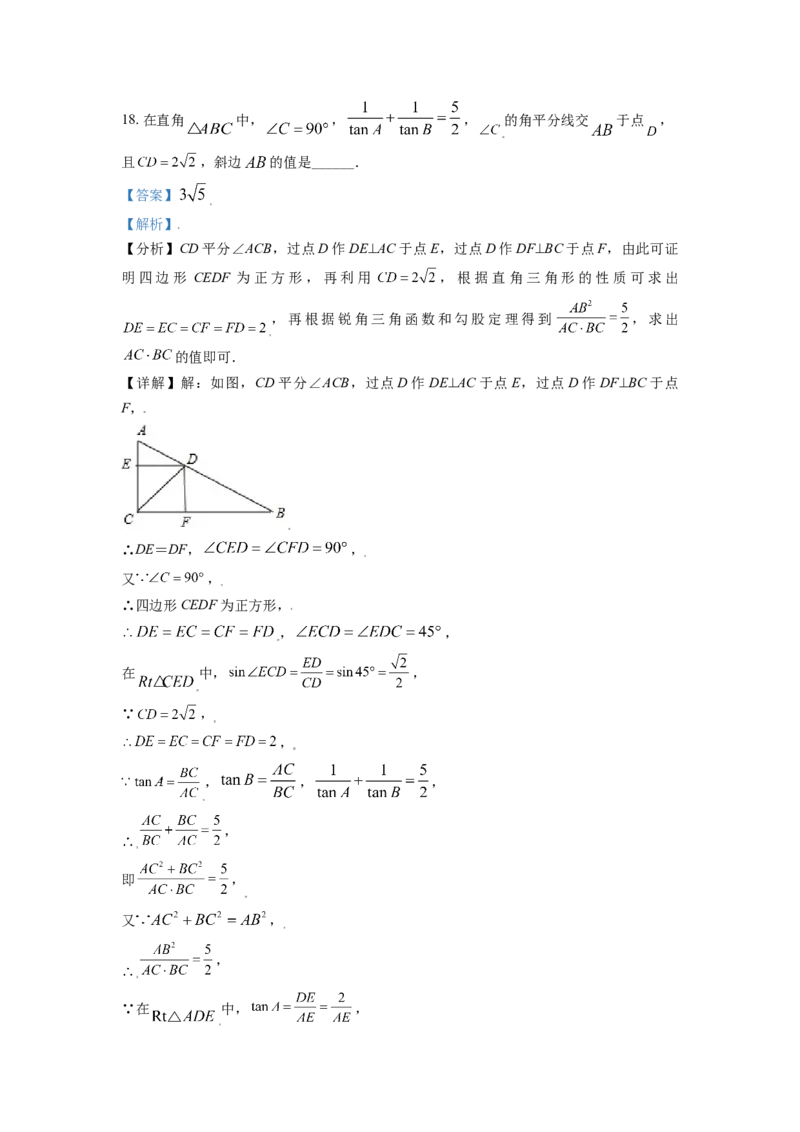
合性,作辅助线,构造直角三角形,利用方程思想是解题的关键.18. 在直角 中, , , 的角平分线交 于点 ,
且 ,斜边 的值是______.
【答案】
【解析】
【分析】CD平分∠ACB,过点D作DE⊥AC于点E,过点D作DF⊥BC于点F,由此可证
明四边形 CEDF 为正方形,再利用 ,根据直角三角形的性质可求出
,再根据锐角三角函数和勾股定理得到 ,求出
的值即可.
【详解】解:如图,CD平分∠ACB,过点D作DE⊥AC于点E,过点D作DF⊥BC于点
F,
∴DE=DF, ,
又 ,
∴四边形CEDF为正方形,
, ,
在 中, ,
∵ ,
,
, , ,
,
即 ,
又 ,
,
∵在 中, ,∴ ,
∵在 中, ,
∴ ,
,
,
,
即 (舍负),
故答案为: .
【点睛】本题考查解直角三角形的应用,掌握直角三角形的边角关系是解决问题的关键.
三、解答题:本大题共7个小题,解答应写出文字说明、证明过程或演算步骤.
19. (1)计算: ;
(2)先化简,再求值: ,其中 , .
【答案】(1)-1;(2) ,2
【解析】
【分析】(1)根据特殊角的三角函数值,绝对值的意义,零指数幂法则以及二次根式的性
质逐步进行计算即可;
(2)先根据分式的运算法则及运算顺序将原式化简,再代入求值即可.
【详解】解:(1)原式;
(2)原式
,
当 , 时,
原式 .
【点睛】本题考查数与式的运算能力,涉及分式的化简求值,实数的运算等知识,熟练掌
握运算法则是解题的关键.
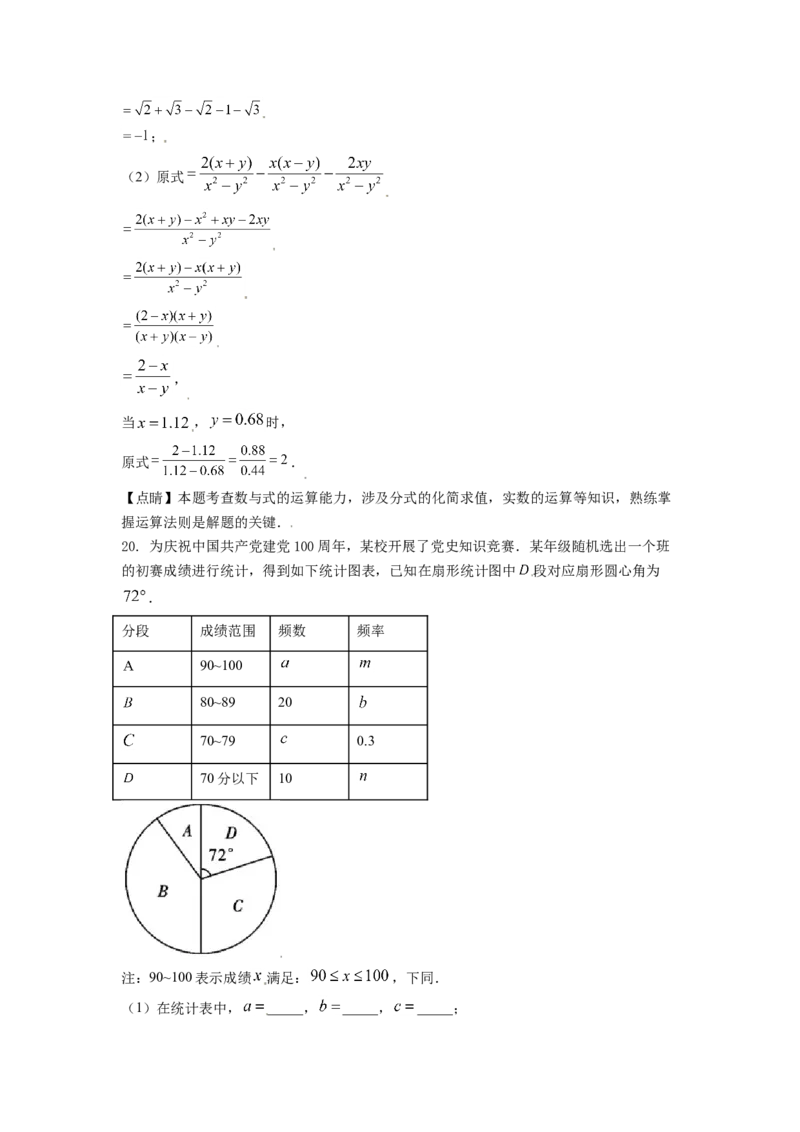
20. 为庆祝中国共产党建党100周年,某校开展了党史知识竞赛.某年级随机选出一个班
的初赛成绩进行统计,得到如下统计图表,已知在扇形统计图中 段对应扇形圆心角为
.
分段 成绩范围 频数 频率
90~100
80~89 20
70~79 0.3
70分以下 10
注:90~100表示成绩 满足: ,下同.
(1)在统计表中, _____, _____, _____;(2)若该年级参加初赛的学生共有2000人,根据以上统计数据估计该年级成绩在90分及
以上的学生人数;
(3)若统计表 段的男生比女生少1人,从 段中任选2人参加复赛,用列举法求恰好
选到1名男生和1名女生的概率.
【答案】(1) , , ;(2)200;(3)列举见解析,
【解析】
【分析】(1)根据扇形统计图中 段对应扇形圆心角为 , 段人数为10人,可求出
总人数,即可求出 , , 的值;
(2)用样本中的频率来估计总体中的频率即可;
(3)通过列举所选情况可知:共10种结果,并且它们出现的可能性相等,其中包含1名
男生1名女生的结果有6种,然后根据概率公式即可得出答案.
【详解】解:(1)总人数为: (人),
, (人),
(人),
故答案为:5,0.4,15;
(2)由题意得:成绩在 之间的人数为5,
随机选出的这个班级总人数为50,
设该年级成绩在 之间的人数为 ,
则 ,
解得: ,
答:该年级成绩在 之间的人数为200人,
(3)由(1)(2)可知: 段有男生2人,女生3人,
记2名男生分别为男1,男2;记3名女生分别为女1,女2,女3,
选出2名学生的结果有:
男1男2,男1女1,男1女2,男1女3,男2女1,
男2女2,男2女3,女1女2,女1女3,女2女3,
共10种结果,并且它们出现的可能性相等,
其中包含1名男生1名女生的结果有6种,
,
即选到1名男生和1名女生的概率为 .
【点睛】本题主要考查了统计表和统计图,列举法求概率,用样本估计总体等知识,解决本题的关键是列举出所有等可能结果.
21. 某工艺厂为商城制作甲、乙两种木制工艺品,甲种工艺品不少于400 件,乙种工艺品不
少于680件.该厂家现准备购买 、 两类原木共150根用于工艺品制作,其中,1根
类原木可制作甲种工艺品4件和乙种工艺品2件,1根 类原木可制作甲种工艺品2件和乙
种工艺品6件.
(1)该工艺厂购买 类原木根数可以有哪些?
(2)若每件甲种工艺品可获得利润50元,每件乙种工艺品可获得利润80元,那么该工艺
厂购买 、 两类原木各多少根时获得利润最大,最大利润是多少?
【答案】(1)50、51、52、53、54、55;(2)50根,100根,最大利润为76000
【解析】
【分析】(1)设工艺厂购买 类原木 根, 类原木(150-x), 根 类原木可制作甲
种工艺品4 件+(150-x)根 类原木可制作甲种工艺品2(150-x))件不少于400, 根
类原木可制作乙种工艺品2 件+(150-x)根 类原木可制作乙种工艺品6(150-x)件不少
于680列不等式组,求出 范围即可;
(2)设获得利润为 元,根据每件甲利润乘以甲件数+每件乙利润乘以乙件数列出函数,
根据函数性质即可求解.
【详解】解:(1)设工艺厂购买 类原木 根, 类原木(150-x)根
由题意可得 ,
可解得 ,
∵ 为整数,
∴ ,51,52,53,54,55.
答:该工艺厂购买A类原木根数可以是:50、51、52、53、54、55.
(2)设获得利润为 元,
由题意, ,
即 .
∵ ,
∴ 随 的增大而减小,
∴ 时, 取得最大值76000.
∴购买A类原木根数50根,购买B类原木根数100根,取得最大值76000元.
【点睛】本题考查列不等式组解应用题,一次函数的增减性质求最值,掌握列不等式组解
应用题方法与步骤,利用一次函数的增减性质求最值方法是解题关键.
22. 如图,点 是 的边 上的动点, ,连接 ,并将线段 绕点
逆时针旋转 得到线段 .(1)如图1,作 ,垂足 在线段 上,当 时,判断点 是
否在直线 上,并说明理由;
(2)如图2,若 , ,求以 、 为邻边的正方形的面积 .
【答案】(1)点 在直线 上,见解析;(2)18
【解析】
【分析】(1)根据 , ,得到 ,可得
线段 逆时针旋转 落在直线 上,即可得解;
(2)作 于 ,得出 ,再根据平行线的性质得到 ,
再根据直角三角形的性质计算即可;
【详解】解:(1)结论:点 在直线 上;
∵ , ,
∴ ,
∴ ,即 .
∴线段 逆时针旋转 落在直线 上,即点 在直线 上.
(2)作 于 ,
∵ , ,
∴ ,
∵ ,
∴ ,
∵ , ,
∴ , ,∴ ,即以 、 为邻边的正方形面积 .
【点睛】本题主要考查了旋转综合题,结合平行线 的性质计算是解题的关键.
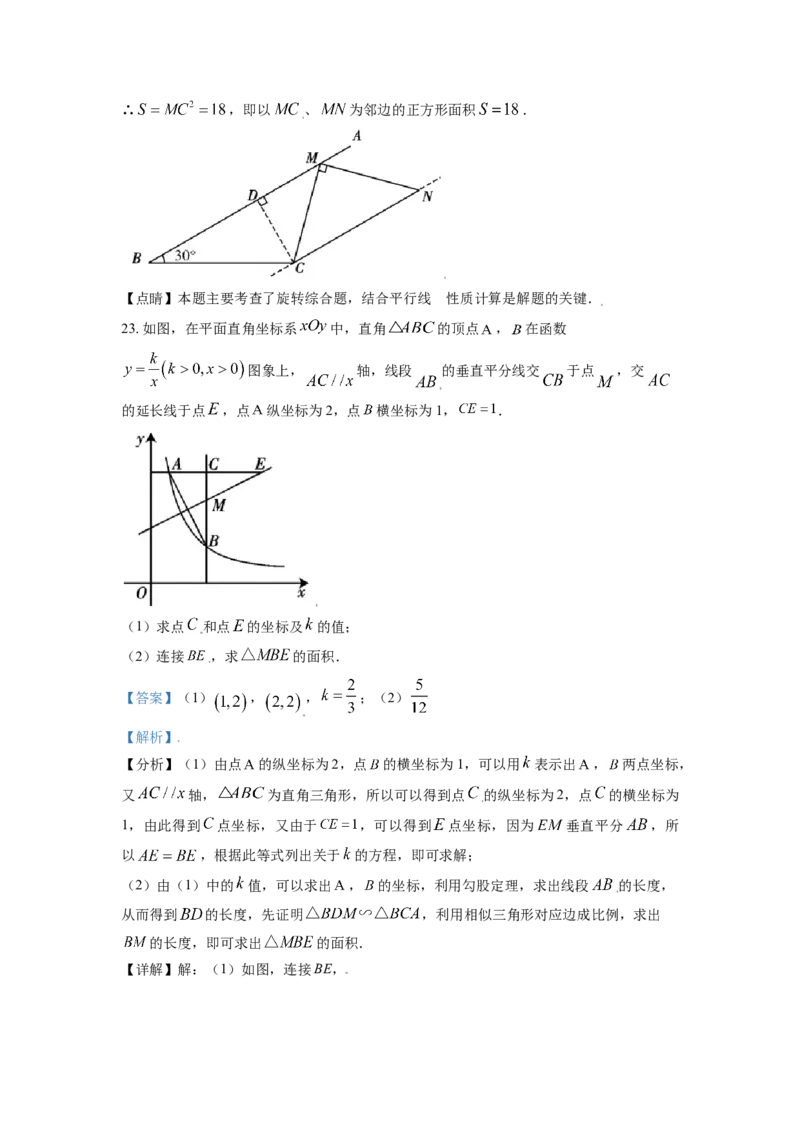
23. 如图,在平面直角坐标系 中,直角 的顶点 , 在函数
图象上, 轴,线段 的垂直平分线交 于点 ,交
的延长线于点 ,点 纵坐标为2,点 横坐标为1, .
(1)求点 和点 的坐标及 的值;
(2)连接 ,求 的面积.
【答案】(1) , , ;(2)
【解析】
【分析】(1)由点 的纵坐标为2,点 的横坐标为1,可以用 表示出 , 两点坐标,
又 轴, 为直角三角形,所以可以得到点 的纵坐标为2,点 的横坐标为
1,由此得到 点坐标,又由于 ,可以得到 点坐标,因为 垂直平分 ,所
以 ,根据此等式列出关于 的方程,即可求解;
(2)由(1)中的 值,可以求出 , 的坐标,利用勾股定理,求出线段 的长度,
从而得到 的长度,先证明 ,利用相似三角形对应边成比例,求出
的长度,即可求出 的面积.
【详解】解:(1)如图,连接BE,由题意得点 的坐标为 , ,点 的坐标为 ,
又 轴,且 为直角三角形,
点 的坐标为 ,
又∵ ,
点 的坐标为 ,
点 在线段 的垂直平分线上,
,
在 中, ,
,
或 ,
当 时,点 , , 三点重合,不能构成三角形,故舍去,
,
, , ;
(2)由(1)可得, , , ,
设 的中点为 ,
, ,
, ,
,
,,
.
【点睛】本题是一道反比例函数的综合题,考查了反比例函数的图象性质,垂直平分线的
性质,勾股定理,相似三角形的判定与性质等相关知识,熟知平行于坐标轴的直线上的点
的坐标特征,是解决此题的关键.
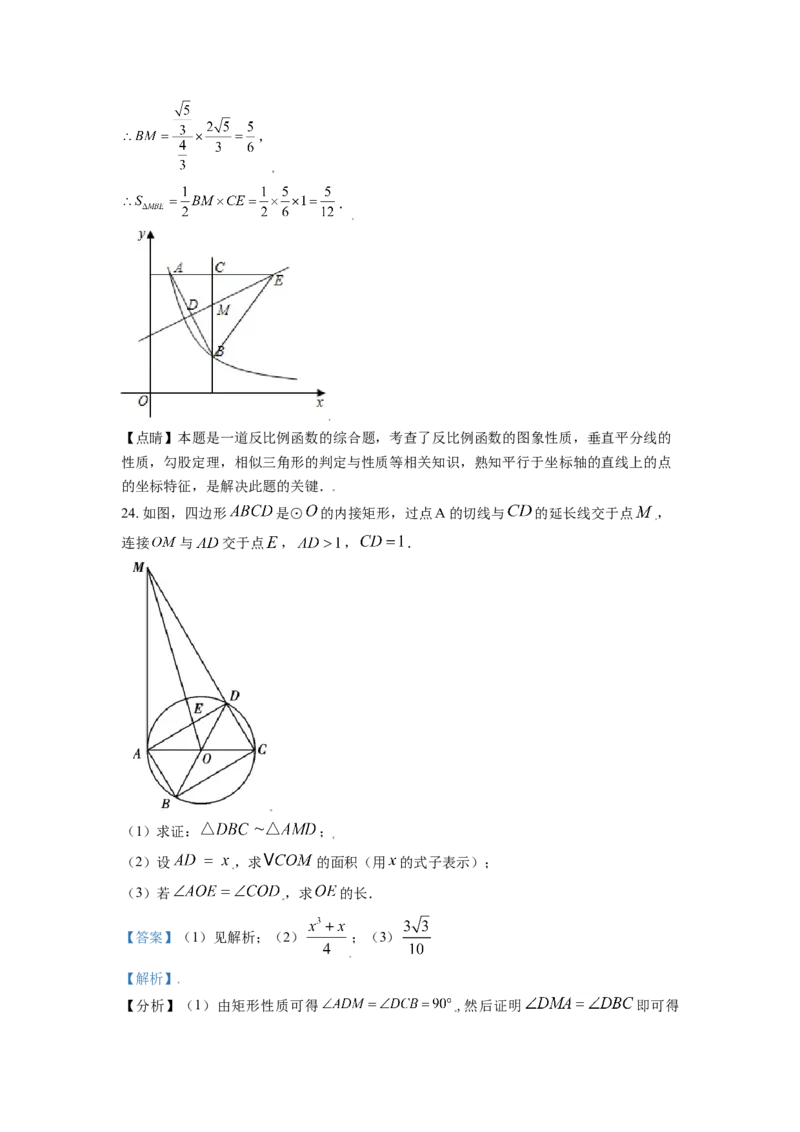
24. 如图,四边形 是⊙ 的内接矩形,过点 的切线与 的延长线交于点 ,
连接 与 交于点 , , .
(1)求证: ;
(2)设 ,求 的面积(用 的式子表示);
(3)若 ,求 的长.
【答案】(1)见解析;(2) ;(3)
【解析】
【分析】(1)由矩形性质可得 ,然后证明 即可得出结论;
(2)根据勾股定理得出 ,根据相似三角形性质得出 ,则
,根据勾股定理得出 的值,运用三角形面积公
式表示即可;
(3)记 与圆弧 交于点 ,连接 ,证明 ,即可得出
,求出 的值,过 作 于 ,过 作 于 .
运用等面积法得出 ,根据勾股定理得出
,代入数据联立 的值,解方程得出
, ,设 ,则 ,根据相似三角形性质
即可得出结论.
【详解】解:(1)∵四边形 为 的内接矩形,
∴ , 过圆心 ,且 .
∵ ,
∴ ,
又∵ 是 的切线,故 ,
由此可得 ,
又∵ 与 都是圆弧 所对的圆周角,
∴ ,
∴ ,
又∵ ,
∴ ;
(2)解:由 , ,则 ,
由题意 .
由(1)知 ,则 ,
代入 , , ,可得 ,解得 .
在直角 中, ,
所以 ;
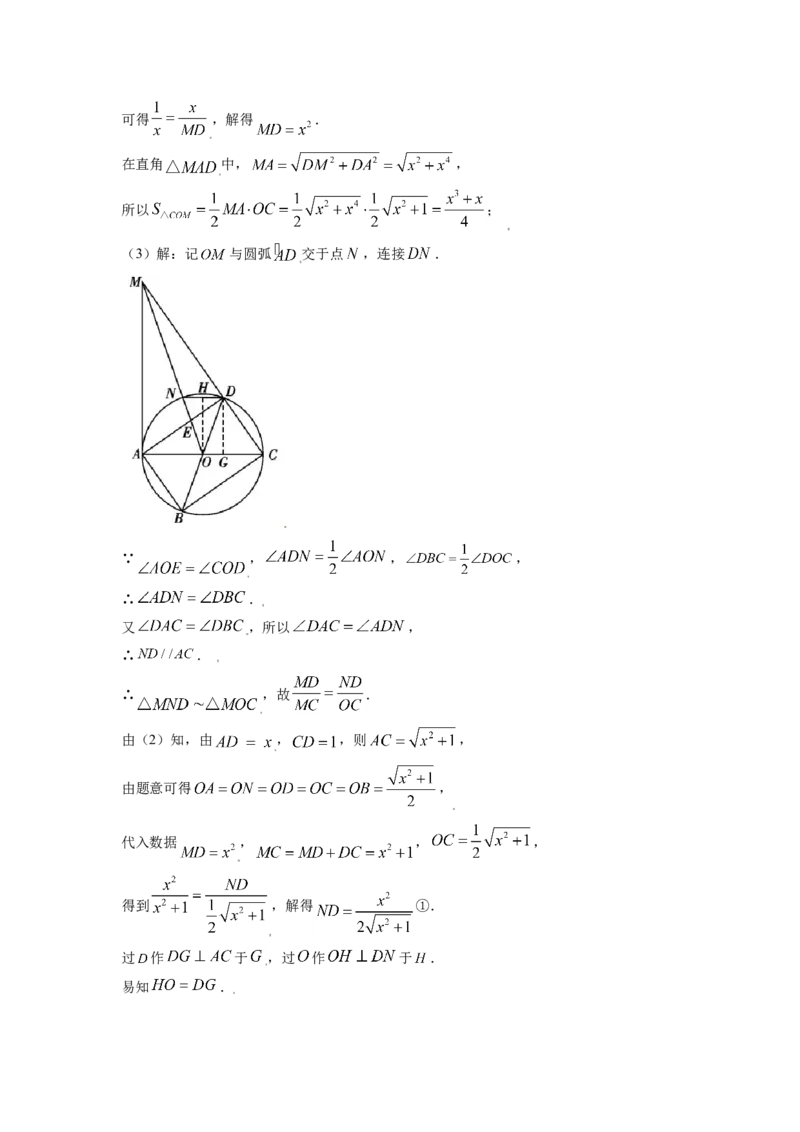
(3)解:记 与圆弧 交于点 ,连接 .
∵ , , ,
∴ .
又 ,所以 ,
∴ .
∴ ,故 .
由(2)知,由 , ,则 ,
由题意可得 ,
代入数据 , , ,
得到 ,解得 ①.
过 作 于 ,过 作 于 .
易知 .由等面积法可得 ,
代入数据得 ,即 .
在直角三角形 中,
.②
由①②可得 ,得 ,
解得 , (舍去).
所以 , .
由 ,故 ,故 .
设 ,则 ,代入得 ,
解得 ,即 的长为 .
【点睛】本题考查了圆的综合问题,相似三角形判定与性质,圆切线的性质,勾股定理,
解一元二次方程等知识点,熟练运用相似三角形性质列出方程是解题的关键.
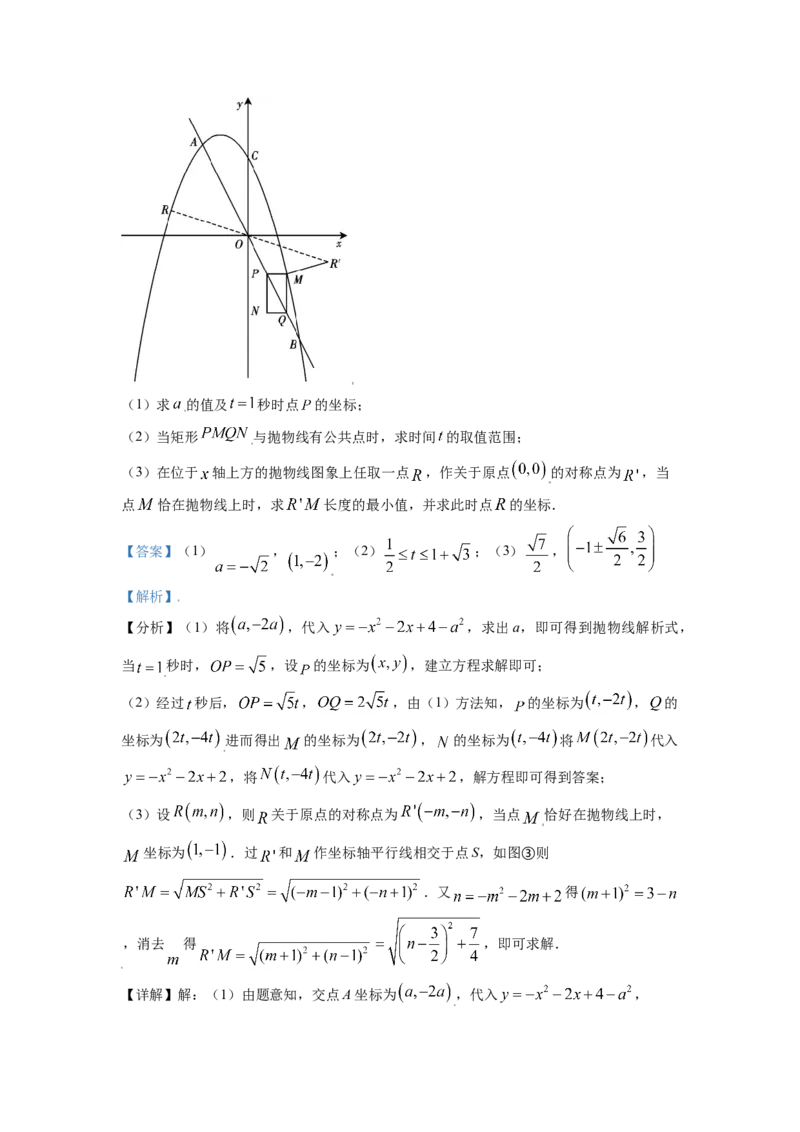
25. 如图,二次函数 的图象与一次函数 的图象交于点 、
(点 在右侧),与 轴交于点 ,点 的横坐标恰好为 .动点 、 同时从原点
出发,沿射线 分别以每秒 和 个单位长度运动,经过 秒后,以 为对角线作
矩形 ,且矩形四边与坐标轴平行.(1)求 的值及 秒时点 的坐标;
(2)当矩形 与抛物线有公共点时,求时间 的取值范围;
(3)在位于 轴上方的抛物线图象上任取一点 ,作关于原点 的对称点为 ,当
点 恰在抛物线上时,求 长度的最小值,并求此时点 的坐标.
【答案】(1) , ;(2) ;(3) ,
【解析】
【分析】(1)将 ,代入 ,求出a,即可得到抛物线解析式,
当 秒时, ,设 的坐标为 ,建立方程求解即可;
(2)经过 秒后, , ,由(1)方法知, 的坐标为 , 的
坐标为 进而得出 的坐标为 , 的坐标为 将 代入
,将 代入 ,解方程即可得到答案;
(3)设 ,则 关于原点的对称点为 ,当点 恰好在抛物线上时,
坐标为 .过 和 作坐标轴平行线相交于点S,如图③则
.又 得
,消去 得 ,即可求解.
【详解】解:(1)由题意知,交点A坐标为 ,代入 ,解得 ,
∴抛物线解析式为 .
当 秒时, ,设 的坐标为 ,
则 ,
解得 或 (舍),
所以 的坐标为 .
(2)经过 秒后, , ,
由(1)方法知, 的坐标为 , 的坐标为 ,
由矩形 的邻边与坐标轴平行可知, 的坐标为 , 的坐标为 .
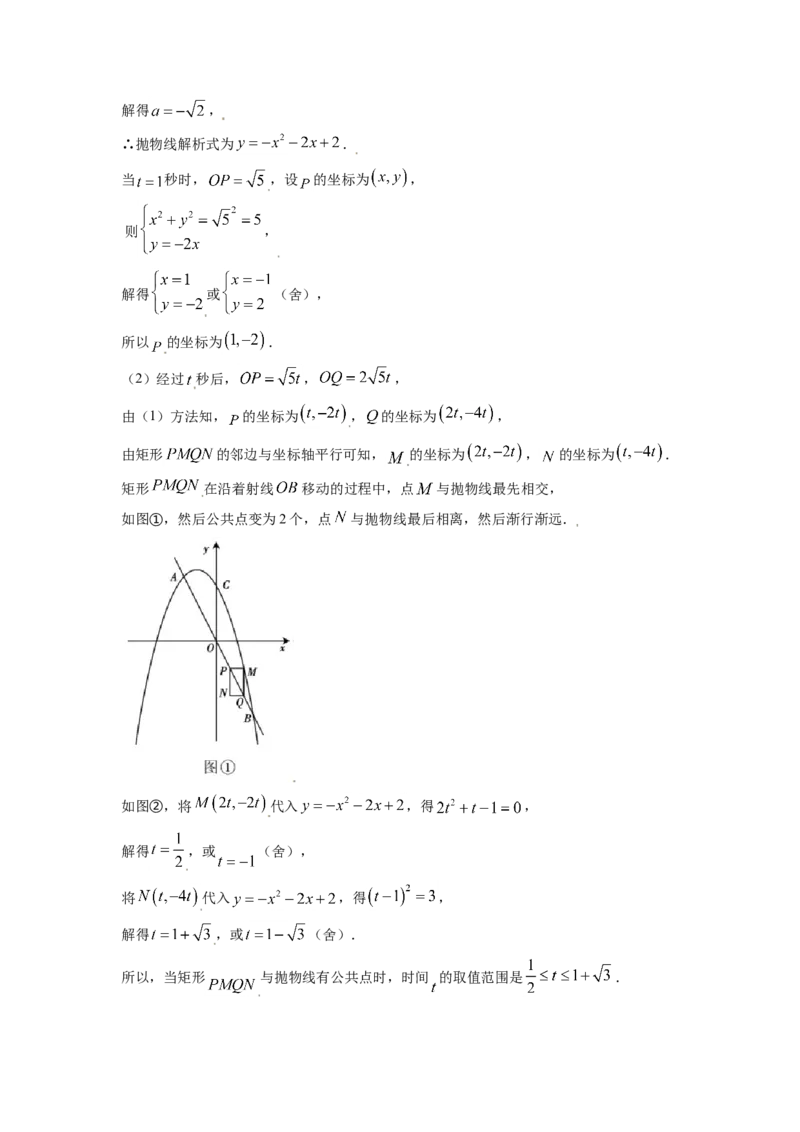
矩形 在沿着射线 移动的过程中,点 与抛物线最先相交,
如图①,然后公共点变为2个,点 与抛物线最后相离,然后渐行渐远.
如图②,将 代入 ,得 ,
解得 ,或 (舍),
将 代入 ,得 ,
解得 ,或 (舍).
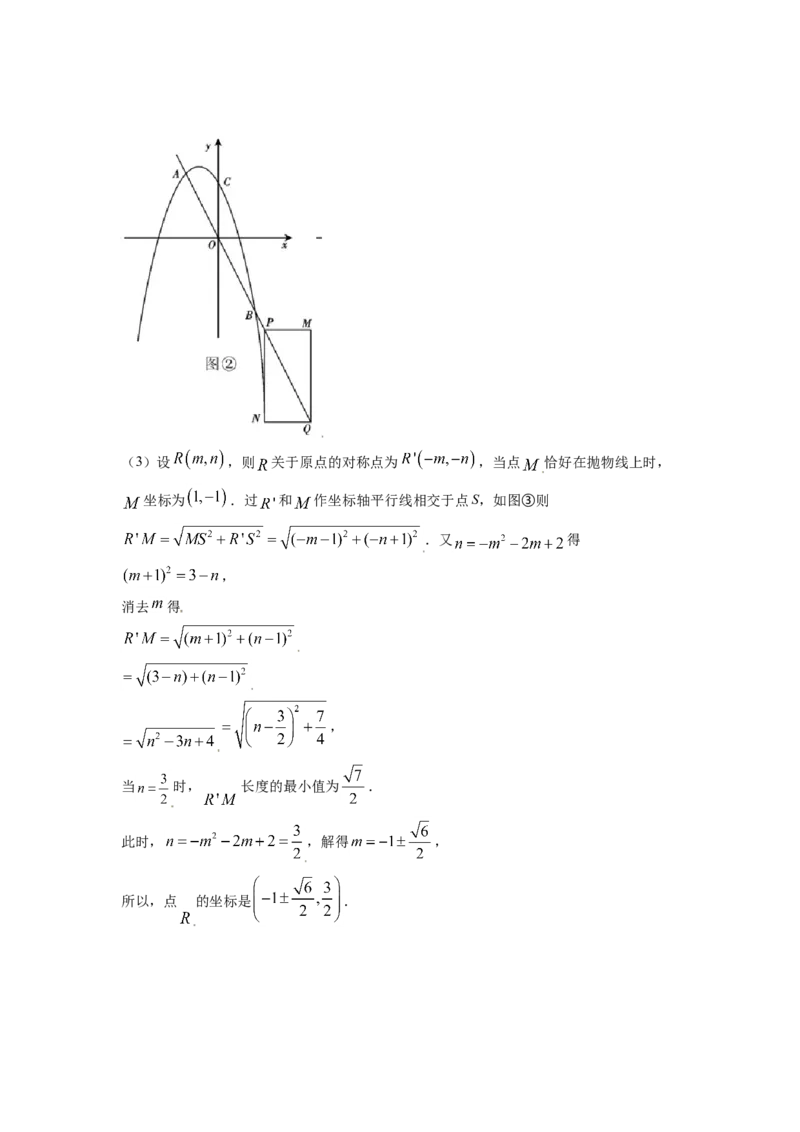
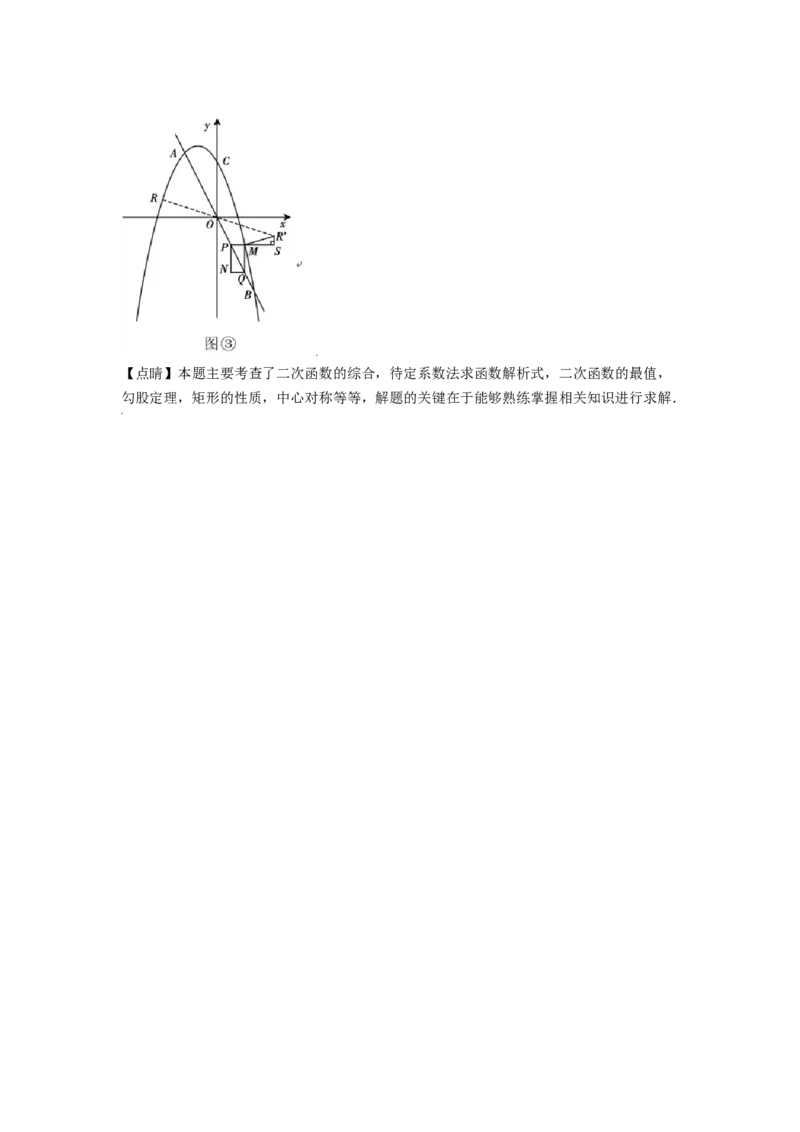
所以,当矩形 与抛物线有公共点时,时间 的取值范围是 .(3)设 ,则 关于原点的对称点为 ,当点 恰好在抛物线上时,
坐标为 .过 和 作坐标轴平行线相交于点S,如图③则
.又 得
,
消去 得
,
当 时, 长度的最小值为 .
此时, ,解得 ,
所以,点 的坐标是 .【点睛】本题主要考查了二次函数的综合,待定系数法求函数解析式,二次函数的最值,
勾股定理,矩形的性质,中心对称等等,解题的关键在于能够熟练掌握相关知识进行求解.