文档内容
绵阳市 2021 年高中阶段学校招生暨初中学业水平考试数学
本试卷分试题卷和答题卡两部分,试题卷共6页,答题卡共6页,考试时间120
分钟.
注意事项:
1.答题前,考生务必将自己的姓名、准考证号用0.5毫米的黑色墨迹签字笔填
写在答题卡上,并认真核对条形码上的姓名、准考证号、考点、考场号.
2.选择题答案使用2B铅笔填涂在答题卡对应题目标号的位置上,非选择题答
案使用0.5毫米的黑色墨迹签字笔书写在答题卡的对应框内.超出答题区域书
写的答案无效;在草稿纸、试题卷上答题无效.
3.考试结束后,将试题卷和答题卡一并交回.
第Ⅰ卷(选择题)
一、选择题:本大题共12个小题,每个小题只有一个选项符合题目要求.
1. 整式 的系数是( )
A. -3 B. 3 C. D.
2. 计算 的结果是( )
A. 6 B. C. D.
3. 下列图形中,轴对称图形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
4. 如图,圆锥的左视图是边长为2的等边三角形,则此圆锥的高是( )
A. 2 B. 3 C. D.
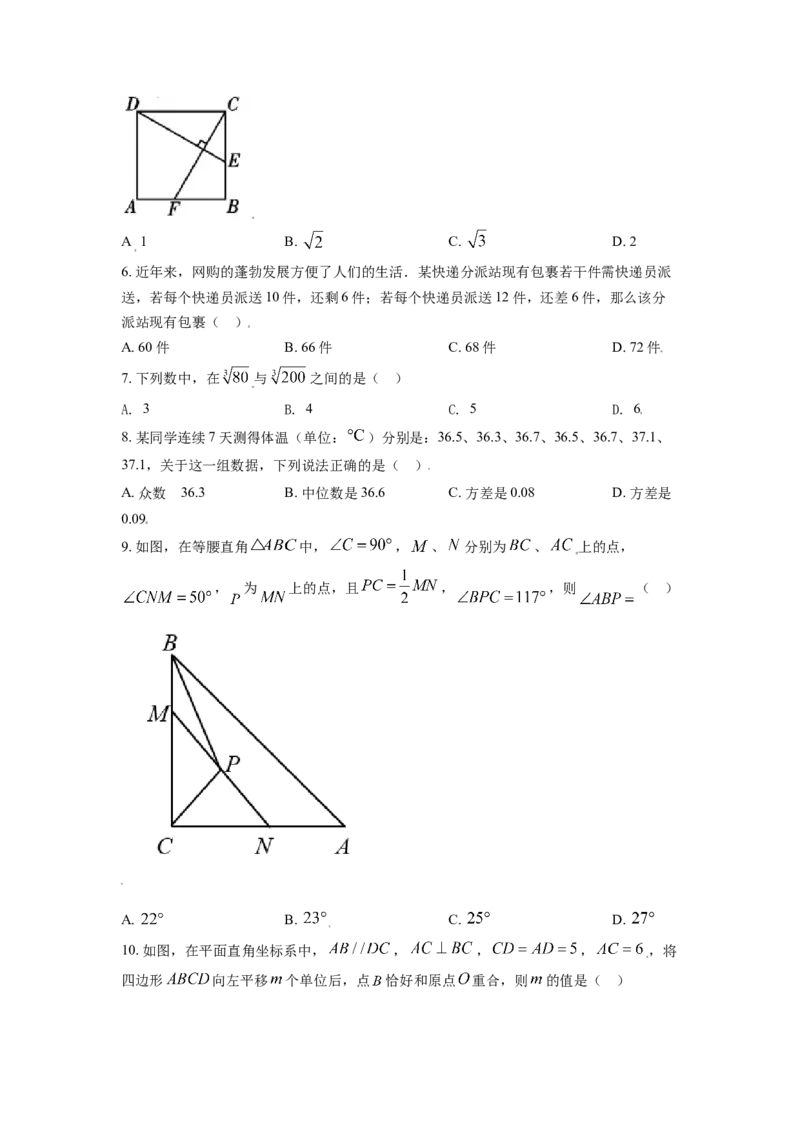
5. 如图,在边长为3的正方形 中, , ,则 的长是(
).
A 1 B. C. D. 2
6. 近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派
送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,那么该分
派站现有包裹( )
A. 60件 B. 66件 C. 68件 D. 72件
7. 下列数中,在 与 之间的是( )
A. 3 B. 4 C. 5 D. 6
8. 某同学连续7天测得体温(单位: )分别是:36.5、36.3、36.7、36.5、36.7、37.1、
37.1,关于这一组数据,下列说法正确的是( )
A. 众数 是36.3 B. 中位数是36.6 C. 方差是0.08 D. 方差是
0.09
9. 如图,在等腰直角 中, , 、 分别为 、 上的点,
, 为 上的点,且 , ,则 ( )
A. B. C. D.
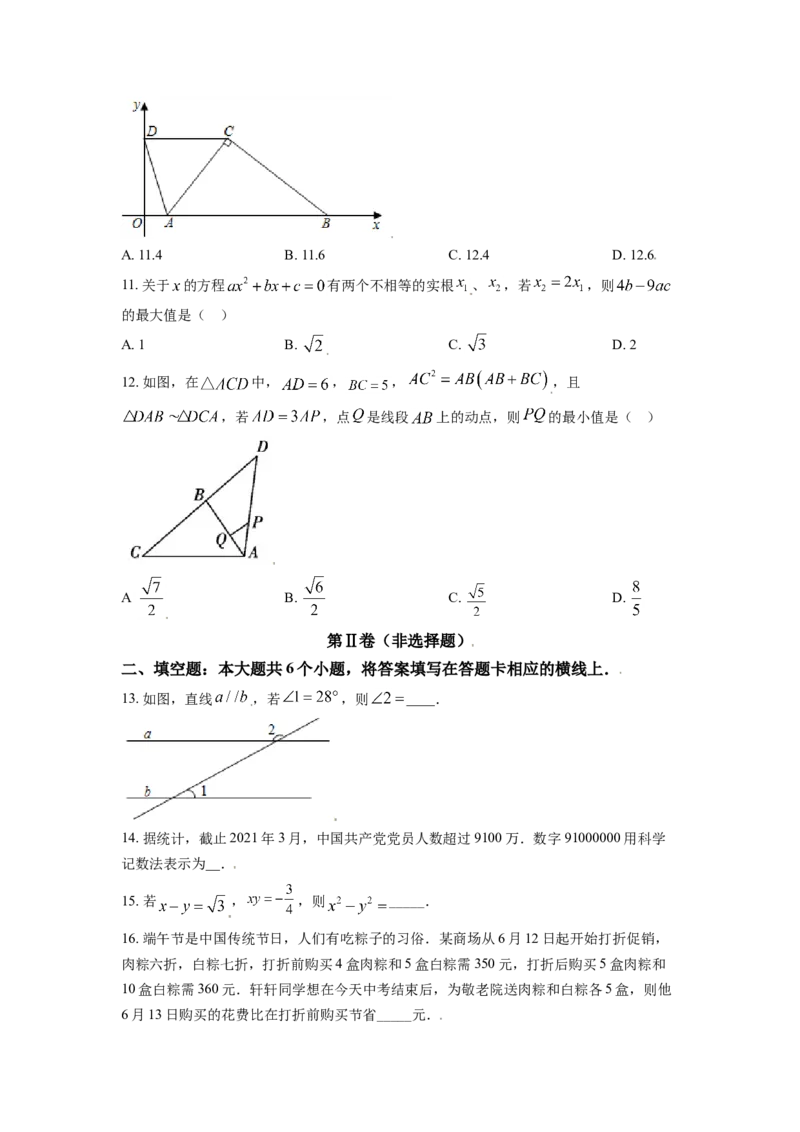
10. 如图,在平面直角坐标系中, , , , ,将
四边形 向左平移 个单位后,点 恰好和原点 重合,则 的值是( )A. 11.4 B. 11.6 C. 12.4 D. 12.6
11. 关于 的方程 有两个不相等的实根 、 ,若 ,则
的最大值是( )
A. 1 B. C. D. 2
12. 如图,在 中, , , ,且
,若 ,点 是线段 上的动点,则 的最小值是( )
.
A B. C. D.
第Ⅱ卷(非选择题)
二、填空题:本大题共6个小题,将答案填写在答题卡相应的横线上.
13. 如图,直线 ,若 ,则 ____.
14. 据统计,截止2021年3月,中国共产党党员人数超过9100万.数字91000000用科学
记数法表示为__.
15. 若 , ,则 _____.
16. 端午节是中国传统节日,人们有吃粽子的习俗.某商场从6月12日起开始打折促销,
肉粽六折,白粽七折,打折前购买4盒肉粽和5盒白粽需350元,打折后购买5盒肉粽和
10盒白粽需360元.轩轩同学想在今天中考结束后,为敬老院送肉粽和白粽各5盒,则他
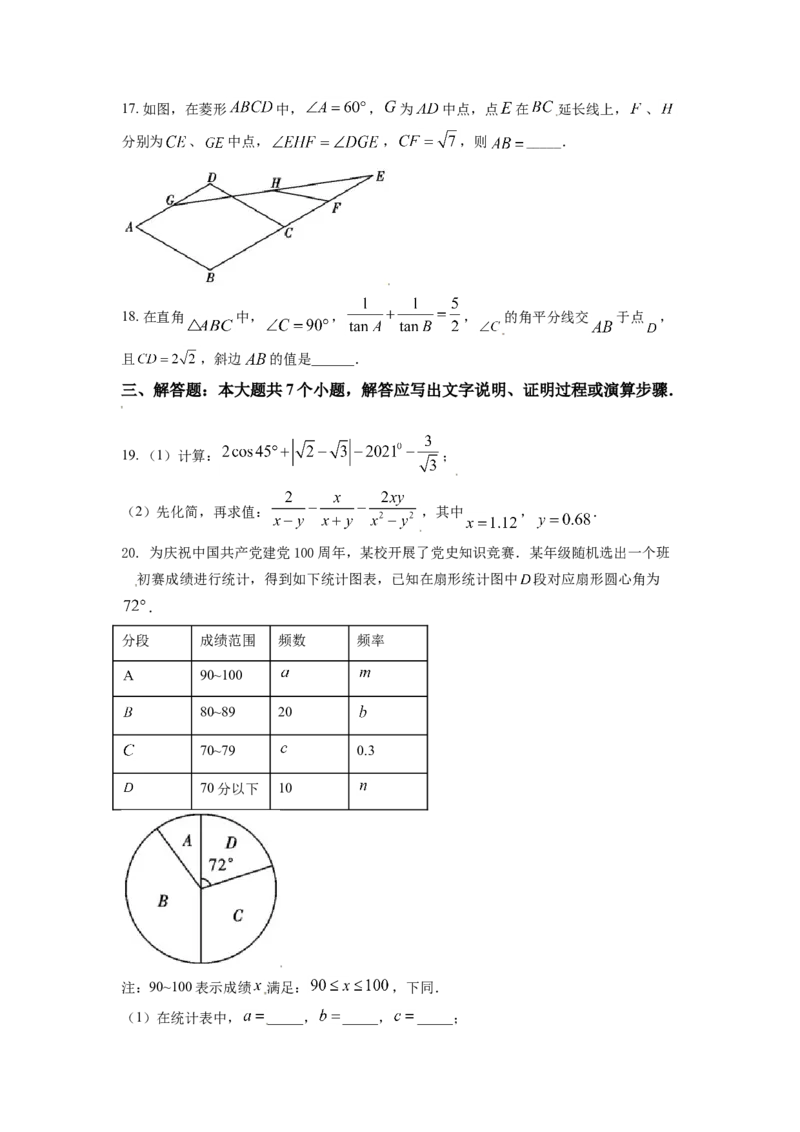
6月13日购买的花费比在打折前购买节省_____元.17. 如图,在菱形 中, , 为 中点,点 在 延长线上, 、
分别为 、 中点, , ,则 _____.
18. 在直角 中, , , 的角平分线交 于点 ,
且 ,斜边 的值是______.
三、解答题:本大题共7个小题,解答应写出文字说明、证明过程或演算步骤.
19. (1)计算: ;
(2)先化简,再求值: ,其中 , .
20. 为庆祝中国共产党建党100周年,某校开展了党史知识竞赛.某年级随机选出一个班
的初赛成绩进行统计,得到如下统计图表,已知在扇形统计图中 段对应扇形圆心角为
.
分段 成绩范围 频数 频率
90~100
80~89 20
70~79 0.3
70分以下 10
注:90~100表示成绩 满足: ,下同.
(1)在统计表中, _____, _____, _____;(2)若该年级参加初赛的学生共有2000人,根据以上统计数据估计该年级成绩在90分及
以上的学生人数;
(3)若统计表 段的男生比女生少1人,从 段中任选2人参加复赛,用列举法求恰好
选到1名男生和1名女生的概率.
21. 某工艺厂为商城制作甲、乙两种木制工艺品,甲种工艺品不少于400 件,乙种工艺品不
少于680件.该厂家现准备购买 、 两类原木共150根用于工艺品制作,其中,1根
类原木可制作甲种工艺品4件和乙种工艺品2件,1根 类原木可制作甲种工艺品2件和乙
种工艺品6件.
(1)该工艺厂购买 类原木根数可以有哪些?
(2)若每件甲种工艺品可获得利润50元,每件乙种工艺品可获得利润80元,那么该工艺
厂购买 、 两类原木各多少根时获得利润最大,最大利润是多少?
22. 如图,点 是 的边 上的动点, ,连接 ,并将线段 绕点
逆时针旋转 得到线段 .
(1)如图1,作 ,垂足 在线段 上,当 时,判断点 是
否在直线 上,并说明理由;
(2)如图2,若 , ,求以 、 为邻边的正方形的面积 .
23. 如图,在平面直角坐标系 中,直角 的顶点 , 在函数
图象上, 轴,线段 的垂直平分线交 于点 ,交
的延长线于点 ,点 纵坐标为2,点 横坐标为1, .
(1)求点 和点 的坐标及 的值;(2)连接 ,求 的面积.
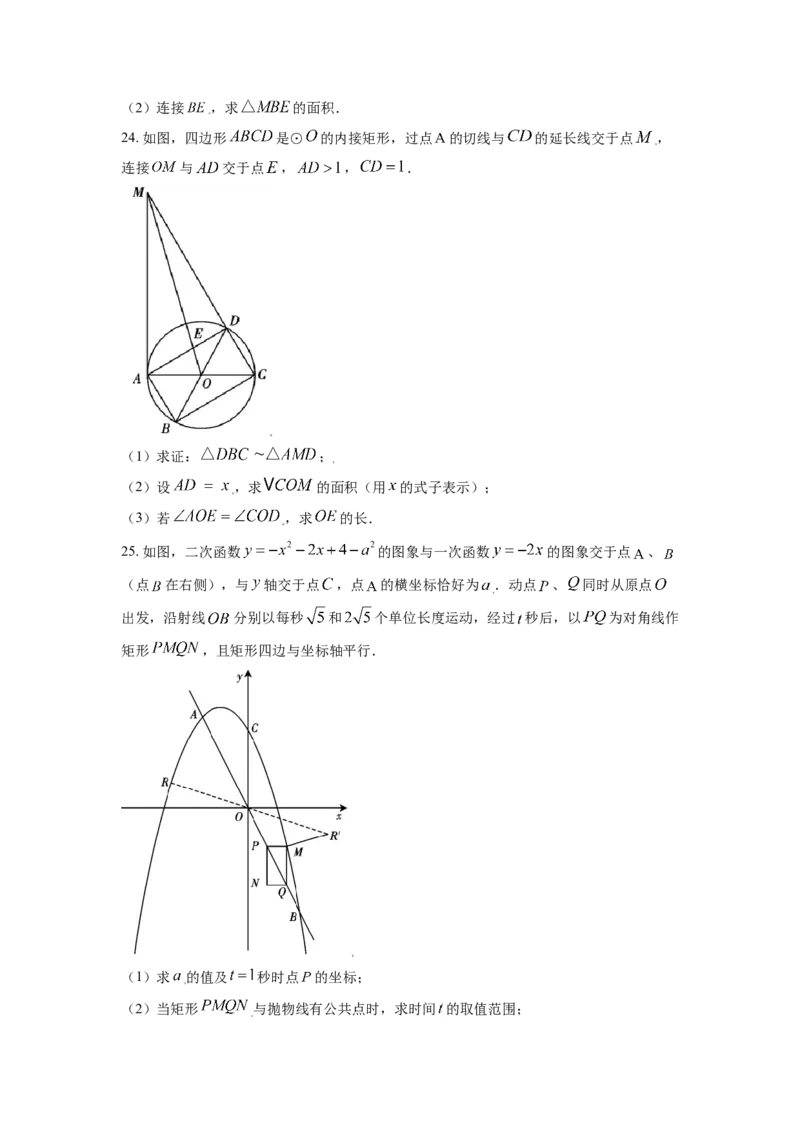
24. 如图,四边形 是⊙ 的内接矩形,过点 的切线与 的延长线交于点 ,
连接 与 交于点 , , .
(1)求证: ;
(2)设 ,求 的面积(用 的式子表示);
(3)若 ,求 的长.
25. 如图,二次函数 的图象与一次函数 的图象交于点 、
(点 在右侧),与 轴交于点 ,点 的横坐标恰好为 .动点 、 同时从原点
出发,沿射线 分别以每秒 和 个单位长度运动,经过 秒后,以 为对角线作
矩形 ,且矩形四边与坐标轴平行.
(1)求 的值及 秒时点 的坐标;
(2)当矩形 与抛物线有公共点时,求时间 的取值范围;(3)在位于 轴上方的抛物线图象上任取一点 ,作关于原点 的对称点为 ,当
点 恰在抛物线上时,求 长度的最小值,并求此时点 的坐标.