文档内容
2023 年高考考前押题密卷(广东卷)
数学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写
在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
(原创)1.已知集合 , ,若 ,则 ( )
A. B. C. D.
(原创)2.已知a, , ,则 ( )
A.5 B. C.3 D.
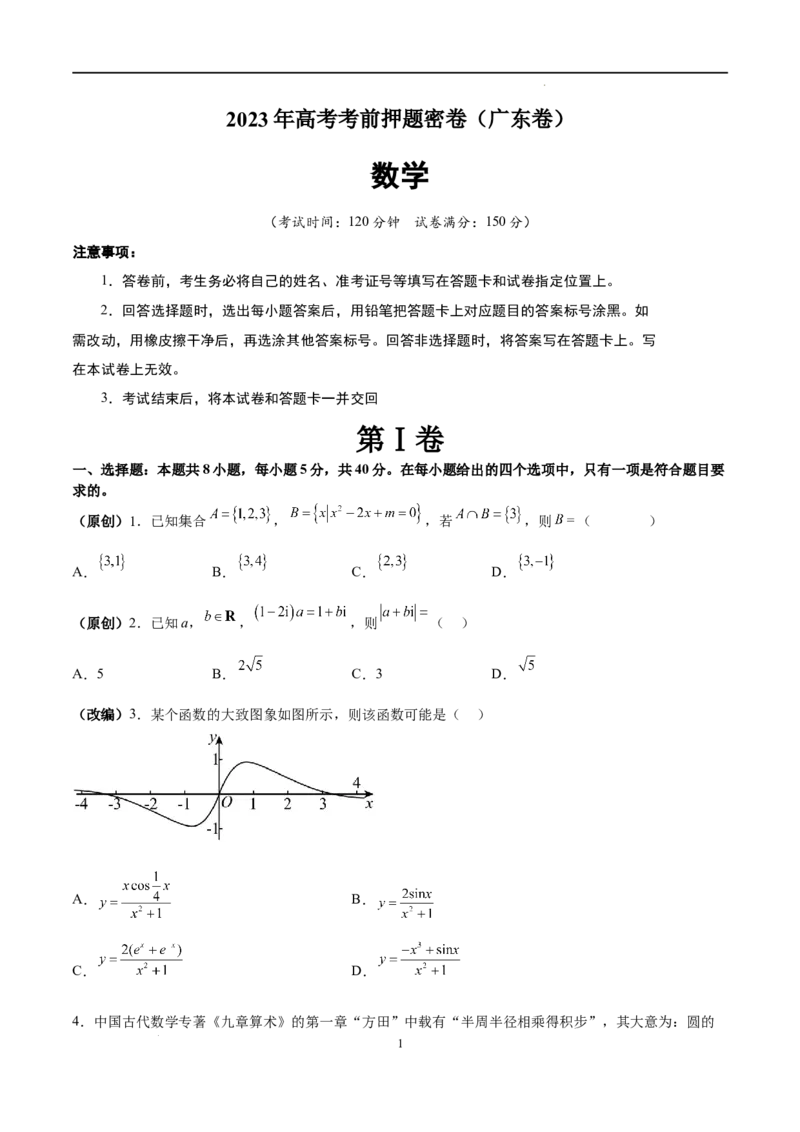
(改编)3.某个函数的大致图象如图所示,则该函数可能是( )
A. B.
C. D.
4.中国古代数学专著《九章算术》的第一章“方田”中载有“半周半径相乘得积步”,其大意为:圆的
1
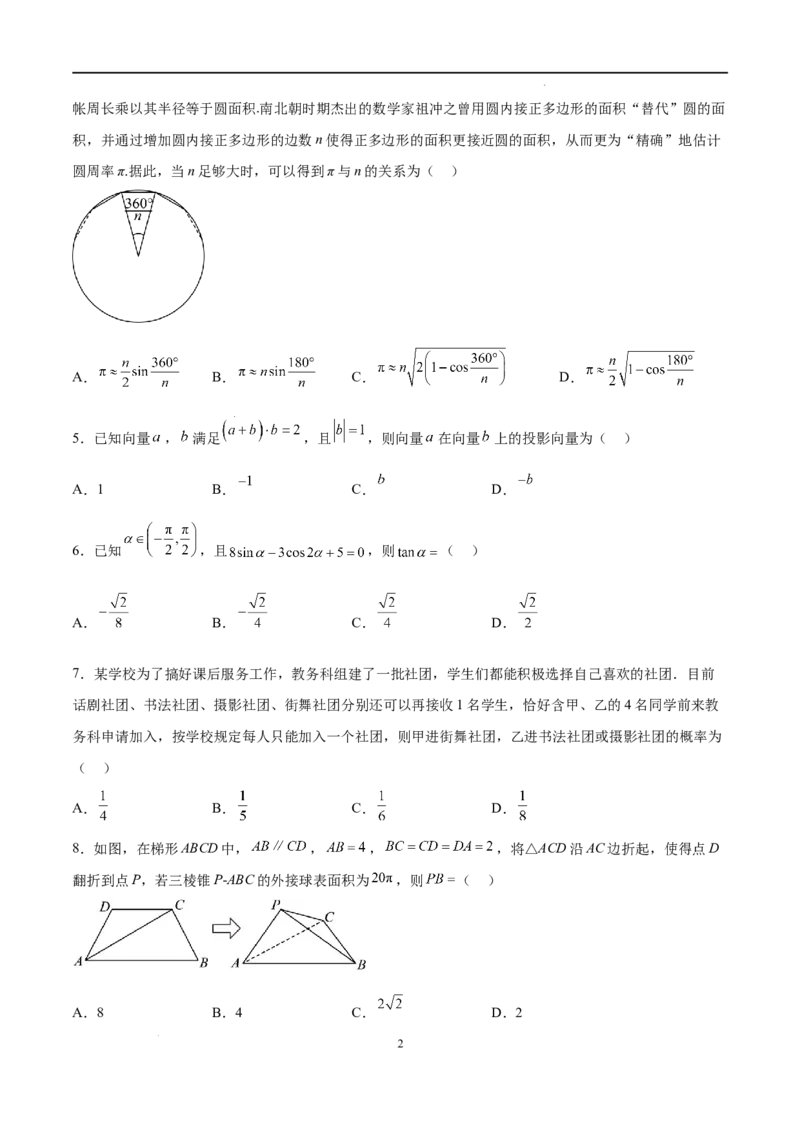
学科网(北京)股份有限公司帐周长乘以其半径等于圆面积.南北朝时期杰出的数学家祖冲之曾用圆内接正多边形的面积“替代”圆的面
积,并通过增加圆内接正多边形的边数n使得正多边形的面积更接近圆的面积,从而更为“精确”地估计
圆周率π.据此,当n足够大时,可以得到π与n的关系为( )
A. B. C. D.
5.已知向量 , 满足 ,且 ,则向量 在向量 上的投影向量为( )
A.1 B. C. D.
6.已知 ,且 ,则 ( )
A. B. C. D.
7.某学校为了搞好课后服务工作,教务科组建了一批社团,学生们都能积极选择自己喜欢的社团.目前
话剧社团、书法社团、摄影社团、街舞社团分别还可以再接收1名学生,恰好含甲、乙的4名同学前来教
务科申请加入,按学校规定每人只能加入一个社团,则甲进街舞社团,乙进书法社团或摄影社团的概率为
( )
A. B. C. D.
8.如图,在梯形ABCD中, , , ,将△ACD沿AC边折起,使得点D
翻折到点P,若三棱锥P-ABC的外接球表面积为 ,则 ( )
A.8 B.4 C. D.2
2
学科网(北京)股份有限公司二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部
选对的得5分,部分选对的得2分,有选错的得0分。
(改编)9.已知函数 的部分图像如图所示,则( )
A.
B. 的图像关于点 对称
C. 的图像关于直线 对称
D.函数 为偶函数
(改编)10.下列命题中正确是( )
A.中位数就是第50百分位数
B.已知随机变量X~ ,若 ,则
C.已知随机变量 ~ ,且函数 为偶函数,则
D.已知采用分层抽样得到的高三年级男生、女生各100名学生的身高情况为:男生样本平均数172,方差
为120,女生样本平均数165,方差为120,则总体样本方差为
11.已知函数 是定义在 上的可导函数,当 时, ,若 且对
任意 ,不等式 成立,则实数 的取值可以是( )
3
学科网(北京)股份有限公司A.-1 B.0 C.1 D.2
12.在平面直角坐标系 中,双曲线 的左、右焦点分别是 , ,渐近线方
程为 ,M为双曲线E上任意一点, 平分 ,且 , ,则( )
A.双曲线的离心率为
B.双曲线的标准方程为
C.点M到两条渐近线的距离之积为
D.若直线 与双曲线E的另一个交点为P,Q为 的中点,则
第Ⅱ卷
三、填空题:本题共4小题,每小题5分,共20分。
(改编)13.已知无穷数列 满足 ,写出满足条件的 的一个通项公式:
___________.(不能写成分段数列的形式)
(原创)14.已知 ,函数 都满足 ,又 ,则 ______.
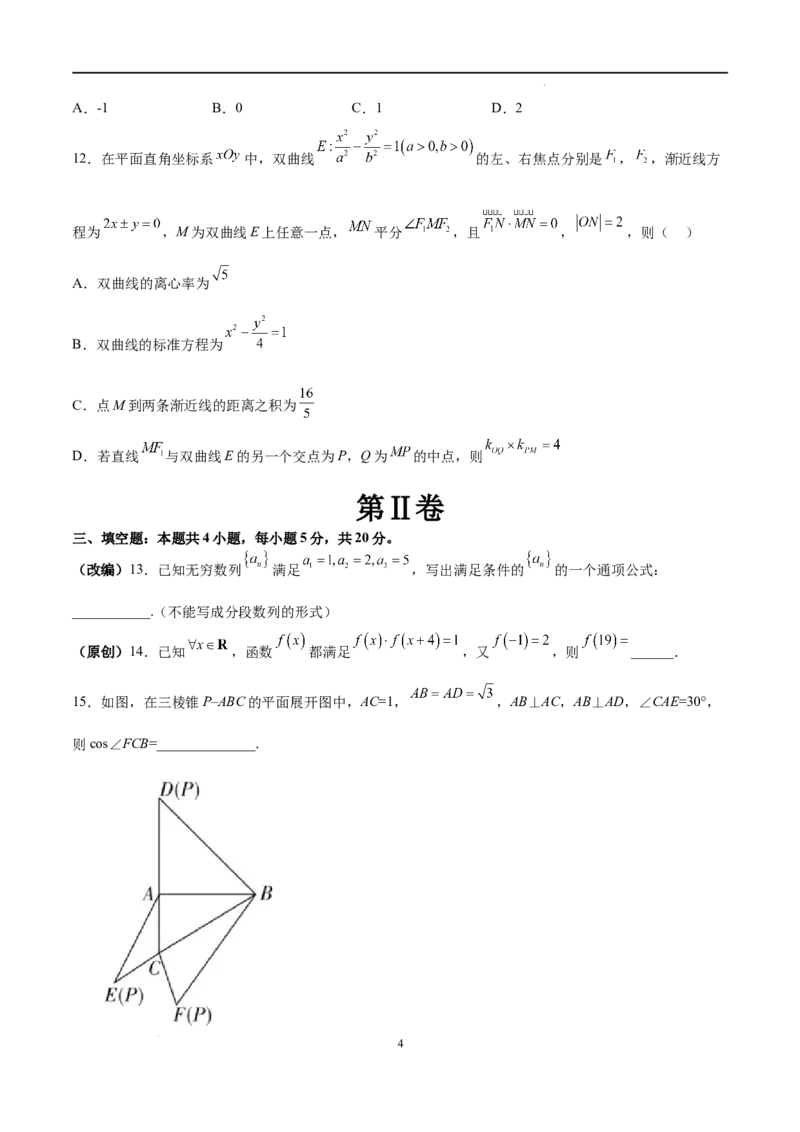
15.如图,在三棱锥P–ABC的平面展开图中,AC=1, ,AB⊥AC,AB⊥AD,∠CAE=30°,
则cos∠FCB=______________.
4
学科网(北京)股份有限公司16.已知抛物线 与圆 ,过圆心 的直线 与抛物线 和圆 分别交于 , ,
, ,其中 , 在第一象限, , 在第四象限,则 最小值是______.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步棸。
17.(10分)
在数列 中, , .
(1)求证:数列 为等比数列,并求数列 的通项公式;
(2)设 ,求数列 的前 项和 .
18.(12分)
已知 的角A,B,C的对边分别为a,b,c,且 .
(1)求A;
(2)若 的面积为 , ,点D为边BC的中点,求AD的长.
19.(12分)
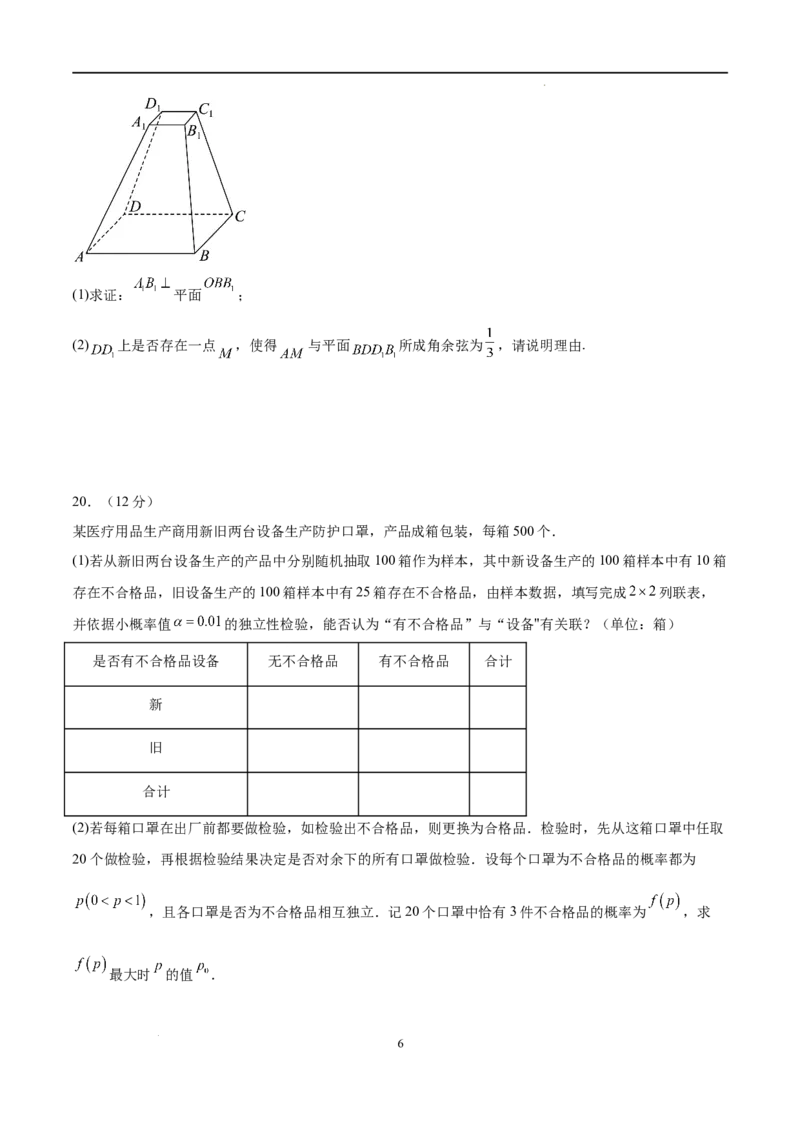
如图,在四棱台 中,底面 是菱形, ,梯形 底面 ,
.设 为 的中点.
5
学科网(北京)股份有限公司(1)求证: 平面 ;
(2) 上是否存在一点 ,使得 与平面 所成角余弦为 ,请说明理由.
20.(12分)
某医疗用品生产商用新旧两台设备生产防护口罩,产品成箱包装,每箱500个.
(1)若从新旧两台设备生产的产品中分别随机抽取100箱作为样本,其中新设备生产的100箱样本中有10箱
存在不合格品,旧设备生产的100箱样本中有25箱存在不合格品,由样本数据,填写完成 列联表,
并依据小概率值 的独立性检验,能否认为“有不合格品”与“设备"有关联?(单位:箱)
是否有不合格品设备 无不合格品 有不合格品 合计
新
旧
合计
(2)若每箱口罩在出厂前都要做检验,如检验出不合格品,则更换为合格品.检验时,先从这箱口罩中任取
20个做检验,再根据检验结果决定是否对余下的所有口罩做检验.设每个口罩为不合格品的概率都为
,且各口罩是否为不合格品相互独立.记20个口罩中恰有3件不合格品的概率为 ,求
最大时 的值 .
6
学科网(北京)股份有限公司(3)现对一箱产品检验了20个,结果恰有3个不合格品,以(2)中确定的 作为 的值.已知每个口罩的
检验费用为0.2元,若有不合格品进入用户手中,则生产商要为每个不合格品支付5元的赔偿费用.以检
验费用与赔偿费用之和的期望为决策依据,是否要对这箱产品余下的480个口罩做检验?
附表:
0.100 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
附: ,其中 .
21.(12分)
已知椭圆 的离心率为 ,且过点 .
(1)求椭圆 的方程;
(2)设直线 与 轴交于点 ,过 作直线 交 于 两点, 交 于 两点.已知直线
交 于点 ,直线 交 于点 .试探究 是否为定值,若为定值,求出定值;若不为定值,说明理由.
22.(12分)
7
学科网(北京)股份有限公司已知函数 .
(1)当 时,求 的零点个数;
(2)若 恒成立,求实数a的值.
8
学科网(北京)股份有限公司9
学科网(北京)股份有限公司