【MATLAB源码】CORDIC-QR :基于Cordic硬件级矩阵QR分解
🎲 CORDIC-QR 硬件级矩阵QR分解
Givens 旋转加速 · 脉动阵列架构 · 线性代数硬核化无开方 QR 分解 (Square-Root-Free) + 最小二乘 (LS) 求解 + 信号子空间正交化
📌 为什么选择 CORDIC-QR?
在大规模 MIMO 通信、自适应滤波和雷达波束成形中,矩阵求逆和分解是计算瓶颈。传统的 Gram-Schmidt 正交化对字长敏感,容易发散。CORDIC-QR 基于 CORDIC 辅助的 Givens 旋转,提供了一种数值高度稳定且无除法/无开方的矩阵分解方案,天然契合 Systolic Array (脉动阵列) 硬件架构。
|
|
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
🎯 核心价值
🔬 学术研究价值
|
💼 工程应用价值
|
⚡ 技术亮点
🌊 CORDIC-QR vs MATLAB qr
|
|
qr |
CORDIC-QR (本平台) |
|---|---|---|
| 算法内核 |
|
Givens 旋转 (CORDIC) |
| 硬件实现难度 |
|
低 (仅移位加减) |
| 并行度 |
|
适用于 FPGA 阵列 |
| 适用场景 |
|
实时信号处理 (MIMO/Radar) |
📊 性能指标 (实测数据)
基于
demo_qr.m(8×5 Matrix)
|
|
|
|
|---|---|---|
| 重构误差
|
< 1e-4 |
|
| 正交性误差
|
< 2e-4 |
|
| LS 求解精度
|
< 1e-4 |
|
📁 项目结构
CORDIC-QR/├── matrix/ # 矩阵运算核心│ ├── cordic_qr.m # QR分解主函数│ ├── givens_rotation.m # Givens旋转单元│ └── qr_solve.m # 最小二乘求解器├── docs/ # 核心文档│ ├── 算法文档.md # QR/Givens/Systolic 理论│ └── 代码文档.md # API 字典└── demo_qr.m # 旗舰演示脚本🎬 一键运行
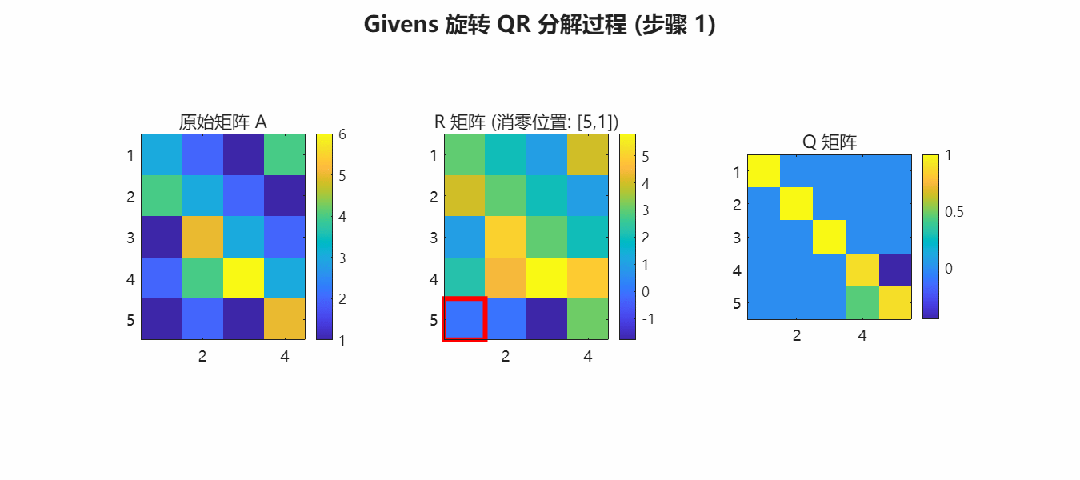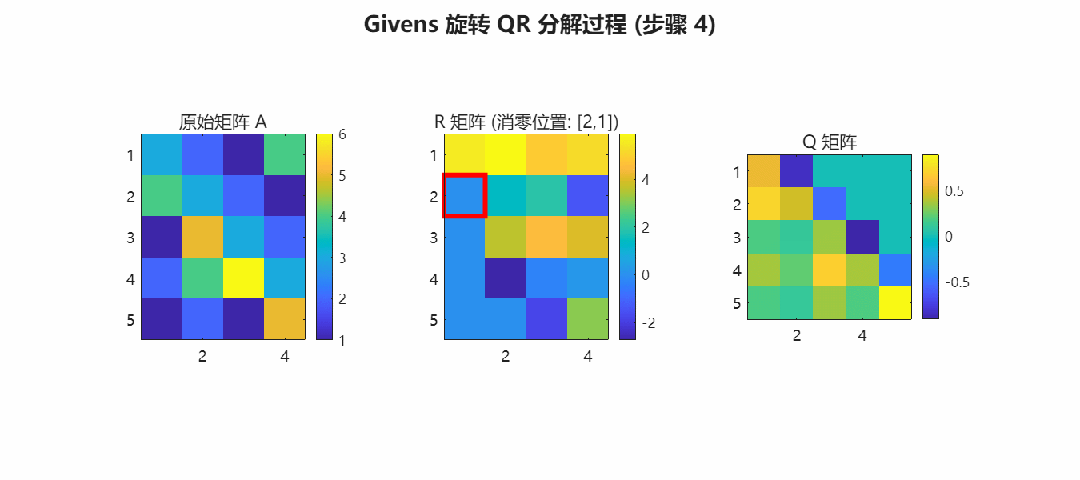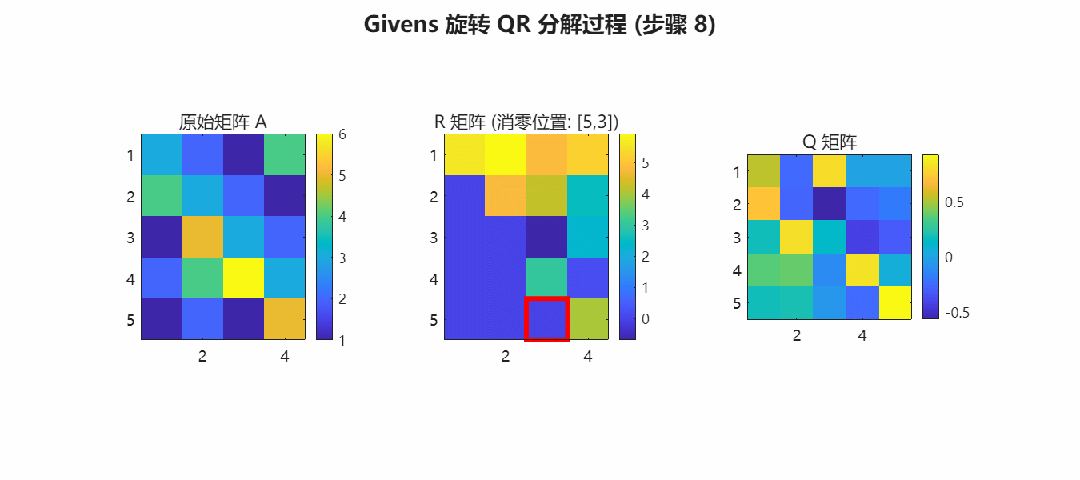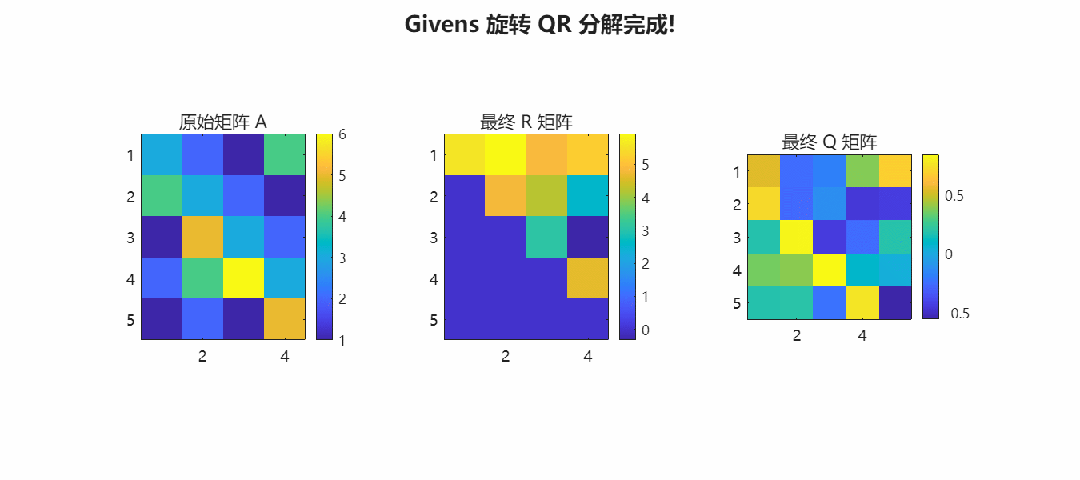
>> addpath(genpath('.'));>> demo_qr结果预览: Givens 旋转消零过程
下图展示了 CORDIC-QR 如何逐个消除矩阵下三角元素,最终将 转化为上三角矩阵 。
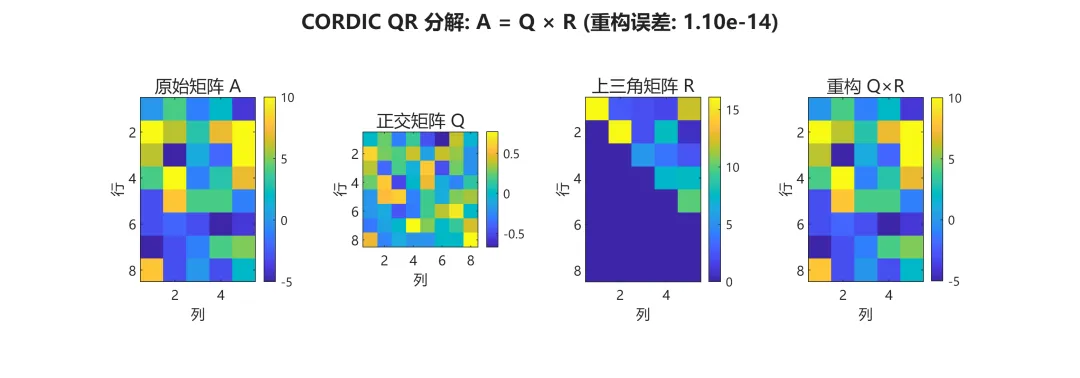
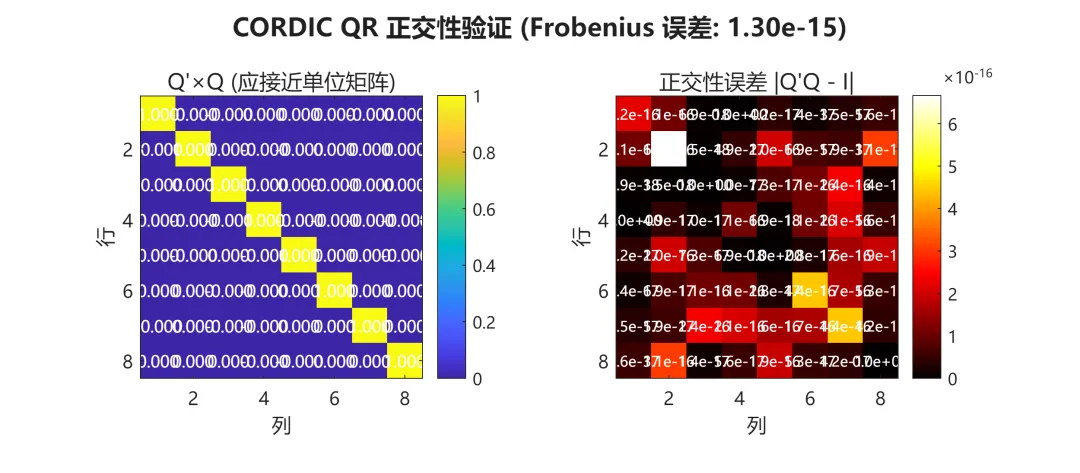
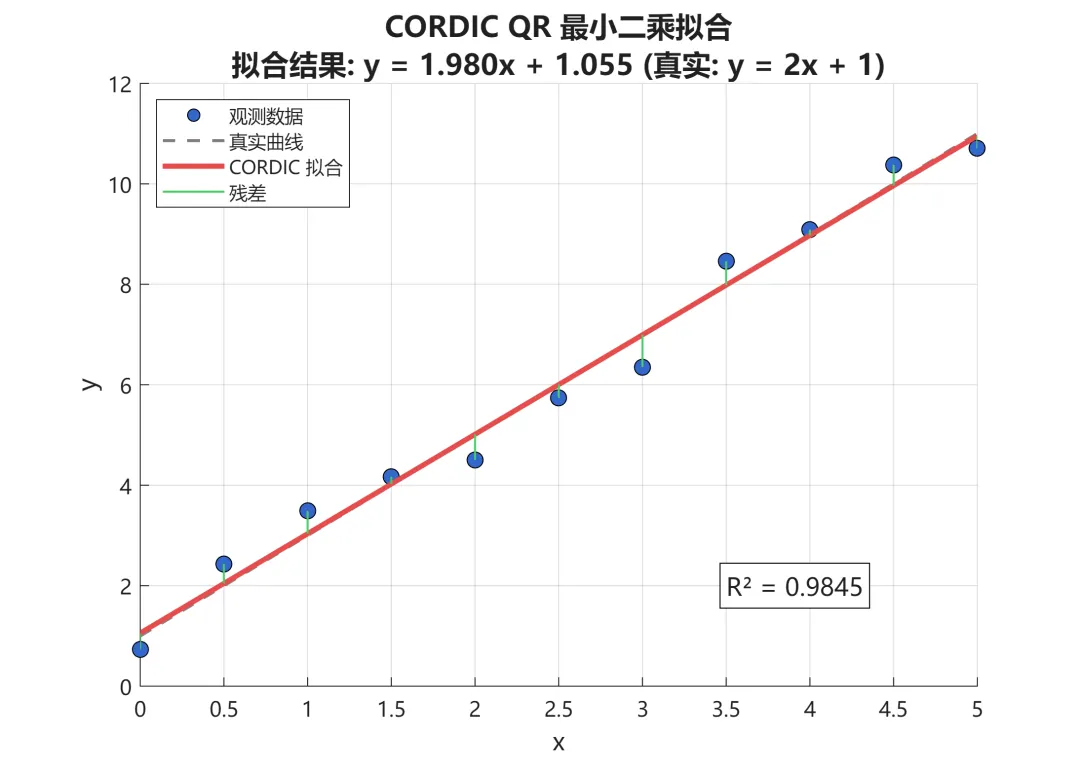
 夜雨聆风
夜雨聆风









