陕西​2025年高考全国二卷数学高考真题解析_1.高考2025全国各省真题+答案_2.高考数学试题及答案

2025 年全国统一高考数学试卷 （新高考Ⅱ卷） 注意事项： 1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上. 2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑； 如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写 在答题卡上，写在试卷上无效. 3.考试结束后，本试卷和答题卡一并交回. 一、单选题：本题共8小题，每小题 5分，共40分.在每小题给出的选项中，只 有一项是符合题目要求的. 1．样本数据2，8，14，16，20的平均数为（ ） A．8 B．9 C．12 D．18 1 2．已知z1i，则 （ ） z1 A．i B．i C．1 D．1 3．已知集合A{4,0,1,2,8},B  x∣x3  x  ,则AB（ ） A．{0,1,2} B．{1,2,8} C．{2,8} D．{0,1} x4 4．不等式 2的解集是（ ） x1 A．{x∣2x1} B．{x∣x2} C．{x∣2x1} D．{x∣x1} 5．在V ABC中，BC 2，AC1 3，AB  6 ，则A（ ） A．45 B．60 C．120 D．135 6．设抛物线C:y2 2px(p0)的焦点为F,点A在C上，过A作C的准线的垂线，垂足为 B，若直线BF的方程为y2x2，则|AF |（ ） A．3 B．4 C．5 D．6 7．记S 为等差数列a 的前n项和，若S 6,S 5,则S （ ） n n 3 5 6 试卷第1页，共3页A．20 B．15 C．10 D．5  5   8．已知0，cos  ，则sin （ ） 2 5  4 2 2 3 2 7 2 A． B． C． D． 10 5 10 10 二、多选题：本题共 3小题，共18分.在每小题给出的选项中，有多项符合题目 要求. 9．记S 为等比数列a 的前n项和，q为a 的公比，q0，若S 7,a 1，则（ ） n n n 3 3 1 1 A．q B．a  2 5 9 C．S 8 D．a S 8 5 n n 10．已知 f(x)是定义在R上的奇函数，且当x0时， f x  x23  ex 2，则（ ） A． f(0)0 B．当x0时， f x  x23  ex 2 C． f(x)2当且仅当x 3 D．x1是 f(x)的极大值点 x2 y2 11．双曲线C:  1(a 0,b0) 的左、右焦点分别是F、F ，左、右顶点分别为A，A ， a2 b2 1 2 1 2 5 以FF 为直径的圆与C的一条渐近线交于M、N两点，且NAM  ，则（ ） 1 2 1 6  A．AMA  B． MA 2 MA 1 2 6 1 2 C．C的离心率为 13 D．当a 2时，四边形NAMA 的面积为8 3 1 2 三、填空题：本题共 3小题，每小题 5分，共 15分.        12．已知平面向量a (x,1),b (x1,2x),若a  ab ，则|a| 13．若x2是函数 f(x)(x1)(x2)(xa)的极值点，则 f(0) 14．一个底面半径为4cm，高为9cm的封闭圆柱形容器（容器壁厚度忽略不计）内有两个 半径相等的铁球，则铁球半径的最大值为 cm． 四、解答题：本题共 5小题，共77分.解答应写出文字说明，证明过程或演算步 骤. 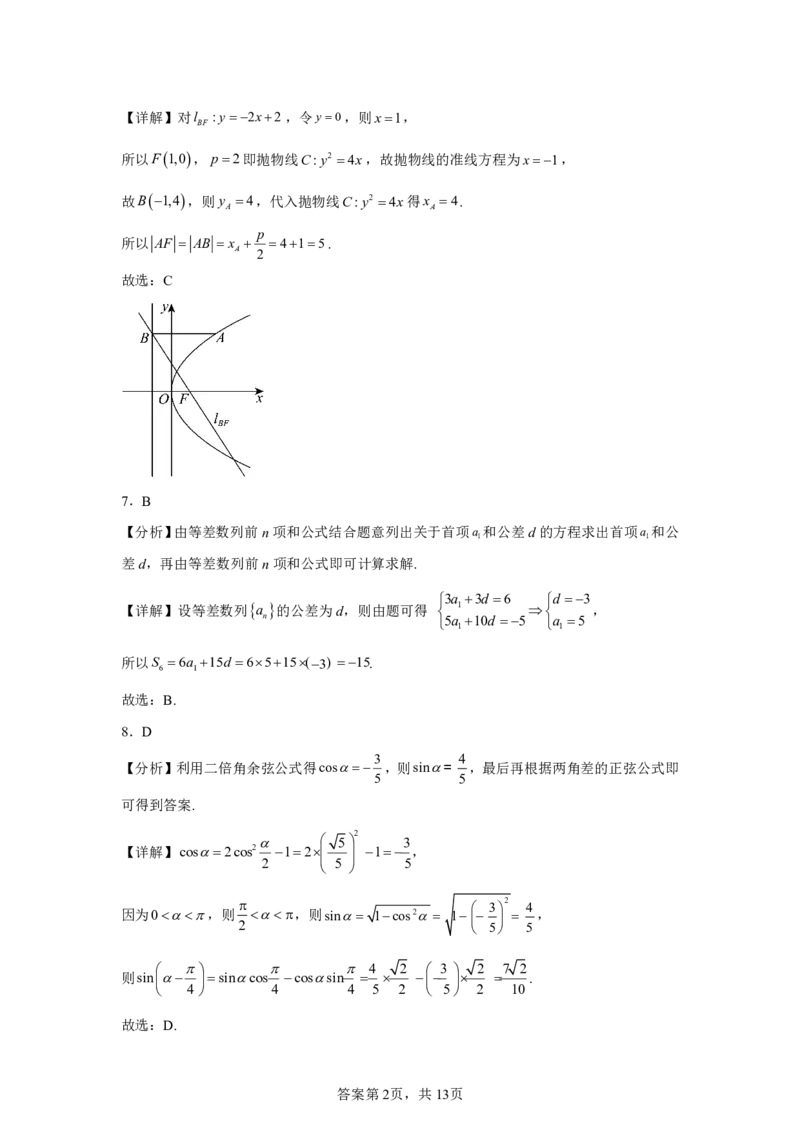1 15．已知函数 f xcos2x(0π), f 0 ． 2 (1)求 ; 试卷第2页，共3页 π (2)设函数g(x) f(x) f x ，求g(x)的值域和单调区间．  6 x2 y2 2 16．已知椭圆C:  1(ab0)的离心率为 ，长轴长为4． a2 b2 2 (1)求C的方程； (2)过点(0,-2)的直线l与C交于A, B两点，O为坐标原点，若△OAB的面积为 2，求|AB|． 17．如图，在四边形ABCD中，AB//CD,DAB90，F为CD的中点，点E在AB上，EF//AD， AB3AD,CD2AD，将四边形EFDA沿EF翻折至四边形EFDA，使得面EFDA与面 EFCB所成的二面角为60． (1)证明:AB//平面CDF； (2)求面BCD与面EFDA所成的二面角的正弦值． 1 1 18．已知函数 f(x)ln(1x)x x2kx3，其中0k  ． 2 3 (1)证明： f(x)在区间(0,)存在唯一的极值点和唯一的零点； (2)设x ,x 分别为 f(x)在区间(0,)的极值点和零点. 1 2 （i）设函数g(t) f x t f x t ·证明：g(t)在区间0,x 单调递减； 1 1 1 （ii）比较2x 与x 的大小，并证明你的结论． 1 2 19．甲、乙两人进行乒乓球练习，每个球胜者得1分，负者得0分．设每个球甲胜的概率为 1  P  p1，乙胜的概率为q，pq1，且各球的胜负相互独立，对正整数k2，记p 2  k 为打完k个球后甲比乙至少多得2分的概率，q 为打完k个球后乙比甲至少多得2分的概 k 率． (1)求p ,p （用p表示）． 3 4 p p (2)若 4 3 4，求p． q q 4 3 (3)证明：对任意正整数m，p q  p q  p q ． 2m1 2m1 2m 2m 2m2 2m2 试卷第3页，共3页1．C 【分析】由平均数的计算公式即可求解. 28141620 60 【详解】样本数据2,8,14,16,20的平均数为  12. 5 5 故选：C. 2．A 【分析】由复数除法即可求解. 1 1 1 i 【详解】因为z1i，所以    i. z1 1i1 i i2 故选：A. 3．D 【分析】求出集合B后结合交集的定义可求AB. 【详解】B  x|x3  x  0,1,1，故AB 0,1， 故选：D. 4．C 【分析】移项后转化为求一元二次不等式的解即可. x4 x2 x2x10 【详解】 2即为 0即 ，故-2£ x< 1， x1 x1 x10 故解集为2,1， 故选：C. 5．A AB2 AC2BC2 【分析】由余弦定理cosA 直接计算求解即可. 2ABAC AB2AC2BC2  6 2 1 3 222 2 【详解】由题意得cosA   ， 2ABAC 2 6 1 3  2 又0  A180，所以A45o. 故选：A 6．C 【分析】先由直线l 求出焦点F 和 p即抛物线C的方程，进而依次得抛物线的准线方程和 BF 点B，从而可依次求出y 和x ，再由焦半径公式即可得解. 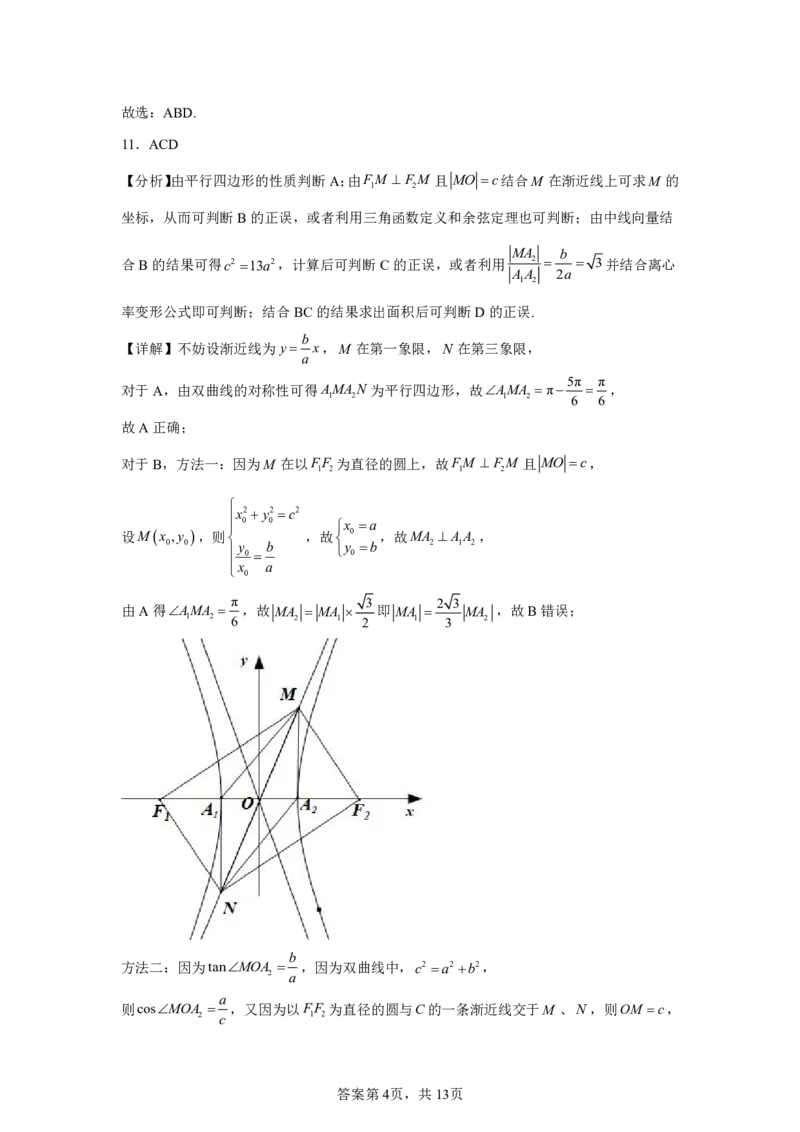A A 答案第1页，共13页【详解】对l :y 2x2，令y0，则x1， BF 所以F1,0， p2即抛物线C:y2 4x，故抛物线的准线方程为x1， 故B1,4，则y 4，代入抛物线C:y2 4x得x 4. A A p 所以 AF  AB  x  415. A 2 故选：C 7．B 【分析】由等差数列前n项和公式结合题意列出关于首项a 和公差d的方程求出首项a 和公 1 1 差d，再由等差数列前n项和公式即可计算求解. 3a 3d 6 d 3 【详解】设等差数列a 的公差为d，则由题可得  1  ， n 5a 10d 5 a 5 1 1 所以S 6a 15d 65153 15. 6 1 故选：B. 8．D 3 4 【分析】利用二倍角余弦公式得cos ，则sin= ，最后再根据两角差的正弦公式即 5 5 可得到答案. 2   5 3 【详解】cos2cos2 12  1 ，   2  5  5   3 2 4 因为0，则 ，则sin 1cos2 1   ， 2  5 5     4 2  3  2 7 2 则sin sincos cossin      .  4  4 4 5 2  5 2 10 故选：D. 答案第2页，共13页9．AD 【分析】对A，根据等比数列通项公式和前n项和公式得到方程组，解出a,q，再利用其通 1 项公式和前n项和公式一一计算分析即可. a 4  a 9  aq2 1  1  1 【详解】对A，由题意得 1 ，结合q0，解得 1或 1（舍去）， a aqaq2 7 q q 1 1 1  2  3 故A正确； 4 1 1 对B，则a aq4 4   ，故B错误； 5 1 2 4  1  对C，S  a 1  1q5  4  1 32    31 ，故C错误； 5 1q 1 4 1 2  1 n n1 41   对D，a n 4    1 2    23n， S n    1 2  82n3 ， 1 2 则a S 23n823n 8，故D正确； n n 故选：AD. 10．ABD 【分析】对A，根据奇函数特点即可判断；对B，利用 f(x)f x代入求解即可；对C， 举反例 f(1)2即可；对D，直接求导，根据极大值点判定方法即可判断. 【详解】对A，因为 f(x)定义在R上奇函数，则 f(0)0，故A正确； 对B，当x0时，x0，则 f(x)f x    x23  ex2     x 23  ex2 ，故B 正确； 对C， f(1)13e22e1 2， 故C错误； 对D，当x0时， f(x)  3x2 ex2，则 f(x)  3x2 ex2xex   x22x3  ex ， 令 f(x)0，解得x1或3（舍去）， 当x,1时， f(x)0，此时 f x单调递增， 当x1,0时， f(x)0，此时 f x单调递减， 则x1是 f(x)极大值点，故D正确； 答案第3页，共13页故选：ABD. 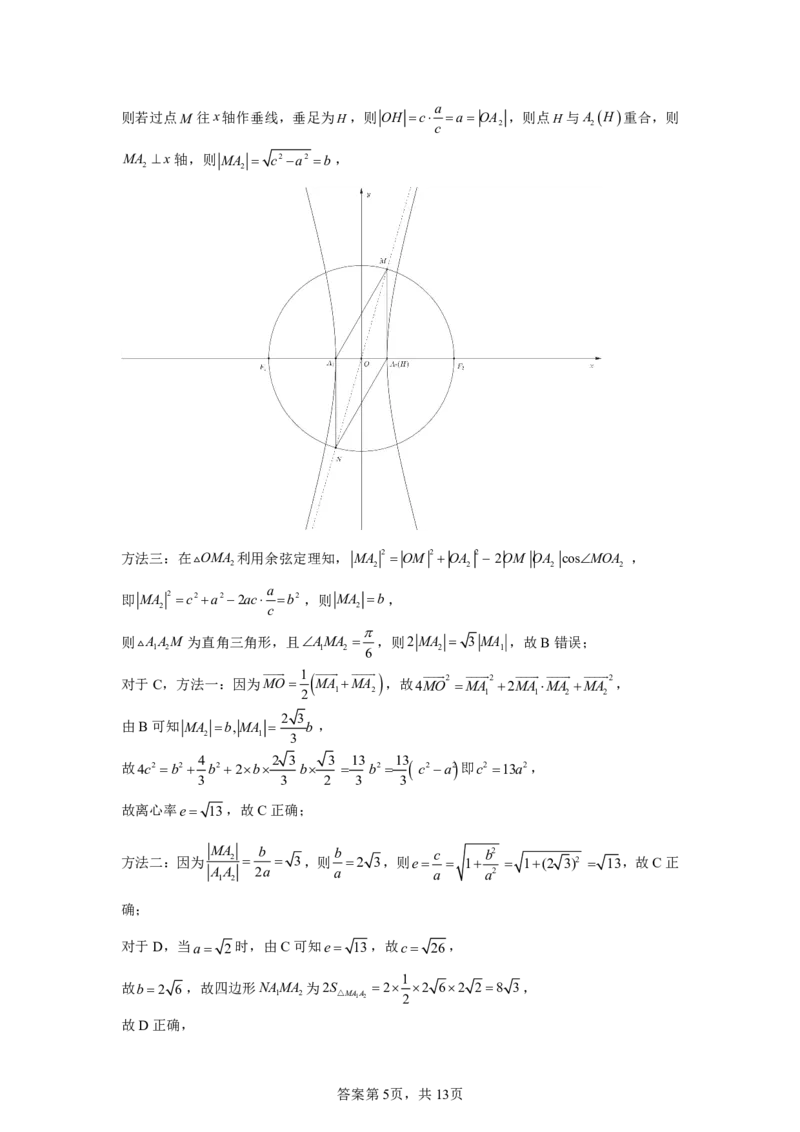11．ACD 【分析】由平行四边形的性质判断A；由FM F M 且 MO c结合M 在渐近线上可求M 的 1 2 坐标，从而可判断B的正误，或者利用三角函数定义和余弦定理也可判断；由中线向量结 MA b 合B的结果可得c2 13a2，计算后可判断C的正误，或者利用 2   3并结合离心 AA 2a 1 2 率变形公式即可判断；结合BC的结果求出面积后可判断D的正误. b 【详解】不妨设渐近线为y x，M 在第一象限，N在第三象限， a 5π π 对于A，由双曲线的对称性可得AMA N为平行四边形，故AMA π  ， 1 2 1 2 6 6 故A正确； 对于B，方法一：因为M 在以FF 为直径的圆上，故FM F M 且 MO c， 1 2 1 2  x2y2 c2   0 0 x a 设Mx ,y ，则 ，故 0 ，故MA AA ， 0 0 y 0  b y 0 b 2 1 2  x a 0 π 3 2 3 由A得AMA  ，故 MA  MA  即 MA  MA ，故B错误； 1 2 6 2 1 2 1 3 2 b 方法二：因为tanMOA  ，因为双曲线中，c2 a2b2， 2 a a 则cosMOA  ，又因为以FF 为直径的圆与C的一条渐近线交于M 、N，则OM c， 2 c 1 2 答案第4页，共13页a 则若过点M 往x轴作垂线，垂足为H，则 OH c a OA ，则点H与A H重合，则 c 2 2 MA x 轴，则 MA  c2a2 b ， 2 2 方法三：在OMA 利用余弦定理知， MA 2  OM 2OA 2 2OM OA cosMOA ， 2 2 2 2 2 a 即 MA 2 c2a22ac b2 ，则 MA b， 2 c 2  则AA M 为直角三角形，且AMA  ，则2 MA  3 MA ，故B错误； 1 2 1 2 6 2 1 对于C，方法一：因为M  O   1 M  A  M  A   ，故4M  O  2 M  A  2 2M  A  M  A  M  A  2， 2 1 2 1 1 2 2 2 3 由B可知 MA b,MA  b ， 2 1 3 故4c2 b2 4 b22b 2 3 b 3  13 b2  13 c2a2即c2 13a2， 3 3 2 3 3 故离心率e 13，故C正确； 方法二：因为 MA 2  b  3，则 b 2 3，则e c  1 b2  1(2 3)2  13，故C正 AA 2a a a a2 1 2 确； 对于D，当a 2时，由C可知e 13，故c 26， 1 故b2 6 ，故四边形NAMA 为2S 2 2 62 2 8 3， 1 2 △MA1A2 2 故D正确， 答案第5页，共13页故选：ACD. 12． 2   【分析】根据向量坐标化运算得ab (1,12x)，再利用向量垂直的坐标表示得到方程，解 出即可.             【详解】ab (1,12x)，因为a ab ，则a ab  0， 则x12x0，解得x1.   则a (1,1)，则|a| 2 . 故答案为： 2. 13．4 【分析】由题意得 f20即可求解a，再代入即可求解. 【详解】由题意有 f xx1x2xa， 所以 fxxax1x1x2xax2， 因为2是函数 f x极值点，所以 f22a0，得a2， 当a2时， fx2x2x1x22 x23x4，  4 4  当x, ,f x0,f x单调递增，当x ,2,f x0,f x单调递减，  3 3  当x2,, fx0, f x单调递增， 所以x2是函数 f xx1x2xa的极小值点，符合题意； 所以 f 012a2a4. 故答案为：4. 14．2.5 【分析】根据圆柱与球的性质以及球的体积公式可求出球的半径； 【详解】 答案第6页，共13页圆柱的底面半径为4cm，设铁球的半径为r，且r4， 由圆柱与球的性质知AB2 (2r)2 (82r)2 (92r)2， 即4r268r1452r52r290，r4， r2.5. 故答案为：2.5. π 15．(1) 3 (2)答案见解析 1 【分析】（1）直接由题意得cos ,0π，结合余弦函数的单调性即可得解； 2  π （2）由三角恒等变换得gx 3cos2x ，由此可得值域，进一步由整体代入法可得  6 函数gx的单调区间. 1 π 【详解】（1）由题意 f 0cos ,0π，所以 ； 2 3  π （2）由（1）可知 f xcos2x ，  3  π  π 所以gx f x f x cos2x cos2x  6  3 1 3 3 3  π  cos2x sin2xcos2x cos2x sin2x 3cos 2x  ， 2 2 2 2  6  所以函数gx的值域为 3, 3，   π π 5π 令2kπ2x π2kπ,kZ，解得 kπ x kπ,kZ， 6 12 12 π 5π 11π 令π2kπ2x 2π2kπ,kZ，解得 kπ x kπ,kZ， 6 12 12  π 5π  所以函数gx的单调递减区间为  kπ, kπ ,kZ，    12 12  5π 11π  函数gx的单调递增区间为  kπ, kπ  ,kZ. 12 12  答案第7页，共13页x2 y2 16．(1)  1 4 2 (2) 5 【分析】（1）根据长轴长和离心率求出基本量后可得椭圆方程； （2）设出直线方程并联立椭圆方程后结合韦达定理用参数t表示面积后可求t的值，从而可 求弦长. 2 【详解】（1）因为长轴长为4，故a2，而离心率为 ，故c 2， 2 x2 y2 故b 2，故椭圆方程为：  1. 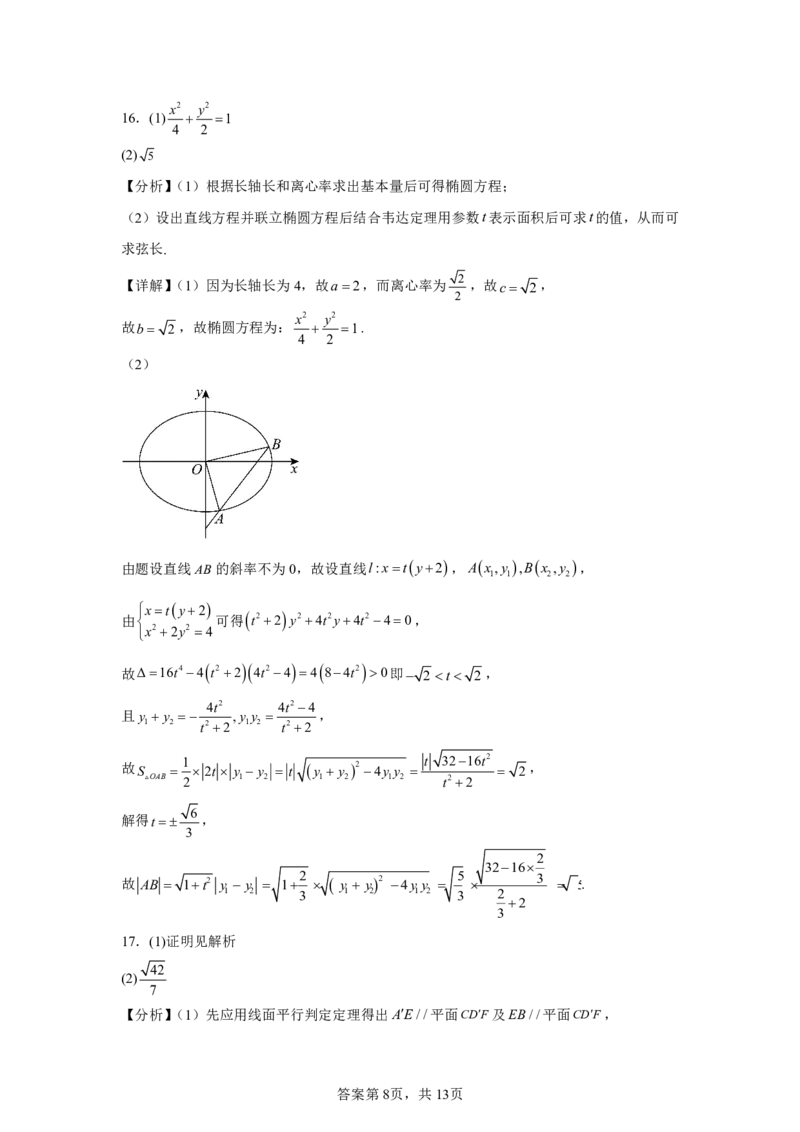4 2 （2） 由题设直线AB的斜率不为0，故设直线l:xty2，Ax,y ,Bx ,y ， 1 1 2 2 xty2 由 可得  t22  y24t2y4t240， x22y2 4 故Δ16t44  t22  4t24  4  84t2 0即 2t 2， 4t2 4t24 且y  y  ,y y  ， 1 2 t22 1 2 t22 故 S  1  2t  y y  t y  y 24y y  t 3216t2  2 ， OAB 2 1 2 1 2 1 2 t22 6 解得t  ， 3 2 3216 故 AB  1t2 y  y  1 2   y  y2 4y y  5  3  5. 1 2 3 1 2 1 2 3 2 2 3 17．(1)证明见解析 42 (2) 7 【分析】（1）先应用线面平行判定定理得出AE//平面CDF及EB//平面CDF， 答案第8页，共13页再应用面面平行判定定理得出平面AEB//平面CDF，进而得出线面平行； （2）建立空间直角坐标系，利用已知条件将点B,C,D,E,F的坐标表示出来，然后将平面 BCD及平面EFDA的法向量求出来，利用两个法向量的数量积公式可将两平面的夹角余弦 值求出来，进而可求得其正弦值. 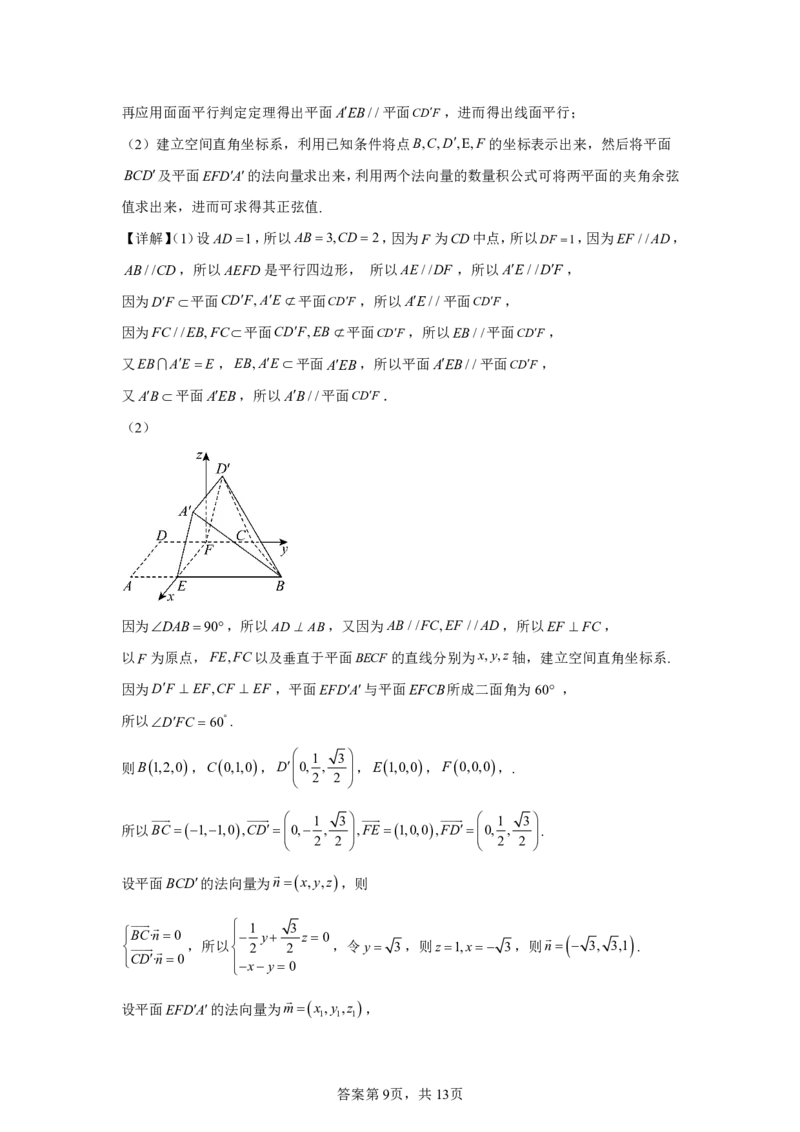【详解】（1）设AD1，所以AB3,CD2，因为F 为CD中点，所以DF 1，因为EF //AD， AB//CD，所以AEFD是平行四边形， 所以AE//DF ，所以AE//DF， 因为DF 平面CDF,AE 平面CDF，所以AE//平面CDF， 因为FC//EB,FC平面CDF,EB平面CDF，所以EB//平面CDF， 又EBAE E ，EB,AE平面AEB，所以平面AEB//平面CDF， 又AB平面AEB，所以AB//平面CDF． （2） 因为DAB90，所以ADAB，又因为AB//FC,EF //AD，所以EF FC， 以F 为原点，FE,FC以及垂直于平面BECF的直线分别为x,y,z轴，建立空间直角坐标系. 因为DF  EF,CF  EF ，平面EFDA与平面EFCB所成二面角为60° ， 所以DFC 60.  1 3 则B1,2,0，C0,1,0，D0, , ，E1,0,0，F0,0,0，.    2 2     1 3    1 3 所以BC 1,1,0,CD0, , ,FE 1,0,0,FD0, , .      2 2   2 2   设平面BCD的法向量为nx,y,z，则    B  C  ·n  0   1 y 3 z 0      ，所以 2 2 ，令y 3，则z1,x 3，则n  3, 3,1 . CD·n0  xy0  设平面EFDA的法向量为mx,y,z ， 1 1 1 答案第9页，共13页   F  E  ·m  0   1 y 3 z0 则  ，所以2 2 ， FD·m0  x0    令y 3，则z1,x0，所以m 0, 3,1 .     m·n 031 1 所以cosm,n      . m n 331 13 7 2  1  42 所以平面BCD与平面EFDA夹角的正弦值为 1    .  7 7 18．(1)证明见解析； (2)（i）证明见解析；（ii）2x  x ，证明见解析. 1 2  1  1 【分析】（1）先由题意求得 fxx2  3k，接着构造函数gx 3k,x0，利 1x  1x 用导数工具研究函数gx的单调性和函数值情况，从而得到函数的单调性，进而得证函数 f x在区间(0,)上存在唯一极值点；再结合 f 00和x时 f x的正负情况即可 得证 f x在区间(0,)上存在唯一零点； 1 （2）（i）由（1）x 1 和gt fx t fx t结合（1）中所得导函数 fx 计 1 3k 1 1 1  x t2 x t 2  算得到gtt 1  1  ，再结合t0,x 得  x t1x 1 x t1x 1  1 1 1 1 1 gt0即可得证； （ii）由函数gt在区间0,x 上单调递减得到0 f 2x ，再结合 f x 0， 1 1 2 和函数 f x的单调性以以及函数值的情况即可得证. 1 x2  1  【详解】（1）由题得 fx 1x3kx2  3kx2 x2  3k， 1x 1x 1x  1 因为x0,，所以x2 0，设gx 3k,x0， 1x 1 则gx  0在(0,)上恒成立，所以gx在(0,)上单调递减， 1x2 1 g013k 0，令gx 0 x  1， 1 1 3k 所以当x0,x 时，gx0，则 fx0；当xx ,时，gx0，则 fx0， 0 0 答案第10页，共13页所以 f x在0,x 上单调递增，在x ,上单调递减， 0 0 所以 f x在(0,)上存在唯一极值点， 1 x 对函数yln1xx有y 1 0在(0,)上恒成立， 1x 1x 所以yln1xx在(0,)上单调递减， 所以yln1xx y| 0 在(0,)上恒成立， x0 1 1 又因为 f 00，x时 x2kx3  x212kx0， 2 2 所以x时 f x0， 所以存在唯一x 0,使得 f x 0，即 f x在(0,)上存在唯一零点. 2 2 1 1  1  （2）（i）由（1）知x  1，则x 1 ， fxx2  3k， 1 3k 1 3k 1x   1   1  则gt fx t fx t x t 2  3k  x t 2  3k 1 1 1 x t1  1 x t1  1 1  1 1   1 1  x t2     x t 2    1 x t1 x 1 1 x t1 x 1 1 1 1 1 tx t2 t x t 2  x t2 x t 2   1  1 t 1  1  x t1x 1 x t1x 1  x t1x 1 x t1x 1  1 1 1 1 1 1 1 1  x t2 x t 2  t 1  1  ，  x t1x 1 x t1x 1  1 1 1 1 x t2 x t 2 因为t0,x ，所以x t10，所以 1  1  0， 1 1 x t1x 1 x t1x 1 1 1 1 1 所以gt0， 所以函数gt在区间0,x 上单调递减； 1 （ii）2x  x ，证明如下： 1 2 由（i）知：函数gt在区间0,x 上单调递减， 1 所以g0gx 即0 f 2x ，又 f x 0， 1 1 2 由（1）可知 f x在x ,上单调递减，x x ,，且对任意x0,x  f x0， 0 2 0 2 所以2x  x . 1 2 答案第11页，共13页19．(1)p  p3， p  p343p 3 4 2 (2)p 3 (3)证明过程见解析 【分析】（1）直接由二项分布概率计算公式即可求解； p p （2）由题意q q3,q q343q，联立 4 3 4， pq1即可求解； 3 4 q q 4 3 （3）首先 p  p Cm1pm1qm，p p Cm pm2qm，同理有q q Cm1qm1pm， 2m 2m1 2m 2m2 2m1 2m1 2m 2m1 2m q q Cm qm2pm，作差有 p q  p q ，另一方面 2m2 2m1 2m1 2m1 2m1 2m 2m 2m1!  m  p  p  pmqmpp ，且同理有 2m2 2m m!m1!  2m1 2m1!  m  q q  pmqmq q ，作差能得到 p q  p q ，由此即可 2m2 2m m!m1!  2m1 2m 2m 2m2 2m2 得证. 【详解】（1）p 为打完3个球后甲比乙至少多得两分的概率，故只能甲胜三场， 3 故所求为 p C31 p0 p3  p3， 3 3 p 为打完4个球后甲比乙至少多得两分的概率，故甲胜三场或四场， 4 故所求为 p C31 p1 p3C41 p0 p4 4p31 p p4  p343p； 4 4 4 （2）由（1）得 p  p3， p  p343p，同理q q3,q q343q， 3 4 3 4 p p 若 4 3 4， pq1， q q 4 3 p  p p343p p3 3p31 p p3q  p 2 则 4 3      4， q q q343qq3 3q31q q3p q 4 3 2 由于0 p,q1，所以p2q21 p0，解得p ； 3 （3）我们有 m1 m1 m1 m1 m1 p p  Ck p2mkqkCk p2m1kqk Ck p2mkqkCk p2m1kqkCk1p2m1kqk 2m 2m1 2m 2m1 2m 2m 2m k0 k0 k0 k0 k0 m1 m1 m1 m1 1 pCk p2mkqkCk1p2m1kqk Ck p2mkqk1Ck1p2m1kqk 2m 2m 2m 2m k0 k0 k0 k0 答案第12页，共13页m1 m2 Ck p2mkqk1 Ck p2mkqk1 Cm1pm1qm. 2m 2m 2m k0 k0 以及 m m1 m m m1 p  p Ck p2m2kqk Ck p2m1kqk Ck1 p2m2kqk Ck p2m2kqk Ck p2m1kqk 2m2 2m1 2m2 2m1 2m1 2m1 2m1 k0 k0 k0 k0 k0 m m 1 Ck1 p2m2kqkCm pm2qm p1Ck p2m1kqk 2m1 2m1 2m1 k0 k0 m m1 Ck1 p2m2kqk Cm pm2qmCk p2m1kqk1 2m1 2m1 2m1 k0 k0 m1 m1 Ck p2m1kqk1Cm pm2qmCk p2m1kqk1Cm pm2qm. 2m1 2m1 2m1 2m1 k0 k0 至此我们得到 p  p Cm1pm1qm， p p Cm pm2qm，同理有 2m 2m1 2m 2m2 2m1 2m1 q q Cm1qm1pm，q q Cm qm2pm. 2m 2m1 2m 2m2 2m1 2m1 故 p  p Cm1pm1qm  p  Cm1pmqm q  Cm1pmqm Cm1qm1pm q q ，即 2m 2m1 2m 2m 2m 2m 2m 2m1 p q  p q . 2m1 2m1 2m 2m 另一方面，由于 p  p p  p p  p Cm pm2qmCm1pm1qm  pmqmp  pCm Cm1 2m2 2m 2m2 2m1 2m 2m1 2m1 2m 2m1 2m  2m1! 2m!  2m1!  m   pmqmp   p m!m1!  m1!m1!     m!m1! pmqmp  p 2m1   2m1!  m  且同理有q q  pmqmq q . 2m2 2m m!m1!  2m1 故结合  m   m  m m m1 pp qq  pq pq   pq  pq   pq   pq 0  2m1  2m1 2m1 2m1 2m1 ， 就能得到 p  p q q ，即 p q  p q ，证毕. 2m2 2m 2m2 2m 2m 2m 2m2 2m2 答案第13页，共13页