文档内容
[机密]2024年6月13日11:00前
重庆市 2024 年初中学业水平暨高中招生考试
数学试题(B 卷)
(全卷共三个大题,满分150分,考试时间120分钟)
注意事项:
1.试题的答案书写在答题卡上,不得在试题卷上直接作答;
2.作答前认真阅读答题卡上的注意事项;
3.作图(包括作辅助线)请一律用黑色2B铅笔完成;
4.考试结束,由监考人员将试题卷和答题卡一并收回.
参考公式:抛物线 的顶点坐标为 ,对称轴为 .
一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代
号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所
对应的方框涂黑.
1. 下列各数中最小的数是( )
A. B. 0 C. 1 D. 2
2. 下列标点符号中,是轴对称图形的是( )
A. B. C. D.
3. 反比例函数 的图象一定经过的点是( )
A. B. C. D.
4. 如图, ,若 ,则 的度数为( )
.
A B. C. D.
5. 若两个相似三角形的相似比为 ,则这两个三角形面积的比是( )
1A. B. C. D.
6. 估计 的值应在( )
A. 8和9之间 B. 9和10之间 C. 10和11之间 D. 11和12之间
7. 用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图
案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑧个图案中,菱形的个数是( )
A. 20 B. 21 C. 23 D. 26
8. 如图, 是 的弦, 交 于点 ,点 是 上一点,连接 , .若
,则 的度数为( )
A. B. C. D.
的
9. 如图,在边长为4 正方形 中,点 是 上一点,点 是 延长线上一点,连接 ,
, 平分 .交 于点 .若 ,则 的长度为( )
2A. 2 B. C. D.
为
10. 已知整式 ,其中 自然数, 为正整数,且
.下列说法:
①满足条件的整式 中有5个单项式;
②不存在任何一个 ,使得满足条件的整式 有且只有3个;
③满足条件的整式 共有16个.
其中正确 的个数是( )
A. 0 B. 1 C. 2 D. 3
二、填空题:(本大题8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡
中对应的横线上.
11. 计算: ______.
12. 甲、乙两人分别从A、B、C三个景区中随机选取一个景区前往游览,则他们恰好选择同一景区的概率
为________.
13. 若正多边形的一个外角是45°,则该正多边形的边数是_________.
14. 重庆在低空经济领域实现了新的突破.今年第一季度低空飞行航线安全运行了200架次,预计第三季
度低空飞行航线安全运行将达到401架次.设第二、第三两个季度安全运行架次的平均增长率为 ,根据
题意,可列方程为________.
15. 如图,在 中, , , 平分 交 于点 .若 ,则
的长度为________.
16. 若关于 的一元一次不等式组 的解集为 ,且关于 的分式方程
3的解均为负整数,则所有满足条件的整数 的值之和是________.
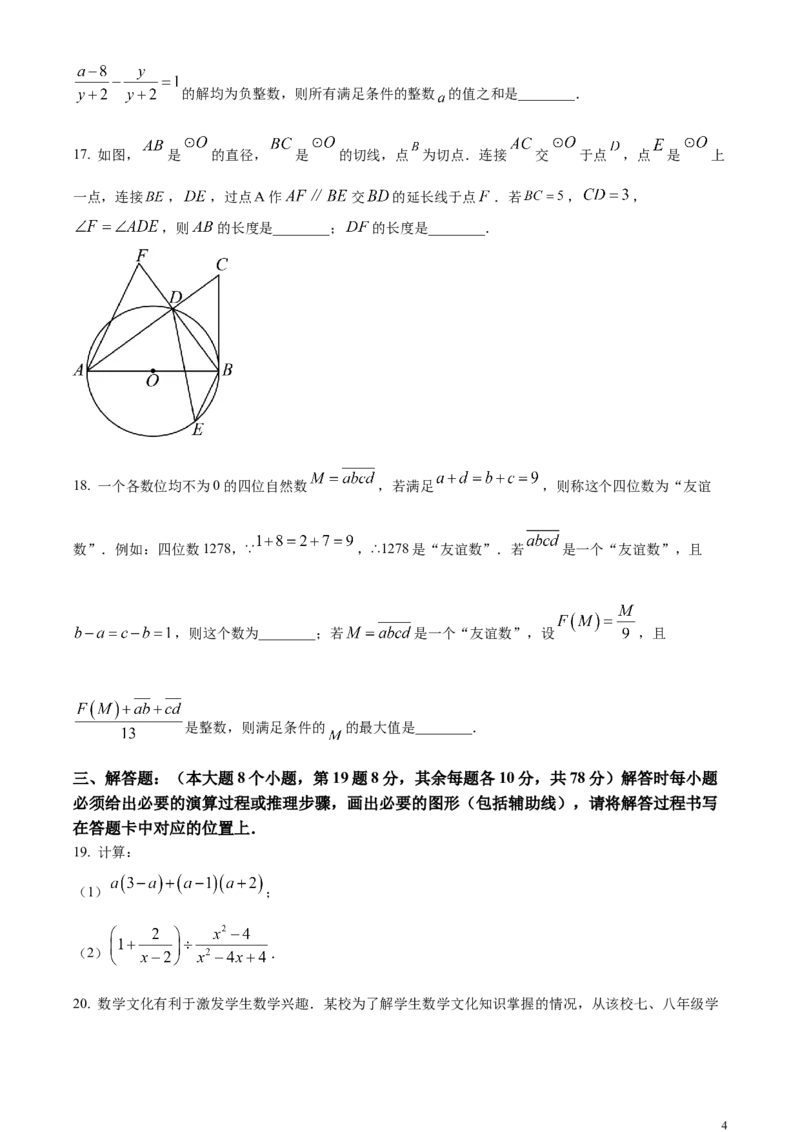
17. 如图, 是 的直径, 是 的切线,点 为切点.连接 交 于点 ,点 是 上
一点,连接 , ,过点 作 交 的延长线于点 .若 , ,
,则 的长度是________; 的长度是________.
18. 一个各数位均不为0的四位自然数 ,若满足 ,则称这个四位数为“友谊
数”.例如:四位数1278,∵ ,∴1278是“友谊数”.若 是一个“友谊数”,且
,则这个数为________;若 是一个“友谊数”,设 ,且
是整数,则满足条件的 的最大值是________.
三、解答题:(本大题8个小题,第19题8分,其余每题各10分,共78分)解答时每小题
必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写
在答题卡中对应的位置上.
19. 计算:
(1) ;
(2) .
20. 数学文化有利于激发学生数学兴趣.某校为了解学生数学文化知识掌握的情况,从该校七、八年级学
4生中各随机抽取10名学生参加了数学文化知识竞赛,并对数据(百分制)进行整理、描述和分析(成绩均
不低于70分,用 表示,共分三组:A. ,B. ,C. ),下面给出了
部分信息:
七年级10名学生的竞赛成绩是:76,78,80,82,87,87,87,93,93,97.
八年级10名学生的竞赛成绩在B组中的数据是:80,83,88,88.
七、八年级抽取的学生竞赛成绩统计表
平均 中位 众
年级
数 数 数
七年
86 87
级
八年
86 90
级
根据以上信息,解答下列问题:
(1)填空: ________, ________, ________;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生数学文化知识较好?请说明理由(写出一条
理由即可);
(3)该校七年级学生有500人,八年级学生有400人.估计该校七、八年级学生中数学文化知识为“优
秀” 的总共有多少人?
21. 在学习了矩形与菱形的相关知识后,小明同学进行了更深入的研究,他发现,过矩形的一条对角线的
中点作这条对角线的垂线,与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形,可利用
证明三角形全等得到此结论.根据他的想法与思路,完成以下作图与填空:
5的
(1)如图,在矩形 中,点 是对角线 中点.用尺规过点 作 的垂线,分别交 ,
于点 , ,连接 , .(不写作法,保留作图痕迹)
(2)已知:矩形 ,点 , 分别在 , 上, 经过对角线 的中点 ,且 .
求证:四边形 是菱形.
证明:∵四边形 是矩形,
∴ .
∴①, .
∵点 是 的中点,
∴②.
∴ (AAS).
∴③.
又∵ ,
∴四边形 是平行四边形.
∵ ,
∴四边形 是菱形.
进一步思考,如果四边形 是平行四边形呢?请你模仿题中表述,写出你猜想的结论:④.
22. 某工程队承接了老旧小区改造工程中1000平方米的外墙粉刷任务,选派甲、乙两人分别用 、 两种
外墙漆各完成总粉刷任务的一半.据测算需要 、 两种外墙漆各300千克,购买外墙漆总费用为15000
元,已知 种外墙漆每千克的价格比 种外墙漆每千克的价格多2元.
(1)求 、 两种外墙漆每千克的价格各是多少元?
(2)已知乙每小时粉刷外墙面积是甲每小时粉刷外墙面积的 ,乙完成粉刷任务所需时间比甲完成粉刷
任务所需时间多5小时.问甲每小时粉刷外墙的面积是多少平方米?
23. 如图,在 中, , ,点 为 上一点,过点 作 交 于点 .设
6的长度为 ,点 , 的距离为 , 的周长与 的周长之比为 .
(1)请直接写出 , 分别关于 的函数表达式,并注明自变量 的取值范围;
(2)在给定的平面直角坐标系中画出函数 , 的图象;请分别写出函数 , 的一条性质;
(3)结合函数图象,直接写出 时 的取值范围.(近似值保留一位小数,误差不超过 )
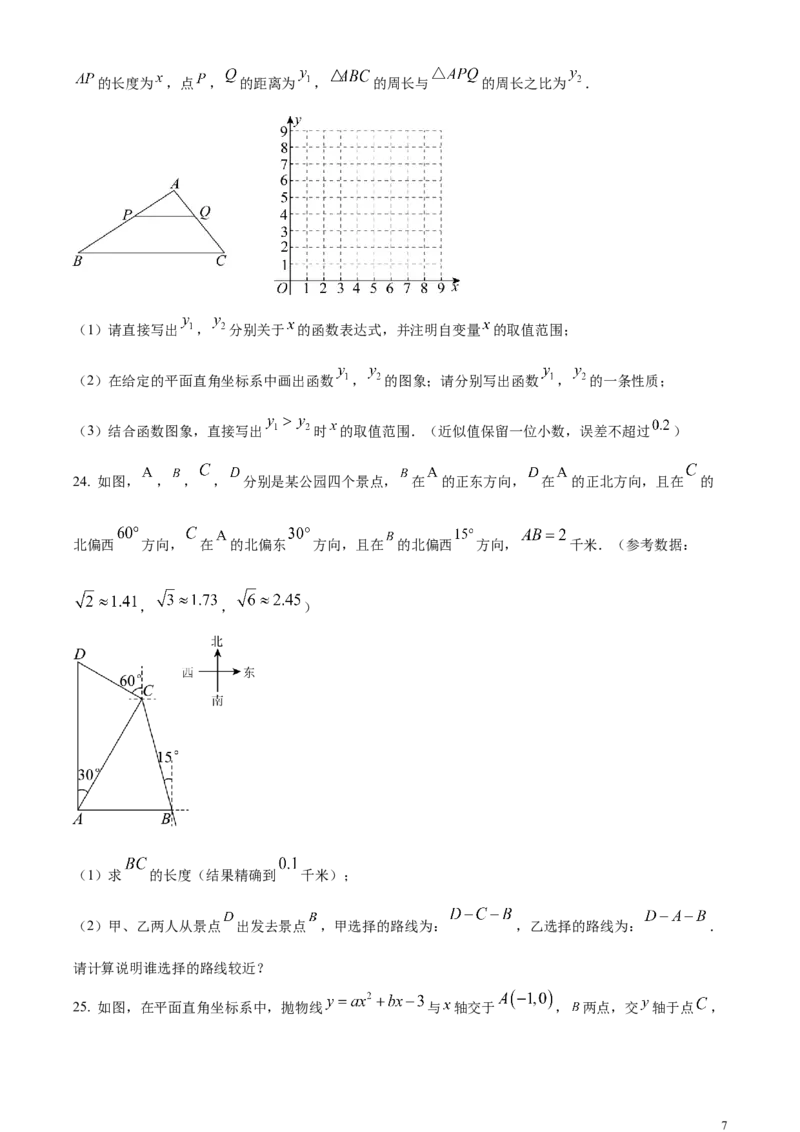
24. 如图, , , , 分别是某公园四个景点, 在 的正东方向, 在 的正北方向,且在 的
北偏西 方向, 在 的北偏东 方向,且在 的北偏西 方向, 千米.(参考数据:
, , )
(1)求 的长度(结果精确到 千米);
(2)甲、乙两人从景点 出发去景点 ,甲选择的路线为: ,乙选择的路线为: .
请计算说明谁选择的路线较近?
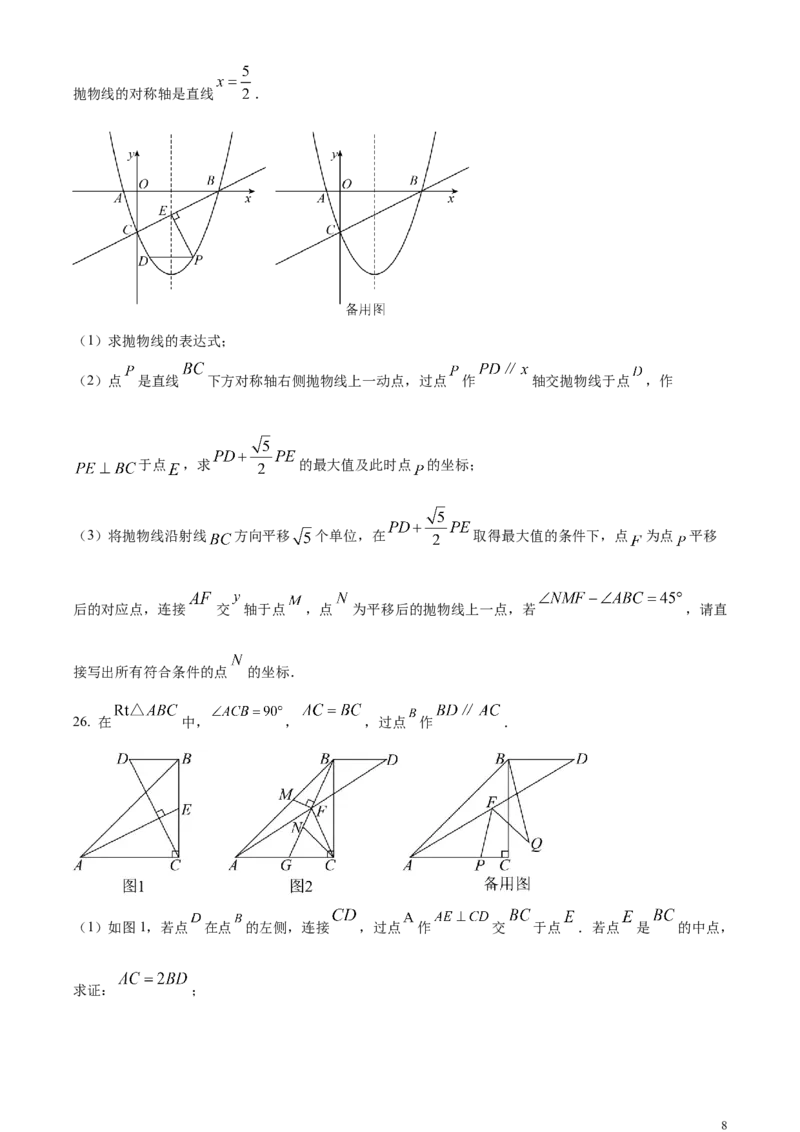
25. 如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点,交 轴于点 ,
7抛物线的对称轴是直线 .
(1)求抛物线的表达式;
(2)点 是直线 下方对称轴右侧抛物线上一动点,过点 作 轴交抛物线于点 ,作
于点 ,求 的最大值及此时点 的坐标;
(3)将抛物线沿射线 方向平移 个单位,在 取得最大值的条件下,点 为点 平移
后的对应点,连接 交 轴于点 ,点 为平移后的抛物线上一点,若 ,请直
接写出所有符合条件的点 的坐标.
26. 在 中, , ,过点 作 .
(1)如图1,若点 在点 的左侧,连接 ,过点 作 交 于点 .若点 是 的中点,
求证: ;
8(2)如图2,若点 在点 的右侧,连接 ,点 是 的中点,连接 并延长交 于点 ,连
接 .过点 作 交 于点 , 平分 交 于点 ,求证:
;
(3)若点 在点 的右侧,连接 ,点 是 的中点,且 .点 是直线 上一动点,
连接 ,将 绕点 逆时针旋转 得到 ,连接 ,点 是直线 上一动点,连接 , .
在点 的运动过程中,当 取得最小值时,在平面内将 沿直线 翻折得到 ,连接 .
在点 的运动过程中,直接写出 的最大值.
9