文档内容
长郡中学 2024 级高一综合能力检测试卷
数学
时量:90分钟 满分 100分
一、选择题:本题共 8小题,每小题 4分,共 32分.在每小题给出的四个选项中,只有一个
选项是符题目要求的.
1.
《孙子算经》中记载:“凡大数之法,万万曰亿,万万亿日兆.”说明了大数之间的关系:1亿=1万1
万,1兆=1万×1万×1亿.若1兆 =10m ,则m的值为( )
A. 4 B. 8 C. 12 D. 16
【答案】D
【解析】
【分析】由指数幂的运算性质即可求解.
【详解】1万=104,所以1亿=108,
所以1兆=108×108 =1016,
所以m=16.
故选:D
2. 二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,
二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨),夏季(立夏、小满、芒种、夏
至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小
寒大寒),若从二十四个节气中随机抽取一个节气,则抽到的节气在夏季的概率为( )
1 1 1 1
A. B. C. D.
2 12 6 4
【答案】D
【解析】
【分析】根据概率的计算公式即可求解.
6 1
【详解】从二十四个节气中随机抽取一个节气,则抽到的节气在夏季的概率为 = ,
24 4
故选:D
3. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作
弧交数轴的正半轴于M,则点M所表示的数为( )
第1页/共28页
学科网(北京)股份有限公司A. 2 B. 10−1 C. 5 D. 5−1
【答案】B
【解析】
【分析】利用勾股定理和数轴的知识求得正确答案.
【详解】由于AC = 32 +12 = 10 ,
( )
所以点M所表示的数为2+ 10−3 = 10−1.
故选:B
x+5
≥ x−3
4. 若关于x的不等式组 2 恰好只有四个整数解,则a的取值范围是( )
2x+2<3 ( x+a )
5 5 4
A. a<− B. − ≤a<−
3 3 3
5 5
C. −22−3a,
由已知可得7≤2−3a<8,
5
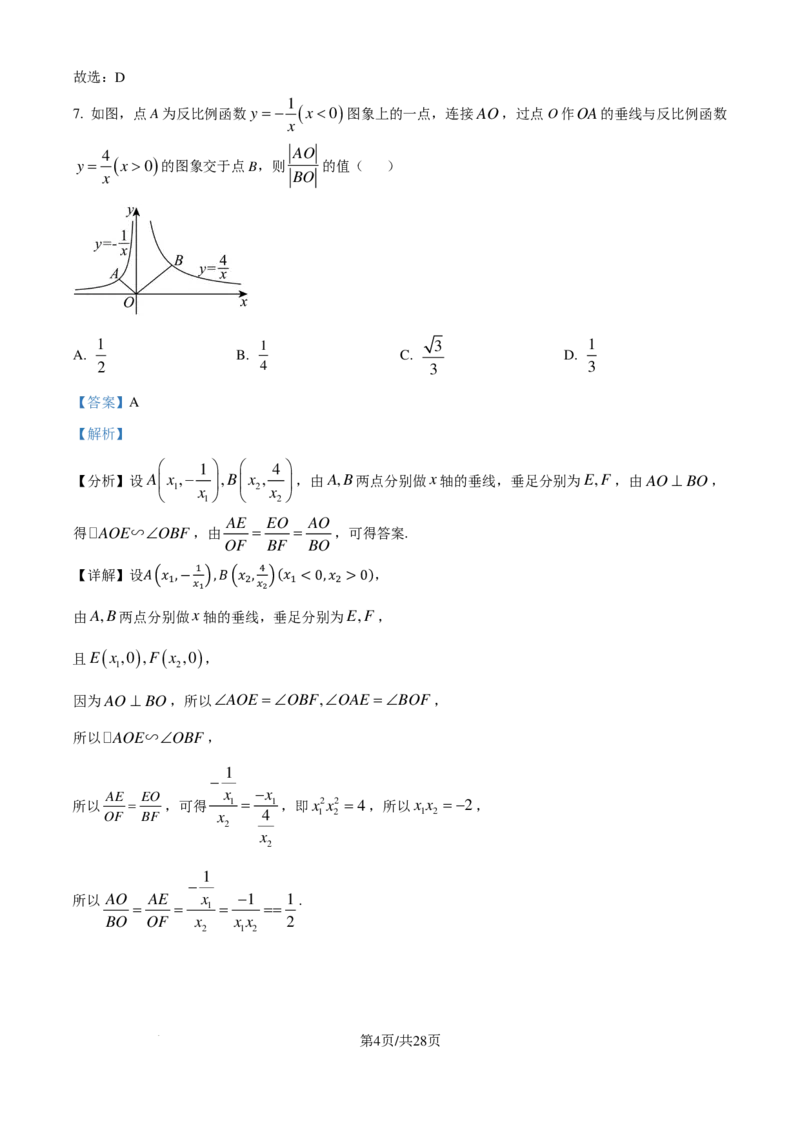
所以−2 AB ,且 PB < AB ,
所以 PB > AB − PA =5−2=3,且 PB <5,
则3−2< PB <3+2,
由圆B的半径为2,圆P的半径为3,
所以圆P与圆B相交.
故选:B.
k+1 k 3+1 3
6. 对于正整数k定义一种运算: f(k)=[ ]−[ ],例: f(3)=[ ]−[ ],[x]表示不超过x的最大
4 4 4 4
整数,例:[3.9]=3,[−1.8]=−2.则下列结论错误的是( )
A. f
(
1
)=0
B. f
(
k
)=0或1
C. f ( k+4 )= f ( k ) D. f ( k+1 )≥ f ( k )
【答案】D
【解析】
【分析】根据给定的定义,逐项计算判断即可.
1 1
【详解】对于A, f(1)=[ ]−[ ]=0−0=0,A正确;
2 4
对于B,取k =4n+i,i =1,2,3,4,n为自然数,
1 1
当i =4时, f(k)=[n+1+ ]−[n+1]=[ ]=0,
4 4
3 3
当i =3时, f(k)=[n+1]−[n+ ]=n+1−(n+[ ])=1,
4 4
i+1 i i+1 i
当i =1,2时, f(k)=[n+ ]−[n+ ]=n+[ ]−(n+[ ])=0,B正确;
4 4 4 4
k+1 k k+1 k
对于C, f(k+4)=[1+ ]−[1+ ]=1+[ ]−(1+[ ])= f(k),C正确;
4 4 4 4
4+1 4 3+1 3
对于D, f(3+1)=[ ]−[ ]=0, f(3)=[ ]−[ ]=1,即 f(3+1)< f(3),D错误.
4 4 4 4
第3页/共28页
学科网(北京)股份有限公司故选:D
1
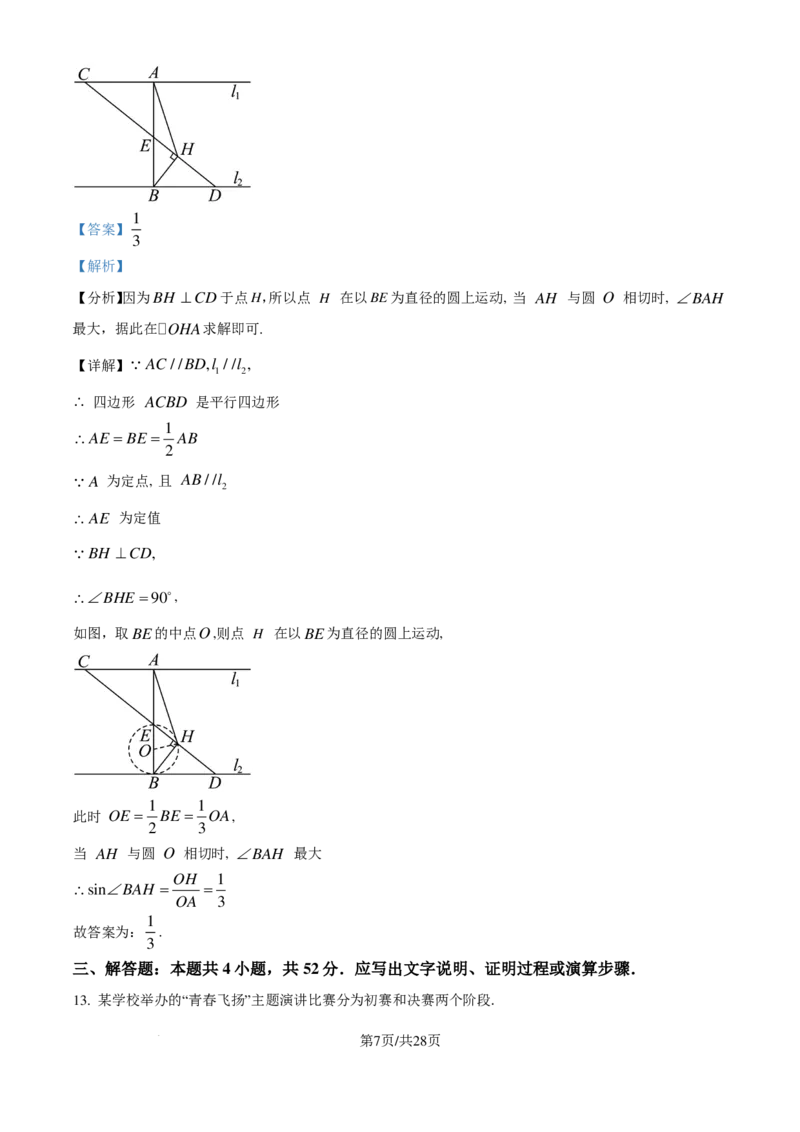
7. 如图,点A为反比例函数y =− ( x<0 )图象上的一点,连接AO,过点O作OA的垂线与反比例函数
x
4 AO
y = ( x>0 )的图象交于点B,则 的值( )
x BO
1 1 3 1
A. B. C. D.
2 4 3 3
【答案】A
【解析】
1 4
【分析】设Ax ,− ,Bx , ,由A,B两点分别做x轴的垂线,垂足分别为E,F,由AO⊥ BO,
1 x 2 x
1 2
AE EO AO
得AOE∽∠OBF,由 = = ,可得答案.
OF BF BO
【详解】设 ,
1 4
𝐴𝐴�𝑥𝑥1,−𝑥𝑥1�,𝐵𝐵�𝑥𝑥2,𝑥𝑥2�(𝑥𝑥1 <0,𝑥𝑥2 >0)
由A,B两点分别做x轴的垂线,垂足分别为E,F,
( ) ( )
且E x ,0 ,F x ,0 ,
1 2
因为AO⊥ BO,所以∠AOE =∠OBF,∠OAE =∠BOF,
所以AOE∽∠OBF,
1
−
AE EO x −x
所以 = ,可得 1 = 1 ,即x2x2 =4,所以x x = −2,
OF BF x 4 1 2 1 2
2
x
2
1
−
所以 AO AE x −1 1.
= = 1 = ==
BO OF x x x 2
2 1 2
第4页/共28页
学科网(北京)股份有限公司故选:A.
8. 若二次函数的解析式为y =( x−2m )( x−2 )( 1≤m≤5 ) ,且函数图象过点 ( p,q ) 和点 ( p+4,q ) ,则q
的取值范围是( )
A. −12≤q≤4 B. −5≤q≤0 C. −5≤q≤4 D. −12≤q≤3
【答案】A
【解析】
p+ p+4
【分析】由二次函数解析式可求得对称轴为x=m+1,进而可得 =m+1,由函数图象过点 ( p,q ) ,
2
可得q=−(m−1)2 +4,可求q的取值范围.
【详解】因为二次函数的解析式为y =( x−2m )( x−2 )( 1≤m≤5 ) ,
所以二次函数的对称轴为x=m+1,
函数图象过点 ( p,q ) 和点 ( p+4,q ) ,故点 ( p,q ) 和点 ( p+4,q ) 关于直线x=m+1对称,
p+ p+4
所以 =m+1,所以 p=m−1∈[0,4],
2
又q=( p−2m )( p−2 )=( m−1−2m )( m−1−2 )=−m2 +2m+3=−(m−1)2 +4,
当m=1,q =4,当m=5,q =−12,所以−12≤q≤4.
max min
故选:A.
二、填空题:本题共 4小题,每小题 4分,共 16分.
9. 分解因式:a4 −4a3+4a2 −9=______.
【答案】(a2 −2a+3)(a+1)(a−3)
【解析】
【分析】根据给定条件,利用公式法及十字相乘法分解因式即可得解.
【详解】a4 −4a3+4a2 −9=(a2 −2a)2 −9=(a2 −2a+3)(a2 −2a−3)=(a2 −2a+3)(a+1)(a−3).
故答案为:(a2 −2a+3)(a+1)(a−3)
第5页/共28页
学科网(北京)股份有限公司10. 直线l :y=x−1与x轴交于点A,将直线l 绕点A逆时针旋转15°,得到直线l ,则直线l 对应的函数
1 1 2 2
表达式是______.
【答案】y = 3x− 3
【解析】
【分析】先求得l 的倾斜角,进而求得直线l 对应的函数表达式.
2 2
【详解】直线l :y=x−1与x轴交于点A1,0,
1
直线l :y=x−1的斜率为1,倾斜角为45°,
1
所以l 的倾斜角为60°,斜率为 3,
2
所以直线l 对应的函数表达式是y = 3 ( x−1 )= 3x− 3.
2
故答案为:y = 3x− 3
2x−a −2x+a
11. 若关于x的分式方程 −4= 的解为整数,则整数a=______.
x−1 x+1
【答案】±1
【解析】
2
【分析】由分式方程有意义可知x≠1且x≠−1,再化简方程求解x= ,由a,x均为整数可求.
a
2x−a −2x+a
【详解】则方程 −4= 可知,x≠1且x≠−1.
x−1 x+1
2x−a −2x+a 2−a 2+a
方程可化为 −2= +2,即 = ,
x−1 x+1 x−1 x+1
2
解得x= ,由x≠1且x≠−1,所以a ≠ 2且a≠−2.
a
由a为整数,且x为整数,
则当a=−1,x = −2,或当a =1,x=2时满足题意.
所以a=±1.
故答案为:±1.
12. 如图,已知两条平行线l ,l ,点A是l 上的定点,AB⊥l 于点B,点C,D分别是l ,l 上的动
1 2 1 2 1 2
点,且满足AC = BD,连接CD交线段AB于点E,BH ⊥CD于点H,则当∠BAH 最大时,sin∠BAH
的值为______.
第6页/共28页
学科网(北京)股份有限公司1
【答案】
3
【解析】
【分析】因为BH ⊥CD于点H,所以点 H 在以BE为直径的圆上运动, 当 AH 与圆 O 相切时, ∠BAH
最大,据此在OHA求解即可.
【详解】AC//BD,l //l ,
1 2
∴ 四边形 ACBD 是平行四边形
1
∴AE = BE = AB
2
A 为定点, 且 AB//l
2
∴AE 为定值
BH ⊥CD,
∴∠BHE =90,
如图,取BE的中点O,则点 H 在以BE为直径的圆上运动,
1 1
此时 OE = BE = OA,
2 3
当 AH 与圆 O 相切时, ∠BAH 最大
OH 1
∴sin∠BAH = =
OA 3
1
故答案为: .
3
三、解答题:本题共 4小题,共 52分.应写出文字说明、证明过程或演算步骤.
13. 某学校举办的“青春飞扬”主题演讲比赛分为初赛和决赛两个阶段.
第7页/共28页
学科网(北京)股份有限公司(1)初赛由10名教师评委和45名学生评委给每位选手打分(百分制),对评委给某位选手的打分进行整
理、描述和分析下面给出了部分信息.
a.教师评委打分:86 88 90 91 91 91 91 92 92 98
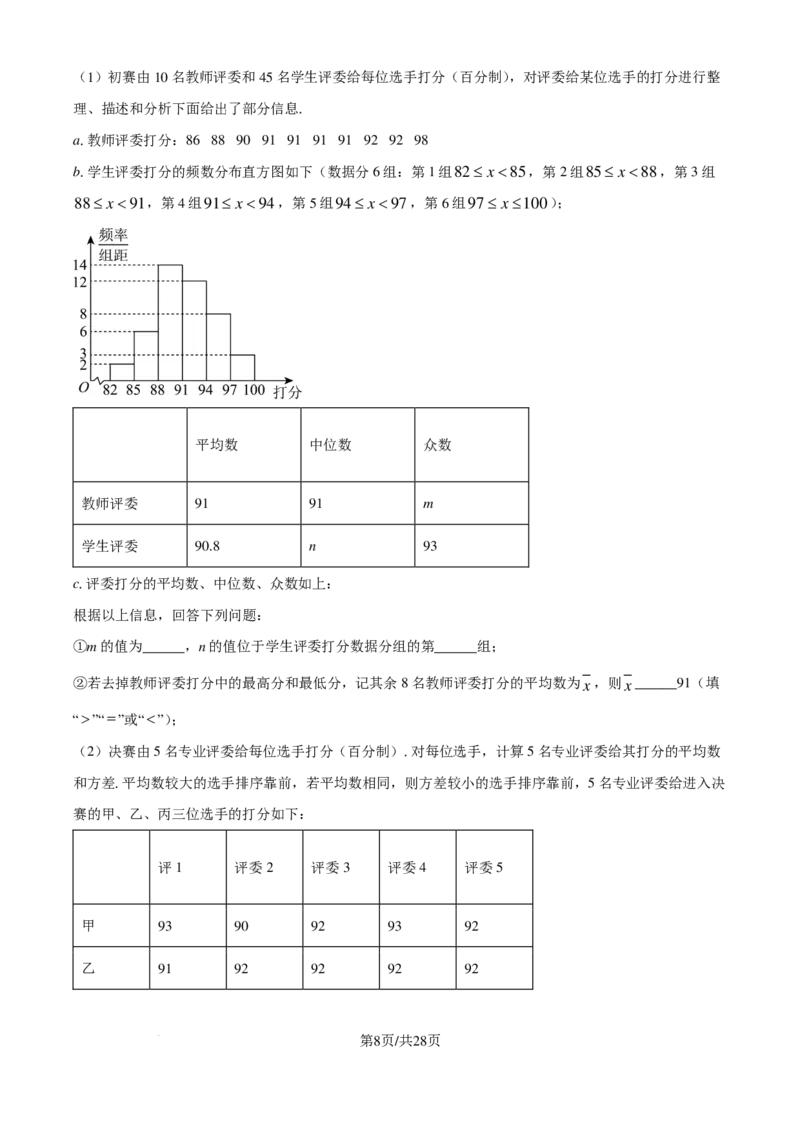
b.学生评委打分的频数分布直方图如下(数据分6组:第1组82≤ x<85,第2组85≤ x<88,第3组
88≤ x<91,第4组91≤ x<94,第5组94≤ x<97,第6组97≤ x≤100);
平均数 中位数 众数
教师评委 91 91 m
学生评委 90.8 n 93
c.评委打分的平均数、中位数、众数如上:
根据以上信息,回答下列问题:
①m的值为______,n的值位于学生评委打分数据分组的第______组;
②若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分的平均数为x,则x______91(填
“>”“=”或“<”);
(2)决赛由5名专业评委给每位选手打分(百分制).对每位选手,计算5名专业评委给其打分的平均数
和方差.平均数较大的选手排序靠前,若平均数相同,则方差较小的选手排序靠前,5名专业评委给进入决
赛的甲、乙、丙三位选手的打分如下:
评1 评委2 评委3 评委4 评委5
甲 93 90 92 93 92
乙 91 92 92 92 92
第8页/共28页
学科网(北京)股份有限公司丙 90 94 90 94 k
若丙在甲、乙、丙三位选手中的排序居中,则这三位选手中排序最靠前的是______,表中k(k为整数)的
值为______.
【答案】(1)①91;4;②<
(2)甲;92
【解析】
【分析】(1)①根据众数以及中位数的定义解答即可;
②根据算术平均数的定义求出8名教师评委打分的平均数,即可得出答案;
(2)根据方差的定义和平均数的意义求解即可.
【小问1详解】
①由题意得,教师评委打分中91出现的次数最多,故众数m =91;
45名学生评委打分数据的中位数是第23个数,故n的值位于学生评委打分数据分组的第4组;
②若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分的平均数为x ,
1
则x = ×(88+90+91+91+91+91+92+92)=90.75,
8
∴x <91.
【小问2详解】
1
甲选手的平均数为 ×(93+90+92+93+92)=92,
5
1
乙选手的平均数为 ×(91+92+92+92+92)=91.8,
5
因为丙在甲、乙、丙三位选手中的排序居中,
所以三位选手中排序最靠前的是甲,且丙的平均数大于或等于乙的平均数,
因为5名专业评委给乙选手的打分为91,92,92,92,92,
1
乙选手的方差S2 = ×[4×(92−91.8)2 +(91−91.8)2]=0.16,
乙
5
5名专业评委给丙选手的打分为90,94,90,94,k ,
所以乙选手的方差小于丙选手的方差,
所以丙选手的平均数大于乙选手的平均数,小于或等于甲选手的平均数,
∴93+90+92+93+92≥90+94+90+94+k >91+92+92+92+92,
∴92≥k >91,
k 为整数,
第9页/共28页
学科网(北京)股份有限公司∴k 的值为92.
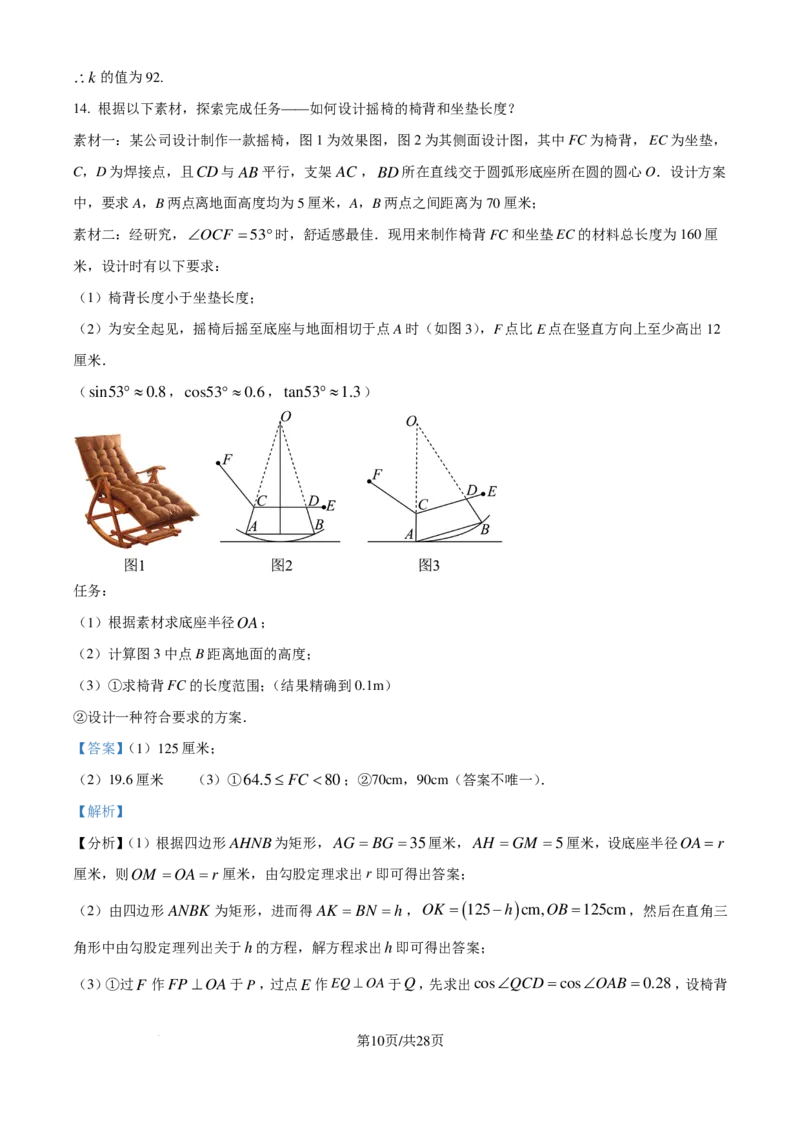
14. 根据以下素材,探索完成任务——如何设计摇椅的椅背和坐垫长度?
素材一:某公司设计制作一款摇椅,图1为效果图,图2为其侧面设计图,其中FC为椅背,EC为坐垫,
C,D为焊接点,且CD与AB平行,支架AC,BD所在直线交于圆弧形底座所在圆的圆心O.设计方案
中,要求A,B两点离地面高度均为5厘米,A,B两点之间距离为70厘米;
素材二:经研究,∠OCF =53°时,舒适感最佳.现用来制作椅背FC和坐垫EC的材料总长度为160厘
米,设计时有以下要求:
(1)椅背长度小于坐垫长度;
(2)为安全起见,摇椅后摇至底座与地面相切于点A时(如图3),F点比E点在竖直方向上至少高出12
厘米.
(sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
任务:
(1)根据素材求底座半径OA;
(2)计算图3中点B距离地面的高度;
(3)①求椅背FC的长度范围;(结果精确到0.1m)
②设计一种符合要求的方案.
【答案】(1)125厘米;
(2)19.6厘米 (3)①64.5≤ FC <80;②70cm,90cm(答案不唯一).
【解析】
【分析】(1)根据四边形AHNB为矩形,AG = BG =35厘米,AH =GM =5厘米,设底座半径OA=r
厘米,则OM =OA=r厘米,由勾股定理求出r 即可得出答案;
(2)由四边形ANBK 为矩形,进而得AK = BN =h,OK =( 125−h ) cm,OB=125cm,然后在直角三
角形中由勾股定理列出关于h的方程,解方程求出h即可得出答案;
(3)①过F 作FP⊥OA于P,过点E作EQ⊥OA于Q,先求出cos∠QCD=cos∠OAB=0.28,设椅背
第10页/共28页
学科网(北京)股份有限公司FC = x厘米,则坐垫EC =(160−x),即可得0.6x−0.28(160−x)≥12,由此解得x≥64.5,据此可得椅
背FC的长度范围;
②在①中椅背FC 的长度范围任取一个FC 的值,再计算出EC 的值即可,例如取FC =70厘米,则
EC =160−70=90(厘米);(答案不唯一,只要在FC的长度范围内即可).
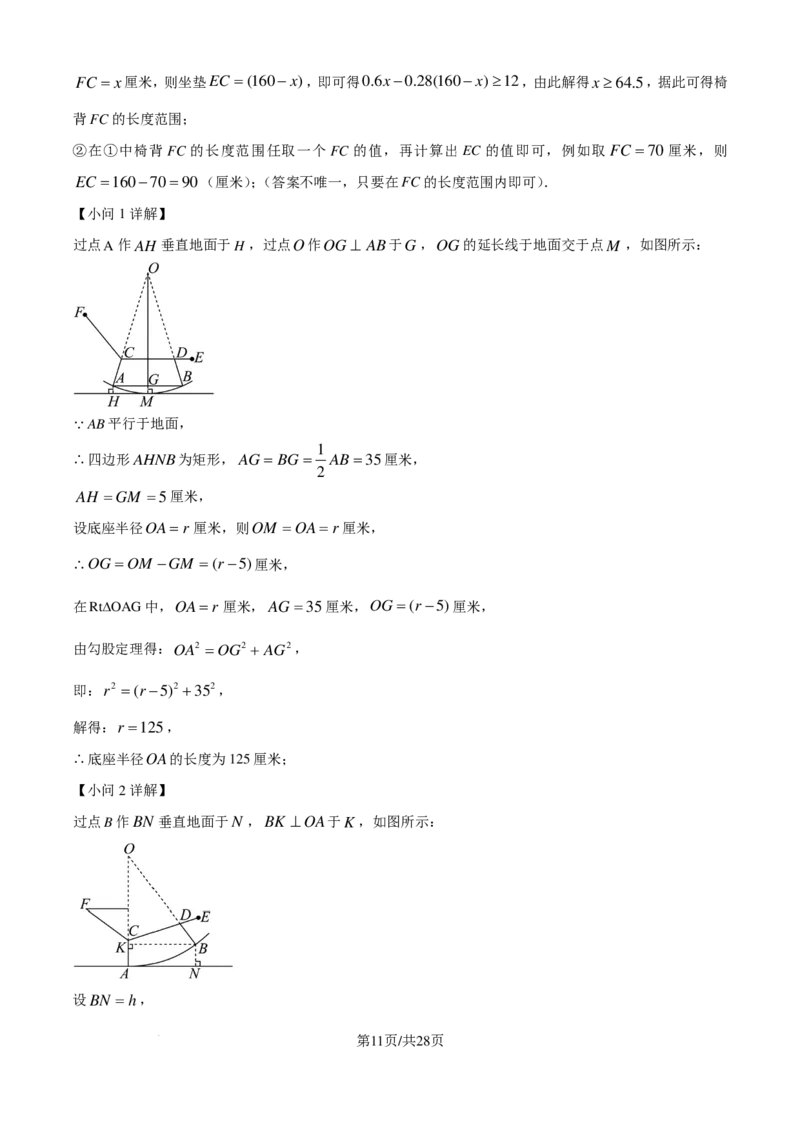
【小问1详解】
过点A作AH 垂直地面于H ,过点O作OG ⊥ AB于G,OG的延长线于地面交于点M ,如图所示:
AB平行于地面,
1
∴四边形AHNB为矩形,AG = BG = AB=35厘米,
2
AH =GM =5厘米,
设底座半径OA=r 厘米,则OM =OA=r厘米,
∴OG =OM −GM =(r−5)厘米,
在Rt∆OAG中,OA=r 厘米,AG =35厘米,OG =(r−5)厘米,
由勾股定理得:OA2 =OG2 + AG2,
即:r2 =(r−5)2 +352,
解得:r =125,
∴底座半径OA的长度为125厘米;
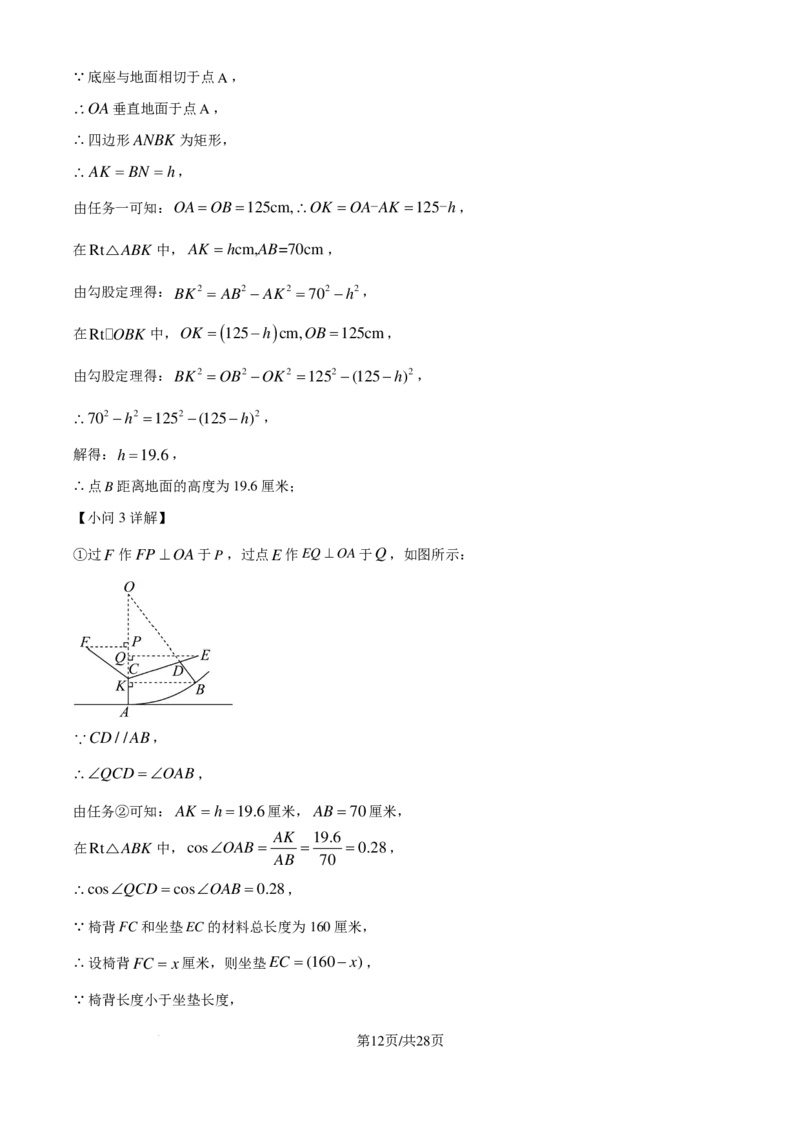
【小问2详解】
过点B作BN 垂直地面于N ,BK ⊥OA于K,如图所示:
设BN =h,
第11页/共28页
学科网(北京)股份有限公司底座与地面相切于点A,
∴OA垂直地面于点A,
∴四边形ANBK 为矩形,
∴AK = BN =h,
由任务一可知:OA=OB=125cm,∴OK =OA-AK =125-h,
在Rt△ABK 中,AK =hcm,AB=70cm,
由勾股定理得:BK2 = AB2 −AK2 =702 −h2,
在RtOBK 中,OK =( 125−h ) cm,OB=125cm,
由勾股定理得:BK2 =OB2 −OK2 =1252 −(125−h)2,
∴702 −h2 =1252 −(125−h)2,
解得:h=19.6,
∴点B距离地面的高度为19.6厘米;
【小问3详解】
①过F 作FP⊥OA于P,过点E作EQ⊥OA于Q,如图所示:
CD//AB,
∴∠QCD=∠OAB,
由任务②可知:AK =h=19.6厘米,AB =70厘米,
AK 19.6
在Rt△ABK 中,cos∠OAB= = =0.28,
AB 70
∴cos∠QCD=cos∠OAB=0.28,
椅背FC和坐垫EC的材料总长度为160厘米,
∴设椅背FC = x厘米,则坐垫EC =(160−x),
椅背长度小于坐垫长度,
第12页/共28页
学科网(北京)股份有限公司∴x<160−x,
解得:x<80,
CQ
在Rt△CQE中,cos∠QCD= =0.28,
CE
∴CQ=0.28CE =0.28(160−x)厘米,
CP
在Rt△CFP中,cos∠OCF = ,
CF
∴CP=CF⋅cos∠OCF = x⋅cos53°≈0.6x(厘米),
F点比E点在竖直方向上至少高出12厘米,
∴AP−AN ≥12,
即:AC+CP−(AC+CQ)≥12,
∴CP−CQ≥12,
∴0.6x−0.28(160−x)≥12,
解得:x≥64.5,
又x<80,
∴64.5≤ x≤80,
即:64.5≤ FC ≤80,
∴椅背FC的长度范围是:64.5≤ FC <80;
②由于64.5≤ FC <80,故取FC =70cm,则EC =160-70=90cm.
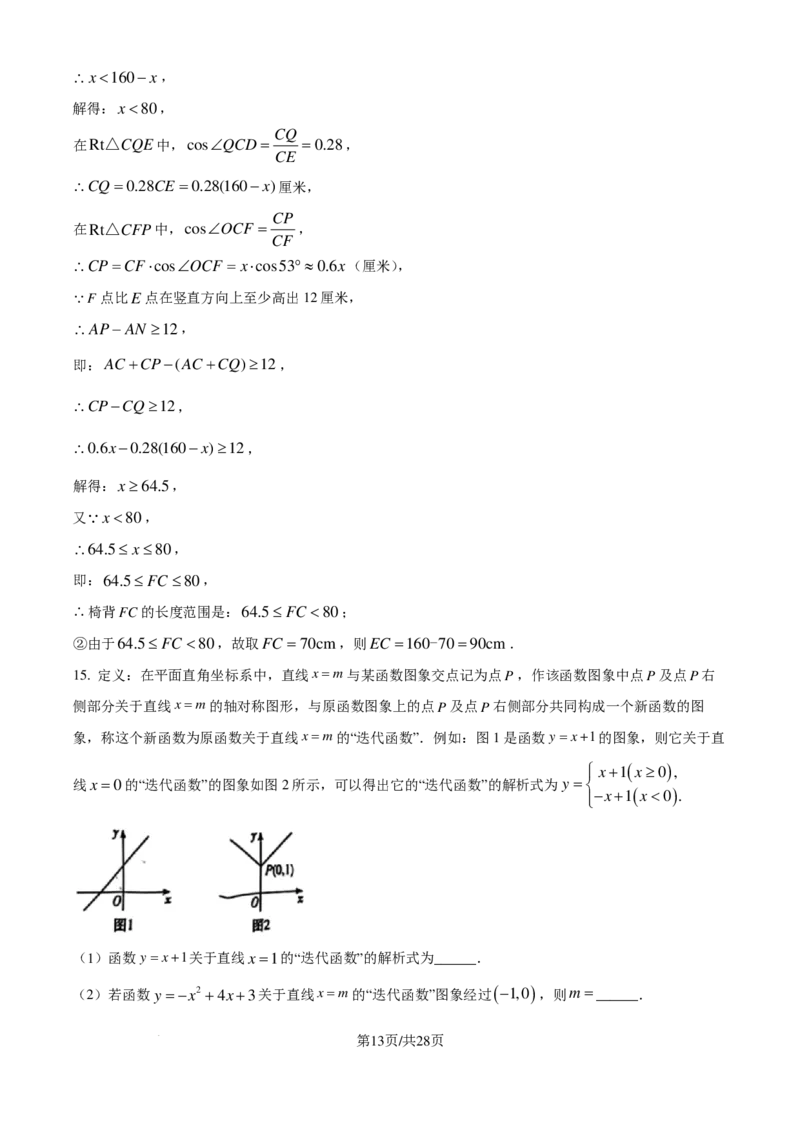
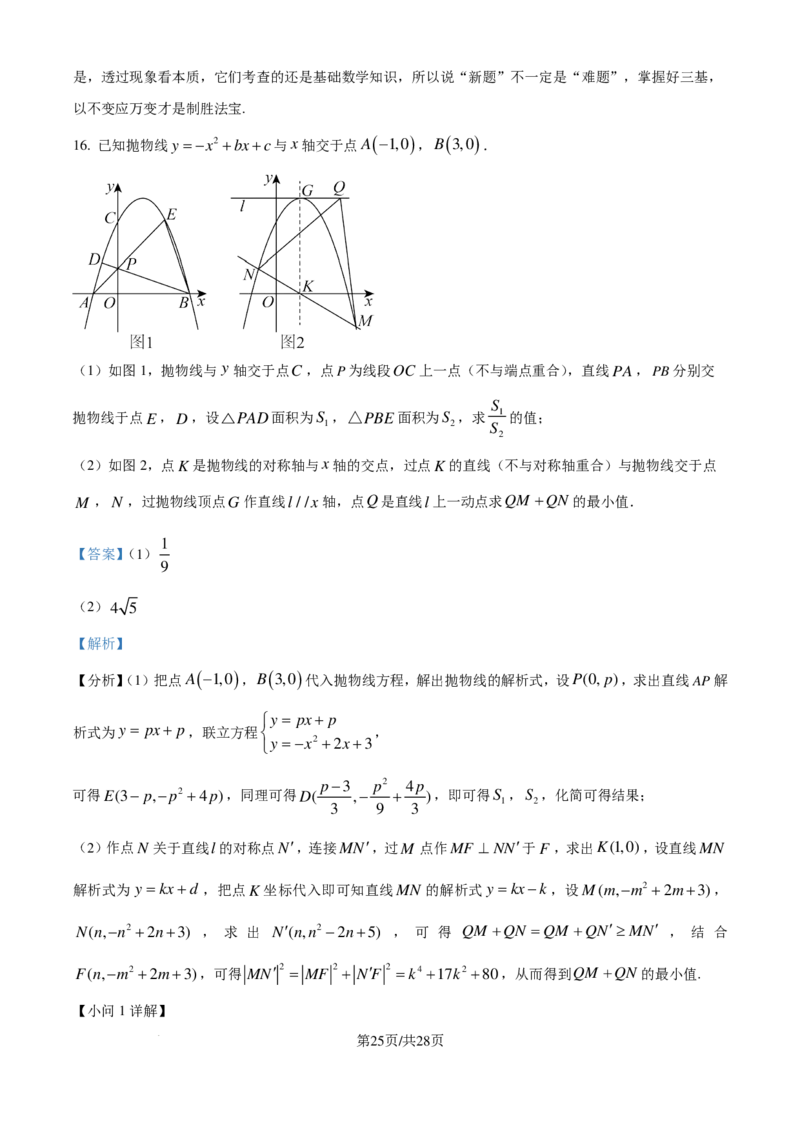
15. 定义:在平面直角坐标系中,直线x=m与某函数图象交点记为点P,作该函数图象中点P及点P右
侧部分关于直线x=m的轴对称图形,与原函数图象上的点P及点P右侧部分共同构成一个新函数的图
象,称这个新函数为原函数关于直线x=m的“迭代函数”.例如:图1是函数y=x+1的图象,则它关于直
x+1 ( x≥0 ) ,
线x=0的“迭代函数”的图象如图2所示,可以得出它的“迭代函数”的解析式为y =
−x+1 ( x<0 ) .
(1)函数y=x+1关于直线x=1的“迭代函数”的解析式为______.
(2)若函数y =−x2 +4x+3关于直线x=m的“迭代函数”图象经过 (−1,0 ) ,则m= ______.
第13页/共28页
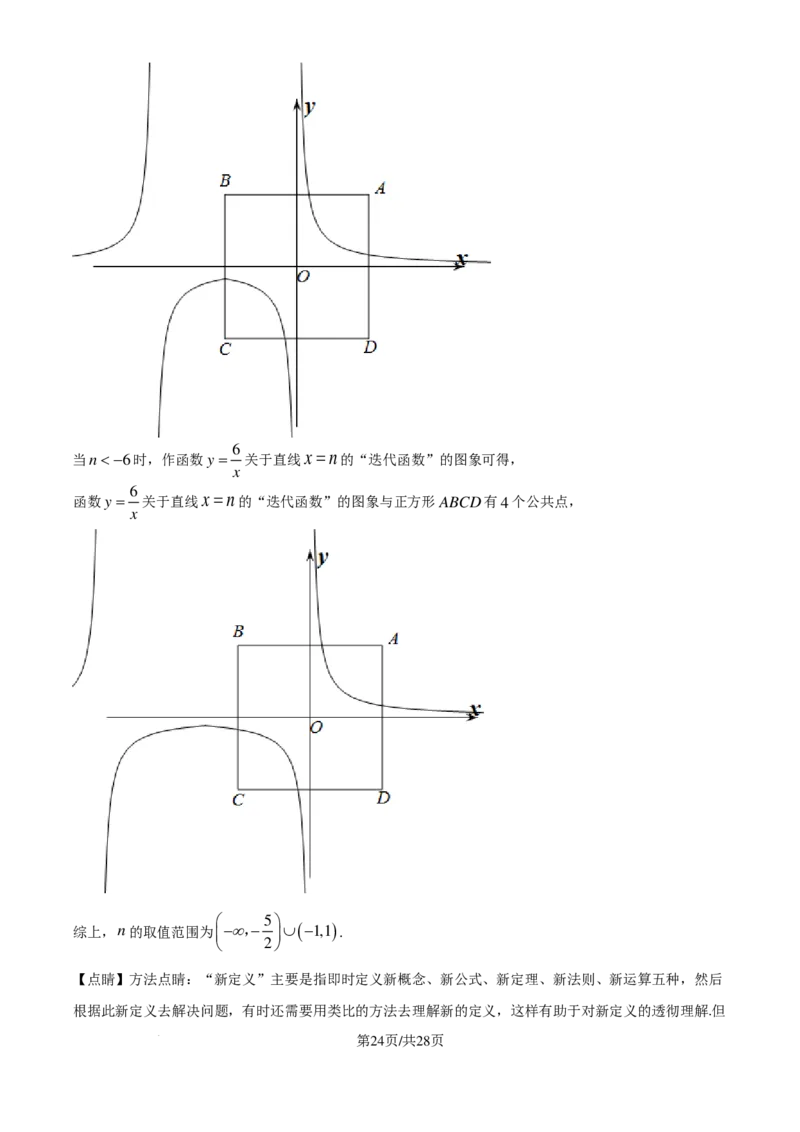
学科网(北京)股份有限公司(3)已知正方形ABCD的顶点分别为:A ( a,a ) ,B ( a,−a ) ,C (−a,−a ) ,D (−a,a ) ,其中a>0.
6
①若函数y = 关于直线x = −2的“迭代函数”的图象与正方形ABCD的边有3个公共点,求a的值;
x
6
②若a=6,函数y = 关于直线x =n的“迭代函数”的图象与正方形ABCD有4个公共点,求n的取值
x
范围.
x+1,x≥1
【答案】(1)y =
−x+3,x<1
1− 7 1+ 7
(2)m= 或m= ,
2 2
5
(3)①3;② −∞,− ∪(−1,1 ) .
2
【解析】
( ) ( )
【分析】(1)取点M 2,3 ,N 3,4 ,求两点关于x=1的对称点,利用待定系数法求左侧图象的解析式,
由此可得结论;
(2)判断点 (−1,0 ) 与函数y =−x2 +4x+3的图象的关系,再求 (−1,0 ) 关于直线x=m的对称点,由条件
列方程求m即可;
6
(3)①求函数y = 关于直线x=−2的“迭代函数”的解析式,作函数图象,观察图象确定a的值;
x
6
②分别在n>0,n=0,n<0时求函数y = 关于直线x=n的“迭代函数”解析式,讨论n,由条件确
x
定n的范围.
【小问1详解】
在函数y=x+1的图象上位于x=1右侧的部分上取点M ( 2,3 ) ,N ( 3,4 ) ,
( )
点M 2,3 关于直线x=1的对称点为 ,
(0,3)
点N
(
3,4
)
关于直线x=1的对称点为
(−1,4 )
,
设函数y=x+1,x>1的图象关于x=1对称的图象的解析式为y =kx+b,x<1,
b=3 k =−1
则 ,解得 ,
−k+b=4 b=3
x+1,x≥1
所以函数y=x+1关于直线x=1的“迭代函数”的解析式为y = ;
−x+3,x<1
第14页/共28页
学科网(北京)股份有限公司【小问2详解】
取x=−1可得,y =−x2 +4x+3=−1−4+3=−2,
故函数y =−x2 +4x+3的图象不过点 (−1,0 ) ,
又点 (−1,0 ) 关于直线x=m的对称点为 ( 2m+1,0 ) ,
由已知可得0=−( 2m+1 )2 +4 ( 2m+1 )+3,m>−1,
1− 7 1+ 7
所以m= 或m= ,
2 2
【小问3详解】
6 6
①当x>0或−2≤ x<0时,函数y = 关于直线x = −2的“迭代函数”的图象的解析式为y = ,
x x
6
当x<−2时,设点 在函数y = 关于直线x = −2的“迭代函数”的图象上,
x
𝐸𝐸(𝑥𝑥,𝑦𝑦) 6
则点 (−4−x,y ) 在函数y = 的图象上,
x
6
所以y = ,
−4−x
6
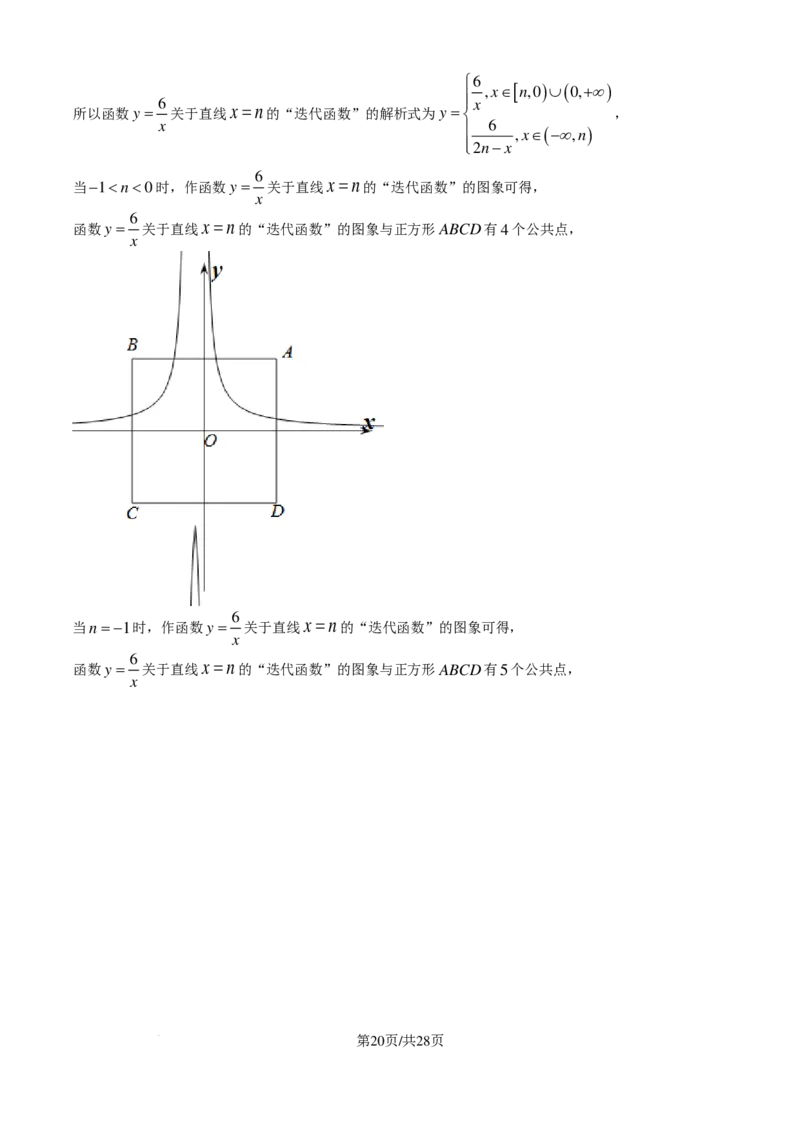
,x∈[−2,0 )∪( 0,+∞)
6 x
所以函数y = 关于直线x = −2的“迭代函数”的解析式为y = ,
x 6 ,x∈(−∞,−2 )
−4−x
6
作函数y = 关于直线x = −2的“迭代函数”的图象如下:
x
第15页/共28页
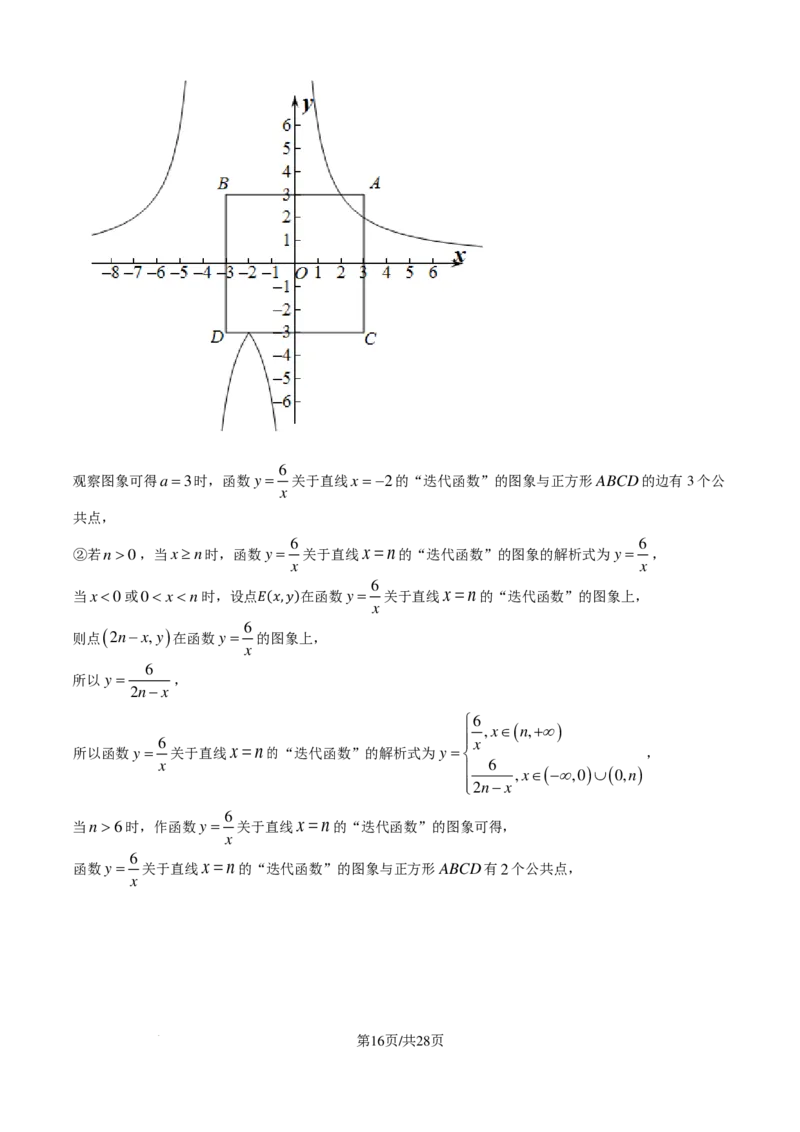
学科网(北京)股份有限公司6
观察图象可得a=3时,函数y = 关于直线x = −2的“迭代函数”的图象与正方形ABCD的边有3个公
x
共点,
6 6
②若n>0,当x≥n时,函数y = 关于直线x =n的“迭代函数”的图象的解析式为y = ,
x x
6
当x<0或0< x6时,作函数y = 关于直线x =n的“迭代函数”的图象可得,
x
6
函数y = 关于直线x =n的“迭代函数”的图象与正方形ABCD有2个公共点,
x
第16页/共28页
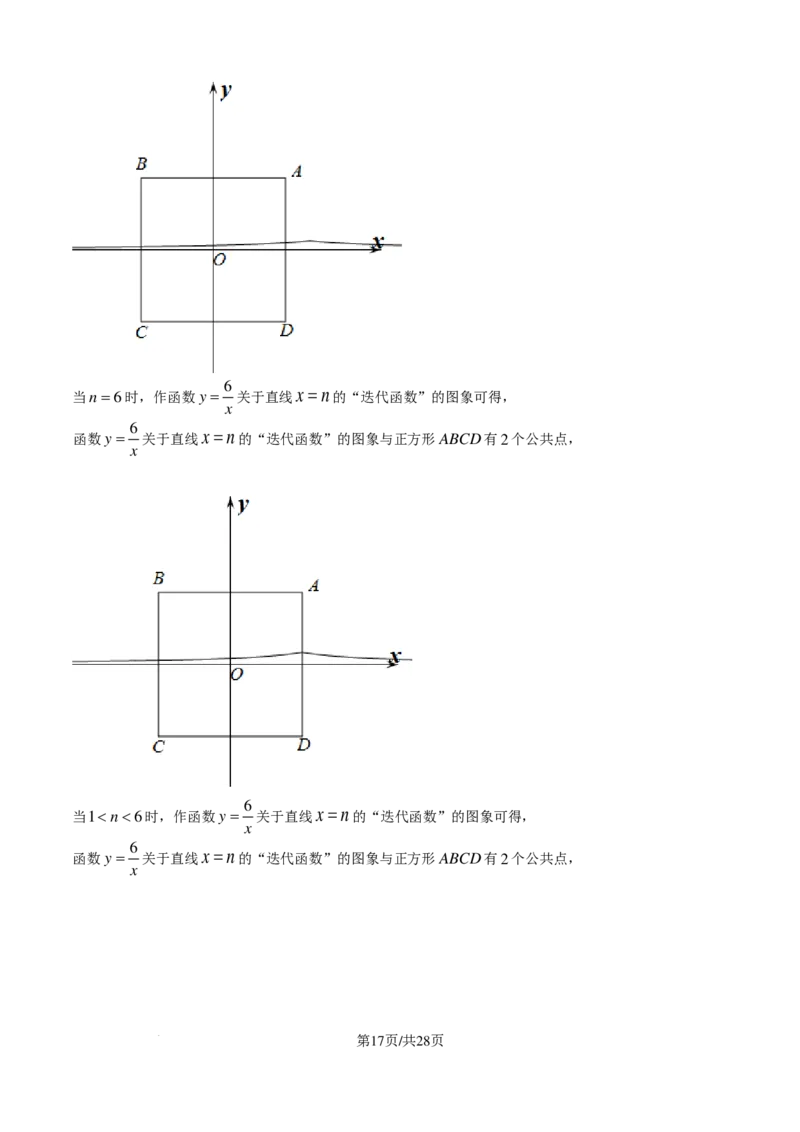
学科网(北京)股份有限公司6
当n=6时,作函数y = 关于直线x =n的“迭代函数”的图象可得,
x
6
函数y = 关于直线x =n的“迭代函数”的图象与正方形ABCD有2个公共点,
x
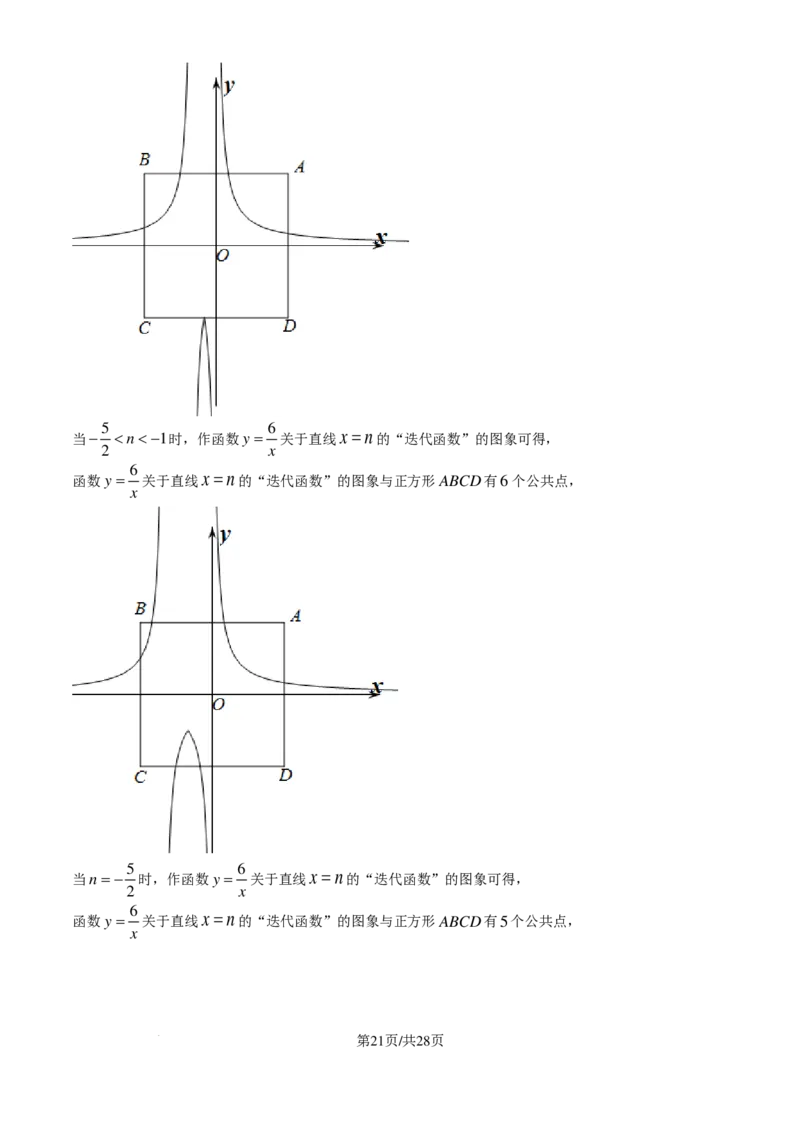
6
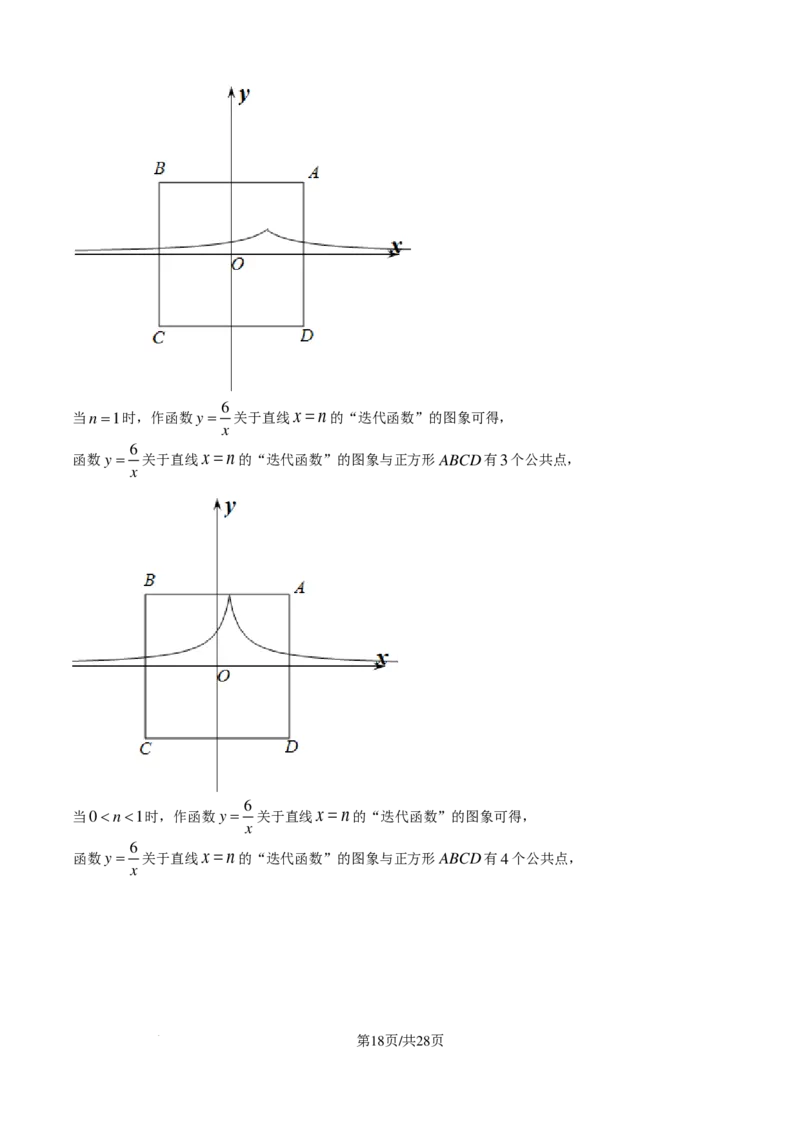
当10
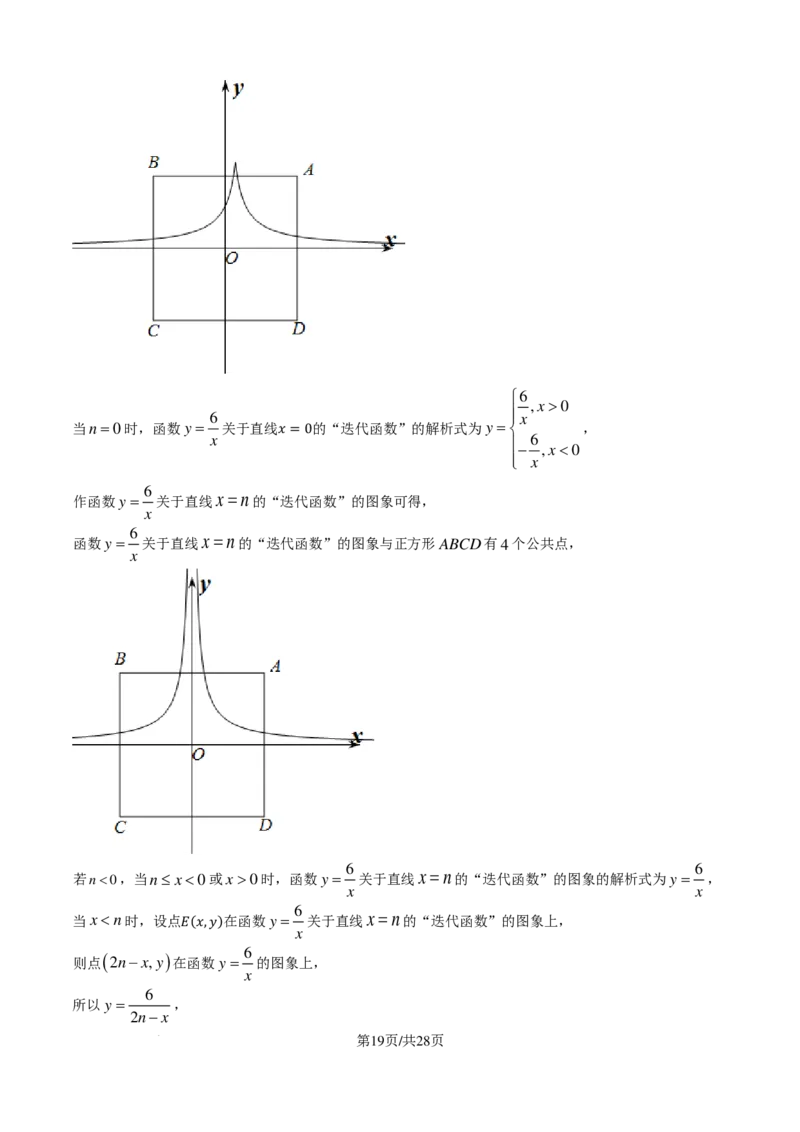
6 x
当n=0时,函数y = 关于直线 的“迭代函数”的解析式为y = ,
x 6
− ,x<0
𝑥𝑥 =0 x
6
作函数y = 关于直线x =n的“迭代函数”的图象可得,
x
6
函数y = 关于直线x =n的“迭代函数”的图象与正方形ABCD有4个公共点,
x
6 6
若n<0,当n≤ x<0或x>0时,函数y = 关于直线x =n的“迭代函数”的图象的解析式为y = ,
x x
6
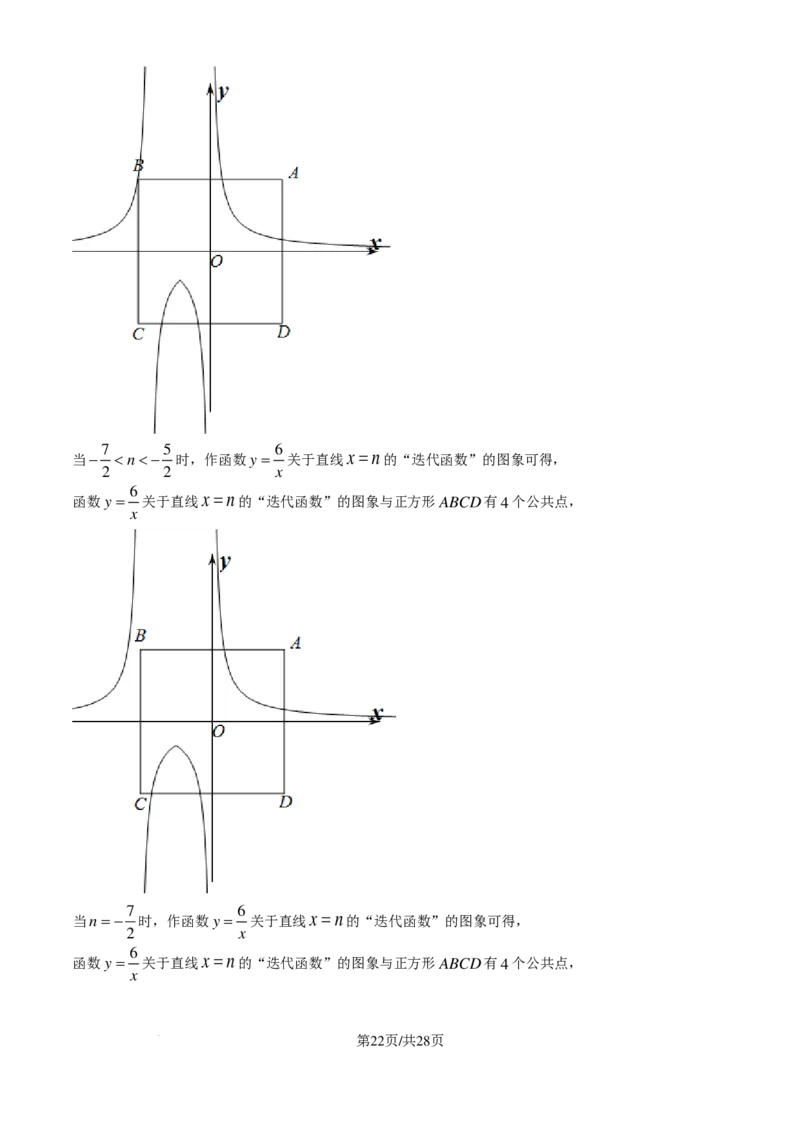
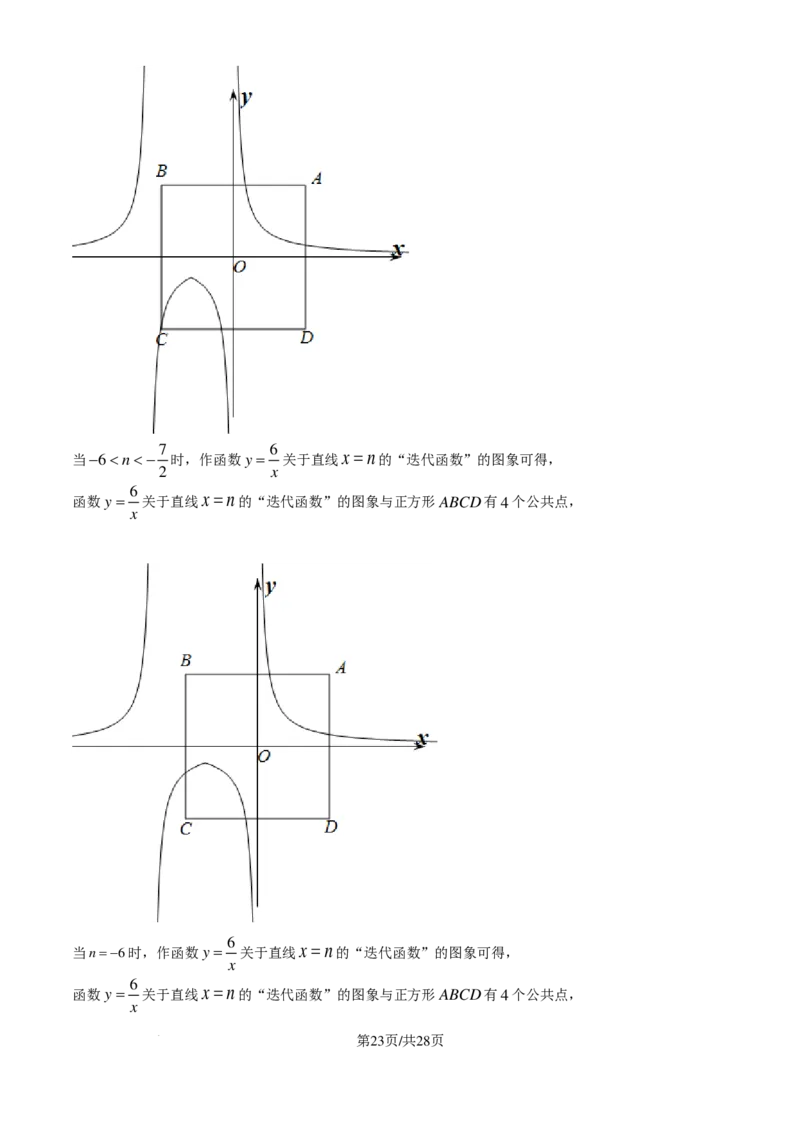
当x