文档内容
长郡中学 2024 级高一综合能力检测试卷
数学
时量:90分钟 满分 100分
一、选择题:本题共 8小题,每小题 4分,共 32分.在每小题给出的四个选项中,只有一个
选项是符题目要求的.
1.
《孙子算经》中记载:“凡大数之法,万万曰亿,万万亿日兆.”说明了大数之间的关系:1亿=1万1
万,1兆=1万×1万×1亿.若1兆 =10m ,则m的值为( )
A. 4 B. 8 C. 12 D. 16
2. 二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,
二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨),夏季(立夏、小满、芒种、夏
至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小
寒大寒),若从二十四个节气中随机抽取一个节气,则抽到的节气在夏季的概率为( )
1 1 1 1
A. B. C. D.
2 12 6 4
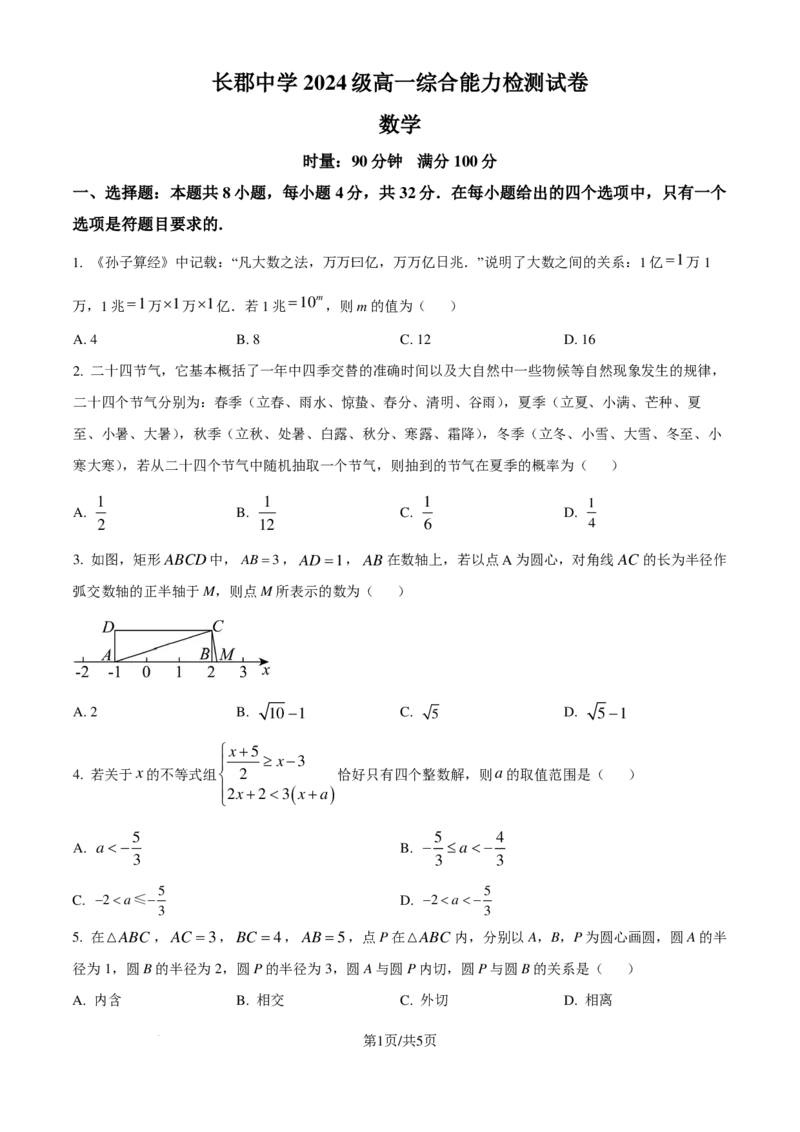
3. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作
弧交数轴的正半轴于M,则点M所表示的数为( )
A. 2 B. 10−1 C. 5 D. 5−1
x+5
≥ x−3
4. 若关于x的不等式组 2 恰好只有四个整数解,则a的取值范围是( )
2x+2<3 ( x+a )
5 5 4
A. a<− B. − ≤a<−
3 3 3
5 5
C. −20 )的图象交于点B,则 的值( )
x BO
1 1 3 1
A. B. C. D.
2 4 3 3
8. 若二次函数的解析式为y =( x−2m )( x−2 )( 1≤m≤5 ) ,且函数图象过点 ( p,q ) 和点 ( p+4,q ) ,则q
的取值范围是( )
A. −12≤q≤4 B. −5≤q≤0 C. −5≤q≤4 D. −12≤q≤3
二、填空题:本题共 4小题,每小题 4分,共 16分.
9. 分解因式:a4 −4a3+4a2 −9=______.
10. 直线l :y=x−1与x轴交于点A,将直线l 绕点A逆时针旋转15°,得到直线l ,则直线l 对应的函数
1 1 2 2
表达式是______.
2x−a −2x+a
11. 若关于x的分式方程 −4= 的解为整数,则整数a=______.
x−1 x+1
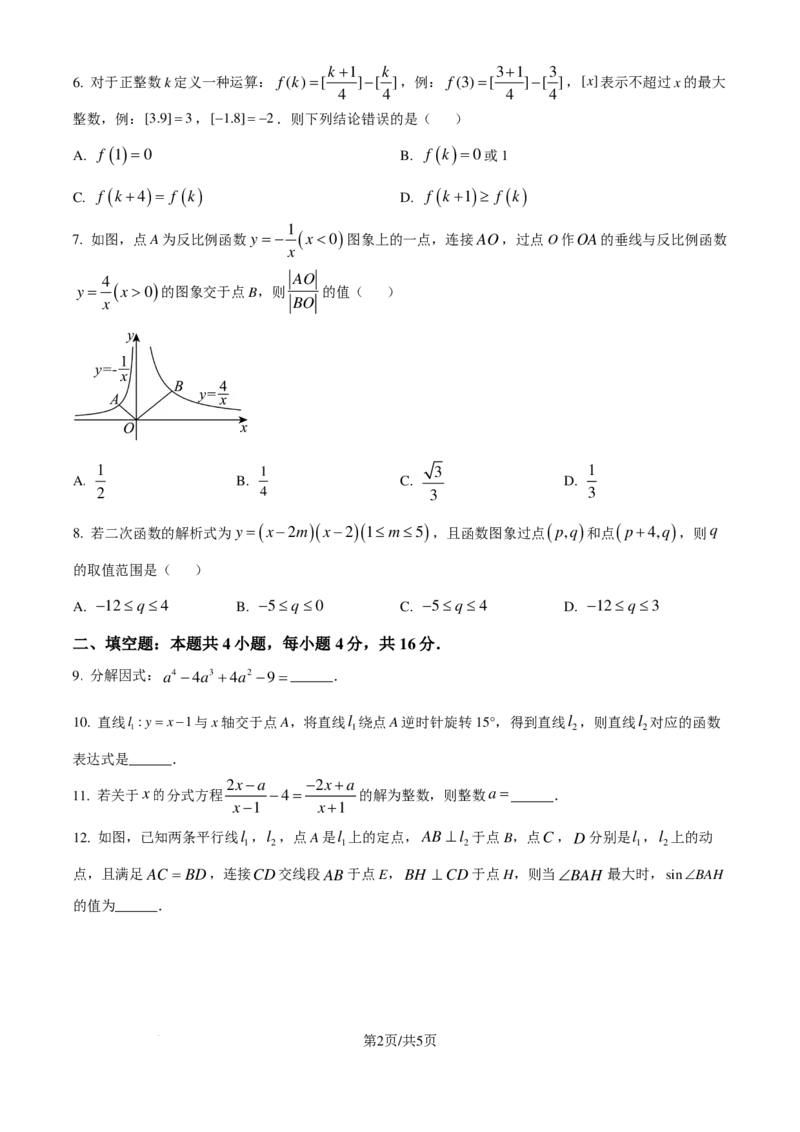
12. 如图,已知两条平行线l ,l ,点A是l 上的定点,AB⊥l 于点B,点C,D分别是l ,l 上的动
1 2 1 2 1 2
点,且满足AC = BD,连接CD交线段AB于点E,BH ⊥CD于点H,则当∠BAH 最大时,sin∠BAH
的值为______.
第2页/共5页
学科网(北京)股份有限公司三、解答题:本题共 4小题,共 52分.应写出文字说明、证明过程或演算步骤.
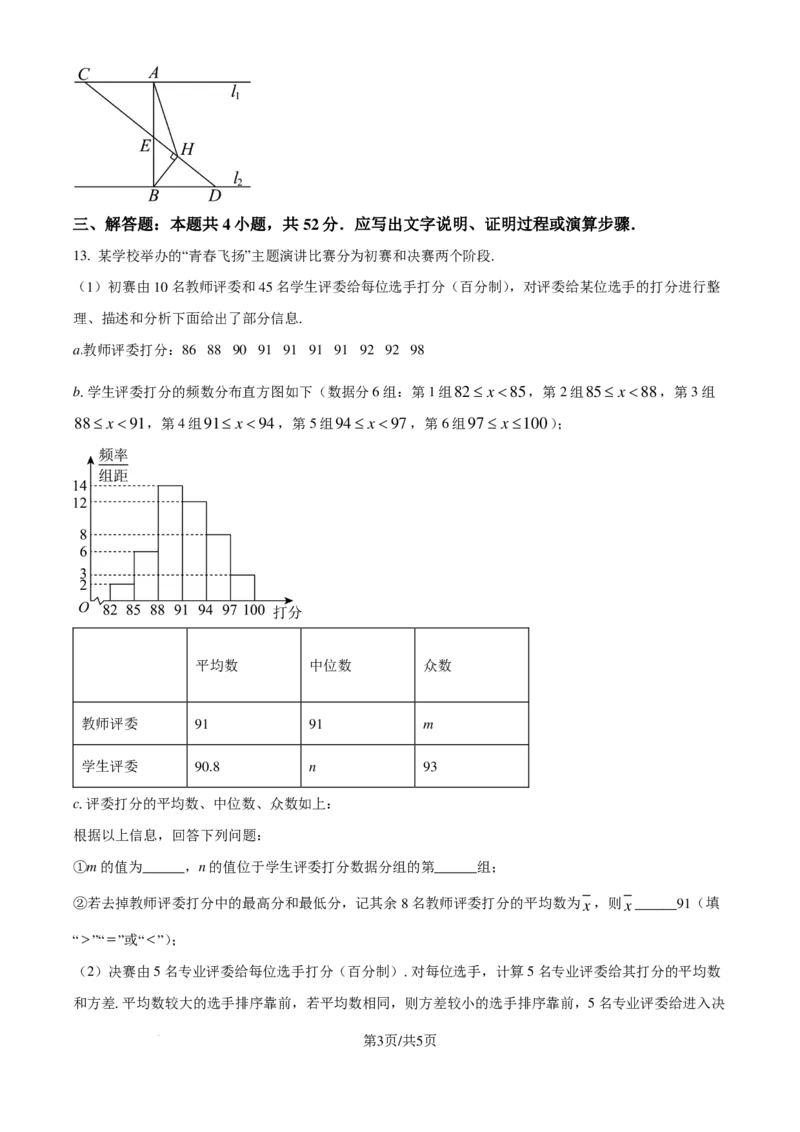
13. 某学校举办的“青春飞扬”主题演讲比赛分为初赛和决赛两个阶段.
(1)初赛由10名教师评委和45名学生评委给每位选手打分(百分制),对评委给某位选手的打分进行整
理、描述和分析下面给出了部分信息.
a.教师评委打分:86 88 90 91 91 91 91 92 92 98
b.学生评委打分的频数分布直方图如下(数据分6组:第1组82≤ x<85,第2组85≤ x<88,第3组
88≤ x<91,第4组91≤ x<94,第5组94≤ x<97,第6组97≤ x≤100);
平均数 中位数 众数
教师评委 91 91 m
学生评委 90.8 n 93
c.评委打分的平均数、中位数、众数如上:
根据以上信息,回答下列问题:
①m的值为______,n的值位于学生评委打分数据分组的第______组;
②若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分的平均数为x,则x______91(填
“>”“=”或“<”);
(2)决赛由5名专业评委给每位选手打分(百分制).对每位选手,计算5名专业评委给其打分的平均数
和方差.平均数较大的选手排序靠前,若平均数相同,则方差较小的选手排序靠前,5名专业评委给进入决
第3页/共5页
学科网(北京)股份有限公司赛的甲、乙、丙三位选手的打分如下:
评1 评委2 评委3 评委4 评委5
甲 93 90 92 93 92
乙 91 92 92 92 92
丙 90 94 90 94 k
若丙在甲、乙、丙三位选手中的排序居中,则这三位选手中排序最靠前的是______,表中k(k为整数)的
值为______.
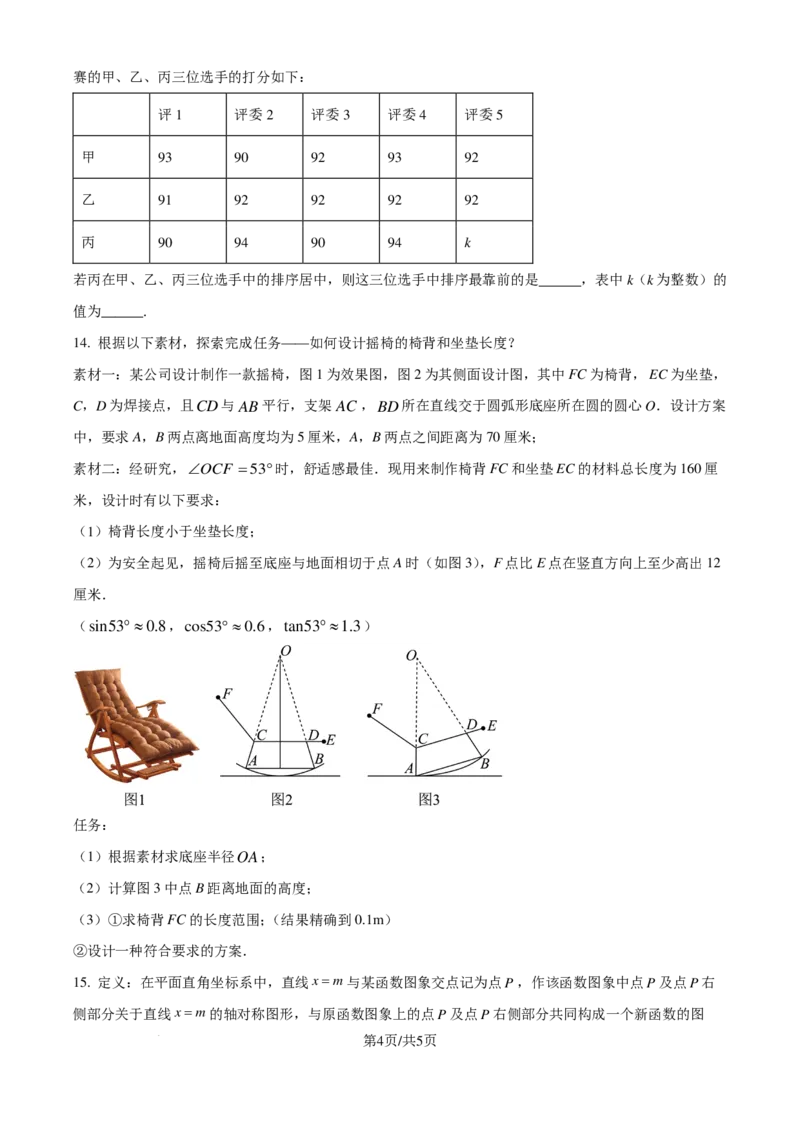
14. 根据以下素材,探索完成任务——如何设计摇椅的椅背和坐垫长度?
素材一:某公司设计制作一款摇椅,图1为效果图,图2为其侧面设计图,其中FC为椅背,EC为坐垫,
C,D为焊接点,且CD与AB平行,支架AC,BD所在直线交于圆弧形底座所在圆的圆心O.设计方案
中,要求A,B两点离地面高度均为5厘米,A,B两点之间距离为70厘米;
素材二:经研究,∠OCF =53°时,舒适感最佳.现用来制作椅背FC和坐垫EC的材料总长度为160厘
米,设计时有以下要求:
(1)椅背长度小于坐垫长度;
(2)为安全起见,摇椅后摇至底座与地面相切于点A时(如图3),F点比E点在竖直方向上至少高出12
厘米.
(sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
任务:
(1)根据素材求底座半径OA;
(2)计算图3中点B距离地面的高度;
(3)①求椅背FC的长度范围;(结果精确到0.1m)
②设计一种符合要求的方案.
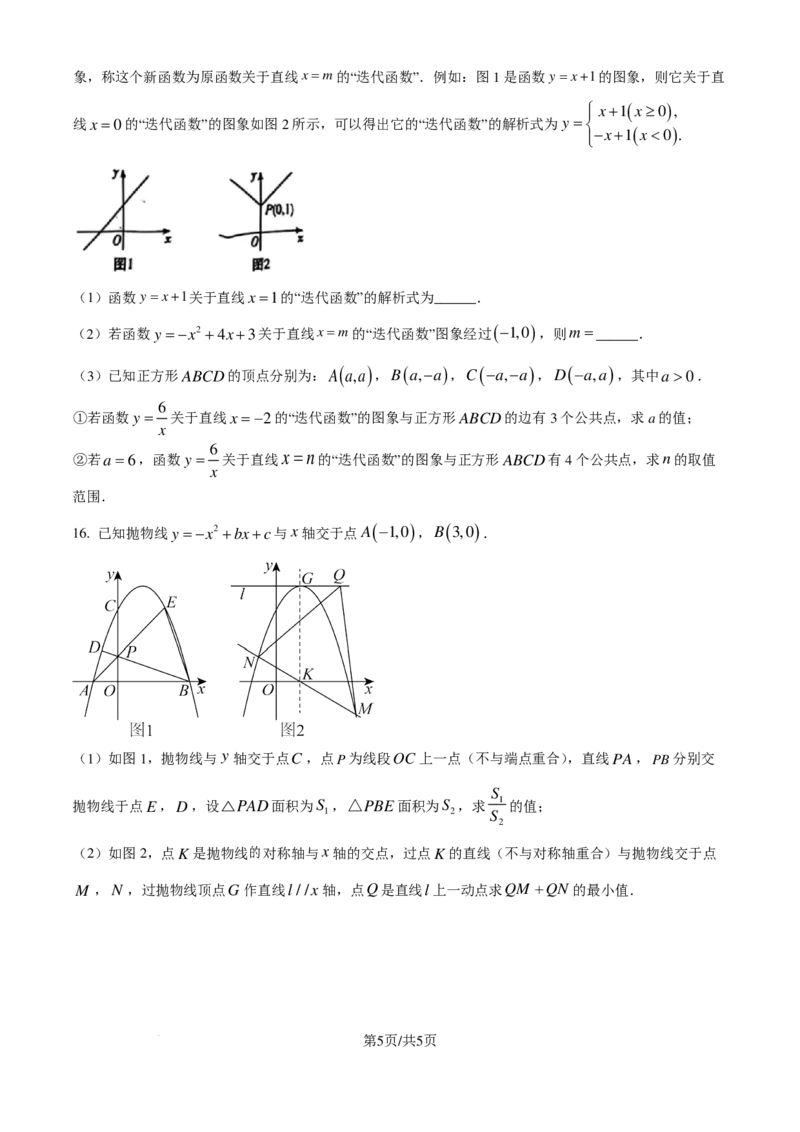
15. 定义:在平面直角坐标系中,直线x=m与某函数图象交点记为点P,作该函数图象中点P及点P右
侧部分关于直线x=m的轴对称图形,与原函数图象上的点P及点P右侧部分共同构成一个新函数的图
第4页/共5页
学科网(北京)股份有限公司象,称这个新函数为原函数关于直线x=m的“迭代函数”.例如:图1是函数y=x+1的图象,则它关于直
x+1 ( x≥0 ) ,
线x=0的“迭代函数”的图象如图2所示,可以得出它的“迭代函数”的解析式为y =
−x+1 ( x<0 ) .
(1)函数y=x+1关于直线x=1的“迭代函数”的解析式为______.
(2)若函数y =−x2 +4x+3关于直线x=m的“迭代函数”图象经过 (−1,0 ) ,则m= ______.
(3)已知正方形ABCD的顶点分别为:A ( a,a ) ,B ( a,−a ) ,C (−a,−a ) ,D (−a,a ) ,其中a>0.
6
①若函数y = 关于直线x = −2的“迭代函数”的图象与正方形ABCD的边有3个公共点,求a的值;
x
6
②若a=6,函数y = 关于直线x =n的“迭代函数”的图象与正方形ABCD有4个公共点,求n的取值
x
范围.
16. 已知抛物线y =−x2 +bx+c与x轴交于点A (−1,0 ) ,B ( 3,0 ) .
(1)如图1,抛物线与 y轴交于点C,点P为线段OC上一点(不与端点重合),直线PA,PB分别交
S
抛物线于点E,D,设△PAD面积为S ,△PBE面积为S ,求 1 的值;
1 2 S
2
(2)如图2,点K是抛物线的对称轴与x轴的交点,过点K的直线(不与对称轴重合)与抛物线交于点
M ,N ,过抛物线顶点G作直线l //x轴,点Q是直线l上一动点求QM +QN的最小值.
第5页/共5页
学科网(北京)股份有限公司