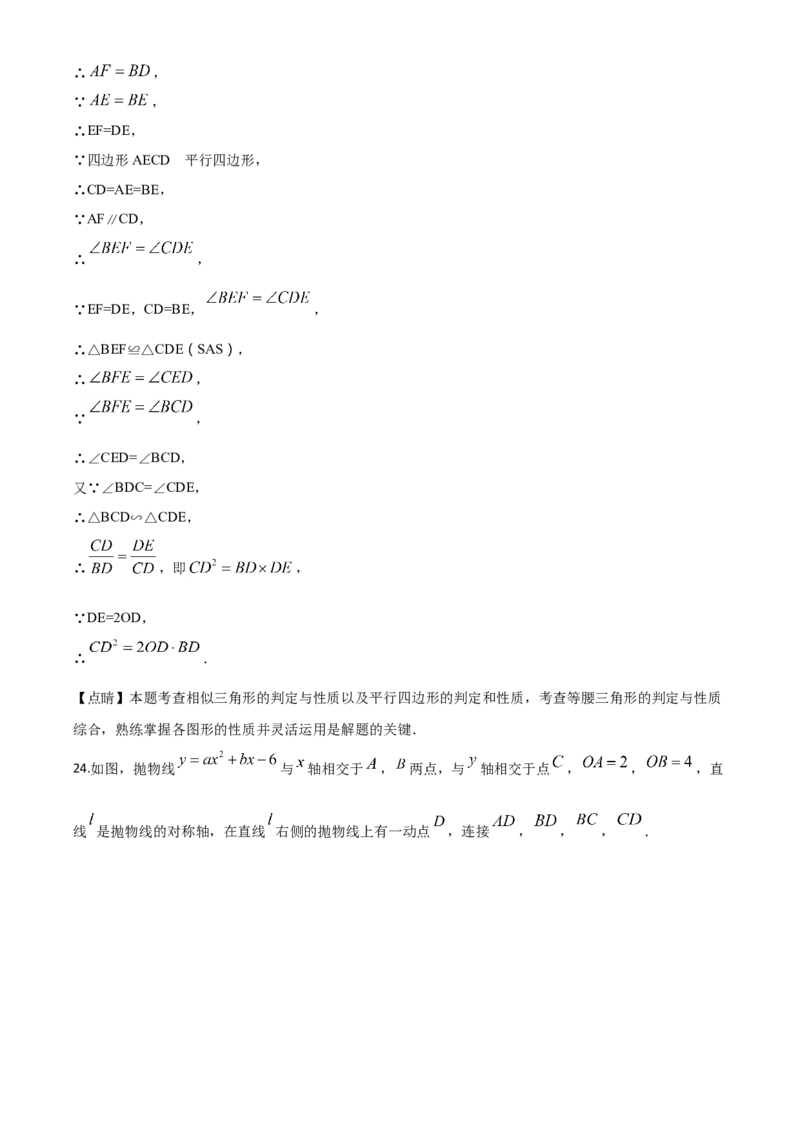文档内容
菏泽市二 0 二 0 年初中学业水平考试(中考)数学试题
注意事项:
1.本试题共24个题,考试时间120分钟.
2.请把答案写在答题卡上,选择题用2B铅笔填涂,非选择题用0.5毫米黑色签字笔书写在
答题卡的指定区域内,写在其他区域不得分.
一、选择题(本大题共8个小题,在每小题给出的四个选项中,只有一个选项是正确的,请
把正确选项的序号涂在答题卡的相应位置.)
1.下列各数中,绝对值最小的数是( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据绝对值的意义,计算出各选项的绝对值,然后再比较大小即可.
【详解】解: , , , ,
∵ ,
∴绝对值最小的数是 ;
故选:B.
【点睛】本题考查的是实数的大小比较,熟知绝对值的性质是解答此题的关键.
2.函数 的自变量 的取值范围是( )
A. B. 且 C. D. 且
【答案】D
【解析】
【分析】
由分式与二次根式有意义的条件得函数自变量的取值范围.
【详解】解:由题意得:解得: 且
故选D.
【点睛】本题考查的是函数自变量的取值范围,掌握分式与二次根式有意义的条件是解题的关键.
3.在平面直角坐标系中,将点 向右平移 个单位得到点 ,则点 关于 轴的对称点的坐标为
( )
A. B. C. D.
【答案】A
【解析】
【分析】
先根据点向右平移 个单位点的坐标特征:横坐标加3,纵坐标不变,得到点 的坐标,再根据关于 轴
的对称点的坐标特征:横坐标不变,纵坐标变为相反数,得到对称点的坐标即可.
【详解】解:∵将点 向右平移 个单位,
∴点 的坐标为:(0,2),
∴点 关于 轴的对称点的坐标为:(0,-2).
故选:A.
【点睛】本题考查平移时点的坐标特征及关于 轴的对称点的坐标特征,熟练掌握对应的坐标特征是解题
的关键.
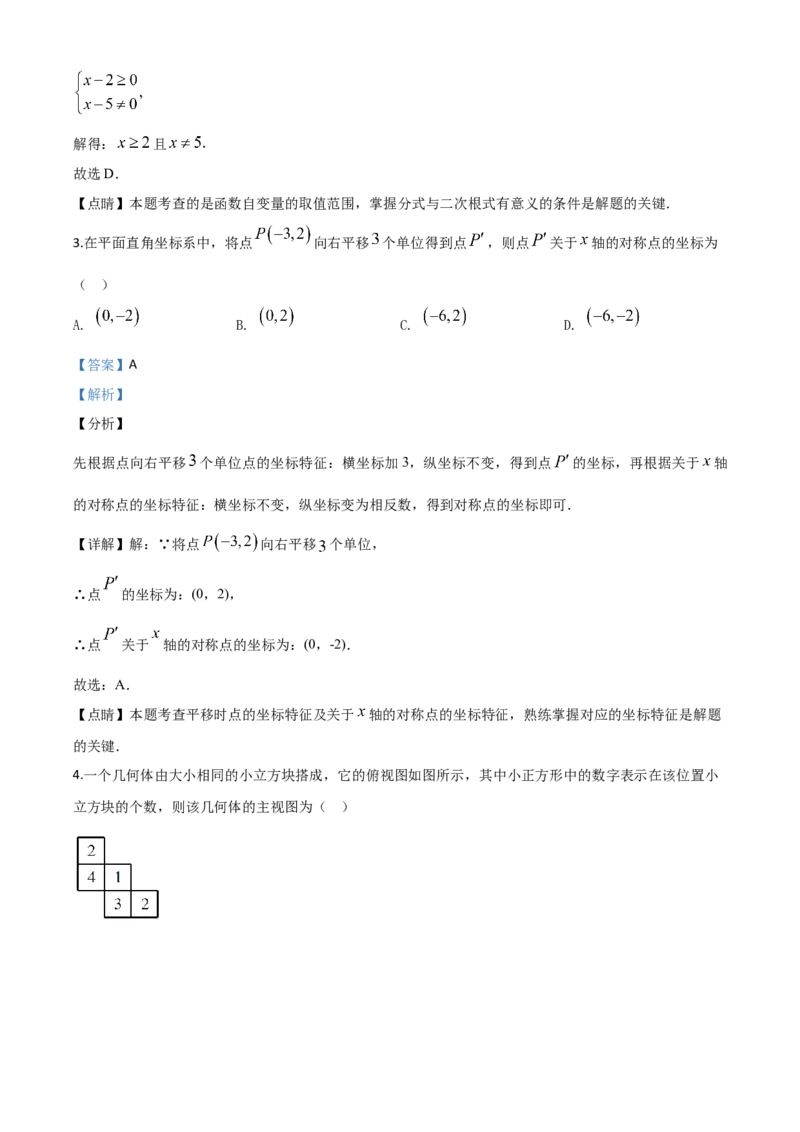
4.一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小
立方块的个数,则该几何体的主视图为( )A. B. C. D.
【答案】A
【解析】
【分析】
从正面看,注意“长对正,宽相等、高平齐”,根据所放置的小立方体的个数判断出主视图图形即可.
【详解】解:从正面看所得到的图形为 选项中的图形.
故选: .
【点睛】考查几何体的三视图的知识,从正面看的图形是主视图,从左面看到的图形是左视图,从上面看
到的图象是俯视图.掌握以上知识是解题的关键.
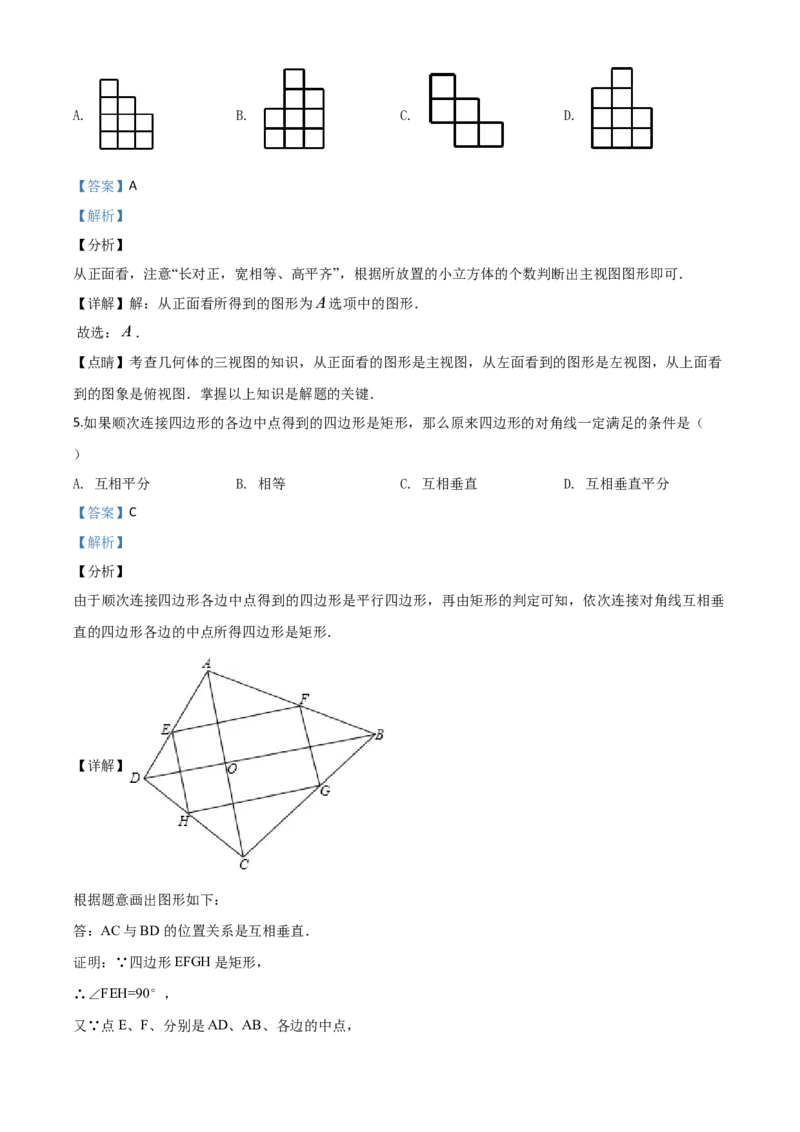
5.如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是(
)
A. 互相平分 B. 相等 C. 互相垂直 D. 互相垂直平分
【答案】C
【解析】
【分析】
由于顺次连接四边形各边中点得到的四边形是平行四边形,再由矩形的判定可知,依次连接对角线互相垂
直的四边形各边的中点所得四边形是矩形.
【详解】
根据题意画出图形如下:
答:AC与BD 的位置关系是互相垂直.
证明:∵四边形EFGH是矩形,
∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD.
故选C.
【点睛】此题主要考查了矩形的判定定理,画出图形进而应用平行四边形的判定以及矩形判定是解决问题
的关键.
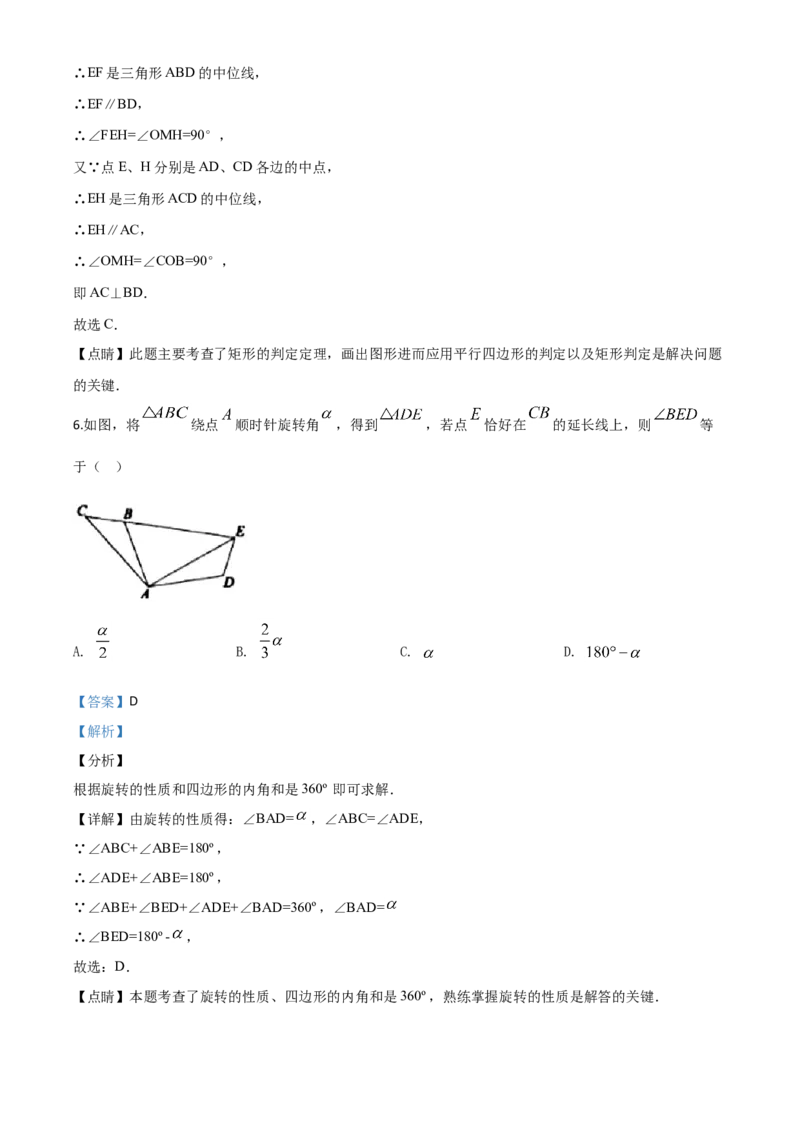
6.如图,将 绕点 顺时针旋转角 ,得到 ,若点 恰好在 的延长线上,则 等
于( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据旋转的性质和四边形的内角和是360º即可求解.
【详解】由旋转的性质得:∠BAD= ,∠ABC=∠ADE,
∵∠ABC+∠ABE=180º,
∴∠ADE+∠ABE=180º,
∵∠ABE+∠BED+∠ADE+∠BAD=360º,∠BAD=
∴∠BED=180º- ,
故选:D.
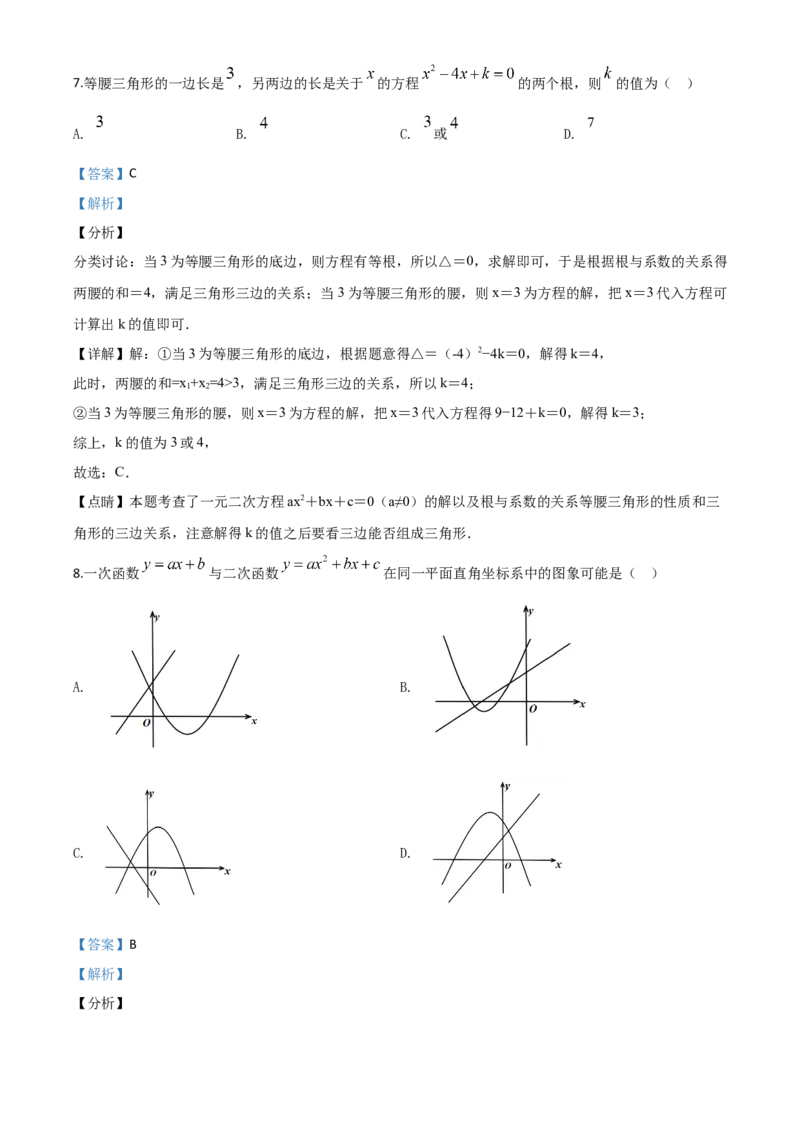
【点睛】本题考查了旋转的性质、四边形的内角和是360º,熟练掌握旋转的性质是解答的关键.7.等腰三角形的一边长是 ,另两边的长是关于 的方程 的两个根,则 的值为( )
A. B. C. 或 D.
【答案】C
【解析】
【分析】
分类讨论:当3为等腰三角形的底边,则方程有等根,所以△=0,求解即可,于是根据根与系数的关系得
两腰的和=4,满足三角形三边的关系;当3为等腰三角形的腰,则x=3为方程的解,把x=3代入方程可
计算出k的值即可.
【详解】解:①当3为等腰三角形的底边,根据题意得△=(-4)2−4k=0,解得k=4,
此时,两腰的和=x+x=4>3,满足三角形三边的关系,所以k=4;
1 2
②当3为等腰三角形的腰,则x=3为方程的解,把x=3代入方程得9−12+k=0,解得k=3;
综上,k的值为3或4,
故选:C.
【点睛】本题考查了一元二次方程ax2+bx+c=0(a≠0)的解以及根与系数的关系等腰三角形的性质和三
角形的三边关系,注意解得k的值之后要看三边能否组成三角形.
8.一次函数 与二次函数 在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【答案】B
【解析】
【分析】逐一分析四个选项,根据二次函数图象的开口以及对称轴与 y轴的关系即可得出a、b的正负,由此即可得
出一次函数图象经过的象限,再与函数图象进行对比即可得出结论.
【详解】解:A、∵二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,A错误;
B、∵二次函数图象开口向上,对称轴在y轴左侧,
∴a>0,b>0,
∴一次函数图象应该过第一、二、三象限,B正确;
C、∵二次函数图象开口向下,对称轴在y轴右侧,
∴a<0,b>0,
∴一次函数图象应该过第一、二、四象限,C错误;
D、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,D错误.
故选:B.
【点睛】本题考查了二次函数的图象以及一次函数图象与系数的关系,根据a、b的正负确定一次函数图象
经过的象限是解题的关键.
二、填空题(本大题共6个小题,只要求把最后结果填写在答题卡的相应区域内)
9.计算 的结果是_______.
【答案】﹣13
【解析】
【分析】
根据平方差公式计算即可.
【详解】 .
故答案为﹣13.
【点睛】本题考查平方差公式和二次根式计算,关键在于牢记公式.
10.方程 的解是______.
【答案】【解析】
【分析】
方程两边都乘以 化分式方程为整式方程,解整式方程得出 的值,再检验即可得出方程的解.
【详解】方程两边都乘以 ,得: ,
解得: ,
检验: 时, ,
所以分式方程的解为 ,
故答案为: .
【点睛】本题主要考查解分式方程,解题的关键是掌握解分式方程的步骤:①去分母;②求出整式方程的
解;③检验;④得出结论.
11.如图,在 中, ,点 为 边的中点,连接 ,若 , ,则
的值为______.
【答案】
【解析】
【分析】
根据直角三角形斜边上的中线是斜边的一半得到DC=DB,∠DCB=∠B,根据锐角三角函数的定义即可求
解.
【详解】∵∠ACB=90°,BC=4,CD=3,点D是AB边的中点,
∴DC=DB,∴∠DCB=∠B,AB=2CD=6,
∴ ,
故答案为: .
【点睛】本题考查了直角三角形的性质,等腰三角形的判定和性质,锐角三角函数的定义,掌握直角三角
形斜边上的中线是斜边的一半和三角函数的定义是解题的关键.
12.从 , , , 这四个数中任取两个不同的数分别作为 , 的值,得到反比例函数 ,则
这些反比例函数中,其图象在二、四象限的概率是______.
【答案】
【解析】
【分析】
从 , , , 中任取两个数值作为 , 的值,表示出基本事件的总数,再表示出其积为负值的基
础事件数,按照概率公式求解即可.
【详解】从 , , , 中任取两个数值作为 , 的值,其基本事件总数有:
共计12种;
其中积为负值的共有:8种,
∴其概率为:
故答案为: .
【点睛】本题结合反比例函数图象的性质,考查了概率的计算,能准确写出基本事件的总数,和满足条件
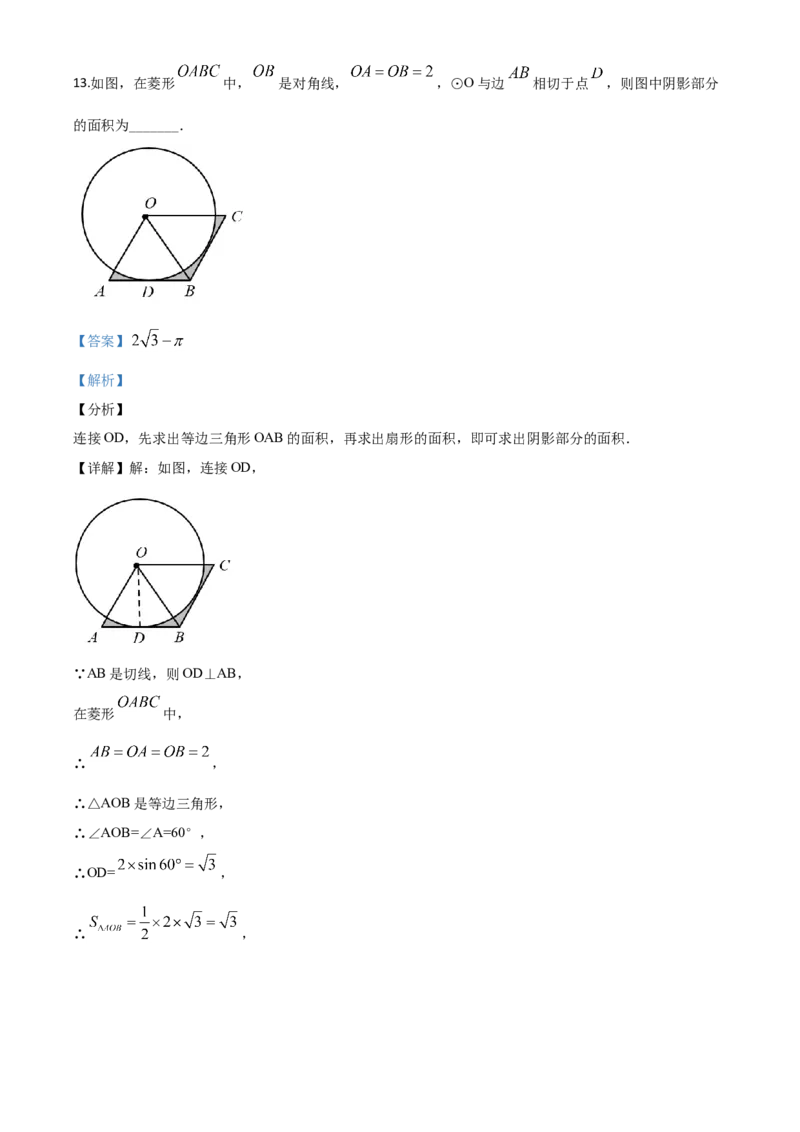
的基本事件数,是解题的关键.13.如图,在菱形 中, 是对角线, ,⊙O与边 相切于点 ,则图中阴影部分
的面积为_______.
【答案】
【解析】
【分析】
连接OD,先求出等边三角形OAB的面积,再求出扇形的面积,即可求出阴影部分的面积.
【详解】解:如图,连接OD,
∵AB是切线,则OD⊥AB,
在菱形 中,
∴ ,
∴△AOB是等边三角形,
∴∠AOB=∠A=60°,
∴OD= ,
∴ ,∴扇形的面积为: ,
∴阴影部分的面积为: ;
故答案为: .
【点睛】本题考查了求不规则图形的面积,扇形的面积,等边三角形的判定和性质,解直角三角形,解题
的关键是正确求出等边三角形的面积和扇形的面积.
14.如图,矩形 中, , ,点 在对角线 上,且 ,连接 并延长,
交 的延长线于点 ,连接 ,则 的长为_______.
【答案】
【解析】
【分析】
由矩形的性质求得BD,进而求得PD ,再由AB∥CD得 ,求得CQ,然后由勾股
定理解得BQ即可.
【详解】∵四边形ABCD是矩形, , ,
∴∠BAD=∠BCD=90º,AB=CD=5,BC=AD=12,AB∥CD,
∴ ,又 =5,
∴PD=8,
∵AB∥DQ,∴ ,即
解得:CQ=3,
在Rt△BCQ中,BC=12,CQ=3,
.
故答案为:
【点睛】本题考查了矩形的性质、平行线分线段成比例定理、勾股定理,熟练掌握矩形的性质,会利用平
行线成比例定理列相关比例式是解答的关键.
三、解答题(把解答或证明过程写在答题卡的相应区域内.)
15.计算: .
【答案】
【解析】
【分析】
根据负整数指数幂,绝对值,特殊角的三角函数值,积的乘方公式的逆向应用进行计算即可.
【详解】
.
【点睛】本题考查了负整数指数幂,绝对值,特殊角的三角函数值,积的乘方公式的逆向应用,熟知以上
运算是解题的关键.
16.先化简,再求值: ,其中 满足 .
【答案】2a2+4a,6【解析】
【分析】
原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,再
代值计算即可求出值.
【详解】解:原式=
=
=
=2a(a+2)
=2a2+4a.
∵ ,
∴a2+2a=3.
∴原式=2(a2+2a)=6.
【点睛】此题主要考查了分式的化简求值,正确化简分式是解题关键.
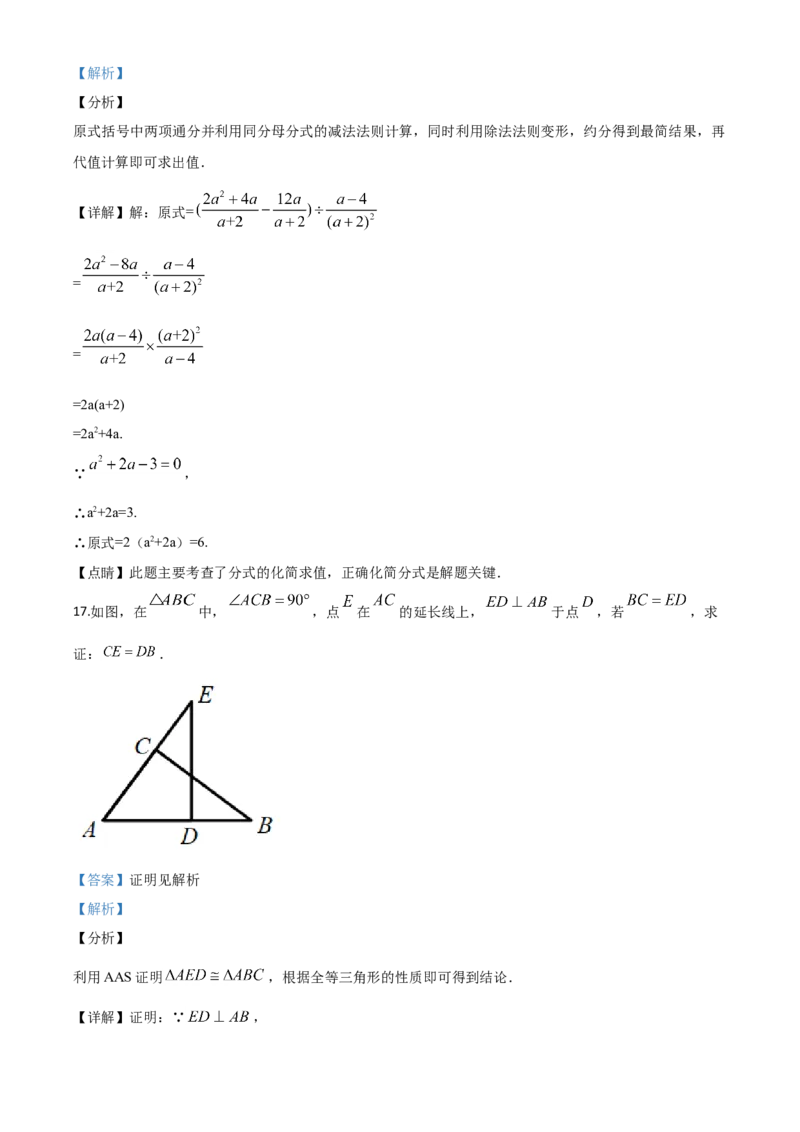
17.如图,在 中, ,点 在 的延长线上, 于点 ,若 ,求
证: .
【答案】证明见解析
【解析】
【分析】
利用AAS证明 ,根据全等三角形的性质即可得到结论.
【详解】证明:∵ ,∴∠ADE=90°,
∵ ,
∴∠ACB=∠ADE,
在 和 中
,
∴ ,
∴AE=AB,AC=AD,
∴AE-AC=AB-AD,即EC=BD.
【点睛】本题考查全等三角形的判定和性质,解题的关键是熟练掌握基本知识.
18.某兴趣小组为了测量大楼 的高度,先沿着斜坡 走了 米到达坡顶点 处,然后在点 处测得
大楼顶点 的仰角为 ,已知斜坡 的坡度为 ,点 到大楼的距离 为 米,求大楼的
高度 .(参考数据: , , )
【答案】大楼的高度 为52米
【解析】
【分析】
过点B作BE⊥AD于点E,作BF⊥CD于点F,在Rt△ABE中,根据坡度 及勾股定理求出BE和
AE的长,进而由三个角是直角的四边形是矩形判断四边形 BEDF是矩形,得到BF和FD的长,再在
Rt△BCF中,根据∠CBF的正切函数解直角三角形,得到CF的长,由CD=CF+FD得解.【详解】解:如下图,过点B作BE⊥AD于点E,作BF⊥CD于点F,
在Rt△ABE中,AB=52,
∵
∴tan∠BAE= = ,
∴AE=2.4BE,
又∵BE2+AE2=AB2,
∴BE2+(2.4BE)2=522,
解得:BE=20,
∴AE=2.4BE=48;
∵∠BED=∠D=∠BFD=90°,
∴四边形BEDF是矩形,
∴FD=BE=20,BF=ED=AD-AE=72-48=24;
在Rt△BCF中,
tan∠CBF= ,
即:tan53°= =
∴CF= BF=32,
∴CD=CF+FD=32+20=52.
答:大楼的高度 为52米.
【点睛】本题考查解直角三角形的实际应用,熟练掌握仰角的定义,准确确定合适的直角三角形并且根据
勾股定理或三角函数列出方程是解题的关键.
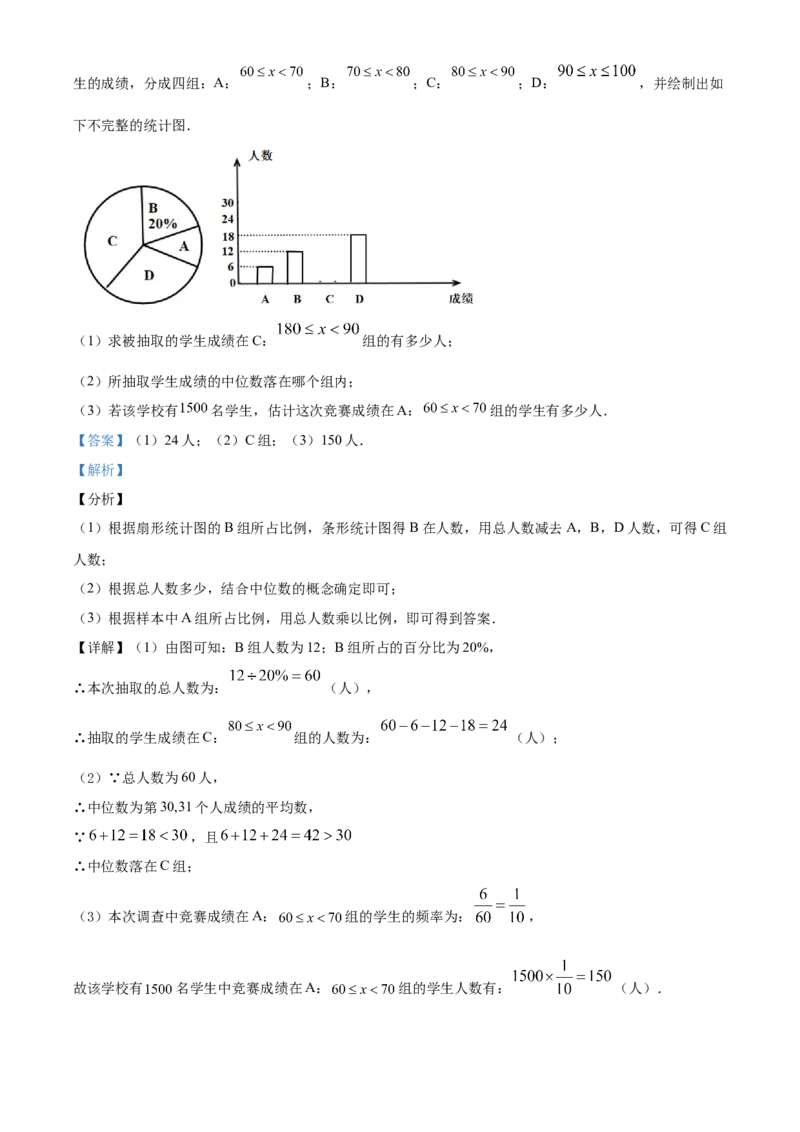
19.某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:A: ;B: ;C: ;D: ,并绘制出如
下不完整的统计图.
(1)求被抽取的学生成绩在C: 组的有多少人;
(2)所抽取学生成绩的中位数落在哪个组内;
(3)若该学校有 名学生,估计这次竞赛成绩在A: 组的学生有多少人.
【答案】(1)24人;(2)C组;(3)150人.
【解析】
【分析】
(1)根据扇形统计图的B组所占比例,条形统计图得B在人数,用总人数减去A,B,D人数,可得C组
人数;
(2)根据总人数多少,结合中位数的概念确定即可;
(3)根据样本中A组所占比例,用总人数乘以比例,即可得到答案.
【详解】(1)由图可知:B组人数为12;B组所占的百分比为20%,
∴本次抽取的总人数为: (人),
∴抽取的学生成绩在C: 组的人数为: (人);
(2)∵总人数为60人,
∴中位数为第30,31个人成绩的平均数,
∵ ,且
∴中位数落在C组;
(3)本次调查中竞赛成绩在A: 组的学生的频率为: ,
故该学校有 名学生中竞赛成绩在A: 组的学生人数有: (人).【点睛】本题考查了条件统计图与扇形统计图的信息读取,以及总数,频数与频率之间的转化计算,熟知
以上知识是解题的关键.
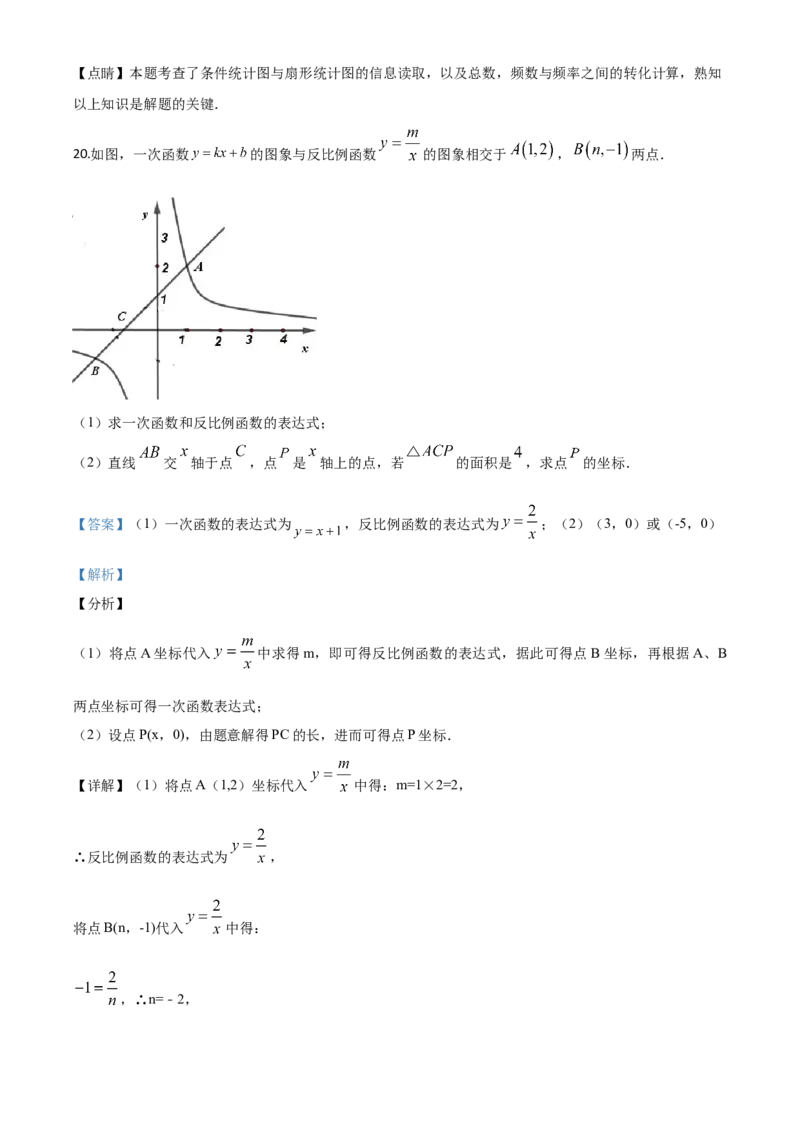
20.如图,一次函数 的图象与反比例函数 的图象相交于 , 两点.
(1)求一次函数和反比例函数的表达式;
(2)直线 交 轴于点 ,点 是 轴上的点,若 的面积是 ,求点 的坐标.
【答案】(1)一次函数的表达式为 ,反比例函数的表达式为 ;(2)(3,0)或(-5,0)
【解析】
【分析】
(1)将点A坐标代入 中求得m,即可得反比例函数的表达式,据此可得点B坐标,再根据A、B
两点坐标可得一次函数表达式;
(2)设点P(x,0),由题意解得PC的长,进而可得点P坐标.
【详解】(1)将点A(1,2)坐标代入 中得:m=1×2=2,
∴反比例函数的表达式为 ,
将点B(n,-1)代入 中得:
,∴n=﹣2,∴B(-2,-1),
将点A(1,2)、B(-2,-1)代入 中得:
解得: ,
∴一次函数的表达式为 ;
(2)设点P(x,0),
∵直线 交 轴于点 ,
∴由0=x+1得:x=﹣1,即C(-1,0),
∴PC=∣x+1∣,
∵ 的面积是 ,
∴
∴解得: ,
∴满足条件的点P坐标为(3,0)或(-5,0).
【点睛】本题考查了反比例函数与一次函数的交点问题,会用待定系数法求函数的解析式,会用坐标表示
线段长是解答的关键.
21.今年史上最长的寒假结束后,学生复学,某学校为了增强学生体质,鼓励学生在不聚集的情况下加强体
育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买 根跳绳和 个毽子共需 元;购买 根跳
绳和 个毽子共需 元.
(1)求购买一根跳绳和一个毽子分别需要多少元;
(2)某班需要购买跳绳和毽子的总数量是 ,且购买的总费用不能超过 元;若要求购买跳绳的数量
多于 根,通过计算说明共有哪几种购买跳绳的方案.
【答案】(1)购买一根跳绳需要6元,一个毽子需要4元;(2)方案一:购买跳绳21根;方案二:购买
跳绳22根
【解析】【分析】
(1)设购买一根跳绳需要x元,一个毽子需要y元,依题意列出二元一次方程组解之即可;
(2)设学校购进跳绳m根,则购进毽子(54-m)根,根据题意列出不等式解之得m的范围,进而可判断
购买方案.
【详解】(1)设购买一根跳绳需要x元,一个毽子需要y元,
依题意,得: ,
解得: ,
答:购买一根跳绳需要6元,一个毽子需要4元;
(2)设学校购进跳绳m根,则购进毽子(54-m)根,
根据题意,得: ,
解得:m≤22,
又m﹥20,且m为整数,
∴m=21或22,
∴共有两种购买跳绳的方案,方案一:购买跳绳21根;方案二:购买跳绳22根.
【点睛】本题考查二元一次方程组以及一元一次不等式的应用,根据题意正确列出方程式及不等式是解答
的关键.
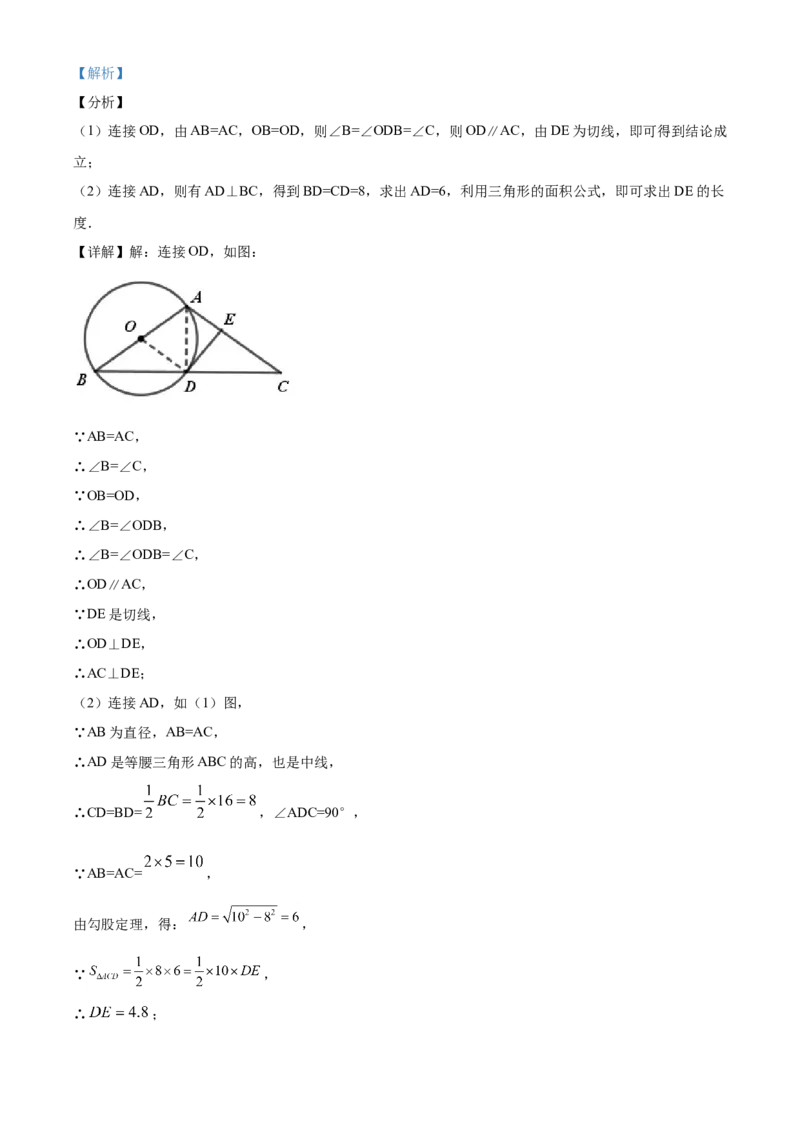
22.如图,在 中, ,以 为直径的⊙O与 相交于点 ,过点 作⊙O的切线交
于点 .
(1)求证: ;
(2)若⊙O的半径为 , ,求 的长.
【答案】(1)见详解;(2)4.8.【解析】
【分析】
(1)连接OD,由AB=AC,OB=OD,则∠B=∠ODB=∠C,则OD∥AC,由DE为切线,即可得到结论成
立;
(2)连接AD,则有AD⊥BC,得到BD=CD=8,求出AD=6,利用三角形的面积公式,即可求出DE的长
度.
【详解】解:连接OD,如图:
∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠B=∠ODB=∠C,
∴OD∥AC,
∵DE是切线,
∴OD⊥DE,
∴AC⊥DE;
(2)连接AD,如(1)图,
∵AB为直径,AB=AC,
∴AD是等腰三角形ABC的高,也是中线,
∴CD=BD= ,∠ADC=90°,
∵AB=AC= ,
由勾股定理,得: ,
∵ ,
∴ ;【点睛】本题主要考查的是切线的性质、等腰三角形的性质、平行线的性质、勾股定理,解题的关键是熟
练掌握所学的性质定理,正确的求出边的长度.
的
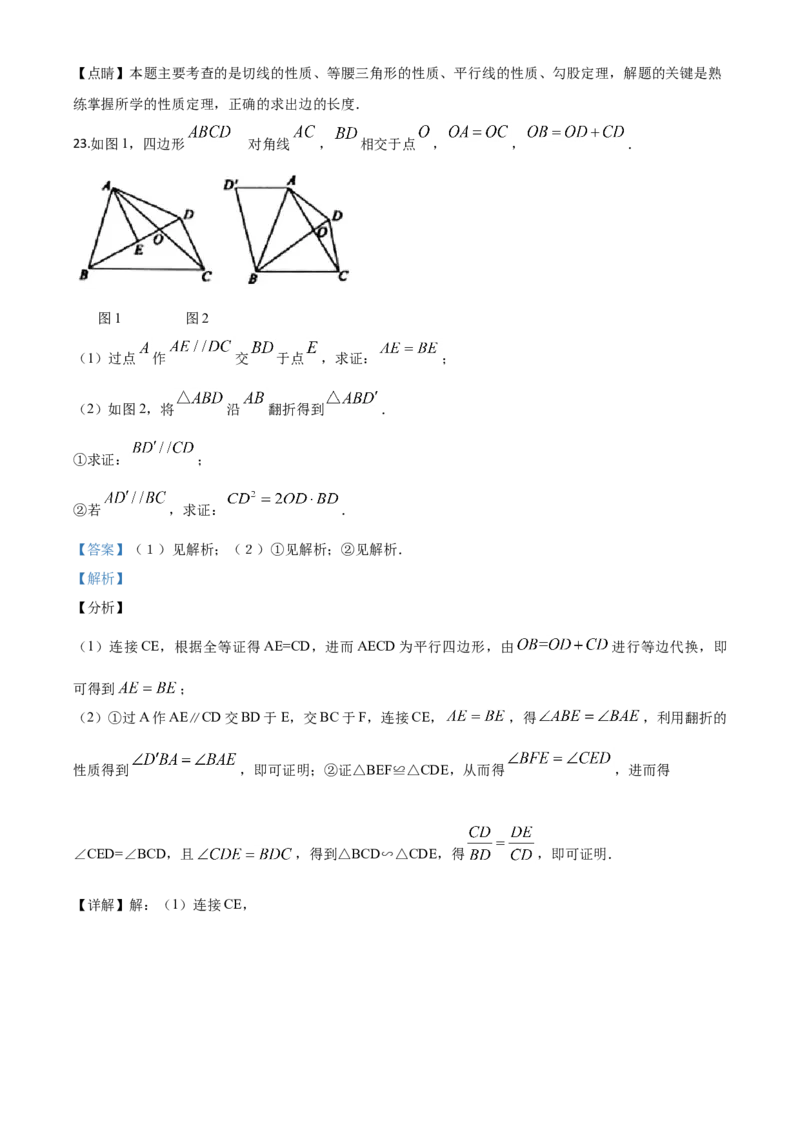
23.如图1,四边形 对角线 , 相交于点 , , .
图1 图2
(1)过点 作 交 于点 ,求证: ;
(2)如图2,将 沿 翻折得到 .
①求证: ;
②若 ,求证: .
【答案】(1)见解析;(2)①见解析;②见解析.
【解析】
【分析】
(1)连接CE,根据全等证得AE=CD,进而AECD为平行四边形,由 进行等边代换,即
可得到 ;
(2)①过A作AE∥CD交BD于E,交BC于F,连接CE, ,得 ,利用翻折的
性质得到 ,即可证明;②证△BEF≌△CDE,从而得 ,进而得
∠CED=∠BCD,且 ,得到△BCD∽△CDE,得 ,即可证明.
【详解】解:(1)连接CE,∵ ,
∴ ,
∵ , , ,
∴△OAE≌△OCD,
∴AE=CD,
∴四边形AECD为平行四边形,
∴AE=CD,OE=OD,
∵ ,
∴CD=BE,
∴ ;
(2)①过A作AE∥CD交BD于E,交BC于F,连接CE,
由(1)得, ,
∴ ,
由翻折的性质得 ,
∴ ,
∴ ,
∴ ;
②∵ , ,
∴四边形 为平行四边形,
∴ , ,∴ ,
∵ ,
∴EF=DE,
∵四边形AECD 是平行四边形,
∴CD=AE=BE,
∵AF∥CD,
∴ ,
∵EF=DE,CD=BE, ,
∴△BEF≌△CDE(SAS),
∴ ,
∵ ,
∴∠CED=∠BCD,
又∵∠BDC=∠CDE,
∴△BCD∽△CDE,
∴ ,即 ,
∵DE=2OD,
∴ .
【点睛】本题考查相似三角形的判定与性质以及平行四边形的判定和性质,考查等腰三角形的判定与性质
综合,熟练掌握各图形的性质并灵活运用是解题的关键.
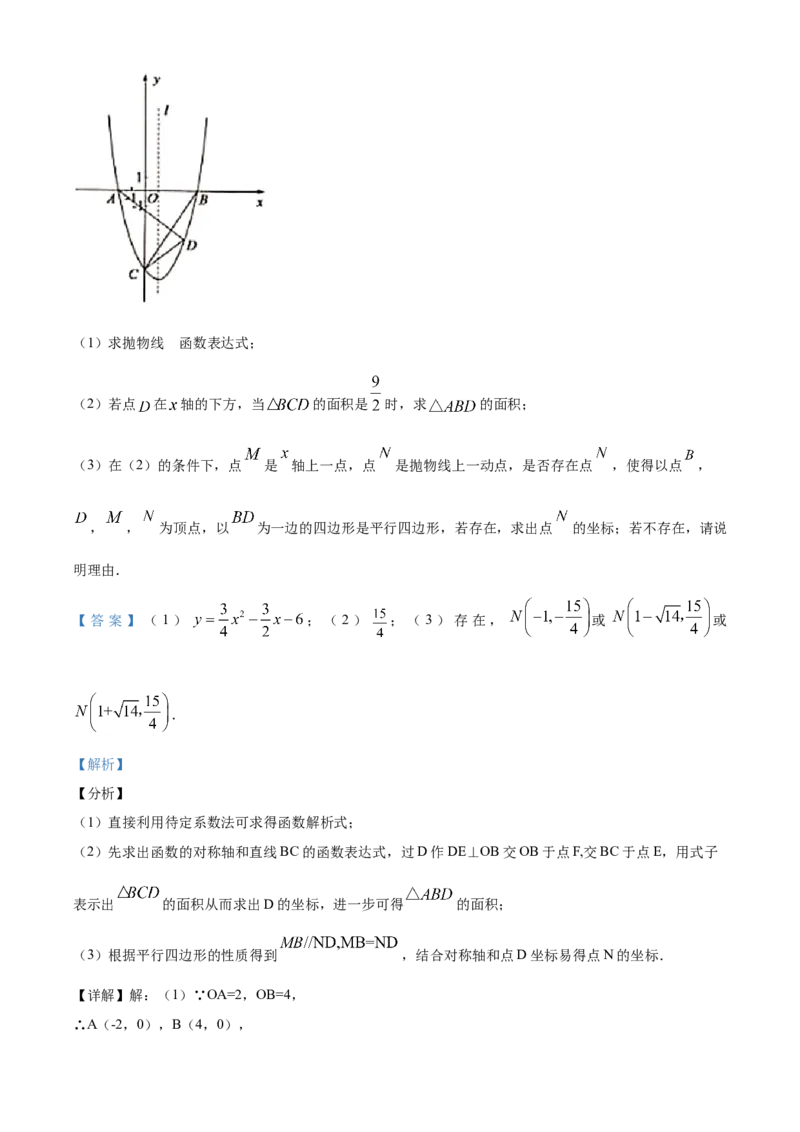
24.如图,抛物线 与 轴相交于 , 两点,与 轴相交于点 , , ,直
线 是抛物线的对称轴,在直线 右侧的抛物线上有一动点 ,连接 , , , .的
(1)求抛物线 函数表达式;
(2)若点 在 轴的下方,当 的面积是 时,求 的面积;
(3)在(2)的条件下,点 是 轴上一点,点 是抛物线上一动点,是否存在点 ,使得以点 ,
, , 为顶点,以 为一边的四边形是平行四边形,若存在,求出点 的坐标;若不存在,请说
明理由.
【答案】(1) ;(2) ;(3)存在, 或 或
.
【解析】
【分析】
(1)直接利用待定系数法可求得函数解析式;
(2)先求出函数的对称轴和直线BC的函数表达式,过D作DE⊥OB交OB于点F,交BC于点E,用式子
表示出 的面积从而求出D的坐标,进一步可得 的面积;
(3)根据平行四边形的性质得到 ,结合对称轴和点D坐标易得点N的坐标.
【详解】解:(1)∵OA=2,OB=4,
∴A(-2,0),B(4,0),将A(-2,0),B(4,0)代入 得:
,
解得:
∴抛物线的函数表达式为: ;
(2)由(1)可得抛物线 的对称轴l: , ,
设直线BC: ,
可得:
解得 ,
∴直线BC的函数表达式为: ,
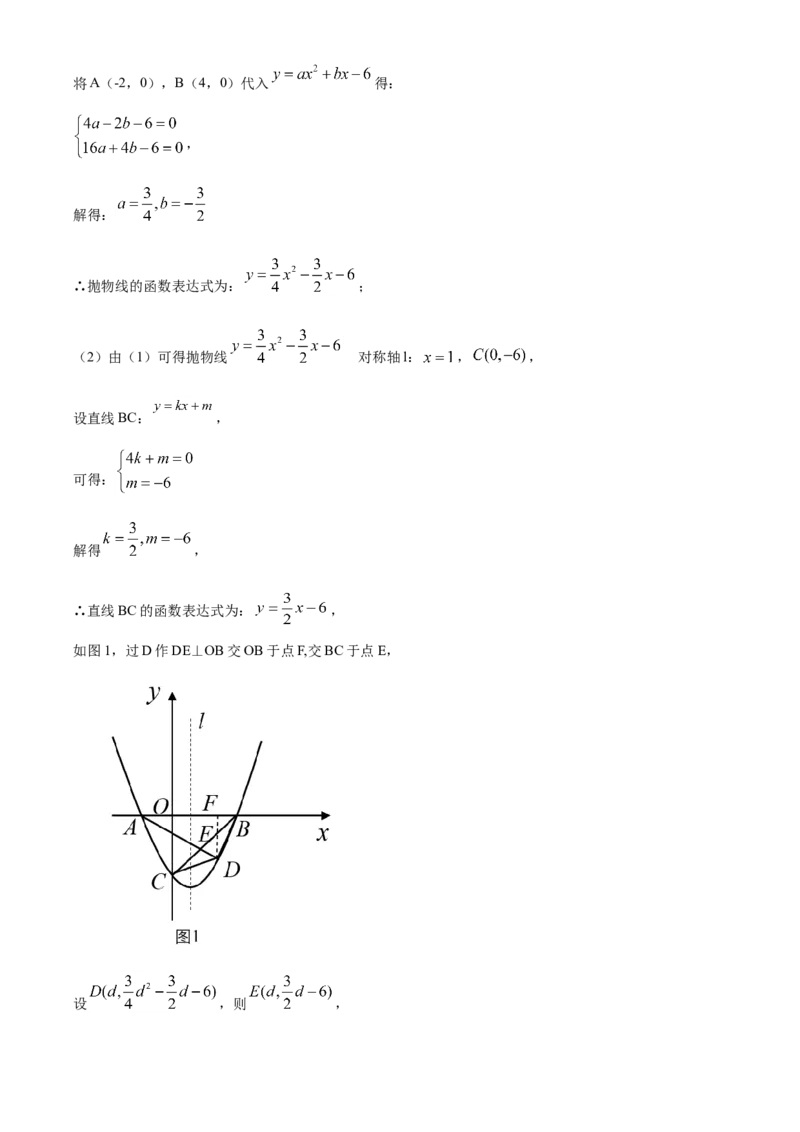
如图1,过D作DE⊥OB交OB于点F,交BC于点E,
设 ,则 ,∴ ,
由题意可得
整理得
解得 (舍去),
∴ ,
∴
∴
;
(3)存在
由(1)可得抛物线 的对称轴l: ,由(2)知 ,
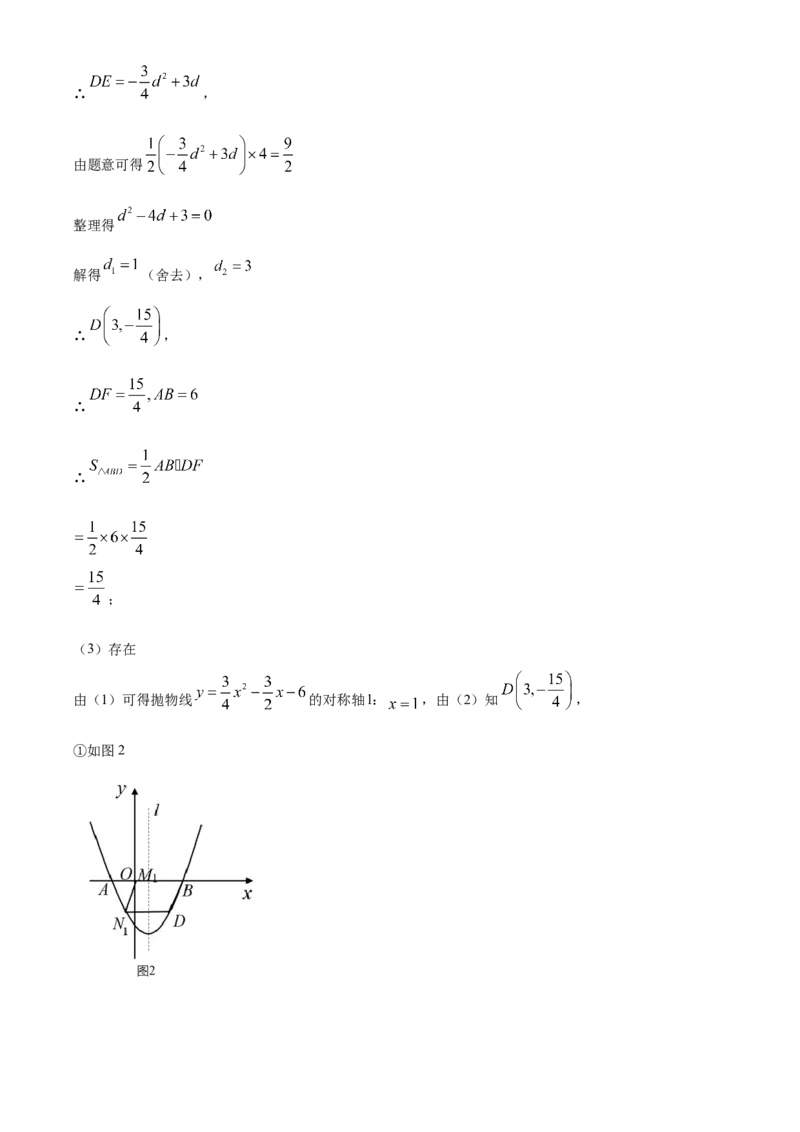
①如图2当 时,四边形BDNM即为平行四边形,
此时MB=ND=4,点M与点O重合,四边形BDNM即为平行四边形,
∴由对称性可知N点横坐标为-1,将x=-1代入
解得
∴此时 ,四边形BDNM即为平行四边形.
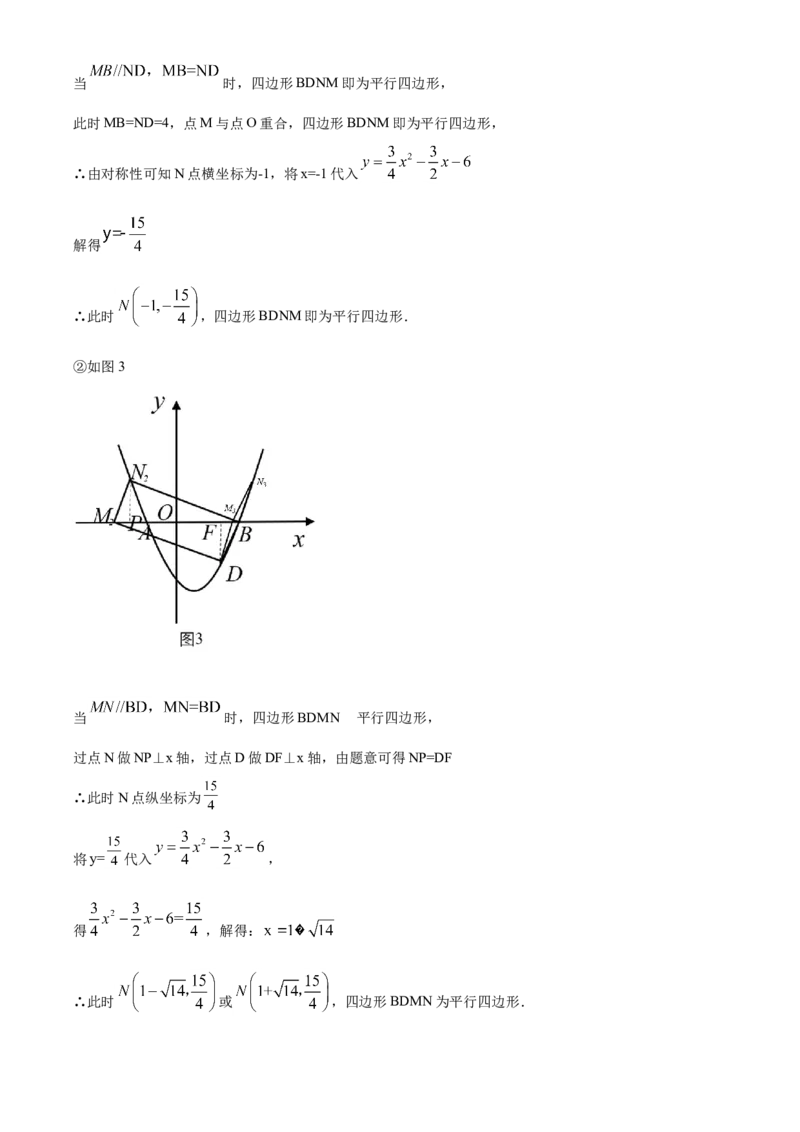
②如图3
为
当 时,四边形BDMN 平行四边形,
过点N做NP⊥x轴,过点D做DF⊥x轴,由题意可得NP=DF
∴此时N点纵坐标为
将y= 代入 ,
得 ,解得:
∴此时 或 ,四边形BDMN为平行四边形.综上所述, 或 或 .
【点睛】本题考查的是二次函数的综合,首先要掌握待定系数法求解析式,其次要添加恰当的辅助线,灵
活运用面积公式和平行四边形的判定和性质,应用数形结合的数学思想解题.本试卷的题干、答案和解析均由组卷网(http://zujuan.xkw.com)专业教师团队编校出品。
登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。
试卷地址:在组卷网浏览本卷
组卷网是学科网旗下的在线题库平台,覆盖小初高全学段全学科、超过900万精品解析试题。
关注组卷网服务号,可使用移动教学助手功能(布置作业、线上考试、加入错题本、错题训练)。
学科网长期征集全国最新统考试卷、名校试卷、原创题,赢取丰厚稿酬,欢迎合作。
钱老师 QQ:537008204 曹老师 QQ:713000635