鲁教版9年级数学上册高清教材_4-教培资料-26年最新资料-同步更新_初中高中教资_03科三专项（进去保存报考的学科即可）_02科三专项（笔记真题思维导图教学设计版本二）

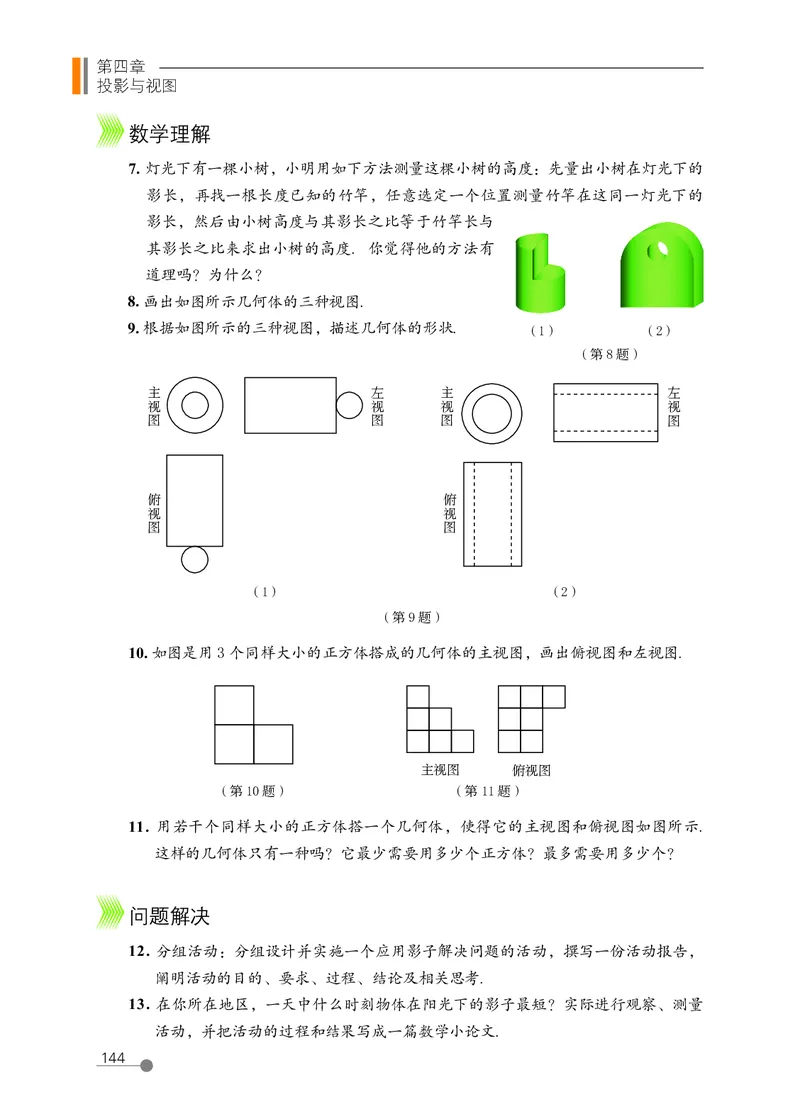
绿色印刷产品 义务教育教科书（五·四学制） 数学 九年级 上册 定价：9.15元 价格批准文号：鲁发改价格核（2021）607010 举报电话：12345YIWU JIAOYU JIAOKESHU （WU·SI XUEZHI） SHUXUE JIU NIANJI SHANG CE 义务教育教科书（五·四学制） 数学 九年级 上册 * 山东出版传媒股份有限公司 山东教育出版社出版 （济南市市中区二环南路 2066 号 4 区 1 号） 山东新华书店集团有限公司发行 山东新华印刷厂潍坊厂印装 * 开本：787 毫米×1092 毫米 1/16 印张：9.75 字数：195 千 定价：9.15 元（上光） ISBN 978-7-5328-8328-8 2014 年 8 月第 1 版 2021 年 7 月第 8 次印刷 著作权所有·请勿擅用本书制作各类出版物·违者必究 山东出版传媒股份有限公司教材中心售后服务电话：（0531）82098188亲爱的同学： 祝贺你步入义务教育的最后一个学年！ 前几年的数学学习生活使你接触到许多数学对象，经历了许 多有意义的数学活动，还学到了一些重要的数学方法，并且能够 用它们去解决问题。更重要的是，我们看到了身边的数学，掌握 了一些学习数学的基本方法，有了学好数学的信心…… 你已经学习了一次函数，反比例函数是另一种函数模型，学 习过后，相信你会对函数的认识更加丰富。 在与变量、函数打交道时，我们初步体验到函数对变化过程 的描述，也感受到一个变化过程中存在“不变因素”。二次函数 是一种较为复杂的“经典”函数，对它的研究将使我们体会到二 次函数的广泛应用和研究函数的基本思路、方法和内容，而这一 切又是你未来数学学习的重要知识基础，切不可掉以轻心呀！ “直角三角形的边角关系”与生活中的许多现象密不可分， 与相似、比例、函数……有着千丝万缕的联系，学习它将有益于 我们了解数形之间的关系，进一步体会到数学的价值。 物体在灯光下、太阳光下都有影子，物体的这些影子有什么 特点和规律？从数学的角度如何来认识它？这部分内容学完后你 将发现“数学会使我们看得更深刻”。 学好数学当然不是轻而易举就能做到的，但也并非高不可 攀。自己想一想、做一做，与同伴们议一议，读一读教科书，听 一听老师的讲解，并在日常生活中尝试使用数学。事实上，对数 学了解得越多，你就越能体会到它的意义与趣味。 让我们一起走进数学新天地！目 录 MULU 第一章 反比例函数 (cid:18)(cid:18)(cid:18)(cid:1318)(cid:1318)(cid:3467)(cid:915)(cid:1126)(cid:2973) 1 反比例函数 …………………… 2 2 反比例函数的图象与性质 …… 5 3 反比例函数的应用 …………… 14 yyyyyyy(cid:62)(cid:62)(cid:62)(cid:62)(cid:33)(cid:33)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20) xxxxxxxx IIII(cid:62)(cid:62)(cid:62) RRRRRRRRR (cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:21)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19) yyyyyyy(cid:62)(cid:62)(cid:62)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19) (cid:26)(cid:26)(cid:26)(cid:26)(cid:26) (cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)xxxxxxxx 回顾与思考 ……………………… 17 yyyyyyy(cid:62)(cid:62)(cid:62)(cid:62)(cid:33)(cid:33)(cid:25)(cid:25)(cid:25)(cid:25)(cid:25)(cid:25)(cid:25)(cid:25) xxxxxxxx (cid:62)(cid:62)(cid:62) (cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:22)(cid:22)(cid:22)(cid:22)(cid:22)(cid:22)(cid:22)(cid:22)(cid:22)(cid:22)(cid:22)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:20)(cid:27)(cid:27)(cid:27)(cid:27)(cid:27)(cid:27)(cid:27)(cid:27)(cid:27) VVVVVV tttttt 复习题 …………………………… 17 y(cid:23) (cid:22) (cid:21) (cid:46)(cid:33)(cid:23)(cid:46)(cid:33)(cid:22)(cid:46)(cid:33)(cid:21)(cid:46)(cid:33)(cid:20) O (cid:20) (cid:46)(cid:33)(cid:20)(cid:20)(cid:21)(cid:22)(cid:23) x (cid:46)(cid:33)(cid:21) (cid:46)(cid:33)(cid:22) (cid:46)(cid:33)(cid:23) 综合与实践 (cid:25)(cid:25)(cid:25)(cid:25)(cid:25)(cid:25)(cid:25)(cid:25)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19)(cid:19) pppppppp(cid:62)(cid:62)(cid:62) SSSSSSSS (cid:18) 能将矩形的周长和面积同时加倍吗 … 19 第二章 直角三角形的边角关系 1 锐角三角函数 ………………… 24 2 30°，45°，60°角的三角函数值 … 30 3 用计算器求锐角的三角函数值… 34 4 解直角三角形 ………………… 40 5 三角函数的应用 ……………… 46 6 利用三角函数测高 …………… 51 回顾与思考 ………………………… 54 复习题 ……………………………… 54 综合与实践 A B 设计遮阳篷 ………………………… 58第三章 二次函数 1 对函数的再认识 ………………… 62 2 二次函数 ………………………… 69 3 二次函数 y = ax 2 的图象与性质 … 71 4 二次函数 y = ax 2 + bx + c 的图象 与性质 …………………………… 78 5 确定二次函数的表达式 ………… 90 6 二次函数的应用 ………………… 96 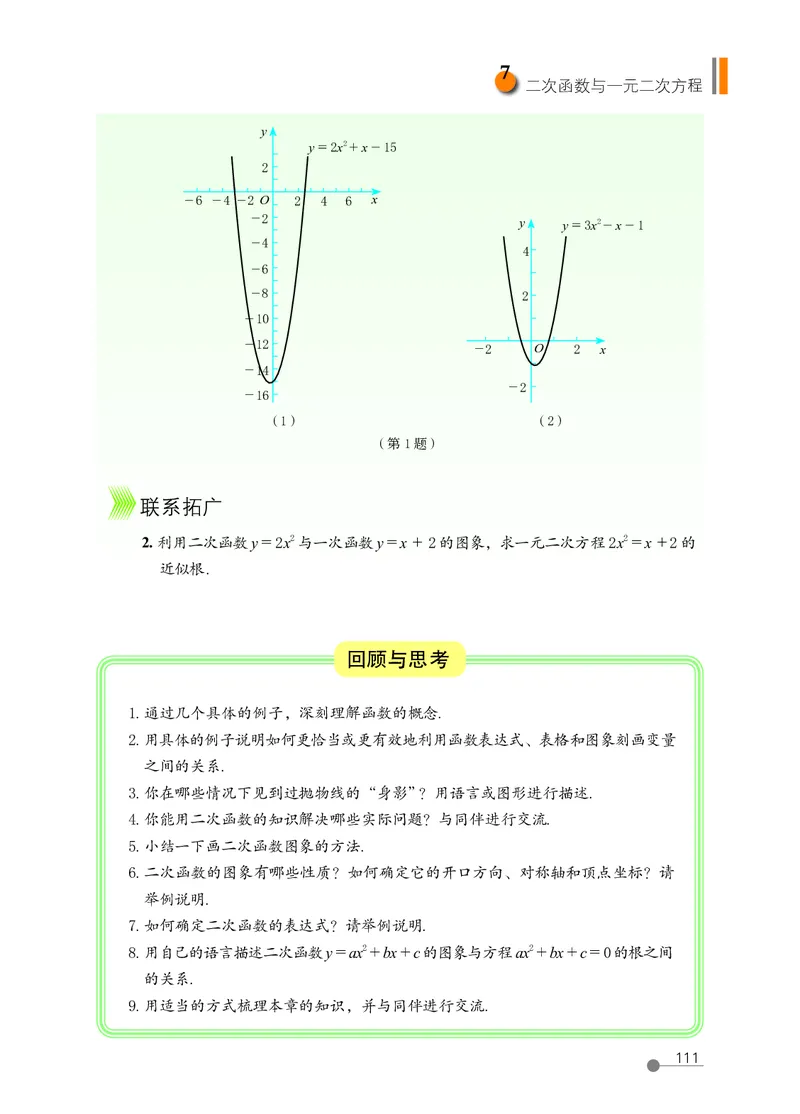7 二次函数与一元二次方程 …… 104 回顾与思考 ………………………… 111 复习题 ……………………………… 112 综合与实践 拱桥形状设计 ……………………… 117 第四章 投影与视图 1 投影 ………………………… 120 2 视图 ………………………… 132 回顾与思考 ……………………… 141 复习题 …………………………… 142 总复习题 ……………………… 1451111 反反反比比比例例例函函函数数数 第一章 反比例函数 当人和木板对地面的压力一定时，随着木板面积的变化，人和木板对地面 的压强将如何变化？当列车行驶的路程一定时，随着列车行驶的平均速度的 变化，列车行驶的时间将如何变化？……这其中的数量关系具有怎样的共同 特征？ 本章将研究反比例函数. 与一次函数一样，反比例函数也是刻画很多现实 问题中变量之间关系的重要数学模型. 77 II == yy == 11 22 22 00 110000 xx yy == xx RR y 4 8 66 1 3 3 yy == 1 xx 2 VV 1 == - 4- 3- 2- 1 tt O 1 2 3 4 x - 1 - 2 - 3 - 4 学习目标 积累从现实问题中抽象出变量之间的依赖 关系并加以表示的经验 体会反比例函数的意义，能根据已知条件 确定反比例函数的表达式 能画出反比例函数的图象 借助图象和表达式探索并理解反比例函数 的性质，体会数形结合的思想 进一步体会用函数解决实际问题的方法与 思想 660000 pp == SS 11第一章 反比例函数 1 反比例函数 电流 I（A）、电阻 R（Ω）、电压 U（V）之间满足关系式 U = I R. 当 U = 220 V 时： （1）你能用含有 R 的代数式表示 I 吗？ （2）利用写出的关系式完成下表： R / Ω 20 40 60 80 100 I / A 当 R 越来越大时，I 怎样变化？当 R 越来越小时呢？ （3）变量 I 是 R 的函数吗？为什么？ 京沪高速铁路全长约为 1 318 km，列车沿京沪 高速铁路从上海驶往北京，列车行完全程所需要的时 间 t（h）与行驶的平均速度 v（km / h）之间有怎样的 关系？变量 t 是 v 的函数吗？为什么？ 已知两个实数的乘积为 - 8，如果其中一个因数为 p，另一个因数为 q， 则 q 与 p 之间的函数关系是什么？ 在上述问题中，变量 I 与 R 之间的关系可以表示成： 220 I = ； R 变量 t 与 v 之间的关系可以表示成： 1 318 t = ； v 21 反比例函数 变量 q 与 p 之间的关系可以表示成： - 8 q = . p 议一议 观察上面列出的三个函数关系式，你发现它们有什么共同特点？ k 一般地，如果两个变量 x，y 之间的关系可以表示成 y = （k 为常数， x k ≠ 0）的形式，那么称 y 是 x 的反比例函数（inverse proportional function）. 想一想 k 对于反比例函数 y = （k ≠0），自变量 x 的取值范围是什么？ x 反比例函数的自变量 x 不能为零. 例 已知 y 是 x 的反比例函数，当 x = - 3 时，y = 4. （1）写出 y 与 x 之间的函数关系式； （2）求当 x = 6 时 y 的值. k 解：（1）设 y = （k ≠0）， x 因为当 x = - 3 时，y = 4， k 所以有 4 = ， - 3 k = - 12. - 12 所以， y 与 x 之间的函数关系式为 y = . x - 12 （2）把 x = 6 代入 y = ，得 x - 12 y = = - 2. 6 3第一章 反比例函数 做一做 1. 一个矩形的面积为 20 cm2，相邻的两条边长分别为 x cm 和 y cm，那么 变量 y 是变量 x 的函数吗？是反比例函数吗？为什么？ 2. 某村有耕地 346.2 公顷，人口数量 n 逐年发生变化，那么该村人均占有 耕地面积 m（公顷 /人）是全村人口数 n 的函数吗？是反比例函数吗？为什么？ 3. y 是 x 的反比例函数，下表给出了 x 与 y 的一些值. 1 1 x - 2 - 1 - 1 3 2 2 2 y 2 - 1 3 （1）写出这个反比例函数的表达式； （2）根据函数表达式完成上表. 随堂练习 1. 在下列函数表达式中，x 均表示自变量，那么哪些是反比例函数？每一个反比例函 数相应的 k 值是多少？ 5 0.4 （1）y = ； （2）y = ； x x x （3）y = ； （4）xy = 2. 2 2. 你能举出两个反比例函数的实例吗？写出函数表达式，与同伴进行交流. 习题 1.1 知识技能 1. 计划修建铁路 1 200 km，那么铺轨天数 y（d）是每日铺轨量 x（km /d）的反比 例函数吗？ 42 反比例函数的图象与性质 2. 三角形的面积 S 是常数，它的一条边长为 y，这条边上的高为 x，那么 y 是 x 的 函数吗？是反比例函数吗？ 数学理解 3. 下列哪些式子表示 y 是 x 的反比例函数？为什么？ 1 （1）xy = - ； （2）y = 5 - x； 3 - 2 2a （3）y = ； （4）y = （a 为常数，a≠0）. 5x x 4. 已知 y 是 x 的反比例函数，当 x = 3 时，y = 6. （1）写出 y 与 x 之间的函数关系式； （2）当 x 为何值时，y = 8？ 5. 电流 I、电阻 R、电功率 P 之间满足关系式 P = I 2R. 已知 P = 5 W，填写下表并 回答问题： I / A 1 2 3 4 5 6 7 8 R / Ω （1）变量 R 是变量 I 的函数吗？ （2）变量 R 是变量 I 的反比例函数吗？ 2 反比例函数的图象与性质 还记得一次函数的图象吗？反比例函数的图象又会是什么样的呢？ 还记得画函数图 象的一般步骤吗？ 4 你能尝试画出反比例函数 y = 的图象吗？你是怎样画的？与同伴交流. 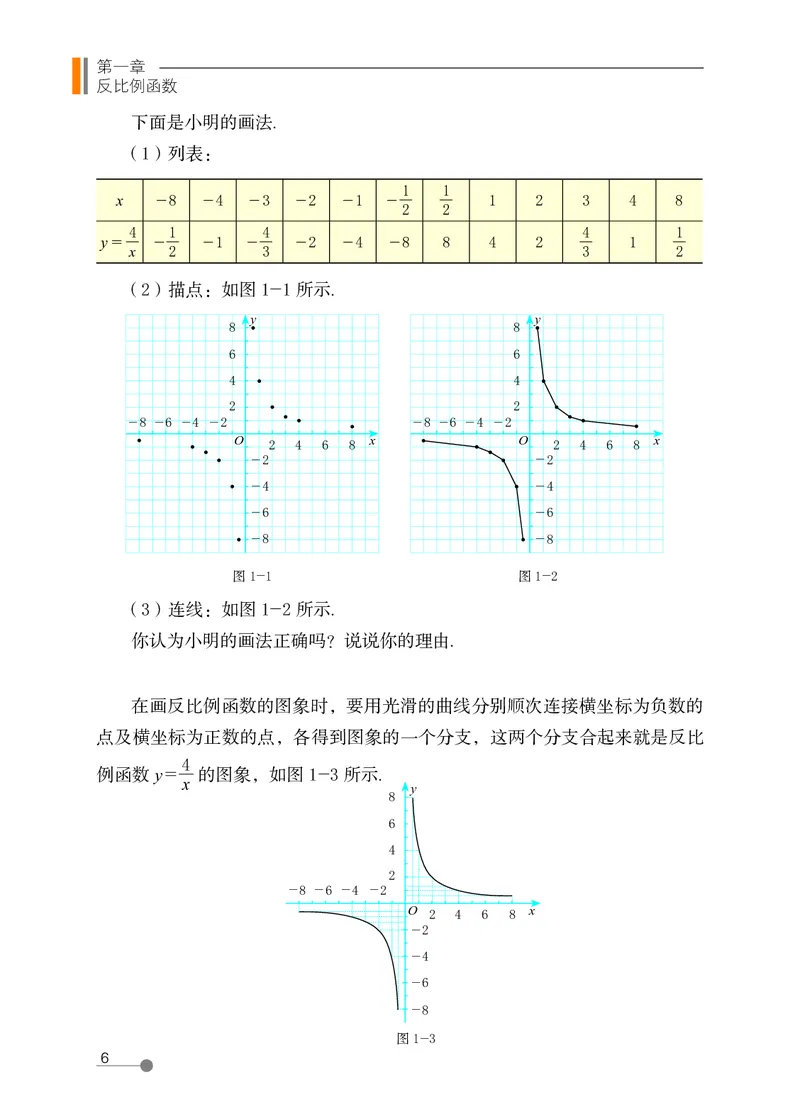x 5第一章 反比例函数 下面是小明的画法. （1）列表： 1 1 x - 8 - 4 - 3 - 2 - 1 - 1 2 3 4 8 2 2 4 1 4 4 1 y = - - 1 - - 2 - 4 - 8 8 4 2 1 x 2 3 3 2 （2）描点：如图 1-1 所示. y y 8 8 6 6 4 4 2 2 - 8 - 6 - 4 - 2 - 8 - 6 - 4 - 2 O 2 4 6 8 x O 2 4 6 8 x - 2 - 2 - 4 - 4 - 6 - 6 - 8 - 8 图 1-1 图 1-2 （3）连线：如图 1-2 所示. 你认为小明的画法正确吗？说说你的理由. 在画反比例函数的图象时，要用光滑的曲线分别顺次连接横坐标为负数的 点及横坐标为正数的点，各得到图象的一个分支，这两个分支合起来就是反比 4 例函数 y = 的图象，如图 1-3 所示. x y 8 6 4 2 - 8 - 6 - 4 - 2 O 2 4 6 8 x - 2 - 4 - 6 - 8 图 1-3 62 反比例函数的图象与性质 议一议 y 8 你认为画反比例函数图象时应注意哪些 6 问题？与同伴进行交流. 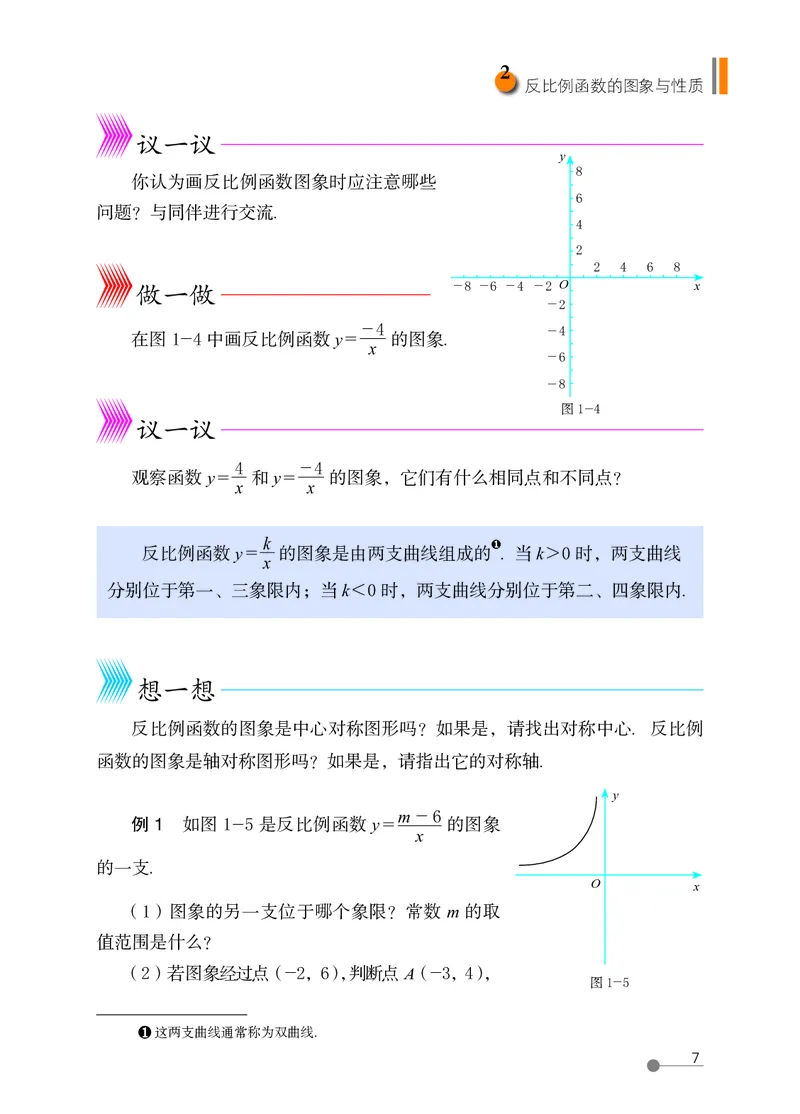4 2 2 4 6 8 做一做 - 8 - 6 - 4 - 2 O x - 2 - 4 - 4 在图 1-4 中画反比例函数 y = 的图象. x - 6 - 8 图 1-4 议一议 4 - 4 观察函数 y = 和 y = 的图象，它们有什么相同点和不同点？ x x k 反比例函数 y = 的图象是由两支曲线组成的 . 当 k > 0 时，两支曲线 x 分别位于第一、三象限内；当 k < 0 时，两支曲线分别位于第二、四象限内. 想一想 反比例函数的图象是中心对称图形吗？如果是，请找出对称中心. 反比例 函数的图象是轴对称图形吗？如果是，请指出它的对称轴. 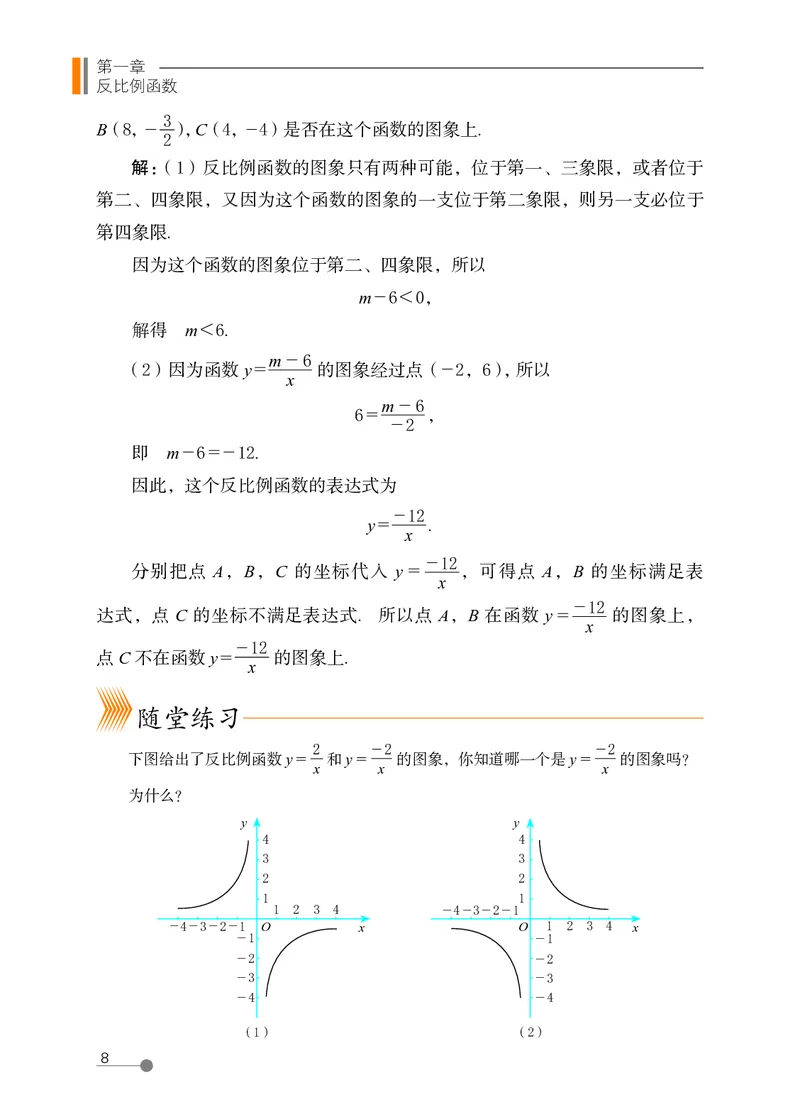y m - 6 例 1 如图 1-5 是反比例函数 y = 的图象 x 的一支. O x （1）图象的另一支位于哪个象限？常数 m 的取 值范围是什么？ （2）若图象经过点（- 2，6），判断点 A（- 3，4）， 图 1-5 这两支曲线通常称为双曲线. 7第一章 反比例函数 3 B（8，- ），C（4，- 4）是否在这个函数的图象上. 2 解：（1）反比例函数的图象只有两种可能，位于第一、三象限，或者位于 第二、四象限，又因为这个函数的图象的一支位于第二象限，则另一支必位于 第四象限. 因为这个函数的图象位于第二、四象限，所以 m - 6 < 0， 解得 m < 6. m - 6 （2）因为函数 y = 的图象经过点（- 2，6），所以 x m - 6 6 = ， - 2 即 m - 6 = - 12. 因此，这个反比例函数的表达式为 - 12 y = . x - 12 分别把点 A，B，C 的坐标代入 y = ，可得点 A，B 的坐标满足表 x - 12 达式，点 C 的坐标不满足表达式. 所以点 A，B 在函数 y = 的图象上， x - 12 点 C 不在函数 y = 的图象上. x 随堂练习 2 - 2 - 2 下图给出了反比例函数 y = 和 y = 的图象，你知道哪一个是 y = 的图象吗？ x x x 为什么？ y y 4 4 3 3 2 2 1 1 1 2 3 4 - 4- 3- 2- 1 - 4- 3- 2- 1 O x O 1 2 3 4 x - 1 - 1 - 2 - 2 - 3 - 3 - 4 - 4 （1） （2） 82 反比例函数的图象与性质 习题 1.2 知识技能 6 - 6 1. 分别画出函数 y = 和 y = 的图象. 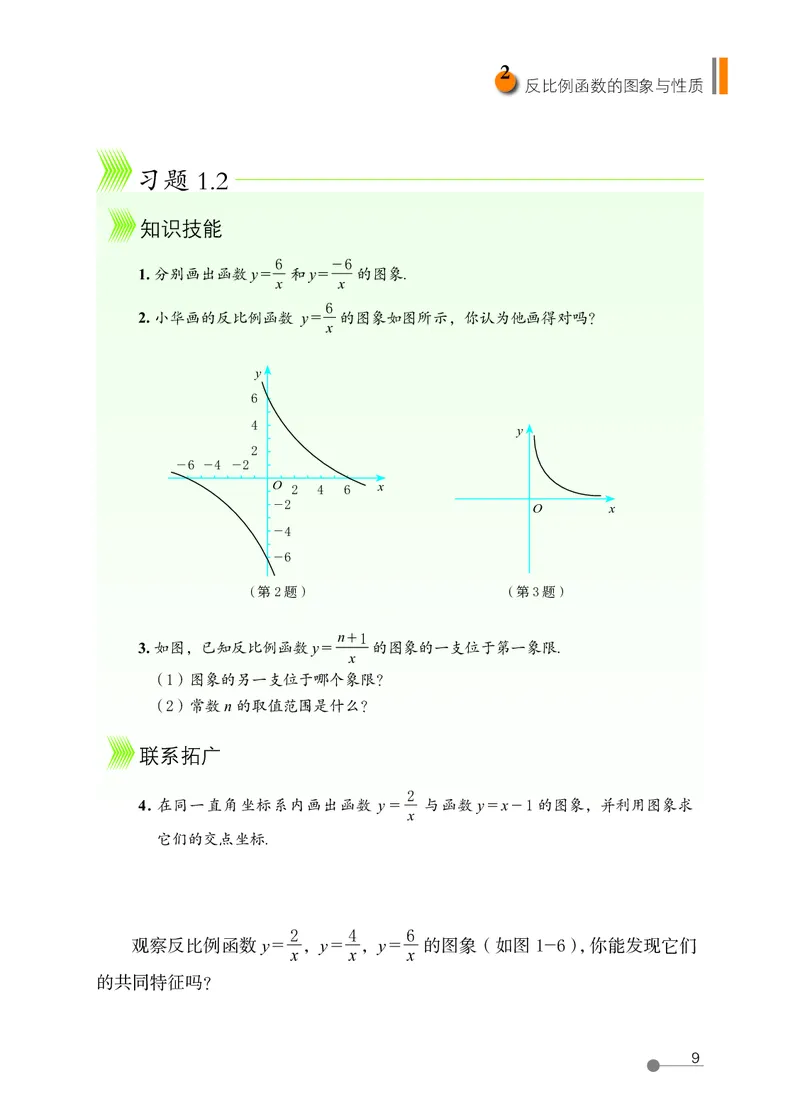x x 6 2. 小华画的反比例函数 y = 的图象如图所示，你认为他画得对吗？ x y 6 4 y 2 - 6 - 4 - 2 O 2 4 6 x - 2 O x - 4 - 6 （第 2 题） （第 3 题） n + 1 3. 如图，已知反比例函数 y = 的图象的一支位于第一象限. x （1）图象的另一支位于哪个象限？ （2）常数 n 的取值范围是什么？ 联系拓广 2 4. 在同一直角坐标系内画出函数 y = 与函数 y = x - 1 的图象，并利用图象求 x 它们的交点坐标. 2 4 6 观察反比例函数 y = ，y = ，y = 的图象（如图 1-6），你能发现它们 x x x 的共同特征吗？ 9第一章 反比例函数 y y y 6 6 6 4 y = 2 4 4 4 y = 6 x y = x x 2 2 2 - 6 - 4 - 2 - 6 - 4 - 2 - 6 - 4 - 2 O 2 4 6 x O 2 4 6 x O 2 4 6 x - 2 - 2 - 2 - 4 - 4 - 4 - 6 - 6 - 6 图 1-6 （1）函数图象分别位于哪几个象限内？ （2）在每一个象限内，随着 x 值的增大，y 的值是怎样变化的？能说明这 是为什么吗？ （3）反比例函数的图象可能与 x 轴相交吗？可能与 y 轴相交吗？为什么？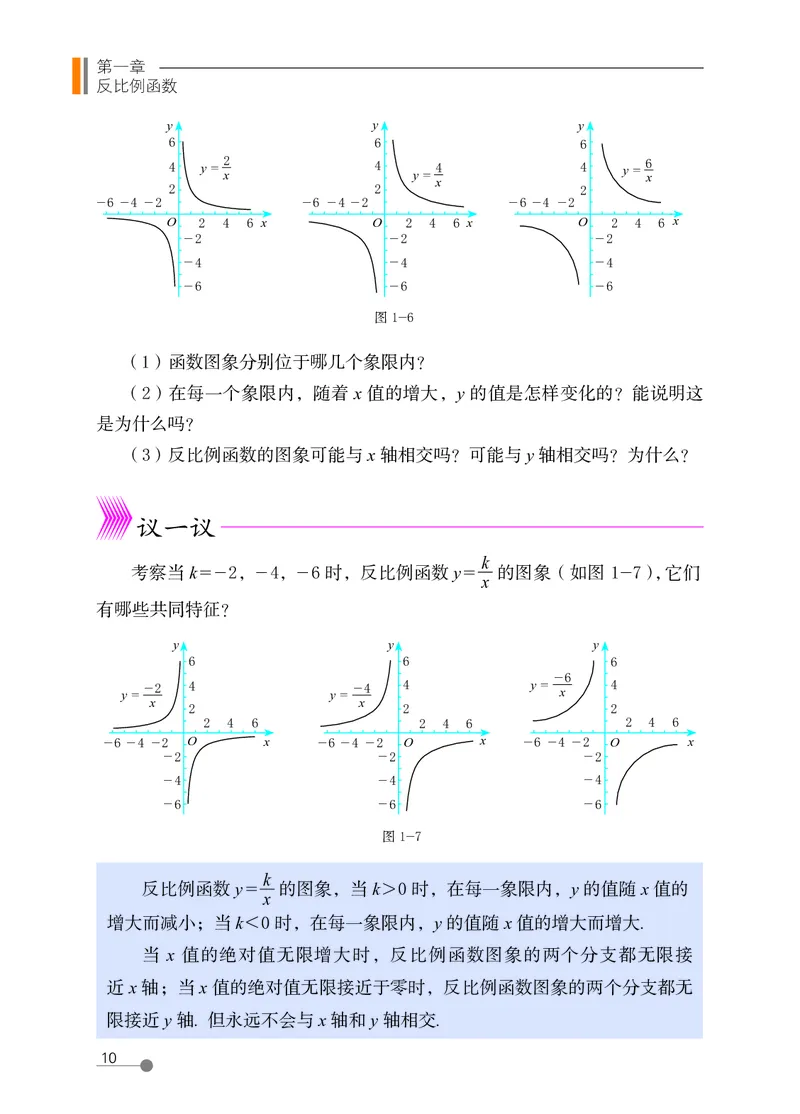 议一议 k 考察当 k = - 2，- 4，- 6 时，反比例函数 y = 的图象（如图 1-7），它们 x 有哪些共同特征？ y y y 6 6 6 - 6 - 2 4 - 4 4 y = 4 y = y = x x 2 x 2 2 2 4 6 2 4 6 2 4 6 - 6 - 4 - 2 O x - 6 - 4 - 2 O x - 6 - 4 - 2 O x - 2 - 2 - 2 - 4 - 4 - 4 - 6 - 6 - 6 图 1-7 k 反比例函数 y = 的图象，当 k > 0 时，在每一象限内，y 的值随 x 值的 x 增大而减小；当 k < 0 时，在每一象限内，y 的值随 x 值的增大而增大. 当 x 值的绝对值无限增大时，反比例函数图象的两个分支都无限接 近 x 轴；当 x 值的绝对值无限接近于零时，反比例函数图象的两个分支都无 限接近 y 轴. 但永远不会与 x 轴和 y 轴相交. 102 反比例函数的图象与性质 例 2 若反比例函数的图象经过点 A（- 3，6）. （1）求这个反比例函数的表达式； （2）在这个函数的图象上任取点 A（a，m）和点 B（b，n），若 a > b > 0， 那么 m 和 n 有怎样的大小关系？ 解：（1）设反比例函数的关系式为 k y = . x k 将 A（- 3，6）的坐标代入 y = 中，得 x k 6 = ， - 3 解得 k = - 18. 所以这个反比例函数的表达式为 18 y = - . x （2）因为 k < 0， 所以在每一象限内，y 的值随 x 值的增大而增大. 又 a > b > 0， 所以 m > n. 议一议 若把例 2 中的条件“a > b > 0”改为条件“a < b < 0”或“a > 0 > b ”， 则 m 与 n 的关系又如何？ 想一想 在一个反比例函数图象上任取两点 P，Q . 过点 P 分别作 x 轴、y 轴的平行 线，与坐标轴围成的矩形面积为 S ；过点 Q 分别作 x 轴、y 轴的平行线，与坐 1 标轴围成的矩形面积为 S . S 与 S 有什么关系？为什么？ 2 1 2 11第一章 反比例函数 随堂练习 6 1.（1）已知点（- 6，y ），（- 4，y ）在反比例函数 y = - 的图象上，试比较 y 与 1 2 x 1 y 的大小. 你是怎么做的？ 2 6 （2）已知点（4，y），（6，y）在反比例函数 y = - 的图象上，试比较 y 与 y 的 3 4 x 3 4 大小. 6 （3）已知点（- 4，y ），（6，y ）在反比例函数 y = - 的图象上，试比较 y 与 y 5 6 x 5 6 的大小. 2. 下列函数中，其图象位于第一、三象限的有 ________；在其图象所在的象限内， y 的值随 x 值的增大而增大的有 ________. 1 0.3 （1）y = ； （2）y = ； 2x x 10 - 7 （3）y = ； （4）y = . x 100x 读一读 反比例函数与三等分角 同学们都知道，关于尺规作图有著名的“三大不能” 问题，其中之一就是三等分 角的问题. 但是，你知道借助反比例函数的图象，就可以完成对一个角的三等分吗？ 它的作法是这样的： （1）如图 1-8，建立直角坐标系，将已知锐角∠AOB 的顶点与原点 O 重合，角的 一边 OB 与 x 轴正方向重合. y A P M Q R N O H B x 图 1-8 倍立方问题、三等分角问题、化圆为方问题. 122 反比例函数的图象与性质 1 （2）在直角坐标系内，绘制函数 y = 的图象，图象与已知角的另一边 OA 交于 x 点 P . 1 （3）以点 P 为圆心、以 2OP 为半径作弧，交函数 y = 的图象于点 R. x （4）分别过点 P 和 R 作 x 轴和 y 轴的平行线，两线相交于点 M . （5）连接 OM，得到∠MOB. 1 这时，∠MOB = ∠AOB . 3 你知道这是为什么吗？ 你可能要问，图 1-8 给出的∠AOB 是锐角，对于钝角或直角怎么办呢？这个问题 就留给你了，相信你可以解决它. 习题 1.3 知识技能 1. 下列函数中，图象位于第一、三象限的有 _________；在图象所在的象限内， y 的值随 x 值的增大而增大的有 _________ . 2 0.1 （1）y = ； （2）y = ； 3x x 5 - 2 （3）y = ； （4）y = . x 75x k 2. 已知点 P（3，2）， Q（- 2，a）都在反比例函数 y = 的图象上. 过点 P 分别 x 作两坐标轴的垂线，垂线与两坐标轴围成的矩形面积为 S ；过点 Q 分别作两坐 1 标轴的垂线，垂线与两坐标轴围成的矩形面积为 S . 求 a，S ，S 的值. 2 1 2 数学理解 3. 已知矩形的面积为 9，试用图象表示出这个矩形两邻边之间的关系. 13第一章 反比例函数 联系拓广 1 ※4.（1）已知点（2，y ），（1，y ），（- 1，y ），（- 2，y ）都在反比例函数 y = 1 2 3 4 x 的图象上，比较 y ，y ，y ，y 的大小； 1 2 3 4 1 （2）已知点（x ，y ），（x ，y ）都在反比例函数 y = 的图象上，且 x > x ， 1 1 2 2 x 1 2 比较 y 1 与 y 2 的大小. k ※5. 已知点 A（- 2，y ），B（- 1，y ）和 C（3，y ）都在反比例函数 y = 的图象 1 2 3 x 上，比较 y ，y ，y 的大小. 1 2 3 3 反比例函数的应用 某校科技小组进行野外考察，利用铺 垫木板的方式通过了一片烂泥湿地，你能 解释他们这样做的道理吗？当人和木板对 湿地的压力一定时，随着木板面积 S（m2） 的变化，人和木板对地面的压强 p（Pa）将 如何变化？ 如果人和木板对湿地地面的压力合 计 600 N，那么 （1）用含 S 的代数式表示 p，p 是 S 的 反比例函数吗？为什么？ （2）当木板面积为 0.2 m2 时，压强是 多少？ （3）如果要求压强不超过 6 000 Pa，木板面积至少要多大？ 143 反比例函数的应用 （4）在图 1-9 所示的直角坐标系中，画出相应的函数 p / Pa 图象. （5）请利用图象对（2）和（3）作出直观解释，并与 同伴进行交流. 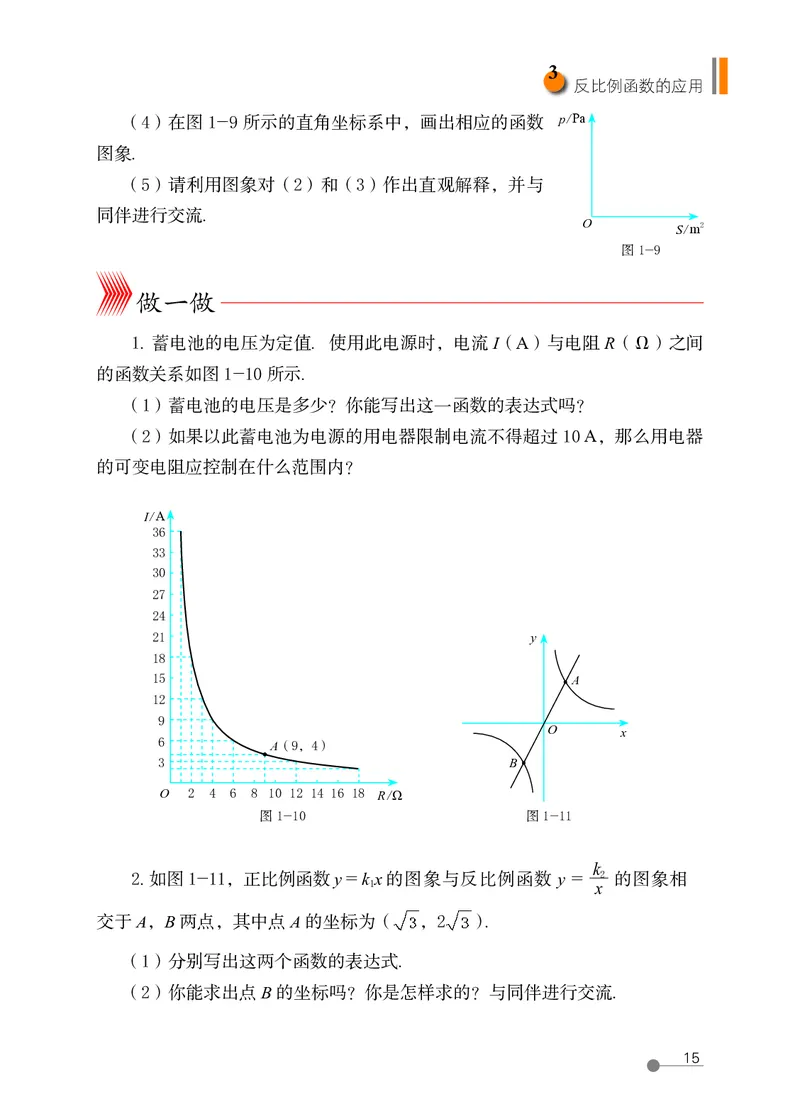O S / m2 图 1-9 做一做 1. 蓄电池的电压为定值. 使用此电源时，电流 I（A）与电阻 R（Ω）之间 的函数关系如图 1-10 所示. （1）蓄电池的电压是多少？你能写出这一函数的表达式吗？ （2）如果以此蓄电池为电源的用电器限制电流不得超过 10 A，那么用电器 的可变电阻应控制在什么范围内？ I / A 36 33 30 27 24 21 y 18 15 A 12 9 O x 6 A（9，4） 3 B O 2 4 6 8 10 12 14 16 18 R / Ω 图 1-10 图 1-11 k 2. 如图 1-11，正比例函数 y = k x 的图象与反比例函数 y = 2 的图象相 1 x 交于 A，B 两点，其中点 A 的坐标为（ ，2 ）. （1）分别写出这两个函数的表达式. （2）你能求出点 B 的坐标吗？你是怎样求的？与同伴进行交流. 15第一章 反比例函数 随堂练习 某蓄水池的排水管每小时排水 8 m3，6 h 可将满池水全部排空. （1）蓄水池的容积是多少？ （2）如果增加排水管，使每小时的排水量达到 Q（m3），那么将满池水排空所需的 时间 t（h）将如何变化？ （3）写出 t 与 Q 之间的关系式； （4）如果准备在 5 h 内将满池水排空，那么每小时的排水量至少为多少？ （5）已知排水管的最大排水量为每小时 12 m3，那么最少多长时间可将满池水全部 排空？ 习题 1.4 知识技能 1. 反比例函数的图象经过点 A（2，3），那么点 B（- ，3 ），C（2 ， - ）， 2 D（9， ）是否在该函数的图象上？ 3 问题解决 2. 某气球内充满了一定质量的气体，当温度不变时， p / kPa 气球内气体的气压 p（kPa）是气体体积 V（m3）的 200 反比例函数，其图象如图所示. 150 A（0.8，120） （1）写出这一函数的表达式； 100 （2）当气体体积为 1 m3时，气压是多少？ 50 （3）当气球内的气压大于 140 kPa 时，气球将爆炸. O 0.5 1 1.5 2 V / m3 为了安全起见，气体的体积应不小于多少？ （第 2 题） 联系拓广 k 3. 已知正比例函数 y = kx 的图象与反比例函数 y = 2 的图象的一个交点是（1，3）. 1 x （1）写出这两个函数的表达式，并确定这两个函数图象的另一个交点的坐标； ※（2）画出草图，并据此写出使反比例函数值大于正比例函数值的 x 的取值范围. 16复习题 回顾与思考 1. 你能举出现实生活中有关反比例函数的几个实例吗？ 2 - 2 2. 说说反比例函数 y = 与 y = 的图象的联系和区别. x x 3. 你能总结一下反比例函数的图象的特征吗？与同伴进行交流. 4. 你能用反比例函数的知识解决有关问题吗？请举例说明. 5. 用适当的方式梳理本章的知识，并与同伴进行交流. 复习题 知识技能 k 1. 点（23，- 3）在反比例函数 y = 的图象上，那么 k = _________，该反比例函数 x 的图象位于第_________象限. k 2. 反比例函数 y = 的图象经过点（32，3），那么点（2，23）是否在该反比例函数 x 的图象上？点（- 32，- 3）呢？为什么？ m + 1 3. 已知反比例函数 y = 的图象具有下列特征：在所在象限内，y 的值随 x 值的 x 增大而增大，那么 m 的取值范围是 _______. k 4. 如果反比例函数 y = 的图象经过点（- 2， ），那么直线 y =（k - 1）x 一定经 x 过点（2，_________）. 2 5. 考察函数 y = 的图象，当 x = - 2 时，y = _________；当 x < -2 时，y 的取值范 x 围是 _________；当 y ≥ - 1 时，x 的取值范围是 _________. 数学理解 a 6. 函数 y = ax - a 与 y = （a ≠ 0）在同一直角坐标系中的图象可能是（ ）. x 17第一章 反比例函数 y y y y O x O x O x O x （A） （B） （C） （D） （第 6 题） 联系拓广 6 - a 7. 已知正比例函数 y = ax 的图象与反比例函数 y = 的图象有一个交点的横坐标 x 是 1，求它们两个交点的坐标. k 8. 在同一直角坐标系中，正比例函数 y = k x 的图象与反比例函数 y = 2 的图象没有 1 x 公共点，则 k k 0. 1 2 ___________ - 2 ※9. 一次函数 y = kx + b 的图象与反比例函数 y = 的图象相交于 A（- 1，m）， x B（n，- 1）两点. （1）写出这个一次函数的表达式； （2）画出这两个函数图象的草图，并据此写出使一次函数值大于反比例函数值的 x 的取值范围. 18能将矩形的周长和面积同时加倍吗 能将矩形的周长和面积同时加倍吗 （1）任意给定一个正方形，是否存在另一个正方形，它的周长和面积分别 是已知正方形周长和面积的 2 倍？你是怎么做的？你有哪些解决方法？你能提 出新的问题吗？ （2）任意给定一个矩形，是否存在另一个矩形，它的周长和面积分别是已 知矩形周长和面积的 2 倍？ 矩形的形状太多 了，我们可以先研究一 个具体的矩形. 做一做 如果已知矩形的长和宽分别为 2 和 1，那么你能找到满足上面要求的矩形 吗？你是怎么做的？与同伴进行交流. 如果已知矩形的长和宽分别为 2 和 1，那么其周长和面积分别为 6 和 2， 所求矩形的周长和面积应分别为 12 和 4. 可以先固定所求矩形的周长：周 长为 12 的矩形有很多，它们的长和宽 如果设所求矩形的长为 x， 可以是 5 和 1，4 和 2，3 和 3，也可以 那么它的宽为 6 - x，而它的 11 1 面积是 x（6 - x）. 这样，问题 是 2 和 2 ……其中是否有面积为 4 就转化成讨论方程 x（6 - x） = 4 是否有解的问题了. 的矩形呢？ 19综合与实践 能将矩形的周长和面积同时加倍吗 也可以先固定所求矩形的面积：面积为 4 的矩形也有很多，它们的长和宽 1 可以是 4 和 1，2 和 2， 和 8……其中是否有周长为 12 的矩形呢？ 2 议一议 当已知矩形的长和宽分别为 3 和 1 时，是否还有相同的结论？当已知矩形 的长和宽分别为 4 和 1，5 和 1，…，n 和 1 时呢？ 更一般地，当已知矩形的长和宽分别为 n 和 m 时，是否仍然有相同的结 论？请说明理由. 任意给定一个矩形，一定存在另一个矩形，它的周长和面积分别是已知矩 形周长和面积的 2 倍. 想一想 任意给定一个矩形，是否一定存在另一个矩形，它的周长和面积分别是已 知矩形周长和面积的一半？你是怎么做的？ 这个结论是肯定的. 理由是：既然任意给定一个矩形，都存在 一个新矩形，它的周长和面积分别是已知矩形周长和面积的 2 倍， 也就是任何一个矩形的周长和面积可以同时“加倍”，那么原矩形 自然满足新矩形的“减半”要求，即原矩形的周长和面积分别是新 矩形周长和面积的一半. 例如，长和宽分别为 3 + 5 和 3 - 5 的 矩形（记为 A，其周长和面积分别是 12 和 4），是由长和宽分别 为 2 和 1 的矩形（记为 B）“加倍”而来的. 因而矩形 B 的周长和面 积分别是矩形 A 的周长和面积的一半. 你同意小明的观点吗？ 20能将矩形的周长和面积同时加倍吗 做一做 如果已知矩形的长和宽仍为 2 和 1，那么是否存在一个矩形，它的周长和 面积分别是已知矩形周长和面积的一半？ 如果已知矩形的长和宽分别是 3 和 1，4 和 1，5 和 1 呢？ 当已知矩形的长和宽为 2 和 1，3 和 1，4 和 1，5 和 1 时，都不存在这样 的矩形，它的周长和面积分别是已知矩形周长和面积的一半. 议一议 当矩形满足什么条件时，才存在一个新的矩形，它的周长和面积分别是已 知矩形周长和面积的一半？ 读一读 换一个角度看 我们在本课中研究的是有关图形性质的问题，而解决问题所采用的基本方法是 “代数”的，但还是可以从“图形”的角度来研究它. 以长和宽分别为 2 和 1 的矩形为例. 我们知道，它的“加倍”矩形（周长和面积 分别是它的 2 倍）满足 x + y = 6，xy = 4（x，y 分别表示所求矩形的长和宽）. 如果固定所求矩形的面积，那么可以发现：满足要求的（x，y）可以看做反比 4 例函数 y = 的图象在第一象限内的点的坐标. 这样的点有无数个，也就是说面积 x 为 4 的矩形有无数个. 如果固定所求矩形的周长，那 y 8 么可以发现：满足要求的（x，y）可以看做一次函 6 数 y = - x + 6 的图象在第一象限内的点的坐标. 这样的 4 点也有无数个，也就是说周长为 12 的矩形有无数个. 2 4 而满足“加倍”要求的（x，y）就可以看做反比 y = x O 2 4 6 8 x 4 例函数 y = 的图象与一次函数 y = - x + 6 的图象在 x y = - x + 6 第一象限内交点的坐标. 从图 1 中看到，这样的交点 图 1 21综合与实践 能将矩形的周长和面积同时加倍吗 y 存在，即满足要求的矩形是存在的. 4 同样地，满足“减半”要求的（x，y）可以看做反比 3 1 3 例函数 y = 的图象与一次函数 y = - x + 的 2 x 2 1 y = 1 图象在第一象限内交点的坐标. x O 1 2 3 4 x 从图 2 中看到，这样的交点不存在，即满足要求的矩 3 y = - x + 2 形是不存在的. 图 2 事实上，我们还可以借助图象探讨以下问题：对于面 积为 1 的矩形来说，它的周长最小是多少——凡是周长要求小于这个值的矩形都是不存 在的；或者，对于周长为 3 的矩形来说，它的面积最大是多少——凡是面积要求大于这 个值的矩形也都是不存在的. 习题 1. 求解下列问题： （1）在 1 ~ 10 这 10 个自然数中，每次取两个数，使得所取两数之和大于 10， 共有多少种取法？ （2）在 1 ~ 100 这 100 个自然数中，每次取两个数，使得所取两数之和大于 100，共有多少种取法？ （3）你还能提出什么问题？ （4）各边长度都是整数、最大边长为 11 的三角形有多少个？本题与上述哪个 问题有联系？它们的区别是什么？ 2. 任意给定一个正三角形. （1）是否存在另一个正三角形，它的周长和面积分别是已知正三角形周长和面 积的 2 倍？ （2）是否存在另一个正三角形，它的周长和面积分别是已知正三角形周长和面 积的一半？你是怎么做的？ 3. 任意给定一个矩形. （1）是否存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的 3 倍？ 1 （2）是否存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的 ？ 3 4. 你还能提出什么问题？在综合与实践的学习过程中，你还学到了什么？ 221 锐角三角函数 第二章 直角三角形的边角关系 小明在 A 处仰望塔顶，测得∠α 的大小，再往塔的方向前进 50 m 到 B 处， 又测得∠β 的大小. 已知小明的身高为 1.5 m，根据这些数据小明就求出了塔的 高度. 你知道他是怎样求的吗？ 在直角三角形中，已知一边和一个锐角，你能求出其他的边和角吗？ 本章我们将借助生活中的实例，探索直角三角形边角之间的关系，并利用 三角函数解决一些简单的实际问题. 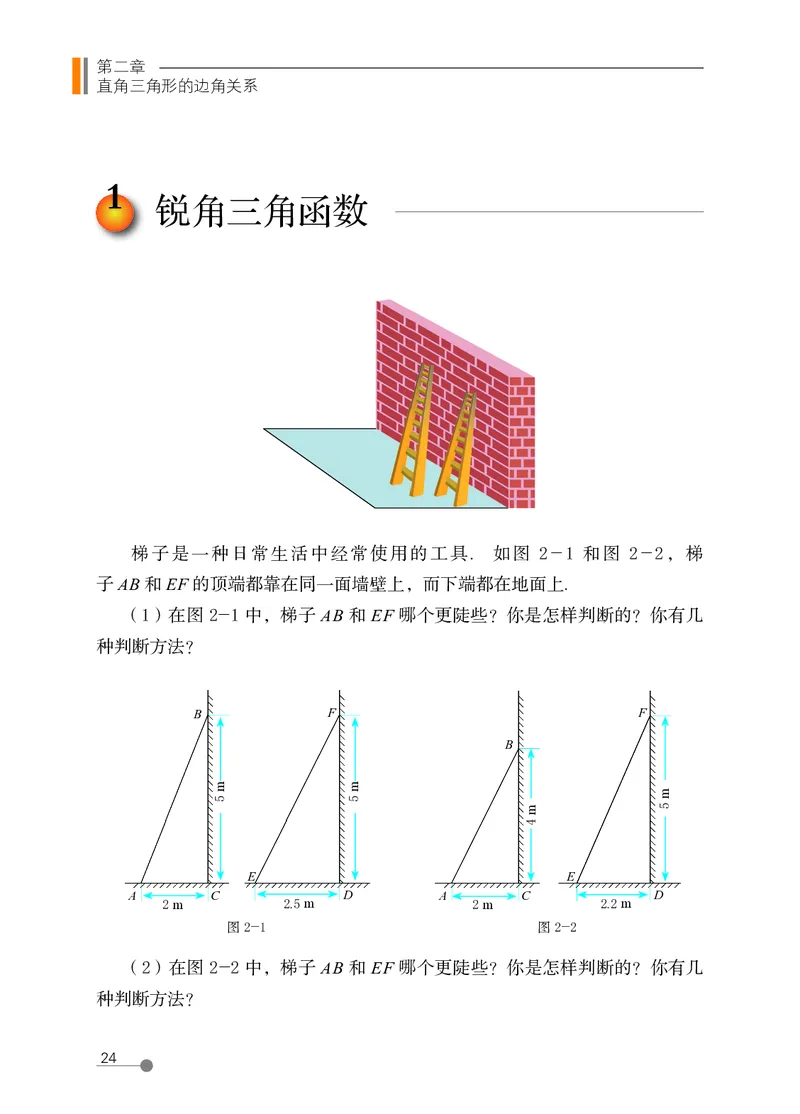学习目标 探索直角三角形的边角关系，发展几何直观 探索 30°，45°，60°角的三角函数值 学会用计算器解决一些三角函数计算问题 用三角函数解决实际问题，发展应用意识 23 A B第二章 直角三角形的边角关系 2 m 24 m 4 m 5 1 锐角三角函数 梯子是一种日常生活中经常使用的工具. 如图 2-1 和图 2-2，梯 子 AB 和 EF 的顶端都靠在同一面墙壁上，而下端都在地面上. （1）在图 2-1 中，梯子 AB 和 EF 哪个更陡些？你是怎样判断的？你有几 种判断方法？ F B E A C D 2 m 2.2 m 图 2-1 图 2-2 （2）在图 2-2 中，梯子 AB 和 EF 哪个更陡些？你是怎样判断的？你有几 种判断方法？ m 5 m 5 B F E A C D 2.5 m1 锐角三角函数 想一想 如图 2-3，B ，B 是梯子 AB 上的点，B C ⊥ AC，垂足为点 C ， 1 2 1 1 1 B C ⊥ AC，垂足为点 C . 小明想通过测量 B C 及 AC ，算出它们的比，来说 2 2 2 1 1 1 明梯子 AB 的倾斜程度；而小亮则认为，通过测量 B C 及 AC ，算出它们的 2 2 2 比，也能说明梯子 AB 的倾斜程度. 你同意他们的看法吗？ B B B 1 B 1 B 2 B 2 A A C C C C C C 2 1 2 1 （1） （2） 图 2-3 在图 2-3（2）中， （1）Rt△AB C 与 Rt△AB C 有什么关系？ 1 1 2 2 B C B C （2） 1 1 与 2 2 有什么关系？ AC AC 1 2 （3）如果改变点 B 在 AB 上的位置并保持 B C ⊥ AC（垂足是点 C ）呢？ 2 2 2 2 由此你能得出什么结论？ 如图 2-4，在 Rt△ABC 中，如果锐角 A 确 B 定，那么∠A 的对边 BC 与邻边 AC 的比便随之 ∠A 的对边 确定，这个比叫做∠A 的正切（tangent），记 A C ∠A 的邻边 作 tan A ，即 图 2-4 ∠A 的对边 tan A = . ∠A 的邻边 tan A 是一个完整的符号，它表示∠A 的正切，记号里习惯省去角的符号“∠”. 下文中的 sin A， cos A 也是这样. 25第二章 直角三角形的边角关系 议一议 在图 2-3 中，你发现梯子的倾斜程度与 tan A 有怎样的关系？与同伴进行 交流. 当锐角 A 变化时，相应的 tan A 也随之变化. tan A 的值越大，梯子越陡. 例 1 图 2-5 表示甲、乙两个自动扶梯，哪一个自动扶梯比较陡？ 13 m 4 m 5 m α β 8 m 甲 乙 图 2-5 解：甲梯中， 4 1 tan α = = . 8 2 乙梯中， 5 5 tan β = = . 132 - 52 12 因为 tan α > tan β，所以甲梯比较陡. 正切也经常用来描述山坡的坡度 . 例如， 有一个山坡，如果沿山坡在水平方向上每前 进 100 m 就升高 60 m（如图 2-6），那么这个山 坡的坡度就是 α 60 3 tan α = = . 100 5 图 2-6 坡面的铅直高度与水平宽度的比称为坡度（或坡比）. 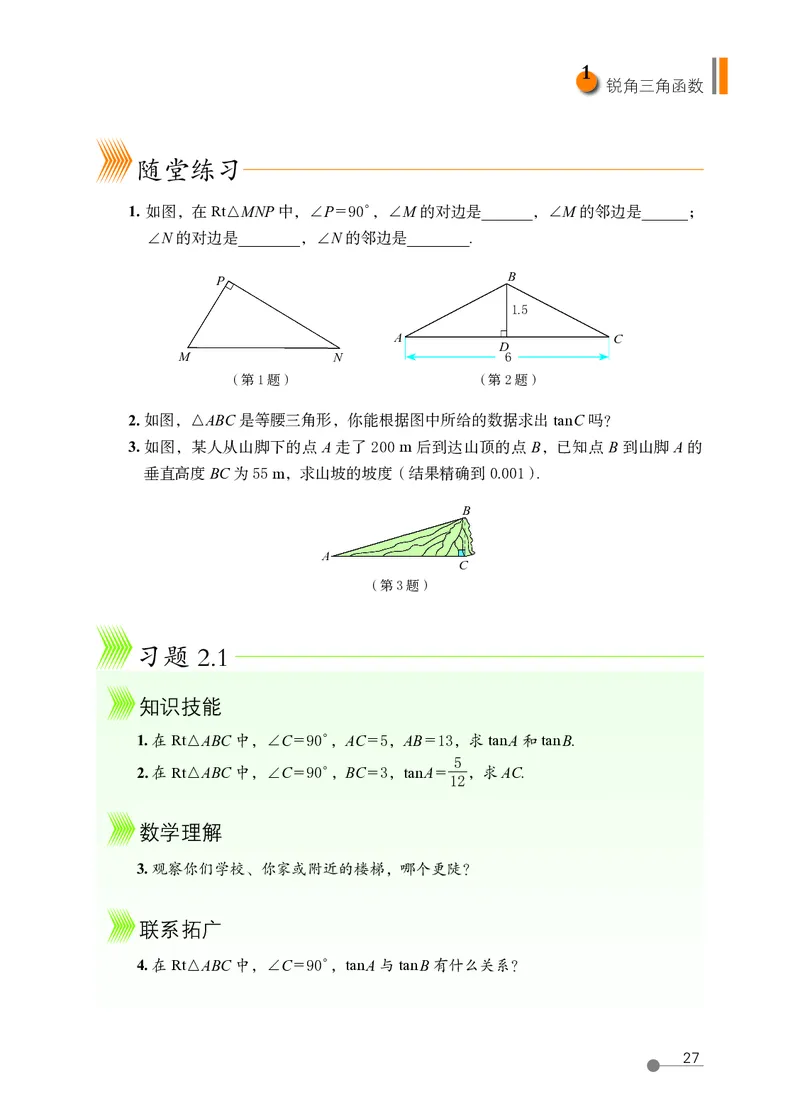26 m 06 100 m1 锐角三角函数 随堂练习 1. 如图，在 Rt△MNP 中，∠P = 90°，∠M 的对边是_______，∠M 的邻边是______； ∠N 的对边是________，∠N 的邻边是________. P B 1.5 A C D M N 6 （第 1 题） （第 2 题） 2. 如图，△ABC 是等腰三角形，你能根据图中所给的数据求出 tan C 吗？ 3. 如图，某人从山脚下的点 A 走了 200 m 后到达山顶的点 B，已知点 B 到山脚 A 的 垂直高度 BC 为 55 m，求山坡的坡度（结果精确到 0.001）. B A C （第 3 题） 习题 2.1 知识技能 1. 在 Rt△ABC 中，∠C = 90°，AC = 5，AB = 13，求 tan A 和 tan B. 5 2. 在 Rt△ABC 中，∠C = 90°，BC = 3，tan A = ，求 AC. 12 数学理解 3. 观察你们学校、你家或附近的楼梯，哪个更陡？ 联系拓广 4. 在 Rt△ABC 中，∠C = 90°，tan A 与 tan B 有什么关系？ 27第二章 直角三角形的边角关系 议一议 B 如图 2-7，当 Rt△ABC 中的锐角 A 确定时， 斜边 ∠A 的对边 ∠A 的对边与邻边的比便随之确定. 此时，其他边 之间的比也确定吗？与同伴进行交流. A ∠A 的邻边 C 图 2-7 在 Rt△ABC 中，如果锐角 A 确定，那么∠A 的对边与斜边的比、邻边与斜 边的比也随之确定. ∠A 的对边与斜边的比叫做∠A 的正弦（sine），记作 sin A，即 ∠A 的对边 sin A = . 斜边 ∠A 的邻边与斜边的比叫做∠A 的余弦（cosine），记作 cos A，即 ∠A 的邻边 cos A = . 斜边 锐角 A 的正弦、余弦和正切都是∠A 的三角函数（trigonometric function）. 想一想 在图 2-3 中，你发现梯子的倾斜程度与 sin A 和 cos A 有关系吗？ 当锐角 A 变化时，相应的 sin A，cos A 也随之变化. sin A 的值越大，梯子 越陡；cos A 的值越小，梯子越陡. 例 2 如图 2-8，在 Rt△ABC 中，∠C = 90°，AB = 5，AC = 2. 求 sin A， cos A. 解：在 Rt△ABC 中， A AC 2 cos A = = . AB 5 又∵AC 2 + BC 2 = AB 2 ， B C ∴BC = AB 2 - AC 2 = 52 - 22 = 21 . 图 2-8 BC 21 ∴sin A = = . AB 5 281 锐角三角函数 例 3 如图 2-9，在 Rt△ABC 中，∠B = 90°，AC = 200，sin A = 0.6， 求 BC 的长. C 解：在 Rt△ABC 中， BC ∵sin A = ， AC BC 即 = 0.6， 200 A B ∴BC = 200×0.6 = 120. 图 2-9 做一做 12 如图 2-10，在 Rt△ABC 中，∠C = 90°，cos A = ，AC = 10，AB 等于多 13 少？sin B 呢？ B C A 图 2-10 随堂练习 1. 在 Rt△ABC 中，∠C = 90°，BC = 1，AB = 9，求 sin A，cos A. 4 2. 在 Rt△ABC 中，∠C = 90°，sin A = ，BC = 20，求△ABC 的周长和面积. 5 习题 2.2 知识技能 1. 如图，分别求∠α 和∠β 的正弦、余弦和正切. β 45 x α 36 （（第第 11 题题）） 29第二章 直角三角形的边角关系 数学理解 2. 如何用正弦、余弦、正切来刻画梯子的倾斜程度？ 联系拓广 3. 在 Rt△ABC 中，∠C = 90°，sin A 与cos B 有什么关系？ 4. 在 Rt△ABC 中，∠BCA = 90°，CD 是边 AB 上的中线，BC = 8，CD = 5，求 sin∠ACD，cos∠ACD 和 tan∠ACD. 5. 在 △ABC 中，∠ABC < 90°，AB = 5，BC = 13，AD 是边 BC 上的高，AD = 4，求 CD 和 sin C. 如果∠ABC > 90°呢？ 2 3300° 45° 60° ， ， 角的三角函数值 观察一副三角尺，其中有几个锐角？它们分别等于多少度？ （1）sin 30°等于多少？你是怎样得到的？与同伴进行交流. （2）cos 30°等于多少？tan 30°呢？ 做一做 （1）60°角的正弦、余弦和正切的值分别是多少？你是怎样得到的？ 302 30°，45°，60°角的三角函数值 （2）45°角的正弦、余弦和正切的值分别是多少？你是怎样得到的？ （3）完成下表： 三角 三角 函 数 值 函数 sin α cos α tan α 角 α 30° 45° 60° 例 1 计算： （1）sin 30°+ cos 45°； （2）sin 260°+ sin 230°- tan 45°. 1 2 1+ 2 解：（1）sin 30°+cos 45°= + = ； 2 2 2 （2）sin 2 60°+ sin 2 30°- tan 45°=（ 3 ） 2 +（ 1 ） 2 - 1 = 3 + 1 - 1 = 0. 2 2 4 4 例 2 一个小孩荡秋千，秋千链子的长度为 2.5 m，当秋千向两边摆动 时，摆角 恰好为 30°，且两边的摆动角度相同（如图 2-11 所示）. 求它摆至 最高位置时与其摆至最低位置时的高度之差（结果精确到 0.01 m）. O 30° C B D A 图 2-11 sin2 60°表示（sin 60°）2 ，cos2 60°表示（cos 60°）2，其余类推. 此处指秋千摆至最高位置时链子所在的直线与铅垂线之间的夹角. 31第二章 直角三角形的边角关系 解：如图 2-11，根据题意可知， ∠AOB = 30°，OB = 2.5 m， 3 所以 OC = OB cos 30°= 2.5× ≈2.165（m）. 2 所以 AC = 2.5 - 2.165 ≈ 0.34（m）. 所以，秋千摆至最高位置与最低位置的高度差约为 0.34 m. 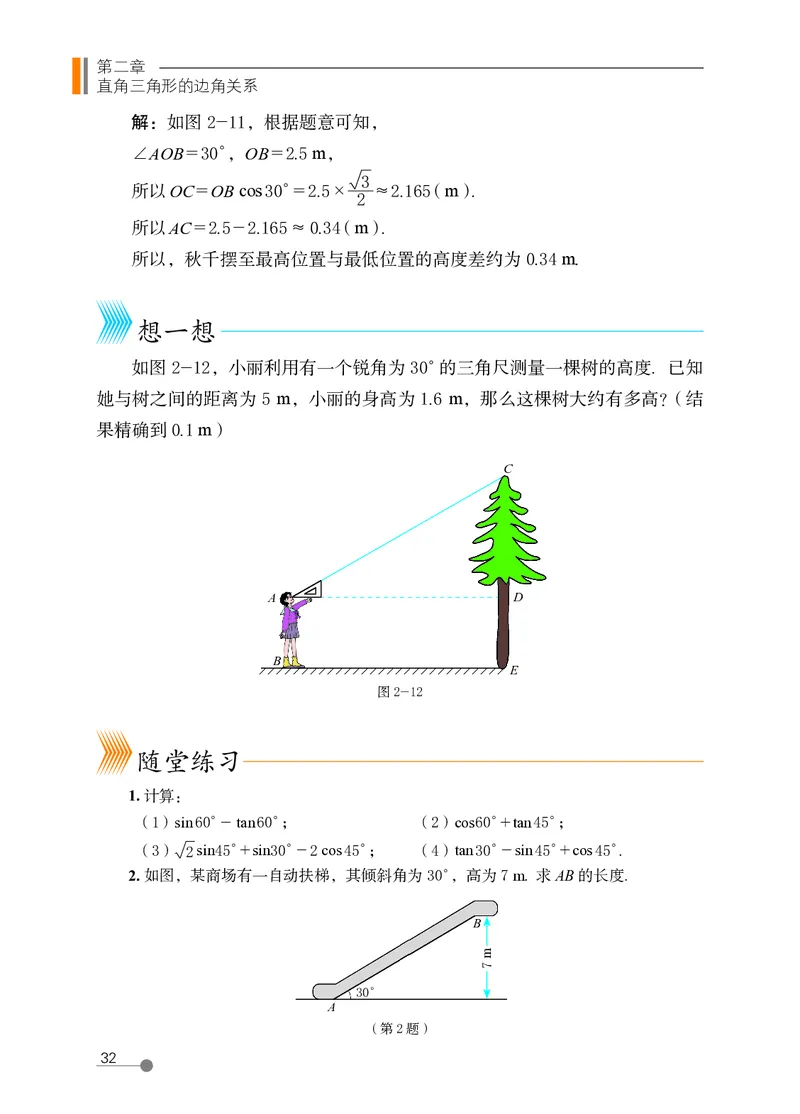想一想 如图 2-12，小丽利用有一个锐角为 30°的三角尺测量一棵树的高度. 已知 她与树之间的距离为 5 m，小丽的身高为 1.6 m，那么这棵树大约有多高？（结 果精确到 0.1 m） C A D B E 图 2-12 随堂练习 1. 计算： （1）sin 60°－ tan 60°； （2）cos60°+ tan 45°； （3） 2 sin45°+ sin30°－2 cos 45°； （4）tan 30°－sin 45°+ cos 45°. 2. 如图，某商场有一自动扶梯，其倾斜角为 30°，高为 7 m. 求 AB 的长度. B 30° A 32 m 7 （第 2 题）2 30°，45°，60°角的三角函数值 习题 2.3 知识技能 1. 计算： （1）tan 45°－sin 30°； （2）cos 60°+ sin 45°－tan 30°； （3）6 tan2 30°－ 3 sin 60°- 2 cos 45°. 2. 如图，一斜坡 AB 的长是 40 m，其倾斜角为 30°，求坡顶到地面的高度. A D B A C B C （第 2 题） （第 3 题） 3. 如图，河岸 AD，BC 互相平行，桥 AB 垂直于两岸，桥长 12 m，在 C 处看桥的 两端 A，B，夹角∠BCA = 60°，求 B，C 之间的距离（结果精确到 1 m）. 问题解决 4. 某阶梯的形状如图所示，其中线段 AB = BC，AB 部分的坡角为 45°，BC 部分的 坡角为 30°，AD = 1.5 m. 如果每个台阶的高不超过 20 cm，那么这一阶梯至少有 多少个台阶？（最后一个台阶的高不足 20 cm 时，按一个台阶计算） C 30° E B 4455° AAAAAAAAAAAAAAAAAAA DDDDDDDDDDDDDDDDDDD （第 4 题） 33第二章 直角三角形的边角关系 联系拓广 1 5. 在 Rt△ABC 中，∠C = 90°，cos A = ，求 sin A 和 tan A. 2 你有几种解法？与同伴进行交流. 3 用用计计算算器器求求锐锐角角的的三三角角函函数数值值 如图 2-13，当登山缆车的吊箱经过点 A 到达点 B 时，它走过了 200 m. 已 知缆车行驶的路线与水平面的夹角∠α = 16°，那么缆车垂直上升的距离是多 少？（结果精确到 0.01 m） 求解中你有哪些困难？ D B A C 图 2-13 在 Rt△ABC 中，∠ACB = 90°，BC = AB sin 16°. 你知道 sin 16°是多少吗？我们可以借助科学计算器求锐角的三角函数值. 怎样用科学计算器求三角函数值呢？ 用科学计算器求三角函数值，要用到 和 键. 例如，求 sin 16°，cos 42°，tan 85°和 sin 72°38′25″的按键顺序如下表所示. 343 用计算器求锐角的三角函数值 按键顺序 计算结果 sin 16° 0.275 637 355 cos 42° 0.743 144 825 tan 85° 11.430 052 3 sin 72°38′25″ 0.954 450 312 对于本节一开始的问题，利用科学计算器可以求得 BC = 200 sin 16°≈55.13（m）. 想一想 在本节一开始的问题中，当缆车继续由点 B 到达点 D 时，它又走过了 200 m，缆车由点 B 到点 D 的行驶路线与水平面的夹角∠β = 42°，由此你还能 计算什么？ 随堂练习 1. 用计算器求下列各式的值： （1）sin 56°； （2）sin 15°49′； （3）cos 20.72°； （4）cos 27°35′12″； （5）tan 29.5°； （6）tan 39°39′39″. 2. 一个人由山底爬到山顶，需先爬 40°的山坡 300 m，再爬 30°的山坡 100 m，求山 高（结果精确到 0.1 m）. 用计算器求三角函数值时，结果一般有 9 个数位. 本书约定，如无特别说明，计算结果一般精确 到万分位. 35第二章 直角三角形的边角关系 习题 2.4 知识技能 1. 用计算器求下列各式的值： （1）tan 32°； （2）cos 24.53°； （3）sin 62°11′； （4）cos 51°42′20″； （5）sin 56°+ cos 61°+ tan 76°； （6）sin 81°32′17″+ cos 38°43′47″. 2. 用计算器求下列各式的值（结果精确到0.01）： cos 45°+ sin 30° （1）sin 35°－3 tan 25°； （2） . sin 60°+ tan 60° 问题解决 3. 一座楼房门前的台阶高出地面 1.2 m，计划拆除台阶，改建成可供轮椅行走的斜 坡. 根据这个城市的规定，供轮椅行走的斜坡倾斜角不得超过 9°. 从斜坡的起点 至楼门的最短水平距离是多少？（结果精确到 0.1 m） 4. 如图所示，一座厂房屋顶人字架的跨度为 10 m，上弦 AB = BD，∠A = 26°. 求中 柱 BC 和上弦 AB 的长（结果精确到 0.01 m）. B 26° A D C 10 m （第 4 题） 联系拓广 5. 用计算器求出下列三角函数的值，并填入下表： α 10° 20° 30° 40° 50° 60° 70° 80° sin α cos α tan α 从上面的表格中，你能发现哪些规律？与同伴进行交流. 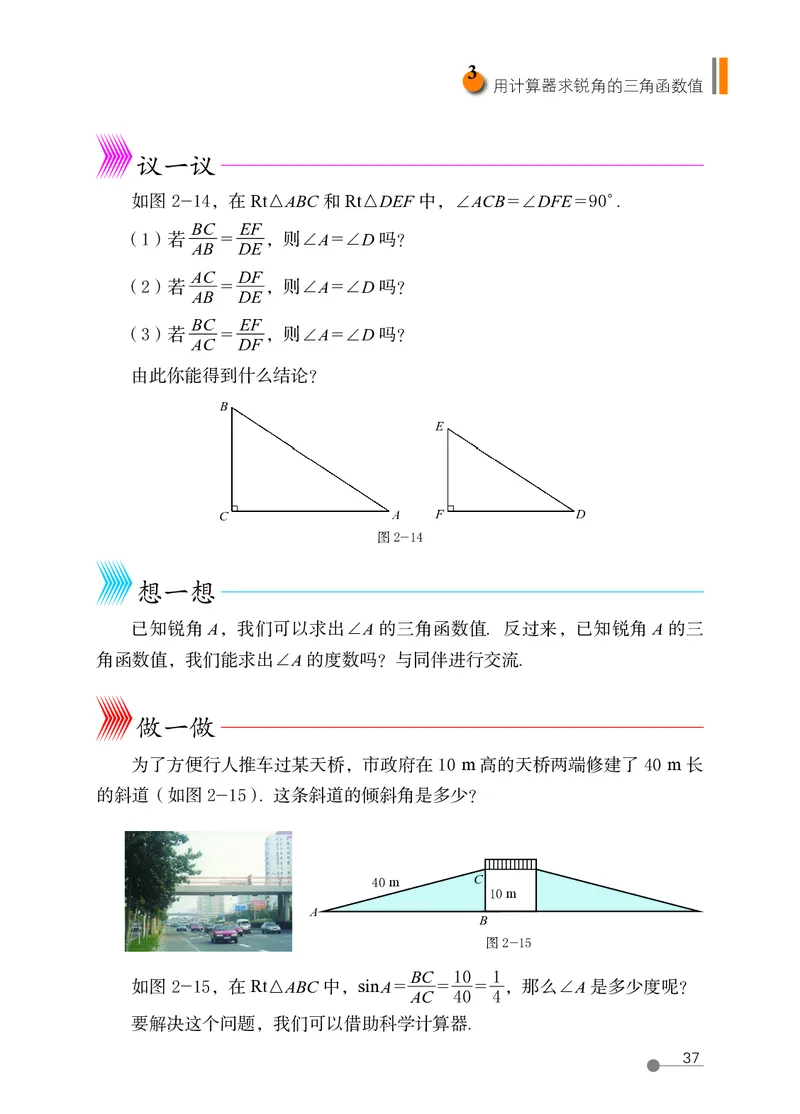363 用计算器求锐角的三角函数值 议一议 如图 2-14，在 Rt△ABC 和 Rt△DEF 中，∠ACB =∠DFE = 90°. BC EF （1）若 = ，则∠A =∠D 吗？ AB DE AC DF （2）若 = ，则∠A =∠D 吗？ AB DE BC EF （3）若 = ，则∠A =∠D 吗？ AC DF 由此你能得到什么结论？ B E C A F D 图 2-14 想一想 已知锐角 A，我们可以求出∠A 的三角函数值. 反过来，已知锐角 A 的三 角函数值，我们能求出∠A 的度数吗？与同伴进行交流. 做一做 为了方便行人推车过某天桥，市政府在 10 m 高的天桥两端修建了 40 m 长 的斜道（如图 2-15）. 这条斜道的倾斜角是多少？ 40 m C 10 m A B 图 2-15 BC 10 1 如图 2-15，在 Rt△ABC 中，sin A = = = ，那么∠A 是多少度呢？ AC 40 4 要解决这个问题，我们可以借助科学计算器. 37第二章 直角三角形的边角关系 -1 已知三角函数值求角度，要用到 键的第二功能“sin ， -1 -1 cos ，tan ”和 键. 按键顺序 计算结果 sin A = 0.981 6 78.991 840 39 cos A = 0.860 7 30.604 730 07 tan A = 0.189 0 10.702 657 49 tan A = 56.78 88.991 020 49 上表的计算结果是以“度”为单位的，再按 键即可显示以“度、 分、秒”为单位的结果. 用“度、分、秒”为单位表示角度时，本书中如果没 有特别说明，结果一般精确到1″. 你能求出图 2-15 中∠A 的大小吗？ D A B 例 1 如图 2-16，工件上有一 V 形槽（AC = BC）， 测得它的上口宽 20 mm，深 19.2 mm，求 V 形角（∠ACB） C 的大小（结果精确到 1°）. AD 10 图 2-16 解：tan∠ACD = = ， CD 19.2 ∴ ∠ACD≈27.5°， ∴ ∠ACB = 2∠ACD≈2×27.5°= 55°. 383 用计算器求锐角的三角函数值 例 2 如图 2-17，一名患者体内某重要器官后面有一肿瘤. 在接受放射性 治疗时，为了最大限度地保证疗效，并且防止伤害器官，射线必须从侧面照射 肿瘤. 已知肿瘤在皮下 6.3 cm 的 A 处，射线从肿瘤右侧 9.8 cm 的 B 处进入身 体，求射线与皮肤的夹角. 解：如图 2-17，在 Rt△ABC 中， 皮肤 9.8 cm C B AC = 6.3 cm，BC = 9.8 cm， 器官 AC 6.3 所以 tan B = = . A BC 9.8 肿瘤 所以 ∠B≈32°44′7″. 图 2-17 因此，射线与皮肤的夹角约为 32°44′7″. 随堂练习 1. 根据下列三角函数值求锐角 α 的大小： （1）sin α = 0.829 1； （2）cos α = 0.785 7； 4 （3）tan α = 30； （4）tan α = . 5 2. 一梯子斜靠在一面墙上. 已知梯长 4 m，梯子位于地面上的一端离墙壁 2.5 m，求梯 子与地面所成的锐角. 习题 2.5 知识技能 1. 根据下列三角函数值求锐角 α 的大小： （1）tan α = 2.988 8； （2）sin α = 0.395 7； （3）cos α = 0.785 0； 5 3 （4）tan α = 0.897 2； （5）sin α = ； （6）cos α = . 6 8 2. 根据下列三角函数值求锐角 β 的大小： 2 2 2 （1）sin β = ； （2）cos β = ； （3）tan β = . 5 5 5 问题解决 3. 一辆汽车沿着一山坡行驶了 1 000 m，其铅直高度上升了 50 m. 求山坡与水平面 所成锐角的大小. 39第二章 直角三角形的边角关系 4. 在 1∶20 000 的平面地图上，量得甲、乙两地的直线距离为 1.5 cm，两地的实际 高度相差 27 m，求甲、乙两地间的坡角. 联系拓广 5. 用计算器求下列正切值对应的锐角 θ，并填入下表： tan θ 0.5 1 2 3 4 5 10 20 50 θ 从上面的表格中，你能发现哪些规律？与同伴进行交流. 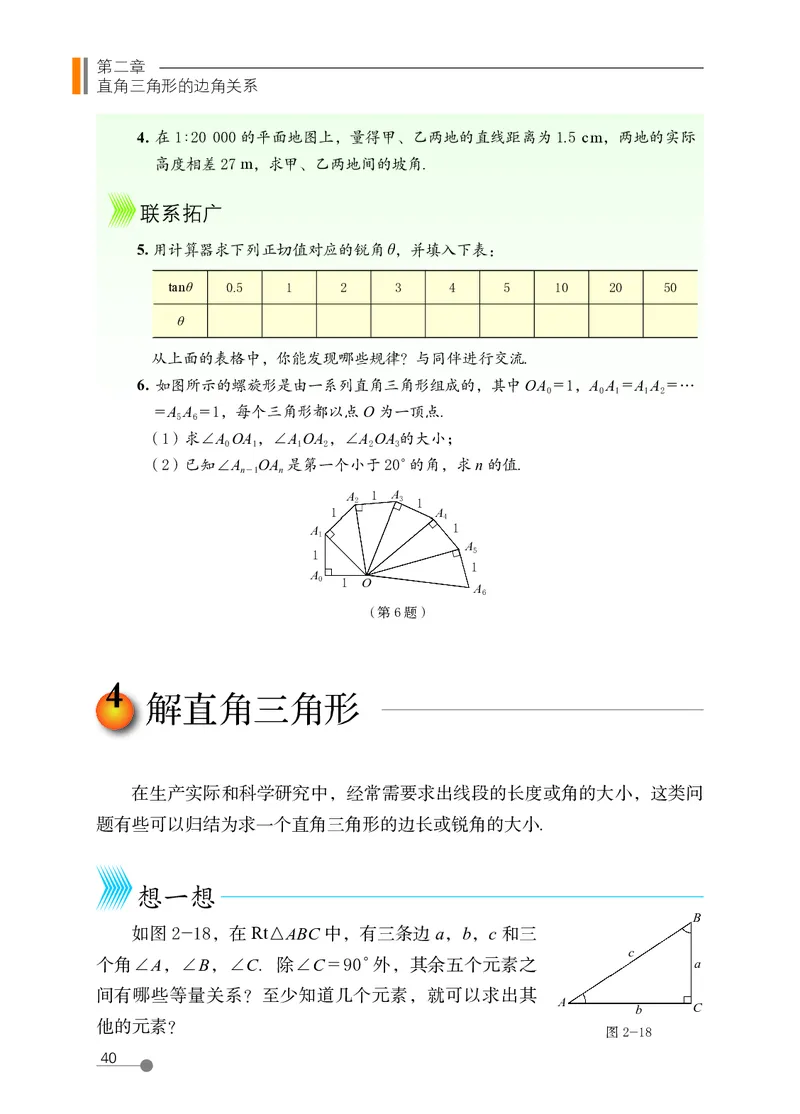6. 如图所示的螺旋形是由一系列直角三角形组成的，其中 OA = 1，A A = A A = … 0 0 1 1 2 = A A = 1，每个三角形都以点 O 为一顶点. 5 6 （1）求∠A OA ，∠A OA ，∠A OA 的大小； 0 1 1 2 2 3 （2）已知∠A OA 是第一个小于 20°的角，求 n 的值. n - 1 n A 2 1 A 3 1 1 A 4 A 1 1 A 1 5 1 A 0 1 O A 6 （第 6 题） 4 解解直直角角三三角角形形 在生产实际和科学研究中，经常需要求出线段的长度或角的大小，这类问 题有些可以归结为求一个直角三角形的边长或锐角的大小. 想一想 B 如图 2-18，在 Rt△ABC 中，有三条边 a，b，c 和三 c 个角∠A，∠B，∠C. 除∠C = 90°外，其余五个元素之 a 间有哪些等量关系？至少知道几个元素，就可以求出其 A b C 他的元素？ 图 2-18 404 解直角三角形 在图 2-18 中，∠C 为直角，可得下列边角关系： （1）锐角之间的关系：∠A +∠B = 90°； （2）三边之间的关系：a 2 + b 2 = c 2 ； （3）角与边之间的关系： a b a b sin A = cos B = ，cos A = sin B = ，tan A = ，tan B = . c c b a 利用上面这些关系，如果知道直角三角形中的两个元素（其中至少一个是 边），就可以求出其他元素. 由直角三角形中已知的元素，求出其他所有未知 元素的过程，叫做解直角三角形. 例 1 如图 2-19，在 Rt△ABC 中，已知∠C = 90°，a = 4，c = 8. 解这个 直角三角形. 解：在 Rt△ABC 中， B ∵a 2 + b 2 = c 2 ，a = 4，c = 8， c a ∴b = c 2 - a 2 = 82 - 42 = 4 3. a 4 1 ∵sin A = c = 8 = 2 ， C b A 图 2-19 ∴∠A = 30°. ∴∠B = 90°- 30°= 60°. 例 2 在 Rt△ABC 中，已知∠C = 90°，a = 35，b = 28，求∠A，∠B 的度 数（结果精确到 1°）和 c 的长（结果精确到 1）. 解：在 Rt△ABC 中， ∵a 2 + b 2 = c 2 ，a = 35，b = 28， ∴c = a 2 + b 2 = 352 + 282 = 2 009 ≈ 45. a 35 ∵tan A = = = 1.25， b 28 ∴∠A≈51°. ∴∠B = 90°－∠A ≈ 90°－51°= 39°. 41第二章 直角三角形的边角关系 议一议 在 Rt△ABC 中，∠C = 90°. （1）已知 a，b，怎样求∠A 的度数？ （2）已知 a，c，怎样求∠A 的度数？ （3）已知 b，c，怎样求∠A 的度数？ 由此你能总结一下已知两边解直角三角形的方法吗？与同伴进行交流. 随堂练习 在 Rt△ABC 中，∠C = 90°. （1）已知 c = 26，b = 24，求 a 的长和∠B 的度数（结果精确到1′）； （2）已知 a = 5，b = 5 3，求 c 的长和∠A，∠B 的度数. 习题 2.6 知识技能 1. 在 Rt△ABC 中，已知∠C = 90°，b = 6，c = 8，解这个直角三角形. 2. 在 Rt△ABC 中，已知∠C = 90°，a = 15，b = 5，解这个直角三角形. 3. 在 Rt△ABC 中，已知∠C = 90°，a = 13.5，c = 9 3，解这个直角三角形. 例 3 在 Rt△ABC 中，已知∠C = 90°，c = 128，∠B = 60°，解这个直角三 角形. 解：在 Rt△ABC 中， ∠ A = 90°－∠B = 90°－60°= 30°. a b ∵cos B = ，sinB = ， c c 1 ∴a = c·cos B = 128 cos 60°= 128× = 64， 2 3 b = c·sin B = 128 sin 60°= 128× = 64 3. 2 424 解直角三角形 例 4 在 Rt△ABC 中，已知∠C = 90°，a = 15，∠A = 35°27′，求∠B 的度 数和 b，c 的长（结果精确到 1）. 解：在 Rt△ABC 中， ∠B = 90°－∠A = 90°－35°27′= 54°33′. b a ∵tan B = ，sin A = ， a c ∴b = a·tan B = 15 tan 54°33′≈ 21， a 15 c = = ≈ 26. sin A sin 35°27' 议一议 在 Rt△ABC 中，∠C = 90°. （1）已知 c，∠A，写出求 a 和 b 的式子； （2）已知 b，∠A，写出求 a 和 c 的式子； （3）已知 a，∠A，写出求 b 和 c 的式子. 由此你能总结一下已知一条边和一个锐角解直角三角形的方法吗？与同伴 进行交流. 随堂练习 在 Rt△ABC 中，∠C = 90°. （1）已知 c = 15，∠B = 60°，求 a 的长； （2）已知 b = 24，∠A = 45°，求 c 的长. 习题 2.7 知识技能 1. 在 Rt△ABC 中，∠C = 90°. （1）已知 c = 15，∠B = 36°，求∠A 的度数和 a，b 的长； （2）已知 a = 24，∠A = 80°，求∠B 的度数和 b，c 的长. 2. 在 Rt△ABC 中，∠C = 90°，根据下列条件解直角三角形： （1）∠A = 30°，b = 5； （2）∠A = 14°，c = 1 200（长度精确到 1）. 43第二章 直角三角形的边角关系 例 5 如图 2-20，在△ABC 中，已知∠A = 60°，∠B = 45°，AC = 12，求 AB 的长. 解：过点 C 作 CD⊥AB，垂足为点 D. C 在 Rt△ACD 中，AC = 12，∠A = 60°， 3 ∴CD = AC·sin A = 12 sin 60°= 12× = 6 3， 2 1 AD = AC·cos A = 12 cos 60°= 12× 2 = 6. A D B 图 2-20 在 Rt△BCD 中，∠B = 45°， CD 6 3 ∴BD = = = 6 3. tan B tan 45 ° ∴AB = AD + BD = 6 + 6 3. 例 6 如图 2-21，在△ABC 中，∠B = 47°，∠ACB = 15°，AC = 6，求 AB 的长（结果精确到 0.01）. 解：过点 C 作 CD⊥AB，交 BA 的延长线于点 D. C ∵∠B = 47°，∠ACB = 15°， ∴∠CAD =∠B +∠ACB = 47°+ 15°= 62°. 在 Rt△ACD 中，AC = 6，∠CAD = 62°， ∴AD = AC·cos∠CAD = 6 cos 62°≈ 2.817， D A B 图 2-21 CD = AC·sin∠CAD = 6 sin 62°≈ 5.298. 在 Rt△BCD 中，∠B = 47°， CD 5.298 ∴BD = ≈ ≈ 4.940. tan B tan 47 ° ∴AB = BD - AD ≈ 4.940 - 2.817 ≈ 2.12. 议一议 （1）对于例 6，是否还有其他作辅助线的解法？ （2）在例 5 和例 6 的解答过程中，如何把问题转化为解直角三角形问题？ 与同伴进行交流. 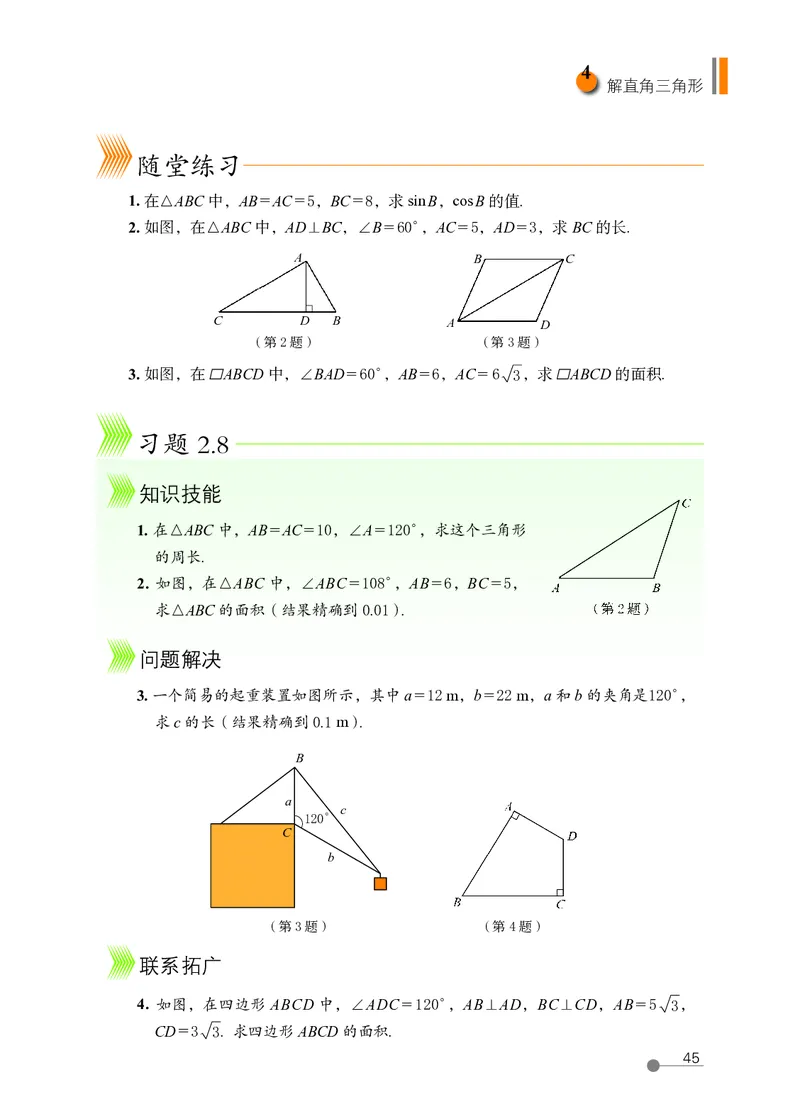444 解直角三角形 随堂练习 1. 在△ABC 中，AB = AC = 5，BC = 8，求 sin B，cos B 的值. 2. 如图，在△ABC 中，AD⊥BC，∠B = 60°，AC = 5，AD = 3，求 BC 的长. A B C C D B A D （第 2 题） （第 3 题） 3. 如图，在 ABCD 中，∠BAD = 60°，AB = 6，AC = 6 3，求 ABCD 的面积. 习题 2.8 知识技能 C 1. 在△ABC 中，AB = AC = 10，∠A = 120°，求这个三角形 的周长. 2. 如图，在△ABC 中，∠ABC = 108°，AB = 6，BC = 5， A B 求△ABC 的面积（结果精确到 0.01）. （第 2 题） 问题解决 3. 一个简易的起重装置如图所示，其中 a = 12 m，b = 22 m，a 和 b 的夹角是120°， 求 c 的长（结果精确到 0.1 m）. B a c A 120° C D b B C （第 3 题） （第 4 题） 联系拓广 4. 如图，在四边形 ABCD 中，∠ADC = 120°，AB⊥AD，BC⊥CD，AB = 5 3， CD = 3 3. 求四边形 ABCD 的面积. 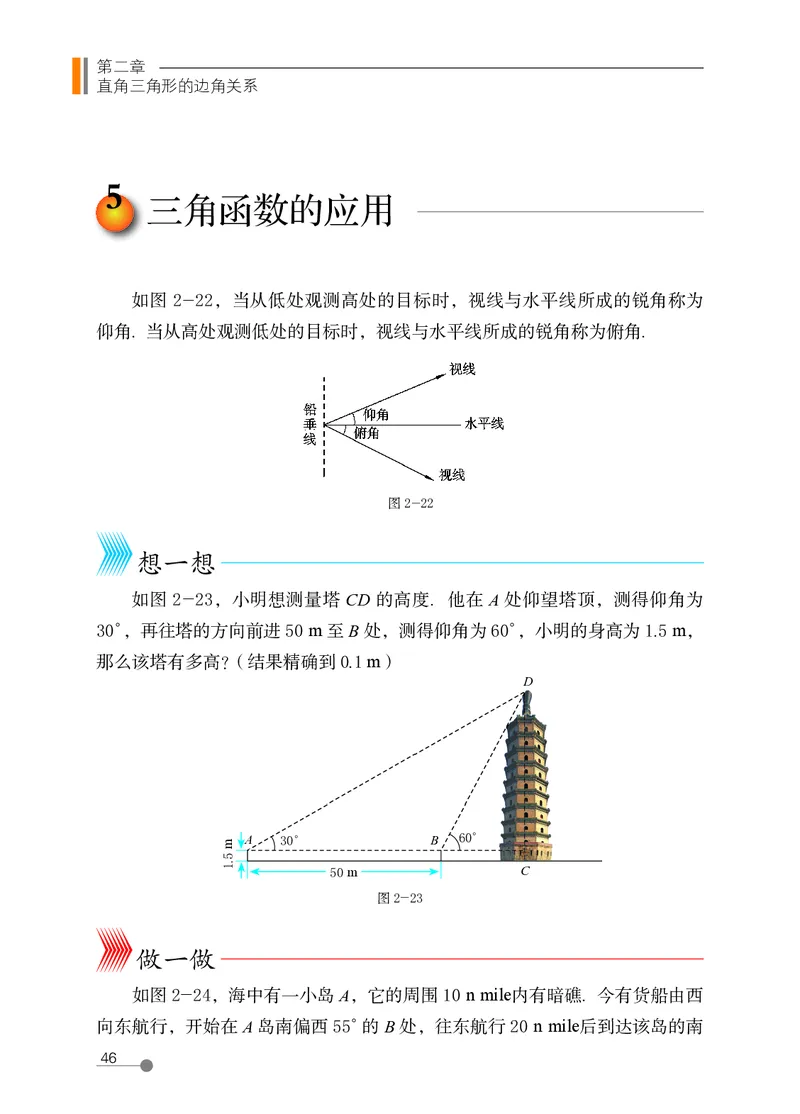45第二章 直角三角形的边角关系 D B 50 m C 46 m 5.1 5 三三角角函函数数的的应应用用 如图 2-22，当从低处观测高处的目标时，视线与水平线所成的锐角称为 仰角. 当从高处观测低处的目标时，视线与水平线所成的锐角称为俯角. 图 2-22 想一想 如图 2-23，小明想测量塔 CD 的高度. 他在 A 处仰望塔顶，测得仰角为 30°，再往塔的方向前进 50 m 至 B 处，测得仰角为 60°，小明的身高为 1.5 m， 那么该塔有多高？（结果精确到 0.1 m） A 30° 60° 图 2-23 做一做 如图 2-24，海中有一小岛 A，它的周围 10 n mile内有暗礁. 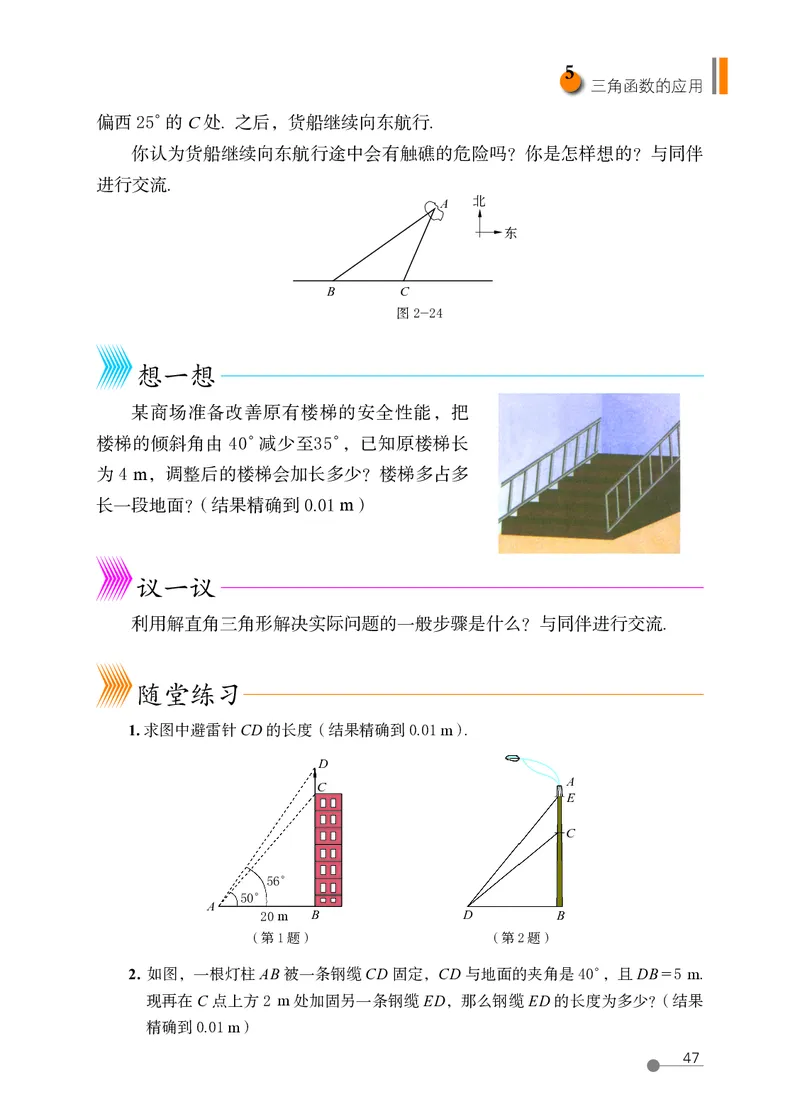今有货船由西 向东航行，开始在 A 岛南偏西 55°的 B 处，往东航行 20 n mile后到达该岛的南5 三角函数的应用 偏西 25°的 C 处. 之后，货船继续向东航行. 你认为货船继续向东航行途中会有触礁的危险吗？你是怎样想的？与同伴 进行交流. A 北 东 B C 图 2-24 想一想 某商场准备改善原有楼梯的安全性能，把 楼梯的倾斜角由 40°减少至35°，已知原楼梯长 为 4 m，调整后的楼梯会加长多少？楼梯多占多 长一段地面？（结果精确到 0.01 m） 议一议 利用解直角三角形解决实际问题的一般步骤是什么？与同伴进行交流. 随堂练习 1. 求图中避雷针 CD 的长度（结果精确到 0.01 m）. D A C E C 56° 50° A 20 m B D B （第 1 题） （第 2 题） 2. 如图，一根灯柱 AB 被一条钢缆 CD 固定，CD 与地面的夹角是 40°，且 DB = 5 m. 现再在 C 点上方 2 m 处加固另一条钢缆 ED，那么钢缆 ED 的长度为多少？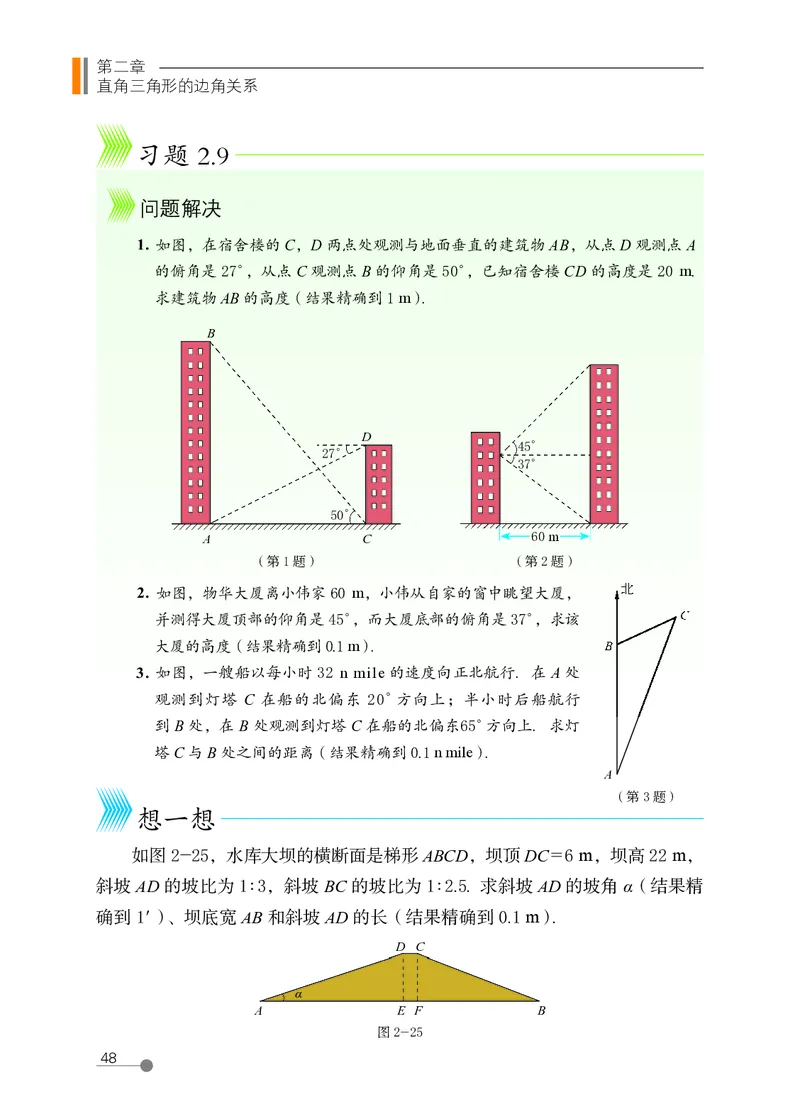（结果 精确到 0.01 m） 47第二章 直角三角形的边角关系 习题 2.9 问题解决 1. 如图，在宿舍楼的 C，D 两点处观测与地面垂直的建筑物 AB，从点 D 观测点 A 的俯角是 27°，从点 C 观测点 B 的仰角是 50°，已知宿舍楼 CD 的高度是 20 m. 求建筑物 AB 的高度（结果精确到 1 m）. B D 45° 27° 37° 50° A C 60 m （第 1 题） （第 2 题） 2. 如图，物华大厦离小伟家 60 m，小伟从自家的窗中眺望大厦， 北 并测得大厦顶部的仰角是 45°，而大厦底部的俯角是 37°，求该 C 大厦的高度（结果精确到 0.1 m）. B 3. 如图，一艘船以每小时 32 n mile 的速度向正北航行. 在 A 处 观测到灯塔 C 在船的北偏东 20°方向上；半小时后船航行 到 B 处，在 B 处观测到灯塔 C 在船的北偏东65°方向上. 求灯 塔 C 与 B 处之间的距离（结果精确到 0.1 n mile）. A （第 3 题） 想一想 如图 2-25，水库大坝的横断面是梯形 ABCD，坝顶 DC = 6 m，坝高 22 m， 斜坡 AD 的坡比为 1∶3，斜坡 BC 的坡比为 1∶2.5. 求斜坡 AD 的坡角 α（结果精 确到 1′）、坝底宽 AB 和斜坡 AD 的长（结果精确到 0.1 m）. 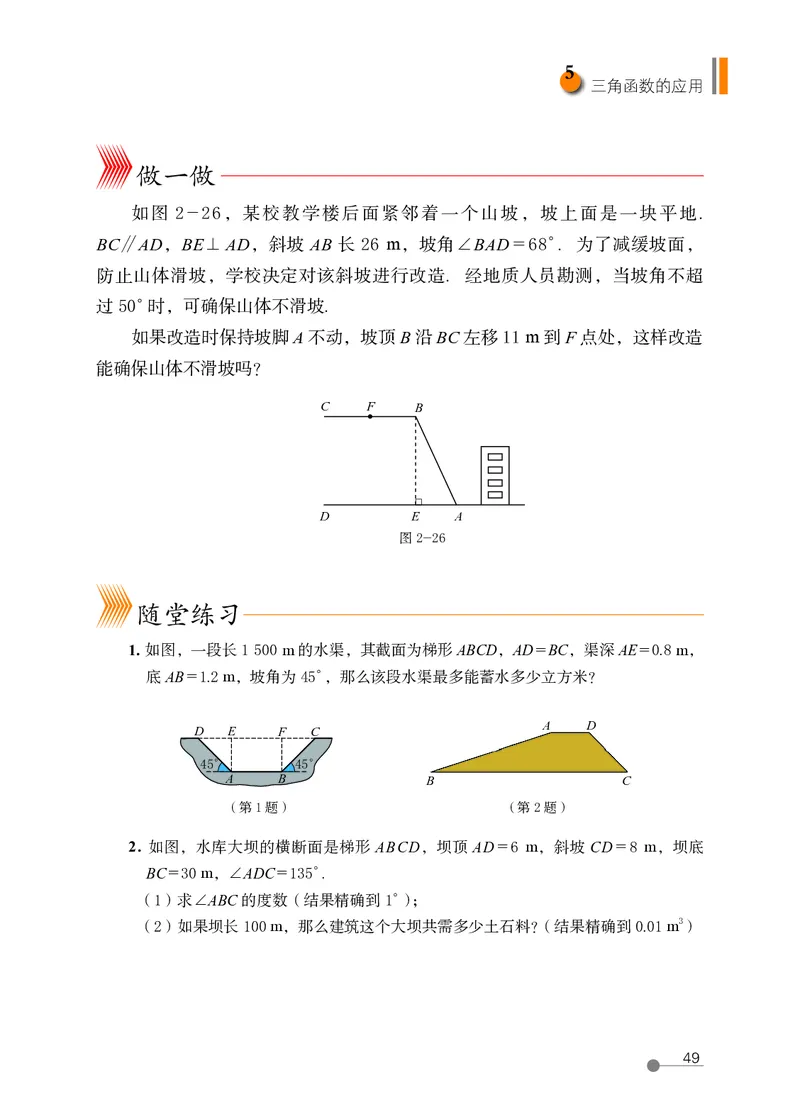D C α A E F B 图 2-25 485 三角函数的应用 做一做 如图 2-26，某校教学楼后面紧邻着一个山坡，坡上面是一块平地. BC∥AD，BE⊥ AD，斜坡 AB 长 26 m，坡角∠BAD = 68°. 为了减缓坡面， 防止山体滑坡，学校决定对该斜坡进行改造. 经地质人员勘测，当坡角不超 过 50°时，可确保山体不滑坡. 如果改造时保持坡脚 A 不动，坡顶 B 沿 BC 左移 11 m 到 F 点处，这样改造 能确保山体不滑坡吗？ C F B D E A 图 2-26 随堂练习 1. 如图，一段长 1 500 m 的水渠，其截面为梯形 ABCD，AD = BC，渠深 AE = 0.8 m， 底 AB = 1.2 m，坡角为 45°，那么该段水渠最多能蓄水多少立方米？ A D D E F C 45° 45° A B B C （第 1 题） （第 2 题） 2. 如图，水库大坝的横断面是梯形 ABCD，坝顶 AD = 6 m，斜坡 CD = 8 m，坝底 BC = 30 m，∠ADC = 135°. （1）求∠ABC 的度数（结果精确到 1°）； （2）如果坝长 100 m，那么建筑这个大坝共需多少土石料？（结果精确到 0.01 m3） 49第二章 直角三角形的边角关系 读一读 三角学的发展 “三角学”（trigonometry）一词源于希腊文的“三角形”与“测量”，原意是“三 角形的测量”. 后来，人们把利用三角函数研究三角形和其他图形的数量关系，进而研 究三角函数的性质及其应用的数学学科称为三角学. 三角学的发展大致可以分为三个时期. 从远古至 11 世纪前为第一个时期. 在此期 间，虽然人们还没有明确提到三角形的边与角之间的数量关系，更没有角的函数的概 念，但是人们已经能够利用当时掌握的数学知识解决属于三角学范围内的一些实际问题. 11—18 世纪是三角学发展的第二个时期. 这一时期，由于测量、贸易和航海等方面 的需要，三角学得到了迅速发展，并逐渐形成一门独立的数学学科. 在此期间，人们编 制出大量的三角函数表，三角函数得到广泛发展. 第三个时期是 18 世纪以后，这时三角学的研究逐步演变为研究三角函数的性质及 其应用，而且引进了现在所使用的三角函数符号. 三角学输入我国开始于明朝. 由邓玉函（1576—1630）撰、汤若望（1591—1666） 订、徐光启（1562—1633）督修的《大测》，是我国第一部三角学著作；罗雅谷 （1593—1638）、徐光启等人合作编译了《测量全义》. 1877 年华衡芳（1833—1902） 与英国人傅兰雅（J. Fryer，1839—1928）合译了英国人海麻士（I. Hymers，1803— 1877）的《三角数理》，这是三角学第二次输入我国. 习题 2.10 问题解决 1. 如图，燕尾槽的横断面是一个梯形，其中 AD ∥ BC，AB = CD，燕尾角 ∠B = 55°，外口宽 AD = 180 mm，燕尾槽深度是 70 mm，求它的里口宽 BC（结果精 确到 1 mm）. 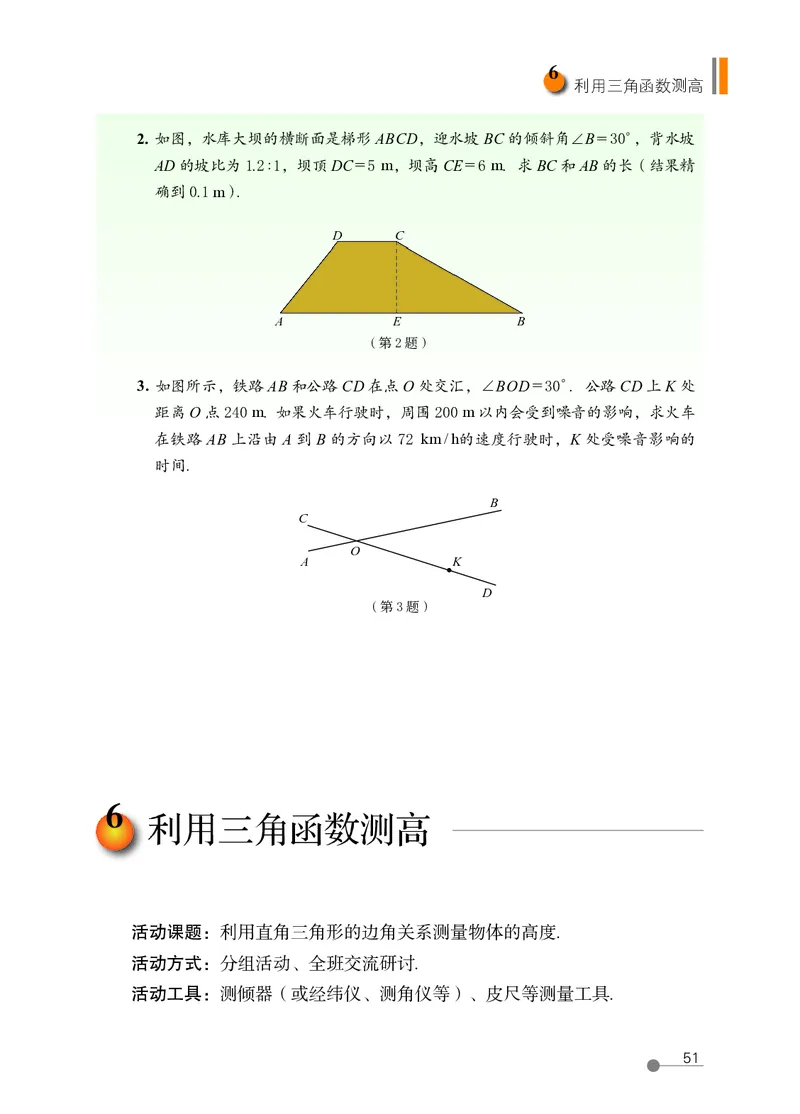A D B C （第 1 题） 506 利用三角函数测高 2. 如图，水库大坝的横断面是梯形 ABCD，迎水坡 BC 的倾斜角∠B = 30°，背水坡 AD 的坡比为 1.2∶1，坝顶 DC = 5 m，坝高 CE = 6 m. 求 BC 和 AB 的长（结果精 确到 0.1 m）. D C A E B （第 2 题） 3. 如图所示，铁路 AB 和公路 CD 在点 O 处交汇，∠BOD = 30°. 公路 CD 上 K 处 距离 O 点 240 m. 如果火车行驶时，周围 200 m 以内会受到噪音的影响，求火车 在铁路 AB 上沿由 A 到 B 的方向以 72 km / h的速度行驶时，K 处受噪音影响的 时间. B C O A K D （第 3 题） 6 利利用用三三角角函函数数测测高高 活动课题：利用直角三角形的边角关系测量物体的高度. 活动方式：分组活动、全班交流研讨. 活动工具：测倾器（或经纬仪、测角仪等）、皮尺等测量工具. 51第二章 直角三角形的边角关系 P Q 活动一：测量倾斜角. 测量倾斜角可以用测倾器. 简单的测倾器由度盘、铅 锤和支杆组成（如图 2-27）. 使用测倾器测量倾斜角的步骤如下： （1）把支杆竖直插入地面，使支杆的中心线、铅垂线 图 2-27 和度盘的 0°刻度线重合，这时度盘的顶线 PQ 在水平位置. （2）转动度盘，使度盘的直径对准目标 M，记下此时铅垂线所指的度数. 根据测量数据，你能求出目标 M 的仰角或俯角吗？说说你的理由. 活动二：测量底部可以到达的物体的高度. 所谓“底部可以到达”，就是在地面上可以无障碍地直接测得测点与被测 物体的底部之间的距离. 如图 2-28，要测量物体 MN 的高度，可以按下列步骤 进行： M C E N A 图 2-28 （1）在测点 A 处安置测倾器，测得 M 的仰角∠MCE = α. （2）量出测点 A 到物体底部 N 的水平距离 AN = l. （3）量出测倾器的高度 AC = a（即度盘的顶线 PQ 成水平位置时，它与地 面之间的距离）. 根据测量数据，你能求出物体 MN 的高度吗？说说你的理由. 活动三：测量底部不可以到达的物体的高度. 所谓“底部不可以到达”，就是在地面上不能直接测得测点与被测物体的 底部之间的距离. 如图 2-29，要测量物体 MN 的高度，可以按下列步骤进行： 526 利用三角函数测高 M D C E N B A 图 2-29 （1）在测点 A 处安置测倾器，测得此时 M 的仰角∠MCE = α. （2）在测点 A 与物体 MN 之间的 B 处安置测倾器（A，B 与 N 在同一条直 线上），测得此时 M 的仰角∠MDE = β. （3）量出测倾器的高度 AC = BD = a，以及测点 A 和测点 B 之间的水平距 离 AB = b. 根据测量数据，你能求出物体 MN 的高度吗？说说你的理由. 议一议 （1）到目前为止，你有哪些测量物体高度的方法？ （2）如果一个物体的高度已知或容易测量，那么如何测量某点到该物体的 水平距离？与同伴进行交流. 习题 2.11 问题解决 1. 分组制作简单的测倾器. 2. 选择一个底部可以到达的物体，测量它的高度，并撰写一份活动报告，阐明活动 课题、测量示意图、测得数据和计算过程等. 3. 选择一个底部不可以到达的物体，测量它的高度，并撰写一份活动报告. 53第二章 直角三角形的边角关系 回顾与思考 1. 举例说明锐角三角函数在现实生活中的应用. 2. 任意给定一个锐角，用计算器探索这个角的正弦、余弦、正切之间的关系. 3. 直角三角形的边角之间有怎样的关系？举例说明. 4. 你能应用锐角三角函数解决哪些问题？ 5. 如何测量一座高楼的高度？你能想出几种方法？ 6. 用适当的方式梳理本章的知识，并与同伴进行交流. 复习题 知识技能 1. 计算： （1）sin 45°－cos 30°+ tan 60°； （2）sin 60°+ tan 45°－cos 30°； （3）cos 60°－tan 30°+ sin 30°； （4）cos230°+ sin230°- tan 45°. 2. 用计算器求下列各式的值： （1）sin 23°5′+ cos 66°55′； （2）cos 14°28′－tan 42°57′； （3）tan 52°39′－sin 61°42′； （4）sin27.8°- cos 65°37′+ tan 49°56″. 3. 在 Rt△ABC 中，∠C = 90°，a，b，c 分别为∠A，∠B，∠C 的对边. （1）已知 a = 3，b = 3，求∠A； （2）已知 b = 4，c = 8，求 a 及∠A； （3）已知∠A = 45°，c = 8，求 a 及 b； （4）已知 a = 22.5，b = 12，求∠A 及∠B 的度数（结果精确到 1′）. 3 4. 已知∠A 是锐角，cos A = ，求 sin A，tan A. 5 5. 根据下列三角函数值，求锐角的大小： （1）sin A = 0.675，求∠A； （2）cos B = 0.078 9，求∠B； （3）tan C = 35.6，求∠C. 54复习题 6. 计算： cos 30°- sin 45° （1） ； sin 60°- cos 45° 3 2 （2） tan 60°- cos 45°； 2 2 （3）sin 60°·cos 60°+ sin 45°·cos 45°- sin 30°·cos 30°. 7. 在 Rt△ABC 中，∠C = 90°，∠B = 60°，AB = 4，求 AC，BC，sin A 和 cos A. 数学理解 8. 如图，在 Rt△ABC 中，∠C = 90°. A B C D （第 8 题） （1）在 BC 边上取一点 D，使得 BD = DC，则 tan∠ABC 和 tan∠ADC 有什么大小 关系？ （2）在 BC 边上取一点 D，使得 BD = 2DC，则 tan∠ABC 和 tan∠ADC 有什么大小 关系？ （3）在 BC 边上取一点 D，使得 BD = nDC（n > 0），则 tan∠ABC 和 tan∠ADC 有 什么大小关系？ 问题解决 9. 如图，在高出海平面 100 m 的悬崖顶 A 处，观测海面上的一艘小船 B，并测得它的 俯角为30°，求船与观测者之间的水平距离（结果精确到 0.1 m）. A 30° B （第 9 题） 10. 一艘船由 A 港沿北偏东 60°方向航行 10 km 至 B 港，然后再沿北偏西 30°方向航 行 10 km 至 C 港. （1）求 A，C 两港之间的距离（结果精确到 0.1 km）； （2）确定 C 港在 A 港的什么方向. 55第二章 直角三角形的边角关系 11. 如图，为了测量一条河流的宽度，一位测量员在河北岸东西方向相距 180 m 的P， Q 两点分别测定对岸河边一棵树 T 的位置，T 在 P 的正南方向，在 Q 的南偏西 50°方向，求河宽 PT（结果精确到 1 m）. P Q 北 T （第 11 题） 12. 一根长 4 m 的竹竿斜靠在墙上. （1）如果竹竿与地面成 60°角，那么竹竿的下端离墙脚有多远？ （2）如果竹竿上端顺墙下滑到高度 2.3 m 处停止，那么此时竹竿与地面所成锐角 的大小是多少？ 13. 如图，甲、乙两楼相距 30 m，甲楼高 40 m，在甲楼楼顶 A 处测得乙楼楼顶 B 处的 仰角为 30°，乙楼有多高？（结果精确到 1 m） 30 m 联系拓广 56 m 04 B B 甲A 30° 乙 D 30° E 60° A C （第 13 题） （第 14 题） 14. 如图，大楼高 30 m，附近有一座塔 BC，某人在楼底 A 处测得塔顶的仰角为 60°， 爬到楼顶 D 处测得塔顶的仰角为 30°，求塔高 BC 及大楼与塔之间的距离 AC（结 果精确到 0.01 m）. 15. 海岛 A 的周围 8 n mile 内有暗礁. 渔船跟踪鱼群由西向东航行，在点 B 处测得海 岛 A 位于北偏东 60°方向上；航行 12 n mile 后到达点 C 处，又测得海岛 A 位于北 偏东 30°方向上. 如果渔船不改变航向继续向东航行，那么它有没有触礁的危险？ ※16. 如图，为了测量山坡的护坡石坝与地面之间的倾斜角 α，把一根长为 4.5 m 的竹竿 AC 斜靠在石坝旁，在竹竿上距 A 点 1 m 远处的 D 点离地面的高度 DE 是 0.6 m， 又量得石坝的坡长 BC = 2.8 m，这样∠α 就可以计算出来了. 请你算一算.复习题 C 50 m m 0 3 D 60° 60° 1 m m 0.6 m α 0 50 m 2 A E B （第 16 题） （第 17 题） ※17. 如图是一块四边形空地，求此空地的面积（结果精确到 0.01 m2）. ※18. 如图，某学校主楼的顶部和大门的上方之间挂了一些彩旗. 经测量，大门 AB 的高 度是 5 m，大门距主楼的距离 BC 是 30 m. 在大门处测得主楼顶部的仰角是 30°， 测倾器到地面的距离 EB 为 1.4 m. （1）求学校主楼的高度（结果精确到 0.01 m）； （2）求大门顶部与主楼顶部的距离 AD（结果精确到 0.01 m）. D A D A 30° E B C E B C （第 18 题） （第 19 题） 19. 如图，正方形 ABCD 的边长为 1，延长边 CB 到点 E，使 BE = BD，连接 DE， ∠CDE 的度数是多少？ 试利用这个图形求出角 67.5°的正切的值. 20. 把一条 1.35 m 的铁丝弯成顶角为 150°的等腰三角形，求此三角形的各边长 （结果精确到 0.01 m）. 57综合与实践 设计遮阳篷 设计遮阳篷 在日常生活中，我们经常可以看到一些窗户上安装有遮阳篷. 你会设计遮 阳篷吗？ 假设某居民楼位于北半球某地，窗户朝南，窗户的高度为 h cm. 此地一年 中的正午时刻，太阳光与地平面的最小夹角为 α，最大夹角为 β. 请你为该窗 户设计一个遮阳篷，要求它既能最大限度地遮挡夏天炎热的阳光，又能最大限 度地使冬天温暖的阳光射入室内. α β 做一做 58 h h （1） （2） 图 1 把图 1 画成图 2，其中 AB 表示窗户（AB = h cm），BCD 表示直角形遮阳篷. 图 2 图 3设计遮阳篷 （1）当太阳光与地平面的夹角为 α 时，要想使太阳光尽可能多地射入 室内，遮阳篷 BCD 应如何设计？请在图 3 中画图表示. 此时，BC 唯一吗？ CD 呢？ （2）当太阳光与地平面的夹角为 β 时，要想使太阳光刚好不射入室内，遮 阳篷 BCD 应如何设计？请在图 3 中画图表示. 此时，BC 唯一吗？CD 呢？ （3）如果要同时满足（1）（2）两个条件，那么遮阳篷 BCD 应如何设计？ 请在图 3 中画图表示. 此时，BC 唯一吗？CD 呢？ 你能用含有 h，α，β 的关系式分别表示 BC 和 CD 吗？ 议一议 就北半球而言，冬至这一天的正午时刻，太阳光与地平面的夹角最小； 夏至这一天的正午时刻，太阳光与地平面的夹角最大. 如果根据上面（3）中 的 BC 和CD 设计遮阳篷 BCD，那么你认为它符合本综合与实践一开始提出的 要求吗？与同伴进行交流. 想一想 如何利用你所学的知识测量你所在地区正午时刻太阳光与地平面的夹角？ 先想一想，再与同伴进行交流. 做一做 查阅有关资料或进行实际测量，获得你所在地区 α 和 β 的相应数据，然后 为你们学校的某个窗户制作一个遮阳篷（模型）. 下表中的数据可供你参考. 纬 度 北纬 24° 北纬 32° 北纬 40° 北纬 48° 冬至（α） 42°34' 34°34' 26°34' 18°34' 冬至（β） 89°26' 81°26' 73°26' 64°26' 59综合与实践 设计遮阳篷 想一想 对于上面你所制作的遮阳篷： （1）如果考虑到防雨功能，遮阳篷往下倾斜 10°（即坡角为10°），那么遮 阳篷的最小宽度为多少？ （2）由于安装防盗网等原因，遮阳篷到窗户顶部的距离应不少于 20 cm （BC ≥ 20 cm），那么遮阳篷的最小宽度为多少？ （3）若同时考虑（1）和（2）的条件，又使遮阳篷可以伸缩，那么应如何 设计？请画出示意图. 先想一想，再与同伴进行交流. 做一做 分组调查遮阳篷的实际设计与制作过程，并撰写调查报告. 议一议 把调查情况和调查报告在全班进行交流. 你能对厂家的设计提出改进建议 吗？ 习题 如图，某一时刻太阳光从窗户射入房间内，与地面的夹角∠DPC = 30°，已知窗 户的高度 AF = 2 m，窗台的高度 CF = 1 m，窗外水平遮阳篷的宽 AD = 0.8 m， 求 CP 的长度（结果精确到 0.1 m）. D A B F C E P 601 对函数的再认识 第三章 二次函数 节日的喷泉给人们带来喜庆，夏日的喷泉给人们带来凉爽. 你是否注意到 喷泉水流所经过的路线？在观看篮球比赛时，你是否注意过篮球入篮的路线？ 它会与某种函数有联系吗？ 本章我们将要探索和研究刻画变量之间关系的一种新模型——二次函数. 类似于以前所学的一次函数和反比例函数，我们也要借助图象发现二次函数的 性质，并利用二次函数解决一些实际问题. 学习目标 进一步认识函数，能恰当地表示函数 探索变量之间的二次函数关系，体会其中的模型思想 会画二次函数的图象，发展几何直观 探究二次函数的性质，进一步积累研究函数性质的经验 会利用二次函数的图象求一元二次方程的近似解，进一 步体会方程和函数的关系 能够用二次函数解决现实生活中的问题，发展应用意识 660000 == PP xx 61第三章 二次函数 1 对函数的再认识 想一想 你还记得什么是函数吗？你能举出几个函数的例子吗？ 做一做 （1）A，B 两地之间的路程为 900 km，一辆汽车从 A 地到 B 地所需时 间 t（h）与汽车的平均速度 v（km/h）之间的关系式是 D C t = _______. 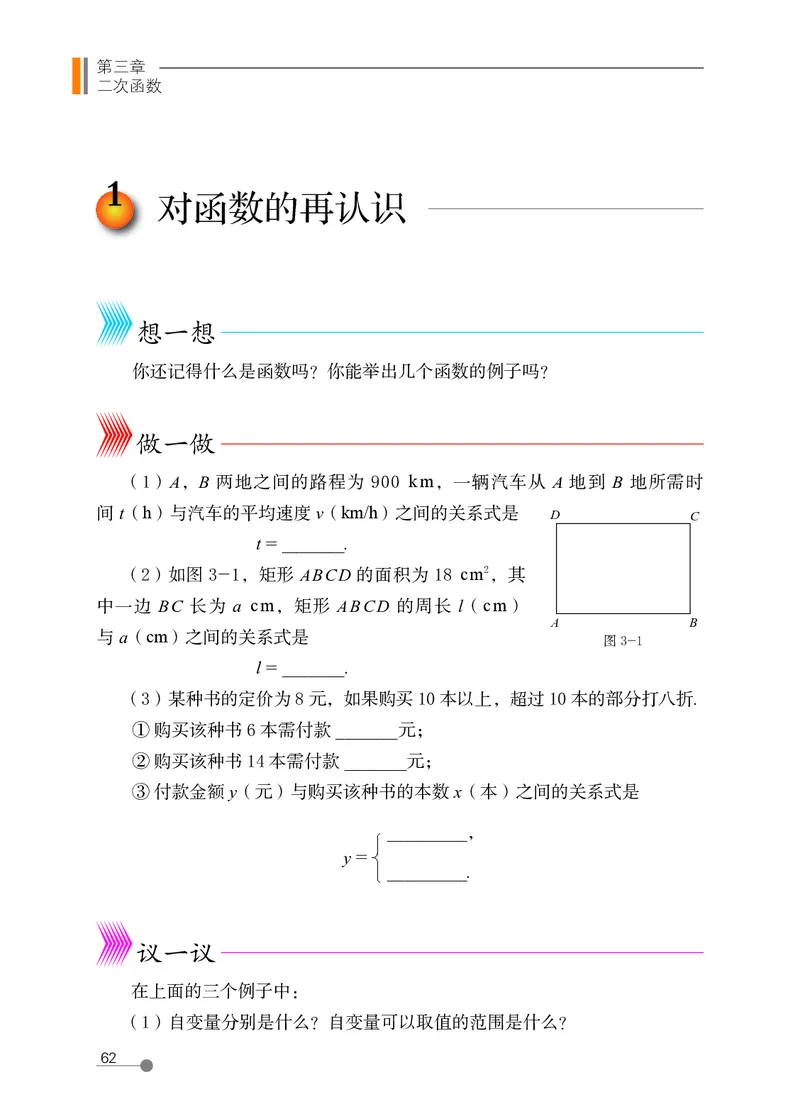（2）如图 3-1，矩形 ABCD 的面积为 18 cm2，其 中一边 BC 长为 a cm，矩形 ABCD 的周长 l（cm） A B 与 a（cm）之间的关系式是 图 3-1 l = _______. （3）某种书的定价为 8 元，如果购买 10 本以上，超过 10 本的部分打八折. ① 购买该种书 6 本需付款 _______元； ② 购买该种书 14 本需付款 _______元； ③ 付款金额 y（元）与购买该种书的本数 x（本）之间的关系式是 _________， y = _________. 议一议 在上面的三个例子中： （1）自变量分别是什么？自变量可以取值的范围是什么？ 621 对函数的再认识 （2）对于自变量在它可以取值的范围内的每一个值，另一个变量是否都有 唯一确定的值与它对应？ （3）由此你对函数有了哪些进一步的认识？与同伴进行交流. 一般地，如果在一个变化过程中有两个变量 x 和 y，并且对于变量 x 在某 一范围内的每一个确定值，变量 y 都有唯一确定的值与它对应，那么我们就 称 y 是 x 的函数，其中 x 是自变量， y 是因变量. 例 1 如图 3-2，正方形 ABCD 的边长为 2，点 P 为 AD 边上一点， 设 AP = x，四边形 BCDP 的面积为 y ，求 y 与 x 之间的函数关系式，并指 出 x 的取值范围 . D C 解：因为 AP = x，AB = 2， 所以△APB 的面积 S = x，正方形 ABCD 的面积 1 S = 4 . P 所以四边形 BCDP 的面积 y = S - S 1 A B 图 3-2 = 4 - x . 所以，y 与 x 之间的函数关系式为 y = 4 - x . 由于点 P 在 AD 边上，因此，0 < x < 2. 例 2 当 x = 3 时，求下列各函数 y 的对应值： （1）y = 3x + 7； （2）y = - 2x 2 - 1； 1 （3）y = 5x + 2 ； （4）y = x - 3 . 解：（1）当 x = 3 时，y = 3 × 3 + 7 = 16； （2）当 x = 3 时，y = - 2×32 - 1 = - 19； 1 1 （3）当 x = 3 时，y = = ； 5 × 3 + 2 17 （4）当 x = 3 时，y = 3 - 3 = 0. 63第三章 二次函数 对于自变量 x 在可以取值范围内的一个确定的值 a，函数 y 有唯一确定的 对应值，这个对应值叫做当 x = a 时函数的值，简称函数值（value of function）. 如对于例 2（1）中的函数 y = 3x + 7，16 就是当 x = 3 时的函数值. 随堂练习 1. 某汽车油箱内现有汽油 50 L，若这辆汽车每行驶 100 km 的耗油量为 6 L，试写出 汽车油箱中剩余油量 y（L）与汽车行驶的路程 x（km）之间的关系式. 1 2. 当 x = - 3， 时，求下列函数的函数值： 2 1 （1）y = 2 x2 + x - 3； （2）y = - 4 x + 8 ； x - 3 1 7 （3）y = x + 1 ； （4）y = 2 x + 4 . 习题 3.1 知识技能 1. 一个等腰三角形的周长为 10 cm，求它的一腰长 y（cm）与底边长 x（cm）之间 的关系式. 2. 当 x 为何值时，下列函数的函数值为 0？ （1）y = 2x + 3； （2）y = 2x2 - x - 6. 问题解决 3. 一根蜡烛长 20 cm，点燃后每小时燃烧 5 cm. （1）写出蜡烛剩余长度 y（cm）与点燃时间 x（h）之间的函数关系式 ； （2）写出自变量 x 的取值范围； （3）蜡烛点燃 2 h 后还剩多长？ 联系拓广 4. 当 x 为何值时，下列函数的函数值为正数？ 1 （1）y = 1 - 2x； （2）y = . 2x + 3 641 对函数的再认识 上节课所举出的例子中，函数都是利用数学式子表示的. 你知道函数还可 以用什么方法表示吗？ 做一做 1. 某届全国图书展销会在 5 月份举行. 本届展销会总收入约 1 800 万元 （包括批发和零售），其中零售收入约 500 万元，展销会期间的零售收入统计 如下： 日期/日 12 13 14 15 16 17 18 19 20 21 22 23 零售收入/万元 40 42 48 50 46 42 40 38 35 37 42 44 （1）展销会期间，哪一日的零售收入最高？ （2）零售收入是日期的函数吗？为什么？它是用什么方法表示的？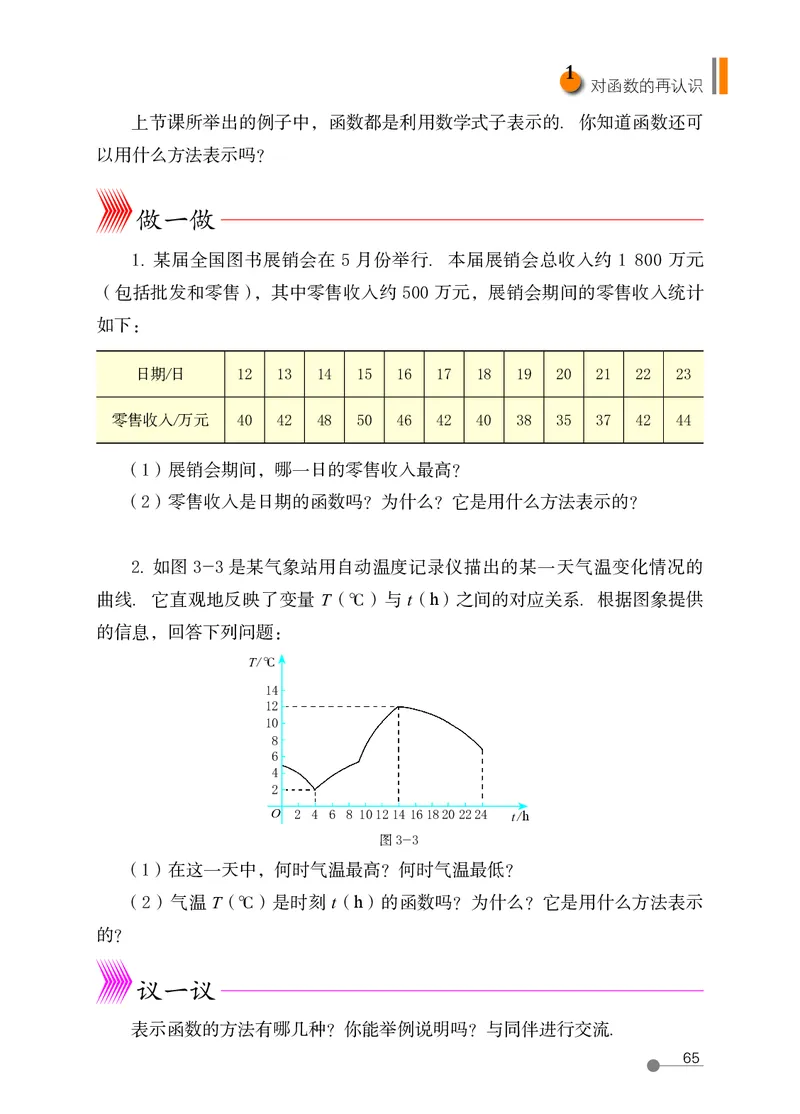 2. 如图 3-3 是某气象站用自动温度记录仪描出的某一天气温变化情况的 曲线. 它直观地反映了变量 T（℃）与 t（h）之间的对应关系. 根据图象提供 的信息，回答下列问题： T / ℃ 14 12 10 8 6 4 2 O 2 4 6 8 1012141618202224 t / h 图 3-3 （1）在这一天中，何时气温最高？何时气温最低？ （2）气温 T（℃）是时刻 t（h）的函数吗？为什么？它是用什么方法表示 的？ 议一议 表示函数的方法有哪几种？你能举例说明吗？与同伴进行交流. 65第三章 二次函数 用来表示函数关系的数学式子叫做函数的表达式（或解析式），用数学式 子表示函数的方法称为解析法. 函数还可以用表格和图象表示，分别称为列表 法和图象法. 你认为用解析法、 列表法和图象法表示函 数关系各有哪些优点？ 想一想 上述例子中，自变量的取值范围分别是什么？ 例 3 求下列函数的自变量 x 的取值范围： 1 （1）y = 2x - 4； （2）y = ； 4x + 3 1 （3）y = 2x + 1； （4）y = . 2 - 3x 解：（1）自变量 x 的取值范围是全体实数. （2）使函数有意义的条件是 4x + 3 ≠ 0， 3 也就是 x ≠ - . 4 1 3 所以，函数 y = 的自变量 x 的取值范围是 x ≠ - 的实数. 4x + 3 4 （3）使函数有意义的条件是 2x + 1 ≥ 0， 1 也就是 x ≥ - . 2 1 所以，函数 y = 2x + 1 的自变量 x 的取值范围是 x ≥ - 2 的实数. （4）使函数有意义的条件是 2 - 3x > 0， 2 也就是 x < . 3 661 对函数的再认识 1 2 所以，函数 y = 的自变量 x 的取值范围是 x < 的实数. 3 2 - 3x 例 4 用总长为 60 m 的篱笆围成矩形场地，求矩形的面积 S（m2）与它的 一边长 x（m）之间的关系式，并求出 x 的取值范围. 解：因为矩形的周长为 60 m，一边长为 x m， 1 所以矩形的另一边长为 （60 - 2x）m，即（30 - x）m. 2 因此，矩形的面积 S（m2）与 x（m）之间的关系式为 S = x（30 - x）. 因为矩形的两边长分别为 x m，（30 - x）m， x > 0， 所以 解得 0 < x < 30. 30 - x > 0， 因此，自变量 x 的取值范围是 0 < x < 30. 如何确定函数 自变量的取值范围？ 函数自变量的取值范围，应使函数表达式有意义. 在解决实际问题时，还 必须考虑使实际问题有意义. 随堂练习 1. 求下列函数的自变量 x 的取值范围： x （1）y = x2（x + 1）； （2）y = ； x - 4 3x （3）y = 1 - 3x； （4）y = . x + 5 2. 从边长分别为 6 cm，8 cm 的矩形纸片的四个角处各剪去一个边长为 x cm 的小正方 形（如图所示），求纸片剩余部分的面积 S（cm2）与 x（cm）之间的关系式，并指 67第三章 二次函数 出 x 的取值范围. 8 习题 3.2 知识技能 1. 求下列函数的自变量 x 的取值范围： x + 1 （1）y = ； （2）y = x + 2 + 3 - x . x2 + 1 2. 小明设计了一个计算程序，输入的数 x 和输出的数 y 的数据如下表： 输入的数 x 1 2 3 4 5 1 2 3 4 5 输出的数 y 2 3 4 5 6 在这个问题中，y 是 x 的函数吗？它们之间的函数关系是用哪种方法表示的？你 能用一个函数表达式表示它们之间的关系吗？ 问题解决 3. 某车间共有工人 20 名. 已知每名工人每天可制造甲种零件 6 个或乙种零件 5 个，每制造一个甲种零件可创利润 150 元，每制造一个乙种零件可创利润 260 元. 车间每天安排 x 名工人制造甲种零件，其余工人制造乙种零件 . （1）请写出此车间每天所创利润 y（元）与 x（人）之间的函数关系式； （2）如果要使车间每天所创利润不低于 24 000 元，你认为至少要安排多少名工 人制造乙种零件？ 68 6 （第 2 题） x2 二次函数 2 二次函数 某果园有 100 棵橙子树，每一棵树平均结 600 个橙子. 现准备多种一些橙子树以提高果园 产量，但是如果多种树，那么树之间的距离和 每一棵树所接受的阳光就会减少. 根据经验估 计，每多种一棵树，平均每棵树就会少结 5 个 橙子. （1）问题中有哪些变量？其中哪些是自变量？哪些是因变量？ （2）假设果园增种 x 棵橙子树，那么果园共有多少棵橙子树？这时平均每 棵树结多少个橙子？ （3）如果果园橙子的总产量为 y 个，那么请你写出 y 与 x 之间的关系式. 果园共有（100 + x）棵橙子树，平均每棵橙子树结（600 - 5x）个橙子， 因此果园橙子的总产量 y =（600 - 5x）（100 + x）= - 5x 2 + 100x + 60 000. 做一做 (cid:18978)(cid:15736)(cid:1492)(cid:14832)(cid:1877)(cid:10419)(cid:15764) 银行的储蓄利率是随时间的变化而变化的， (cid:19)(cid:17)(cid:18)(cid:18)(cid:14)(cid:19)(cid:14)(cid:26) (cid:4228)(cid:8298)(cid:19877)(cid:11290) (cid:5024)(cid:1877)(cid:10419)(cid:8) 也就是说，利率是一个变量. 在我国，利率的调 (cid:8807)(cid:7243)(cid:4228)(cid:8298) (cid:19)(cid:17)(cid:23)(cid:19) (cid:821)(cid:854)(cid:7220) (cid:21)(cid:17)(cid:25)(cid:19) 整是由中国人民银行根据国民经济发展的情况而 (cid:2166)(cid:5024) (cid:21)(cid:17)(cid:27)(cid:19) (cid:812)(cid:5024) (cid:22)(cid:17)(cid:19)(cid:19) (cid:6816)(cid:4228)(cid:6816)(cid:2306) 决定的. (cid:952)(cid:5024) (cid:22)(cid:17)(cid:28)(cid:19) (cid:821)(cid:5024) (cid:23)(cid:17)(cid:24)(cid:19) (cid:4294) (cid:960)(cid:5024) (cid:24)(cid:17)(cid:19)(cid:19) 设人民币一年定期储蓄的年利率是 x，一年到 (cid:7243) (cid:19490)(cid:4228)(cid:6816)(cid:2306)(cid:543) (cid:812)(cid:5024) (cid:21)(cid:17)(cid:25)(cid:19) (cid:4228) (cid:6816)(cid:4228)(cid:19490)(cid:2306)(cid:543) (cid:821)(cid:5024) (cid:21)(cid:17)(cid:27)(cid:19) 期后，银行将本金和利息自动按一年定期储蓄转 (cid:8298) (cid:4228)(cid:7256)(cid:2306)(cid:5531) (cid:960)(cid:5024) (cid:22)(cid:17)(cid:19)(cid:19) (cid:6197)(cid:812)(cid:5024)(cid:1041)(cid:1713)(cid:4294)(cid:7243)(cid:6816)(cid:4228)(cid:6816)(cid:2306)(cid:3) (cid:4294)(cid:8807)(cid:848)(cid:1259) 存. 如果存款额是 100 元，那么请你写出两年后 (cid:2360)(cid:7567)(cid:8269)(cid:1877)(cid:10419)(cid:6015)(cid:3)(cid:25)(cid:3)(cid:6084) (cid:2171)(cid:4294)(cid:4228)(cid:8298) (cid:20)(cid:17)(cid:21)(cid:20) (cid:812)(cid:3669) (cid:19)(cid:17)(cid:27)(cid:24) 的本息和 y（元）的表达式. (cid:17734)(cid:11537)(cid:4228)(cid:8298) (cid:815)(cid:3669) (cid:20)(cid:17)(cid:22)(cid:28) 69第三章 二次函数 想一想 （1）已知矩形的周长为 40 cm，它的面积可能是 100 cm2 吗？可能是 75 cm2 吗？还可能是多少？你能表示这个矩形的面积与其一边长的关系吗？ （2）两数的和是 20，设其中一个数是 x，你能写出这两数之积 y 的表达式 吗？ 一般地，形如 y = ax 2 + bx + c（a，b，c 是常数，a ≠ 0）的函数叫做 x 的 二次函数（quadratic function）. 例如，y = - 5x 2 + 100x + 60 000，y = 100x 2 + 200x + 100 和 y = - x 2 + 20x 都是二次函数. 我们以前学过的正方形面积 A 与边长 a 的关系A = a 2，圆面 积 S 与半径 r 的关系 S = r 2，自由落体运动物体下落的高度 h 与下落的时 1 间 t 的关系 h = gt 2 等也是二次函数的例子. 2 随堂练习 1. 下列函数中（x，t 是自变量），哪些是二次函数？ 1 1 y = - + 3x2，y = x2 - x3 + 25，y = 22 + 2x，s = 1 + t + 5t 2. 2 2 2. 圆的半径是 1 cm，假设半径增加 x cm 时，圆的面积增加 y cm2. （1）写出 y 与 x 之间的关系式； （2）当圆的半径分别增加 1 cm， 2 cm，2 cm 时，圆的面积各增加多少？ 习题 3.3 知识技能 1. 物体从某一高度落下，已知下落的高度 h（m）和下落的时间 t（s）的关系是： h = 4.9 t2，填表表示物体在前 5 s 下落的高度： t / s 1 2 3 4 5 h / m 703 二次函数 y = ax2 的图象与性质 数学理解 2. 举出一个生活中有关二次函数的例子. 问题解决 3. 某工厂计划为一批长方体形状的产品涂上油漆，长方体的长和宽相等，高比长 多 0.5 m. （1）长方体的长和宽用 x（m）表示，长方体需要涂漆的表面积 S（m2）如何表示？ （2）如果涂漆每平方米所需要的费用是 5 元，油漆每个长方体所需费用用 y（元） 表示，那么 y 的表达式是什么？ 4. 某超市欲购进一种今年新上市的产品，购进价为 20 元/件. 为了调查这种新产品 的销路，该超市进行了试销售，得知该产品每天的销售量 t（件）与每件的销售 价 x（元 / 件）之间有如下关系：t = - 3x + 70. 请写出该超市销售这种产品每天 的销售利润 y（元）与 x 之间的函数关系式. 3 = 2 二次函数 y ax 的图象与性质 在二次函数 y = x 2 中，y 的值随 x 值的变化而变化的规律是什么？你想直 观地了解它的性质吗？ 画二次函数 y = x 2 的图象. （1）观察 y = x 2 的表达式，选择适当的 x 值，并计算相应的 y 值，完成 下表： x y （2）在直角坐标系中描点. 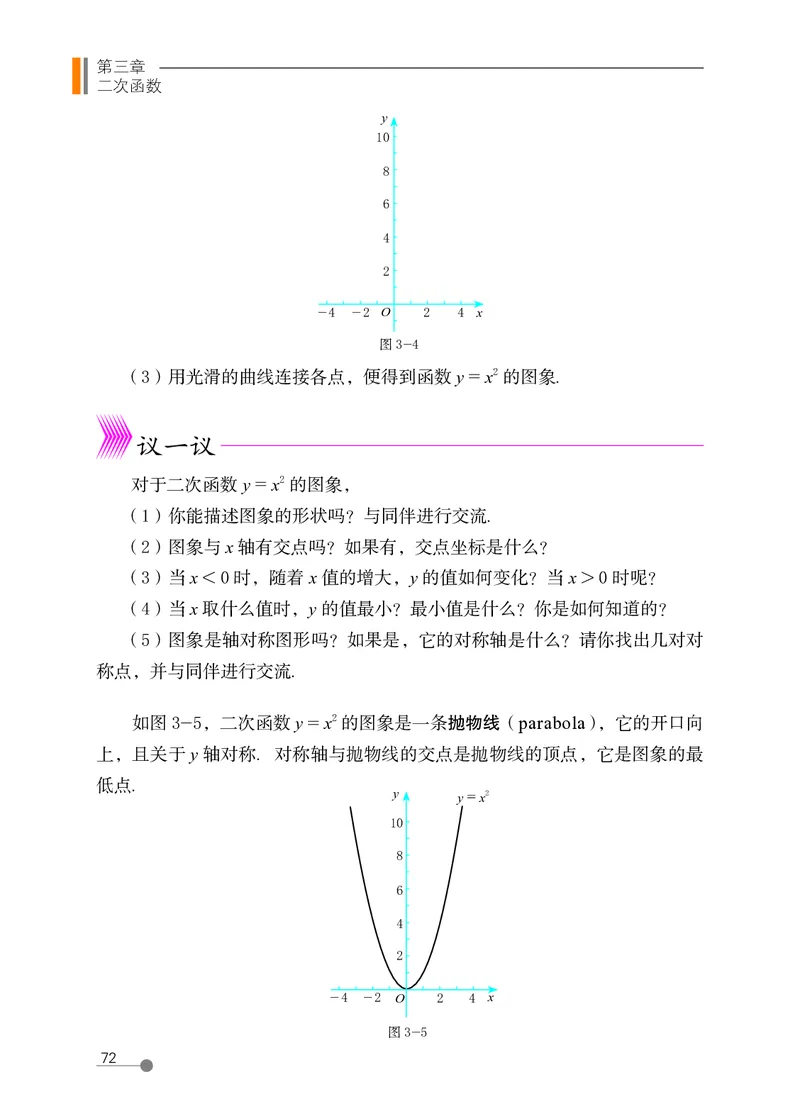71第三章 二次函数 y 10 8 6 4 2 - 4 - 2 O 2 4 x 图 3-4 （3）用光滑的曲线连接各点，便得到函数 y = x 2 的图象. 议一议 对于二次函数 y = x 2 的图象， （1）你能描述图象的形状吗？与同伴进行交流. （2）图象与 x 轴有交点吗？如果有，交点坐标是什么？ （3）当 x < 0 时，随着 x 值的增大，y 的值如何变化？当 x > 0 时呢？ （4）当 x 取什么值时，y 的值最小？最小值是什么？你是如何知道的？ （5）图象是轴对称图形吗？如果是，它的对称轴是什么？请你找出几对对 称点，并与同伴进行交流. 如图 3-5，二次函数 y = x 2 的图象是一条抛物线（parabola），它的开口向 上，且关于 y 轴对称. 对称轴与抛物线的交点是抛物线的顶点，它是图象的最 低点. y y = x2 10 8 6 4 2 - 4 - 2 O 2 4 x 图 3-5 723 二次函数 y = ax2 的图象与性质 做一做 二次函数 y = - x 2的图象是什么形状？先想一想，然后画出它的图象. 它 与二次函数 y = x 2 的图象有什么关系？与同伴进行交流. y - 4 - 2 O 2 4 x - 2 - 4 - 6 - 8 - 10 图 3-6 随堂练习 在同一直角坐标系中，画出函数 y = x2 与 y = - x2 的图象，并根据图象回答下列问题： （1）y = x2 的图象与 y = - x2 的图象关于哪条直线对称？ （2）这两个图象关于哪个点对称？ （3）由 y = x2 的图象如何得到 y = - x2 的图象？ 读一读 二次函数的广泛应用 二次函数是刻画客观世界许多现象的一种重要模型. 请看下面的一些例子. 1. 某一物体的质量为 m，它运动时的能量 E 与它的运动速度 v 之间的关系是： 1 E = mv2（m 为定值）. 2 2. 导线的电阻为 R，当导线中有电流通过时，单位时间所产生的热量 Q 与电流强 度 I 之间的关系是： Q = RI 2（R 为定值）. 3. g 表示重力加速度，当物体自由下落时，下落的距离 h 与下落时间 t 之间的关 73第三章 二次函数 系是： 1 h = gt 2（g 为定值）. 2 此外，二次函数在建筑学上也有重要应用，生活中不少建筑都设计成抛物线形 状，如桥拱、隧道等. 我们常见的卫星天线也是抛物线形的，喷泉、抛球、流星雨，甚 至是人的眉毛和微笑的嘴唇，无不蕴藏着抛物线的影子. 习题 3.4 知识技能 1. 设正方形的边长为 a，面积为 S，试画出 S 随 a 的变化而变化的图象. 数学理解 2. 点 A（2，4）在二次函数 y = x2 的图象上吗？请分别写出点 A 关于 x 轴的对称 点 B 的坐标、关于 y 轴的对称点 C 的坐标、关于原点 O 的对称点 D 的坐标. 点 B，C，D 在二次函数 y = x2 的图象上吗？在二次函数 y = - x2 的图象上吗？ 743 二次函数 y = ax2 的图象与性质 你知道两辆汽车在同向行驶 时为什么要保持一定距离吗？汽 车刹车时向前滑行的距离（称为 刹车距离）与什么因素有关？ 影响刹车距离的最主要因素 是汽车行驶的速度及路面的摩擦系数. 有研究表明，某种型号的汽车晴天在某 段公路上行驶时，速度 v（km/h）与刹车距离 s（m）之间的关系式为 1 s = v 2， 100 雨天行驶时，v 与 s 之间的关系式为 1 s = v 2 . 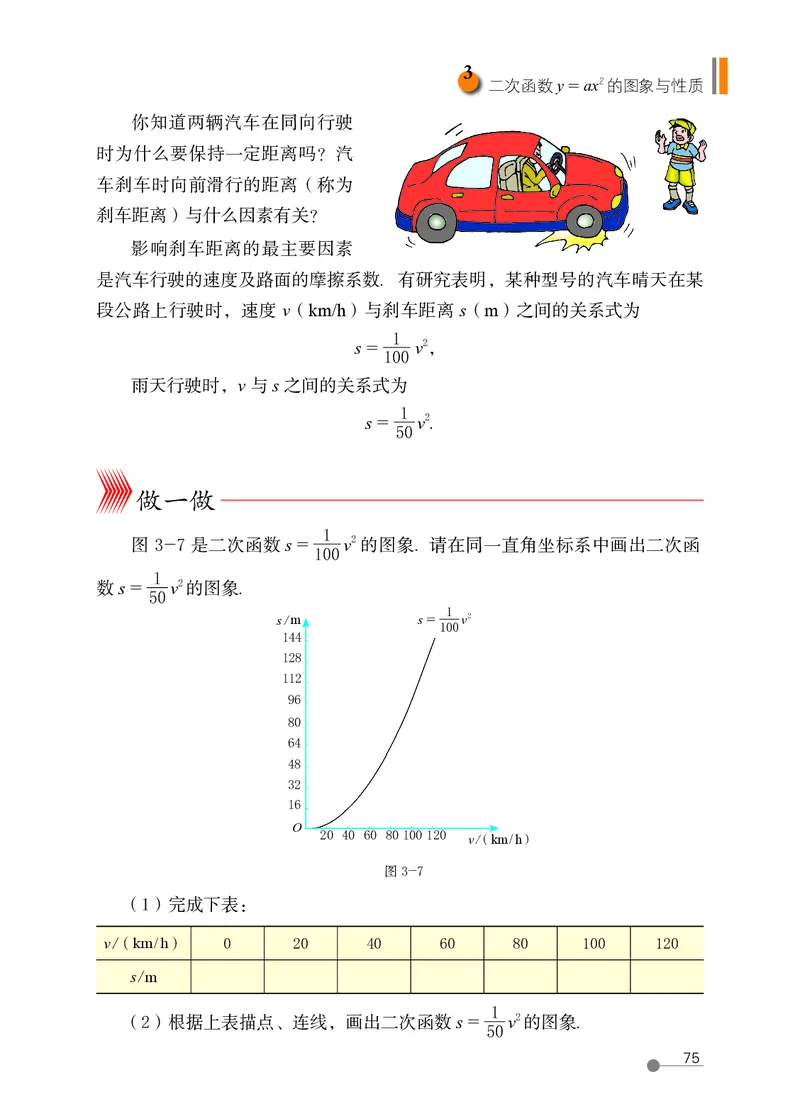50 做一做 1 图 3-7 是二次函数 s = v 2 的图象. 请在同一直角坐标系中画出二次函 100 1 数 s = v 2 的图象. 50 1 s/m s = v2 100 144 128 112 96 80 64 48 32 16 O 20 40 60 80100120 v /（km / h） 图 3-7 （1）完成下表： v /（km / h） 0 20 40 60 80 100 120 s / m 1 （2）根据上表描点、连线，画出二次函数 s = v 2 的图象. 50 75第三章 二次函数 议一议 1 1 （1）在上述函数 s = v 2 和 s = v 2 中，自变量 v 可以取任何值吗？为 100 50 什么？ 1 1 （2）s = v 2 和 s = v 2 的图象有什么相同点与不同点？ 100 50 （3）如果该汽车行驶的速度是 60 km/h，那么在雨天行驶和在晴天行驶相 比，刹车距离相差多少米？你是怎么知道的？ 做一做 画出二次函数 y = 2x 2 的图象. （1）完成下表： x y （2）在图 3-8 中画出 y = 2x 2 的图象. yy 88 66 44 22 -- 44 -- 22 OO 22 44 xx 图 3-8 （3）二次函数 y = 2x 2 的图象是什么形状？它与二次函数 y = x 2 的图象有 什么相同点和不同点？它的开口方向、对称轴和顶点坐标分别是什么？ 议一议 （1）二次函数 y = - 2x 2 的图象是什么形状？它的开口方向、对称轴和顶点 763 二次函数 y = ax2 的图象与性质 坐标分别是什么？在图 3-9 中画出它的图象 y 2 验证一下. （2）结合前面学习的内容，你能发现二 - 4 - 2 O 2 4 x - 2 次函数 y = ax 2 的图象具有什么共同特点吗？ - 4 - 6 - 8 - 10 图 3-9 一般地，二次函数 y = ax 2 的图象是抛物线. 我们把二次函数 y = ax 2 的 图象叫做抛物线 y = ax 2 . 抛物线 y = ax 2 的对称轴是 y 轴，它的顶点是坐标原点. 当 a > 0 时，抛 物线的开口向上，顶点是它的最低点；当 a < 0 时，抛物线的开口向下，顶 点是它的最高点. 随堂练习 1. 二次函数 y = - 3x2 的图象与二次函数 y = 3x2 的图象有什么关系？它们是轴对称图 形吗？它们的开口方向、对称轴和顶点坐标分别是什么？先想一想，如果需要， 1 1 画草图看一看. 二次函数 y = - x2 的图象与 y = x2 的图象呢？ 2 2 1 2. 二次函数 y = x2 的图象与二次函数 y = 3x2 的图象有什么相同点和不同点？ 3 3.（1）已知抛物线 y = ax2 通过点（2，4），求 a 的值； 1 （2）如果点（2，a），（b，- 8）都在抛物线 y = - x2 上，求 a，b 的值 . 2 习题 3.5 知识技能 1. 判断对错： （1）抛物线 y = 6x2 的开口向上； 77第三章 二次函数 （2）二次函数 y = ax2（a ≠ 0）的图象经过点（- 1，a）； （3）二次函数 y = ax2（a < 0）的图象是轴对称图形； （4）二次函数 y = ax2（a < 0）的图象有最低点； （5）若点（m，n）在抛物线 y = ax2 上，那么点（- m，n）也在这条抛物线上 . 2.（1）写出圆的面积 S 与它的直径 d 之间的函数关系式； （2）画出这个函数的图象； （3）从图象上求出直径为 3.4 cm 时圆的面积（结果精确到 0.1 cm2）. 3. 已知点 A（2，- 1），B（- 3，m）都在抛物线 y = ax2上，求 a 及 m 的值. 1 4. 已知二次函数 y = - x2. 2 （1）画出这个函数的图象； （2）当 x = 2，- 1.8 时，求 y 的值； （3）当 y = - 2，- 1.28 时，求 x 的值. 4 = 2 + + 二次函数 y ax bx c 的图象与性质 二次函数 y = 2x 2 + 1 的表达式与 y = 2x 2 有什么关系？由此猜想，它的图 象与二次函数 y = 2x 2 的图象有什么关系？与同伴进行交流. 做一做 画出二次函数 y = 2x 2 + 1 的图象. （1）完成下表，并指出 2x 2 与 2x 2 + 1 的值之间的关系. 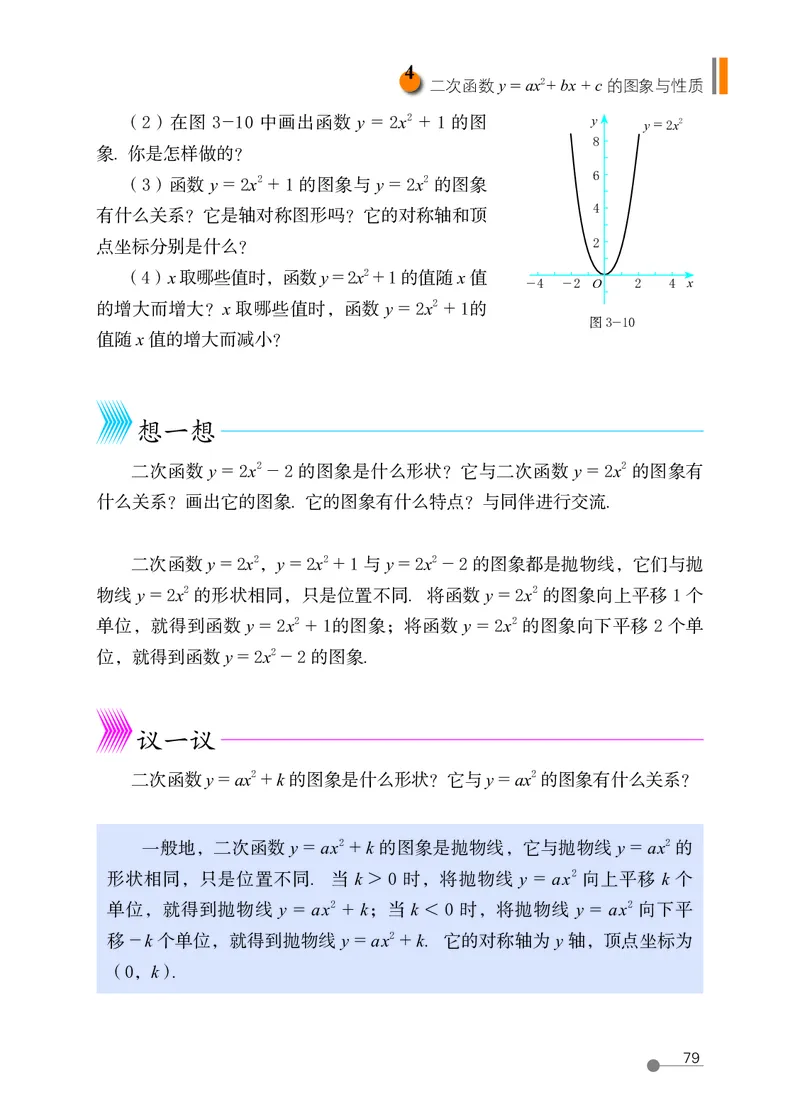x - 3 - 2 - 1 0 1 2 3 y = 2x2 y = 2x2 + 1 784 二次函数 y = ax2+ bx + c 的图象与性质 （2）在图 3-10 中画出函数 y = 2x 2 + 1 的图 y y = 2x2 8 象. 你是怎样做的？ 6 （3）函数 y = 2x 2 + 1 的图象与 y = 2x 2 的图象 4 有什么关系？它是轴对称图形吗？它的对称轴和顶 点坐标分别是什么？ 2 （4）x 取哪些值时，函数 y = 2x 2 + 1 的值随 x 值 - 4 - 2 O 2 4 x 的增大而增大？x 取哪些值时，函数 y = 2x 2 + 1的 图 3-10 值随 x 值的增大而减小？ 想一想 二次函数 y = 2x 2 - 2 的图象是什么形状？它与二次函数 y = 2x 2 的图象有 什么关系？画出它的图象. 它的图象有什么特点？与同伴进行交流. 二次函数 y = 2x 2，y = 2x 2 + 1 与 y = 2x 2 - 2 的图象都是抛物线，它们与抛 物线 y = 2x 2 的形状相同，只是位置不同. 将函数 y = 2x 2 的图象向上平移 1 个 单位，就得到函数 y = 2x 2 + 1的图象；将函数 y = 2x 2 的图象向下平移 2 个单 位，就得到函数 y = 2x 2 - 2 的图象. 议一议 二次函数 y = ax 2 + k 的图象是什么形状？它与 y = ax 2 的图象有什么关系？ 一般地，二次函数 y = ax 2 + k 的图象是抛物线，它与抛物线 y = ax 2 的 形状相同，只是位置不同. 当 k > 0 时，将抛物线 y = ax 2 向上平移 k 个 单位，就得到抛物线 y = ax 2 + k；当 k < 0 时，将抛物线 y = ax 2 向下平 移 - k 个单位，就得到抛物线 y = ax 2 + k. 它的对称轴为 y 轴，顶点坐标为 （0，k）. 79第三章 二次函数 随堂练习 1 1. 二次函数 y = 3x2 - 的图象与二次函数 y = 3x2 的图象有什么关系？它是轴对称图 2 形吗？它的开口方向、对称轴和顶点坐标分别是什么？画图看一看. 1 1 2. 二次函数 y = - 2x2 - 的图象与二次函数 y = - 2x2 + 的图象有什么关系？ 2 2 习题 3.6 知识技能 1. 在同一直角坐标系中画出下列二次函数的图象： 1 1 1 y = - x2，y = - x2 + 2，y = - x2 - 2. 2 2 2 根据图象，填写下表： 性质 x 取哪些值时，y 的值随 x 开口方向 对称轴 顶点坐标 二次函数 值的增大而增大 1 y = - 2 x2 1 y = - 2 x2 + 2 1 y = - 2 x2 - 2 2. 下列二次函数在同一直角坐标系中的图象如图所示，将函数图象的序号填在对 应函数表达式后面的括号里： y A B C 2 D 1 E O x - 1 - 2 （第 2 题） （1）y = 2x2； （ ） （2）y = 2x2 + 1； （ ） 804 二次函数 y = ax2+ bx + c 的图象与性质 （3）y = 2x2 + 2； （ ） （4）y = 2x2 - 1； （ ） （5）y = 2x2 - 2. （ ） 数学理解 3. 请写出两个二次函数的表达式，要求这两个函数图象的开口方向不同. 我们已经知道 y = 2x 2 的图象，那么二次函数 y = 2（x - 1）2 的图象与 y = 2x 2 的图象有什么关系？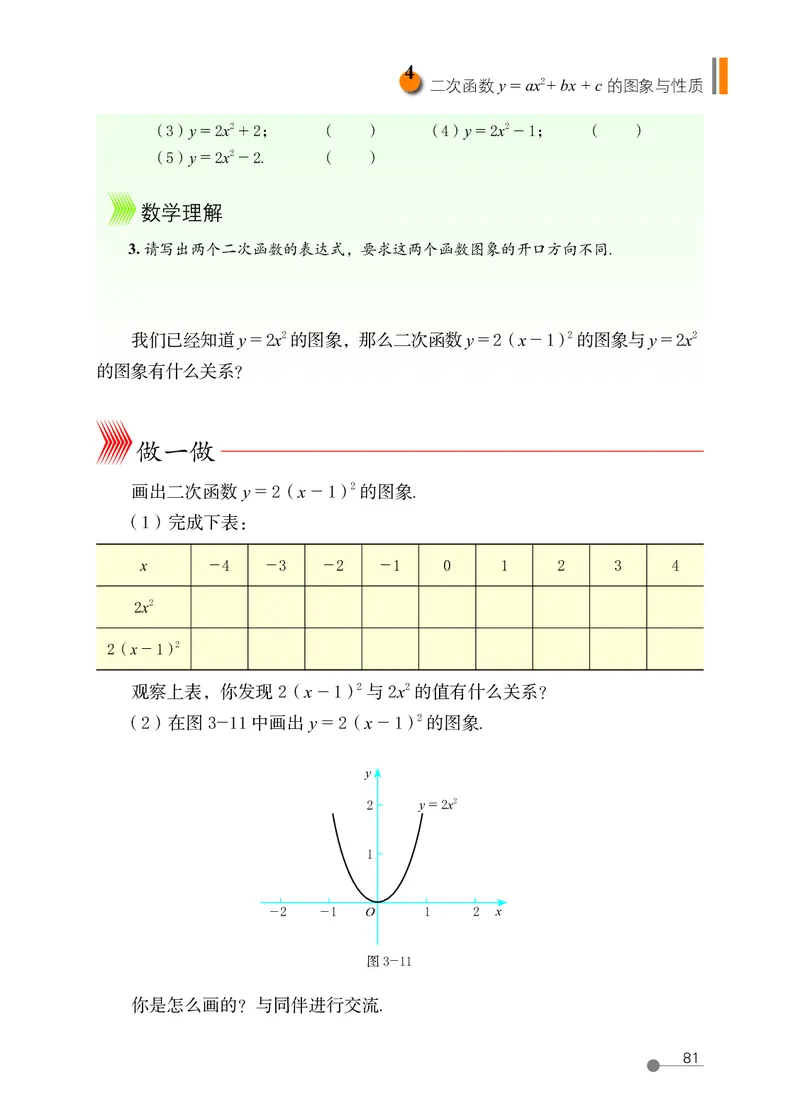 做一做 画出二次函数 y = 2（x - 1）2 的图象. （1）完成下表： x - 4 - 3 - 2 - 1 0 1 2 3 4 2x2 2（x - 1）2 观察上表，你发现 2（x - 1）2 与 2x 2 的值有什么关系？ （2）在图 3-11 中画出 y = 2（x - 1）2 的图象. y 2 y = 2x2 1 - 2 - 1 O 1 2 x 图 3-11 你是怎么画的？与同伴进行交流. 81第三章 二次函数 议一议 二次函数 y = 2（x - 1）2 的图象与二次函数 y = 2x 2 的图象有什么关系？它 的开口方向、对称轴和顶点坐标分别是什么？当 x 取哪些值时，y 的值随 x 值 的增大而增大？当 x 取哪些值时，y 的值随 x 值的增大而减小？ 类似地，你能发现二次函数 y = 2（x + 1）2 的图象与二次函数 y = 2x 2 的图 象有什么关系吗？ 二次函数 y = 2x 2，y = 2（x - 1）2，y = 2（x + 1）2 的图象都是抛物线，并且 形状相同，只是位置不同. 将二次函数 y = 2x 2 的图象向右平移 1 个单位，就得 到函数 y = 2（x - 1）2 的图象；将二次函数 y = 2x 2 的图象向左平移 1 个单位， 就得到函数 y = 2（x + 1）2 的图象. 想一想 1 1 1 （1）函数 y = - （x + 1）2，y = - （x - 2）2 的图象分别与 y = - x 2 的 2 2 2 图象有什么关系？它们是轴对称图形吗？对称轴和顶点坐标分别是什么？ 1 （2）x 取哪些值时，函数 y = - （x + 1）2 的值随 x 值的增大而增大？ x 取哪 2 1 1 些值时，函数 y = - （x + 1）2 的值随 x 值的增大而减小？函数 y = - （x - 2）2 2 2 呢？ 1 1 二次函数 y = - （x + 1）2，y = - （x - 2）2 的图象都是抛物线，它们与 2 2 1 1 抛物线 y = - x 2 的形状相同，只是位置不同. 将函数 y = - x 2 的图象向左平 2 2 1 1 移 1 个单位，就得到函数 y = - （x + 1）2 的图象；将函数 y = - x 2 的图象 2 2 1 向右平移 2 个单位，就得到函数 y = - （x - 2）2 的图象. 2 824 二次函数 y = ax2+ bx + c 的图象与性质 议一议 二次函数 y = a（x - h）2 的图象是什么形状？它与二次函数 y = ax 2 的图象 有什么关系？你能说出二次函数 y = a（x - h）2 的图象具有哪些性质吗？与同 伴进行交流. 随堂练习 1. 图中有七条形状相同的抛物线，如果中间一条抛物线 y 对应的函数表达式是 y = 2x2，那么，从左到右其余六 条抛物线对应的函数表达式是什么？ 2. 对于二次函数 y = - 3（x + 2）2： - 3- 2- 1O 1 2 3 x （1）它的图象与二次函数 y = - 3 x2 的图象有什么关 系？它是轴对称图形吗？它的开口方向、对称轴 （第 1 题） 和顶点坐标分别是什么？ （2）当 x 取哪些值时，y 的值随 x 值的增大而增大？当 x 取哪些值时，y 的值随 x 值 的增大而减小？ 习题 3.7 知识技能 1. 在同一直角坐标系中画出下列二次函数的图象： 1 1 1 y = x2，y = （x + 2）2，y = （x - 2）2. 2 2 2 根据图象，填写下表： 性质 x 取哪些值时，y 的值随 x 开口方向 对称轴 顶点坐标 二次函数 值的增大而增大 1 y = 2 x2 1 y = 2（x + 2）2 1 y = 2（x - 2）2 83第三章 二次函数 1 2. 对于二次函数 y = - 3（x - ）2，它的图象与二次函数 y = - 3x2 的图象有什么 2 关系？它是轴对称图形吗？它的开口方向、对称轴和顶点坐标分别是什么？ 数学理解 3. 怎样由 y = 2x2 的图象得到函数 y = 2（x - 1）2 的图象？当 x 取哪些值时，y 的值 随 x 值的增大而增大？当 x 取哪些值时，y 的值随 x 值的增大而减小？ 4. 分别写出两个符合下列条件的二次函数表达式： （1）函数的图象不经过第三、四象限； （2）函数图象只有顶点坐标不同. 议一议 1 二次函数 y = - （x + 1）2 - 1 的图象是什么形状？它与二次函数 2 1 1 y = - （x + 1）2 的图象有什么关系？你能说出二次函数 y = - （x + 1）2 - 1 的 2 2 1 图象具有哪些性质吗？二次函数 y = - （x + 1）2 + 2 呢？ 2 做一做 1 1 （1）在同一直角坐标系中，分别画出二次函数 y = - x 2，y = - x 2 - 1， 2 2 1 y = - （x + 1）2 - 1 的图象，验证你的结论，并与同伴进行交流. 2 （2）填写下表： 性质 开口方向 对称轴 顶点坐标 二次函数 1 y = - x2 2 1 y = - x2 - 1 2 1 y = - （x + 1）2 - 1 2 844 二次函数 y = ax2+ bx + c 的图象与性质 1 1 二次函数 y = - （x + 1）2 - 1 的图象是抛物线，它与抛物线 y = - x 2 2 2 1 的形状相同，只是位置不同. 将二次函数 y = - x 2 的图象向下平移 1 个单位就得 2 1 1 到函数 y = - x 2 - 1 的图象，再向左平移 1 个单位就得到函数 y = - （x + 1）2 - 1 2 2 的图象. 一般地，二次函数 y = a（x - h）2 + k 的图象是抛物线，它与抛物线 y = ax 2 的形状相同，只是位置不同. 平移二次函数 y = ax 2 的图象便可得到二次函 数 y = a（x - h）2 + k 的图象. 它的开口方向、对称轴和顶点坐标与 a，h，k 的 值有关. 议一议 二次函数 y = a（x - h）2 + k 的图象具有哪些性质？填写下表，并与同伴 进行交流. y = a（x - h）2 + k 开口 顶点 x 取哪些值时，y 的值 x 取哪些值时，y 的值 对称轴 的性质 方向 坐标 随 x 值的增大而增大 随 x 值的增大而减小 a > 0 a < 0 1 5 例 求二次函数 y = - x 2 + x - 的顶点坐标和对称轴，并画出函数 2 2 图象. 1 5 解： y = - x 2 + x - 画二次函数的图象 2 2 时，首先要找出顶点坐 1 = - （x - 1）2 - 2. 标和对称轴，这样便于 2 正确迅速地画图. 所以它的顶点坐标是（1，- 2）， 对称轴是直线 x = 1. 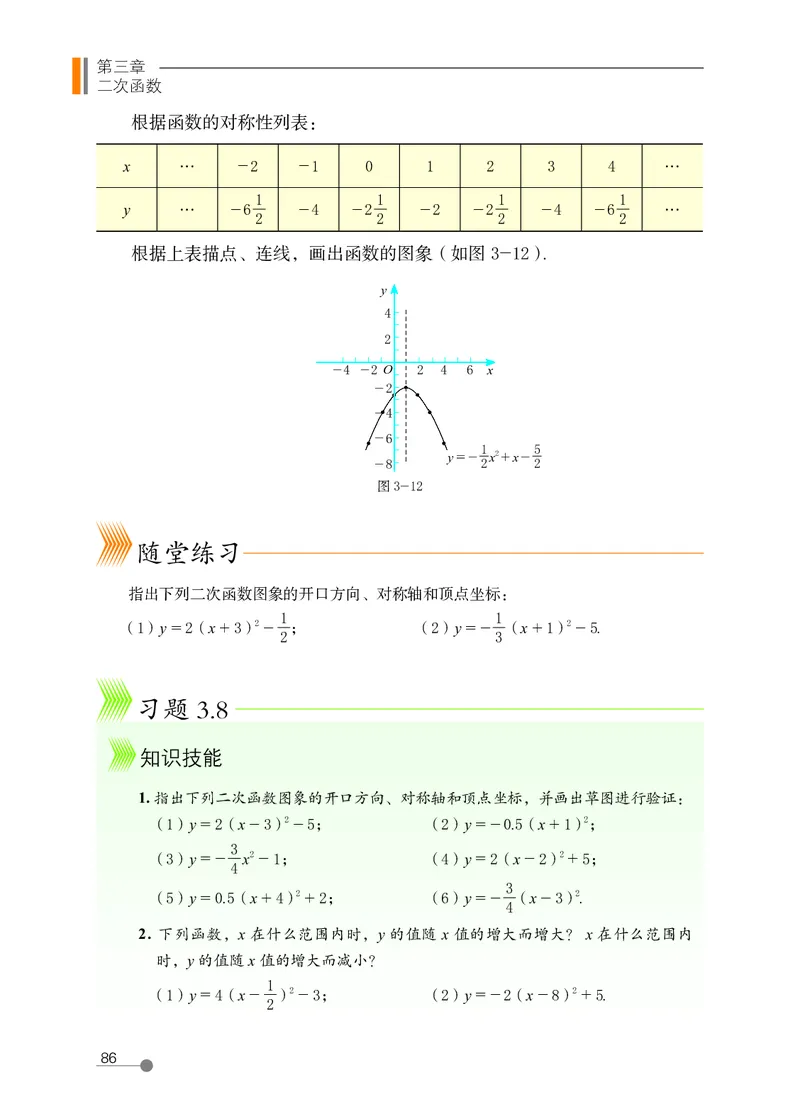85第三章 二次函数 根据函数的对称性列表： x … - 2 - 1 0 1 2 3 4 … 1 1 1 1 y … - 6 - 4 - 2 - 2 - 2 - 4 - 6 … 2 2 2 2 根据上表描点、连线，画出函数的图象（如图 3-12）. y 4 2 - 4 - 2 O 2 4 6 x - 2 - 4 - 6 1 5 - 8 y = - 2 x2 + x - 2 图 3-12 随堂练习 指出下列二次函数图象的开口方向、对称轴和顶点坐标： 1 1 （1）y = 2（x + 3）2 - ； （2）y = - （x + 1）2 - 5. 2 3 习题 3.8 知识技能 1. 指出下列二次函数图象的开口方向、对称轴和顶点坐标，并画出草图进行验证： （1）y = 2（x - 3）2 - 5； （2）y = - 0.5（x + 1）2； 3 （3）y = - x2 - 1； （4）y = 2（x - 2）2 + 5； 4 3 （5）y = 0.5（x + 4）2 + 2； （6）y = - （x - 3）2. 4 2. 下列函数，x 在什么范围内时，y 的值随 x 值的增大而增大？ x 在什么范围内 时，y 的值随 x 值的增大而减小？ 1 （1）y = 4（x - ）2 - 3； （2）y = - 2（x - 8）2 + 5. 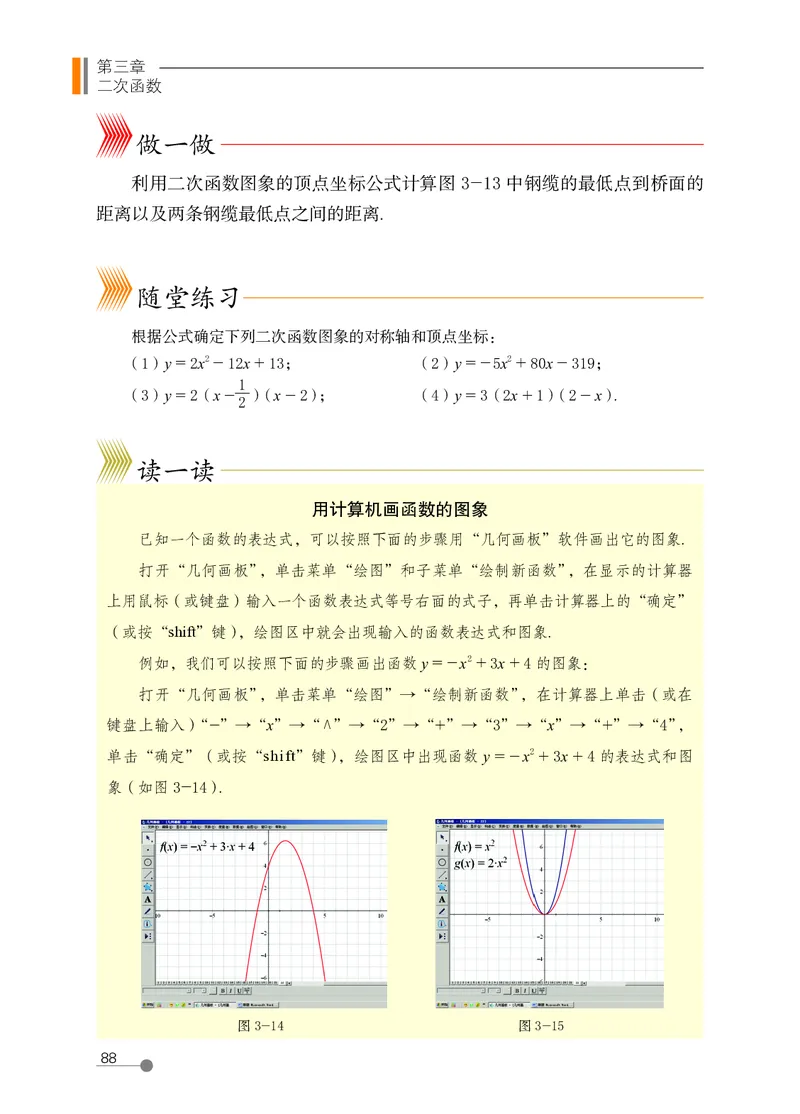2 864 二次函数 y = ax2+ bx + c 的图象与性质 做一做 如图 3-13 所示，某座桥梁相邻两条钢缆的形状是两段相同的抛物线，两 条钢缆的公共端点到桥面的距离为 10 m. 按照图中的直角坐标系，左边的一段 抛物线可以用 9 9 y = x 2 + x + 10（- 40 ≤ x ≤ 0） 400 10 表示，而且左、右两段抛物线关于 y 轴对称. y / m 10 桥面 - 5 O 5 x / m 图 3-13 （1）钢缆的最低点到桥面的距离是多少？ （2）两条钢缆最低点之间的距离是多少？ 你是怎样计算的？与同伴进行交流. 一般地，对于二次函数 y = ax 2 + bx + c，我们可以利用配方法推导出它的 图象的对称轴和顶点坐标公式. 把二次函数 y = ax 2 + bx + c 的右边配方，得 y = ax 2 + bx + c b = a（x 2 + x）+ c a b b b = a［ x 2 + 2· x +（ ）2 -（ ）2］+ c 2a 2a 2a b 4ac - b 2 = a（x + ）2 + . 2a 4a 因此，二次函数 y = ax 2 + bx + c 的图象是一条抛物线，它的对称轴是直 b b 4ac - b 2 线 x = - ，顶点坐标是（- ， ）. 2a 2a 4a 87第三章 二次函数 做一做 利用二次函数图象的顶点坐标公式计算图 3-13 中钢缆的最低点到桥面的 距离以及两条钢缆最低点之间的距离. 随堂练习 根据公式确定下列二次函数图象的对称轴和顶点坐标： （1）y = 2x2 - 12x + 13； （2）y = - 5x2 + 80x - 319； 1 （3）y = 2（x - 2 ）（x - 2）； （4）y = 3（2x + 1）（2 - x）. 读一读 用计算机画函数的图象 已知一个函数的表达式，可以按照下面的步骤用“几何画板”软件画出它的图象. 打开“几何画板”，单击菜单“绘图”和子菜单“绘制新函数”，在显示的计算器 上用鼠标（或键盘）输入一个函数表达式等号右面的式子，再单击计算器上的“确定” （或按“shift”键），绘图区中就会出现输入的函数表达式和图象. 例如，我们可以按照下面的步骤画出函数 y = - x2 + 3x + 4 的图象： 打开“几何画板”，单击菜单“绘图”→“绘制新函数”，在计算器上单击（或在 键盘上输入）“-”→“x”→“∧”→“2”→“+”→“3”→“x”→“+”→“4”， 单击“确定”（或按“shift”键），绘图区中出现函数 y = - x2 + 3x + 4 的表达式和图 象（如图 3-14）. 图 3-14 图 3-15 884 二次函数 y = ax2+ bx + c 的图象与性质 几点说明： （1）如果要在同一直角坐标系中画出多个函数图象，可以先画出一个函数图象， 再单击“图表”→“绘制新函数”……画出其他的函数图象（如图 3-15）. （2）用鼠标拖曳坐标原点可以平移坐标系，拖曳坐标原点右边的红点（坐标 为（1，0）的点），可以调整坐标系的单位长度；选中函数图象，单击菜单“显 示”→“颜色/线型”，可以编辑图象的颜色和线型；单击菜单“图表”→“隐藏网 格”，可以隐藏坐标系中的网格；还可以在文本工具栏中编辑函数表达式等. 你不妨上 机试一试. 习题 3.9 知识技能 1. 指出下列二次函数图象的开口方向、对称轴和顶点坐标，必要时画草图进行 验证： （1）y = 2（x - 2）2 + 5； （2）y = 2x2 - 4x - 1； （3）y = 3x2 - 6x + 2； （4）y = - 3（x + 3）（x + 9）. 数学理解 2. 将二次函数 y = x2 的图象向上平移 2 个单位，再向左平移 3 个单位，得到抛物线 y = x2 + bx + c，求 b，c 的值，并求出这条抛物线的开口方向、对称轴和顶点坐 标，必要时画草图进行验证. 问题解决 3. 当一枚火箭被竖直向上发射时，如果它的高度 h（m）与时间 t（s）之间的关系 可以用公式 h = - 5t 2 + 150t + 10 表示，那么经过多长时间，火箭到达它的最高 点？最高点的高度是多少？ 4. 有心理学家研究发现，学生对某类概念的接受能力 y 与讲授概念所用时间 x （min）之间满足函数关系 y = - 0.1x2 + 2.6x + 43（0 ≤ x ≤ 30）. y 值越大， 表示接受能力越强. 根据这一结论回答下列问题： 89第三章 二次函数 （1）x 在什么范围内，学生的接受能力逐渐增强？在什么范围内，学生的接受 能力逐渐降低？ （2）经过多长时间，学生的接受能力最强？ ※5. 你知道图 3-13 中右边钢缆的表达式是什么吗？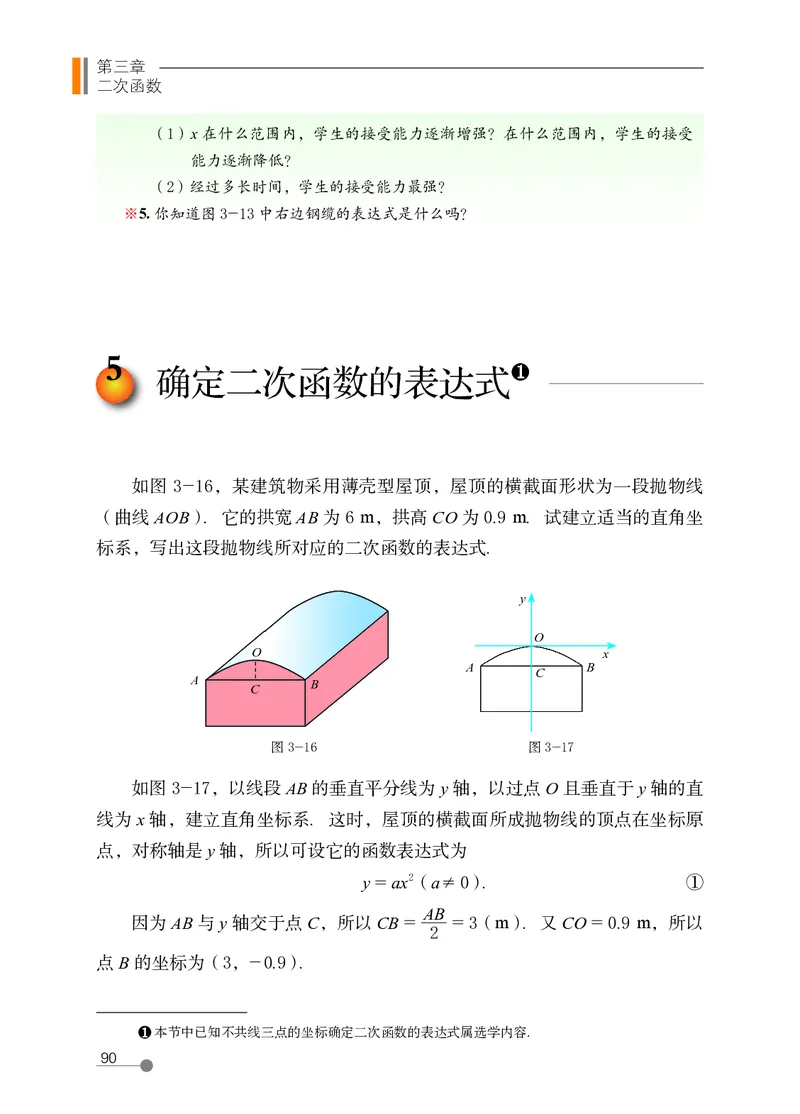 5 确定二次函数的表达式 如图 3-16，某建筑物采用薄壳型屋顶，屋顶的横截面形状为一段抛物线 （曲线 AOB）. 它的拱宽 AB 为 6 m，拱高 CO 为 0.9 m. 试建立适当的直角坐 标系，写出这段抛物线所对应的二次函数的表达式. y O O x A B C A B C 图 3-16 图 3-17 如图 3-17，以线段 AB 的垂直平分线为 y 轴，以过点 O 且垂直于 y 轴的直 线为 x 轴，建立直角坐标系. 这时，屋顶的横截面所成抛物线的顶点在坐标原 点，对称轴是 y 轴，所以可设它的函数表达式为 y = ax 2（a≠ 0）. ① AB 因为 AB 与 y 轴交于点 C，所以 CB = = 3（m）. 又 CO = 0.9 m，所以 2 点 B 的坐标为（3，- 0.9）. 本节中已知不共线三点的坐标确定二次函数的表达式属选学内容. 905 确定二次函数的表达式 因为点 B 在这段抛物线上，将它的坐标代入 ①，得 - 0.9 = a × 32， 所以 a = - 0.1. 因此，这段抛物线所对应的二次函数的表达式是 y = - 0.1x 2（- 3 ≤ x ≤ 3）. 例 1 已知一个二次函数的图象的对称轴为 x = - 2，与 y 轴交点的纵坐标 为 2，且经过点（- 3，- 1），求这个二次函数的表达式. 解：设二次函数的表达式为 待定系数法可以 确定 a，b，c 的值. y = ax 2 + bx + c（a ≠ 0）， 因为二次函数的图象与 y 轴交点的纵坐标为 2，即经过点（0，2）， 可得 c = 2. 所以 y = ax 2 + bx + 2. ① 又因为二次函数的对称轴为 x = - 2， b 所以 - = - 2， 2a 即 b = 4a. ② 因为二次函数的图象经过点（- 3，- 1），将坐标代入 ① 式，得 9a - 3b + 2 = - 1. ③ 由 ②③，解得 a = 1，b = 4. 所以，这个二次函数的表达式为 y = x 2 + 4 x + 2. 想一想 （1）例 1 还有没有其他解法？与同伴进行交流. （2）如果二次函数 y = ax 2 + bx + c 的图象的顶点坐标为（h，k），那么这 个二次函数的表达式可表示成什么形式呢？ 91第三章 二次函数 若二次函数的图象 的顶点坐标为（h，k）， 可以设二次函数的表达 式为 y = a（x - h）2 + k . 例 2 已知二次函数图象的顶点坐标是（- 1，- 6），并且该图象经过点 （2，3），求这个二次函数的表达式. 解：因为二次函数图象的顶点坐标是（- 1，- 6），所以可设这个二次函 数的表达式为 y = a（x + 1）2 - 6（a≠ 0）. 又因为该图象经过点（2，3），将坐标代入上式，得 3 = a（2 + 1）2 - 6， 解得 a = 1. 所以，这个二次函数的表达式是 y =（x + 1）2 - 6，即 y = x 2 + 2x - 5. 随堂练习 根据下列条件，分别求出对应的二次函数表达式： （1）已知图象的顶点在坐标原点，且图象经过点（2，8）； （2）已知图象的顶点坐标是（- 1，- 2），且图象经过点（1，10）. 习题 3.10 数学理解 1. 已知抛物线 y = ax2 + bx + c 的顶点坐标为（2，1），且这条抛物线与 x 轴的一 个交点坐标是（3，0）. （1）求这条抛物线的表达式； （2）求这条抛物线与 x 轴的另一个交点的坐标. 925 确定二次函数的表达式 2. 已知二次函数图象的顶点在坐标原点，且图象经过点（3，- 27）. 将它向左平 移 2 个单位，再向上平移 3 个单位，求平移后对应的二次函数的表达式. 3. 二次函数 y = x2 + bx + c 的图象经过点 A（0，1），B（2，- 1），试判断点 P（- 1，2）是否在这个二次函数的图象上 . 问题解决 4. 有一个抛物线形拱桥，桥洞离水面的最大高度为 4 m，跨度为 10 m. 如图所示， 建立直角坐标系. （1）求这条抛物线所对应的函数表达式； （2）如图，在这条抛物线的对称轴右边 1 m 处，桥洞离水面的高度是多少？ y 4 m 1 m O M x 10 m （第 4 题） 想一想 已知一个二次函数的图象所经过的三个点，可以确定这个二次函数的表达 式吗？怎样确定这个二次函数的表达式？ 例 3 已知一个二次函数的图象经过（- 1，10），（1，4），（2，7）三 点，求这个二次函数的表达式，并写出它的对称轴和顶点坐标. 解：设所求的二次函数的表达式为 y = ax 2 + bx + c， 由已知，将三点（- 1，10），（1，4），（2，7）分别代入表达式，得 10 = a - b + c， 4 = a + b + c， 7 = 4a + 2b + c. 93第三章 二次函数 解这个方程组，得 a = 2， b = - 3， c = 5. 故所求函数表达式为 y = 2x 2 - 3x + 5. 3 31 y = 2x 2 - 3x + 5 = 2（x - ）2 + . 4 8 3 3 31 所以二次函数 y = 2x 2 - 3x + 5 的对称轴为直线 x = ，顶点坐标为（ ， ）. 4 4 8 做一做 若二次函数的图象经过点（- 2，3），（- 1，0），（1，6），试确定这个二 次函数的表达式 . 例 4 某商贸公司成立以来，5 年的利润情况如图 3-18 所示，图中的折线 近似于抛物线的一部分 . y / 百万元 8 6.9 7 E 6 5 5 3.8 D 4 3 2.6 3 C B 2 A 1 O 第 1 年第 2 年 第 3 年 第 4 年第 5 年 x 图 3-18 （1）试求出图象过 A，C，D 三点的二次函数的表达式； （2）利用（1）的结果，分别求出当 x = 2 和 x = 5 时该二次函数的函数 值，并分别与点 B、点 E 的纵坐标比较； （3）利用（1）中求得的二次函数的表达式，预测该商贸公司第 6 年的 利润. 解：（1）设图象过 A，C，D 三点的二次函数的表达式为 y = ax 2 + bx + c. 945 确定二次函数的表达式 将 A（1，2.6），C（3，3.8），D（4，5）分别代入 y = ax 2 + bx + c，得 a + b + c = 2.6， 9a + 3b + c = 3.8， 16a + 4b + c = 5. 解这个方程组，得 a = 0.2， b = - 0.2， c = 2.6. 所以，图象过 A，C，D 三点的二次函数的表达式为 y = 0.2x 2 - 0.2x + 2.6. （2）当 x = 2 时，y = 0.2 × 4 - 0.2 × 2 + 2.6 = 3. 此时，y 的值与点 B 的纵坐标相等. 当 x = 5 时，y = 0.2 × 25 - 0.2 × 5 + 2.6 = 6.6. 此时，y 的值小于点 E 的纵坐标. （3）当 x = 6 时，y = 0.2 × 36 - 0.2 × 6 + 2.6 = 8.6. 估计该商贸公司第 6 年的利润可达 860 万元. 随堂练习 1. 已知二次函数 y = ax2 + b 的图象经过点（2，3），（- 1，- 3）. （1）求 a，b 的值，并写出这个二次函数的表达式； （2）如果点 M（m，13）在这个二次函数的图象上，求 m 的值. 2. 小明用力地将篮球向篮筐抛出，篮球离地的高度 h（m）与时间 t（s）的关系可以 1 表示为：h = v t - gt2 + h （其中 v 表示篮球离手时的速度，g 表示重力加速度， 0 2 0 0 取 g = 10（m/s2），h 表示篮球离手时的高度）. 如果 v = 9（m/s），h = 2（m）， 0 0 0 问： （1）篮球从抛出到落地需多少时间？ （2）篮球离地最高有多少米？ 95第三章 二次函数 问题解决 3. 高尔夫球手击出的高尔夫球的运动路线是一 条抛物线，当球水平运动了 24 m 时，达到 最高点. 落球点比击球点的海拔低 1 m，水 平距离为 50 m. （1）建立适当的坐标系，求高度 h（m）关于 水平距离 x（m）的二次函数表达式； （2）与击球点相比，球运动到最高点时有多高？ 6 二次函数的应用 如图 3-19，在一个直角三角形的内部作一个矩形 ABCD，其中 AB 和 AD 分 别在两直角边上. 96 m 03 习题 3.11 知识技能 1. 已知一个关于 x 的二次函数，当 x 分别为 1，2，3 时，对应函数值分别为 3， 0，4，求这个二次函数的表达式. 2. 已知抛物线与 x 轴的交点的横坐标为 - 2 和 1，且经过点（0，3），求这个二次 函数的表达式. C D A B 40 m 图 3-19 （1）如果设矩形的一边 AB = x m，那么 AD边的长度如何表示？6 二次函数的应用 议一议 x x y 例 1 某建筑物的窗户如图 3-21 所示，它的上半部是半圆，下半部是矩 形，制造窗框的材料总长（图中所有黑线的长度和）为 15 m. 当 x 等于多少 时，窗户通过的光线最多（结果精确到 0.01 m）？此时，窗户的面积是多少？ 解：根据题意，得 7x + 4y + x = 15， 15 - 7x - x 所以 y = . 4 15 - 7x - x 因为 x > 0，且 > 0， 4 所以 0 < x < 1.479. 设窗户的面积是 S m2，则 1 S = x 2 + 2xy 2 1 15 - 7x - x = x 2 + 2x· 2 4 7 15 = - x 2 + x 2 2 7 15 225 = - （x - ）2 + . 2 14 56 15 225 所以，当 x = ≈1.07 时，S = ≈4.02. 14 最大 56 即当 x ≈1.07 m 时，S ≈4.02 m2 . 此时，窗户通过的光线最多. 最大 97 m 03 （2）设矩形的面积为 y m2，当 x 取何值时，y 的值最大？最大值是多少？ 在上面的问题中，如果把矩形改为如图 3-20 所示的位置，其他条件不 变，那么矩形的最大面积是多少？你是怎样知道的？ 40 m 图 3-20 图 3-21第三章 二次函数 随堂练习 图 3-19 的问题中，如果设 AD 边的长为 x m，那么问题的结果会怎样？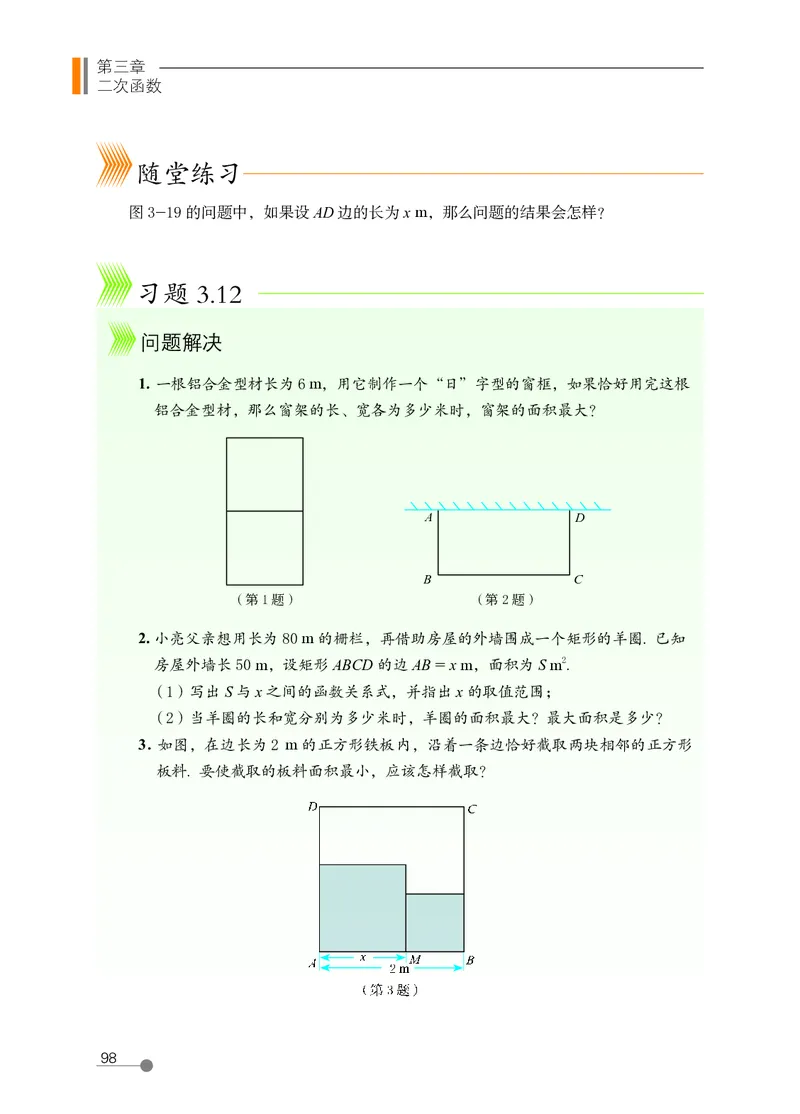 习题 3.12 问题解决 1. 一根铝合金型材长为 6 m，用它制作一个“日”字型的窗框，如果恰好用完这根 铝合金型材，那么窗架的长、宽各为多少米时，窗架的面积最大？ A D B C （第 1 题） （第 2 题） 2. 小亮父亲想用长为 80 m 的栅栏，再借助房屋的外墙围成一个矩形的羊圈. 已知 房屋外墙长 50 m，设矩形 ABCD 的边 AB = x m，面积为 S m2. （1）写出 S 与 x 之间的函数关系式，并指出 x 的取值范围； （2）当羊圈的长和宽分别为多少米时，羊圈的面积最大？最大面积是多少？ 3. 如图，在边长为 2 m 的正方形铁板内，沿着一条边恰好截取两块相邻的正方形 板料. 要使截取的板料面积最小，应该怎样截取？ D C A x 22 mm M B （第 3 题） 986 二次函数的应用 服装厂生产某品牌的 T 恤衫，每件的成本是 10 元. 根据市场调查，以单价 13 元批发给经销商，经销商愿 意经销 5 000 件，并且表示每件降价 0.1 元，愿意多经 销 500 件. 请你帮助分析，厂家批发单价是多少时可以获得最 大利润. 例 2 某旅社有客房 120 间，每间房的日租金为 160 元时，每天都客满. 经市场调查发现，如果每间客房的日租金每增加 10 元时，那么客房每天出租 数会减少 6 间. 不考虑其他因素，旅社将每间客房的日租金提高到多少元时， 客房日租金的总收入最高？ 解：设每间客房的日租金提高 x 个 10 元，则每天客房出租数会减少 6x 间. 设客房日租金总收入为 y 元，则 y =（160 + 10x）（120 - 6x） = - 60（x - 2）2 + 19 440. 因为 x ≥ 0，且 120 - 6x > 0， 所以 0 ≤ x < 20. 当 x = 2 时，y 有最大值 19 440. 这时每间客房的日租金为 160 + 10×2 = 180（元）. 客房日租金的总收入最高为 19 440元. 议一议 还记得本章第 2 节中“种多少棵橙子 y / 个 60 600 树”的问题吗？我们得到表示增种橙子树的 60 500 60 400 数量 x（棵）与橙子总产量 y（个）的二次 60 300 函数表达式 60 200 60 100 y =（600 - 5x）（100 + x） 60 000 = - 5x 2 + 100x + 60 000. O 5 10 15 20 x / 棵 图 3-22 99第三章 二次函数 （1）当 x 为何值时，y 取最大值 ？最大值为多少？ （2）利用函数图象描述橙子的总产量与增种橙子树的棵数之间的关系. （3）结合函数图象，增种多少棵橙子树，可以使橙子的总产量在 60 400 个 以上？ 随堂练习 某商店购进一批单价为 20 元的日用商品，如果以单价 30 元销售，那么半月内可售 出 400 件. 根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高 1 元， 销售量相应减少 20 件. 售价为多少元时，才能在半月内获得最大利润？ 读一读 平均数、方差与二次函数 在科学实验中，经常需要测定某一个量 a 的大小. 由于测量工具和测量方法的限 制，测量的结果往往只是 a 的近似值. 为此，需对它做 n 次观测，测得 n 个数据 a， 1 _ a + a + … + a a ，…，a ，然后取它们的平均数 x = 1 2 n，作为对 a 的测定值. 你能说出 2 n n 这样做的道理吗？ 为了回答这个问题，考虑关于变量 x 的二次函数 1 y = ［（x - a ）2 +（x - a ）2 + … + （x - a ）2］. n 1 2 n 由于 1 y = ［nx2 - 2（a + a + … + a ）x +（a2 + a2 + … + a2）］ n 1 2 n 1 2 n 2 1 = x2 - （a + a + … + a ）x + （a2 + a2 + … + a2）， n 1 2 n n 1 2 n a + a + … + a _ 所以，当 x = 1 2 n = x 时，y 取最小值. 这时 n 1 _ _ _ y = ［（x - a）2 +（x - a ）2 + … +（x - a ）2］. 最小 n 1 2 n y 正是数据 a ，a ，…，a 的方差. 最小 1 2 n _ 因此，我们通常把观测数据的平均数 x 作为对 a 的测定值. 1006 二次函数的应用 习题 3.13 问题解决 1. 某旅行社组团去外地旅游，30 人起组团，每人单价 800 元. 旅行社对超过 30 人 的团给予优惠，即旅行团每增加 1 人，每人的单价就降低 10 元. 你能帮助算一 下，当一个旅游团的人数是多少时，旅行社可以获得最大营业额？ 2. 某商店购进一批单价为 8 元的商品，如果按每件 10 元出售，那么每天可销 售 100 件. 经调查发现，这种商品的销售单价每提高 1 元，其销售量相应减 少 10 件. 将销售价定为多少，才能使每天所获销售利润最大？最大利润是 多少？ 3. 在测量时，为了确定被测对象的最佳值，经常要对同一对象测量若干次，然 后选取与各测量数据的差的平方和为最小的数作为最佳近似值. 例如，在测量 了 5 个大麦穗长之后，得到的数据（单位：cm）是： 6.5，5.9，6.0，6.7，4.5， 那么这些大麦穗的最佳近似长度可以取使函数 y =（x - 6.5）2 +（x - 5.9）2 +（x - 6.0）2 +（x - 6.7）2 +（x - 4.5）2 为最小值的 x 值. 整理上式，并求出大麦穗长的最佳近似长度. 如图 3-23，某公司的大门呈抛物线形，大门底 C 部 AB 宽为 4 m，顶部 C 距地面的高度为 4.4 m. （1）试建立适当的直角坐标系，求抛物线对应的 二次函数表达式； （2）一辆满载货物的汽车欲通过大门，货物顶部 A 4 m B 距地面 2.65 m，装货宽度为 2.4 m，那么这辆汽车能否 顺利通过大门？ 想一想 在上面的问题中，如果装货宽度为 2.4 m 的汽车能顺利通过大门，那么货 物顶部距地面的最大高度是多少？（结果精确到 0.01 m） 101 m 4.4 图 3-23第三章 二次函数 例 3 如图 3-24 所示，公园要建造一个圆形喷水池，在水池中央点 O 处 安装一根垂直于水面的柱形喷水装置 OA，OA = 1.25 m. 水流由顶端 A 处的喷 头向外喷出，在各个方向上沿形状相同的抛物线路径落下. 为使水流形状看起 来较为美观，设计要求水流在与 OA 的距离为 1 m 处达到最高点，这时距水面 的最大高度为 2.25 m. 如果不计其他因素，那么水池的半径至少是多少米时， 才能使喷出的水流不致落到池外？ y B A A O C O C x 图 3-24 图 3-25 解：如图 3-25，以 OC 所在的直线为 x 轴，OA 所在的直线为 y 轴，建立 直角坐标系. 由条件知点 A 的坐标为（0，1.25），若点 B 为右边抛物线的顶点，则其坐 标为（1，2.25），因此，可设右边的抛物线的表达式为 y = a（x - 1）2 + 2.25， 将点 A 的坐标代入 y = a（x - 1）2 + 2.25，得 1.25 = a + 2.25. 解得 a = - 1. 故右边抛物线的表达式为 y = -（x - 1）2 + 2.25. 当 y = 0 时，x = - 0.5，x = 2.5. 1 2 即点 C 的坐标为（2.5，0）. 所以，水池的半径至少为 2.5 m 时，才能使喷出的水流不致落到池外. 议一议 （1）对于例 3，你还有其他解法吗？与同伴进行交流. （2）你能求出图 3-25 中左边抛物线的表达式吗？ （3）回顾本课时的两个问题的解法，你能总结出此类问题的一般解法吗？ 1026 二次函数的应用 随堂练习 如图，一条隧道的截面由一段抛物线和一个矩形的三条边围成. 矩形的长是 8 m，宽 1 是 2 m，在如图所示的直角坐标系中，抛物线可以用 y = - x2 + 4 表示. 4 （1）一辆货运卡车高 4 m，宽 2 m，它能通过该隧道吗？ （2）如果该隧道内的路面为双车道，那么这辆货运卡车是否可以通过？ y 3 2 1 O - 3 - 2- 1 1 2 3 x - 1 - 3 习题 3.14 问题解决 5 1. 如图，一个运动员推铅球，铅球在点 A 处出手，出手时铅球距地面约 m；铅 3 球落在点 B 处. 铅球运行中在运动员前方 4 m 处（即 OC = 4 m）达到最高点， 最高点距地面的高度为 3 m. 已知铅球经过的路线是抛物线，根据图中的直角坐 标系，你能算出该运动员的成绩吗？ S / 万元 4 3 2 y 1 - 2- 1O 1 2 3 4 5 6 t / 月 A - 1 - 2 O C B x （第 1 题） （第 2 题） 2. 某公司研发一种新的软件，年初上市后，该产品经历了从亏损到盈利的过 程. 如图所示的图象是抛物线的一段，它刻画了该产品年初以来累积利润 103第三章 二次函数 S（万元）与销售时间 t（月）之间的关系（即前 t 个月的利润总和 S 与 t 之间 的关系）. 根据图象提供的信息，解答下列问题： （1）由已知图象上三点的坐标，求 S 与 t 之间的关系式； （2）截止到几月底该产品累积利润可达 30 万元？ （3）预计 8 月份该产品所获的利润将达到多少万元？ 3. 如图，有一个抛物线形的水泥门洞 . 门洞的地面宽度为 8 m，两侧距地面 4 m 高 处各有一盏灯，两灯间的水平距离为 6 m. 求这个门洞的高度 （精确到 0.1 m）. 6 m y 5 C O D x 8 m A B （第 4 题） ※4. 如图，有一座抛物线形拱桥，在正常水位时水面宽 AB = 20 m，当水位上升 3 m 时，水面宽 CD = 10 m. （1）按如图所示的直角坐标系，求表示此抛物线的函数表达式； （2）有一条船以 5 km/h 的速度向此桥驶来，当船距离此桥 35 km 时，桥下水位 正好在 AB 处，之后水位每小时上涨 0.25 m，当水位达到 CD 处时，将禁 止船只通行. 如果该船按原来的速度行驶，那么它能否在水位达到 CD 前 通过此桥？ 7 二次函数与一元二次方程 我们已经知道，竖直上抛物体的高度 h（m）与运动时间 t（s）的关系可 以用公式 h = - 5t 2 + v t + h 表示，其中 h （m）是抛出时的高度，v （m/s） 0 0 0 0 是抛出时的速度. 一个小球从地面被以 40 m/s 的速度竖直向上抛起，小球距 离地面的高度 h（m）与运动时间 t（s）的关系如图 3-26 所示，那么 104 m 4 （第 3 题）7 二次函数与一元二次方程 h/m 80 70 60 50 40 30 20 10 O 1 2 3 4 5 6 7 8 t/s 图 3-26 （1）h 与 t 之间的关系式是什么？ （2）小球经过多少秒后落地？你有几种求解方法？与同伴进行交流. 议一议 二次函数 y = x 2 + 2x，y = x 2 - 2x + 1，y = x 2 - 2x + 2 的图象如图 3-27 所 示. y y y 6 5 5 4 4 4 3 3 3 2 2 2 1 1 1 - 3- 2- 1 O 1 x - 1 O 1 2 3 x - 1 O 1 2 3 x - 1 - 1 - 1 （1） （2） （3） 图 3-27 （1）每个图象与 x 轴各有几个交点？ （2）一元二次方程 x 2 + 2x = 0，x 2 - 2x + 1 = 0 有几个根？用判别式验证 一下，一元二次方程 x 2 - 2x + 2 = 0 有根吗？ （3）二次函数 y = ax 2 + bx + c 的图象和 x 轴交点的坐标与一元二次方程 ax 2 + bx + c = 0 的根有什么关系？ 105第三章 二次函数 二次函数 y = ax 2 + bx + c 的图象与 x 轴的交点有三种情况：有两 个交点、有一个交点、没有交点. 当二次函数 y = ax 2 + bx + c 的图象 与 x 轴有交点时，交点的横坐标就是当 y = 0 时自变量 x 的值，即一 元二次方程 ax 2 + bx + c = 0 的根. 此时，判别式 Δ = b 2 - 4ac ≥ 0. 当 二次函数 y = ax 2 + bx + c 的图象与 x 轴没有交点时，一元二次方 程 ax 2 + bx + c = 0 无实数根，此时，判别式 Δ = b 2 - 4ac < 0. 想一想 在本节一开始的小球上抛问题中，何时小球离地面的高度是 60 m？你是如 何知道的？ 随堂练习 一个足球被从地面向上踢出，它距地面的高度 h（m）可以用公式 h = - 4.9t 2 + 19.6t 来 表示，其中 t（s）表示足球被踢出后经过的时间. （1）画出函数 h = - 4.9t 2 + 19.6t 的图象； （2）当 t = 1，t = 2 时，足球距地面的高度分别是多少？ （3）方程 - 4.9t 2 + 19.6t = 0，- 4.9t 2 + 19.6t = 14.7 的根的实际意义分别是什么？你能 在图象上表示出来吗？ 习题 3.15 知识技能 1. 求下列二次函数的图象与 x 轴的交点的坐标，并画草图验证： 1 （1）y = x2 - x + 3； （2）y = - 2x2 + 20x - 49. 2 数学理解 2. 一元二次方程 x2 - 6x + 4 = 1 的根与二次函数 y = x2 - 6x + 4 的图象有什么关 1067 二次函数与一元二次方程 系？试把方程的根在图象上表示出来. 3. 二次函数 y = - x2 + 3x + 4 的图象与一次函数 y = 2x - 1 的图象相交吗？如果相 交，请求出它们的交点坐标. 4. 若二次函数 y = ax2 + bx + c 的图象经过（- 3，5），且方程 ax2 + bx + c = 0 的两 实根为 x = - 1，x = 2，求该二次函数的表达式 . 1 2 你能利用二次函数的图象估计一元二次方程 x 2 + 2x - 10 = 0 的根吗？ 图 3-28 是函数 y = x 2 + 2x - 10 的图象. y 2 O - 5 - 3 - 1 1 3 x - 2 - 4 - 6 - 8 - 10 图 3-28 y 2 由图象可知方程有两个根，一个 O 在 - 5 和 - 4 之间，另一个在 2 和 3 之间. - 5 - 3 - 1 1 3 x （1）先求 - 5 和 - 4 之间的根. 利用 - 2 计算器进行探索： - 4 - 4.5 - 4 - 6 x - 4.1 - 4.2 - 4.3 - 4.4 - 8 y - 1.39 - 0.76 - 0.11 0.56 - 10 因此，x = - 4.3 是方程的一个近似 根 . 图 3-29 本书规定：用图象法求一元二次方程的近似根时，结果只取到十分位. 107第三章 二次函数 （2）另一个根可以类似地求出： y 2 x 2.1 2.2 2.3 2.4 O - 5 - 3 - 1 1 3 x y - 1.39 - 0.76 - 0.11 0.56 - 2 - 4 因此，x = 2.3 是方程的另一个近似 - 6 2 2.5 根. - 8 - 10 用一元二次方程的求根公式验证一 下，看是否有相同的结果. 图 3-30 做一做 （1）请利用图 3-31 求一元二次方程 x 2 + 2x - 10 = 3 的近似根. y y 5 f（x）= x2+ 2x - 13 5 g（x）= x2+ 2x - 10 - 5 O 5 x - 5 O 5 x - 5 - 5 - 10 - 10 图 3-31 图 3-32 （2）你还能利用图 3-32 求一元二次方程 x 2 + 2x - 10 = 3 的近似根吗？ 1087 二次函数与一元二次方程 随堂练习 利用二次函数的图象求一元二次方程 - 2x2 + 4x + 1 = 0 的近似根. y 4 2 - 4 - 2 O 2 4 x - 2 - 4 读一读 走近函数大家庭 我们已经学过一次函数、反比例函数和二次函数. 除了这些函数之外，在函数大 家庭里还有许多其他成员. 如函数 y = a 2 （ea x + e- a x ）（a > 0，e = 2.718 281 8…），它的面孔尽管陌生，但是 它的图象就是我们所熟悉的那种下垂的高压输电线（如图 3-33）. y O x 图 3-33 又如下面的脑电波图，常人看上去也许觉得它们杂乱无章，但是对于一个临床医 生来说，它们却是发现脑部异常的重要依据. 脑细胞活动时会产生生物电流，脑电波图 反映了生物电流随人脑活动的变化而变化的情况. 109第三章 二次函数 精神稳定时的脑电波 图 3-34 精神紧张时的脑电波 图 3-35 急性脑炎患者的脑电波 图 3-36 利用函数图象的方法帮助进行医疗诊断，除了脑电波图之外，还有心电图等，它 们都早已成为临床诊断常用的辅助手段. 还有一种函数的图象不是连续的，像下面表示某种公共汽车票价与乘坐距离之间 关系的图象（图 3-37）就是如此. 结合乘车购票的经验，相信你一定可以读懂它. y / 元 5 4 3 2 1 O 5 10 15 20 x / 千米 图 3-37 另外，数学上还有一些非常重要的函数，例如 y =［x］（［x］表示不超过 x 的最大 1（x > 0）， 整数，如［3.8］= 3，［4］= 4，［- 4.1］= - 5）；符号函数 sgn（x）= 0（x = 0），等. - 1（x < 0） 函数大家庭的成员尽管都个性十足，但它们却能够和谐相处，因为它们都反映了 变量之间的关系，都反映了函数随自变量的变化而变化这一共性. 习题 3.16 知识技能 1. 利用二次函数的图象求下列一元二次方程的近似根： （1）2x2 + x - 15 = 0； （2）3x2 - x - 1 = 0. 1107 二次函数与一元二次方程 y y = 2x2 + x - 15 2 - 6 - 4 - 2 O 2 4 6 x - 2 y y = 3x2 - x - 1 - 4 4 - 6 - 8 2 - 10 - 12 - 2 O 2 x - 14 - 2 - 16 （1） （2） （第 1 题） 联系拓广 2. 利用二次函数 y = 2 x2 与一次函数 y = x ＋ 2 的图象，求一元二次方程 2 x2 = x ＋2 的 近似根 . 回顾与思考 1. 通过几个具体的例子，深刻理解函数的概念. 2. 用具体的例子说明如何更恰当或更有效地利用函数表达式、表格和图象刻画变量 之间的关系. 3. 你在哪些情况下见到过抛物线的“身影”？用语言或图形进行描述. 4. 你能用二次函数的知识解决哪些实际问题？与同伴进行交流. 5. 小结一下画二次函数图象的方法. 6. 二次函数的图象有哪些性质？如何确定它的开口方向、对称轴和顶点坐标？请 举例说明. 7. 如何确定二次函数的表达式？请举例说明. 8. 用自己的语言描述二次函数 y = ax2 + bx + c 的图象与方程 ax2 + bx + c = 0 的根之间 的关系. 9. 用适当的方式梳理本章的知识，并与同伴进行交流. 111第三章 二次函数 复习题 知识技能 1. 两个数的和为 6，这两个数的积最大可以达到多少？利用图象描述乘积与因数之间 的关系. 2. 求下列二次函数图象的对称轴和顶点坐标： （1）y = 2 - 2x2 ； （2）y = - 3（x - 1）2 + 5； （3）y = 4（x + 3）2 - 1； （4）y = x（5 - x）； （5）y = 1 + 2x - x2； （6）y = 2x2 - 7x + 12. 3. 求下列二次函数的图象与 x 轴的交点坐标，并画草图验证： （1）y = x2 + 6x + 9； （2）y = 9 - 4x2； （3）y =（x + 1）2 - 9. 4. 把一根长 120 cm 的铁丝分为两部分，每一部分均弯曲成一个正方形，它们的面积 和是多少？它们的面积和最小是多少？ 5. 当运动中的汽车撞到物体时，汽车所受到的损坏程度可以用“撞击影响”来衡量. 某型汽车的撞击影响可以用公式 I = 2v2 来表示，其中 v（千米/分）表示汽车的速 度. （1）列表表示 I 与 v 的关系； （2）当汽车的速度扩大为原来的 2 倍时，撞击影响扩大为原来的多少倍？ 6. 自由落体运动是由于引力的作用而造成的，地球上物体自由下落的时间 t（s）和下落 1 的距离 h（m）的关系是 h = 4.9t 2. 我们知道，月球的引力大约是地球引力的 ，因 6 此月球上物体自由下落的时间 t（s）和下落的距离 h（m）的关系大约是h = 0.8t2. （1）在同一直角坐标系中画图，分别表示地球、月球上 h 与 t 之间的关系； （2）比较物体下落 4 s 时，在地球上和月球上分别下落的距离； （3）比较物体下落 10 m 时，在地球上和月球上分别所需要的时间（结果精确到 0.1 s）. 7. 二次函数 y = x2 - x - 5 与一次函数 y = 2x - 1的交点坐标是什么？利用函数表达 式、表格和图象三种方法求解. 1 1 8. 方程 - x2 + 2x + = 0 的根与二次函数 y = - x2 + 2x + 的图象之间有什么关系？ 2 2 9. 利用二次函数的图象求下列一元二次方程的近似根： 112复习题 （1）x2 + 11x = 9； （2）x2 + 3x = 20； （3）x2 + 2x - 9 = 0； （4）x2 + 3 = 3x . 10. 写出等边三角形的面积 S 与其边长 a 之间的关系表达式，并分别计算当 a = 1， ， 2 时三角形的面积. 数学理解 11. 正方形的边长是 x，面积是 A，周长是 l. （1）分别写出 A，l 与 x 的关系式； （2）在同一直角坐标系中画出（1）中两个函数的图象，比较它们的变化趋势； （3）你所画的函数 A = x2 的图象与函数 y = x2 的图象有什么不同？为什么？ 12. 已知平行四边形的高与底边的比 h∶a = 2∶5，用表达式表示平行四边形的面积 S 与它的底边 a 的关系，并从图象观察平行四边形的面积 y 9 随其底边的变化而变化的情况. 8 13. 如图，将一个小球从斜坡的点 O 处抛出，小球的抛出路 7 6 1 5 线可以用二次函数 y = 4x - x2 刻画，斜坡可以用一次 2 4 3 A 1 函数 y = x 刻画. 2 2 1 （1）求小球到达的最高点的坐标； O 1 2 3 4 5 6 7 8 x （2）小球的落点是 A，求点 A 的坐标. （第 13 题） 问题解决 14. 如图，假设篱笆（虚线部分）的长度是 15 m，如何围篱笆才能使其所围矩形的面 积最大？ B C A D 10 10 A D B 10 C l （第 14 题） （第 15 题） 15. 如图（单位：m），等腰直角三角形 ABC 以 2 m/s 的速度沿直线 l 向正方形移动， 直到 AB 与 CD 重合. 设 x s 时，三角形与正方形重叠部分的面积为 y m2. （1）写出 y 与 x 之间的关系式； （2）当 x = 2，3.5 时，y 分别是多少？ （3）当重叠部分的面积是正方形面积的一半时，三角形移动了多长时间？ 113第三章 二次函数 16. 科研人员在测试一枚火箭竖直向上升空时发现，火箭的高度 h（m）与时间 t（s） 的关系数据如下： 时间 t / s 1 5 10 15 20 25 火箭高度 h / m 155 635 1 010 1 135 1 010 635 （1）根据上表，以时间 t 为横轴，高度 h 为纵轴建立直角坐标系，并描出上述 各点； （2）你能根据坐标系中各点的变化趋势确定 h 关于 t 的函数类型吗？ （3）请由以上数据确定 h 与 t 的函数表达式； （4）你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗？你是根据 哪种表示方式求解的？ 17. 如图，喷水池的喷水口位于水池中心，离水面高为 0.5 m，喷出水柱呈抛物线，最 9 高点离水面 m，落水点离池中心 1 m. 16 9 0.5 m 16m 1 m （第 17 题） （1）请你建立适当的直角坐标系； （2）在你建立的坐标系中，用函数表达式描述右边的这条水柱，并说明自变量的 取值范围； （3）描述左边水柱的函数表达式是怎样的？ 18. 把一个数 a 拆成两数之和，何时它们的乘积最大？你能得出 A D 一个一般性的结论吗？ 19. 相框边的宽窄影响可放入相片的大小. 如图，相框长 26 cm， 宽 22 cm，相框边的宽为 x cm，相框内的面积为 y cm2. （1）写出 y 与 x 的函数表达式； B C （2）画出这个函数的图象； （第 19 题） （3）当 x = 1，1.5，2 时，分别可以放入面积为多少的相片？ 20. 竖直向上发射的物体的高度 h（m）满足关系式 h = - 5 t2 + vt，其中 t（s）是物体 0 运动的时间，v （m/s）是物体被发射时的速度. 某公园计划设计园内喷泉，喷水 0 的最大高度要求达到 15 m，那么喷水的速度应该达到多少？（结果精确到 0.01 m/s） 114复习题 21. 如图，隧道的截面由一段抛物线和矩形的三边构成. 矩形的长为 16 m，宽为 6 m， 抛物线的最高点 C 到路面 AA 的距离为 8 m. 1 （1）按如图所示的直角坐标系，求表示该抛物线的函数表达式； （2）一辆大型货运汽车装载某大型设备后高为 7 m，宽为 4 m. 如果该隧道内设双 向行车道，那么这辆货车能否安全通过？ y C B B 1 A O A x 1 （第 21 题） （第 22 题） ※22. 一座抛物线形拱桥如图所示，桥下水面宽度是 4 m 时，拱顶到水面的距离是 2 m . 当水面下降 1 m 后，水面宽度是多少？（结果精确到 0.1 m） 联系拓广 23. 已知，在△ABC 中，AB = AC = 10，BC = 12. 在 A △ABC 中截出一个矩形 DEFG （如图），设 EF = x， D G S = y ，写出 y 与 x 之间的函数关系式，列出表 矩形DEFG 格，并画出相应的图象. 根据以上三种表示方法回答 B E F C 下列问题： （第 23 题） （1）自变量 x 的取值范围是什么？ （2）图象的对称轴和顶点坐标分别是什么？ （3）你能描述 y 的值随 x 值的变化而变化的情况吗？ ※24. 某种蔬菜的销售单价与销售月份之间的关系如图（1）所示，成本与销售月份之间 的关系如图（2）所示（图（1）的图象是线段，图（2）的图象是抛物线）. 哪个 月出售这种蔬菜每千克的收益最大？（收益 = 售价 - 成本） 每千克售价 / 元 每千克成本 / 元 5 4 4 3 3 2 2 1 1 O O 1 2 3 4 5 6 1 2 3 4 5 6 月份 月份 （1） （2） （第 24 题） 115第三章 二次函数 ※25.（1）如图，第 n 个图形中有多少个小正方形？ 你是如何计算的？ （2）求 1 + 3，1 + 3 + 5，1 + 3 + 5 + 7， （第 25 题） 1 + 3 + 5 + 7 + 9，…， 1 + 3 + 5 + 7 + 9 + … + （2n - 1）. ※26.（1）如图，你知道每一个图形 中各有多少个小圆圈吗？ 第 6 个图形中应该有多少 个小圆圈？为什么？ （第 26 题） （2）完成下表： 一条边上的小圆圈数 1 2 3 4 5 每个图中小圆圈的总数 （3）如果用 n 表示等边三角形一条边上的小圆圈数，m 表示这个三角形中小圆圈的总 数，那么 m 和 n 的关系是什么？ ※27.（1）你知道下面每一个图形中各有多少个小圆圈吗？第 5 个图形中应该有多少个小 圆圈？为什么？ （2）完成下表： 一条边上的小圆圈数 1 2 3 4 5 每个图中小圆圈的总数 （3）如果用 n 表示六边形一条边上的小圆圈数，m 表示这个六边形中小圆圈的总 数，那么 m 和 n 的关系是什么？ （第 27 题） ※28. 求如图所示的海星图中的小圆圈的总数. （第 28 题） 116拱桥形状设计 拱桥形状设计 拱桥是桥梁家族中的重要一员. 拱桥跨度大，造型优美灵活，可雄伟壮 观，可小巧玲珑. 拱桥按桥拱的形状可分为圆弧拱挢、抛物线拱桥和悬链线拱桥. 桥拱形状 的选择主要根据力学上的分析，另外还有桥的跨度、施工条件等方面因素的 考虑. 北京颐和园的十七孔桥始建于清朝乾隆年间，桥身和 桥拱的面中间高，两边低，形成优美的抛物线 某桥梁建筑公司需在两山之间的峡谷上架设一座公路桥，桥下是一条宽 100 m 的河流，河面距所要架的公路桥桥面的高度是 50 m . 根据各方面条件的 分析，专家认为抛物线形拱桥是最好的选择. 如果要修建这座横跨峡谷的公路 桥，请你设计并作出抛物线桥拱设计图. 一、个人及小组活动 1. 搜集有关桥梁的图片，它们的桥拱分别是什么形状的？你知道哪些有关 它们的事情？ 2. 查阅资料或访问专家，了解桥梁的种类、桥梁的历史及有关计算公式等 117综合与实践 拱桥形状设计 习题 支 柱 支柱 长 度 顺序 1 2 3 4 5 6 7 8 9 抛物线表达式 118 m 05 桥梁设计方面的知识. 3. 在此基础上，自己进行设计并作出抛物线桥拱设计图（注意桥梁与峡谷 衔接的地方），并标出桥拱的跨度、桥拱与峡谷衔接的地方距河面的高度、桥 拱的最高点到桥面的距离等. 4. 设桥拱抛物线的表达式为 y = ax 2 + b + c，那么影响桥拱形状的量有 哪些？ 5. 如果有条件，请制作所设计桥梁的模型. 二、班级交流 1. 展示你所搜集的桥梁图片. 2. 展示你的拱桥设计图（模型），说明桥拱抛物线的表达式、设计思路及 设计过程（比如，你受到了哪些启发，桥拱是如何作出的，遇到了哪些困难， 你是如何克服困难的等）. 3. 说明抛物线 y= ax 2 + b + c 的系数是如何影响桥拱形状的. 4. 听取同学、老师或专家的意见，并回答他们提出的问题. 三、改进与自我评价 1. 改进自己的设计. 2. 加入个人的评语或心得，把自己满意的设计结果放入成长记录. 一座抛物线形拱桥的示意图如图所示，相邻两支柱间的距离为10 m. （1）在图中再画出两条弯曲程度不同的抛物 y 线桥拱（自己设计）； O x （2）在图中的直角坐标系中，你画的两条抛 物线的顶点坐标分别是什么？抛物线的 表达式分别是什么？ （3）计算你所设计的两个抛物线拱桥中每 根 100 m 支柱的长度，并把结果填入下表：1 投影 第四章 投影与视图 影子是我们司空见惯的，但你知道数学中是如何描述它们的吗？ 从正面、左面、上面观察一个物体，可以得到它三个方向的形状图，这其 实就是“视图”. 蒙古包可以看成怎样的几何体？你能画出它的视图吗？ 本章将探究灯光下影子的特点、太阳光下影子的特点，学习如何画一个物 体的视图. 在设计、制造、建筑等许多领域，视图有着广泛的应用. 学习目标 在观察、操作、想象等活动中增强对空间物体的把 握和理解能力 通过实例了解中心投影与平行投影 会画直棱柱、圆柱、圆锥和球的三种视图 能根据三种视图描述简单的几何体 119第四章 投影与视图 1 投影 在日常生活中，我们可以看到各种各样的影子. 比如，太阳光照射在窗 框、长椅等物体上时，会在墙壁或地面上留下影子；而皮影和手影都是在灯光 照射下形成的影子. 窗框的影子 长椅的影子 皮影 手影 物体在光线的照射下，会在地面或其他平面上留下它的影子，这就是投影 （projection）现象. 影子所在的平面称为投影面. 做一做 取一些长短不等的小棒和三角形、矩形纸片，用手电筒（或台灯）等去照 射这些小棒和纸片. （1）固定手电筒（或台灯），改变小棒或纸片的摆放位置和方向，它们的 影子分别发生了什么变化？ （2）固定小棒或纸片，改变手电筒（或台灯）的摆放位置和方向，它们的 1201 投影 影子发生了什么变化？ 手电筒、路灯和台灯的光线可以看成是从一个点发出的，这样的光线所形 成的投影称为中心投影（central projection）. 例 1 确定图 4-1 中路灯灯泡所在的位置. 图 4-1 解：如图 4-2，过一根木杆的顶端及其影子的顶端作一条直线，再过另一 根木杆的顶端及其影子的顶端作一条直线，两线相交于点 O. 点 O 就是路灯灯 泡所在的位置. O 图 4-2 议一议 如图 4-3，一个广场中央有一盏路灯. （1）高矮相同的两个人在这盏路灯下的影子一定一样长吗？如果不一定， 那么什么情况下他们的影子一样长？ （2）高矮不同的两个人在这盏路灯下的影子有可能一样长吗？请实际试一 试，并与同伴交流. 121第四章 投影与视图 图 4-3 随堂练习 1. 举例说明生活中的中心投影现象. 2. 两棵小树在一盏路灯下的影子如图所示. （1）确定该路灯灯泡所在的位置； （2）画出图中表示婷婷身影长的线段. 婷婷 （第 2 题） 读一读 日晷与皮影 日晷（guǐ）是我国古代利用日影测定时刻的一种计时仪器，它由“晷面”和“晷 针”组成. 当太阳光照在日晷上时，晷针的影子就会投向晷面. 随着时间的推移，晷针 的影子在晷面上慢慢地移动，以此来显示时刻. 1221 投影 日晷 皮影戏 皮影戏是用兽皮或纸板做成的人物剪影来表演故事的戏曲. 表演时，用灯光把剪 影照射在银幕上，艺人在幕后一边操纵剪影，一边演唱，并配以音乐. 皮影戏也称为影 戏、灯影戏、土影戏等. 皮影戏最早兴起于中国、印度、印度尼西亚等亚洲国家，随后传入欧美各国. 皮影 戏的产生和兴盛，大都与宗教活动有关，甚至在近代某些国家，它仍作为一种祭祀仪式 的演出. 后来发展起来的欧美国家的皮影戏则是一种娱乐性的戏剧艺术. 相传，汉武帝的宠妃李夫人死后，汉武帝对她日思夜想，以至于茶饭不思. 一天， 他命令法师把李夫人的灵魂召来，不然就要砍头. 法师急中生智，想出一条妙计：把李 夫人的画像临摹在一张羊皮上，绘上颜色，用灯光一照，影子映在一层布帘上，仿佛真 人一般，汉武帝见了竟信以为真. 这虽然是传说，却说明了皮影戏的历史悠久，也道出 了皮影戏的特点. 习题 4.1 知识技能 1. 如图是两棵小树在同一灯光下的影子，请在图中画出形成树影的光线. 你能确定 光源的位置吗？ （第 1 题） 123第四章 投影与视图 2. 在下图中，一个广告牌挡住了路灯的灯泡. （1）确定图中路灯灯炮所在的位置； （2）在图中画出表示小赵身高的线段. 小赵 小张 小李 （第 2 题） （第 3 题） 3. 平地上立有三根等高的木杆，从上面看如图所示，图中画出了其中一根木杆在路灯 灯光下的影子. 你能分别在图中画出另外两根木杆在同一路灯灯光下的影子吗？ 数学理解 4. 一个人在路灯下走动时，影子的长度与他到灯杆的距离有什么关系？ 问题解决 5. 一个人站在一盏路灯下，利用他在这盏路灯下的影子可以估算出路灯灯泡的高 度，请你设计一个估测方案. 物体在太阳光下形成的影子与在灯光下形成的影子有什么不同呢？ 做一做 取若干长短不等的小棒及三角形、矩形纸片，观察它们在太阳光下的影子. （1）固定投影面，改变小棒或纸片的摆放位置和方向，它们的影子分别发 生了什么变化？ （2）固定小棒或纸片，改变投影面的摆放位置和方向，它们的影子分别发 生了什么变化？ 1241 投影 太阳光线可以看成平行光线，平行光线所形成的投影称为平行投影 （parallel projection）. 如图 4-4 表示的都是平行投影. （1） （2） 图 4-4 议一议 图 4-5 中的三幅图是在我国北方某地某天上午不同时刻的同一位置拍摄的. （1） （2） （3） 图 4-5 （1）在三个不同时刻，同一棵树的影子长度不同，请将它们按拍摄的先后 顺序进行排列，并说明你的理由. （2）在同一时刻，两棵树影子的长度与它们的高度之间有什么关系？与同 伴交流. 例 2 某校墙边有甲、乙两根木杆，已知乙木杆的高度为 1.5 m. （1）某一时刻甲木杆在阳光下的影子如图 4-6 所示，画出此时乙木杆的 影子； （2）如果此时测得甲、乙木杆的影子长分别为 1.24 m 和 1 m，那么你能求 出甲木杆的高度吗？ 125第四章 投影与视图 D D E E 甲 乙 甲 乙 A D' B A D' B E' 图 4-6 图 4-7 解：（1）如图 4-7，连接 DD'，过点 E 作 DD' 的平行线，交 AD' 所在的直 线于点 E'. BE' 就是乙木杆的影子. AD AD' AD 1.24 （2）因为△ADD' ∽ △BEE'，所以， = ，即 = . BE BE' 1.5 1 1.5×1.24 所以，甲木杆的高度为 AD = = 1.86（m）. 1 做一做 （1）图 4-8 是两棵小树在同一时刻的影子，请在图中画出形成树影的光 线. 它们是太阳的光线还是灯光的光线？与同伴交流. 图 4-8 （2）图 4-9 的影子是在太阳光下形成的还是在灯光下形成的？画出同一时 刻旗杆的影子（用线段表示），并与同伴交流这样做的理由. 1261 投影 图 4-9 随堂练习 如图所示是某一天上午不同时刻同一根旗杆的影子，则它们按时间先后排列应 为（ ）. （A）①②③④ （B）④③②① （C）④①③② （D）②③④① ① ② ③ ④ 读一读 窗框的影子 一个矩形窗框被太阳光照射后，留在地面上的影子是什么形 状？它还是矩形吗？在不同时刻，它的形状一样吗？如果窗框是圆 形呢？假如影子不是落在地面上，而是落在与窗户平行的平面上， 情况又会怎样？ 经过认真观察你会发现：在太阳光照射下，矩形窗框在地面上 图 4-10 的影子常常是平行四边形（如图 4-10），而且在不同时刻，这些平行四边形的形状一 127第四章 投影与视图 般也不一样；圆形窗框在地面上的影子一般是椭圆形. 如果影子落在与窗户平行的 平面上，那么窗框与其影子全等. 把太阳光换成灯光，你又能发现什么？ 有兴趣的同学，可以通过实际操作或查阅有关资料，进行更深入的探究. 习题 4.2 知识技能 1. 一天下午，秦老师先参加了校运动会男子 200 m 比赛，然后又参加了男子 400 m 比赛，摄影师在同一位置拍摄了他参加这两场比赛的照片（如图）. 你认为秦老 师参加 400 m 比赛的照片是哪一张？为什么？ （1） （2） （第 1 题） 数学理解 2. 如图（1），中间是一盏路灯，周围有一圈栏杆，图（2）（3）表示的是这些栏杆 在灯光或太阳光下的阴影，但没有画完，请你把图（2）（3）补充完整. （1） （2） （3） （第 2 题） 1281 投影 问题解决 3. 分组活动：选一个阳光明媚的日子，4 人一组在校园内平坦的空地上立一根木 杆，分别在上午、中午、下午观察这根木杆影子的方向，同时测量木杆的影 长，并将有关结果填入下表： 杆影长度 时间 杆影方向 杆影长度 木杆长度 通过观察和测量，你发现了什么？把你发现的结论及有关思考整理成一篇数学 小论文. 4. 设计一个方案，利用人和旗杆的影子，估计旗杆的高度. ※5. 在太阳光下摆弄一个立方块，观察立方块的影子，你得到的影子分别是几边形？ 与同伴交流. 在我国的北方，晴天时无论上午、中午和下午，阳光总是倾斜地照射在地 面上. （1）地球上的居民能不能看到阳光垂直照射在地面上的情况？ （2）当阳光垂直照射在地面上时，如果拿起一根细木棒，它在地面上的影 子会出现哪些可能的情况？ 在平行投影中，当投影线垂直于投影面（即投影线正对着投影面）时，物 体在投影面上的投影称为正投影（orthographic projection）. 如图 4-11，相对于线段 AB 与 投 投影面的三种不同的位置关系，线 影 方 段 AB 的正投影分别有以下三种不 向 同情况：可能是与线段 AB 等长的 一条线段，也可能是长度较短的一 图 4-11 条线段，甚至还可能是一个点. 129第四章 投影与视图 议一议 图 4-12 表示矩形 ABCD 在投影面上的三种正投影，分析这三种情况，你 能发现平面图形的正投影有什么规律吗？先想一想，再与同伴进行交流. 投 影 方 向 图 4-12 例 3 一个长方体与投影面的相对位置如图 4-13 所示，矩形 A′B′C′D′是长 方体在投影面上的正投影，你能说出长方体的各个面在投影面上的正投影吗？ 图 4-13 解：面 ABCD 与面 EFGH 的正投影都是矩形 A′B′C′D′； 面 ABFE 的正投影是线段 A′B′，面 DCGH 的正投影是线段 D′C′； 面 BCGF 的正投影是线段 B′C′，面 ADHE 的正投影是线段 A′D′. 想一想 例 3 中，长方体的各个面与它们的正投影的形状和大小分别有什么联系？ 与同伴进行交流. 1301 投影 随堂练习 1. 回答下列问题： （1）球的正投影是什么图形？ （2）长方体的正投影一定是矩形吗？ 2. 分别按图中投影线的方向，画出圆柱体的正投影. （第 2 题） 习题 4.3 知识技能 1. 按图中投影线的方向，分别画出这个几何体的正投影. （第 1 题） 2. 下图中的几何体是用 3 个大小相同的正方体拼成的，它的正投影不可能是 （ ）. （第 2 题） （A） （B） （C） （D） 数学理解 3. 一个几何体在投影面上的正投影是一个圆，那么这个几何体可能是什么？说出 其中两种不同几何体的名称. 131第四章 投影与视图 2 视图 上面 如图 4-14，假设有一束平行光线 从正面投射到图中的物体上，你能想象 出它在这束平行光线下的正投影吗？把 左面 你想象的正投影画出来，并与同伴交流. 如果平行光线从左面投射到图中的 物体上，情况又如何？如果平行光线从 上面投射到图中的物体上呢？ 正面 从某一角度看物体，将所见物体的 图 4-14 轮廓形状图用平面图形画出来，这其实就是“视图”. 在实际生活和工程中， 人们常常从正面、左面和上面三个不同方向观察一个物体，分别得到这个物体 的三种视图，这样大体上就把一个物体的形状特征用平面图形表示出来了. 通 常我们把从正面得到的视图叫做主视图（front view），从左面得到的视图叫做 左视图（left view），从上面得到的视图叫做俯视图（planform view）. 例如，图 4-14 所示物体的主视图、左视图和俯视图分别是： 上面 主 左 视 视 图 图 左面 俯 视 图 正面 图 4-15 1322 视图 议一议 （1）图 4-16 中物体的形状分别可以看成什么样的几何体？你能想象出它 们的主视图、左视图和俯视图吗？与同伴交流. （1） （2） （3） 图 4-16 （2）在图 4-17 中分别找出上述几何体的主视图. （1） （2） （3） （4） （5） （6） 图 4-17 （3）图 4-16 中各物体的左视图是什么？俯视图呢？与同伴交流. 图4-16（1）（2）（3）物体的形状分别可以看成是圆柱、圆锥和球. 圆 柱、圆锥和球的三种视图如下表所示： 几何体 主视图 左视图 俯视图 133第四章 投影与视图 想一想 图 4-18 是一个蒙古包的照片，小明认为这个蒙古包可以看成图 4-19 所 示的几何体，你能帮小明画出这个几何体的三种视图吗？ 图 4-18 图 4-19 随堂练习 1. 找出图中每一物品所对应的主视图. （1） （2） （3） （4） （A） （B） （C） （D） （第 1 题） 2. 将两个圆盘、一个茶叶桶、一个皮球和一个蒙古包模型按如图所示的方式摆放在一 起，其主视图是（ ）. （A） （B） （第 2 题） （C） （D） 1342 视图 习题 4.4 知识技能 1. 画出下列物体的三种视图. （1） （2） （第 1 题） （第 2 题） 2. 把一个圆锥的上部截去一个小圆锥（如图），画出剩余部分的三种视图. 3.（1）画出图中各物体的主视图、左视图和俯视图； （2）请找出一些类似形状的物体，并尝试画出它们的三种视图. （1） （2） （3） （第 3 题） 图 4-20 是一个直三棱柱. （1）你能想象出这个直三棱柱的主视图、左视图和俯视图 吗？你能画出它们吗？ （2）你所画的主视图与俯视图中有哪些部分对应相等？主视 图与左视图中有哪些部分对应相等？左视图与俯视图呢？与同伴 交流. 图 4-20 在三种视图中，主视图反映物体的长和高，俯视图反映物体的长和宽，左 视图反映物体的高和宽. 因此在画三种视图时，对应部分的长度要相等，而且 通常把俯视图画在主视图下面，把左视图画在主视图右面. 例如，图 4-20 所 示几何体的三种视图可以表示为图 4-21. 135第四章 投影与视图 主 左 高 高 视 视 图 图 长 宽 长 俯 视 宽 图 图 4-21 例 1 画出图 4-22 所示的四棱柱的主视图、左视图和俯视图. 解：这个四棱柱的三种视图如图 4-23 所示. 主 左 视 视 图 图 俯 视 图 图 4-22 图 4-23 在画视图时，看得见部分的 轮廓线通常画成实线，看不见部 分的轮廓线通常画成虚线. 做一做 有两个底面为等腰直角三角形的直三棱柱，它们的俯视图分别如图 4-24 （1）（2）所示，画出它们的主视图和左视图. （1） （2） 图 4-24 1362 视图 随堂练习 1. 已知直四棱柱的俯视图如图所示，画出它的主视图和左视图. （第 1 题） （第 2 题） 2. 画出如图所示几何体的主视图、左视图和俯视图. 习题 4.5 知识技能 1. 如图是空心圆柱的两种视图，哪个有错误？为什么？ 主 视 图 俯 视 图 （1） （2） （3） （第 1 题） 2. 画出如图所示几何体的三种视图. （1） （2） （第 2 题） 137第四章 投影与视图 3. 一个直五棱柱的俯视图如图所示，请你画出它的主视图和左视图. （第 3 题） 数学理解 4. 画出如图所示几何体的主视图、左视图和俯视图. （1） （2） （3） （第 4 题） 观察图 4-25 中的三种视图，你能在图 4-26 中找出与之对应的几何体吗？ 主 左 视 视 图 图 （1） （2） 俯 视 图 （3） （4） 图 4-25 图 4-26 1382 视图 议一议 根据图 4-27 中的三种视图，你能想象出相应几何体的形状吗？先独立思 考，再与同伴交流. 主 左 视 视 图 图 俯 视 图 图 4-27 做一做 图 4-28 是由若干个同样大小的正方体所搭几何体的俯 2 1 视图，小正方形中的数字表示在该位置正方体的个数. 请画 1 1 出这个几何体的主视图和左视图，并画出几何体的草图. 图 4-28 随堂练习 根据如图所示的三种视图，你能想象出几何体的形状吗？（画出几何体的草图） 主 左 视 视 图 图 俯 视 图 139第四章 投影与视图 习题 4.6 知识技能 1. 根据下列主视图和俯视图，分别找出所对应的物体，并将视图的序号填在相应物 体下面的括号里： 主 视 图 俯 视 图 （1） （2） （3） （4） （ ） （ ） （ ） （ ） （第 1 题） 2. 根据如图所示的三种视图，分别说出它们所对应的几何体的形状： （1） （2） （3） （4） （5） （第 2 题） 1402 视图 数学理解 3. 根据如图所示的三种视图，你能想象出几何体的形状吗？（画出几何体的草图） （1） （2） （第 3 题） 4. 下面的两幅图是由若干个同样大小的正方体所搭几何体的俯视图，小正方形中的 数字表示在该位置的正方体的个数. 请画出相应几何体的主视图和左视图. 1 1 2 1 2 1 1 （1） （2） （第 4 题） 回顾与思考 1. 列举一些中心投影和平行投影的实例. 2. 举例说明灯光及其影子、太阳光及其影子的应用. 3. 你能找出主视图和左视图完全相同的几何体吗？你能找出三种视图完全相同的 几何体吗？请各举两例. 4. 如何画直棱柱的三种视图？请举例说明. 5. 与同伴结对，互相提供视图，让对方根据所提供的视图描述相应几何体的形状. 6. 用适当的方式梳理本章的知识，并与同伴进行交流. 141第四章 投影与视图 复习题 知识技能 1.（1）确定图（1）中路灯灯泡的位置，并画出此时婷婷在路灯下的影子； （2）画出图（2）中旗杆在阳光下的影子. （第 1 题） 2. 下列几何体的三种视图有没有错误（不考虑尺寸）？为什么？如果错了，应该怎样 改正？ （1） （2） 主 左 主 左 视 视 视 视 图 图 图 图 俯 俯 视 视 图 图 142复习题 3. 添线补全下面几何体的三种视图. 主 左 视 视 图 图 （1） 俯 视 图 主 左 视 视 （2） 图 图 俯 视 图 4. 补全下列几何体的三种视图. 主 视 图 （1） 俯 视 图 主 视 图 （2） 俯 视 图 5. 两个底面为梯形的直四棱柱的俯视图分别如图所示，画出它们的主视图和左视图. （1） （2） （第 5 题） 6. 画出下列几何体的三种视图. （1） （2） （第 6 题） 143第四章 投影与视图 数学理解 7. 灯光下有一棵小树，小明用如下方法测量这棵小树的高度：先量出小树在灯光下的 影长，再找一根长度已知的竹竿，任意选定一个位置测量竹竿在这同一灯光下的 影长，然后由小树高度与其影长之比等于竹竿长与 其影长之比来求出小树的高度. 你觉得他的方法有 道理吗？为什么？ 8. 画出如图所示几何体的三种视图. 9. 根据如图所示的三种视图，描述几何体的形状. （1） （2） （第 8 题） 主 左 主 左 视 视 视 视 图 图 图 图 俯 俯 视 视 图 图 （1） （2） （第 9 题） 10. 如图是用 3 个同样大小的正方体搭成的几何体的主视图，画出俯视图和左视图. 主视图 俯视图 （第 10 题） （第 11 题） 11. 用若干个同样大小的正方体搭一个几何体，使得它的主视图和俯视图如图所示. 这样的几何体只有一种吗？它最少需要用多少个正方体？最多需要用多少个？ 问题解决 12. 分组活动：分组设计并实施一个应用影子解决问题的活动，撰写一份活动报告， 阐明活动的目的、要求、过程、结论及相关思考. 13. 在你所在地区，一天中什么时刻物体在阳光下的影子最短？实际进行观察、测量 活动，并把活动的过程和结果写成一篇数学小论文. 144总复习题 总复习题 ● 整理本学期学过的数学知识和方法，并与同伴进行交流． ●在自己经历过的解决问题活动中，选择一个最具有挑战性的问题，写下解决它的 过程，包括遇到的困难、克服困难的方法与过程及所获得的体会，并解释选择 这个问题的原因． ● 通过本学期的数学学习，你有哪些收获？有哪些需要改进的地方？ 知识技能 1. 将 50 kg 的气体装在体积为 V m3 的容器中，气体的密度为 ρ kg / m3．写出密度与体 积之间的关系式． k 2. 已知反比例函数 y = 的图象经过点（3，- 2），那么点（- 2，3）和点（- 3，2） x 是否在这个函数的图象上？为什么？ a 3. 反比例函数 y = （a 为非零常数）的图象在其所在象限内 y 的值随 x 值的增大而 2x 2 增大，那么函数 y = 的图象位于哪些象限内？y 的值随 x 值的增大怎样变化？为 ax 什么？ m 4. 已知 A（m + 3，2）和 B（ 3， ）是同一个反比例函数图象上的两个点． 3 （1）求 m 的值； （2）画出这个反比例函数的图象； （3）将 A，B 两点标在函数图象上. 5. 计算： （1）sin 60°- cos 45°+ tan 45°； （2）cos260°+ sin245°. 1 6.（1）已知∠A 是锐角，sin A = ，求∠A 的其他三角函数值； 5 8 （2）已知∠A 是锐角，tan A = ，求∠A 的其他三角函数值. 15 7. 根据条件求锐角： （1）sin A = 0.753，求∠A； （2）cos B = 0.083 2，求∠B； （3）tan C = 45.8，求∠C. 8. 求下列抛物线的对称轴和顶点坐标： （1）y = -（x - 2）2 + 4； （2）y = -2（x + 5）2 - 3； 145总复习题 （3）y = x - 2x 2； （4）y = 2x（3 - x）； （5）y = 9 - 2x - x 2 . 9. 求下列二次函数的图象与 x 轴的交点坐标，并画草图验证： （1）y = -（x + 2）（x - 2）； （2）y = 9x 2 - 49； （3）y = 5 + x - 4x 2； （4）y =（x + 1）2 - 9. 10. 用图象法求下列一元二次方程的近似根： （1）x 2 - 5x + 5 = 0； （2）2x 2 - 4x = 5； （3）x 2 - 6x = 3； （4）5x 2 + 4x - 3 = 0. 11. 婷婷、小张在路灯下的影子如图所示，画出小高在该路灯下的影子（可以用线段 表示影子）. 婷婷 小张 小高 （第 11 题） 12. 下面四幅照片是在同一天下午的不同时刻拍摄的，请将它们按拍摄时间的先后顺 序进行排列． （1） （2） （3） （4） （第 12 题） 13. 甲、乙两人在太阳光下行走，同一时刻他们的身高与其影长的比之间有什么关系？ 14. 小明和小颖在太阳光下行走，小明身高 1.75 m，他的影长 2.0 m，小颖比他矮 5 cm， 此刻她的影长是多少？ 146总复习题 15. 分别画出如图所示的实物的三种视图. （1） （2） （1） （2） （第 15 题） （第 16 题） 16. 画出如图所示的几何体的三种视图. 数学理解 17. 如图，婷婷在太阳光下的影子如图所示，画出此时小高在太阳光下的影子（用线 段表示影子）. 婷婷 小高 （第 17 题） （第 18 题） 18. 如图所示的图形是一个水平放置的直三棱柱被斜着截去一部分后形成的，请画出 它的主视图、左视图和俯视图. 19. 根据下面两种视图，你能想象出几何体的形状吗？（画出几何体的草图） （1） （2） （3） （4） 主 主 主 主 视 视 视 视 图 图 图 图 俯 俯 俯 俯 视 视 视 视 图 图 图 图 （第 19 题） 147总复习题 问题解决 20. 学校组织学生参加实践活动，教师要求学生测量学校附近的高压电线杆的高度， 具体有以下条件： ① 工具：测角仪（可测水平角、倾斜角等）、米尺、标杆（长度小于 2 m）等； ② 为了安全，不允许到距离电线杆约 5 m 的范围内； ③ 电线杆周围比较平坦. 请你按下列要求设计一个测量电线杆高度的方案： （1）简述测量方法； （2）画出示意图（标出有关的角及线段）； （3）求出电线杆的高 h（用字母表示）. 说明：角度用字母α，β，γ 等表示；距离（线段长度）用字母 a，b，c 等表示. 21. 用一块宽度为 5 m 的矩形铁片弯折成如图所示的等腰梯形（即 AB = CD）流水槽. 要使流水的截面面积最大，弯折的长度（梯形的腰）应为多少？ E D A 120° 120° B C （第 21 题） （第 22 题） 22. 如图，某运动场跑道的周长为 400 m 且两端为半圆形，要使矩形内部操场的面积 最大，直线跑道的长应为多少？ 23. 甲船从 A 处起以 15 海里 / 时的速度向正北方向航行，这时乙船从 A 的正东方向 20 海里的 B 处起以 20 海里 / 时的速度向西航行. 多长时间后，两船的距离最小？最 小距离是多少？ 24. 如图，一块长 x m、宽 y m 的矩形绿地由篱笆围着，并且由一条与长边平行的篱 笆分开，篱笆的总长为 600 m. （1）用含 x 的代数式表示矩形绿地的面积 S； （2）求矩形绿地的最大面积. （第 24 题） 148总复习题 25. 一名身高 1.8 m 的篮球运动员在距篮板 4 m 处跳起投篮，球在运动员头顶上方 0.25 m 处出手. 按如图所示的直角坐标系，球在空中运行的路线可以用 y = -0.2x 2 + 3.5 来 描述. （1）球能达到的最大高度是多少？ （2）球出手时，运动员跳离地面的高度是多少？ y O x 149 8.1 0.25 50.3 （第 25 题） 联系拓广 k 26. 正比例函数 y = kx 和反比例函数 y = 的图象相交于 A，B 两点，已知点 A 的横 x 坐标为 1，点 B 的纵坐标为 -3. （1）求 A，B 两点的坐标； （2）写出这两个函数的表达式.出 版 说 明 为了更好地满足五四学制实验区义务教育教学的需要，2003年山东省教育 厅决定以全国中小学教材审定委员会初审通过的义务教育课程标准实验教科书 为基础，委托山东教育出版社等单位改编、出版一套五四学制的义务教育课程 标准实验教科书。该套实验教科书经全国中小学教材审定委员会初审通过后供 山东省的烟台、威海、淄博、莱芜等五四学制地区的学生选用，受到了广大师 生的欢迎和肯定。 2011年7月，教育部启动了义务教育课程标准实验教科书的修订送审工 作。为了做好五四学制实验教科书初中《数学》的修订送审工作，山东教 育出版社与北京师范大学出版社签署了合作协议。五四学制实验教科书《数 学》（六~九年级）的修订、编写依据教育部制定的《义务教育数学课程标准 （2011年版）》，以马复主编的北师大版六三学制义务教育教科书《数学》 （七~九年级）为基础，吸取了五四学制实验区多年来在教学实践中探索、积 累的丰硕成果。 本套教科书经教育部审定通过，供五四学制地区的学生选用。参加本册改 编的人员有马复、韩际清、赵水祥、陈杰、柳圣明、云鹏、刘崇渭、王德刚、 辛珍文，由马复、韩际清主编。 本书的改编、出版得到了山东省教育厅、山东出版集团、山东省教学研究 室、烟台市教育科学研究院、威海市教育教学研究中心、淄博市教研室、莱芜 市教研室以及泰安、青岛、济宁等教研单位的领导，特别是北京师范大学出版 社的领导和学科专家的大力帮助和支持，在此表示由衷的感谢。 欢迎广大师生在使用过程中提出修改意见和建议，以利于教科书的不断改 进和完善。 山东教育出版社