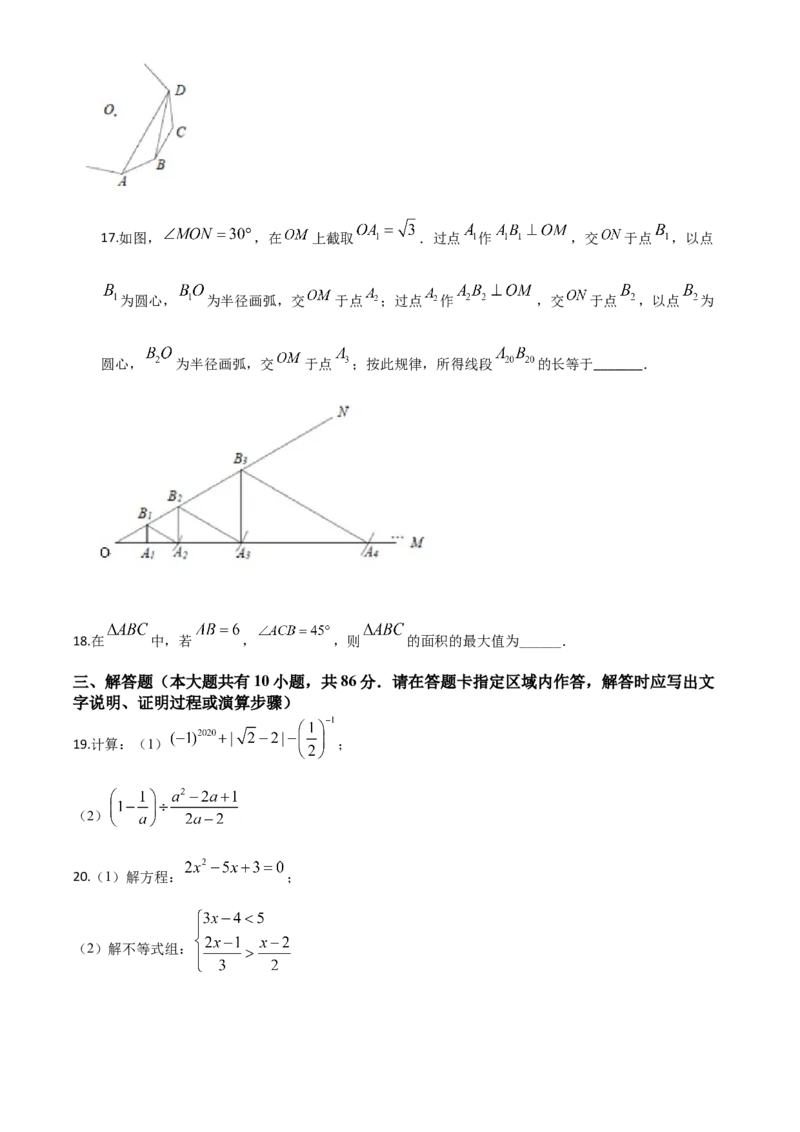文档内容
徐州市 2020 年初中学业水平考试
数学试题
注意事项
1.本试卷共6页,满分140分,考试时间120分钟.
2.答题前,请将姓名、文化考试证号用0.5毫米黑色字迹签字笔填写在本卷和答题卡的指
定位置.
3.答案全部涂、写在答题卡上,写在本卷上无效.考试结束后,将本卷和答题卡一并交回.
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰
有一项是符合要求的,请将正确选项前的字母代号填涂在答题卡相应位置)
1.3的相反数是( ).
A. B. 3 C. D.
的
2.下列垃圾分类标识 图案既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
的
3.三角形 两边长分别为 和 ,则第三边长可能为( )
A. B. C. D.
的
4.在一个不透明 袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出
红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )
A. B. C. D.
5.小红连续 天的体温数据如下(单位相 ): , , , , .关于这组数据下列
说法正确的是( )
A. 中位数是 B. 众数是 C. 平均数是 D. 极差是
6.下列计算正确的是( )
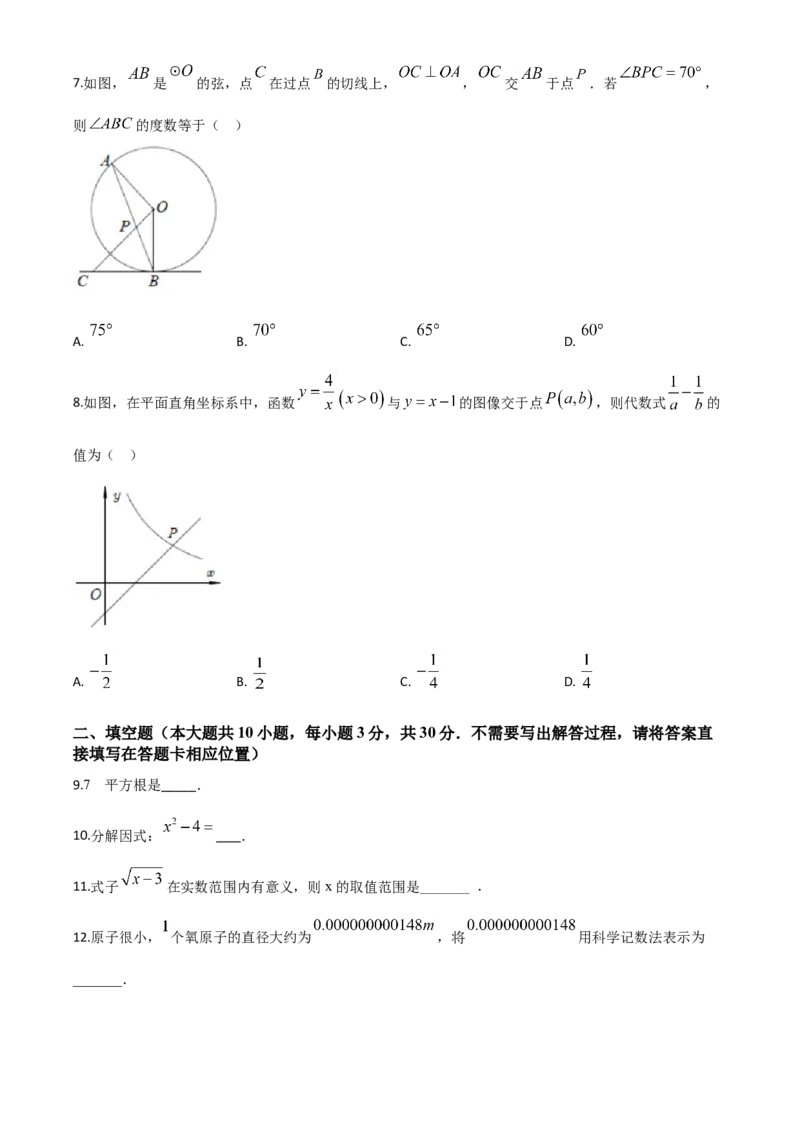
A. B. C. D.7.如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,
则 的度数等于( )
A. B. C. D.
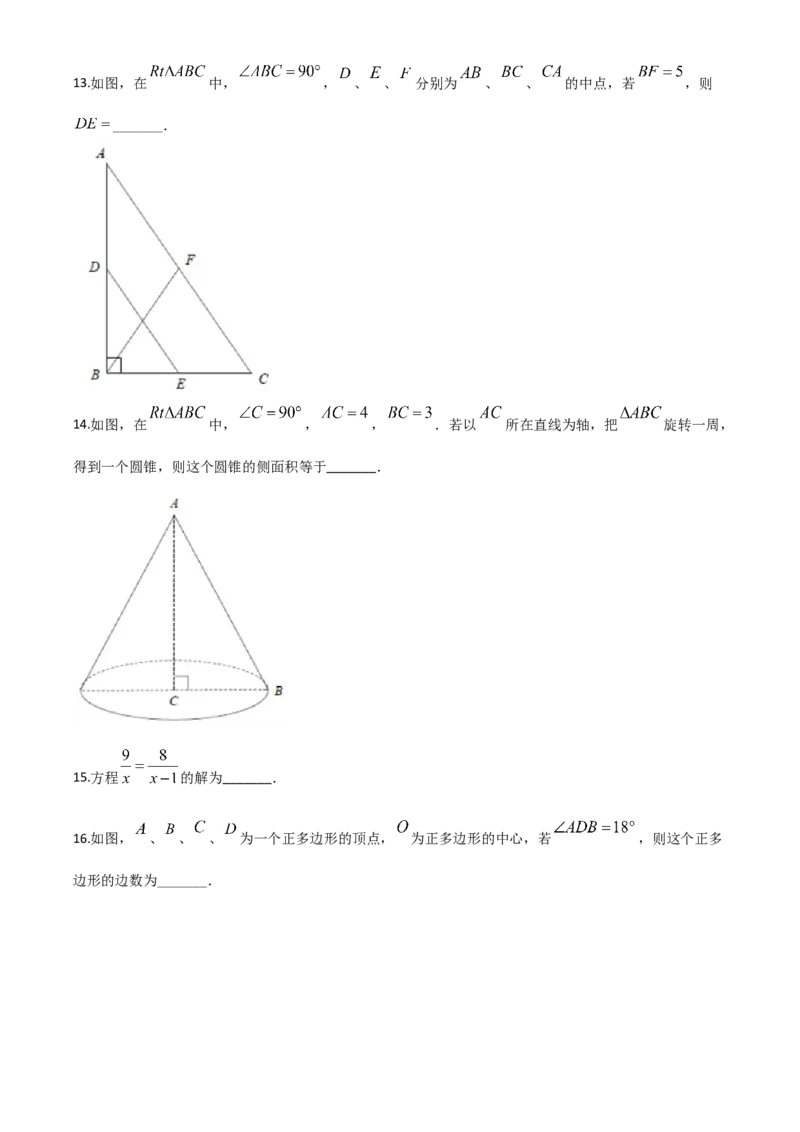
8.如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的
值为( )
A. B. C. D.
二、填空题(本大题共10小题,每小题3分,共30分.不需要写出解答过程,请将答案直
接填写在答题卡相应位置)
的
9.7 平方根是_____.
10.分解因式: .
11.式子 在实数范围内有意义,则 x 的取值范围是_______ .
12.原子很小, 个氧原子的直径大约为 ,将 用科学记数法表示为
_______.13.如图,在 中, , 、 、 分别为 、 、 的中点,若 ,则
_______.
14.如图,在 中, , , .若以 所在直线为轴,把 旋转一周,
得到一个圆锥,则这个圆锥的侧面积等于_______.
15.方程 的解为_______.
16.如图, 、 、 、 为一个正多边形的顶点, 为正多边形的中心,若 ,则这个正多
边形的边数为_______.17.如图, ,在 上截取 .过点 作 ,交 于点 ,以点
为圆心, 为半径画弧,交 于点 ;过点 作 ,交 于点 ,以点 为
圆心, 为半径画弧,交 于点 ;按此规律,所得线段 的长等于_______.
18.在 中,若 , ,则 的面积的最大值为______.
三、解答题(本大题共有10小题,共86分.请在答题卡指定区域内作答,解答时应写出文
字说明、证明过程或演算步骤)
19.计算:(1) ;
(2)
20.(1)解方程: ;
(2)解不等式组:21.小红的爸爸积极参加社区抗疫志愿服务工作.根据社区的安排志愿者被随机分到 组(体温检测)、
组(便民代购)、 组(环境消杀).
(1)小红的爸爸被分到 组的概率是______;
(2)某中学王老师也参加了该社区的志愿者队伍,他和小红爸爸被分到同一组的概率是多少?(请用画
树状图或列表的方法写出分析过程)
22.某市为了解市民每天的阅读时间,随机抽取部分市民进行调查.根据调查结果绘制了如下尚不完整的统
计图表:
市民每天的阅读时间统计表
类别
阅读时间
频数
市民每天的类别阅读时间扇形统计图
根据以上信息解答下列问题:
(1)该调查的样本容量为______, ______;
(2)在扇形统计图中,“ ”对应扇形的圆心角等于______ ;
(3)将每天阅读时间不低于 的市民称为“阅读爱好者”.若该市约有 万人,请估计该市能称为
“阅读爱好者”的市民有多少万人.
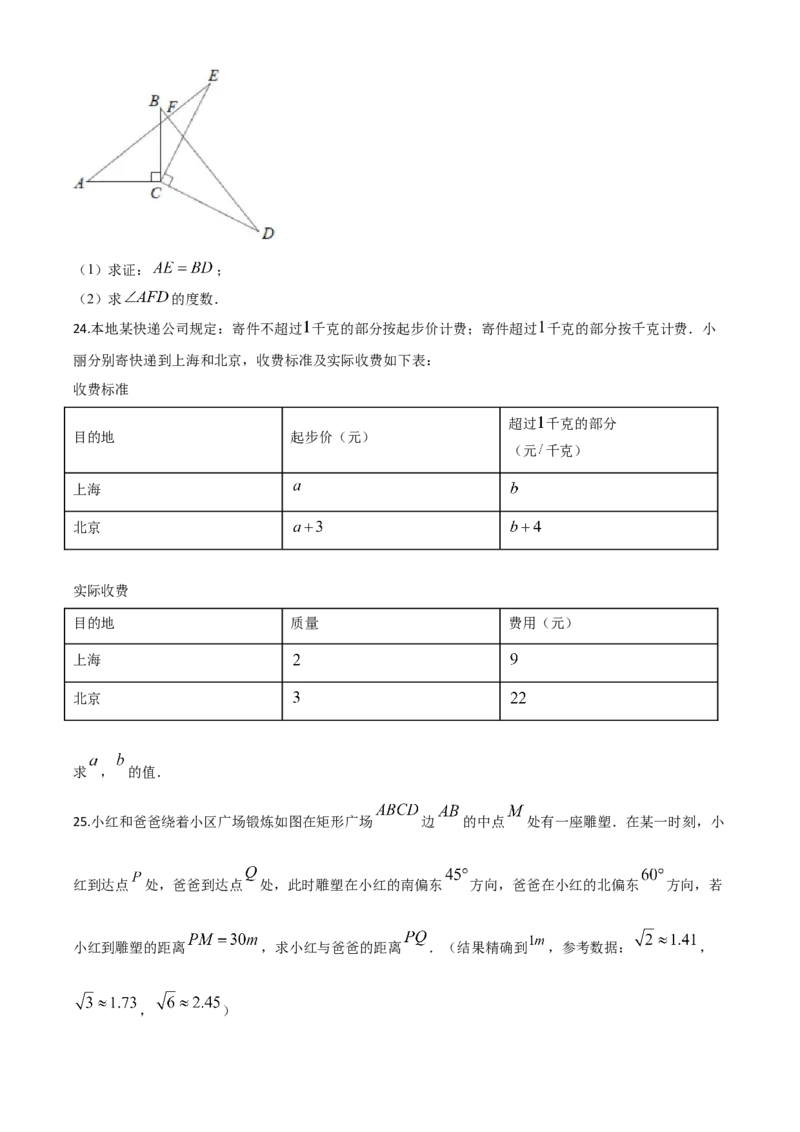
23.如图, , , . , 与 交于点 .(1)求证: ;
(2)求 的度数.
24.本地某快递公司规定:寄件不超过 千克的部分按起步价计费;寄件超过 千克的部分按千克计费.小
丽分别寄快递到上海和北京,收费标准及实际收费如下表:
收费标准
超过 千克的部分
目的地 起步价(元)
(元 千克)
上海
北京
实际收费
目的地 质量 费用(元)
上海
北京
求 , 的值.
25.小红和爸爸绕着小区广场锻炼如图在矩形广场 边 的中点 处有一座雕塑.在某一时刻,小
红到达点 处,爸爸到达点 处,此时雕塑在小红的南偏东 方向,爸爸在小红的北偏东 方向,若
小红到雕塑的距离 ,求小红与爸爸的距离 .(结果精确到 ,参考数据: ,
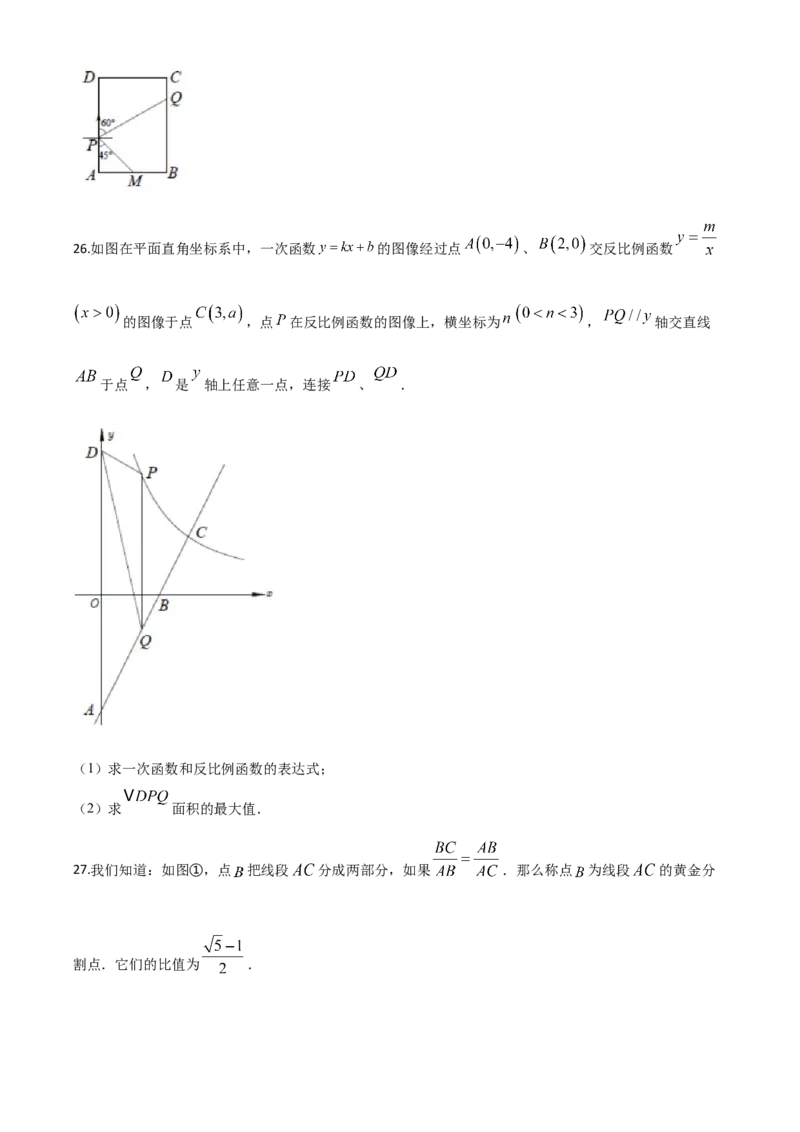
, )26.如图在平面直角坐标系中,一次函数 的图像经过点 、 交反比例函数
的图像于点 ,点 在反比例函数的图像上,横坐标为 , 轴交直线
于点 , 是 轴上任意一点,连接 、 .
(1)求一次函数和反比例函数的表达式;
(2)求 面积的最大值.
27.我们知道:如图①,点 把线段 分成两部分,如果 .那么称点 为线段 的黄金分
割点.它们的比值为 .(1)在图①中,若 ,则 的长为_____ ;
(2)如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,
将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;
(3)如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,
作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰
好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.
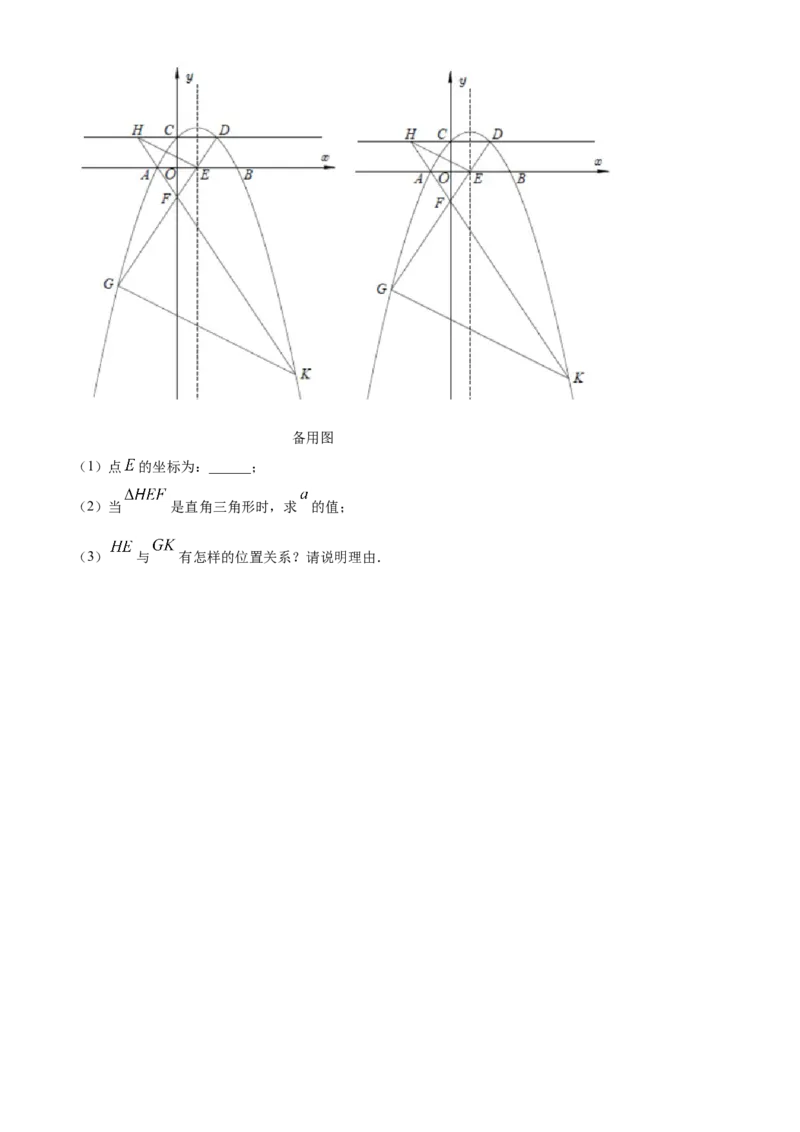
28.如图,在平面直角坐标系中,函数 的图像交 轴于点 、 ,交 轴于点
,它的对称轴交 轴于点 .过点 作 轴交抛物线于点 ,连接 并延长交 轴于点 ,
交抛物线于点 .直线 交 于点 ,交抛物线于点 ,连接 、 .备用图
(1)点 的坐标为:______;
(2)当 是直角三角形时,求 的值;
(3) 与 有怎样的位置关系?请说明理由.本试卷的题干、答案和解析均由组卷网(http://zujuan.xkw.com)专业教师团队编校出品。
登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。
试卷地址:在组卷网浏览本卷
组卷网是学科网旗下的在线题库平台,覆盖小初高全学段全学科、超过900万精品解析试题。
关注组卷网服务号,可使用移动教学助手功能(布置作业、线上考试、加入错题本、错题训练)。
学科网长期征集全国最新统考试卷、名校试卷、原创题,赢取丰厚稿酬,欢迎合作。
钱老师 QQ:537008204 曹老师 QQ:713000635