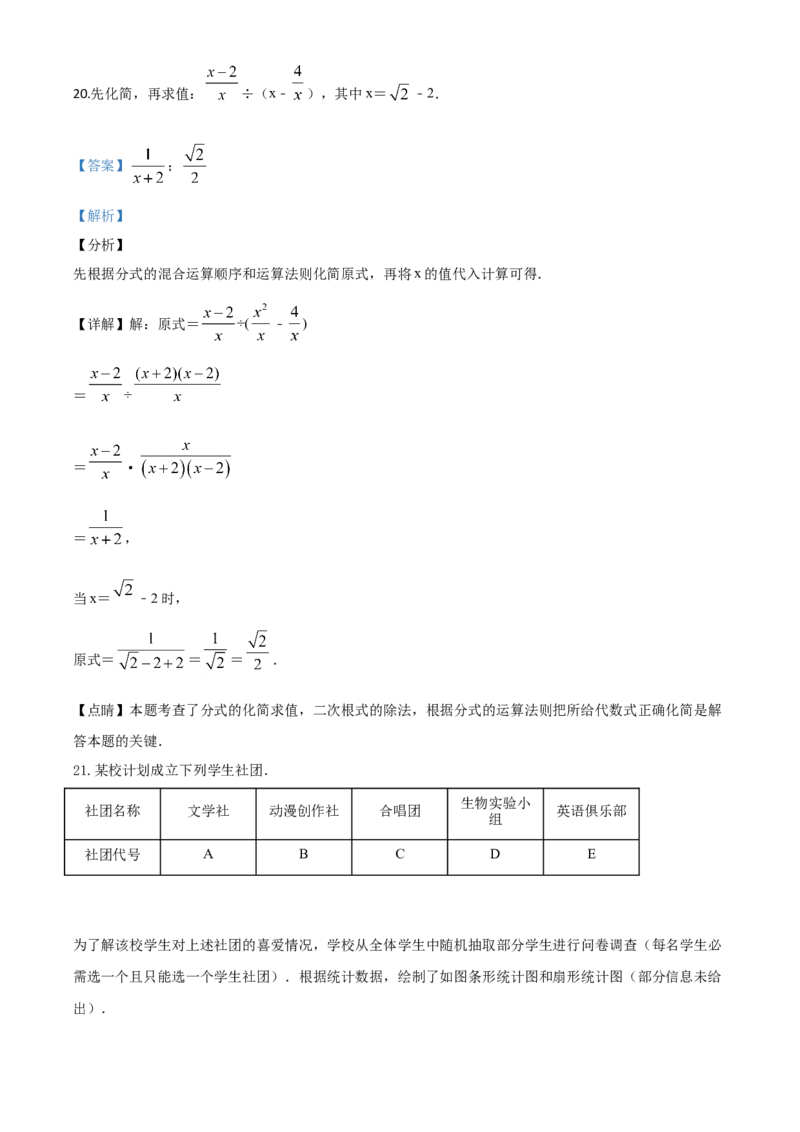文档内容
2020 年江苏省宿迁市中考数学试卷
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一
项是符合题目要求的)
1.2的绝对值是( )
A. ﹣2 B. C. 2 D. ±2
【答案】C
【解析】
【分析】
利用绝对值的意义进行求解即可.
【详解】解:2的绝对值就是在数轴上表示2的点到原点的距离,即|2|=2,
故选:C.
【点睛】本题考查了绝对值的意义,一个正数的绝对值等于它本身,一个负数的绝对值等于它的相反数,
0的绝对值等于0.
2.下列运算正确的是( )
A. m2•m3=m6 B. m8÷m4=m2 C. 3m+2n=5mn D. (m3)2=m6
【答案】D
【解析】
【分析】
根据同底数幂的乘除法、幂的乘方的计算法则进行计算即可.
【详解】m2•m3=m2+3=m5,因此选项A不正确;
m8÷m4=m8﹣4=m4,因此选项B不正确;
3m与2n不是同类项,因此选项C不正确;
(m3)2=m3×2=m6,因此选项D正确;
故选:D.
【点睛】本题考查了同底数幂的乘除法、幂的乘方的计算方法,掌握计算方法是正确计算的前提.
3.已知一组数据5,4,4,6,则这组数据的众数是( )
A. 4 B. 5 C. 6 D. 8
【答案】A
【解析】
【分析】
根据题目中的数据和众数的含义,可以得到这组数据的众数,本题得以解决.【详解】解:∵一组数据5,4,4,6,
∴这组数据的众数是4,
故选:A.
【点睛】本题考查了众数,解答本题的关键是明确众数的含义,会求一组数据的众数.
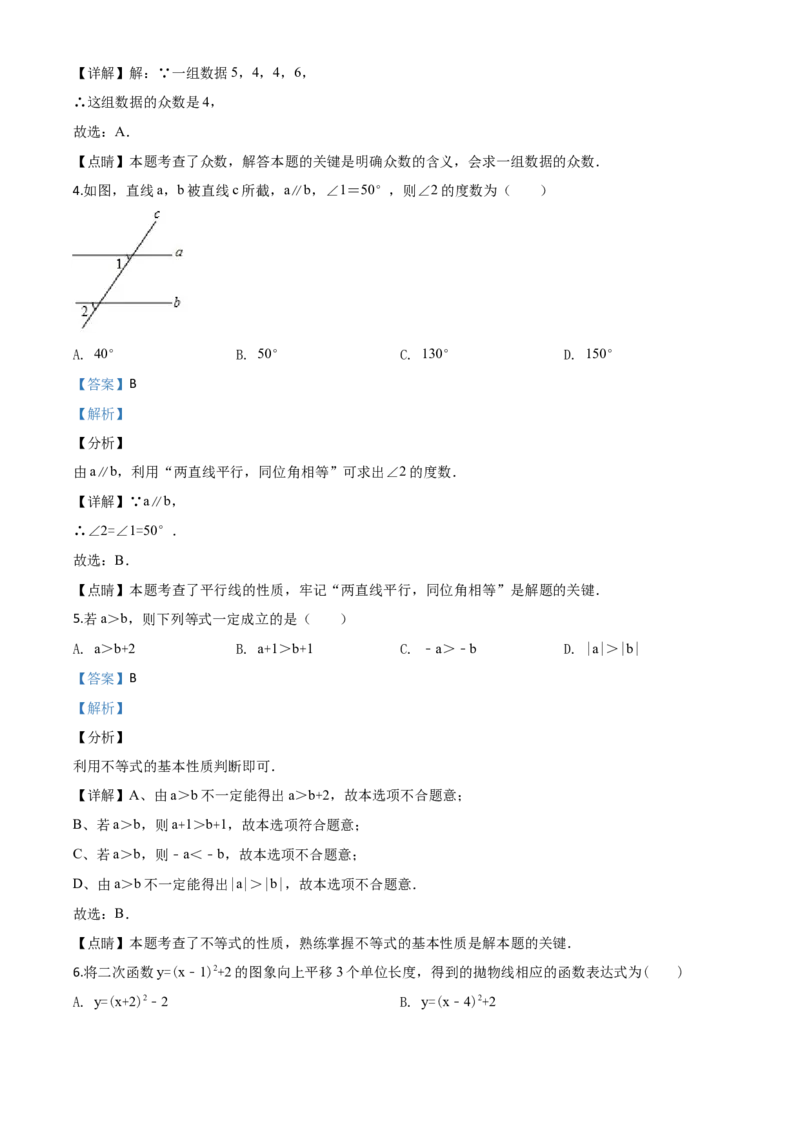
4.如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数为( )
A. 40° B. 50° C. 130° D. 150°
【答案】B
【解析】
【分析】
由a∥b,利用“两直线平行,同位角相等”可求出∠2的度数.
【详解】∵a∥b,
∴∠2=∠1=50°.
故选:B.
【点睛】本题考查了平行线的性质,牢记“两直线平行,同位角相等”是解题的关键.
5.若a>b,则下列等式一定成立的是( )
A. a>b+2 B. a+1>b+1 C. ﹣a>﹣b D. |a|>|b|
【答案】B
【解析】
【分析】
利用不等式的基本性质判断即可.
【详解】A、由a>b不一定能得出a>b+2,故本选项不合题意;
B、若a>b,则a+1>b+1,故本选项符合题意;
C、若a>b,则﹣a<﹣b,故本选项不合题意;
D、由a>b不一定能得出|a|>|b|,故本选项不合题意.
故选:B.
【点睛】本题考查了不等式的性质,熟练掌握不等式的基本性质是解本题的关键.
6.将二次函数y=(x﹣1)2+2的图象向上平移3个单位长度,得到的拋物线相应的函数表达式为( )
A. y=(x+2)2﹣2 B. y=(x﹣4)2+2C. y=(x﹣1)2﹣1 D. y=(x﹣1)2+5
【答案】D
【解析】
【分析】
根据“上加下减”的原则进行解答即可.
【详解】由“上加下减”的原则可知,将二次函数 的图象向上平移3个单位长度,
所得抛物线的解析式为: ,即 ;
故选:D.
【点睛】本题考查了二次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.
7.在△ABC中,AB=1,BC= ,下列选项中,可以作为AC长度的是( )
A. 2 B. 4 C. 5 D. 6
【答案】A
【解析】
【分析】
根据三角形三边关系,两边之差小于第三边,两边之和大于第三边,可以得到AC的长度可以取得的数值
的取值范围,从而可以解答本题.
【详解】∵在△ABC中,AB=1,BC= ,
∴ ﹣1<AC< +1,
∵ ﹣1<2< +1,4> +1,5> +1,6> +1,
∴AC的长度可以是2,
故选项A正确,选项B、C、D不正确;
故选:A.
【点睛】本题考查了三角形三边关系以及无理数的估算,解答本题的关键是明确题意,利用三角形三边关
系解答.
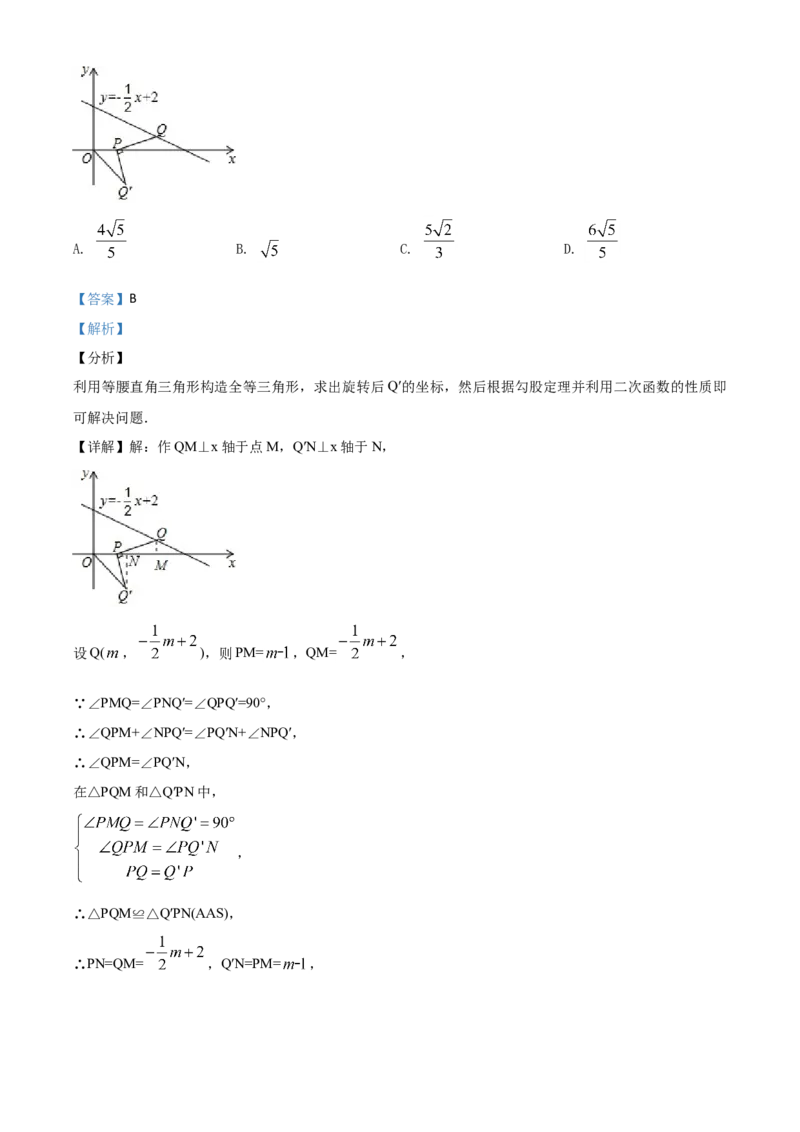
8.如图,在平面直角坐标系中,Q是直线y=﹣ x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得
到点 ,连接 ,则 的最小值为( )A. B. C. D.
【答案】B
【解析】
【分析】
利用等腰直角三角形构造全等三角形,求出旋转后Q′的坐标,然后根据勾股定理并利用二次函数的性质即
可解决问题.
【详解】解:作QM⊥x轴于点M,Q′N⊥x轴于N,
设Q( , ),则PM= ,QM= ,
∵∠PMQ=∠PNQ′=∠QPQ′=90°,
∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,
∴∠QPM=∠PQ′N,
在△PQM和△Q′PN中,
,
∴△PQM≌△Q′PN(AAS),
∴PN=QM= ,Q′N=PM= ,∴ON=1+PN= ,
∴Q′( , ),
∴OQ′2=( )2+( )2= m2﹣5m+10= (m﹣2)2+5,
当m=2时,OQ′2有最小值为5,
∴OQ′的最小值为 ,
故选:B.
【点睛】本题考查了一次函数图象上点的坐标特征,一次函数的性质,三角形全等的判定和性质,坐标与
图形的变换-旋转,二次函数的性质,勾股定理,表示出点的坐标是解题的关键.
二、填空题(本大题共10小题,每小题3分,共30分)
9.分解因式: _____.
【答案】
【解析】
【分析】
直接提取公因式分解因式得出即可.
【详解】解: .
故答案为: .
【点睛】本题主要考查了提取公因式法分解因式,正确得出公因式是解题关键.
10.若代数式 有意义,则实数x的取值范围是________.
【答案】x≠1
【解析】
【分析】
分式有意义时,分母x-1≠0,据此求得x的取值范围.
【详解】解:依题意得:x-1≠0,解得x≠1,
故答案为:x≠1.
【点睛】本题考查了分式有意义的条件.(1)分式有意义的条件是分母不等于零.(2)分式无意义的条
件是分母等于零.
11.2020年6月30日,北斗全球导航系统最后一颗组网卫星成功定点在距离地球36000千米的地球同步轨
道上,请将36000用科学记数法表示为_____.
【答案】3.6×104
【解析】
【分析】
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于36000
有5位,所以可以确定n=5-1=4.
【详解】解:36000=3.6×104.
故答案为:3.6×104.
【点睛】本题考查了科学记数法表示较大的数的方法,准确确定n值是关键.
12.不等式组 的解集是_____.
【答案】x>1
【解析】
【分析】
解不等式x+2>0得x>﹣2,结合x>1,利用口诀“同大取大”可得答案.
【详解】解:解不等式x+2>0,得:x>﹣2,
又x>1,
∴不等式组的解集为x>1,
故答案为:x>1.
【点睛】此题主要考查了解一元一次不等式组,能根据不等式的解集找出不等式组的解集是解此题的关键.
13.用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为_____.
【答案】1
【解析】
【分析】
设这个圆锥的底面圆半径为r,利用弧长公式得到并解关于r的方程即可.
【详解】设这个圆锥的底面圆半径为r,根据题意得2πr= ,
解得r=1,
所以这个圆锥的底面圆半径为1.
故答案为1.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇
形的半径等于圆锥的母线长.
14.已知一次函数y=2x﹣1的图象经过A(x,1),B(x,3)两点,则x_____x(填“>”“<”或
1 2 1 2
“=”).
【答案】<
【解析】
【分析】
由k=2>0,可得出y随x的增大而增大,结合1<3,即可得出x<x.
1 2
【详解】解:∵k=2>0,
∴y随x的增大而增大.
又∵1<3,
∴x<x.
1 2
故答案为:<.
【点睛】本题考查了一次函数的性质以及一次函数图象上点的坐标特征,解题的关键是牢记“当k>0时,
y随x的增大而增大;当k<0时,y随x的增大而减小”.
15.如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,
AD=8,则DE的长为_____.
【答案】5
【解析】
【分析】
利用勾股定理求出AB,再利用直角三角形斜边中线的性质求解即可.
【详解】解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD=6,∴∠ADB=90°,
∴AB= ,
∵E为AB的中点,
∴DE= AB=5,
故答案为:5.
【点睛】本题考查了等腰三角形的性质,勾股定理,直角三角形斜边中线的性质等知识,解题的关键是熟
练掌握基本知识.
16.已知a+b=3,a2+b2=5,则ab的值是
【答案】2
【解析】
【分析】
根据完全平方公式可得 ,再整体代入求解即可.
【详解】解:当 , 时,
, ,解得 .
故答案为:2.
【点睛】本题考查了完全平方公式,解题的关键熟练掌握完全平方公式: .
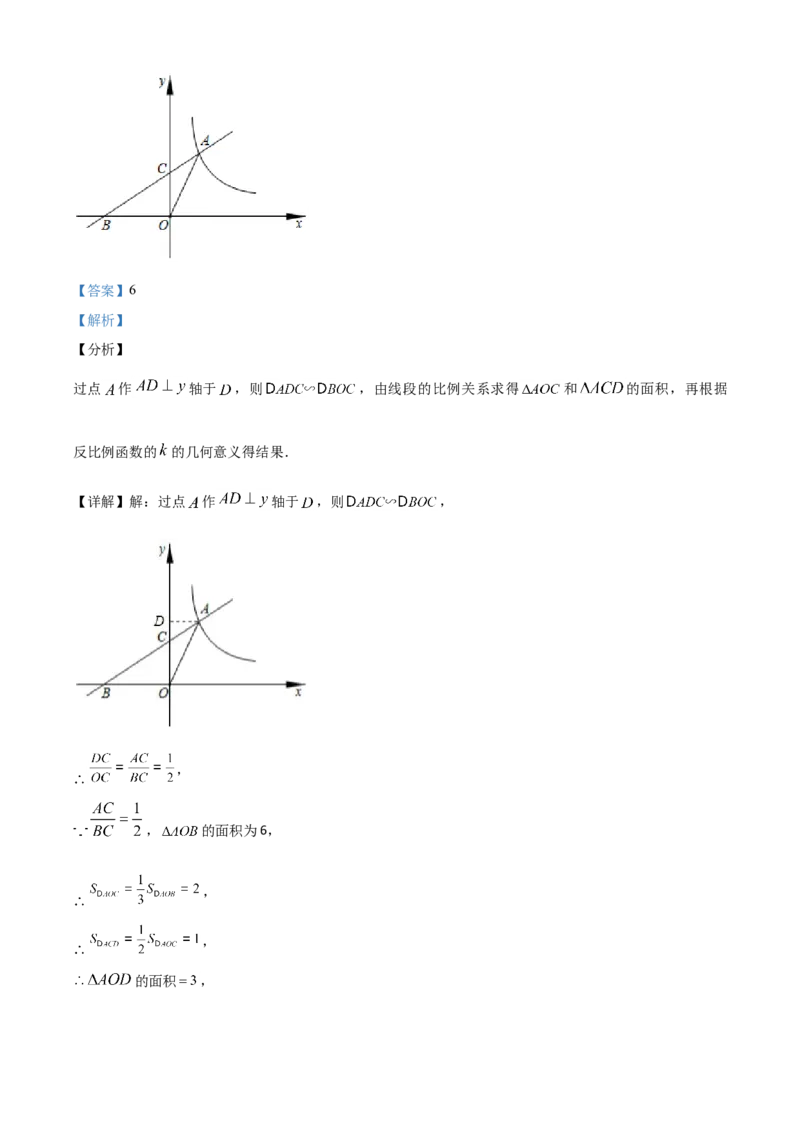
17.如图,点A在反比例函数y= (x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若
= , AOB的面积为6,则k的值为_____.
△【答案】6
【解析】
【分析】
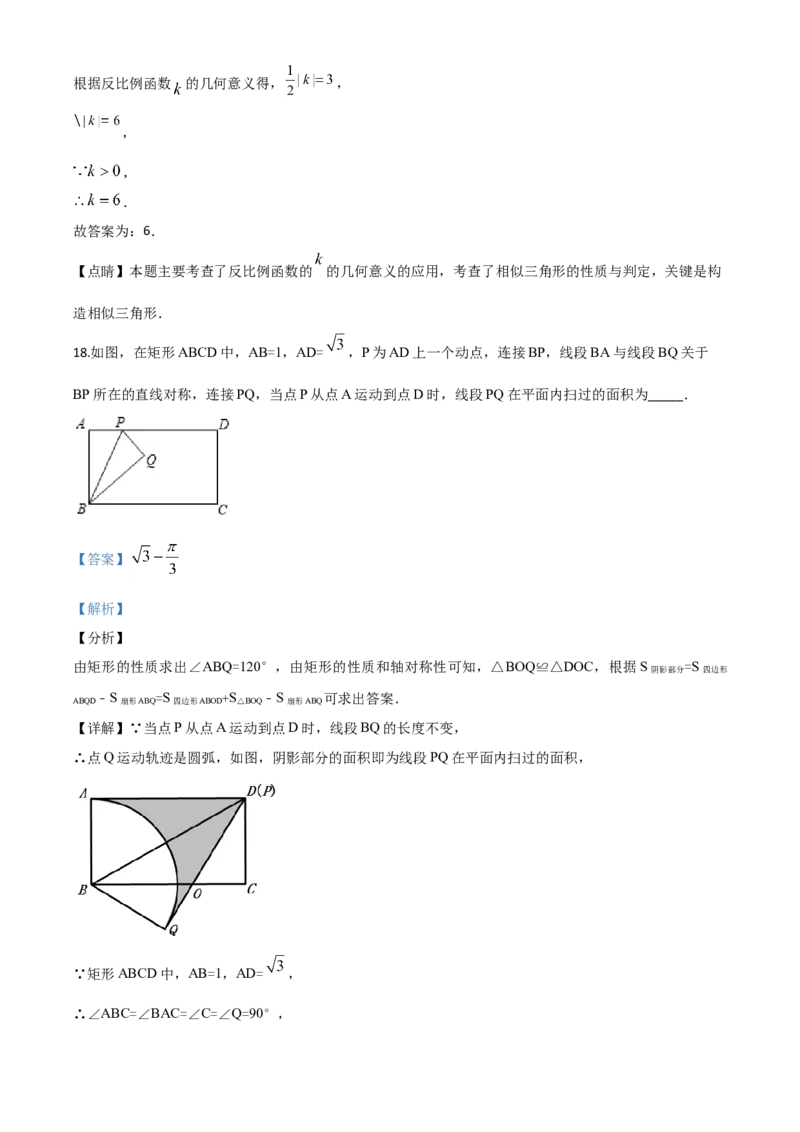
过点 作 轴于 ,则 ,由线段的比例关系求得 和 的面积,再根据
反比例函数的 的几何意义得结果.
【详解】解:过点 作 轴于 ,则 ,
,
, 的面积为6,
,
,
的面积 ,根据反比例函数 的几何意义得, ,
,
,
.
故答案为:6.
【点睛】本题主要考查了反比例函数的 的几何意义的应用,考查了相似三角形的性质与判定,关键是构
造相似三角形.
18.如图,在矩形ABCD中,AB=1,AD= ,P为AD上一个动点,连接BP,线段BA与线段BQ关于
BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为_____.
【答案】
【解析】
【分析】
由矩形的性质求出∠ABQ=120°,由矩形的性质和轴对称性可知,△BOQ≌△DOC,根据S =S
阴影部分 四边形
﹣S =S +S ﹣S 可求出答案.
ABQD 扇形ABQ 四边形ABOD △BOQ 扇形ABQ
【详解】∵当点P从点A运动到点D时,线段BQ的长度不变,
∴点Q运动轨迹是圆弧,如图,阴影部分的面积即为线段PQ在平面内扫过的面积,
∵矩形ABCD中,AB=1,AD= ,
∴∠ABC=∠BAC=∠C=∠Q=90°,∴∠ADB=∠DBC=∠ODB=∠OBQ=30°,
∴∠ABQ=120°,
由轴对称性得:BQ=BA=CD,
在△BOQ和△DOC中,
,
∴△BOQ≌△DOC,
∴S =S ﹣S =S +S ﹣S ,
阴影部分 四边形ABQD 扇形ABQ 四边形ABOD △BOQ 扇形ABQ
=S +S ﹣S ,
四边形ABOD △COD 扇形ABQ
=S ﹣S =1× - .
矩形ABCD △ABQ
故答案为: .
【点睛】本题考查了矩形的性质,扇形的面积公式,轴对称的性质,熟练掌握矩形的性质是解题的关键.
三、解答题(本大题共10小题,共96分.解答时应写出必要的计算过程、推演步骤或文字
说明)
19.计算:(﹣2)0+( )﹣1﹣ .
【答案】1
【解析】
【分析】
根据负整数指数幂、零次幂以及二次根式的化简方法进行计算即可.
【详解】解:(﹣2)0+( )﹣1- ,
=1+3﹣3,
=1.
【点睛】本题考查了负整数指数幂、零次幂以及二次根式的化简,掌握运算的性质和计算的方法是得出正
确答案的前提.20.先化简,再求值: ÷(x﹣ ),其中x= ﹣2.
【答案】 ;
【解析】
【分析】
先根据分式的混合运算顺序和运算法则化简原式,再将x的值代入计算可得.
【详解】解:原式= ÷( ﹣ )
= ÷
= ·
= ,
当x= ﹣2时,
原式= = = .
【点睛】本题考查了分式的化简求值,二次根式的除法,根据分式的运算法则把所给代数式正确化简是解
答本题的关键.
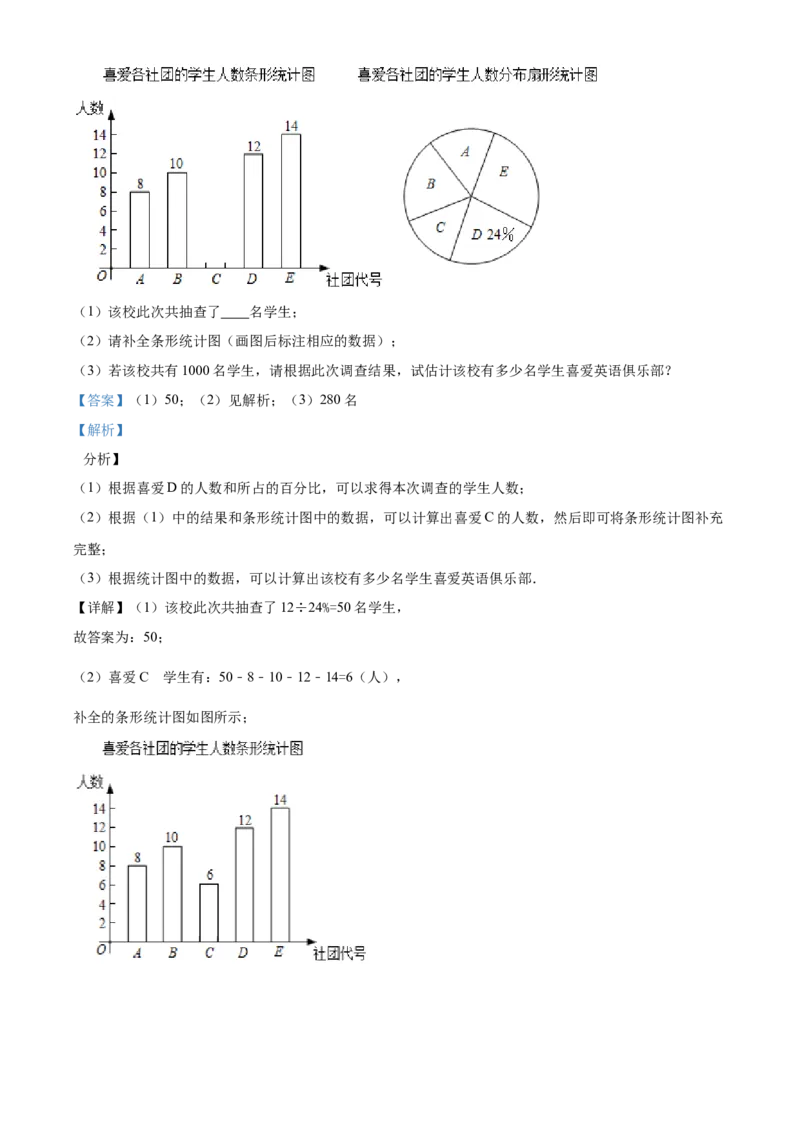
21.某校计划成立下列学生社团.
生物实验小
社团名称 文学社 动漫创作社 合唱团 英语俱乐部
组
社团代号 A B C D E
为了解该校学生对上述社团的喜爱情况,学校从全体学生中随机抽取部分学生进行问卷调查(每名学生必
需选一个且只能选一个学生社团).根据统计数据,绘制了如图条形统计图和扇形统计图(部分信息未给
出).(1)该校此次共抽查了 名学生;
(2)请补全条形统计图(画图后标注相应的数据);
(3)若该校共有1000名学生,请根据此次调查结果,试估计该校有多少名学生喜爱英语俱乐部?
【答案】(1)50;(2)见解析;(3)280名
【解析】
【分析】
(1)根据喜爱D的人数和所占的百分比,可以求得本次调查的学生人数;
(2)根据(1)中的结果和条形统计图中的数据,可以计算出喜爱C的人数,然后即可将条形统计图补充
完整;
(3)根据统计图中的数据,可以计算出该校有多少名学生喜爱英语俱乐部.
【详解】(1)该校此次共抽查了12÷24%=50名学生,
故答案为:50;
的
(2)喜爱C 学生有:50﹣8﹣10﹣12﹣14=6(人),
补全的条形统计图如图所示;(3)1000× =280(名),
答:该校有280名学生喜爱英语俱乐部.
【点睛】本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,读懂统计图,从不同的统计图
中得到必要的信息,利用数形结合的思想解答.
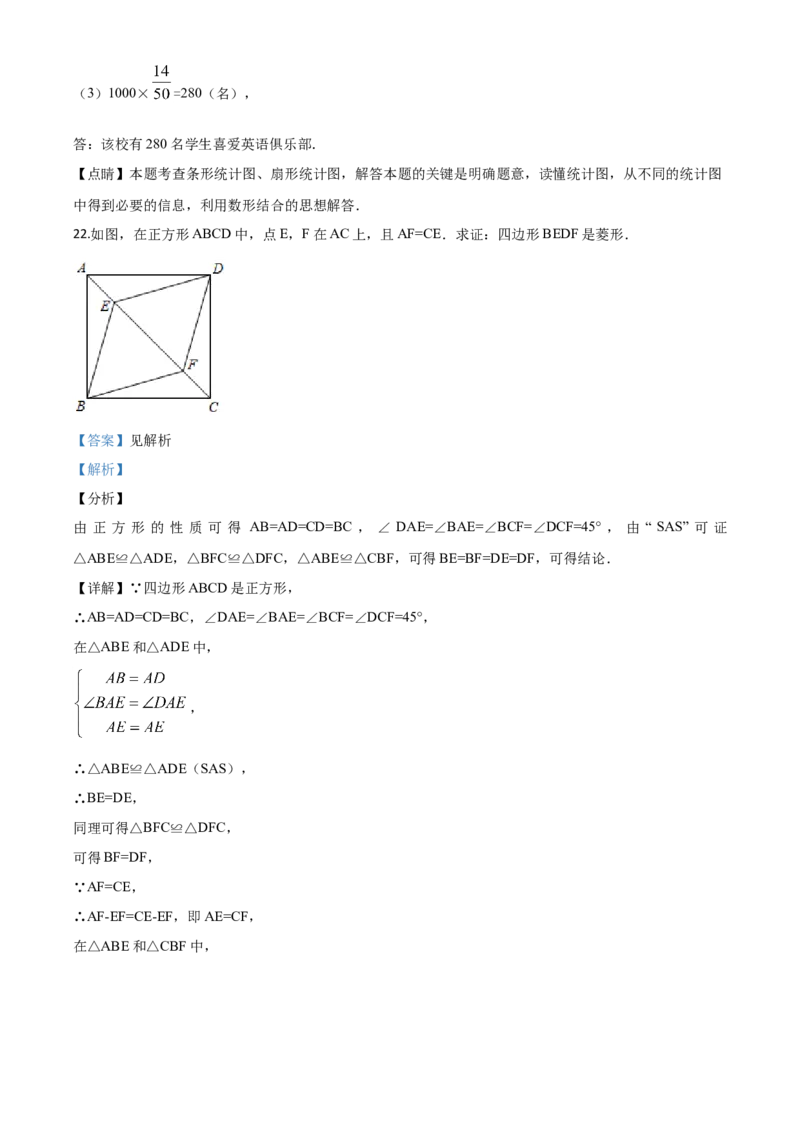
22.如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.
【答案】见解析
【解析】
【分析】
由 正 方 形 的 性 质 可 得 AB=AD=CD=BC , ∠ DAE=∠BAE=∠BCF=∠DCF=45° , 由 “ SAS” 可 证
△ABE≌△ADE,△BFC≌△DFC,△ABE≌△CBF,可得BE=BF=DE=DF,可得结论.
【详解】∵四边形ABCD是正方形,
∴AB=AD=CD=BC,∠DAE=∠BAE=∠BCF=∠DCF=45°,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE,
同理可得△BFC≌△DFC,
可得BF=DF,
∵AF=CE,
∴AF-EF=CE-EF,即AE=CF,
在△ABE和△CBF中,,
∴△ABE≌△CBF(SAS),
∴BE=BF,
∴BE=BF=DE=DF,
∴四边形BEDF是菱形.
【点睛】本题考查了正方形的性质,菱形的判定,全等三角形的判定和性质,掌握正方形的性质是本题的
关键.
23.将4张印有“梅”“兰”“竹”“菊”字样的卡片(卡片的形状、大小、质地都相同)放在一个不透明
的盒子中,将卡片搅匀.
(1)从盒子中任意取出1张卡片,恰好取出印有“兰”字的卡片的概率为 .
(2)先从盒子中任意取出1张卡片,记录后放回并搅匀,再从中任意取出1张卡片,求取出的两张卡片中,
至少有1张印有“兰”字的概率(请用画树状图或列表等方法求解).
【答案】(1) ;(2)
【解析】
【分析】
(1)直接利用概率公式求解可得;
的
(2)画树状图列出所有等可能结果,从中找到符合条件 结果数,再利用概率公式求解可得.
【详解】(1)从盒子中任意取出1张卡片,恰好取出印有“兰”字的卡片的概率为 ,
故答案为: ;
(2)画树状图如下:由树状图知,共有16种等可能结果,其中至少有1张印有“兰”字的有7种结果,
∴至少有1张印有“兰”字的概率为 .
【点睛】本题考查了用列表法或树状图法求随机事件的概率,解题时需要注意是放回试验还是不放回试验.
用到的知识点为:概率=所求情况数与总情况数之比.
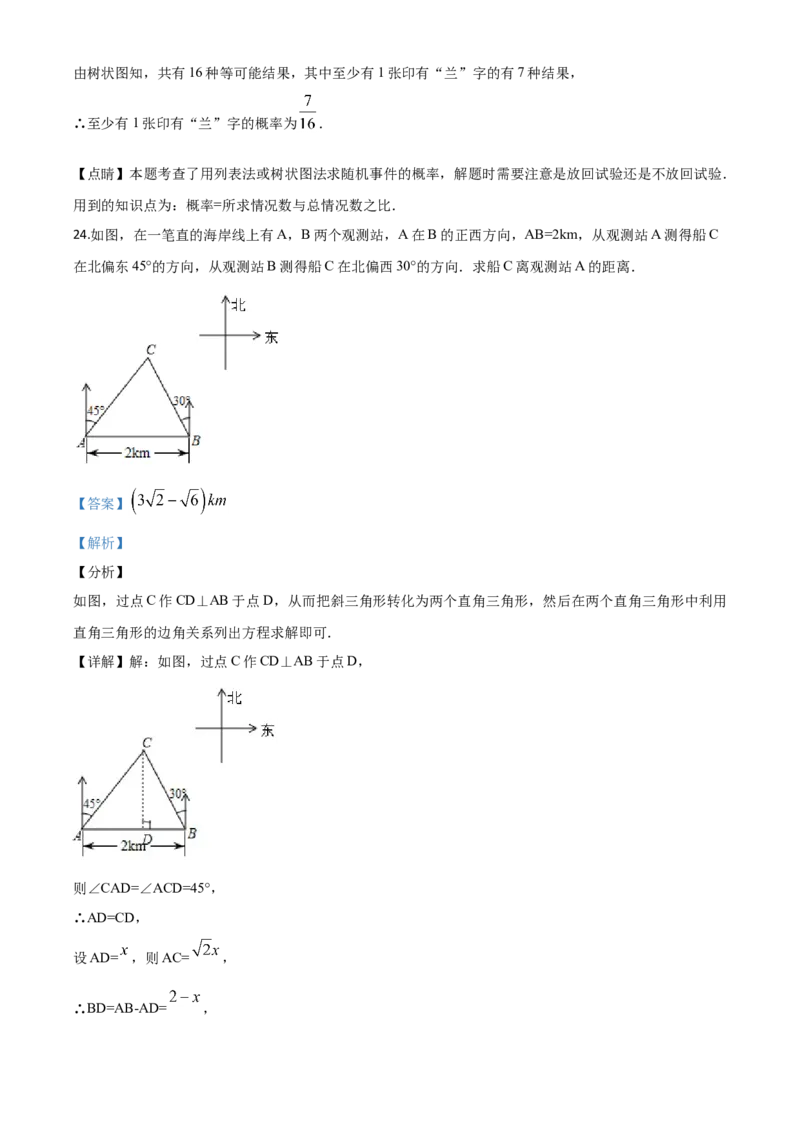
24.如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从观测站A测得船C
在北偏东45°的方向,从观测站B测得船C在北偏西30°的方向.求船C离观测站A的距离.
【答案】
【解析】
【分析】
如图,过点C作CD⊥AB于点D,从而把斜三角形转化为两个直角三角形,然后在两个直角三角形中利用
直角三角形的边角关系列出方程求解即可.
【详解】解:如图,过点C作CD⊥AB于点D,
则∠CAD=∠ACD=45°,
∴AD=CD,
设AD= ,则AC= ,
∴BD=AB-AD= ,∵∠CBD=60°,
在Rt△BCD中,
∵tan∠CBD= ,
∴ ,
解得 ,
经检验, 是原方程的根,
∴AC= = ( )=( - )km.
答:船C离观测站A的距离为( - )km.
【点睛】本题考查了解直角三角形的应用-方向角问题,解决本题的关键是掌握方向角定义.
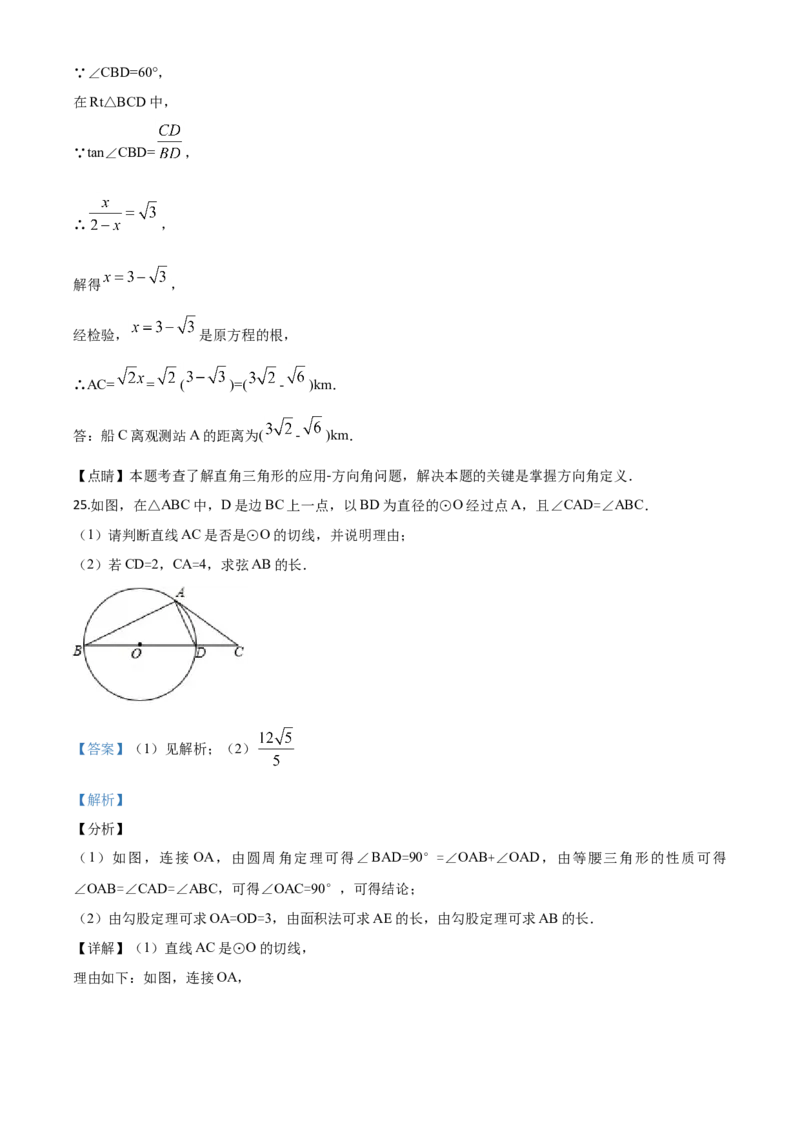
25.如图,在△ABC中,D是边BC上一点,以BD为直径的⊙O经过点A,且∠CAD=∠ABC.
(1)请判断直线AC是否是⊙O的切线,并说明理由;
(2)若CD=2,CA=4,求弦AB的长.
【答案】(1)见解析;(2)
【解析】
【分析】
(1)如图,连接 OA,由圆周角定理可得∠BAD=90°=∠OAB+∠OAD,由等腰三角形的性质可得
∠OAB=∠CAD=∠ABC,可得∠OAC=90°,可得结论;
(2)由勾股定理可求OA=OD=3,由面积法可求AE的长,由勾股定理可求AB的长.
【详解】(1)直线AC是⊙O的切线,
理由如下:如图,连接OA,∵BD为⊙O的直径,
∴∠BAD=90°=∠OAB+∠OAD,
∵OA=OB,
∴∠OAB=∠ABC,
又∵∠CAD=∠ABC,
∴∠OAB=∠CAD=∠ABC,
∴∠OAD+∠CAD=90°=∠OAC,
∴AC⊥OA,
又∵OA是半径,
∴直线AC是⊙O的切线;
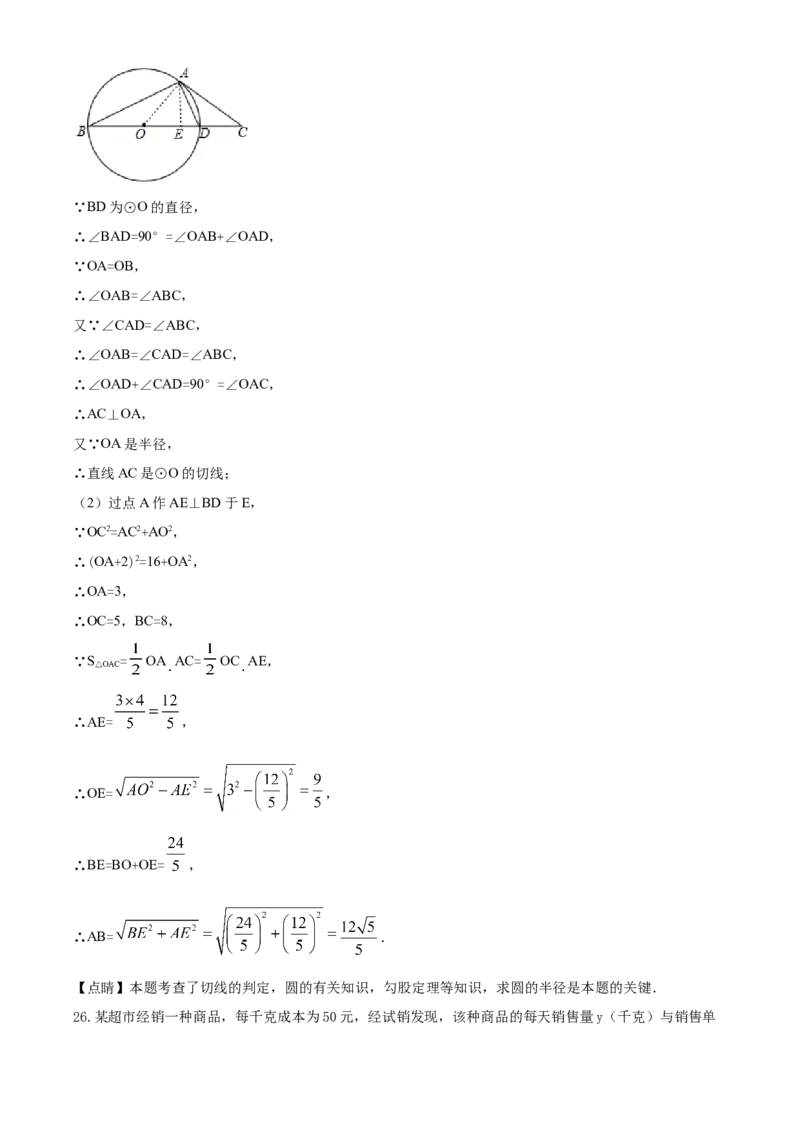
(2)过点A作AE⊥BD于E,
∵OC2=AC2+AO2,
∴(OA+2)2=16+OA2,
∴OA=3,
∴OC=5,BC=8,
∵S = OA AC= OC AE,
△OAC
∴AE= ,
∴OE= ,
∴BE=BO+OE= ,
∴AB= .
【点睛】本题考查了切线的判定,圆的有关知识,勾股定理等知识,求圆的半径是本题的关键.
26.某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
销售单价x(元/千
55 60 65 70
克)
销售量y(千克) 70 60 50 40
(1)求y(千克)与x(元/千克)之间的函数表达式;
(2)为保证某天获得600元的销售利润,则该天的销售单价应定为多少?
(3)当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
【答案】(1) ;(2)60元/千克或80元/千克;(3)70元/千克;800元
【解析】
【分析】
(1)利用待定系数法来求一次函数的解析式即可;
(2)依题意可列出关于销售单价x的方程,然后解一元二次方程组即可;
(3)利用每件的利润乘以销售量可得总利润,然后根据二次函数的性质来进行计算即可.
【详解】解:(1)设y与x之间的函数表达式为 ( ),将表中数据(55,70)、(60,
60)代入得:
,
解得: ,
∴y与x之间的函数表达式为 ;
(2)由题意得: ,
整理得 ,
解得 ,
答:为保证某天获得600元的销售利润,则该天的销售单价应定为60元/千克或80元/千克;
(3)设当天的销售利润为w元,则:,
∵﹣2<0,
∴当 时,w =800.
最大值
答:当销售单价定为70元/千克时,才能使当天的销售利润最大,最大利润是800元.
【点睛】本题考查了待定系数法求一次函数的解析式、一元二次方程和二次函数在实际问题中的应用,理
清题中的数量关系是解题的关键.
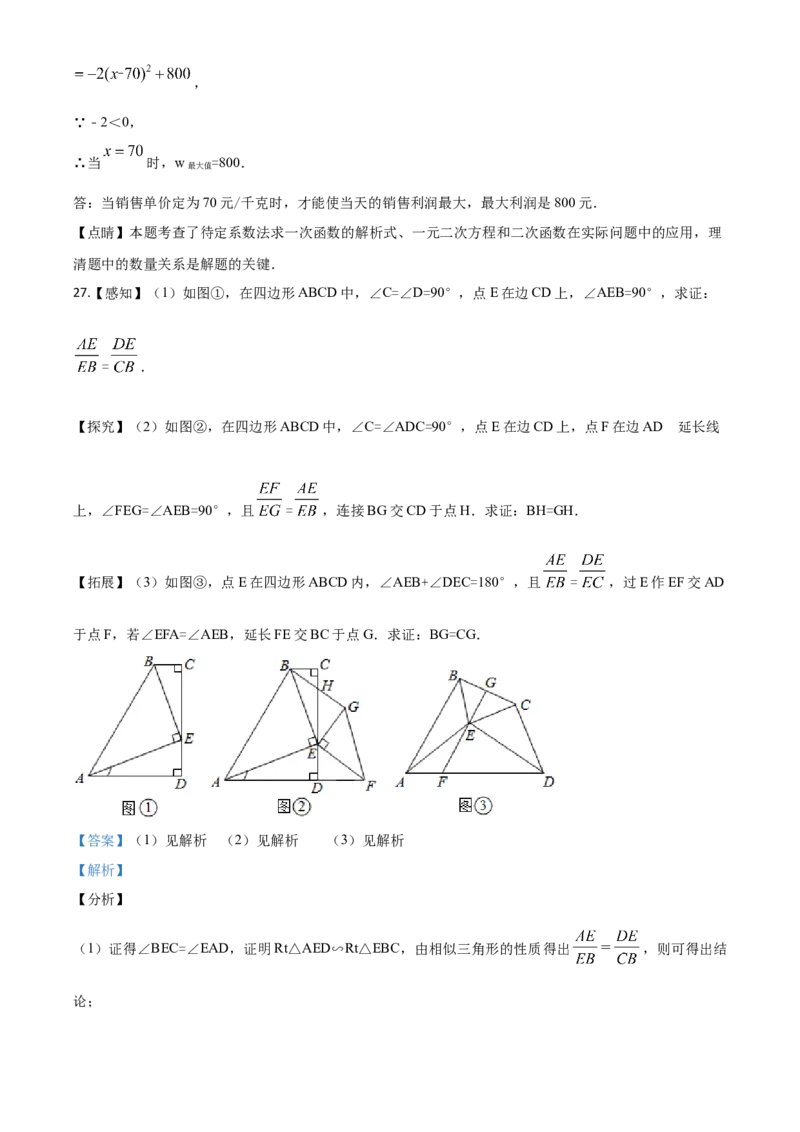
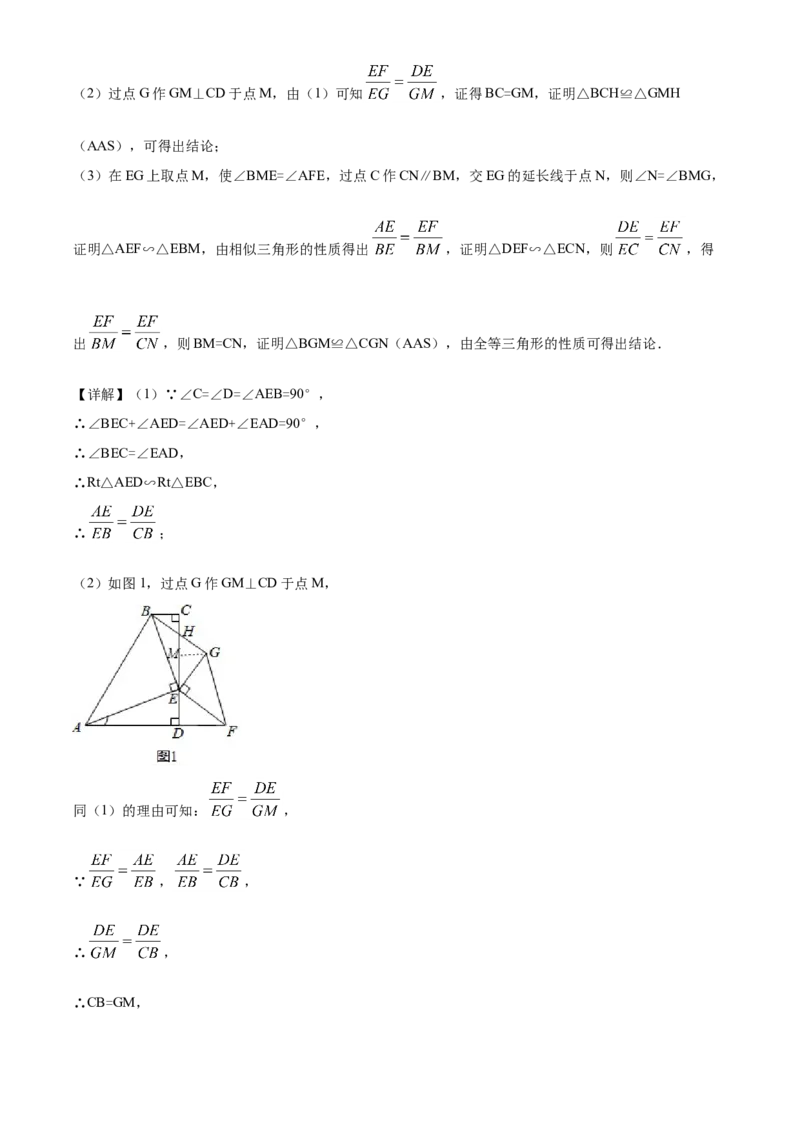
27.【感知】(1)如图①,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,∠AEB=90°,求证:
= .
的
【探究】(2)如图②,在四边形ABCD中,∠C=∠ADC=90°,点E在边CD上,点F在边AD 延长线
上,∠FEG=∠AEB=90°,且 = ,连接BG交CD于点H.求证:BH=GH.
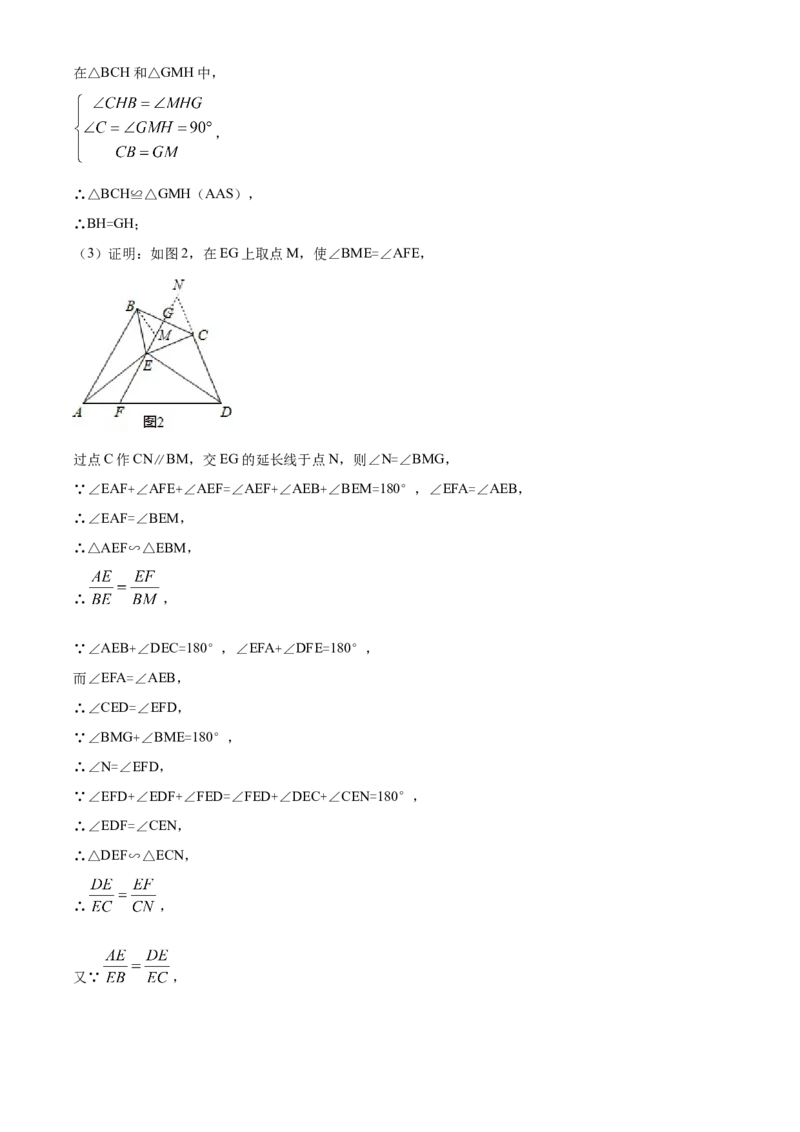
【拓展】(3)如图③,点E在四边形ABCD内,∠AEB+∠DEC=180°,且 = ,过E作EF交AD
于点F,若∠EFA=∠AEB,延长FE交BC于点G.求证:BG=CG.
【答案】(1)见解析 (2)见解析 (3)见解析
【解析】
【分析】
(1)证得∠BEC=∠EAD,证明Rt△AED∽Rt△EBC,由相似三角形的性质得出 ,则可得出结
论;(2)过点G作GM⊥CD于点M,由(1)可知 ,证得BC=GM,证明△BCH≌△GMH
(AAS),可得出结论;
(3)在EG上取点M,使∠BME=∠AFE,过点C作CN∥BM,交EG的延长线于点N,则∠N=∠BMG,
证明△AEF∽△EBM,由相似三角形的性质得出 ,证明△DEF∽△ECN,则 ,得
出 ,则BM=CN,证明△BGM≌△CGN(AAS),由全等三角形的性质可得出结论.
【详解】(1)∵∠C=∠D=∠AEB=90°,
∴∠BEC+∠AED=∠AED+∠EAD=90°,
∴∠BEC=∠EAD,
∴Rt△AED∽Rt△EBC,
∴ ;
(2)如图1,过点G作GM⊥CD于点M,
同(1)的理由可知: ,
∵ , ,
∴ ,
∴CB=GM,在△BCH和△GMH中,
,
∴△BCH≌△GMH(AAS),
∴BH=GH;
(3)证明:如图2,在EG上取点M,使∠BME=∠AFE,
过点C作CN∥BM,交EG的延长线于点N,则∠N=∠BMG,
∵∠EAF+∠AFE+∠AEF=∠AEF+∠AEB+∠BEM=180°,∠EFA=∠AEB,
∴∠EAF=∠BEM,
∴△AEF∽△EBM,
∴ ,
∵∠AEB+∠DEC=180°,∠EFA+∠DFE=180°,
而∠EFA=∠AEB,
∴∠CED=∠EFD,
∵∠BMG+∠BME=180°,
∴∠N=∠EFD,
∵∠EFD+∠EDF+∠FED=∠FED+∠DEC+∠CEN=180°,
∴∠EDF=∠CEN,
∴△DEF∽△ECN,
∴ ,
又∵ ,∴ ,
∴BM=CN,
在△BGM和△CGN中,
,
∴△BGM≌△CGN(AAS),
∴BG=CG.
【点睛】本题考查了直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,平行线的
性质等知识,熟练掌握相似三角形的判定与性质是解题的关键.
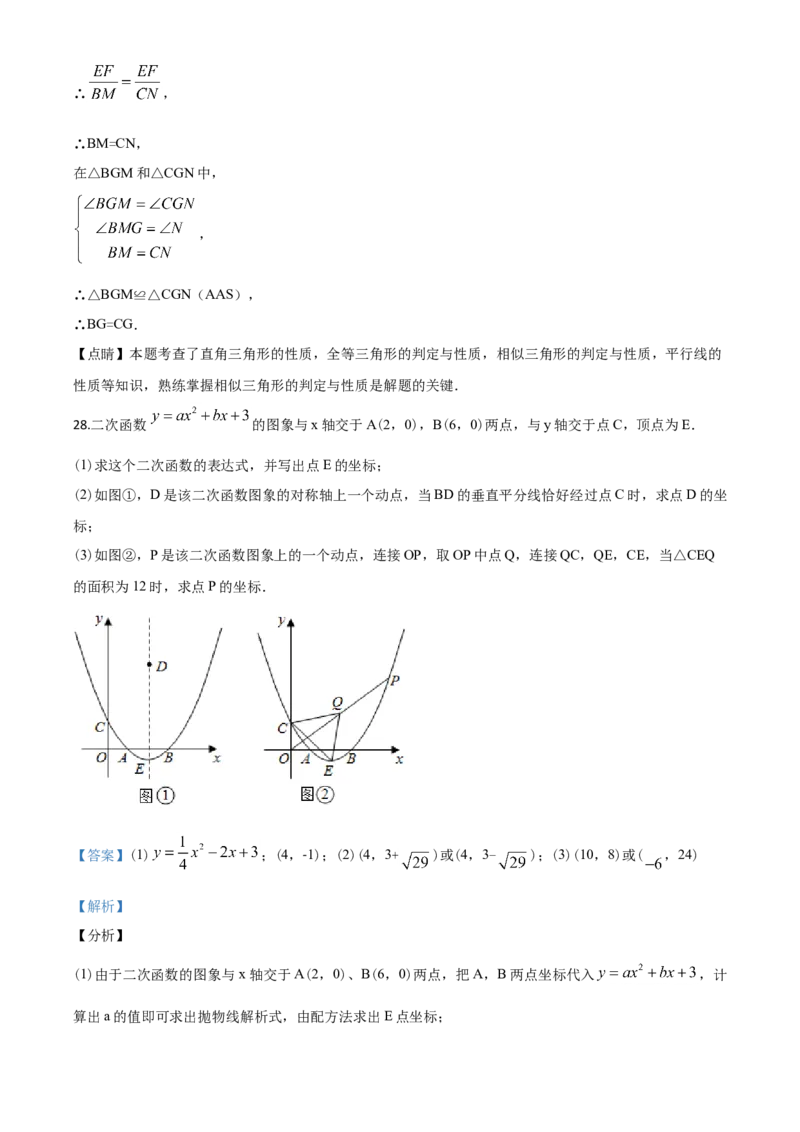
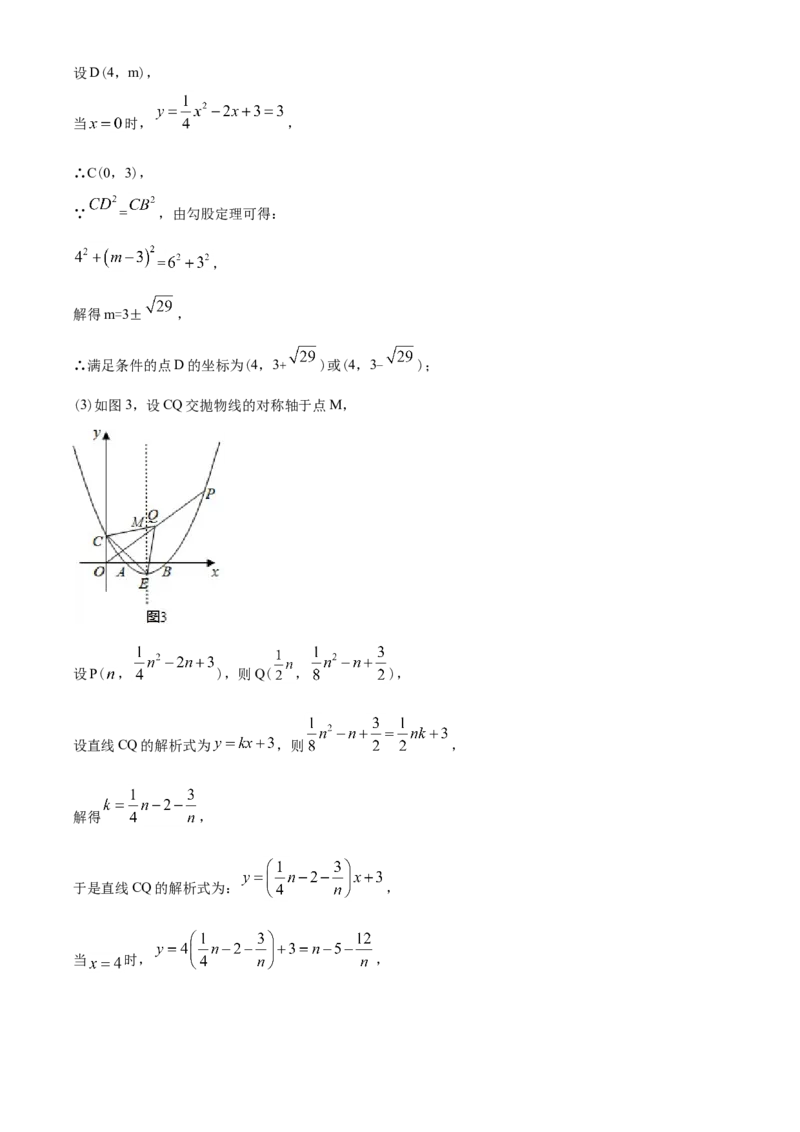
28.二次函数 的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C,顶点为E.
(1)求这个二次函数的表达式,并写出点E的坐标;
(2)如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐
标;
(3)如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ
的面积为12时,求点P的坐标.
【答案】(1) ;(4,-1);(2)(4,3+ )或(4,3- );(3)(10,8)或( ,24)
【解析】
【分析】
(1)由于二次函数的图象与x轴交于A(2,0)、B(6,0)两点,把A,B两点坐标代入 ,计
算出a的值即可求出抛物线解析式,由配方法求出E点坐标;(2)由线段垂直平分线的性质可得出CB=CD,设D(4,m),由勾股定理可得 = ,解方
程可得出答案;
(3)设CQ交抛物线的对称轴于点M,设P( , ),则Q( , ),设直线CQ
的解析式为 ,则 ,解得 ,求出M( , ),
ME= ,由面积公式可求出n的值,则可得出答案.
【详解】(1)将A(2,0),B(6,0)代入 ,
得 ,
解得 ,
∴二次函数的解析式为 ;
∵ ,
∴E(4, );
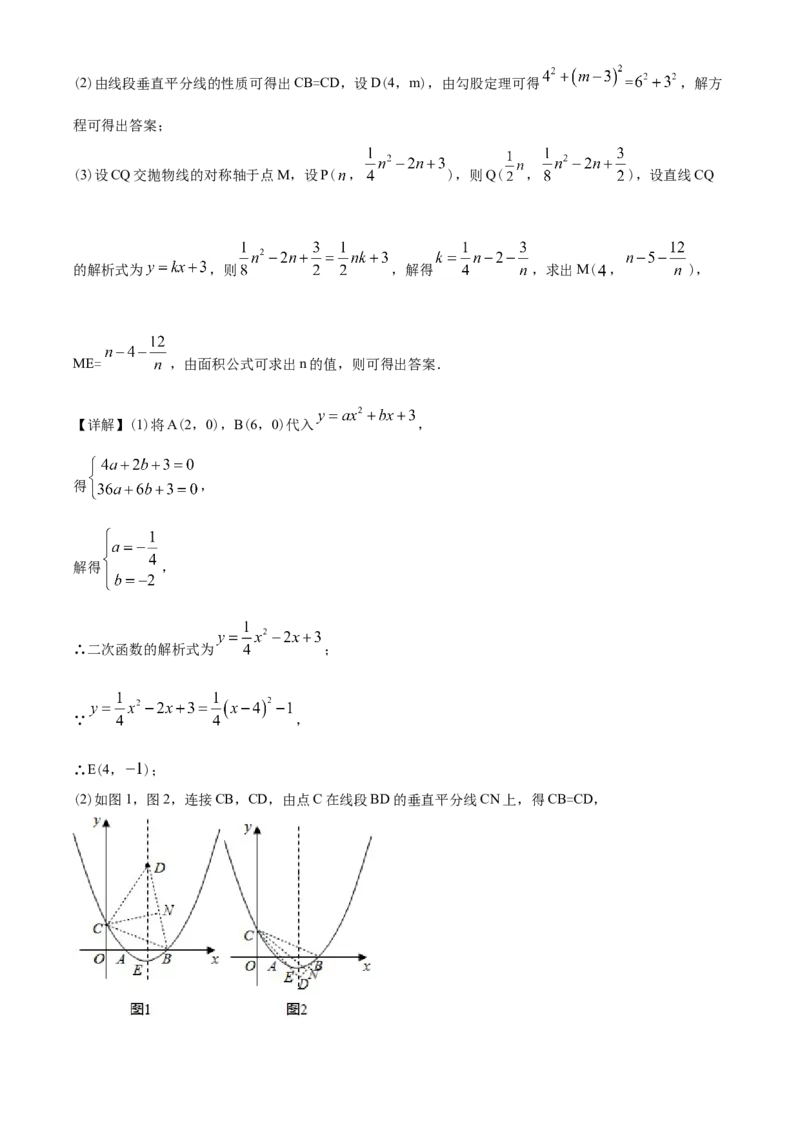
(2)如图1,图2,连接CB,CD,由点C在线段BD的垂直平分线CN上,得CB=CD,设D(4,m),
当 时, ,
∴C(0,3),
∵ = ,由勾股定理可得:
= ,
解得m=3± ,
∴满足条件的点D的坐标为(4,3+ )或(4,3- );
(3)如图3,设CQ交抛物线的对称轴于点M,
设P( , ),则Q( , ),
设直线CQ的解析式为 ,则 ,
解得 ,
于是直线CQ的解析式为: ,
当 时, ,∴M( , ),ME= = ,
∵S =S +S = ,
△CQE △CEM △QEM
∴ ,
解得 或 ,
当 时,P(10,8),
当 时,P( ,24).
综合以上可得,满足条件的点P的坐标为(10,8)或( ,24).
【点睛】本题是二次函数综合题,考查了待定系数法,二次函数图象与性质,垂直平分线的性质,勾股定
理,三角形的面积;熟练掌握二次函数的性质及方程思想是解题的关键.本试卷的题干、答案和解析均由组卷网(http://zujuan.xkw.com)专业教师团队编校出品。
登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。
试卷地址:在组卷网浏览本卷
组卷网是学科网旗下的在线题库平台,覆盖小初高全学段全学科、超过900万精品解析试题。
关注组卷网服务号,可使用移动教学助手功能(布置作业、线上考试、加入错题本、错题训练)。
学科网长期征集全国最新统考试卷、名校试卷、原创题,赢取丰厚稿酬,欢迎合作。
钱老师 QQ:537008204 曹老师 QQ:713000635