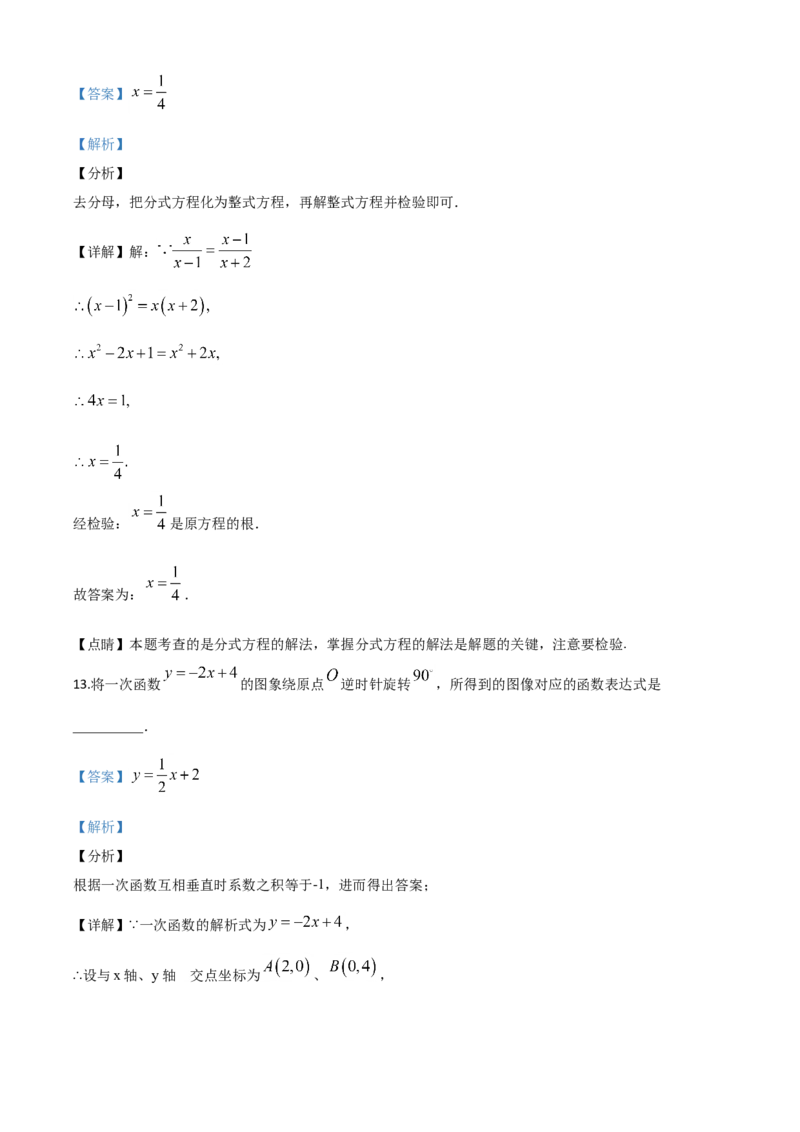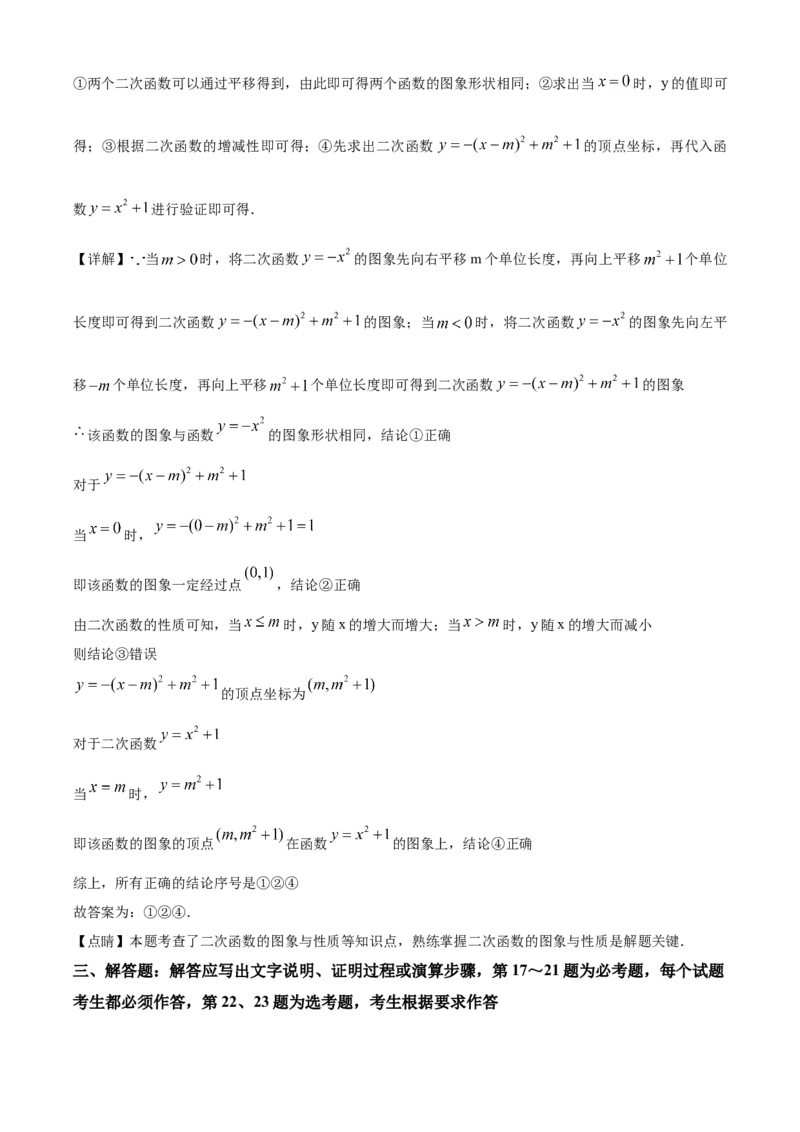文档内容
南京市 2020 年初中学业水平考试数学
第Ⅰ卷
一、选择题:本大题共12个小题,在每小题给出的四个选项中,只有一项是符合题目要求的
1.计算 的结果是( )
A. B. C. D. 5
【答案】D
【解析】
【分析】
利用有理数的减法法则转化为加法,再计算即可.
【详解】解:
故选D.
【点睛】本题考查的是有理数的减法,掌握有理数的减法法则是解题的关键.
2.3的平方根是( )
A. 9 B. C. D.
【答案】D
【解析】
【分析】
直接根据平方根的概念即可求解.
【详解】∵
∴3的平方根是 .
故选:D.
【点睛】本题主要考查了平方根的概念,解决本题的关键是熟记平方根的定义.
3.计算 的结果是( )
A. B. C. D.
【答案】B
【解析】【分析】
先计算幂的乘方,再计算同底数幂的除法,从而可得答案.
【详解】解:
故选B.
【点睛】本题考查的是幂的乘方,同底数幂的除法,掌握以上运算的运算法则是解题的关键.
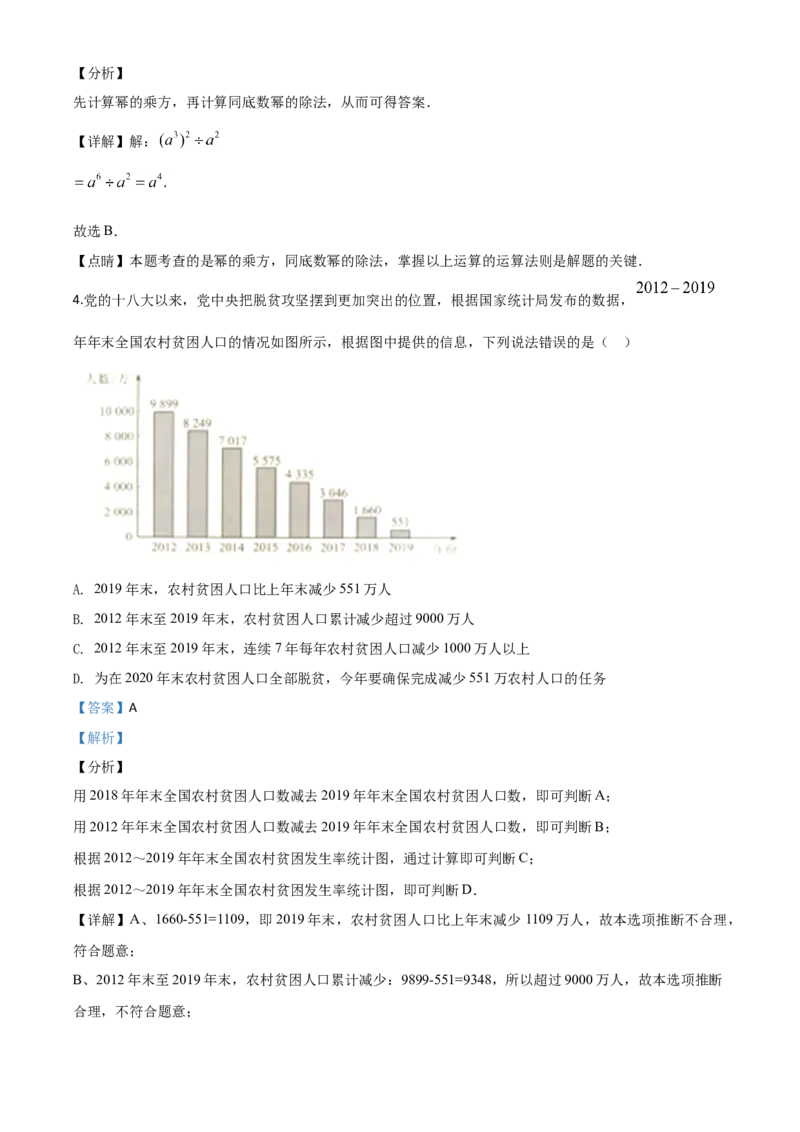
4.党的十八大以来,党中央把脱贫攻坚摆到更加突出的位置,根据国家统计局发布的数据,
年年末全国农村贫困人口的情况如图所示,根据图中提供的信息,下列说法错误的是( )
A. 2019年末,农村贫困人口比上年末减少551万人
B. 2012年末至2019年末,农村贫困人口累计减少超过9000万人
C. 2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上
D. 为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村人口的任务
【答案】A
【解析】
【分析】
用2018年年末全国农村贫困人口数减去2019年年末全国农村贫困人口数,即可判断A;
用2012年年末全国农村贫困人口数减去2019年年末全国农村贫困人口数,即可判断B;
根据2012~2019年年末全国农村贫困发生率统计图,通过计算即可判断C;
根据2012~2019年年末全国农村贫困发生率统计图,即可判断D.
【详解】A、1660-551=1109,即2019年末,农村贫困人口比上年末减少1109万人,故本选项推断不合理,
符合题意;
B、2012年末至2019年末,农村贫困人口累计减少:9899-551=9348,所以超过9000万人,故本选项推断
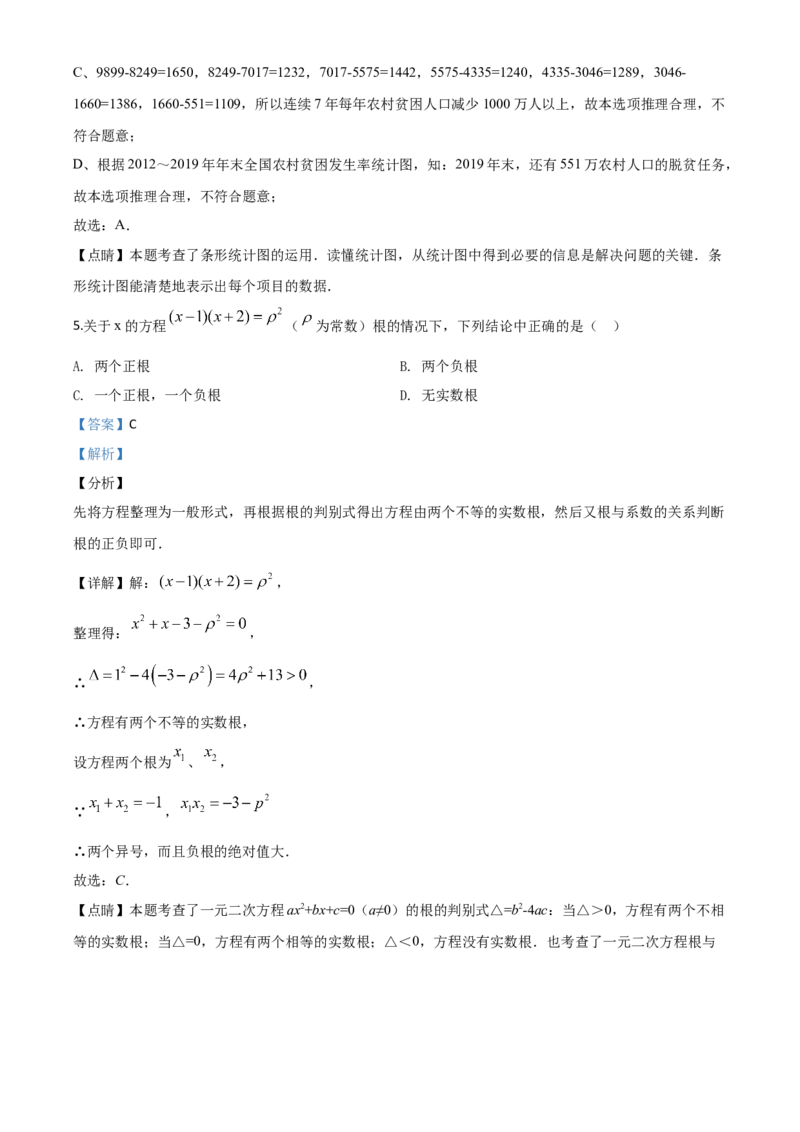
合理,不符合题意;C、9899-8249=1650,8249-7017=1232,7017-5575=1442,5575-4335=1240,4335-3046=1289,3046-
1660=1386,1660-551=1109,所以连续7年每年农村贫困人口减少1000万人以上,故本选项推理合理,不
符合题意;
D、根据2012~2019年年末全国农村贫困发生率统计图,知:2019年末,还有551万农村人口的脱贫任务,
故本选项推理合理,不符合题意;
故选:A.
【点睛】本题考查了条形统计图的运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条
形统计图能清楚地表示出每个项目的数据.
5.关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )
A. 两个正根 B. 两个负根
C. 一个正根,一个负根 D. 无实数根
【答案】C
【解析】
【分析】
先将方程整理为一般形式,再根据根的判别式得出方程由两个不等的实数根,然后又根与系数的关系判断
根的正负即可.
【详解】解: ,
整理得: ,
∴ ,
∴方程有两个不等的实数根,
设方程两个根为 、 ,
∵ ,
∴两个异号,而且负根的绝对值大.
故选:C.
【点睛】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相
等的实数根;当△=0,方程有两个相等的实数根;△<0,方程没有实数根.也考查了一元二次方程根与系数的关系: ,
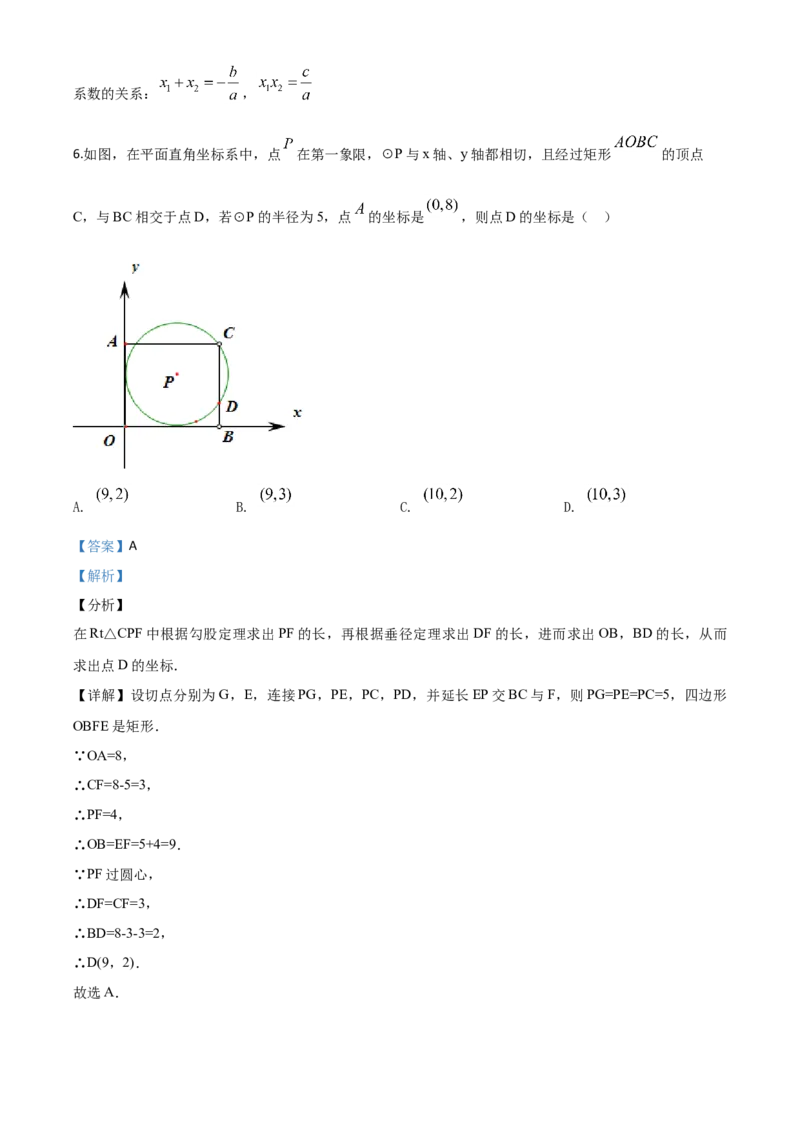
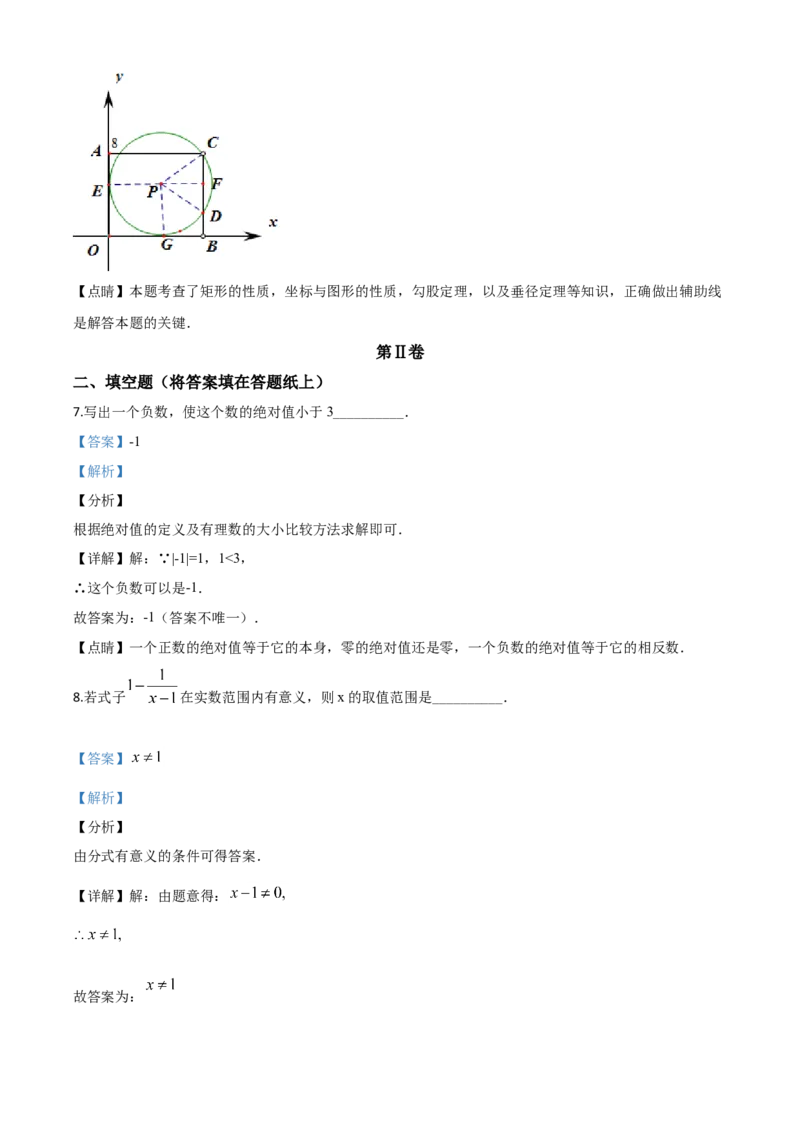
6.如图,在平面直角坐标系中,点 在第一象限,⊙P与x轴、y轴都相切,且经过矩形 的顶点
C,与BC相交于点D,若⊙P的半径为5,点 的坐标是 ,则点D的坐标是( )
A. B. C. D.
【答案】A
【解析】
【分析】
在Rt△CPF中根据勾股定理求出PF的长,再根据垂径定理求出DF的长,进而求出OB,BD的长,从而
求出点D的坐标.
【详解】设切点分别为G,E,连接PG,PE,PC,PD,并延长EP交BC与F,则PG=PE=PC=5,四边形
OBFE是矩形.
∵OA=8,
∴CF=8-5=3,
∴PF=4,
∴OB=EF=5+4=9.
∵PF过圆心,
∴DF=CF=3,
∴BD=8-3-3=2,
∴D(9,2).
故选A.【点睛】本题考查了矩形的性质,坐标与图形的性质,勾股定理,以及垂径定理等知识,正确做出辅助线
是解答本题的关键.
第Ⅱ卷
二、填空题(将答案填在答题纸上)
7.写出一个负数,使这个数的绝对值小于3__________.
【答案】-1
【解析】
【分析】
根据绝对值的定义及有理数的大小比较方法求解即可.
【详解】解:∵|-1|=1,1<3,
∴这个负数可以是-1.
故答案为:-1(答案不唯一).
【点睛】一个正数的绝对值等于它的本身,零的绝对值还是零,一个负数的绝对值等于它的相反数.
8.若式子 在实数范围内有意义,则x的取值范围是__________.
【答案】
【解析】
【分析】
由分式有意义的条件可得答案.
【详解】解:由题意得:
故答案为:【点睛】本题考查的是分式有意义的条件,掌握分式有意义的条件是解题的关键.
9.纳秒 是非常小的时间单位, ,北斗全球导航系统的授时精度优于 ,用科学计数法
表示 是__________.
【答案】 s.
【解析】
【分析】
根据科学记数法的表示形式进行表示即可.
【详解】∵ ,
∴ =20×10-9s,
用科学记数法表示得 s,
故答案为: s.
【点睛】本题考查了科学记数法,掌握科学记数法的表示方法是解题关键.
10.计算 的结果是__________.
【答案】
【解析】
【分析】
先化成最简二次根式,再根据二次根式的加减法法则计算出分母,最后约分即可.
【详解】
,故答案为: .
【点睛】本题考查了二次根式的混合运算,掌握二次根式的加减法法则是解题的关键.
11.已知x、y满足方程组 ,则 的值为__________.
【答案】1
【解析】
【分析】
先解方程组求解 ,从而可得答案.
【详解】解:
① 得: ③
③-②得:
把 代入①:
所以方程组的解是:
故答案为:
【点睛】本题考查的是解二元一次方程组,掌握二元一次方程组的解法是解题的关键.
12.方程 的解是__________.【答案】
【解析】
【分析】
去分母,把分式方程化为整式方程,再解整式方程并检验即可.
【详解】解:
经检验: 是原方程的根.
故答案为: .
【点睛】本题考查的是分式方程的解法,掌握分式方程的解法是解题的关键,注意要检验.
13.将一次函数 的图象绕原点 逆时针旋转 ,所得到的图像对应的函数表达式是
__________.
【答案】
【解析】
【分析】
根据一次函数互相垂直时系数之积等于-1,进而得出答案;
【详解】∵一次函数的解析式为 ,
∴设与x轴、y轴 的交点坐标为 、 ,∵一次函数 的图象绕原点 逆时针旋转 ,
∴旋转后得到的图象与原图象垂直,旋转后的点为 、 ,
令 ,代入点得 , ,
∴旋转后一次函数解析式为 .
故答案为 .
【点睛】本题主要考查了一次函数图像与几何变换,正确把握互相垂直的两直线的位置关系是解题的关键.
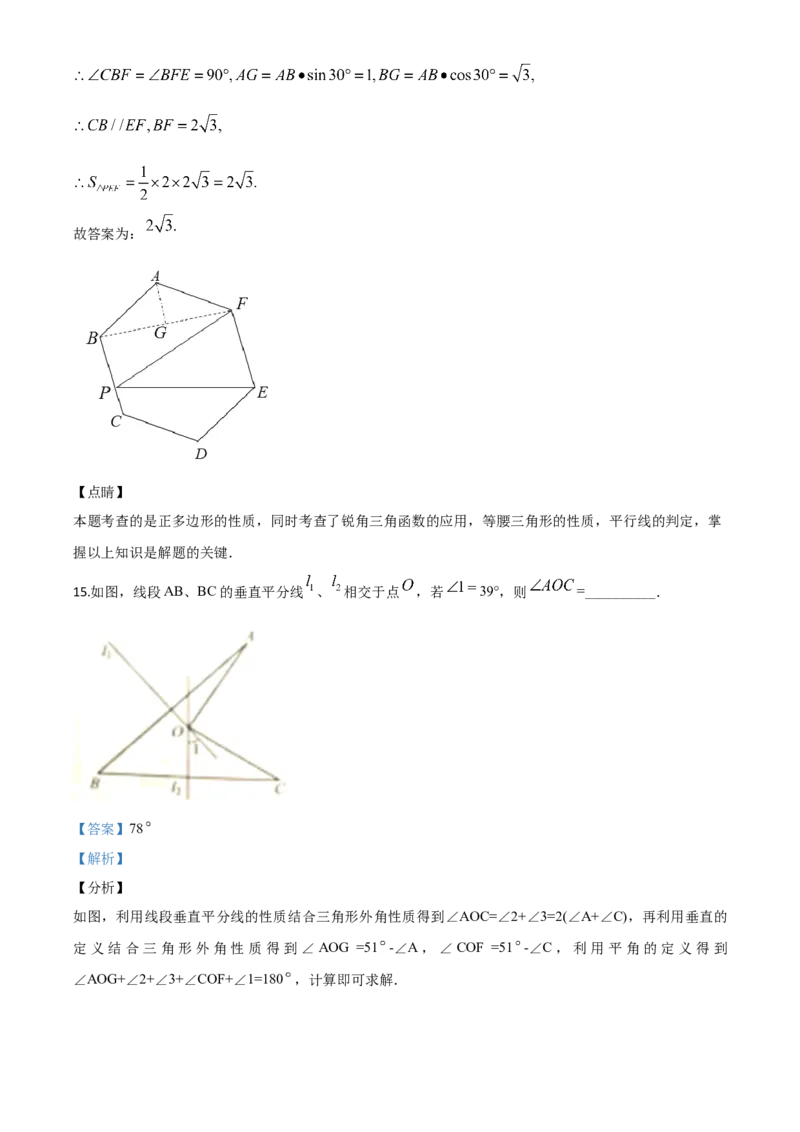
14.如图,在边长为 的正六边形 中,点P在BC上,则 的面积为__________.
【答案】
【解析】
【分析】
如图,连接 过 作 于 ,利用正六边形的性质求解 的长,利用 与 上的高相等,
从而可得答案.
【详解】解:如图,连接 过 作 于 ,
正六边形 ,故答案为:
【点睛】
本题考查的是正多边形的性质,同时考查了锐角三角函数的应用,等腰三角形的性质,平行线的判定,掌
握以上知识是解题的关键.
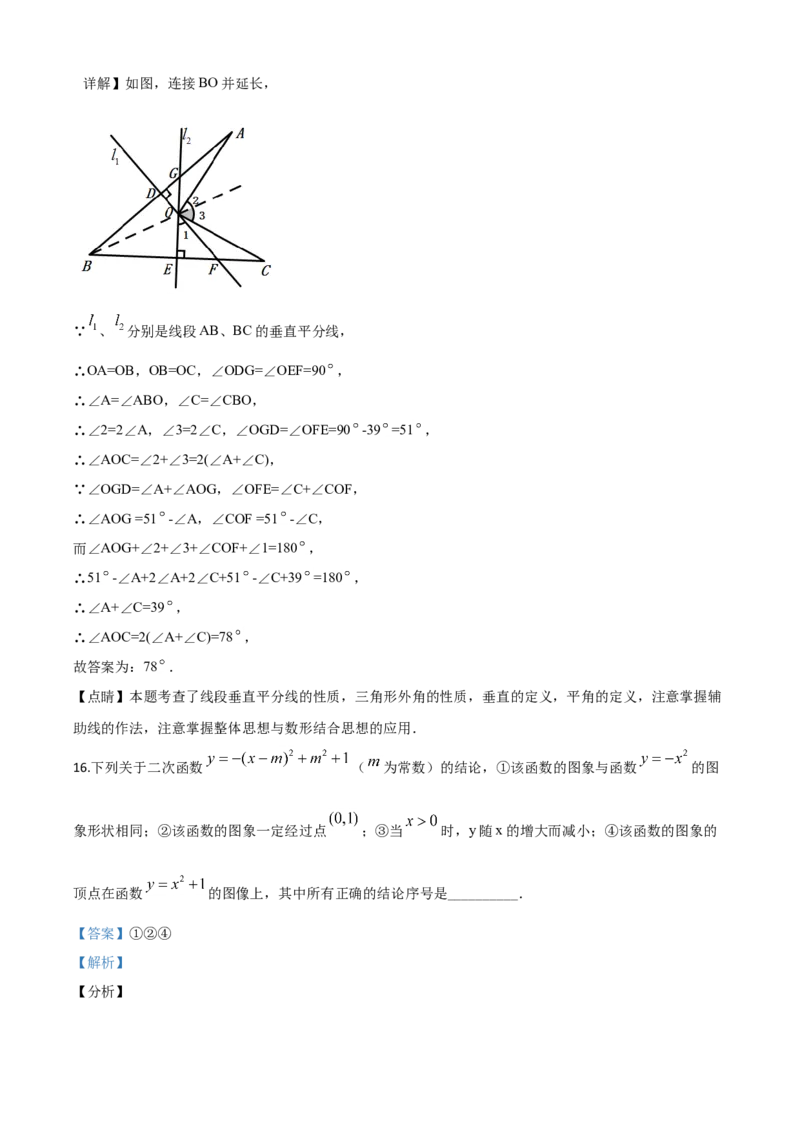
15.如图,线段AB、BC的垂直平分线 、 相交于点 ,若 39°,则 =__________.
【答案】78
【解析】
【分析】
如图,利用线段垂直平分线的性质结合三角形外角性质得到∠AOC=∠2+∠3=2(∠A+∠C),再利用垂直的
定义结合三角形外角性质得到∠AOG =51 -∠A,∠COF =51 -∠C,利用平角的定义得到
∠AOG+∠2+∠3+∠COF+∠1=180 ,计算即可求解.【详解】如图,连接BO并延长,
∵ 、 分别是线段AB、BC的垂直平分线,
∴OA=OB,OB=OC,∠ODG=∠OEF=90 ,
∴∠A=∠ABO,∠C=∠CBO,
∴∠2=2∠A,∠3=2∠C,∠OGD=∠OFE=90 -39 =51 ,
∴∠AOC=∠2+∠3=2(∠A+∠C),
∵∠OGD=∠A+∠AOG,∠OFE=∠C+∠COF,
∴∠AOG =51 -∠A,∠COF =51 -∠C,
而∠AOG+∠2+∠3+∠COF+∠1=180 ,
∴51 -∠A+2∠A+2∠C+51 -∠C+39 =180 ,
∴∠A+∠C=39 ,
∴∠AOC=2(∠A+∠C)=78 ,
故答案为:78 .
【点睛】本题考查了线段垂直平分线的性质,三角形外角的性质,垂直的定义,平角的定义,注意掌握辅
助线的作法,注意掌握整体思想与数形结合思想的应用.
16.下列关于二次函数 ( 为常数)的结论,①该函数的图象与函数 的图
象形状相同;②该函数的图象一定经过点 ;③当 时,y随x的增大而减小;④该函数的图象的
顶点在函数 的图像上,其中所有正确的结论序号是__________.
【答案】①②④
【解析】
【分析】①两个二次函数可以通过平移得到,由此即可得两个函数的图象形状相同;②求出当 时,y的值即可
得;③根据二次函数的增减性即可得;④先求出二次函数 的顶点坐标,再代入函
数 进行验证即可得.
【详解】 当 时,将二次函数 的图象先向右平移m个单位长度,再向上平移 个单位
长度即可得到二次函数 的图象;当 时,将二次函数 的图象先向左平
移 个单位长度,再向上平移 个单位长度即可得到二次函数 的图象
该函数的图象与函数 的图象形状相同,结论①正确
对于
当 时,
即该函数的图象一定经过点 ,结论②正确
由二次函数的性质可知,当 时,y随x的增大而增大;当 时,y随x的增大而减小
则结论③错误
的顶点坐标为
对于二次函数
当 时,
即该函数的图象的顶点 在函数 的图象上,结论④正确
综上,所有正确的结论序号是①②④
故答案为:①②④.
【点睛】本题考查了二次函数的图象与性质等知识点,熟练掌握二次函数的图象与性质是解题关键.
三、解答题:解答应写出文字说明、证明过程或演算步骤,第17~21题为必考题,每个试题
考生都必须作答,第22、23题为选考题,考生根据要求作答17.计算:
【答案】
【解析】
【分析】
先把括号里通分,再把除法转化为乘法,然后约分化简即可.
【详解】解:
.
【点睛】分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,
有括号的先算括号里面的;最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.
18.解方程: .
【答案】
【解析】
【分析】
将方程的左边因式分解后即可求得方程的解
【详解】解:因式分解得:(x+1)(x-3)=0,
即x+1=0或x-3=0,
解得:x=-1,x=3
1 2
【点睛】本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,
这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.
19.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:BD=CE.【答案】证明见解析.
【解析】
试题分析:根据全等三角形的判定定理 ASA可以证得△ACD≌△ABE,然后由“全等三角形的对应边相
等”可得AD =AE ,继而可得结论.
试题解析:在△ABE与△ACD中,
,
∴△ACD≌△ABE(ASA),
∴AD=AE(全等三角形的对应边相等),
∴AB-AD=AC-AE,
即:BD=CE.
20.已知反比例函数 的图象经过点
(1)求 的值
(2)完成下面的解答
解不等式组
解:解不等式①,得 .
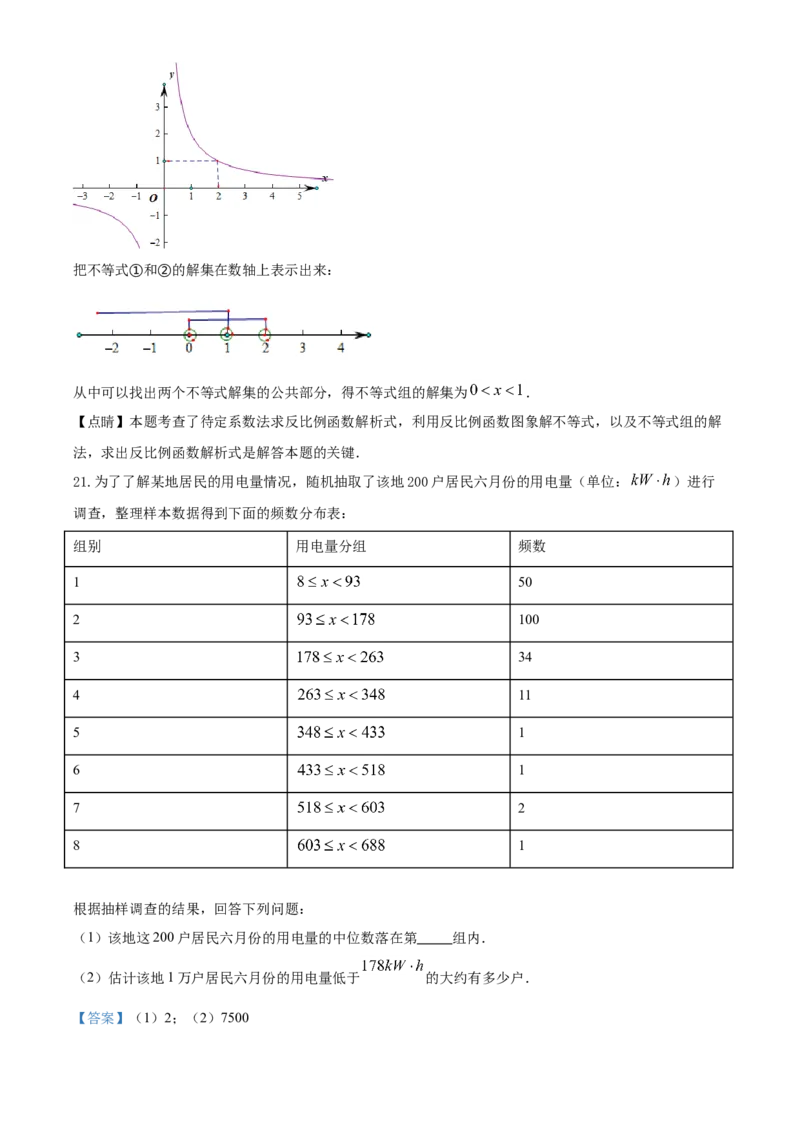
根据函数 的图象,得不等式②得解集 .
把不等式①和②的解集在数轴上表示出来从中可以找出两个不等式解集的公共部分,得不等式组的解集 .
【答案】(1)2;(2) , ,见解析,
【解析】
【分析】
(1)利用待定系数法求解即可;
(2)根据移项、合并同类项、系数化为1求出不等式①的解集;根据反比例函数的图像求出不等式②的解
集,进而求出公共部分即可.
【详解】解:(1)因为点 在反比例函数 的图像上,
所以点 的坐标满足 ,
即 ,解得 ;
(2) ,
解不等式①,得 ;
∵y=1时,x=2,
∴根据函数 的图象,得不等式②得解集 .把不等式①和②的解集在数轴上表示出来:
从中可以找出两个不等式解集的公共部分,得不等式组的解集为 .
【点睛】本题考查了待定系数法求反比例函数解析式,利用反比例函数图象解不等式,以及不等式组的解
法,求出反比例函数解析式是解答本题的关键.
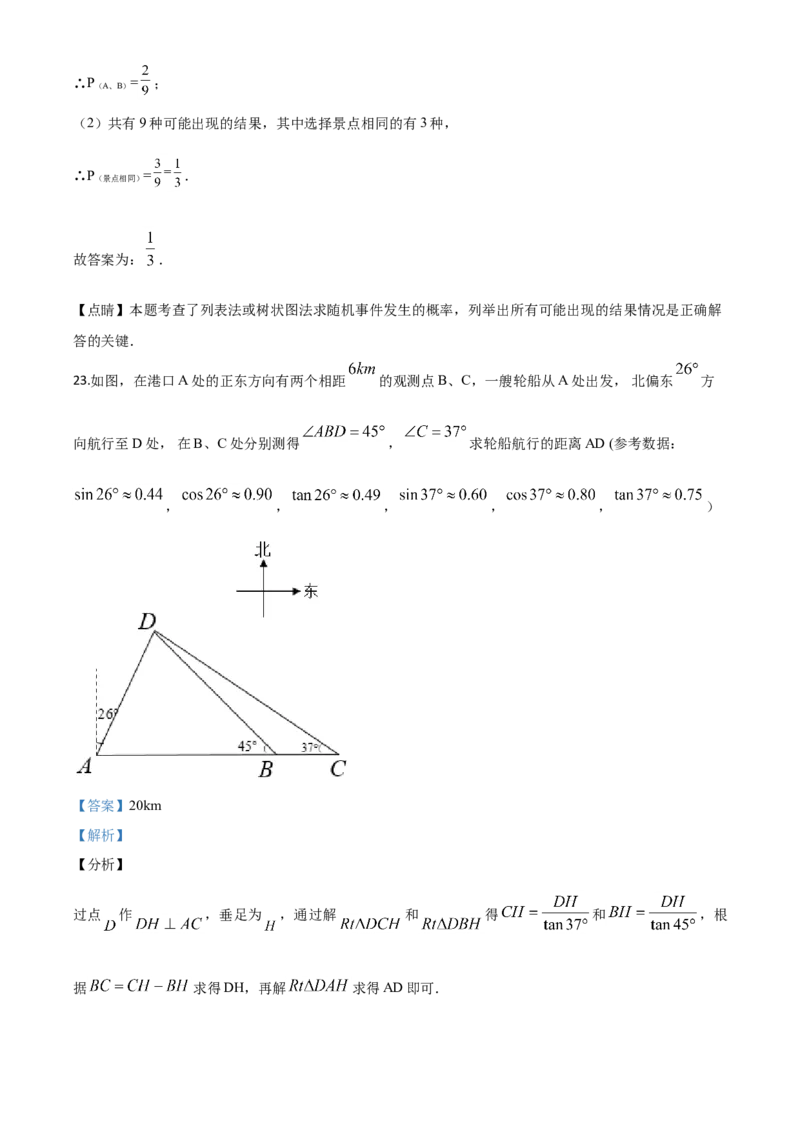
21.为了了解某地居民的用电量情况,随机抽取了该地200户居民六月份的用电量(单位: )进行
调查,整理样本数据得到下面的频数分布表:
组别 用电量分组 频数
1 50
2 100
3 34
4 11
5 1
6 1
7 2
8 1
根据抽样调查的结果,回答下列问题:
(1)该地这200户居民六月份的用电量的中位数落在第 组内.
(2)估计该地1万户居民六月份的用电量低于 的大约有多少户.
【答案】(1)2;(2)7500【解析】
【分析】
(1)将200个数据按大小顺序排列最中间两个数的平均数即为中位数,进而可解决问题;
(2)求出用电量低于 的户数的百分比,根据总户数求出答案..
【详解】解:(1)将200个数据按大小顺序排列最中间两个数即第100和101个数,它们的平均数即为中
位数,这两个数都落在第2组,
故答案为:2;
(2) (户)
因此,估计该地1万户居民六月的用电量低于 的大约有 户.
【点睛】本题考查频数分布表,利用统计表获取信息的能力,以及利用样本估计总体,利用统计表获取信
息时,必须认真观察、分析、研究统计表,才能作出正确的判断和解决问题.
22.甲、乙两人分别从A、B、C这3个景点随机选择2个景点游览.
(1)求甲选择的2个景点是A、B的概率.
(2)甲、乙两人选择的2个景点恰好相同的概率是 .
【答案】(1) ;(2)
【解析】
【分析】
(1)列举出所有可能出现的结果,利用概率公式求解即可;
(2)根据树状图求得恰好只有两人选择相同的情况,再根据概率公式求解即可.
的
【详解】(1)解:用列表法表示所有可能出现 结果如下:
(1)共有9种可能出现的结果,其中选择A、B的有2种,∴P = ;
(A、B)
(2)共有9种可能出现的结果,其中选择景点相同的有3种,
∴P = .
(景点相同)
故答案为: .
【点睛】本题考查了列表法或树状图法求随机事件发生的概率,列举出所有可能出现的结果情况是正确解
答的关键.
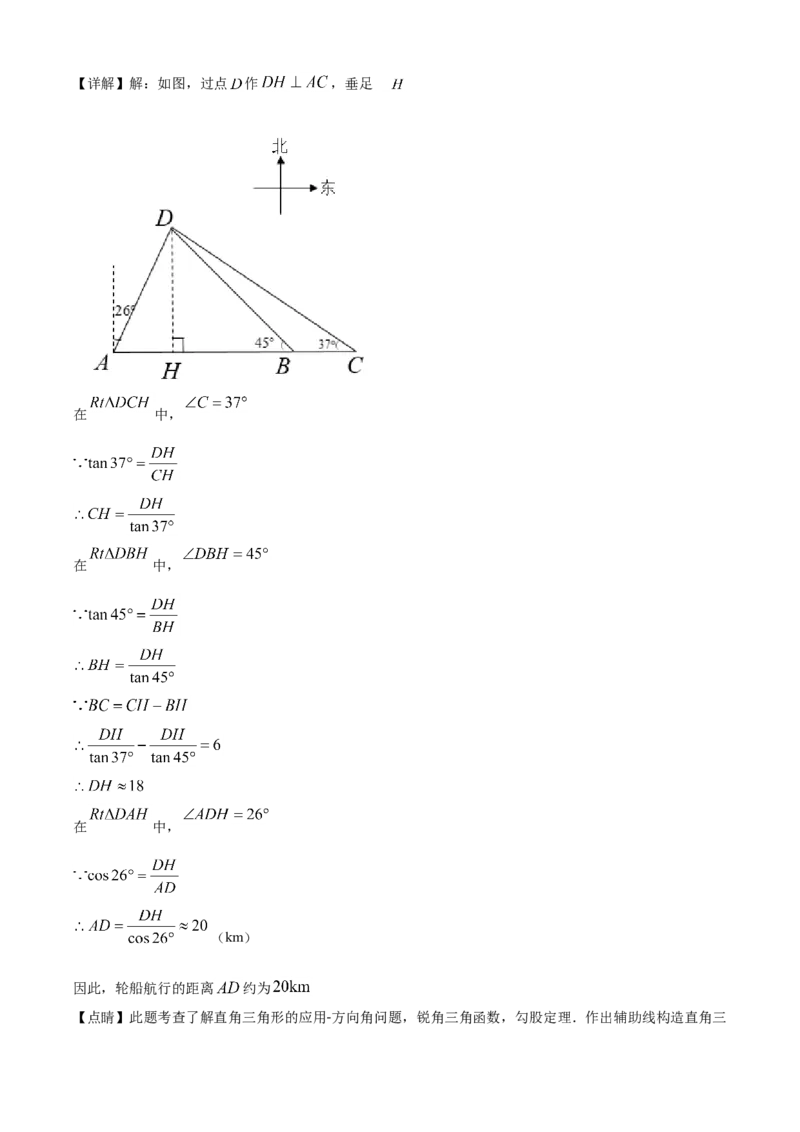
23.如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方
向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据:
, , , , , )
【答案】20km
【解析】
【分析】
过点 作 ,垂足为 ,通过解 和 得 和 ,根
据 求得DH,再解 求得AD即可.【详解】解:如图,过点 作 ,垂足 为
在 中,
在 中,
在 中,
(km)
因此,轮船航行的距离 约为
【点睛】此题考查了解直角三角形的应用-方向角问题,锐角三角函数,勾股定理.作出辅助线构造直角三角形是解题的关键.
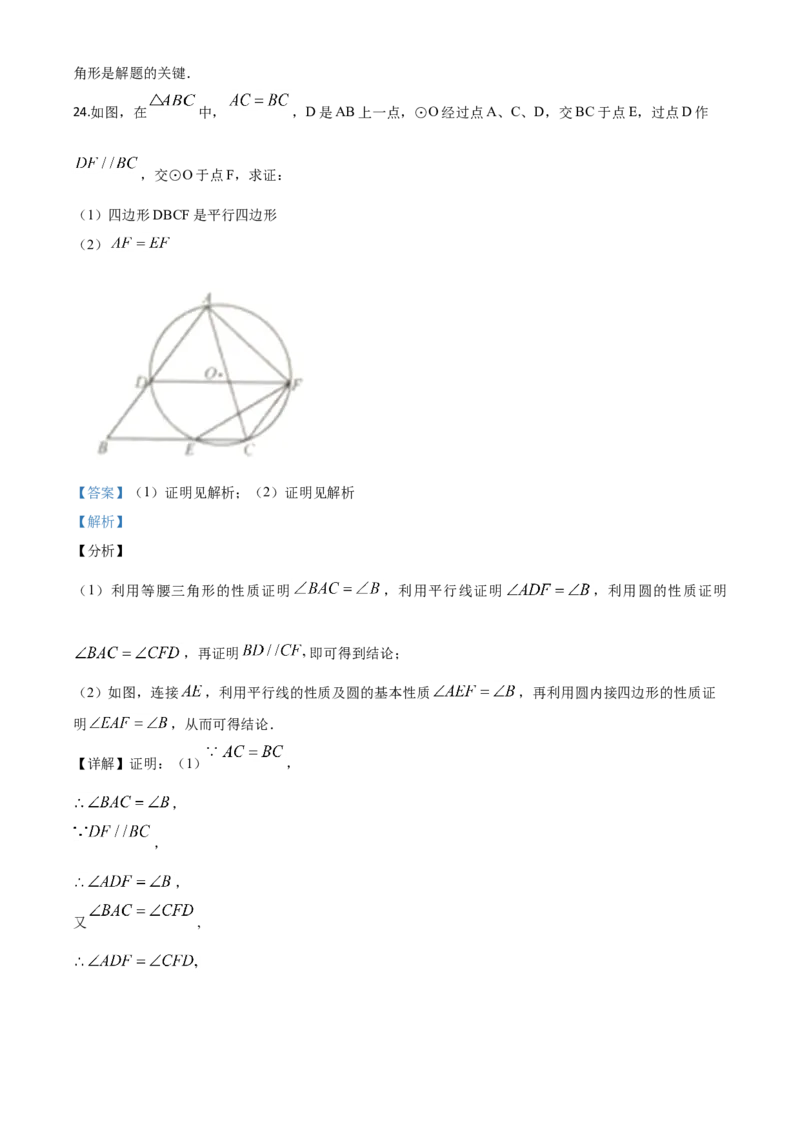
24.如图,在 中, ,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作
,交⊙O于点F,求证:
(1)四边形DBCF是平行四边形
(2)
【答案】(1)证明见解析;(2)证明见解析
【解析】
【分析】
(1)利用等腰三角形的性质证明 ,利用平行线证明 ,利用圆的性质证明
,再证明 即可得到结论;
(2)如图,连接 ,利用平行线的性质及圆的基本性质 ,再利用圆内接四边形的性质证
明 ,从而可得结论.
【详解】证明:(1) ,
,
,
,
又 ,四边形 是平行四边形.
(2)如图,连接
,
四边形 是 的内接四边形
【点睛】本题考查平行四边形的判定,圆的基本性质,平行线的性质与判定,等腰三角形的性质,圆内接
四边形的性质,掌握以上知识是解题的关键.
25.小明和小丽先后从A地出发同一直道去B地, 设小丽出发第 时, 小丽、小明离地的距离分别为
、 , 与x之间的数表达式 , 与x之间的函数表达式是
.
(1)小丽出发时,小明离A地的距离为 .(2)小丽发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?
【答案】(1)250;(2)当小丽出发第 时,两人相距最近,最近距离是
【解析】
【分析】
(1)由x=0时,根据 - 求得结果即可;
(2)求出两人相距的函数表达式,求出最小值即可.
【详解】解(1)当x=0时, =2250, =2000
∴ - =2250-2000=250(m)
故答案为:250
(2)设小丽出发第 时,两人相距 ,
则
即
其中
因此,当 时
S有最小值,
也就是说,当小丽出发第 时,两人相距最近,最近距离是
【点睛】此题主要考查了二次函数的性质的应用,熟练掌握二次函数的性质是解答本题的关键.
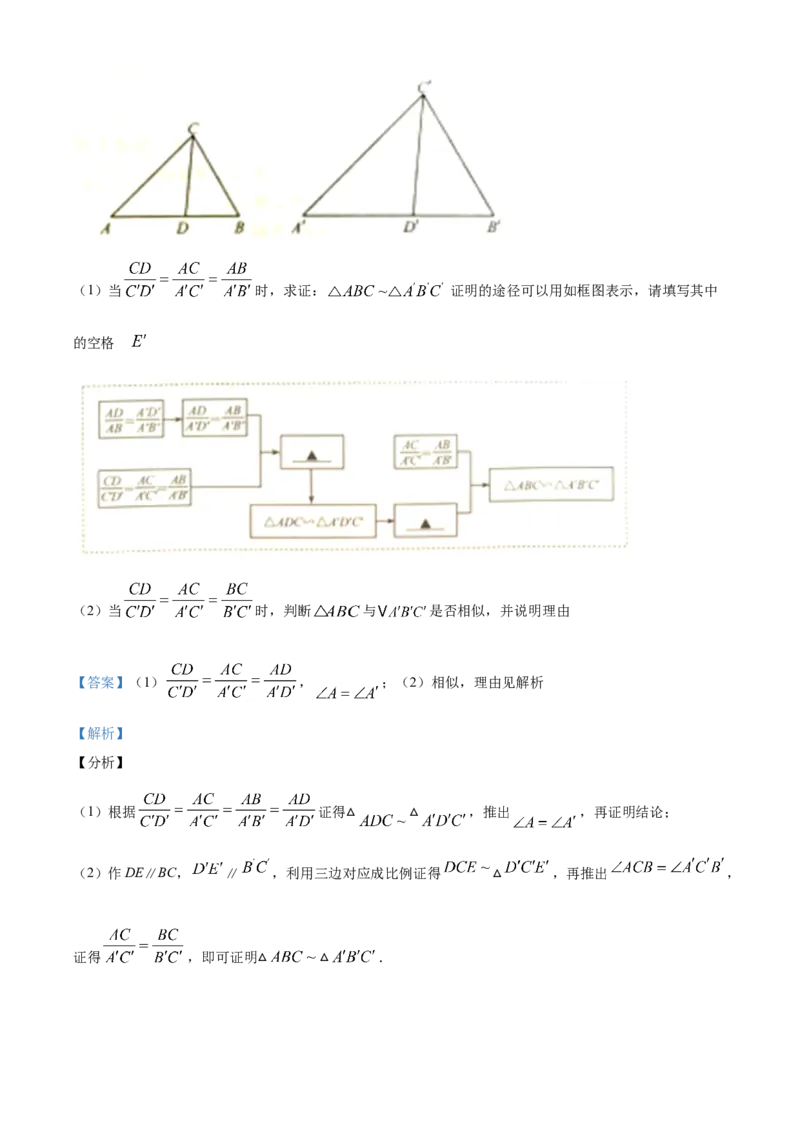
26.如图,在 和 中,D、 分别是AB、 上一点, .(1)当 时,求证: 证明的途径可以用如框图表示,请填写其中
的空格
(2)当 时,判断 与 是否相似,并说明理由
【答案】(1) , ;(2)相似,理由见解析
【解析】
【分析】
(1)根据 证得 ,推出 ,再证明结论;
△ △
(2)作DE∥BC, ∥ ,利用三边对应成比例证得 ,再推出 ,
△
证得 ,即可证明 .
△ △【详解】(1)∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
△ △
∴ ,
∵ ,
∴ ,
△ △
故答案为: , ;
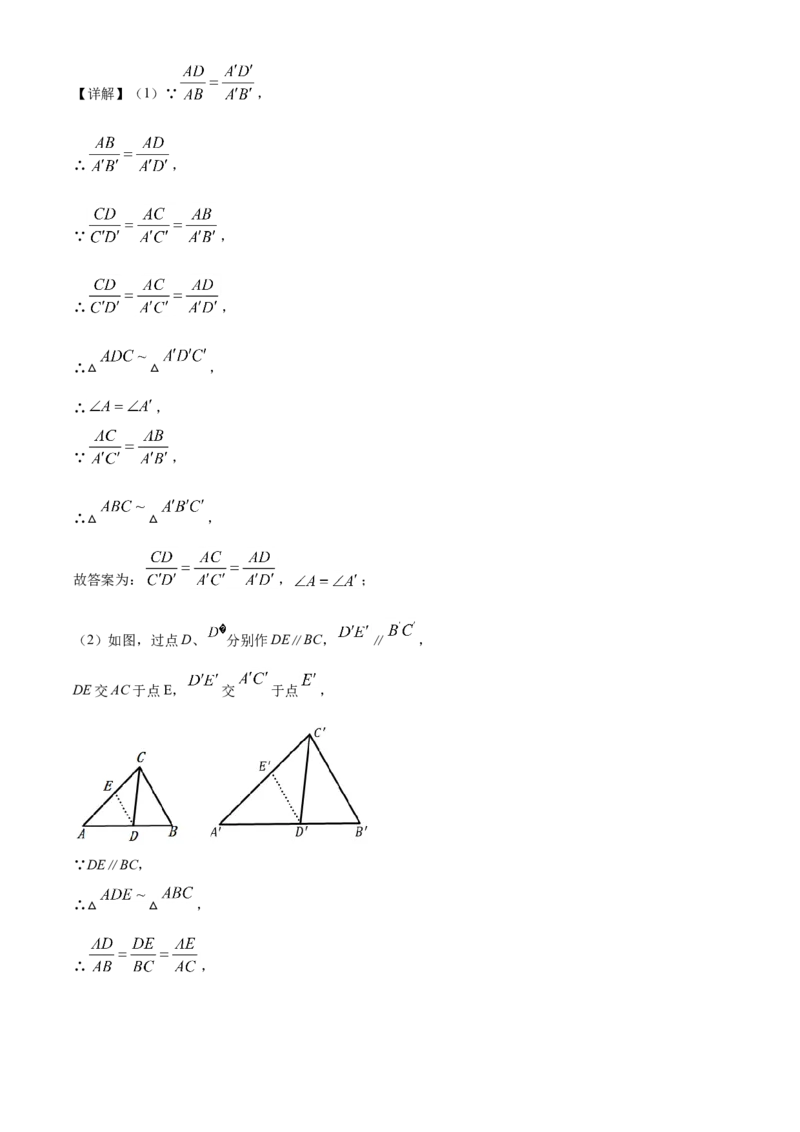
(2)如图,过点D、 分别作DE∥BC, ∥ ,
DE交AC于点E, 交 于点 ,
∵DE∥BC,
∴ ,
△ △
∴ ,同理: ,
又 ,
∴ ,
∴ ,
同理: ,
∴ ,
即 ,
∴ ,
又 ,
∴ ,
∴ ,
△ △
∴ ,
∵DE∥BC,
∴ ,
同理: ,
∴ ,又 ,
∴ .
△ △
【点睛】本题考查了相似三角形的判定和性质,平行线的性质,比例的性质,正确作出辅助线是解答第2
问的关键.
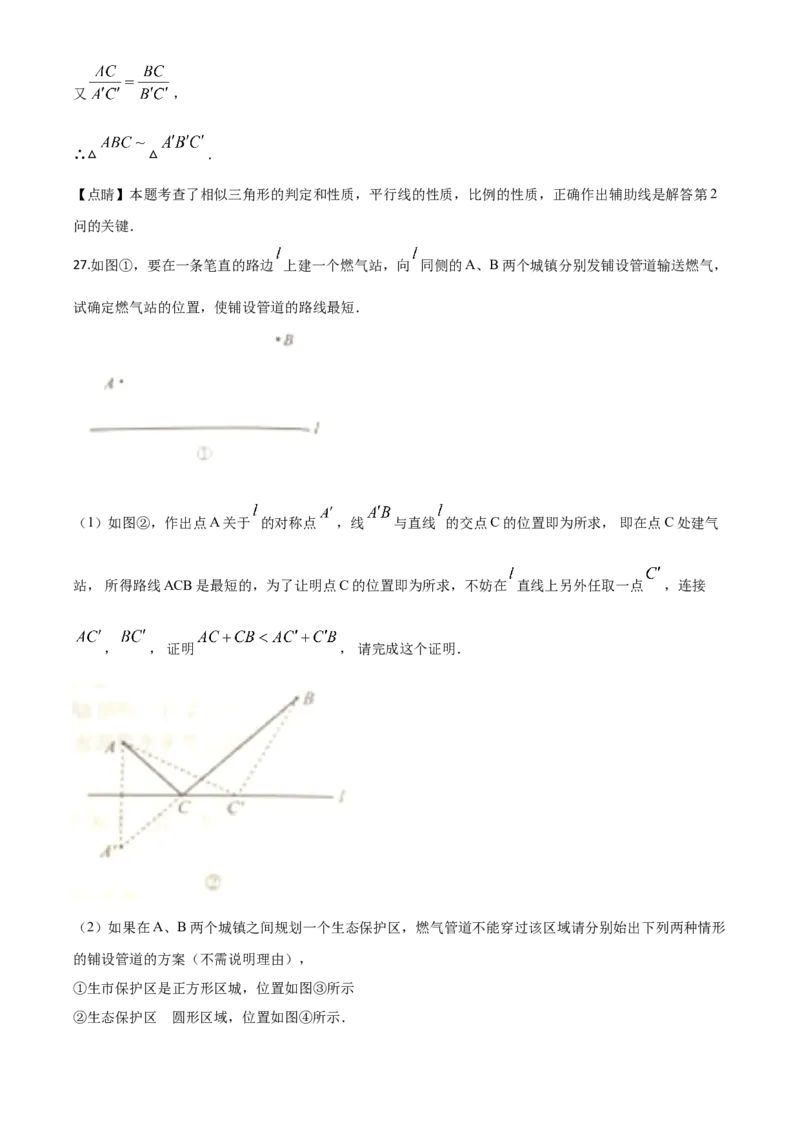
27.如图①,要在一条笔直的路边 上建一个燃气站,向 同侧的A、B两个城镇分别发铺设管道输送燃气,
试确定燃气站的位置,使铺设管道的路线最短.
(1)如图②,作出点A关于 的对称点 ,线 与直线 的交点C的位置即为所求, 即在点C处建气
站, 所得路线ACB是最短的,为了让明点C的位置即为所求,不妨在 直线上另外任取一点 ,连接
, , 证明 , 请完成这个证明.
(2)如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域请分别始出下列两种情形
的铺设管道的方案(不需说明理由),
①生市保护区是正方形区城,位置如图③所示
②生态保护区 是圆形区域,位置如图④所示.【答案】(1)证明见解析;(2)①见解析,②见解析
【解析】
【分析】
(1)连接 ,利用垂直平分线的性质,得到 ,利用三角形的三边关系,即可得到答案;
(2)由(1)可知,在点C处建燃气站,铺设管道的路线最短.分别对①、②的道路进行设计分析,即可
求出最短的路线图.
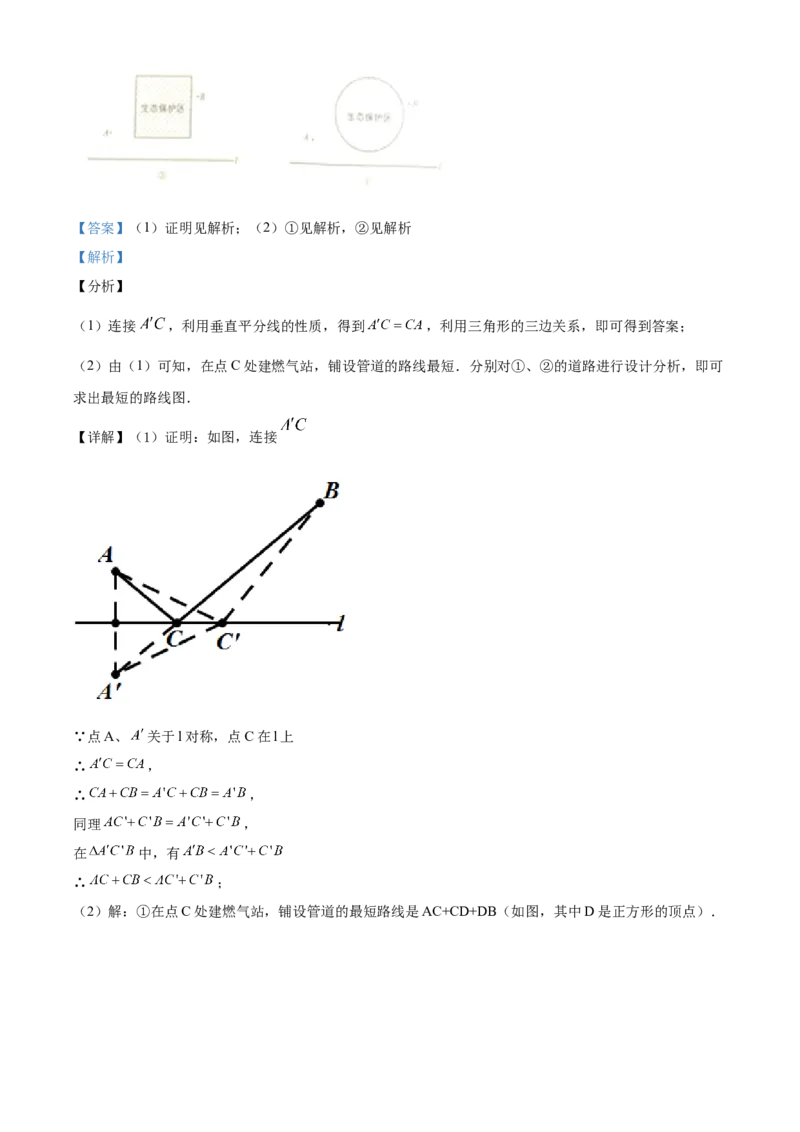
【详解】(1)证明:如图,连接
∵点A、 关于l对称,点C在l上
∴ ,
∴ ,
同理 ,
在 中,有
∴ ;
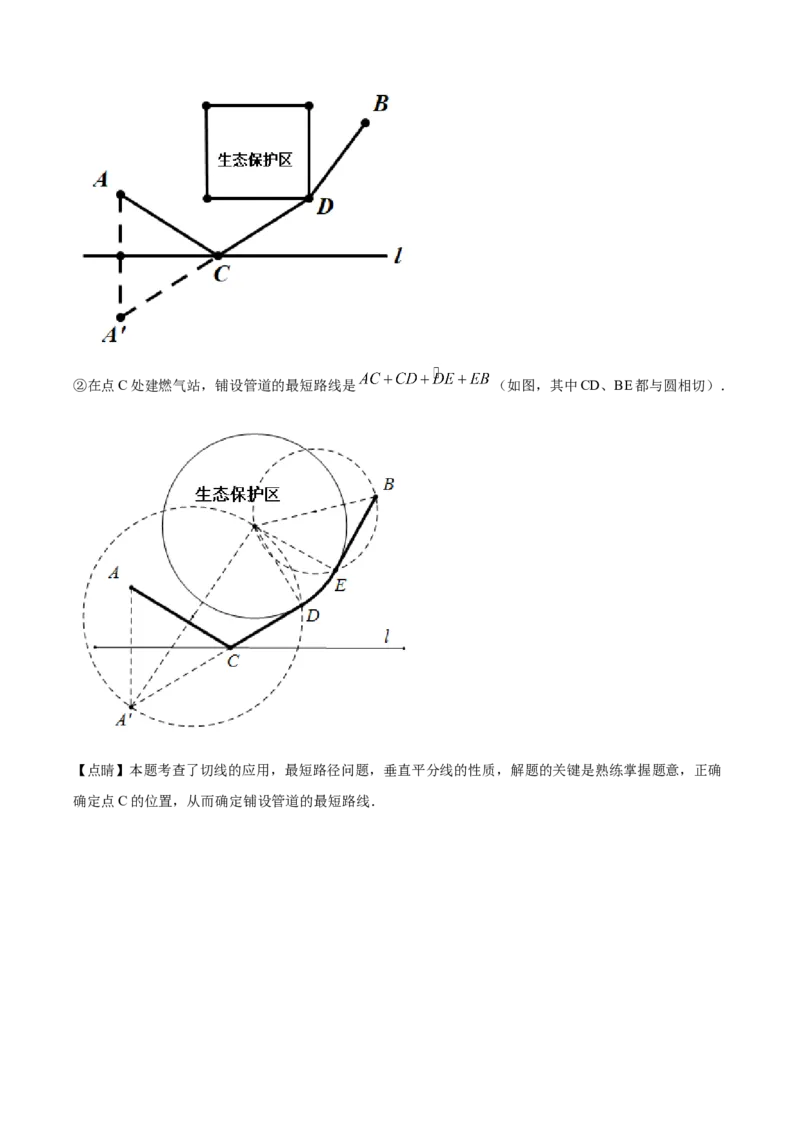
(2)解:①在点C处建燃气站,铺设管道的最短路线是AC+CD+DB(如图,其中D是正方形的顶点).②在点C处建燃气站,铺设管道的最短路线是 (如图,其中CD、BE都与圆相切).
【点睛】本题考查了切线的应用,最短路径问题,垂直平分线的性质,解题的关键是熟练掌握题意,正确
确定点C的位置,从而确定铺设管道的最短路线.本试卷的题干、答案和解析均由组卷网(http://zujuan.xkw.com)专业教师团队编校出品。
登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。
试卷地址:在组卷网浏览本卷
组卷网是学科网旗下的在线题库平台,覆盖小初高全学段全学科、超过900万精品解析试题。
关注组卷网服务号,可使用移动教学助手功能(布置作业、线上考试、加入错题本、错题训练)。
学科网长期征集全国最新统考试卷、名校试卷、原创题,赢取丰厚稿酬,欢迎合作。
钱老师 QQ:537008204 曹老师 QQ:713000635