文档内容
届高三年级第三次质量检测
2025
数 学
注意 事项:
本试卷共 页 满分 分 考试时间 分钟 答卷前 考生务必将自己的姓名 考生
1. 4 , 150 , 120 。 , 、
号等填写在试卷和答题卡上 并将条形码粘贴在答题卡上的指定位置
, 。
回答选择题时 选出每小题答案后 用铅笔把答题卡上对应题目的答案标号涂黑 如需
2. , , ,
改动 用橡皮擦干净后 再选涂其他答案标号 回答非选择题时 将答案写在答题卡上对应的
, , 。 ,
答题区域内 写在本试卷上无效
, 。
考试结束后 将本试卷和答题卡一并交回
3. , 。
一、选择题:本题共 小题,每小题 分,共 分。在每小题给出的四个选项中,只有一项是符
8 5 40
合题目要求的。
已知集合A B x Nx2 则 A B
1. = 1,2,3 , = ∈ | <4 , ∩ =
A. 1 B. 1,2 C. 0,1,2,3 D. -1,0,1,2,3
已知向量a b 若xa yb 则x y
2. =(1,0),=(-1,2), + =(0,1), + =
A.-2 B.-1 C.0 D.1
3.
已知S
n
是等差数列 a
n
的前n项和
,
且a
4 =4,
则S
7=
A.14 B.16 C.21 D.28
z
已 知z a bab 则 是纯虚数 是a b 的
4. = +i( ≠0), “z ” “= ”
充分不必要条件 必要不充分条件
A. B.
充要条件 既不充分也不必要条件
C. D.
正四棱台ABCD ABCD 中 AB AB 直线AA 与平面ABCD所成角的大
5. - 1 1 1 1 , =2, 1 1=1, 1
小为 则该棱台的高为
60°,
6 6 2 3
A. B. C. D.
6 2 2 2
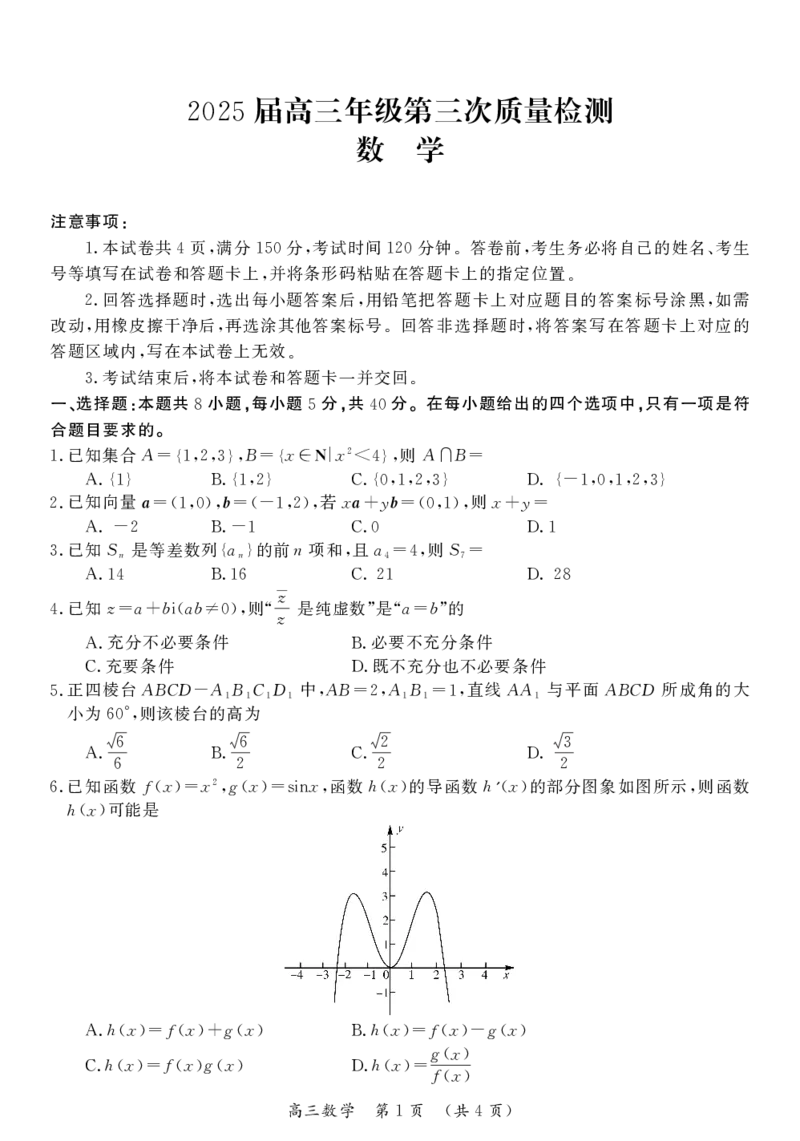
已知函数fx x2gx x 函数hx 的导函数h x 的部分图象如图所示 则函数
6. ()= ,()=sin , () '() ,
hx 可能是
()
.hx fx gx .hx fx gx
A ()= ()+ () B ()= ()- ()
gx
.hx fxgx .hx ()
C ()= ()() D ()=fx
()
高三数学 第 页 (共 页)
1 4.已知函数fx x在区间aa π
7 ()=cos2 ,+
2
高三数学 第 页 (共 页)
4
上的最大值为Ma 最小值为ma .当a变化
(), ()
时 下列选项中不可能成立的是
,
.Ma 且ma .Ma 且ma
A ()=1, ()=-1 B ()=1, ()=0
.Ma 1 且ma 1 .Ma 1 且ma
C ()= , ()=- D ()= , ()=-1
2 2 2
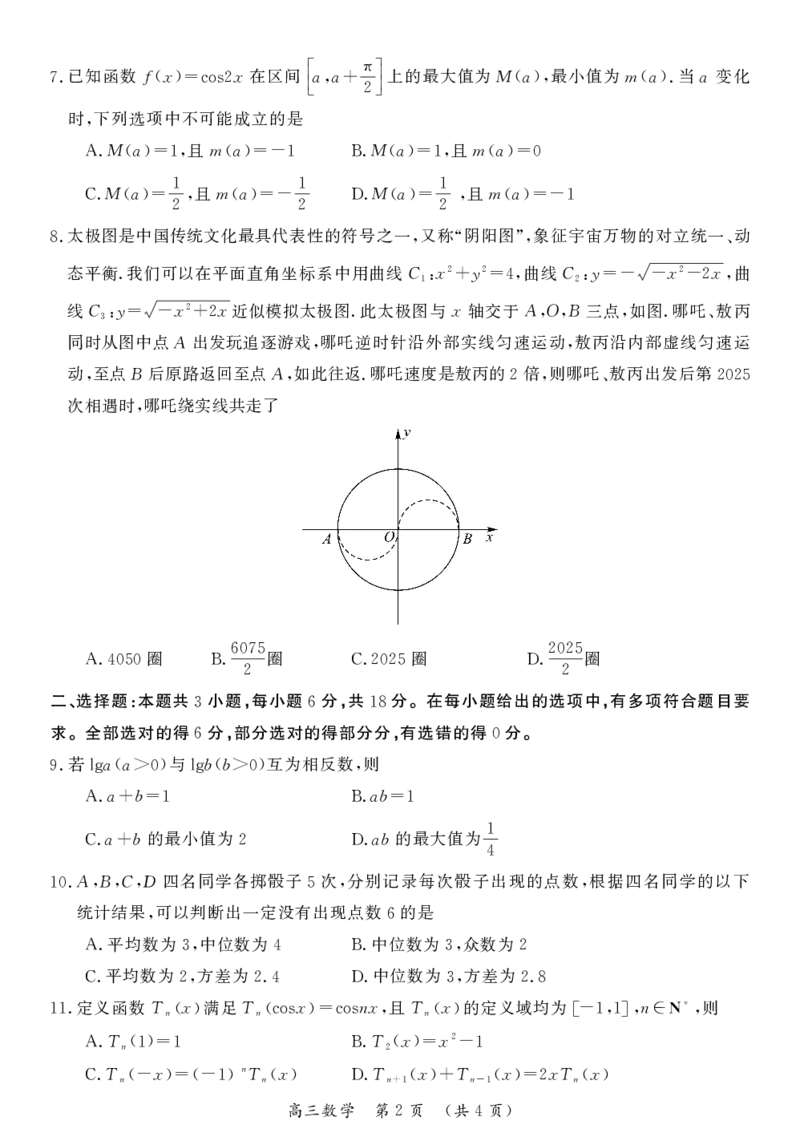
.太极图是中国传统文化最具代表性的符号之一 又称 阴阳图 象征宇宙万物的对立统一 动
8 , “ ”, 、
态平衡.我们可以在平面直角坐标系中用曲线C x2 y2 曲线C y x2 x 曲
1: + =4, 2:=- - -2 ,
线C y x2 x近似模拟太极图.此太极图与x轴交于AOB三点 如图.哪吒 敖丙
3:= - +2 , , , 、
同时从图中点A出发玩追逐游戏 哪吒逆时针沿外部实线匀速运动 敖丙沿内部虚线匀速运
, ,
动 至点B后原路返回至点A 如此往返.哪吒速度是敖丙的 倍 则哪吒 敖丙出发后第
, , 2 , 、 2025
次相遇时 哪吒绕实线共走了
,
圈 6075圈 圈 2025圈
A.4050 B. C.2025 D.
2 2
二、选择题:本题共 小题,每小题 分,共 分。在每小题给出的选项中,有多项符合题目要
3 6 18
求。全部选对的得 分,部分选对的得部分分,有选错的得 分。
6 0
若 aa 与 bb 互为相反数 则
9. lg (>0) lg (>0) ,
.a b .ab
A + =1 B =1
.a b的最小值为 .ab的最大值为1
C + 2 D
4
.ABCD四名同学各掷骰子 次 分别记录每次骰子出现的点数 根据四名同学的以下
10 , , , 5 , ,
统计结果 可以判断出一定没有出现点数 的是
, 6
平均数为 中位数为 中位数为 众数为
A. 3, 4 B. 3, 2
平均数为 方差为 中位数为 方差为
C. 2, 2.4 D. 3, 2.8
11.
定义函数T
n
x 满足T
n cos
x
=cos
nx
,
且T
n
x 的定义域均为
-1,1 ,
n
∈
N*
,
则
A
.T
n(1)=1 B
.T
2(
x
)=
x2
-1
.T x nT x .T x T x xT x
C n(- )=(-1) n() D n +1()+ n -1()=2 n()
2三、填空题:本题共 小题,每小题 分,共 分。
3 5 15
. 在 xn 的展开式中 若各项的二项式系数的和为 则各项系数的和为 .
12 (1-2 ) , 32,
.已知圆Ox2 y2 r2 r 经过椭圆C
x2 y2
a b 的上 下顶点和焦点 则椭
13 : + = (>0) :a2+b2=1(> >0) 、 ,
圆C的离心率e .
=
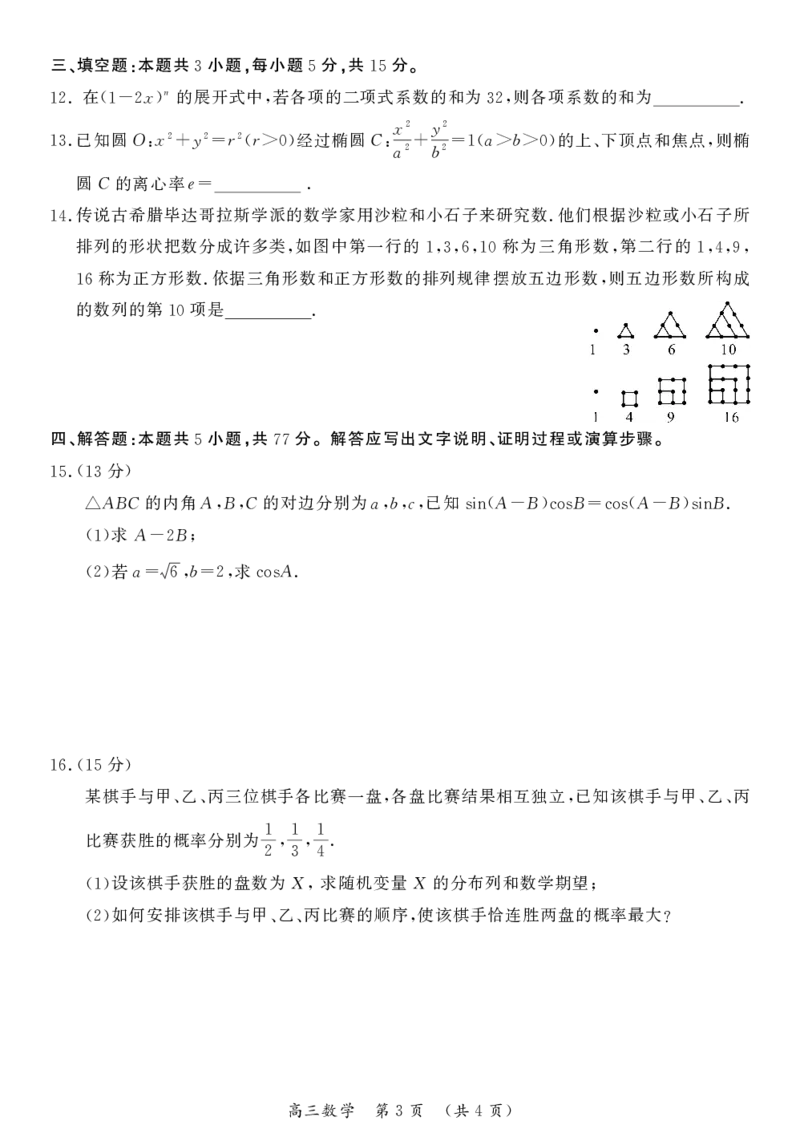
.传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数.他们根据沙粒或小石子所
14
排列的形状把数分成许多类 如图中第一行的 称为三角形数 第二行的
, 1,3,6,10 , 1,4,9,
称为正方形数.依据三角形数和正方形数的排列规律摆放五边形数 则五边形数所构成
16 ,
的数列的第 项是 .
10
四、解答题:本题共 小题,共 分。解答应写出文字说明、证明过程或演算步骤。
5 77
. 分
15 (13 )
ABC的内角ABC的对边分别为abc 已知 A B B A B B.
△ , , ,,, sin( - )cos =cos( - )sin
求 A B
(1) -2 ;
若a b 求 A.
(2) = 6,=2, cos
. 分
16 (15 )
某棋手与甲 乙 丙三位棋手各比赛一盘 各盘比赛结果相互独立 已知该棋手与甲 乙 丙
、 、 , , 、 、
比赛获胜的概率分别为1 1 1.
, ,
2 3 4
设该棋手获胜的盘数为X 求随机变量X的分布列和数学期望
(1) , ;
如何安排该棋手与甲 乙 丙比赛的顺序 使该棋手恰连胜两盘的概率最大
(2) 、 、 , ?
高三数学 第 页 (共 页)
3 4. 分
17 (15 )
已知函数fx - xx2 ax a R
()=e ( + +1),∈ .
证明fx 存在斜率为 的切线
(1) :() 0 ;
若fx 存在极小值 且极小值小于 求a的取值范围.
(2) () , 0,
. 分
18 (17 )
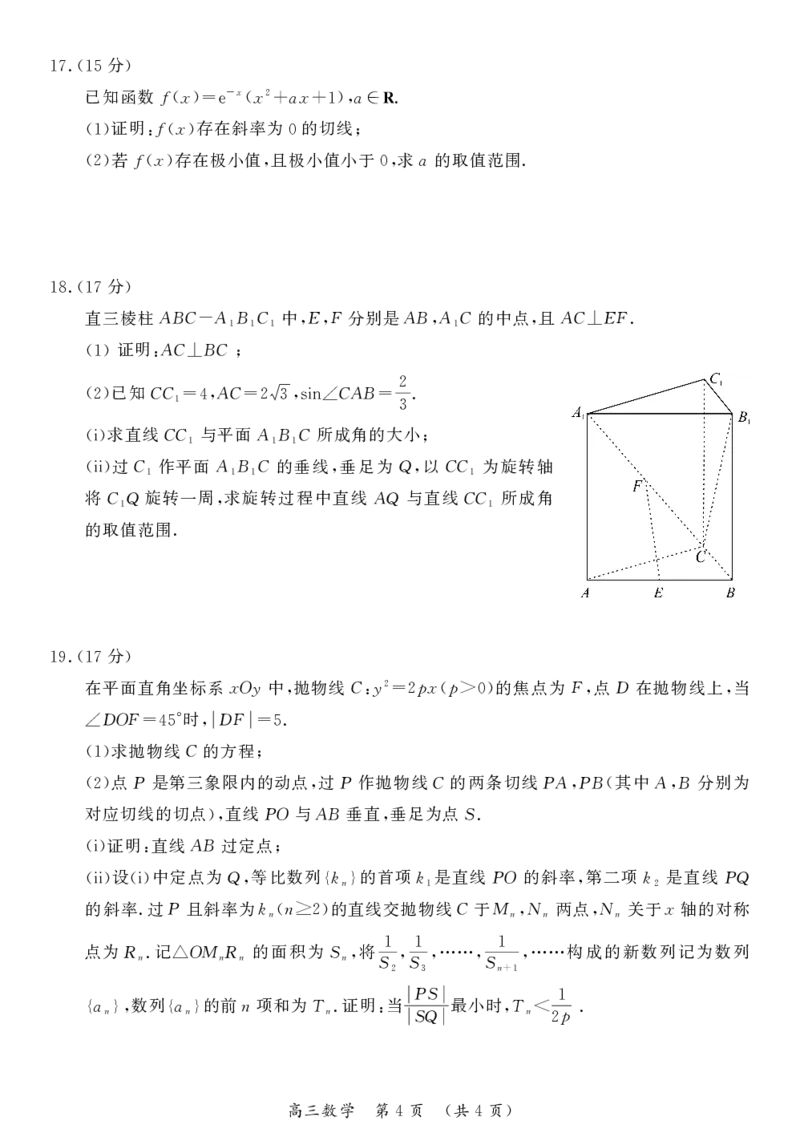
直三棱柱ABC ABC 中 EF分别是ABAC的中点 且AC EF.
- 1 1 1 , , ,1 , ⊥
证明 AC BC
(1) : ⊥ ;
已知CC AC CAB 2.
(2) 1=4, =23,sin∠ =
3
求直线CC 与平面ABC所成角的大小
(i) 1 1 1 ;
过C 作平面ABC的垂线 垂足为Q 以CC 为旋转轴
(ii) 1 1 1 , , 1
将CQ旋转一周 求旋转过程中直线AQ与直线CC 所成角
1 , 1
的取值范围.
. 分
19 (17 )
在平面直角坐标系xOy中 抛物线Cy2 pxp 的焦点为F 点D在抛物线上 当
, : =2 ( >0) , ,
DOF 时 DF .
∠ =45° , =5
求抛物线C的方程
(1) ;
点P是第三象限内的动点 过P作抛物线C的两条切线PAPB 其中AB分别为
(2) , , ( ,
对应切线的切点 直线PO与AB垂直 垂足为点S.
), ,
证明 直线AB过定点
(i) : ;
(ii)
设
(i)
中定点为Q
,
等比数列 k
n
的首项k
1
是直线PO的斜率
,
第二项k
2
是直线PQ
的斜率.过P且斜率为k n 的直线交抛物线C于M N 两点 N 关于x轴的对称
n(⩾2) n, n , n
点为R .记 OMR 的面积为S 将1 1 1 构成的新数列记为数列
n △ n n n, S ,S ,……,S ,……
n
2 3 +1
PS
a 数列a 的前n项和为T .证明 当 最小时 T 1 .
n , n n : SQ ,n< p
2
高三数学 第 页 (共 页)
4 4