文档内容
2013年普通高等学校夏季招生全国统一考试数学文史类
(广东卷)
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.(2013广东,文1)设集合S={x|x2+2x=0,x∈R},T={x|x2-2x=0,x∈R},则S∩T=( ).
A.{0} B.{0,2} C.{-2,0} D.{-2,0,2}
lg(x+1)
2.(2013广东,文2)函数y = 的定义域是( ).
x-1
A.(-1,+∞) B.[-1,+∞)
C.(-1,1)∪(1,+∞) D.[-1,1)∪(1,+∞)
3.(2013广东,文3)若i(x+yi)=3+4i,x,y∈R,则复数x+yi的模是( ).
A.2 B.3 C.4 D.5
æ5π ö 1
4.(2013广东,文4)已知sin ç +a ÷ = ,那么cos α=( ).
è 2 ø 5
2 1 1 2
- -
5 5 5 5
A. B. C. D.
5.(2013广东,文5)执行如图所示的程序框图,若输入n的值为3,则输出s
的值是( ).
A.1 B.2 C.4 D.7
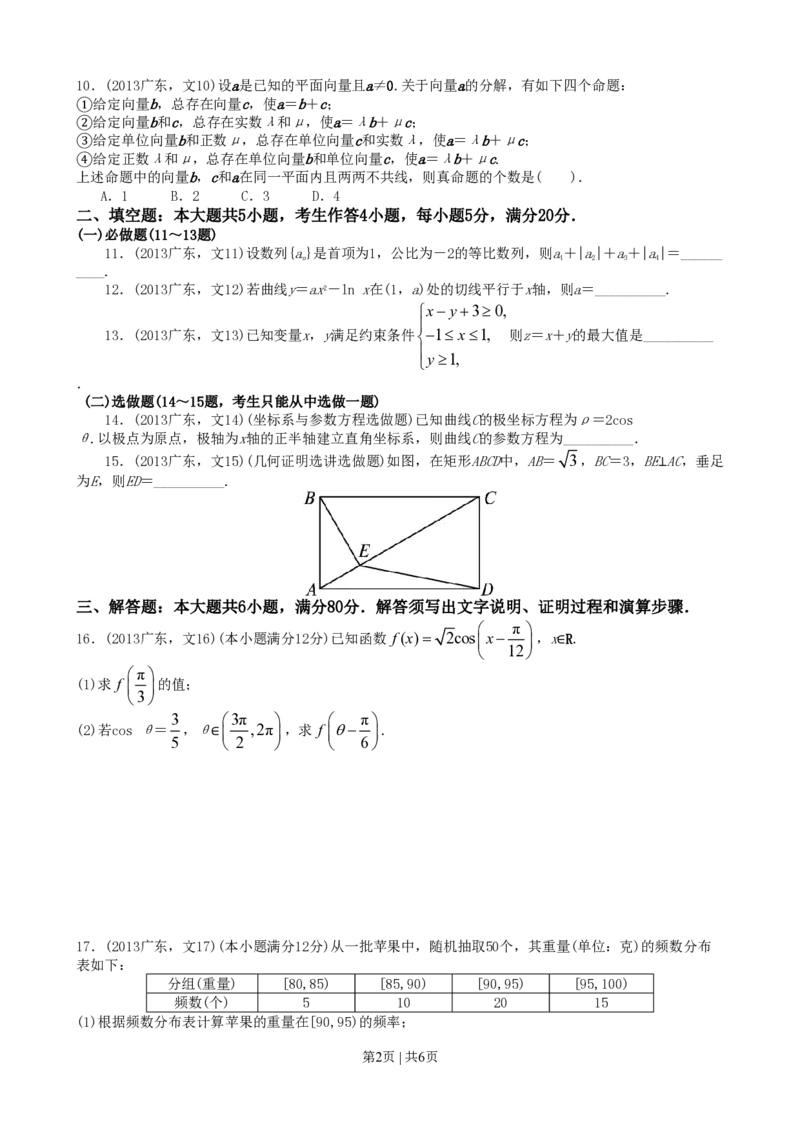
6.(2013广东,文6)某三棱锥的三视图如图所示,则该三棱锥的体积是(
).
1 1 2
6 3 3
A. B. C. D.1
7.(2013广东,文7)垂直于直线y=x+1且与圆x2+y2=1相切于第Ⅰ象限的直线方程是( ).
2 2
A.x+y- =0 B.x+y+1=0 C.x+y-1=0 D.x+y+ =0
8.(2013广东,文8)设l为直线,α,β是两个不同的平面.下列命题中正确的是( ).
A.若l∥α,l∥β,则α∥β B.若l⊥α,l⊥β,则α∥β
C.若l⊥α,l∥β,则α∥β D.若α⊥β,l∥α,则l⊥β
1
9.(2013广东,文9)已知中心在原点的椭圆C的右焦点为F(1,0),离心率等于 ,则C的方程是( ).
2
x2 y2 x2 y2 x2 y2 x2 y2
+ =1 + =1 + =1 + =1
3 4 4 3 4 2 4 3
A. B. C. D.
第1页 | 共6页10.(2013广东,文10)设a是已知的平面向量且a≠0.关于向量a的分解,有如下四个命题:
①给定向量b,总存在向量c,使a=b+c;
②给定向量b和c,总存在实数λ和μ,使a=λb+μc;
③给定单位向量b和正数μ,总存在单位向量c和实数λ,使a=λb+μc;
④给定正数λ和μ,总存在单位向量b和单位向量c,使a=λb+μc.
上述命题中的向量b,c和a在同一平面内且两两不共线,则真命题的个数是( ).
A.1 B.2 C.3 D.4
二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.
(一)必做题(11~13题)
11.(2013广东,文11)设数列{a}是首项为1,公比为-2的等比数列,则a+|a|+a+|a|=______
n 1 2 3 4
____.
12.(2013广东,文12)若曲线y=ax2-ln x在(1,a)处的切线平行于x轴,则a=__________.
ìx- y+3³0,
ï
13.(2013广东,文13)已知变量x,y满足约束条件í-1£ x£1, 则z=x+y的最大值是__________
ï
y³1,
î
.
(二)选做题(14~15题,考生只能从中选做一题)
14.(2013广东,文14)(坐标系与参数方程选做题)已知曲线C的极坐标方程为ρ=2cos
θ.以极点为原点,极轴为x轴的正半轴建立直角坐标系,则曲线C的参数方程为__________.
15.(2013广东,文15)(几何证明选讲选做题)如图,在矩形ABCD中,AB= 3,BC=3,BE⊥AC,垂足
为E,则ED=__________.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
æ π ö
16.(2013广东,文16)(本小题满分12分)已知函数 f(x)= 2cos ç x- ÷,x∈R.
è 12ø
æπö
(1)求 f ç ÷的值;
è3ø
3 æ3π ö æ πö
(2)若cos θ= ,θ∈ç ,2π ÷,求 f ç q- ÷.
5 è 2 ø è 6ø
17.(2013广东,文17)(本小题满分12分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布
表如下:
分组(重量) [80,85) [85,90) [90,95) [95,100)
频数(个) 5 10 20 15
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
第2页 | 共6页(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.
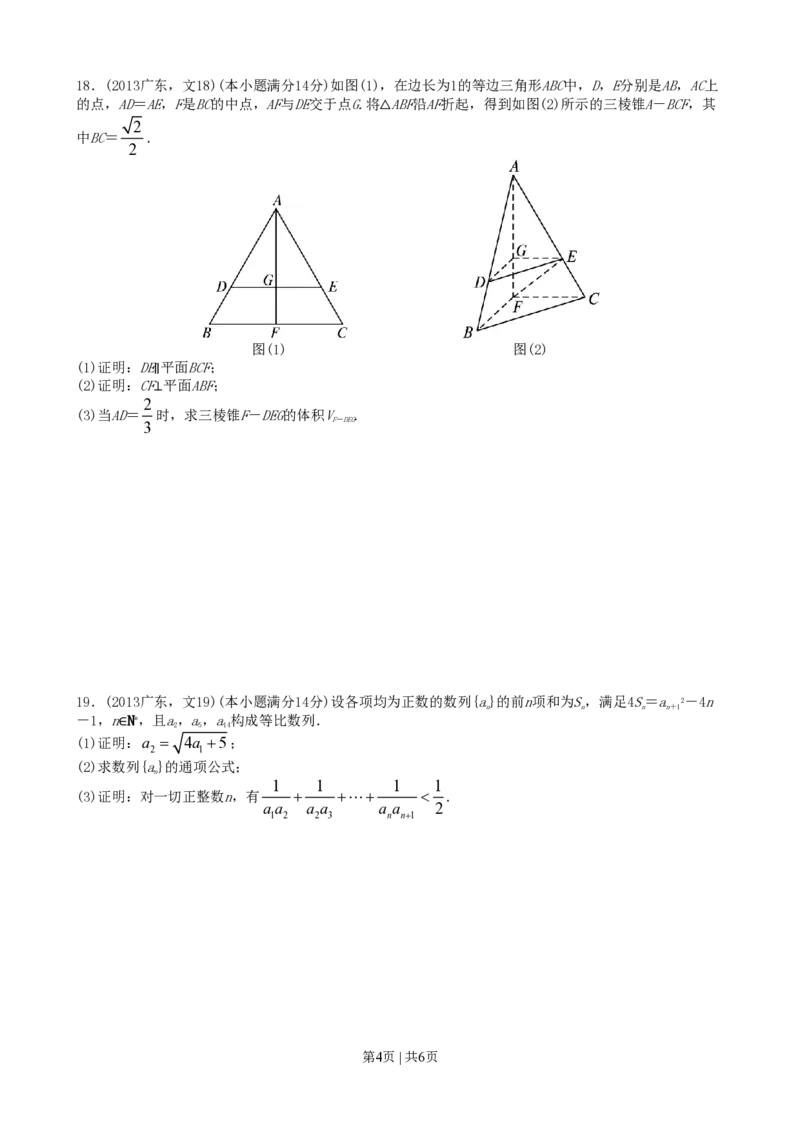
第3页 | 共6页18.(2013广东,文18)(本小题满分14分)如图(1),在边长为1的等边三角形ABC中,D,E分别是AB,AC上
的点,AD=AE,F是BC的中点,AF与DE交于点G.将△ABF沿AF折起,得到如图(2)所示的三棱锥A-BCF,其
2
中BC= .
2
图(1) 图(2)
(1)证明:DE∥平面BCF;
(2)证明:CF⊥平面ABF;
2
(3)当AD= 时,求三棱锥F-DEG的体积V .
F-DEG
3
19.(2013广东,文19)(本小题满分14分)设各项均为正数的数列{a}的前n项和为S,满足4S=a 2-4n
n n n n+1
-1,n∈N*,且a,a,a构成等比数列.
2 5 14
(1)证明:a = 4a +5;
2 1
(2)求数列{a}的通项公式;
n
1 1 1 1
(3)证明:对一切正整数n,有 + + + < .
L
aa a a a a 2
1 2 2 3 n n+1
第4页 | 共6页20.(2013广东,文20)(本小题满分14分)已知抛物线C的顶点为原点,其焦点F(0,c)(c>0)到直线l:x
3 2
-y-2=0的距离为 .设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
2
(1)求抛物线C的方程;
(2)当点P(x,y)为直线l上的定点时,求直线AB的方程;
0 0
(3)当点P在直线l上移动时,求|AF|·|BF|的最小值.
第5页 | 共6页21.(2013广东,文21)(本小题满分14分)设函数f(x)=x3-kx2+x(k∈R).
(1)当k=1时,求函数f(x)的单调区间;
(2)当k<0时,求函数f(x)在[k,-k]上的最小值m和最大值M.
第6页 | 共6页