2023~2024学年度第一学期四校联考（二）参考答案(1)(1)_2023年10月_0210月合集

2023~2024 学年第一学期四校联考（二）参考答案 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B D D B C C B BC BCD BCD ABD 2 4 13. 6 14. 15. k 1 16. (2, ). 2 ln21 部分试题答案详解 7.【答案】C x2 3x1 【解答】解：由题意知 x2 3x1kex 0有两个不同的解，即y 与 y  k 有 ex x2 3x1 x2 x2 (x2)(x1) 两个不同的交点，记g(x) ，则g(x)  ， ex ex ex 当x2时，g(x)0，g(x)单调递增;当2 x 1时，g(x)0，g(x)单调递减； 当x 1时，g(x)0，g(x)单调递增. 所以当x2时，函数g(x)有极大值e2，当x 1时，函 5 数g(x)有极小值 . 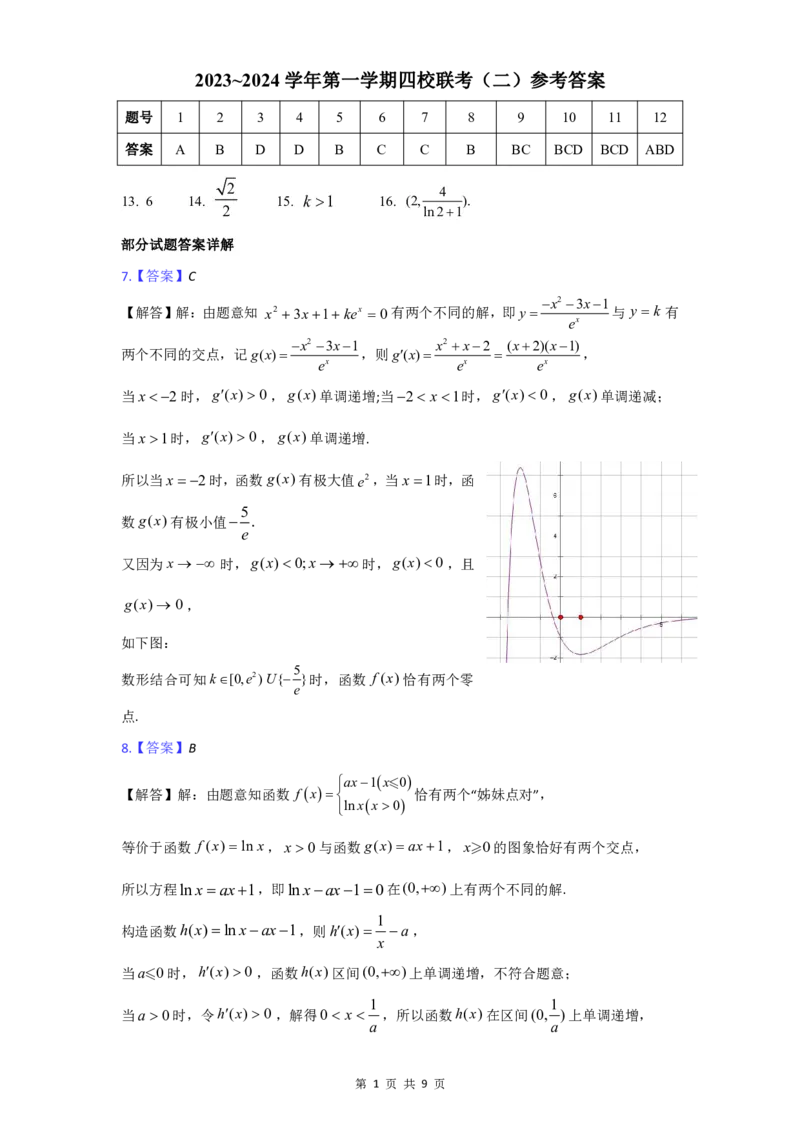e 又因为x   时，g(x)0;x 时，g(x)0，且 g(x) 0， 如下图： 5 数形结合可知k[0,e2)U{ }时，函数 f (x)恰有两个零 e 点. 8.【答案】B ax1x„0 【解答】解：由题意知函数 f x 恰有两个“姊妹点对”， lnxx0 等价于函数 f (x)  ln x，x0与函数g(x) ax1，x 0的图象恰好有两个交点， 所以方程lnxax1，即lnxax10在(0,)上有两个不同的解. 1 构造函数h(x)lnxax1，则h(x) a， x 当a„0时，h(x) 0，函数h(x)区间(0,)上单调递增，不符合题意； 1 1 当a 0时，令h(x) 0，解得0 x  ，所以函数h(x)在区间(0, )上单调递增， a a 第 1 页 共 9 页 {#{QQABIQaAoggoQAAAAAhCQwUQCAKQkBACCAoORBAIIAIAARFABAA=}#}1 1 令h(x) 0，解得x ，所以函数h(x)在区间( ,)上单调递减， a a 1 所以h( )0，解得0 a  e2 ， a 又h(e)lneae1ae0， 1 所以函数h(x)在(e, )上有且仅有一个零点， a 1 1 2 x 令M(x)lnx x 1，则M(x)   ， x 2 x 2x 令M(x)0，解得0 x 4， 所以函数M(x)在(0,4)上单调递增， 令M(x) 0，解得x4， 所以函数M(x)在区间(4,)上单调递减. 所以M(x) M(4)ln430， max 所以M(x)lnx x 1„M(4)0，即lnx x 1. 2 2 2 2 2 2 又h( )ln a 1 1a 1 (1 2)0， a2 a2 a2 a2 a2 a2 1 2 所以函数h(x)在( , )上有且仅有一个零点. a a2 综上可得0  a  e2. 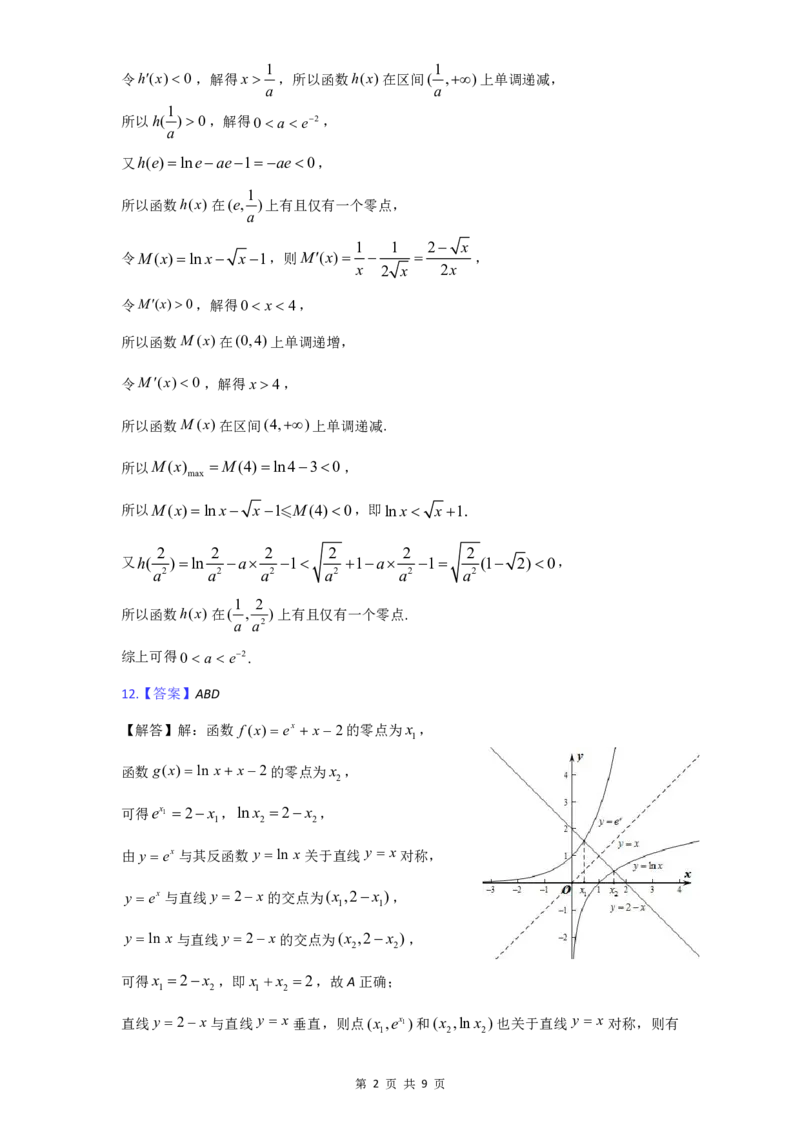12.【答案】ABD 【解答】解：函数 f (x) ex  x2的零点为x ， 1 函数g(x) ln x x2的零点为x ， 2 可得ex 1 2x ，lnx 2x ， 1 2 2 由 y ex 与其反函数 y ln x 关于直线 y  x对称， y ex 与直线 y 2 x的交点为(x ,2x )， 1 1 y ln x 与直线 y 2 x的交点为(x ,2x )， 2 2 可得x 2x ，即x x 2，故A正确； 1 2 1 2 直线 y 2 x与直线 y  x 垂直，则点(x ,ex1)和(x ,lnx )也关于直线 y  x 对称，则有 1 2 2 第 2 页 共 9 页 {#{QQABIQaAoggoQAAAAAhCQwUQCAKQkBACCAoORBAIIAIAARFABAA=}#}x lnx ，则有ex 1 lnx ex 1 x 2，故B正确； 1 2 2 1 3 3 1 3 又g(1) ln112 1 0，g ln  ln ln e 0， 2 2 2 2 1 1 1 3 g( e)ln e  e 2e2 22.252 0 ， 2 2 3 所以  x  e，则x x  x (2x ) x lnx ， 2 2 1 2 2 2 2 2 3  因为 y  xln x，x , e， 2  y 1lnx 0， 3  所以 y  xln x在 , e上单调递增， 2  e 所以x x  x ln x  eln e  ，故C错误； 1 2 2 2 2 3 3 由上可知x x  x ln x  ln ， 1 2 2 2 2 2 3 3 1 1 27  1 27 因为 ln   ln 1 ln 0， 2 2 2 2 8  2 8e 3 3 1 1 所以 ln  ，即x x  ，则x2 x 2 x x 2 2xx 42xx 3， 2 2 2 1 2 2 1 2 1 2 1 2 1 2 所以x2 x2 3，故D正确. 1 2 15.【答案】解：(1)令x  y 0，得 f(00) f(0) f(0)，所以 f(0)0. 证明：令 y x，得 f(xx) f(x) f(x) f(0)0， 所以 f(x)f(x)，所以 f(x)为奇函数． 由题知： f(k2x) f(4x18x 2x)0 f(0) ， 即 f(k2x 4x18x 2x) f(0) ， 又 y  f(x)是定义在R上的增函数， 所以k2x 4x18x 2x 0对任意x[1,2]恒成立， 所以k2x 2x 8x 4x1， 即k 122x 2x2， 1 令2x t ，t[ ,4]， 2 则g(t)t2 4t1，所以k  g(t) ， max 第 3 页 共 9 页 {#{QQABIQaAoggoQAAAAAhCQwUQCAKQkBACCAoORBAIIAIAARFABAA=}#}当t 4 时，g(t)  g(4)161611， max 所以k 1. 16.【解答】解： f(x) 2xa(lnx1)， 2 若函数 f(x) x2 axlnx 在( ,2)上不单调， e 2 则方程 f(x) 0在( ,2)上有根 e 2x 2 即方程a  在( ,2)上有根且方程的根是函数 f(x)的变号零点， lnx1 e 2x 2lnx 令g(x) ，则g(x) ， lnx1 (lnx1)2 2 x( ,1)时，g(x)0，g(x)递减，x(1,2)时，g(x)0，g(x)递增， e 2 4 4 2 4 4 又g(1) 2，g( ) ，g(2) ，由g(2) g( )  0， e eln2 ln21 e ln21 eln2 4 得g(x)(2, ), ln21 4 故a(2, ), ln21 4 故答案为：(2, ). ln21  f(0)b3, 17.【答案】解：(1)fxx2 2axb ，结合题意可得 ................1分 f(3)6ab90, a2 解得 ，经检验符合题意，. ..............................................3分 b3 1 故 f x x3 2x2 3x1. 3 所以在点  0, f 0 处的切线方程为y3x1. .............................................4分 （2）由(1)知 fx x2 4x3. 令 f(x)0，解得x3或x1，令 f(x)0，解得1 x3， 故 f(x)在,1,3,上单调递增，在1,3上单调递减， ...................................6分 所以 f x  f 1 7 ， f x  f 31； ...................................7分 极大值 3 极小值 （3） f(x)在  0,3  上有极大值，无极小值， 又因为 f 01， f 31，. 所以要使不等式 f  x m0能成立，则 f  x  m .............................8分 min 第 4 页 共 9 页 {#{QQABIQaAoggoQAAAAAhCQwUQCAKQkBACCAoORBAIIAIAARFABAA=}#}所以m1. ...........................................9分 故m取值取值范围是是  1，+ . ...........................................10分 3 18.【答案】解：(1)角θ 的终边上一点p1,y，且sin 得 2 所以θ为第四象限角，则y<0， ........................................1分 所以由 sin y ，y 3. .......................................3分 1y2 所以tanθ＝－ 3. ........................................4分 (2)因为tanθ＝－ 3，  cos( ) －cos () 所以 2 = sin ＋cos  .......................................6分 sin （）+cos （+） sin －cos  tanθ＋1 － 3＋1 ＝ ＝ ＝2－ 3. ........................................8分 tanθ－1 － 3－1      10 （3）因为   ,0， 0， ，且sin（+） 得  2   2 10  3 10 +(0, )，所以co（s +） 1sin（2 +） ， ...........................10分 2 10 .....................11分 所以coscos（ +）-cos（+）cossin（+）sin 3 10 1 10 3 =  + （- ） 10 2 10 2 3 10  30 = 20 ...........................................................12分 19.【答案】解：(1)当n 1时，a S 1;. .........................................................1分 1 1 当n 2时，a S S n2 (n1)2 2n1，.. .........................................................2分 n n n1 经检验，当n 1时，满足a 2n1，因此a 2n1. ......................................3分 n n 当n 1时，b T 3;. ....................................4分 1 1  n2n 3 T 当n 2时，b n  T n   n12n1 ( 3)2n 3n，. .....................................5分 n1 3 当n 1时，满足b 3n，因此b 3n. ......................................6分 n n 第 5 页 共 9 页 {#{QQABIQaAoggoQAAAAAhCQwUQCAKQkBACCAoORBAIIAIAARFABAA=}#}(2)由(1)知a b (2n1)3n， n n M 13332 533 (2n1)3n， ......................................7分 n 3M 132 333 534 (2n3)3n (2n1)3n1， ......................................8分 n 两式相减得 2M 32(32 33 34 3n)(2n1)3n1. .....................................9分 n 93n1 32 (2n1)3n1.. ....................................10分 13 6(2n2)3n1， ......................................11分 故M 3(n1)3n1. .........................................................12分 n 20.【答案】解：(1)f (x) (x22x)ex， 求导得 f(x)ex(x22). .........................................................1分 因为ex 0，令 f(x)ex(x22)0，即x2 20， 解得x 2 或x 2， 令 f(x)ex(x22)0，即x2 20， 解得 2  x 2 ， ........................................................4分 函数 f(x)在(, 2)和( 2,)上单调递增，在( 2, 2)上单调递减．..........5分 (2)①当0m„ 2时，  f(x)在[ 2, 2]上单调递减，  f(x)在区间[0,m]上的最大值为 f(0)0， f(x)在区间[0,m]上的最小值为 f(m)(m2 2m)em.......................................................7分 ②当 2 m„2时，  f(x)在[ 2, 2]上单调递减，在[ 2,)上单调递增， 且 f(0) f(2)0，  f(x)在区间[0,m]上的最大值为 f(0)0， f(x)在区间[0,m]上的最小值为 f( 2)(22 2)e 2. .................................9分 第 6 页 共 9 页 {#{QQABIQaAoggoQAAAAAhCQwUQCAKQkBACCAoORBAIIAIAARFABAA=}#}③当m2时，  f(x)在[ 2, 2]上单调递减，在[ 2,)上单调递增， 且 f(m)0 f(0)，  f(x)在区间[0,m]上的最大值为 f(m)(m2 2m)em， f(x)在区间[0,m]上的最小值为 f( 2)(22 2)e 2. ..................................11分 综上所述，当0m„ 2时，最大值为 f(0)0，最小值为 f(m)(m2 2m)em. 当 2 m„2时，最大值为 f(0)0，最小值为 f( 2)(22 2)e 2. 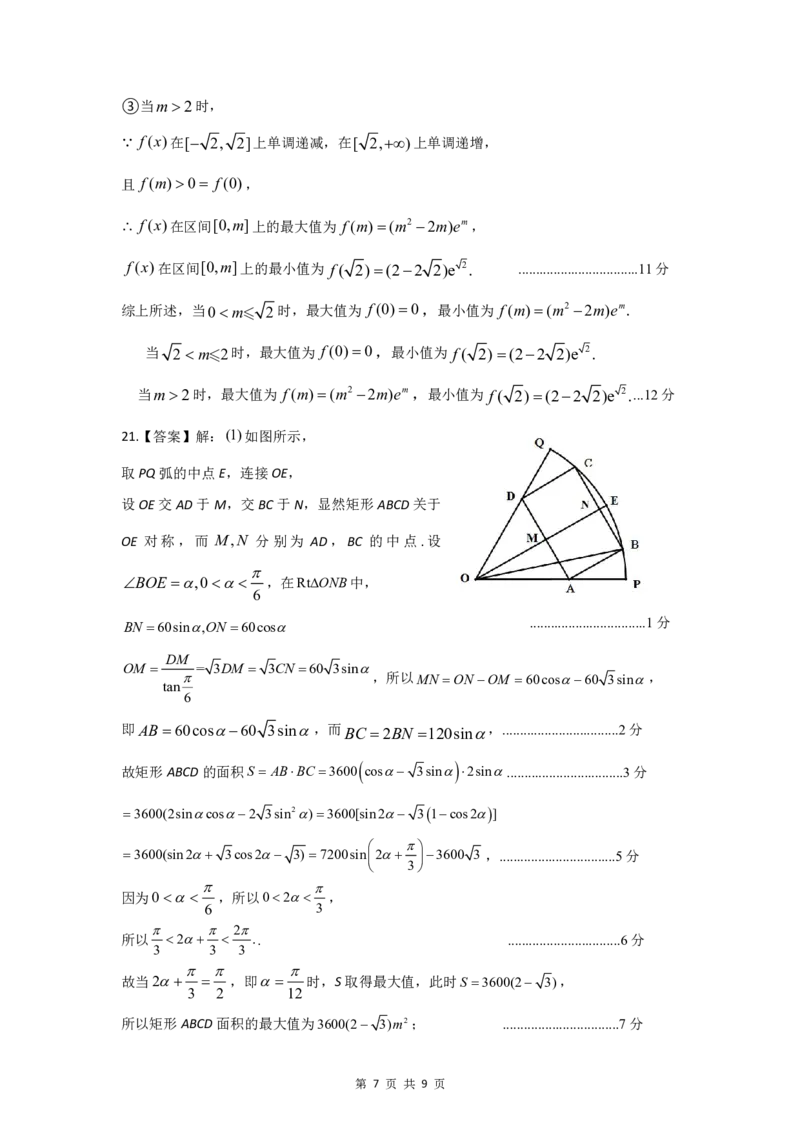当m2时，最大值为 f(m)(m2 2m)em，最小值为 f( 2)(22 2)e 2....12分 21.【答案】解：(1)如图所示， 取PQ弧的中点E，连接OE， 设OE交AD于M，交BC于N，显然矩形ABCD关于 OE 对称，而 M,N 分别为 AD，BC 的中点.设  BOE ,0 ，在RtONB中， 6 BN 60sin,ON 60cos .................................1分 DM OM  = 3DM  3CN 60 3sin  ，所以MN ON OM 60cos60 3sin， tan 6 即AB 60cos60 3sin，而 BC 2BN 120sin，.................................2分   故矩形ABCD的面积S  ABBC 3600 cos 3sin 2sin.................................3分 3600(2sincos2 3sin2)3600[sin2 31cos2]   3600(sin2 3cos2 3) 7200sin2 3600 3，.................................5分  3   因为0 ，所以02 ， 6 3   2 所以 2  .. 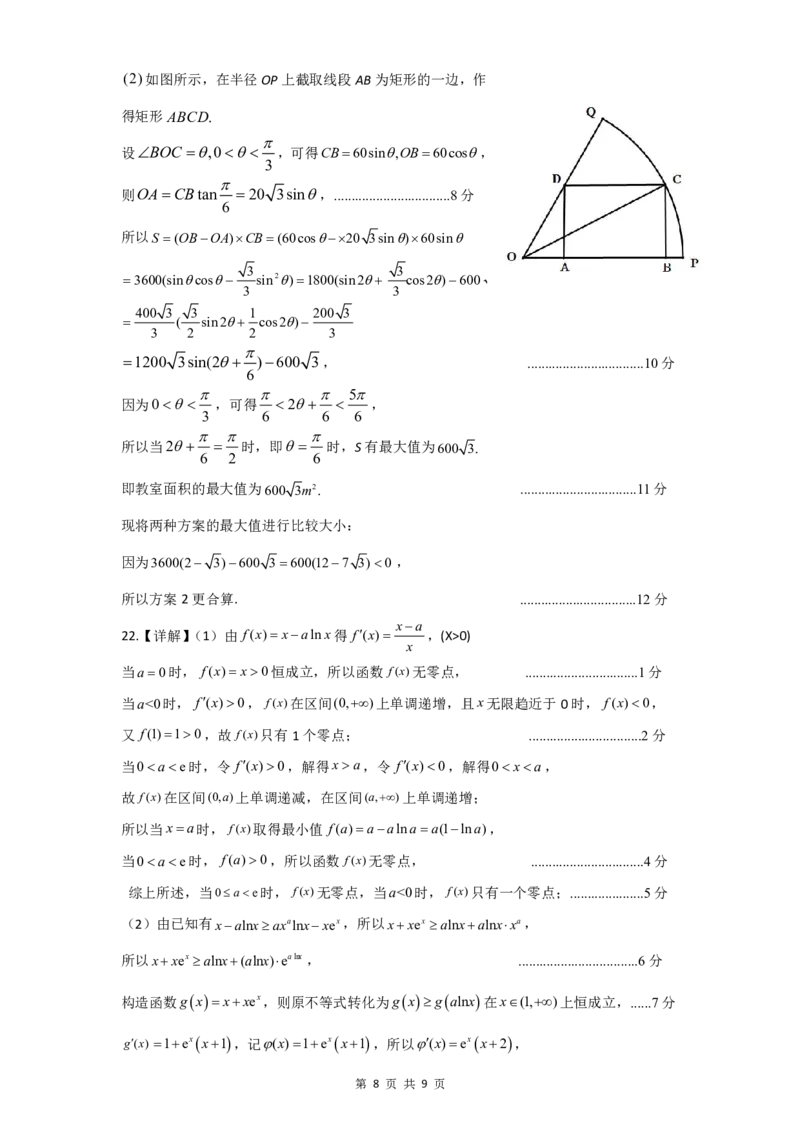................................6分 3 3 3    故当2  ，即 时，S取得最大值，此时S 3600(2 3)， 3 2 12 所以矩形ABCD面积的最大值为3600(2 3)m2； .................................7分 第 7 页 共 9 页 {#{QQABIQaAoggoQAAAAAhCQwUQCAKQkBACCAoORBAIIAIAARFABAA=}#}(2)如图所示，在半径OP上截取线段AB为矩形的一边，作 得矩形 ABCD.  设BOC ,0 ，可得CB60sin,OB60cos， 3  则OACBtan 20 3sin，.................................8分 6 所以S (OBOA)CB(60cos20 3sin)60sin 3 3 3600(sincos sin2)1800(sin2 cos2)600 3 3 3 400 3 3 1 200 3  ( sin2 cos2) 3 2 2 3  1200 3sin(2 )600 3， .................................10分 6    5 因为0 ，可得 2  ， 3 6 6 6    所以当2  时，即 时，S有最大值为600 3. 6 2 6 即教室面积的最大值为600 3m2. .................................11分 现将两种方案的最大值进行比较大小： 因为3600(2 3)600 3600(127 3)0 ， 所以方案2更合算. .................................12分 xa 22.【详解】（1）由 f(x) xalnx得 f(x) ，(X>0) x 当a0时， f(x) x0恒成立，所以函数 f(x)无零点， ................................1分 当a<0时， f(x)0， f(x)在区间(0,)上单调递增，且x无限趋近于0时， f(x)0， 又 f(1)10，故 f(x)只有1个零点； ................................2分 当0ae时，令 f(x)0，解得xa，令 f(x)0，解得0xa， 故 f(x)在区间(0,a)上单调递减，在区间(a,)上单调递增； 所以当xa时， f(x)取得最小值 f(a)aalnaa(1lna)， 当0ae时， f(a)0，所以函数 f(x)无零点， ................................4分 综上所述，当0ae时， f(x)无零点，当a<0时， f(x)只有一个零点；.....................5分 （2）由已知有xalnxaxalnxxex，所以xxex alnxalnxxa， 所以xxex alnx(alnx)ealnx ， ..................................6分 构造函数gxxxex，则原不等式转化为gxgalnx在x(1,)上恒成立，......7分 g(x) 1exx1，记(x)1exx1，所以(x)exx2， 第 8 页 共 9 页 {#{QQABIQaAoggoQAAAAAhCQwUQCAKQkBACCAoORBAIIAIAARFABAA=}#}令(x)0，解得x2，令(x)0，解得x<2，... 故(x)在区间(,2)上单调递减，在区间(2,)上单调递增， 1 所以(x)(2)1 0，所以g(x)0，即g(x)单调递增，..................................8分 e2 所以xalnx在x(1,)上恒成立， x 即a 在x(1,)上恒成立，. ..................................9分 lnx 令hx x ，(x1)，则h(x) lnx1 ， lnx lnx2 令h(x)0，解得xe，令h(x)0，解得1xe， ..................................10分 e 故h(x)在(1,e)单调递减，(e,)单调递增，则h(x)的最小值为h(e) e，...........11分 lne 所以a的取值范围是(,e]. .................................12分 第 9 页 共 9 页 {#{QQABIQaAoggoQAAAAAhCQwUQCAKQkBACCAoORBAIIAIAARFABAA=}#}