文档内容
%&%’届!皖南八校"高三开学考试#数学
参考答案$解析及评分细则
!!(!因为")(#"#)%$))%&**+&*%)(#"#)槡!,$%))+&*!,*所以"#%)%&*!,*故选(!
%,. %%,.&%!,%.& /.
%!-!因为&%!*%.&)%,.*所以&) ) ), ),.*故选-!
!*%. %!*%.&%!,%.& /
’!(!由题可知*!$"),%,%’)&*解得’),!!故选(0
1!$!()234&!5 /$234&!/ /$234&!/ &!5))$!**)&!5,&!/%!*故*%)%(*故选$!
/!6!频率分布直方图中*最低小矩形所在的区间为%%&*%/,*故选项-错误!
由频率分布直方图可得*前三个小矩形的面积之和为%&!&%*&!&1*&!&15&7/)&!/’/%&!/*所以估计该
小区居民在该滑冰馆的锻炼天数的中位数小于!/*故选项(错误-
,
由频率分布直方图可得*$)&!&%7/7%!/*&!&17/75!/*&!&157/7!%!/*&!&"7/7!5!/*&!&!’7
/7%%!/*&!&%7/7%5!/)!1!!/%!1*故选项6正确-
由频率分布直方图可得*该小区居民在该滑冰馆的锻炼天数超过!/天的概率为%&!&"*&!&!’*&!&%&7
/)&!1"/*故选项$错误!故选6!
"!(!由题意*设数列公差为+!因为*
’
**
/
)%*
!
*"+),!&*,
"
)"*
!
*!/+),1%*
解得*),!5*+)1*所以, )!&**1/+),!5&*1/71)!&*故选(!
! !& !
! !
5!-!因为’),!*所以直线-
!
.,$*%#*!)&*直线-
%
.
%
$,#*
%
)&*-
!
与-
%
平行*故充分条件成立-当
! !
直线-
!
.’$*%#*!)&与直线-
%
.
%
$*’#*
%
)&平行时*’%)!*解得’)!或’),!*当’)!时*直线
-
!
.$*%#*!)&与直线-
%
.$*%#*!)&重合*当’),!时*直线-
!
.$,%#,!)&*直线-
%
.$,%#*!)&平
行*故充要条件成立!故选-!
!
8!6!设切线的切点坐标为%$
&
*#& &*#)29$*$%*#.)
$
*%$*
’ !
$)
! & % ($ & )! %! ! !&
#."$)$& )
$ &
*%$
&
)’*解得&
(
#& )29
!
%
*
!
1
*或
#& )!
*所以切点坐标为%!*!&或
%
*29
%
*
1
*
/
所求的切线方程为’$,#,%)&或’$,#, ,29%)&!故选6!
1
! /! /! !
:!$!由%$, ) */)!*可得$) * */)!
’ % 1 "
! ! ! /!
当/)&时*$) *当/)!时*$) * ) *
" 1 " !%
! ! ! % ! &
当/),!时*$), * ), *所以 , *& 为0%$&图象的一个对称中心*故选$!
1 " !% !%
!&!(!取11
!
*12的中点分别为"*%*连接3"*"%*3%*则易证明3"*45*
因为3"+平面3
!
45*45,平面3
!
45*所以3"*平面3
!
45*又因为3
!
4*
"%*"%+平面3
!
45*3
!
4,平面3
!
45*所以"%*平面3
!
45*"%#3")
"*所以平面3
!
45*平面3"%*36,平面3"%*所以36*平面3
!
45*当
36-"%时*36有最小值*则易求出3")3%)槡/*"%)槡%*6为"%的中
!"皖八#高三开学$数学试卷参考答案!第!!!!!页%共"页&’ #$
书书书点*36)槡3%%, %"%&% ) ’槡% *所以36的最小值为 ’槡% *故选(!
% % %
!!!6!设"%’*7&*因为点"在抛物线2.#%)%8$上*所以7%)%8’*
8
以点"为圆心的圆与2的准线相切*所以’* )/*圆"与$轴相交的弦长为"*所以’%*7%)/%*所以
%
8%,!&8*!")&*解得8)%或8)8*故选60
!%!$!;函数#)0%$*!&的图关于直线$),’对称*
<函数#)0%$&的图关于直线$),%对称*
<0%,%*$&)0%,%,$&!
;对.$)"有0%$&*0%,$&)%*
<函数#)0%$&的图象关于%&*!&中心对称*
<0%,%*$*%&)0+,%,%$*%&,*即0%$&)0%,1,$&)%,0%,$&!
又;0%,1,$&*0%$*1&)%*即0%,1,$&)%,0%$*1&*
<0%$*1&)0%,$&*
<0+%$*1&*1,)0+,%$*1&,)0%$&*即0%$*8&)0%$&*
<0%$&的周期9)8*<0%%&%%&)0%%/%78*"&)0%"&)0%%*1&)0%,%&)%,0%%&)%,%%*%&),%!
% !&1 % !&:
!’!"! $,
$
的通项为9
:*!
)6:
1
$1,: ,
$
)6:
1
$%,!&:$$1,%:*令1,%:)&*得:)%*所以常数项为9
’
)
6%$%,!&%)"!
1
!1! !’ !因为&$!$ ! *=.9!) ’ *所以>3=!)槡!,=.9%!)槡!, : ) 1 *
: % / %/ /
=.9! ’ !
所以?@9!) ) !因为?@9%!," &), *
>3=! 1 ’
所以?@9")?@9+!,%!," &,)
!
?
*
@
?
9
@
!
9!
,?
$
@
?
9
@
%
9
!
%!
,"
,"
&
&
’ % !& !’
, ,
1 ’ !% !’
) ) ) !
’ % !& ’ :
!* 7 ,
1 ’ 1
/!
!/!
1&
!如图所示*该四棱锥为5 3421*底面中心为;
!
*外接球球心为;*
设;;)+*由题意;3);5*即槡+%* : )+*%*解得+) ! *
! % 8
因为/542是等腰三角形*42)’*42边上的高为槡1* :
1
) /
%
*所以,
/542
) !
1
/ *
!
设点;到平面542的距离为<*则三棱锥; 542的体积为 , $<)
’ /542
! !/ : %! & /!
, $;5*即 7<) 7 *% *解得<) !
’ /;!42 1 1 8 1&
!"!槡%$,#,’槡%)&或槡%$*#,’槡%)&!设直线-的方程为#)/%$,’&*
(#)/%$,’&*
联立方程组 得%%/%,!&$%,!%/%$*!8/%*")&*
$%,%#%)"*
!"皖八#高三开学$数学试卷参考答案!第!!!!%页%共"页&’ #$因为O3,符合题意;......,,....................................................... 8分
4 4
当n=5时,此时 所有产品均选择方案甲测试, 则X~B作,一 2) ,
所以E(X+Y)= E(X) =5X— 1 =— 5 <3,不符合题意; ......................................................... 10分
2 2
当n=l,2,3,4时,X~的分),Y-B(5-11,¾),
所以E(X+Y)= E(X)+E(Y)=—
2
1
.
'
1.1+.
3(5-
4
11) =一15-—
4
-
11
,
15-n
若使,ECX+Y)= 4 �3,解得咚;;;3,则n=l,2.3
综上,选择甲方案测试的产品个数为0,1,2,3时,测试合格的产品个数的期望不小于3. ............ 12分
20.(1)证明:?PA=PC,O为AC的中点,...PO上AC.
p
·:AB=BC,O为AC的中点,.· .AC上OB. ············································· 2分
·:po上AC,AC上OB,oBnPO=O,OB,PO仁平面PBO,
:.AC上平面PBO.··········································································· 4分
(2) 解:·:AB上BC,AB= BC= 2, PA= PB= PC= 2,,/z,0为AC的中点,AC=勾2, A c
:.BO=石,PO=顶,. . .PO'-+OB'= PB',:P. O上OB.
/3
又?AC上OB,AcnPO= O,AC,PO已平面PAC,
图1
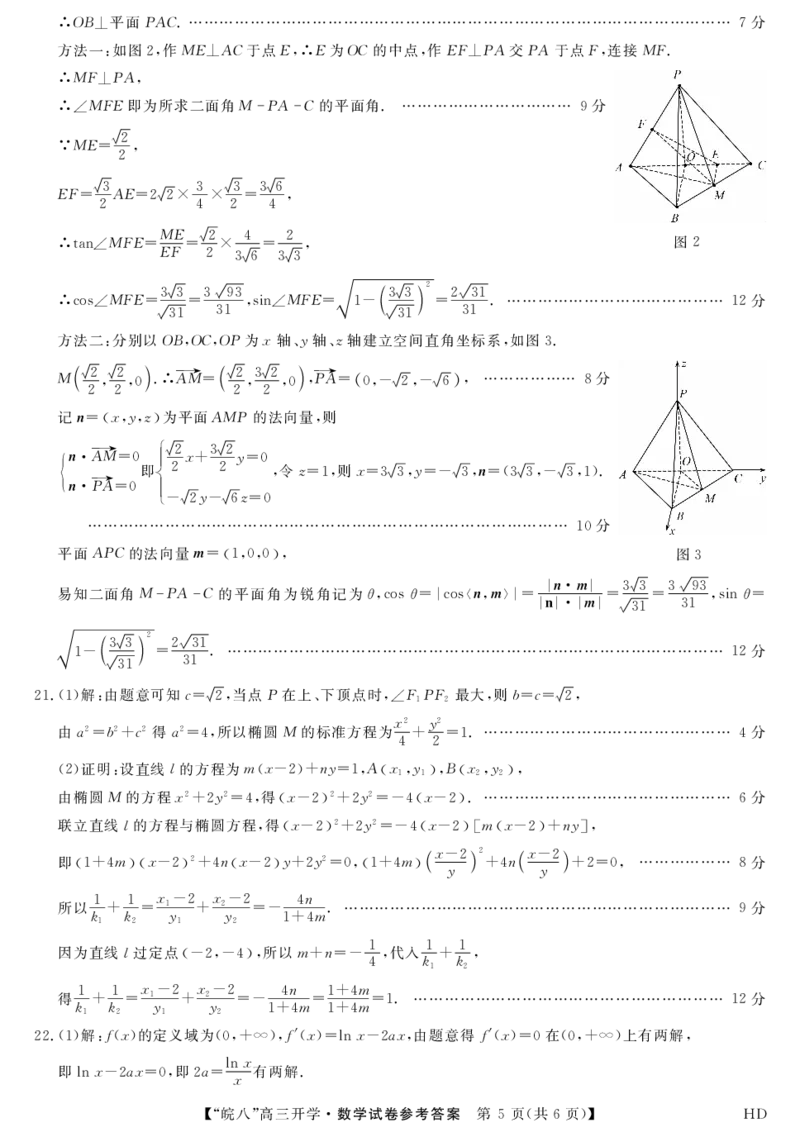
【 “ 皖八 “ 高三开学.数学试卷参考答案 第4页(共6页)】 HD:.QB上平面PAC. ......................................................................................................... 7分
方法一:如图2,作ME上AC于点£,:.£为0C的中点,作EF上PA交PA于点F,连接MF.
p
:.MF..lPA,
.立MF£即为所求二面角M-PA -C的平面角 ................................. 9分
:· ME=
迈—,
2 A r
-
EF=— 万 AE=泣X— 3灯X—=3 — 万 ,
2 4 2 4
B
.二tan乙MF£= M
E
—
F
E 孜=-
2
X
3
—
病
4
袁
=— 2 ' 图2
[勹陑尸辛
cos乙MFE=慧=�,sin乙MFE= .......................................... 12分
方法二:分别以OB,OC,OP为工.轴、y轴、z轴建立空间直角坐标系,如图3.
M 停享 0). :.諒=停琴, o) ,丙=( o ,-迈,-顶), ... ··•············ 8分
IP
记11=(x,y,z)为平面AMP的法向队,则
{'
昼
1 ·諒=0 x+立y=0
即{ 2 2 ,令z=1,则又·=3万,y=-寂,n=(3万,-石,I) A
ll •亢=0
-迈y-顶z=O
............................................................................................. 10分
平面APC的法向址,11=(1,0,0),
易知二面角M-PA-C的平面角为锐角记为0,cos 0= I cos (11,111〉| = In·m l袁 =——= 3旱 ,sin 0=
lln · 1ml,/3f 31
平
厂`尸 ................................................................................................ 12分
21. (1)解:由题意可知c=J',.了,当点P在上、下顶点时,乙F,PF2最大,则b=c=拉一,
z
由矿=bz+cz 得a2=4,所以椭圆M的标准方程为�+立=1~.· ..................…........................... 4分
4. 2
(2)证明:设直线l的方程为m(x-2)+11y=l,A(x1,Y1),B(立,Yz),
由椭圆M的方程又,z+2yz =4,得(几一· 2)2+2y2=-4( x-2), ................................................ 6分
联立直线l的方程与椭圆方程,得(x-2)2+2y'=-4(x-2)[m(x-Z)+ny],
即0+4m)(x-2)2+4n(x-2)y+2y2 =0, 0+4m)( �) ) '+4n( ( �) ) +2=0, .................. 8分
y y
所以上十上=立二色卜丑二2=- 4n ........................................................................... 9分
',k 2k y1'y2 l+4m'
1 1. 1
因为直线l过定点(-2,-4),所以m+1/=-— 4 ,"代"人/'一 1k 十'一 2k '
得— 1, + — 1 = .'.Xl,-一2,+ x2-2 = 411 = 1+4m = 1. ............................................................ 12分
lk 2k y,'yz l+4m 1+4m
22. (1)解:f(x)的定义域为(0,十oo),/(x)=ln工呵-2ax,由题意得f'釭)=0在(0,十oo)上有两解,
即In丑:-2ax=O,即2a=宁有两解
【 “ 皖八 “ 高三开学.数学试卷参考答案 第5页(共6页)】 HD<;4-平面532!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 5分
方法一.如图%*作"@-32于点@*<@为;2的中点*作@A-53交53于点A*连接"A!
<"A-53*
<3"A@即为所求二面角" 53 2的平面角! !!!!!!!!!!! :分
槡%
;"@) *
%
槡’ ’ 槡’ ’槡"
@A) 3@)%槡%7 7 ) *
% 1 % 1
3=3"A@) ) *=.93"A@)槡!, ) !!!!!!!!!!!!!!! !%分
槡’! ’! 槡’! ’!
方法二.分别以;4*;2*;5为$轴0#轴0&轴建立空间直角坐标系*如图’!
" %槡% * 槡% *& & !<3 554 ") %槡% * ’槡% *& & *5 554 3)%&*,槡%*,槡"&* !!!!!! 8分
% % % %
记#)%$*#*&&为平面3"5的法向量*则
554 ’槡% ’槡%
(#$3")& $* #)&
即& % % *令&)!*则$)’槡’*#),槡’*#)%’槡’*,槡’*!&!
554
#$53)&
(,槡%#,槡"&)&
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !&分
平面352的法向量$)%!*&*&&* 图’
"#$$" ’槡’ ’槡:’
易知二面角" 53 2的平面角为锐角记为#*>3=#)">3=1#*$2") ) ) *=.9#)
"#"$"$" 槡’! ’!
%’槡’&%
%槡’!
槡!, ) !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !%分
槡’! ’!
%!!%!&解.由题意可知()槡%*当点5在上0下顶点时*3A
!
5A
%
最大*则))()槡%*
$% #%
由*%))%*(%得*%)1*所以椭圆"的标准方程为 * )!!!!!!!!!!!!!!!!!! 1分
1 %
%%&证明.设直线-的方程为’%$,%&*7#)!*3%$
!
*#! &*4%$
%
*#% &*
由椭圆"的方程$%*%#%)1*得%$,%&%*%#%),1%$,%&!!!!!!!!!!!!!!!!! "分
联立直线-的方程与椭圆方程*得%$,%&%*%#%),1%$,%&+’%$,%&*7#,*
%$,%&% %$,%&
即%!*1’&%$,%&%*17%$,%&#*%#%)&*%!*1’& *17 *%)&* !!!!!! 8分
# #
! ! $,% $,% 17
所以 * ) ! * % ), !!!!!!!!!!!!!!!!!!!!!!!!!! :分
/ ! / % #! #% !*1’
! ! !
因为直线-过定点%,%*,1&*所以’*7), *代入 * *
1 / /
! %
! ! $,% $,% 17 !*1’
得 * ) ! * % ), ) )!! !!!!!!!!!!!!!!!!!!!! !%分
/ ! / % #! #% !*1’ !*1’
%%!%!&解.0%$&的定义域为%&**+&*0.%$&)29$,%*$*由题意得0.%$&)&在%&**+&上有两解*
29$
即29$,%*$)&*即%*) 有两解!
$
!"皖八#高三开学$数学试卷参考答案!第!!!!/页%共"页&’ #$29$
令B%$&) %$%&&*即B%$&的图象与直线#)%*有两个交点!!!!!!!!!!!!!!!! %分
$
!,29$
B.%$&) )&*得$)B*当$)%&*B&时*B.%$&%&*B%$&单调递增-
$%
!
当$)%B**+&时*B.%$&$&*B%$&单调递减*