文档内容
专题 11 立体几何的基本概念、点线面位置关系
及表面积、体积的计算小题综合
考点 十年考情(2015-2024) 命题趋势
2024·全国甲卷、2024·天津卷、2022·全国乙卷
考点1 点线面 2021·浙江卷、2021·全国新Ⅱ卷、2019·全国卷
的位置关系及 2019·全国卷、2019·北京卷、2017·全国卷
1.理解、掌握空间中点线面的
其判断 2016·浙江卷、2016·山东卷、2016·全国卷
位置关系及相关的图形和符号
(10年7考) 2015·浙江卷、2015·湖北卷、2015·广东卷
语言,熟练掌握平行关系的判
2015·福建卷、2015·北京卷
定定理和性质定理及其应用,
熟练掌握垂直关系的判定定理
2024·全国新Ⅰ卷、2024·天津卷、2024·全国甲卷
和性质定理及其应用,该内容
2024·北京卷、2023·全国甲卷、2023·全国乙卷
是新高考卷的常考内容,需强
2023·全国新Ⅰ卷、2023·天津卷、2023·全国新Ⅰ卷
化巩固复习.
2023·全国新Ⅱ卷、2022·天津卷、2022·全国甲卷
考点2 求几何
2022·全国新Ⅰ卷、2022·全国新Ⅱ卷、2021·全国新
体的体积 2.了解柱、锥、台体及简单组
Ⅱ卷2021·北京卷、2021·全国新Ⅰ卷、2020·海南卷
(10年10 合体的结构特征及其相关性
2020·江苏卷、2019·江苏卷、2019·全国卷
考) 质,会运用柱体、锥体、台体
2019·天津卷、2018·江苏卷、2018·全国卷
等组合体的表面积和体积的计
2018·天津卷、2018·天津卷、2017·全国卷
算公式求解相关问题,该内容
2016·浙江卷、2015·上海卷、2015·江苏卷 是新高考卷的常考内容,一般
2015·全国卷、2015·山东卷、2015·山东卷 给定柱、锥、台体及简单组合
体,求对应的表面积与体积,
考点3 求几何
需强化复习.
体的侧面积、 2023·全国甲卷、2021·全国新Ⅰ卷、2021·全国甲卷
表面积 2020·全国卷、2018·全国卷、2018·全国卷
(10年4考)考点01 点线面的位置关系及其判断
1.(2024·全国甲卷·高考真题)设 为两个平面, 为两条直线,且 .下述四个命题:
①若 ,则 或 ②若 ,则 或
③若 且 ,则 ④若 与 , 所成的角相等,则
其中所有真命题的编号是( )
A.①③ B.②④ C.①②③ D.①③④
2.(2024·天津·高考真题)若 为两条不同的直线, 为一个平面,则下列结论中正确的是( )
A.若 , ,则 B.若 ,则
C.若 ,则 D.若 ,则 与 相交
3.(2022·全国乙卷·高考真题)在正方体 中,E,F分别为 的中点,则( )
A.平面 平面 B.平面 平面
C.平面 平面 D.平面 平面
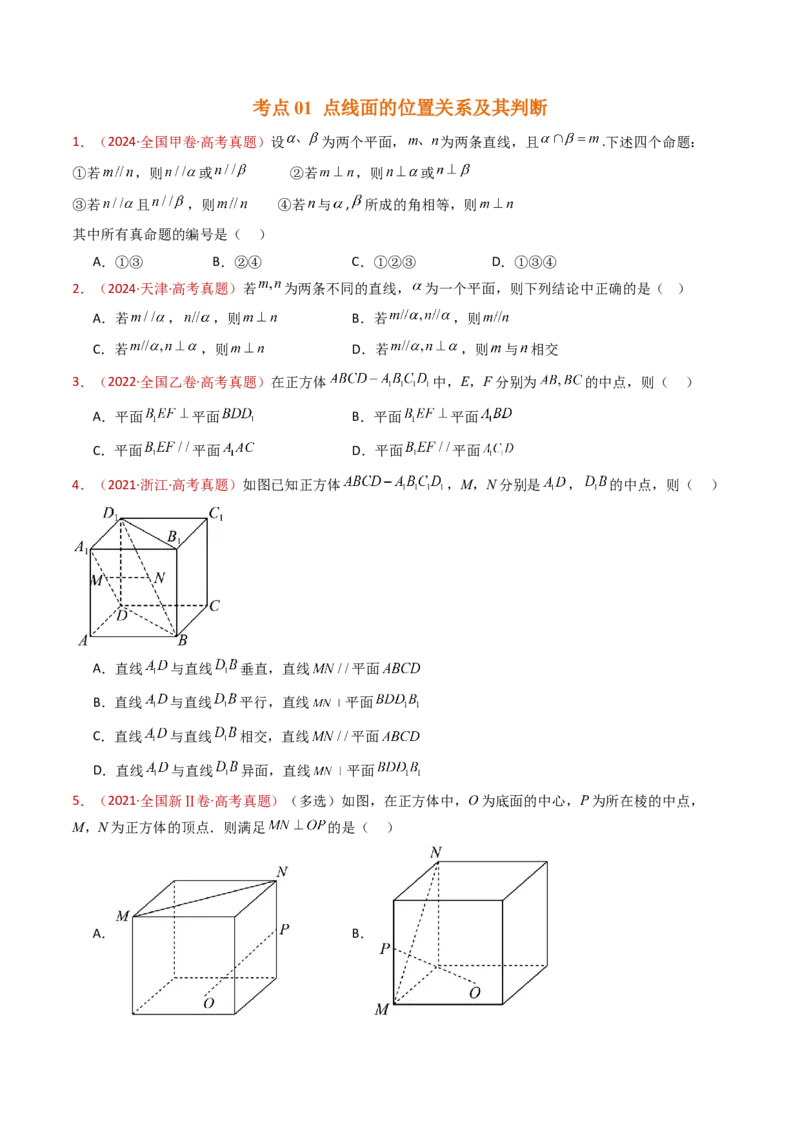
4.(2021·浙江·高考真题)如图已知正方体 ,M,N分别是 , 的中点,则( )
A.直线 与直线 垂直,直线 平面
B.直线 与直线 平行,直线 平面
C.直线 与直线 相交,直线 平面
D.直线 与直线 异面,直线 平面
5.(2021·全国新Ⅱ卷·高考真题)(多选)如图,在正方体中,O为底面的中心,P为所在棱的中点,
M,N为正方体的顶点.则满足 的是( )
A. B.C. D.
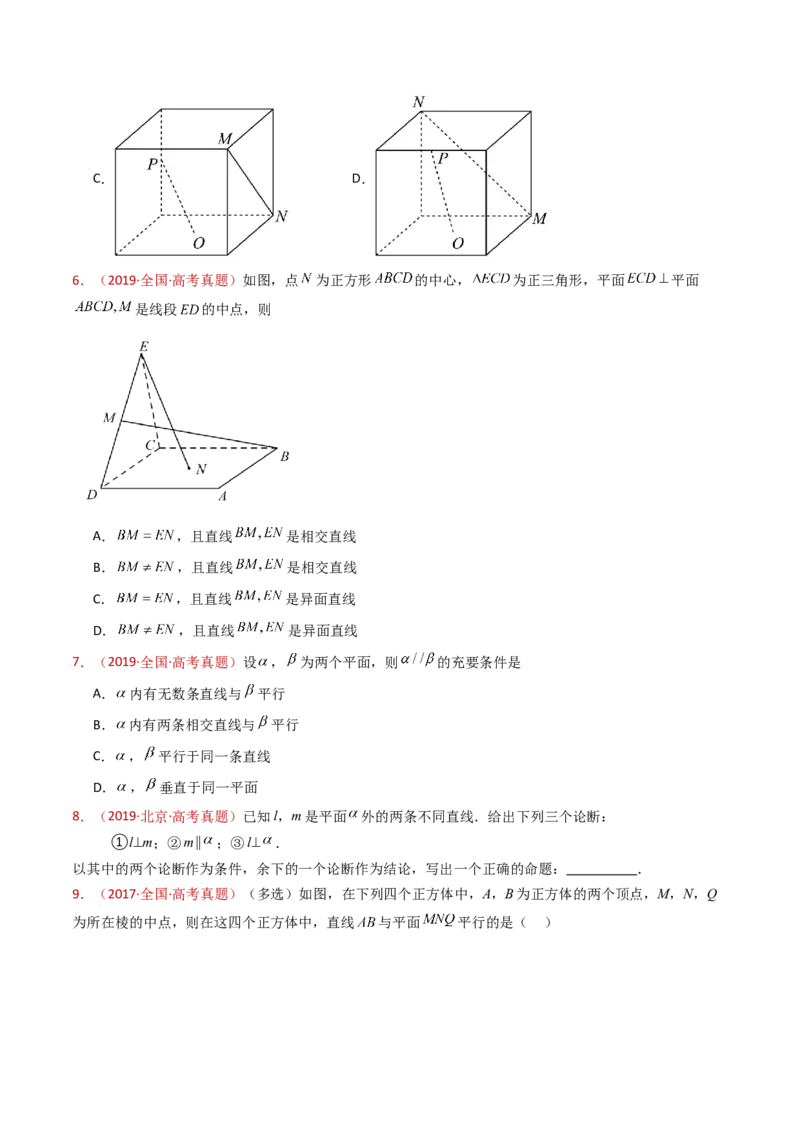
6.(2019·全国·高考真题)如图,点 为正方形 的中心, 为正三角形,平面 平面
是线段 的中点,则
A. ,且直线 是相交直线
B. ,且直线 是相交直线
C. ,且直线 是异面直线
D. ,且直线 是异面直线
7.(2019·全国·高考真题)设 , 为两个平面,则 的充要条件是
A. 内有无数条直线与 平行
B. 内有两条相交直线与 平行
C. , 平行于同一条直线
D. , 垂直于同一平面
8.(2019·北京·高考真题)已知l,m是平面 外的两条不同直线.给出下列三个论断:
①l⊥m;②m∥ ;③l⊥ .
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题: .
9.(2017·全国·高考真题)(多选)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q
为所在棱的中点,则在这四个正方体中,直线 与平面 平行的是( )A. B.
C. D.
10.(2016·浙江·高考真题)已知互相垂直的平面 交于直线l.若直线m,n满足m∥α,n⊥β,则
A.m∥l B.m∥n C.n⊥l D.m⊥n
11.(2016·山东·高考真题)已知直线a,b分别在两个不同的平面 , 内 则“直线a和直线b相交”是
“平面 和平面 相交”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12.(2016·全国·高考真题)α、β是两个平面,m、n是两条直线,有下列四个命题:
(1)如果m⊥n,m⊥α,n∥β,那么α⊥β.(2)如果m⊥α,n∥α,那么m⊥n.
(3)如果α∥β,m α,那么m∥β. (4)如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
13.(2015·浙江·高考真题)设 , 是两个不同的平面, , 是两条不同的直线,且 ,
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
14.(2015·湖北·高考真题) 表示空间中的两条直线,若p: 是异面直线;q: 不相交,则
A.p是q的充分条件,但不是q的必要条件
B.p是q的必要条件,但不是q的充分条件
C.p是q的充分必要条件
D.p既不是q的充分条件,也不是q的必要条件
15.(2015·广东·高考真题)若直线 和 是异面直线, 在平面 内, 在平面 内,l是平面 与平面的交线,则下列命题正确的是
A. 与 , 都相交 B. 与 , 都不相交
C. 至少与 , 中的一条相交 D. 至多与 , 中的一条相交
16.(2015·福建·高考真题)若 是两条不同的直线, 垂直于平面 ,则“ ”是“ ”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
17.(2015·北京·高考真题)设 , 是两个不同的平面, 是直线且 .“ ”是“ ”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
考点02 求几何体的体积
1.(2024·全国新Ⅰ卷·高考真题)已知圆柱和圆锥的底面半径相等,侧面积相等,且它们的高均为 ,
则圆锥的体积为( )
A. B. C. D.
2.(2024·天津·高考真题)一个五面体 .已知 ,且两两之间距离为1.并已知
.则该五面体的体积为( )
A. B. C. D.
3.(2024·全国甲卷·高考真题)已知圆台甲、乙的上底面半径均为 ,下底面半径均为 ,圆台的母线长分
别为 , ,则圆台甲与乙的体积之比为 .
4.(2024·北京·高考真题)汉代刘歆设计的“铜嘉量”是龠、合、升、斗、斛五量合一的标准量器,其中
升量器、斗量器、斛量器的形状均可视为圆柱.若升、斗、斛量器的容积成公比为10的等比数列,底面直
径依次为 ,且斛量器的高为 ,则斗量器的高为 ,升量器的高为
.
5.(2023·全国甲卷·高考真题)在三棱锥 中, 是边长为2的等边三角形,
,则该棱锥的体积为( )
A.1 B. C.2 D.3
6.(2023·全国乙卷·高考真题)已知圆锥PO的底面半径为 ,O为底面圆心,PA,PB为圆锥的母线,,若 的面积等于 ,则该圆锥的体积为( )
A. B. C. D.
7.(2023·全国新Ⅰ卷·高考真题)下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容
器壁厚度忽略不计)内的有( )
A.直径为 的球体
B.所有棱长均为 的四面体
C.底面直径为 ,高为 的圆柱体
D.底面直径为 ,高为 的圆柱体
8.(2023·天津·高考真题)在三棱锥 中,点M,N分别在棱PC,PB上,且 , ,
则三棱锥 和三棱锥 的体积之比为( )
A. B. C. D.
9.(2023·全国新Ⅰ卷·高考真题)在正四棱台 中, ,则该棱台的
体积为 .
10.(2023·全国新Ⅱ卷·高考真题)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面
边长为2,高为3的正四棱锥,所得棱台的体积为 .
11.(2022·天津·高考真题)如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方
形,直三棱柱的底面是顶角为 ,腰为3的等腰三角形,则该几何体的体积为( )
A.23 B.24 C.26 D.27
12.(2022·全国甲卷·高考真题)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 ,侧面积
分别为 和 ,体积分别为 和 .若 ,则 ( )
A. B. C. D.13.(2022·全国新Ⅰ卷·高考真题)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄
入某水库.已知该水库水位为海拔 时,相应水面的面积为 ;水位为海拔 时,相应水
面的面积为 ,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔 上升到
时,增加的水量约为( )( )
A. B. C. D.
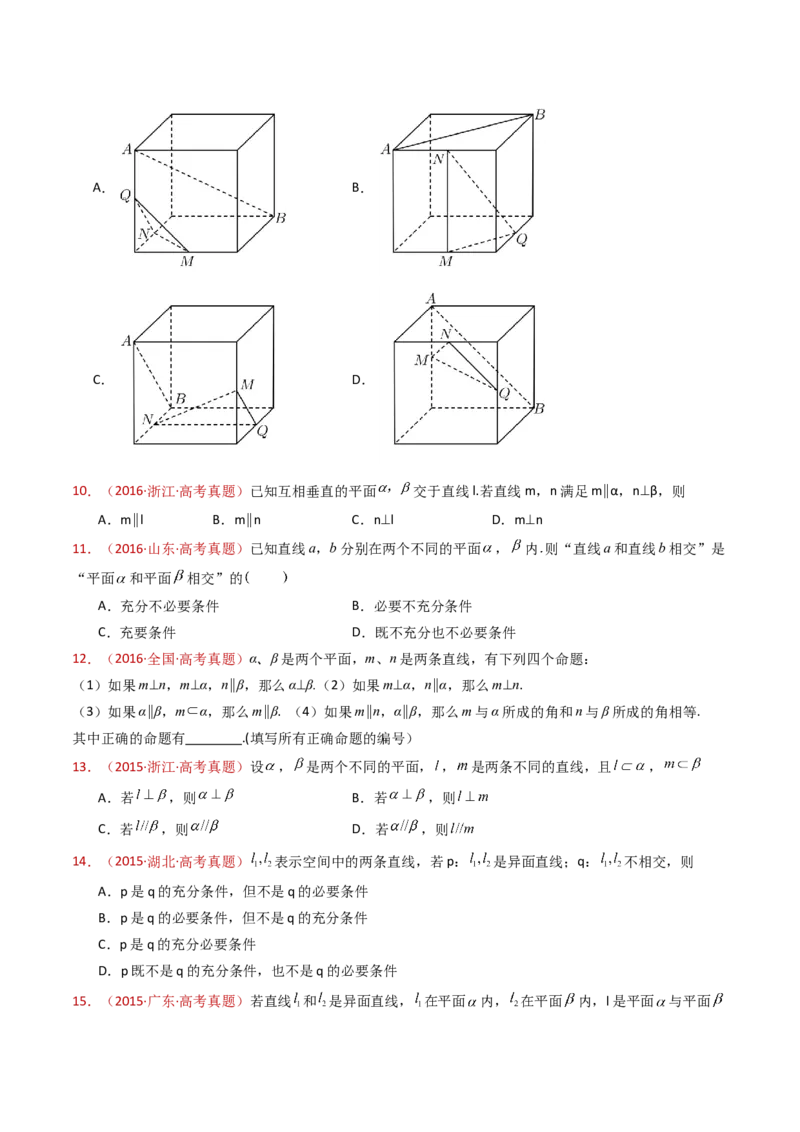
14.(2022·全国新Ⅱ卷·高考真题)如图,四边形 为正方形, 平面 ,
,记三棱锥 , , 的体积分别为 ,则( )
A. B.
C. D.
15.(2021·全国新Ⅱ卷·高考真题)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为(
)
A. B. C. D.
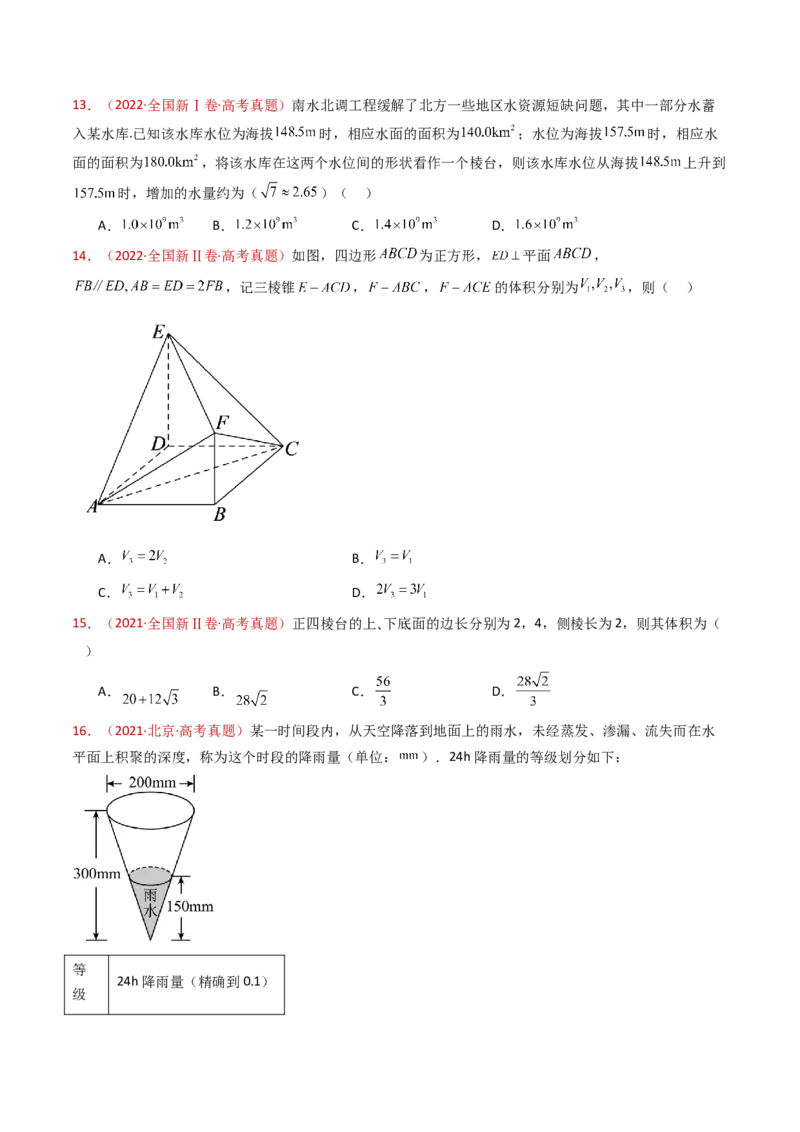
16.(2021·北京·高考真题)某一时间段内,从天空降落到地面上的雨水,未经蒸发、渗漏、流失而在水
平面上积聚的深度,称为这个时段的降雨量(单位: ).24h降雨量的等级划分如下:
等
24h降雨量(精确到0.1)
级…
……
…
小
0.1~9.9
雨
中
10.0~24.9
雨
大
25.0~49.9
雨
暴
50.0~99.9
雨
…
……
…
在综合实践活动中,某小组自制了一个底面直径为200 mm,高为300 mm的圆锥形雨量器.若一次降雨过
程中,该雨量器收集的24h的雨水高度是150 mm(如图所示),则这24h降雨量的等级是
A.小雨 B.中雨 C.大雨 D.暴雨
17.(2021·全国新Ⅰ卷·高考真题)在正三棱柱 中, ,点 满足 ,
其中 , ,则( )
A.当 时, 的周长为定值
B.当 时,三棱锥 的体积为定值
C.当 时,有且仅有一个点 ,使得
D.当 时,有且仅有一个点 ,使得 平面
18.(2020·海南·高考真题)已知正方体ABCD-A B C D 的棱长为2,M、N分别为BB 、AB的中点,则三棱
1 1 1 1 1
锥A-NMD 的体积为
1
19.(2020·江苏·高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的
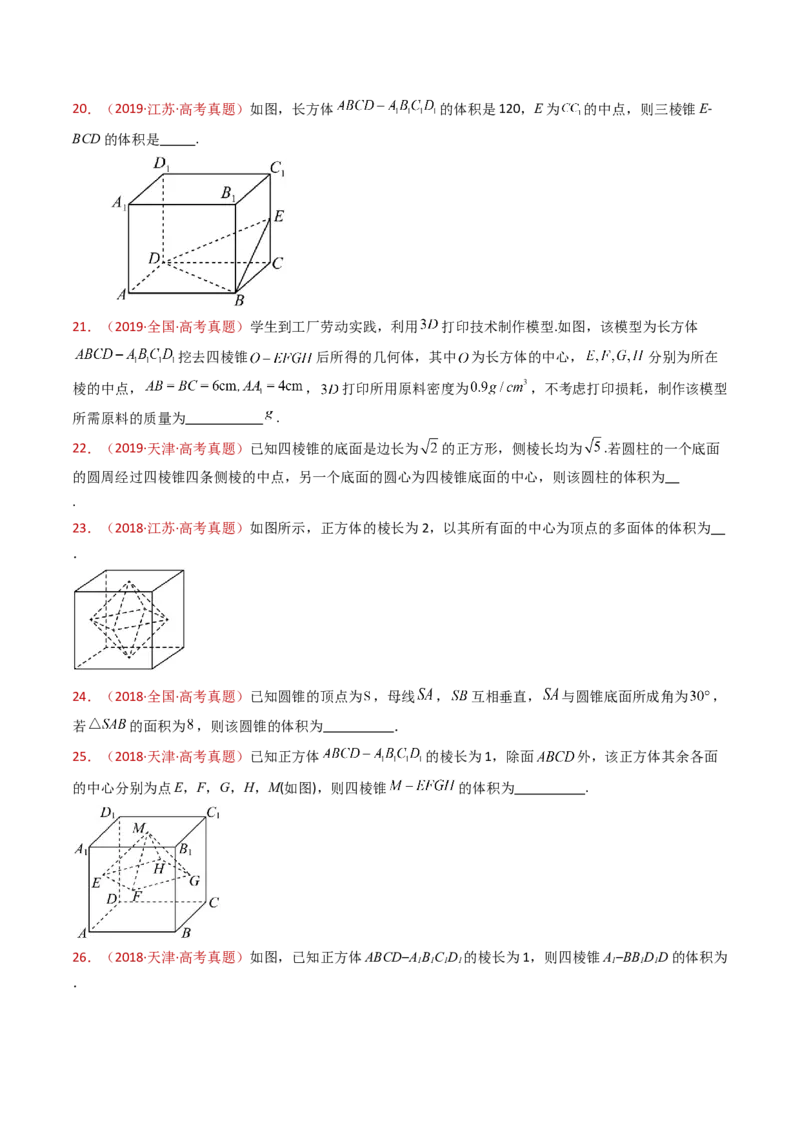
底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是 cm3.20.(2019·江苏·高考真题)如图,长方体 的体积是120,E为 的中点,则三棱锥E-
BCD的体积是 .
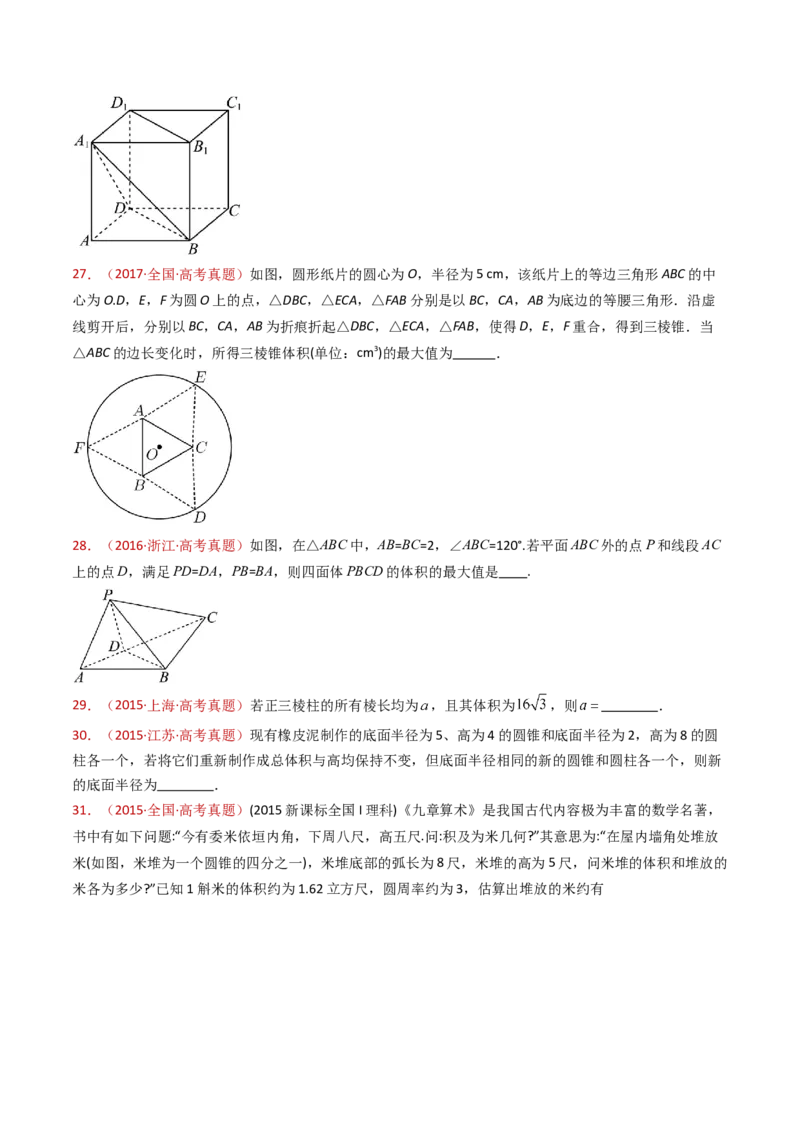
21.(2019·全国·高考真题)学生到工厂劳动实践,利用 打印技术制作模型.如图,该模型为长方体
挖去四棱锥 后所得的几何体,其中 为长方体的中心, 分别为所在
棱的中点, , 打印所用原料密度为 ,不考虑打印损耗,制作该模型
所需原料的质量为 .
22.(2019·天津·高考真题)已知四棱锥的底面是边长为 的正方形,侧棱长均为 .若圆柱的一个底面
的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为
.
23.(2018·江苏·高考真题)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为
.
24.(2018·全国·高考真题)已知圆锥的顶点为 ,母线 , 互相垂直, 与圆锥底面所成角为 ,
若 的面积为 ,则该圆锥的体积为 .
25.(2018·天津·高考真题)已知正方体 的棱长为1,除面 外,该正方体其余各面
的中心分别为点E,F,G,H,M(如图),则四棱锥 的体积为 .
26.(2018·天津·高考真题)如图,已知正方体ABCD–ABC D 的棱长为1,则四棱锥A–BBDD的体积为
1 1 1 1 1 1 1
.27.(2017·全国·高考真题)如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中
心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚
线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当
△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为 .
28.(2016·浙江·高考真题)如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC
上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .
29.(2015·上海·高考真题)若正三棱柱的所有棱长均为 ,且其体积为 ,则 .
30.(2015·江苏·高考真题)现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2,高为8的圆
柱各一个,若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新
的底面半径为 .
31.(2015·全国·高考真题)(2015新课标全国I理科)《九章算术》是我国古代内容极为丰富的数学名著,
书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放
米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的
米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有A.14斛 B.22斛
C.36斛 D.66斛
32.(2015·山东·高考真题)已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转
一周而形成的曲面所围成的几何体的体积为
A. B. C. D.
33.(2015·山东·高考真题)在梯形 中, , , .将梯形
绕 所在直线旋转一周而形成的曲面所围成的几何体的体积为
A. B. C. D.
考点03 求几何体的侧面积、表面积
1.(2023·全国甲卷·高考真题)已知四棱锥 的底面是边长为4的正方形,
,则 的面积为( )
A. B. C. D.
2.(2021·全国新Ⅰ卷·高考真题)已知圆锥的底面半径为 ,其侧面展开图为一个半圆,则该圆锥的母
线长为( )
A. B. C. D.
3.(2021·全国甲卷·高考真题)已知一个圆锥的底面半径为6,其体积为 则该圆锥的侧面积为
.
4.(2020·全国·高考真题)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以
该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底
面正方形的边长的比值为( )A. B. C. D.
5.(2018·全国·高考真题)已知圆柱的上、下底面的中心分别为 , ,过直线 的平面截该圆柱所
得的截面是面积为8的正方形,则该圆柱的表面积为
A. B. C. D.
6.(2018·全国·高考真题)已知圆锥的顶点为 ,母线 , 所成角的余弦值为 , 与圆锥底面所成
角为45°,若 的面积为 ,则该圆锥的侧面积为 .