文档内容
2024 年普通高中学业水平选择性考试(湖南卷)
物理试题本试卷共100分,考试时间75分钟.
一、选择题:本题共6小题,每小题4分,共24分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
的
1. 量子技术是当前物理学应用研究 热点,下列关于量子论的说法正确的是( )
A. 普朗克认为黑体辐射的能量是连续的
B. 光电效应实验中,红光照射可以让电子从某金属表面逸出,若改用紫光照射也可以让电子从该金属表
面逸出
C. 康普顿研究石墨对X射线散射时,发现散射后仅有波长小于原波长的射线成分
D. 德布罗意认为质子具有波动性,而电子不具有波动性
2. 如图,健身者在公园以每分钟60次的频率上下抖动长绳的一端,长绳自右向左呈现波浪状起伏,可近
似为单向传播的简谐横波。长绳上A、B两点平衡位置相距 , 时刻A点位于波谷,B点位于波峰,两
者之间还有一个波谷。下列说法正确的是( )
A. 波长为 B. 波速为
C. 时刻,B点速度为0 D. 时刻,A点速度为0
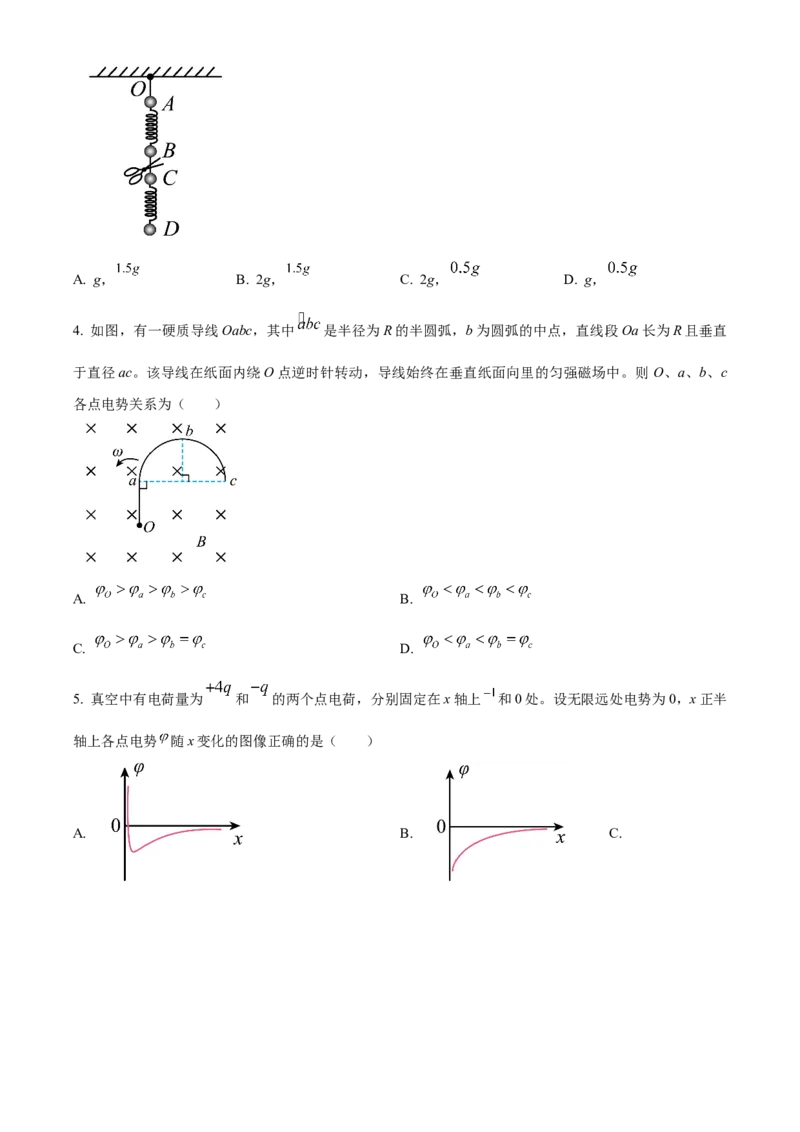
3. 如图,质量分别为 、 、 、m的四个小球A、B、C、D,通过细线或轻弹簧互相连接,悬挂
于O点,处于静止状态,重力加速度为 g。若将B、C间的细线剪断,则剪断瞬间B和C的加速度大小分
别为( )A. g, B. 2g, C. 2g, D. g,
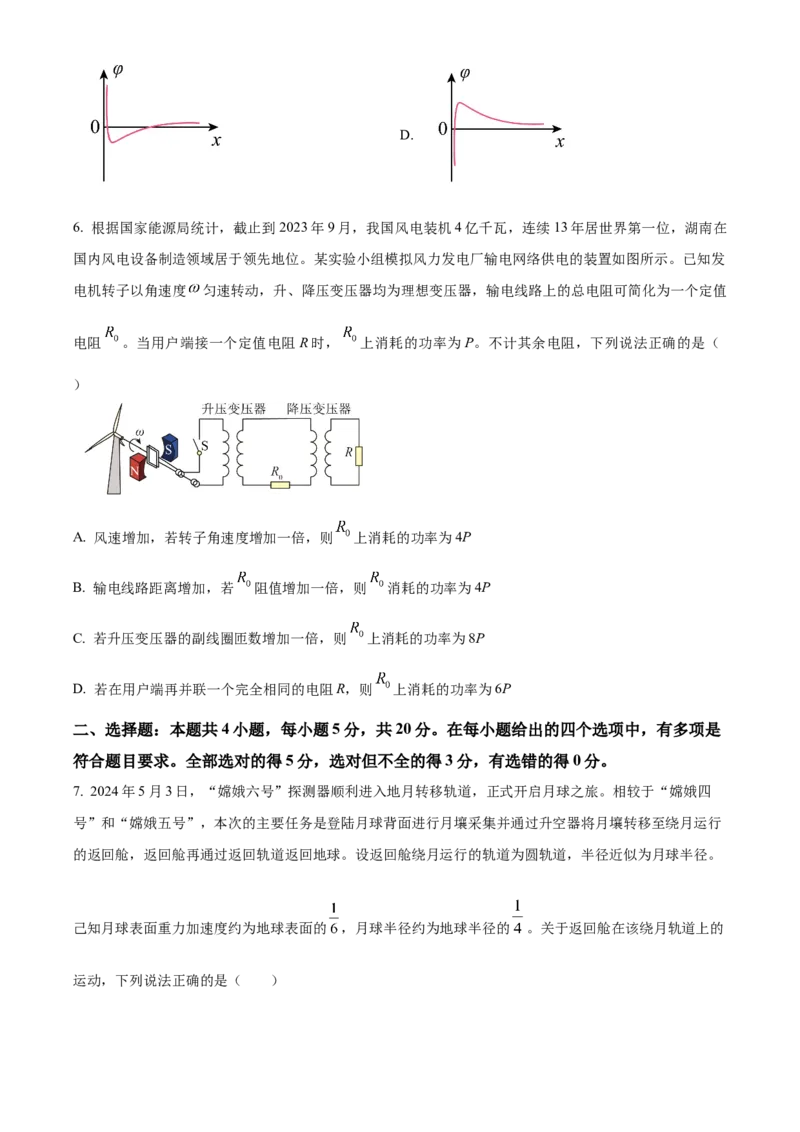
4. 如图,有一硬质导线Oabc,其中 是半径为R的半圆弧,b为圆弧的中点,直线段Oa长为R且垂直
于直径ac。该导线在纸面内绕O点逆时针转动,导线始终在垂直纸面向里的匀强磁场中。则 O、a、b、c
各点电势关系为( )
A. B.
C. D.
5. 真空中有电荷量为 和 的两个点电荷,分别固定在x轴上 和0处。设无限远处电势为0,x正半
轴上各点电势 随x变化的图像正确的是( )
A. B. C.D.
6. 根据国家能源局统计,截止到2023年9月,我国风电装机4亿千瓦,连续13年居世界第一位,湖南在
国内风电设备制造领域居于领先地位。某实验小组模拟风力发电厂输电网络供电的装置如图所示。已知发
电机转子以角速度 匀速转动,升、降压变压器均为理想变压器,输电线路上的总电阻可简化为一个定值
电阻 。当用户端接一个定值电阻R时, 上消耗的功率为P。不计其余电阻,下列说法正确的是(
)
A. 风速增加,若转子角速度增加一倍,则 上消耗的功率为4P
B. 输电线路距离增加,若 阻值增加一倍,则 消耗的功率为4P
C. 若升压变压器的副线圈匝数增加一倍,则 上消耗的功率为8P
D. 若在用户端再并联一个完全相同的电阻R,则 上消耗的功率为6P
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是
符合题目要求。全部选对的得5分,选对但不全的得3分,有选错的得0分。
7. 2024年5月3日,“嫦娥六号”探测器顺利进入地月转移轨道,正式开启月球之旅。相较于“嫦娥四
号”和“嫦娥五号”,本次的主要任务是登陆月球背面进行月壤采集并通过升空器将月壤转移至绕月运行
的返回舱,返回舱再通过返回轨道返回地球。设返回舱绕月运行的轨道为圆轨道,半径近似为月球半径。
己知月球表面重力加速度约为地球表面的 ,月球半径约为地球半径的 。关于返回舱在该绕月轨道上的
运动,下列说法正确的是( )的
A. 其相对于月球 速度大于地球第一宇宙速度
B. 其相对于月球的速度小于地球第一宇宙速度
C. 其绕月飞行周期约为地球上近地圆轨道卫星周期 倍
的
D. 其绕月飞行周期约为地球上近地圆轨道卫星周期的 倍
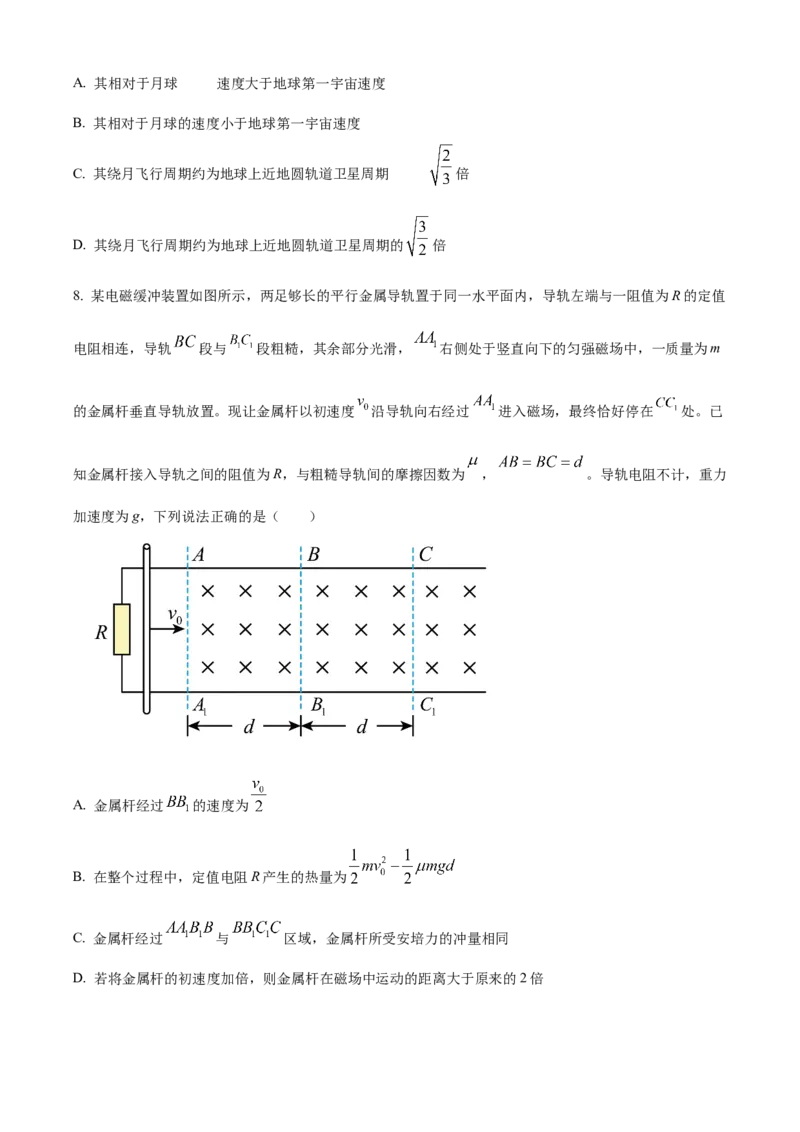
8. 某电磁缓冲装置如图所示,两足够长的平行金属导轨置于同一水平面内,导轨左端与一阻值为R的定值
电阻相连,导轨 段与 段粗糙,其余部分光滑, 右侧处于竖直向下的匀强磁场中,一质量为m
的金属杆垂直导轨放置。现让金属杆以初速度 沿导轨向右经过 进入磁场,最终恰好停在 处。已
知金属杆接入导轨之间的阻值为R,与粗糙导轨间的摩擦因数为 , 。导轨电阻不计,重力
加速度为g,下列说法正确的是( )
A. 金属杆经过 的速度为
B. 在整个过程中,定值电阻R产生的热量为
C. 金属杆经过 与 区域,金属杆所受安培力的冲量相同
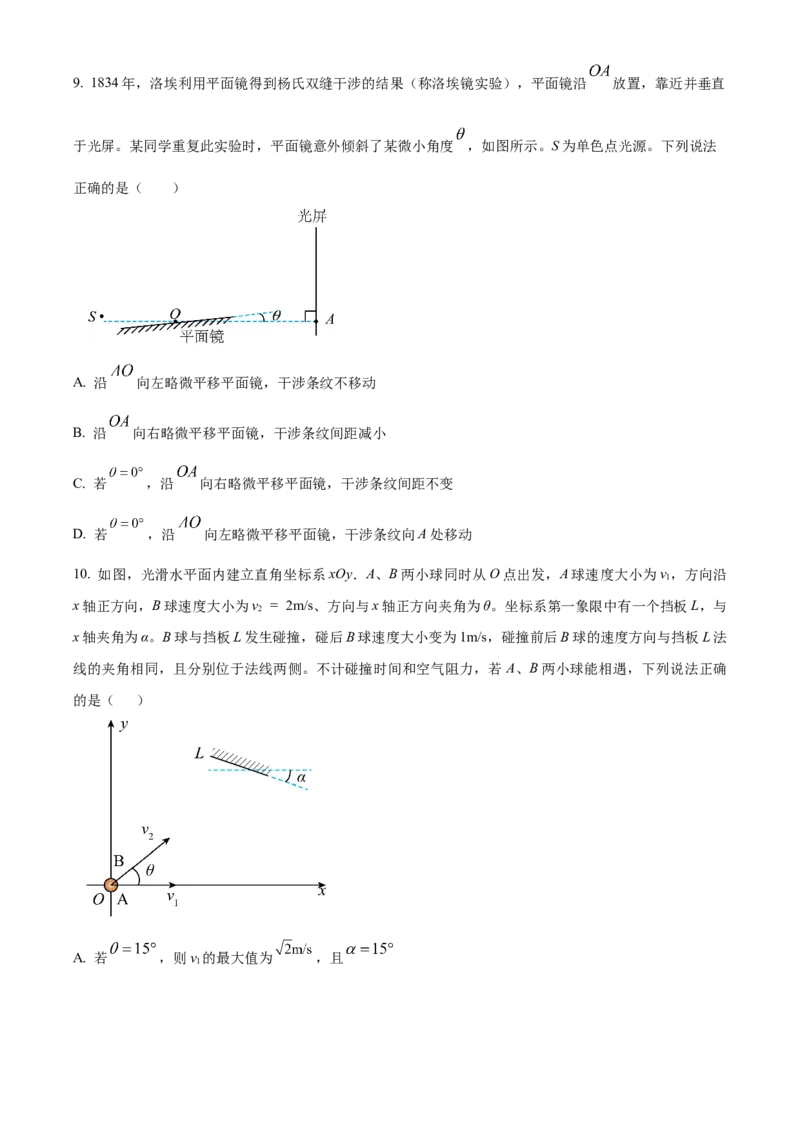
D. 若将金属杆的初速度加倍,则金属杆在磁场中运动的距离大于原来的2倍9. 1834年,洛埃利用平面镜得到杨氏双缝干涉的结果(称洛埃镜实验),平面镜沿 放置,靠近并垂直
于光屏。某同学重复此实验时,平面镜意外倾斜了某微小角度 ,如图所示。S为单色点光源。下列说法
正确的是( )
A. 沿 向左略微平移平面镜,干涉条纹不移动
B. 沿 向右略微平移平面镜,干涉条纹间距减小
C. 若 ,沿 向右略微平移平面镜,干涉条纹间距不变
D. 若 ,沿 向左略微平移平面镜,干涉条纹向A处移动
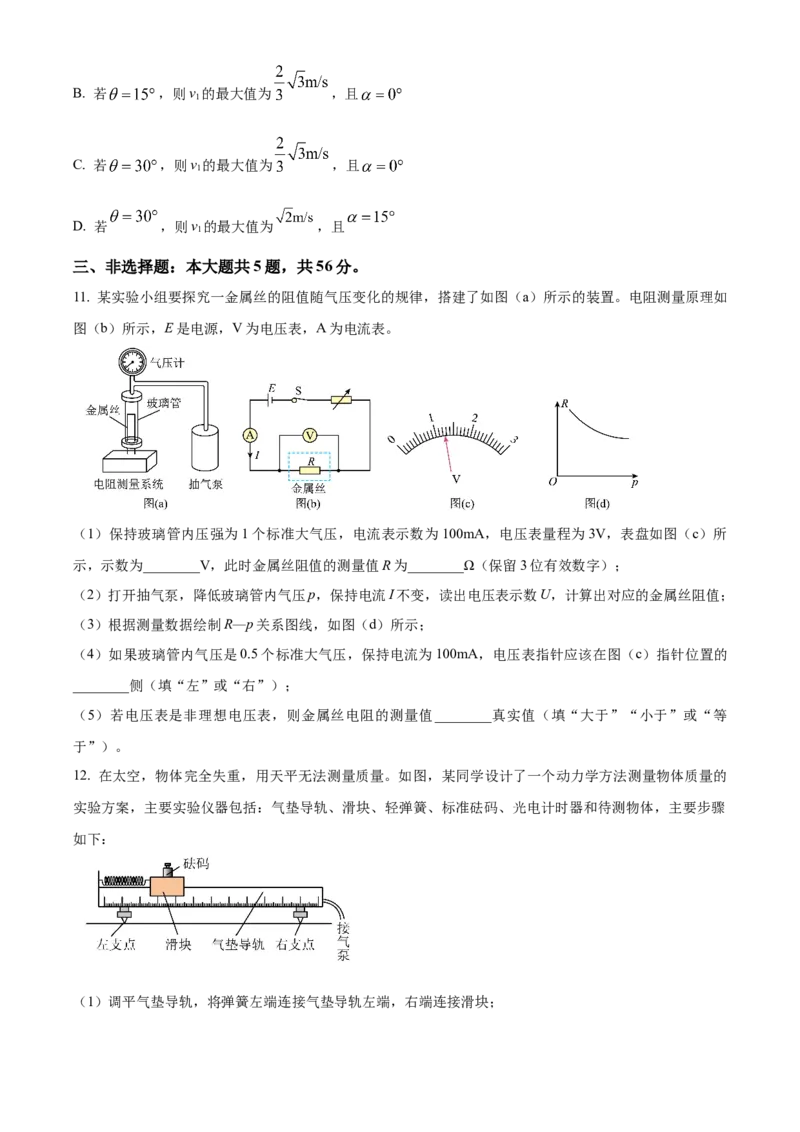
10. 如图,光滑水平面内建立直角坐标系xOy.A、B两小球同时从O点出发,A球速度大小为v ,方向沿
1
x轴正方向,B球速度大小为v = 2m/s、方向与x轴正方向夹角为θ。坐标系第一象限中有一个挡板L,与
2
x轴夹角为α。B球与挡板L发生碰撞,碰后B球速度大小变为1m/s,碰撞前后B球的速度方向与挡板L法
线的夹角相同,且分别位于法线两侧。不计碰撞时间和空气阻力,若 A、B两小球能相遇,下列说法正确
的是( )
A. 若 ,则v 的最大值为 ,且
1B. 若 ,则v 的最大值为 ,且
1
C. 若 ,则v 的最大值为 ,且
1
D. 若 ,则v 的最大值为 ,且
1
三、非选择题:本大题共5题,共56分。
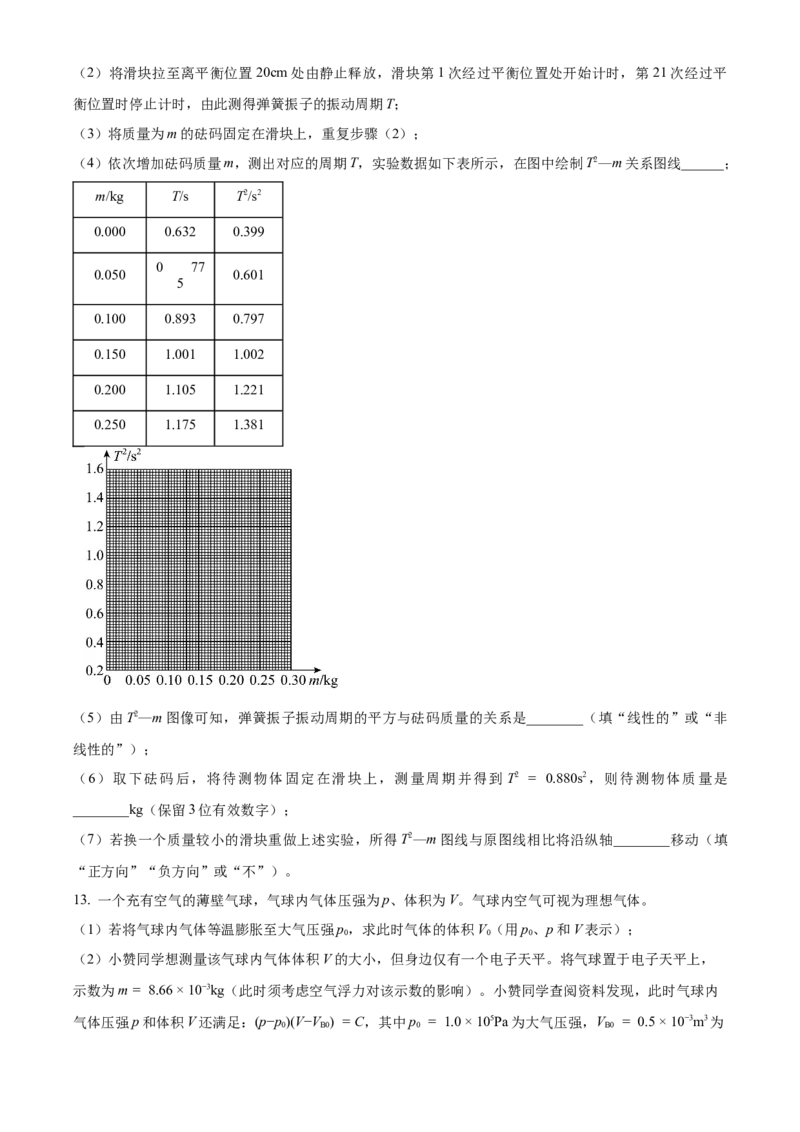
11. 某实验小组要探究一金属丝的阻值随气压变化的规律,搭建了如图(a)所示的装置。电阻测量原理如
图(b)所示,E是电源,V为电压表,A为电流表。
(1)保持玻璃管内压强为1个标准大气压,电流表示数为100mA,电压表量程为3V,表盘如图(c)所
示,示数为________V,此时金属丝阻值的测量值R为________Ω(保留3位有效数字);
(2)打开抽气泵,降低玻璃管内气压p,保持电流I不变,读出电压表示数U,计算出对应的金属丝阻值;
(3)根据测量数据绘制R—p关系图线,如图(d)所示;
(4)如果玻璃管内气压是0.5个标准大气压,保持电流为100mA,电压表指针应该在图(c)指针位置的
________侧(填“左”或“右”);
(5)若电压表是非理想电压表,则金属丝电阻的测量值________真实值(填“大于”“小于”或“等
于”)。
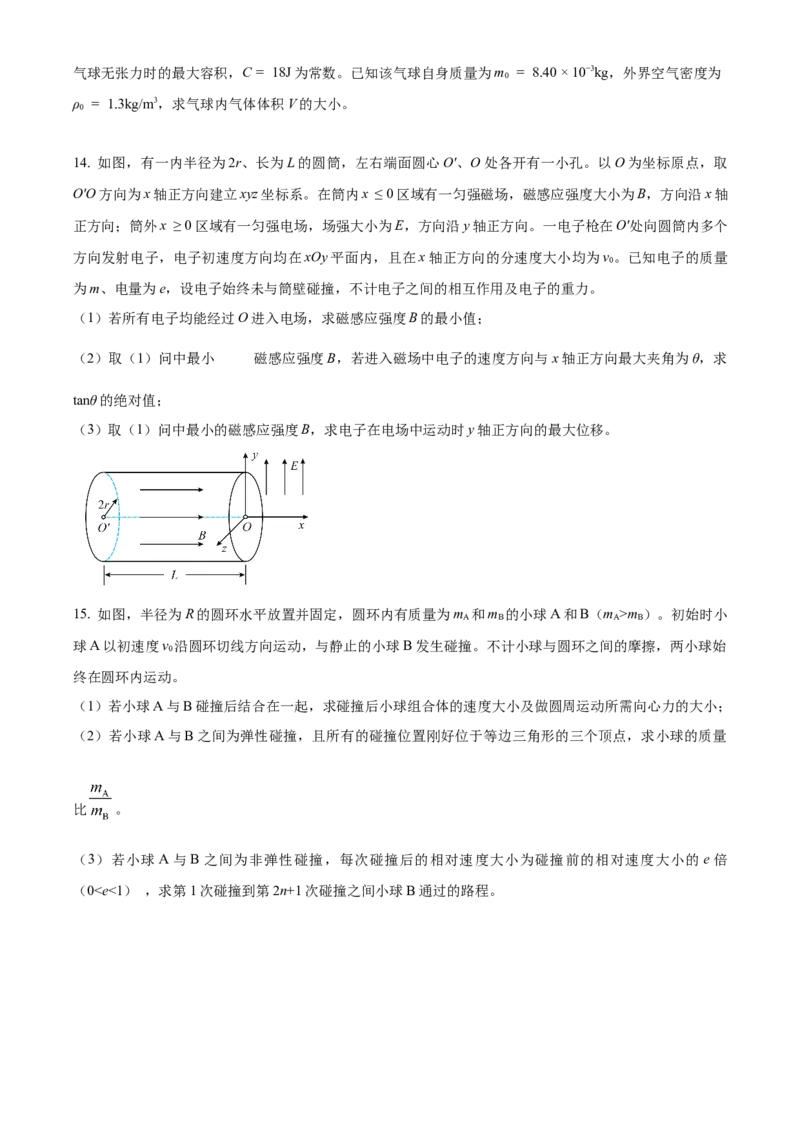
12. 在太空,物体完全失重,用天平无法测量质量。如图,某同学设计了一个动力学方法测量物体质量的
实验方案,主要实验仪器包括:气垫导轨、滑块、轻弹簧、标准砝码、光电计时器和待测物体,主要步骤
如下:
(1)调平气垫导轨,将弹簧左端连接气垫导轨左端,右端连接滑块;(2)将滑块拉至离平衡位置20cm处由静止释放,滑块第1次经过平衡位置处开始计时,第21次经过平
衡位置时停止计时,由此测得弹簧振子的振动周期T;
(3)将质量为m的砝码固定在滑块上,重复步骤(2);
(4)依次增加砝码质量m,测出对应的周期T,实验数据如下表所示,在图中绘制T2—m关系图线______;
m/kg T/s T2/s2
0.000 0.632 0.399
.
0 77
0.050 0.601
5
0.100 0.893 0.797
0.150 1.001 1.002
0.200 1.105 1.221
0.250 1.175 1.381
(5)由T2—m图像可知,弹簧振子振动周期的平方与砝码质量的关系是________(填“线性的”或“非
线性的”);
(6)取下砝码后,将待测物体固定在滑块上,测量周期并得到 T2 = 0.880s2,则待测物体质量是
________kg(保留3位有效数字);
(7)若换一个质量较小的滑块重做上述实验,所得T2—m图线与原图线相比将沿纵轴________移动(填
“正方向”“负方向”或“不”)。
13. 一个充有空气的薄壁气球,气球内气体压强为p、体积为V。气球内空气可视为理想气体。
(1)若将气球内气体等温膨胀至大气压强p,求此时气体的体积V(用p、p和V表示);
0 0 0
(2)小赞同学想测量该气球内气体体积V的大小,但身边仅有一个电子天平。将气球置于电子天平上,
示数为m = 8.66 × 10−3kg(此时须考虑空气浮力对该示数的影响)。小赞同学查阅资料发现,此时气球内
气体压强p和体积V还满足:(p−p)(V−V ) = C,其中p = 1.0 × 105Pa为大气压强,V = 0.5 × 10−3m3为
0 B0 0 B0气球无张力时的最大容积,C = 18J为常数。已知该气球自身质量为m = 8.40 × 10−3kg,外界空气密度为
0
ρ = 1.3kg/m3,求气球内气体体积V的大小。
0
14. 如图,有一内半径为2r、长为L的圆筒,左右端面圆心O′、O处各开有一小孔。以O为坐标原点,取
O′O方向为x轴正方向建立xyz坐标系。在筒内x ≤ 0区域有一匀强磁场,磁感应强度大小为B,方向沿x轴
正方向;筒外x ≥ 0区域有一匀强电场,场强大小为E,方向沿y轴正方向。一电子枪在O′处向圆筒内多个
方向发射电子,电子初速度方向均在xOy平面内,且在x轴正方向的分速度大小均为v 。已知电子的质量
0
为m、电量为e,设电子始终未与筒壁碰撞,不计电子之间的相互作用及电子的重力。
(1)若所有电子均能经过O进入电场,求磁感应强度B的最小值;
的
(2)取(1)问中最小 磁感应强度B,若进入磁场中电子的速度方向与x轴正方向最大夹角为θ,求
tanθ的绝对值;
(3)取(1)问中最小的磁感应强度B,求电子在电场中运动时y轴正方向的最大位移。
15. 如图,半径为R的圆环水平放置并固定,圆环内有质量为m 和m 的小球A和B(m >m )。初始时小
A B A B
球A以初速度v 沿圆环切线方向运动,与静止的小球B发生碰撞。不计小球与圆环之间的摩擦,两小球始
0
终在圆环内运动。
(1)若小球A与B碰撞后结合在一起,求碰撞后小球组合体的速度大小及做圆周运动所需向心力的大小;
(2)若小球A与B之间为弹性碰撞,且所有的碰撞位置刚好位于等边三角形的三个顶点,求小球的质量
比 。
(3)若小球A与B之间为非弹性碰撞,每次碰撞后的相对速度大小为碰撞前的相对速度大小的e倍
(0