文档内容
海南中学 2026 届高三年级第三次月考数学试题
时间: 120 分钟 满分: 150分
命题、审核:李园、杨菲
一、单项选择题:本题共 8小题,每小题5分,共40分.在每小题给出的
四个选项中,只有一项是符合题目要求的.
1.若复数 z=a2-3a+2+(2a-4)i(a∈R)为纯虚数,则a=()
A. 2 B. 1 C. 0 D. 1或2
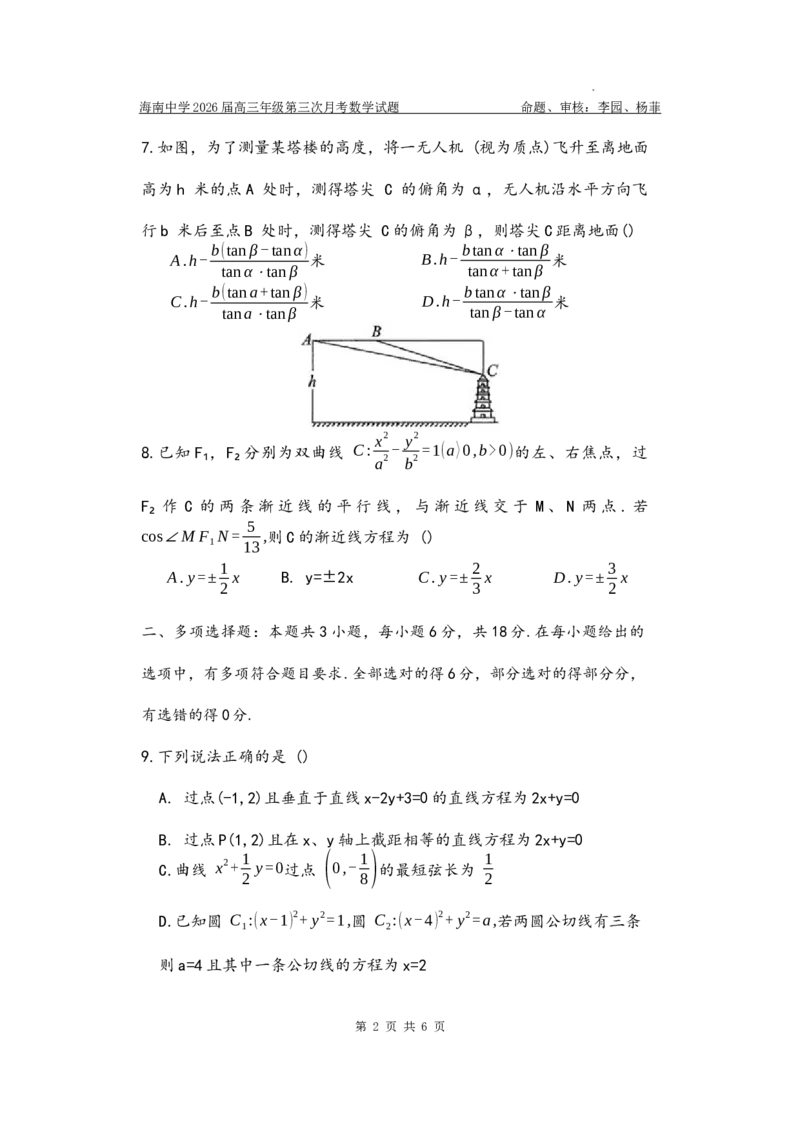
2. 已知集合A={x|00)的左、右焦点,过
a2 b2
F₂ 作 C 的两条渐近线的平行线,与渐近线交于 M、N 两点.若
5
cos∠M F N= ,则C的渐近线方程为 ()
1 13
1 2 3
A.y=± x B. y=±2x C.y=± x D.y=± x
2 3 2
二、多项选择题:本题共 3小题,每小题6分,共18分.在每小题给出的
选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,
有选错的得0分.
9.下列说法正确的是 ()
A. 过点(-1,2)且垂直于直线x-2y+3=0的直线方程为2x+y=0
B. 过点P(1,2)且在x、y轴上截距相等的直线方程为2x+y=0
C.曲线 x2+ 1 y=0过点 ( 0,- 1) 的最短弦长为 1
2 8 2
D.已知圆 C :(x-1) 2+ y2=1,圆 C :(x-4) 2+ y2=a,若两圆公切线有三条
1 2
则a=4且其中一条公切线的方程为x=2
第 2 页 共 6 页
学科网(北京)股份有限公司海南中学 202 6 届高三年级第三次月考数学试题 命题、审核:李园、杨菲
10.已知向量ā=(1,1), b=(-1,x),下列结论正确的是 ()
A. 若 ⃗a⊥⃗b,则x=1
→ →
B. 若 a‖b,则x=1
C.若a,b的夹角为钝角,则x的取值范围为(-∞,1)
D.设ā在b方向上的投影向量为m,则|m|的取值范围为[0, ❑√2
π
11. 在△ABC中, 内角A, B, C所对的边分别为a, b, c, ∠ABC= ,内角B的平分
3
线交AC于点D且. BD=❑√3,则下列结论正确的是 ()
1 1
A. + =1 B. b的最小值是2
a c
C. a+3c的最小值是 4❑√3 D. ΔABC的面积最小值是 ❑√3
三.填空题:本题共3小题,每小题5分,共15分.
12. 若 log 3=a,2b=5,则用a,b表示 log 15=__________.
2 6
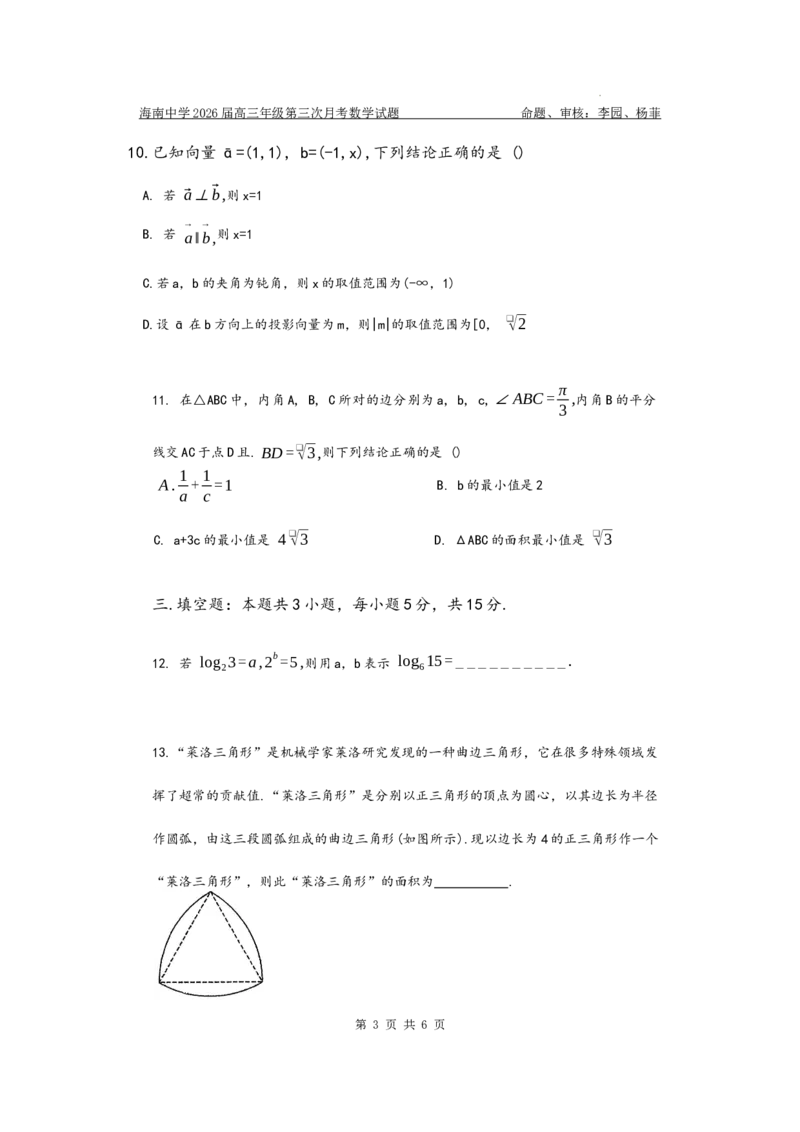
13.“菜洛三角形”是机械学家莱洛研究发现的一种曲边三角形,它在很多特殊领域发
挥了超常的贡献值.“莱洛三角形”是分别以正三角形的顶点为圆心,以其边长为半径
作圆弧,由这三段圆弧组成的曲边三角形(如图所示).现以边长为4的正三角形作一个
“莱洛三角形”,则此“莱洛三角形”的面积为 .
第 3 页 共 6 页
学科网(北京)股份有限公司学科网(北京)股份有限公司海南中学 202 6 届高三年级第三次月考数学试题 命题、审核:李园、杨 菲
14.若在曲线. y=-xeax-1(e为自然对数的底数)存在不同的两点P、Q,使
P、Q两点关于x轴的对称点P'、Q'在曲线y= lnx+ ax上, 则实数a的取值范围是
.
四.解答题:本题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤.
15.(13分) 设向量 ⃗a=(sinx,cosx),⃗b=(cosx,cosx),x∈R,函数 f (x)=⃗a⋅(⃗a+⃗b).
(1)求函数f(x)的最大值与最小正周期;
3
(2)求使不等式 f (x)≥ 成立的x的取值集合及函数f(x)的对称中心.
2
第 4 页 共 6 页
学科网(北京)股份有限公司海南中学 202 6 届高三年级第三次月考数学试题 命题、审核:李园、杨 韭
16.(15分) 21世纪某次机器人展览会上,已知某公司共有 25个汽车模
型,其外观和内饰的颜色分布如下表所示:
外观
红色外观 蓝色外观
内饰
棕色内饰 10 10
米色内饰 2 3
(1)若小明从这些模型中随机拿一个模型,记事件A为小明取到红色外观
的模型,事件B为小明取到棕色内饰的模型,求P(B)和P(B|A),并判断
事件A和事件B是否独立并说明理由..
(2)该公司举行了一个抽奖活动,规定在一次抽奖中,每人可以从这些模
型中拿两个汽车模型,给出以下假设:
假设1:拿到的两个模型会出现三种结果,即外观和内饰均为同色,外
观和内饰都异色,以及仅外观或内饰同色.
假设2:按抽奖的可能性大小,概率越小奖金越高.
假设3:该抽奖活动的奖金额为:一等奖800元,二等奖500元,三等奖
300元.
请你分析奖金对应的结果,设 X为奖金额,写出X的分布列并求出X的
数学期望.
第 5 页共 6页
学科网(北京)股份有限公司海南中学 2026 届高三年级第三次月考数学试题 命题、审核:李园、杨菲
17.(15分) 已知a,b,c分别为锐角△ABC三个内角A,B,C的对边, △ABC的
a2-(b-c) 2
面积 S= ,
2
(1) 求 sin A,cosA的值;
b+2c
(2) 求 的取值范围.
a
x2 y2
18. (17分) 已知椭圆E: + =1(a⟩b>0),以椭圆E的焦点和短轴端点为
a2 b2
顶点的四边形是边长为2的正方形.已知斜率k存在且不为0的直线l过点
( 1)
(0,t)(t⟩❑√2),直线l与椭圆E交于不同的两点A,B,过点A和 C 0, 的直
2
线AC与椭圆E的另一个交点为D.
(1)求椭圆E的方程及离心率;
(2)若直线BD的斜率为0,求t的值及斜率k的取值范围.
19. (17分) 已知函数 f (x)=ex+cosx-2,f'(x)为f(x)的导数.
(1)当x≥0时, 求f'(x)的最小值;
π
(2)当 x≥- 时, xex+xcosx-ax2-2x≥0恒成立,求实数a的取值范围.
2
学科网(北京)股份有限公司第 6 页 共 6 页
学科网(北京)股份有限公司